Numerical Modeling of the Ultimate Bearing Capacity of Strip Footings on Reinforced Sand Layer Overlying Clay with Voids

Abstract

The presence of underground voids within a failure zone usually results in a reduction in the bearing capacity of footings. This paper presents results for the ultimate bearing capacity ratio, qu/γB, of a strip footing on top of a sand layer overlying a clay layer with voids, with and without the placing of geotextile reinforcement at the interface between the sand and clay layers. Using the finite difference software FLAC 2D, the bearing capacity ratio of the strip footing was calculated for voids with different depths and horizontal distance for two configurations: parallel and symmetrical. The effect of parameters on the ultimate bearing capacity ratio was also investigated, including the undrained shear stress ratio of the soil, the thickness of the top layer and the size, location, height, width and spacing of the voids, with and without placing of geotextile layers at the interface between the sand and clay layers. It was found that the influence of a void on the ultimate bearing capacity ratio of the strip footing vanished when the void was located outside the failure zone beneath the footing and increased further with reinforcement until it reached a constant limit value.

1. Introduction

Establishing the ultimate bearing capacity of shallow foundations has long been an important component of geotechnical engineering design. The presence of underground voids due to multiple reasons relating to human activities, such as tunnelling, mining and decomposition of soluble material from subway excavations, can affect the ultimate bearing capacity of shallow foundations. These voids can cause structure collapse, settlement of roads and loss of life and need special attention in engineering practice. The theory of bearing capacity developed by Terzaghi [1] is generally used for single homogeneous soil layers. However, in reality, soils are naturally deposited in layers. In addition, ground improvement techniques are often used in soft clays soils. Replacement of the top layer of clay with cohesionless soil artificially forms a sand layer overlying the clay. The use of bearing capacity factors that fit with Terzaghi’s bearing capacity theory is not possible for this type of non-homogeneous soil, especially in the presence of voids. Several studies have been carried out to assess the stability of the strip footing over soils with voids. Baus and Wang [2] investigated the bearing capacity behaviour of shallow footings located above a continuous rectangular or circular void in silty soil using experimental research and numerical modelling. They concluded that the bearing capacity of the strip footing depended strongly on the size and location of the void. Badie and Wang [3] and Wang and Badie [4] extensively studied the effects of subterranean voids on the stability of strip footings on cohesive soils using the finite element method (FEM). They undertook both experimental and numerical research programs and then compared the results from the two programs. They stated that there was a critical region under the footing [3,4]. Kiyosumi et al. [5] evaluated the effect of multiple voids on the bearing capacity of strip footings using the finite element code PLAXIS (1998). They concluded that a rupture zone was initially developed towards the nearest void, which usually has no effect on other voids. Kiyosumi et al. [6] reported the results of laboratory-scale model tests of strip footings on stiff ground with continuous square voids and revealed three types of collapse modes for a single void: bearing failure without void collapse, void failure without bearing failure and bearing failure with void collapse. Al-Tabbaa et al. [7] performed plane-strain model tests of strip footings over a mixture of sandy gypsum soil that contained continuous circular voids. Their results indicate that the greater the depth and offset of voids, the greater the bearing capacity. Wood and Larnach [8] conducted another study on this subject using physical modelling and numerical simulation. They reported similar behaviour to that observed in Wang’s work. Wang et al. [9] investigated the effects of void on footing behaviour under eccentric and inclined loading conditions using the finite element method. They demonstrated that the bearing capacity of a footing with a central circular void underlying it decreases as the load eccentricity and the inclined loads increase. Azam et al. [10] explored the bearing capacity of strip footings that was centred above a stratified single layer of soil with a circular void using the two-dimensional finite element method and provided design equations. Wang and Hsieh [11] analysed the footing collapse load above a circular void using the upper boundary analysis theorem and summarised the three failure mechanisms, taking into account the influence of the footing size and the size and location of voids on the footing collapse load. Sreng et al. [12] obtained results for the rotation reaction response of strip footings above a continuous square void, which were acquired by estimating both vertical and even removals during 1 G centrifuge model tests. Wang et al. [13] broadened the work by Wang and Hsich [11] and identified ten failure mechanisms. The effect of the surface base on reinforced sand layers in the presence of voids has also been investigated [14,15,16]. For undrained conditions, Lee et al. [17] adopted the finite element code PLAXIS (2012) to study the stability without drainage of a strip footing on homogeneous and inhomogeneous clay with continuous voids. The impact of load inclination was also investigated by Lee et al. [18], who revealed that failure envelopes could be used by engineers. Lavasan et al. [19] utilised the PLAXIS finite element program to investigate strip footing behaviour on soils over double voids. Based on this study, Xiao et al. [20,21] used the finite element limit analysis (FELA) method to study the performance of footing on two-layered clays and the rock mass of single and dual voids. Zhou et al. [22] used discontinuity arrangement optimisation (DLO) techniques to study the influence of square voids on the performance of strip footings over cohesive soils and identified typical fracture patterns. A reduction coefficient was introduced to assess the bearing capacity of the strip footing with different factors.

Recently, the use of geosynthetics for soil reinforcement has increased considerably. Reinforced soil is widely utilised in geotechnical engineering applications due to its low cost, ease of construction, reinforcement benefits and visual appeal. It is thus economically practical to improve the load-bearing capacity of strip foundations by using geosynthetically reinforced soil. Many researchers have examined and reported the effects and benefits of using a reinforcement to increase the bearing capacity of footing and enhance its stability [23,24,25,26,27,28,29,30,31,32]. Full-scale studies conducted by Blivet et al. [33] have shown that a planar geosynthetic reinforcement can effectively reduce the risk of serious accidents posed by localised sinkholes under highways and railway embankments. Ast and Haberland [34] successfully used high-tensile geogrids together with cement-stabilised soil blocks under high-speed train traffic to bridge underlying sinkholes. Many researchers have used several analytical methods in the design of overlying voids and sinkholes that are supported by geosynthetic soil systems [35,36,37]. An experimental study was conducted by Moghaddas Tafreshi and Khalaj [38] to investigate the beneficial effect of geogrid reinforcement on the deformation of pipes with small diameters and the surface collapse of the soil under repeated loads, simulating vehicle packing. They reported that the geogrid reduced the change in the vertical pipe diameter and soil surface collapse significantly. Several researchers reported that the geotechnical performance of a compacted granular fill layer over soft clay layers can be significantly improved by placing a layer of geosynthetic reinforcement on top of the surface of clay layer prior to placement of the fill [39,40,41,42,43,44]. Despite the previous development of research, no publication in the literature has focused on studying the bearing capacity of a strip footing on sand over clay layers with voids and the use of reinforcement.

This paper investigates the bearing capacity of a strip footing placed over sand with voids overlying a clay layer using the finite difference software FLAC 2D. The purpose of this study was to assess the bearing capacity of the footings above voids in stratified soil layers consisting of sand overlying clay, and the use of soil reinforcements to stabilise the strip footing and mitigate the undesirable effects of the voids. The FEM has been previously used by several researchers to analyse soil behaviour in relation to voids and reinforcement [14,16,28,31]. This study focused particularly on the effects of geosynthetic reinforcement on the ultimate bearing capacities of strip footings, qu, in terms of the dimensionless parameters qu/γB as a function of the dimensionless strength parameter, Cu/γB, the normalised thickness of the sand layer, H/B, location, size, width, height and spacing of the voids and the effect of soil reinforcement. Here, B is the footing width, γ is the unit weight of sand, Cu is the undrained shear strength of clay, and H is the thickness of sand layer. The results of this study demonstrate the impact of using a sand layer reinforced with geosynthetic layers over a clay layer with voids on the ultimate bearing capacity of a strip footing.

2. Objectives of the Study

This paper aims to discuss the numerical modelling of the ultimate bearing capacity of strip footings on a reinforced sand layer overlying clay with voids. The bearing capacity ratio of strip footing was computed for voids with different depths and horizontal distances for two configurations, parallel and symmetrical. The impact of many factors, such as the soil’s undrained shear stress ratio, the top layer’s thickness, the size, location, height, width and spacing of the voids, and the use of geotextile layers at the interface between the sand and clay layers was also examined. This work demonstrates that when digging into the ground at a certain depth in the presence of underground voids, a layer of sand placed at a specific depth can increase the bearing capacity. Additionally, in the case of placing geotextile layers, the bearing capacity can be increased two-fold.

3. Defining the Problem

Figure 1 shows the proposed model with the main geometric parameters included and a schematic diagram of the numerical model. A strip footing of width B is constructed on a sand layer overlying a clay layer, as shown in (Figure 2). H is the thickness of the sand layer, γ is the unit weight, and φ is the friction angle of the sand. The top layer is underlain by a clay layer with an undrained shear strength, Cu. The sand and clay layers are assumed to be fully drained and fully undrained, respectively. A rough interface was assumed between the footing and the sand soil. To ensure the accuracy of the results, the bottom boundary of the model is fixed in both vertical and horizontal directions, while the lateral borders are only constrained in the horizontal direction. The performance of a footing over voids is influenced by the shape, location and number of voids [4,5]. As for individual voids, the void shape is presumed to be either square or rectangular, as expressed by the dimension parameters H’ and B’, for the width and height of the void. The symbols H’ and B’ indicate the void’s height and void’s width, respectively, as illustrated in Figure 1a. For the parallel configuration, one void is located right under the footing and the other void is located to the right of the previous void at distance S, as illustrated in Figure 1b. For the symmetrical void configurations, two voids are located symmetrically around the central line of the footing at s distance, as illustrated in Figure 1c. The voids are assumed to have the same depth, size and shape in both the parallel and symmetrical void configurations. The horizontal distance from the centre of the single void to the centreline of the footing is given by E, and the vertical distance is determined to be from the top of the single void to the bottom of the footing, and is indicated by the symbol D. The horizontal distance between the centres of the two voids is defined as S. One reinforcement layer is placed at the interface between the sand and the clay layer. The symbol b in (Figure 1) indicates the length of a layer of the geotextile reinforcement at the interface. Numerical modelling was utilised to estimate the bearing capacity [28,32,41]. These models focus on evaluating the effect of placing a single reinforcement layer at the sand–clay interface on the ultimate bearing capacity of the strip footing. It has been observed that, with the provision of reinforcement, the magnitude of the ultimate bearing capacity increases substantially. The dimensionless ultimate bearing capacity qu/γB can be calculated using the normalisation method, which eliminates the influence of the unit weight of sand γ and the width of strip footing B on the ultimate bearing capacity qu of the stratified soils, which can be expressed as follows:

$$\frac{q_u}{\gamma B}=f\left(\frac{H}{B},\frac{D}{B}, \frac{E}{B},\frac{Cu}{\gamma B},\frac{H^{\prime }}{B},\frac{B^{\prime }}{B},\phi \right)$$

(1)

4. Finite Difference Method

A two-dimensional FLAC code was used to simulate the performance of strip footing resting on a sand layer overlying a clay layer with one or two voids, and to determine the bearing capacity of the strip footing. In this FLAC code, the rigid body is split by a user into a finite-difference grid consisting of quadrilateral elements. The FLAC code is best suited to analysing the nonlinear behaviour of materials and the related instability and failure phenomena. Since no matrix is formed, the large two-dimensional calculations can be performed without excessive memory requirements. It is assumed that the interface between the sand and clay is completely rough (full contact), and therefore a continuous mesh is used. Due to symmetry, only half of the footing and the soil mass were taken into account in the calculation scheme. In this research, the finite difference programme, FLAC2D (Fast Lagrangian Analysis of Continua) (Itasca, 2011), was applied for modelling the strip foundation resting on a reinforced sand layer above a clay layer in the presence of voids. Numerical modelling was conducted to determine the improvement in the bearing capacity of soil for foundations resting on overly stratified soil with voids and a reinforcement layer placed at the sand–clay interface. (Figure 2) illustrates a model of the strip footing for the case of a single void. A strip footing of width B is constructed on a sand layer overlying clay. In the model, H is the thickness of the sand layer, γ is the unit weight of the sand, and φ is the friction angle of the sand. The clay layer below the sand has an undrained shear strength of Cu. The domain size of the area for analysis is set as 30B and 20B in the horizontal and vertical directions, respectively, to minimise possible effects of the boundary. The bottom boundary of the model is fixed in both the vertical and horizontal directions, while the lateral boundaries are only constrained in the horizontal direction. The strip footing is subjected to a distributed vertical load. The footing is modelled as a weightless rigid material, and the interface between the footing and soil is assumed to be perfectly rough to ensure the accuracy of the results. The bottom of the footing is simulated as perfectly rough by specifying a tied contact constraint at the soil–footing interface. The soil is treated as a linearly elastic-perfectly plastic material obeying the linear Mohr–Coulomb yield criterion with the associated flow rule. The material parameters for soil and geotextile are presented in

Table 1. Material properties used in the finite difference mouthed.

Type	Description	Value
Soil	Unit weight of sand γ (kN/m3) Unit weight of clay γ (kN/m3) Friction angle φ ᵒ Dilatancy angle ψ ᵒ Shear modulus G (kPa) Bulk modulus K (kPa) Interface reduction factor sand and clay	20.00 16.00 40 35 3.45 33.33 1.0, 0.5
Geotextile	Normal stiffness EA (KN/m)	2000

. It is noteworthy that the soil unit weight has a negligible effect on the undrained bearing capacity of the strip footing above voids.

5. Verification

To verify the accuracy of the established model, the bearing capacity of a strip footing placed on a sand layer overlying clay with no embedment was simulated using FLAC 2D, and the results were compared with results from prior studies in the literature. This includes comparison with the results of Burd and Frydman [45] based on the finite element method; the results of Hanna and Meyerhof [46] using the semi-empirical method; the results of Michalowski and Shi [47] based on the upper-bound limit analysis; and the results of Shiau et al. [48] using the finite element method of limit analysis theorems. Figure 3 presents the results for the normalised bearing capacity qu/γB versus the normalised undrained shear strength of clay (Cu/γB) for the thickness-to-width ratio of H/B = 1, H/B = 2 and for a friction angle of φ = 40°, φ = 45° for sand. As compared with the upper-bound solution of Michalowski and Shi [47], a more conservative kinetic solution was obtained by Shiau et al. [48]. Burd and Frydman [45] demonstrated the lowest bearing capacity, which was obtained based on the finite element method. The comparison shows that the results of FLAC 2D are in good agreement with the rigorous upper-bound solutions of Shiau et al. [48]. In the case where φ = 45° and H/B = 2, the semi-empirical approach of Hanna and Meyerhof [46] overestimated the bearing capacity, particularly when Cu/γB is large. Generally, consistencies were found between the FLAC 2D results and the numerical limit analysis of Shiau et al. [48] for both scenarios.

6. Results and Discussion

6.1. Effect of the Parameter Clay and Angle of Sand on the Ultimate Bearing Capacity Ratio qu/γB

Figure 4 presents the effect of the sand friction angle φ and undrained shear strength ratio Cu/γB on the ultimate bearing capacity ratio qu/γB for a strip footing on sand overlying clay without void. The value of qu/γB increases with increasing H/B. For a sand layer with a thin thickness, a large amount of radial shear strain was developed in the clay layer. However, with an increase in H/B, the failure surface in the clay layer is greatly reduced. The corresponding qu/γB value increases as the sand contributing to the bearing capacity increases. When H/B is sufficiently large, the failure surface is completely confined within the sand layer. Interestingly, the results obtained show that an increase in either φ or Cu/γB leads to a significant increase in the bearing capacity ratio qu/γB. The required sand layer thickness is dependent on both the φ and Cu/γB parameters. Lower Cu/γB and φ values require a thicker sand layer, and vice versa. For a given Cu/γB, Figure 4 shows that for every φ value, there is a critical value of H/B where the bearing capacity ratio reaches a constant stationary value. The figure also shows that H/Bφ30 < H/Bφ35 < H/Bφ40. It must be mentioned here that there is a critical value of the thickness of the sand layer that gives the greatest value for the bearing capacity ratio. The change in the critical value of the sand layer depends on each of the parameters’ φ and Cu/γB; after that, all values for bearing capacity are constant regardless of changes in each of the parameters’ φ and Cu/γB.

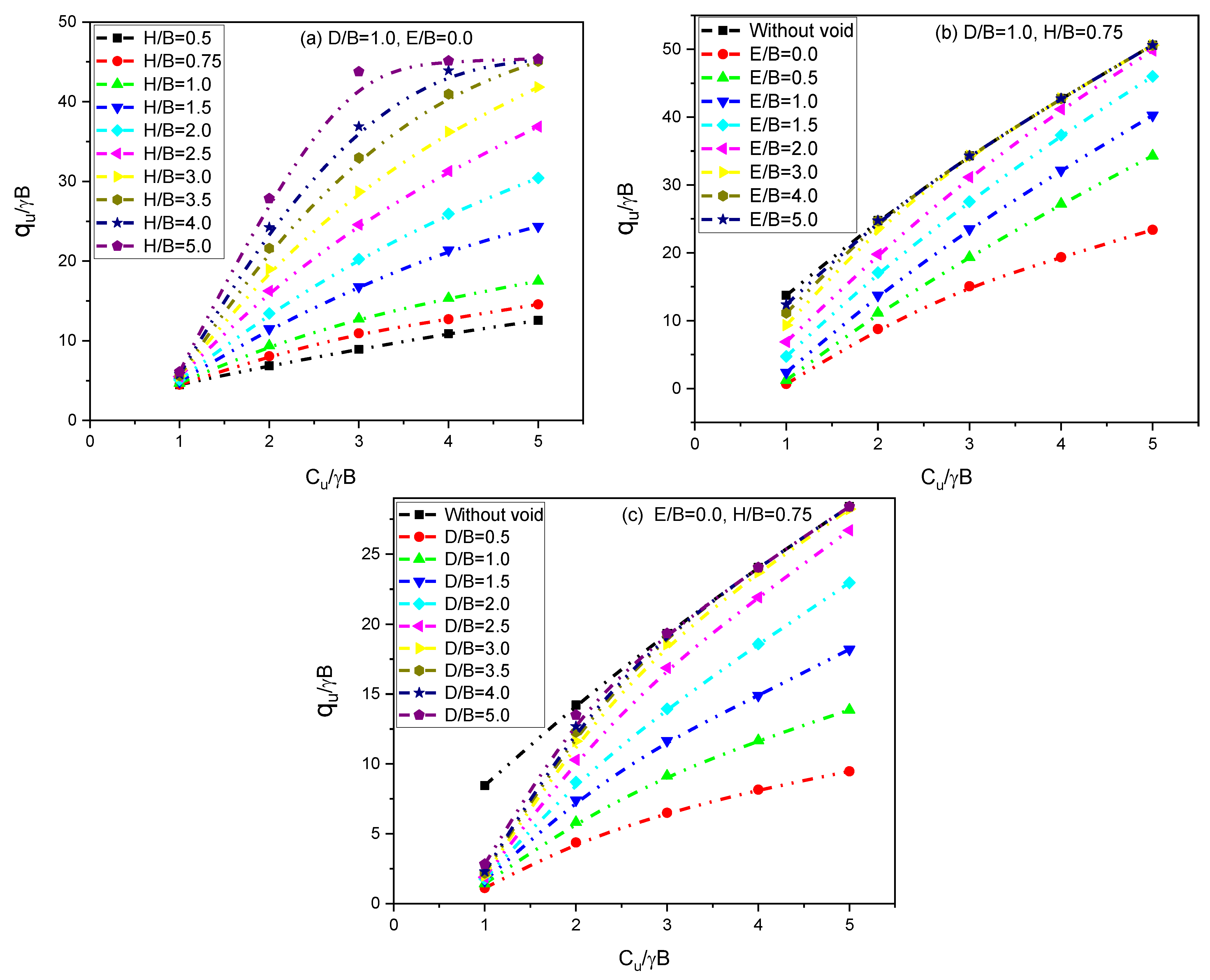
6.2. Effect of the Undrained Shear Strength Ratio (Cu/γB)

The influence of the undrained shear strength ratio Cu/γB on the bearing capacity ratio qu/γB of the strip footing on the sand layer over clay with one void is shown in (Figure 5a), where the void located under the strip footing has a constant depth. The simulation for many thicknesses of the top layer is shown in (Figure 5). As shown in the charts, the value of qu/γB increases as the Cu/γB ratio increases, regardless of the void location and the value of H/B. The rate of change (increase or decrease) in the qu/γB ratio is related to the parameters H/B, D/B and E/B, which needs to be discussed further. It can be seen in (Figure 5a) that the rate of increase in qu/γB increases with increasing values of the Cu/γB and H/B parameters. On the contrary, the rate of reduction in the ultimate bearing capacity ratio qu/γB is mainly related to the void parameters D/B and E/B, and also increases with increasing H/B and Cu/γB parameters. Again, Figure 5a shows that the rate of increase in qu/γB increases with increasing values of both Cu/γB and H/B. However, when H/B is ≥ 4.0, the qu/γB ratio maintains an almost constant value for Cu/γB ≥ 3.5. It should be noted here that the qu/γB ratio value increases at a faster rate with increasing H/B for a Cu/γB ratio ≥ 2.0 as compared to the increase for a Cu/γB ratio < 2.0. The results in (Figure 5b,c) show an initial reduction in the bearing capacity ratio qu/γB due to the presence of a void, which then increases gradually as the clay strength ratio Cu/γB increases when the value of D/B is ≥ 1.0, and the value of E/B is ≥ 0.5. Interestingly, the figures show a similar trend for the effect of void parameters E/B and D/B on the decrease in the bearing capacity ratio. qu/γB.

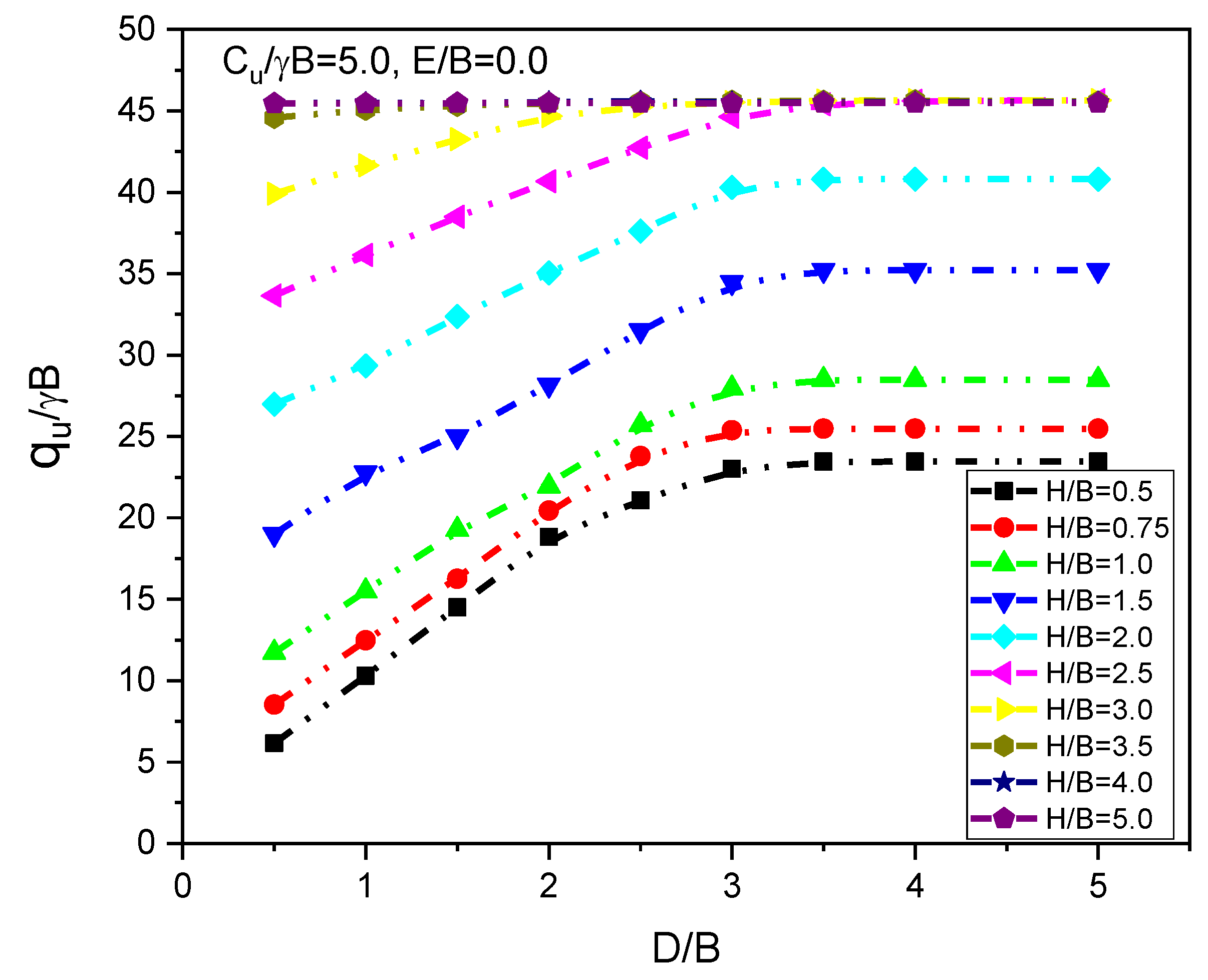
6.3. Effect of the Vertical Distance of the Void (D/B)

The effect of the ratio of the depth of a single void to the width of the strip footing D/B on the bearing capacity ratio qu/γB was studied, and the results are illustrated graphically in (Figure 6). The figure demonstrates that, for the entire range of H/B values, the ratio of qu/γB increases with an increasing D/B value. However, after reaching a certain value of D/B, the qu/γB ratio becomes constant. As illuminated in (Figure 6) for the case of a shear strength ratio of Cu/γB = 5.0, the value of qu/γB reaches a plateau at about D/B = 3.0 for H/B = 3.0 and at about D/B = 2.0 for H/B = 3.5, and for H/B > 3.5, the value of D/B does not have any impact on the carrying bearing capacity of the strip footing. One can conclude that there is a critical depth of void which gives the largest value for the bearing capacity ratio, after which all values are constant regardless of the changes in D/B.

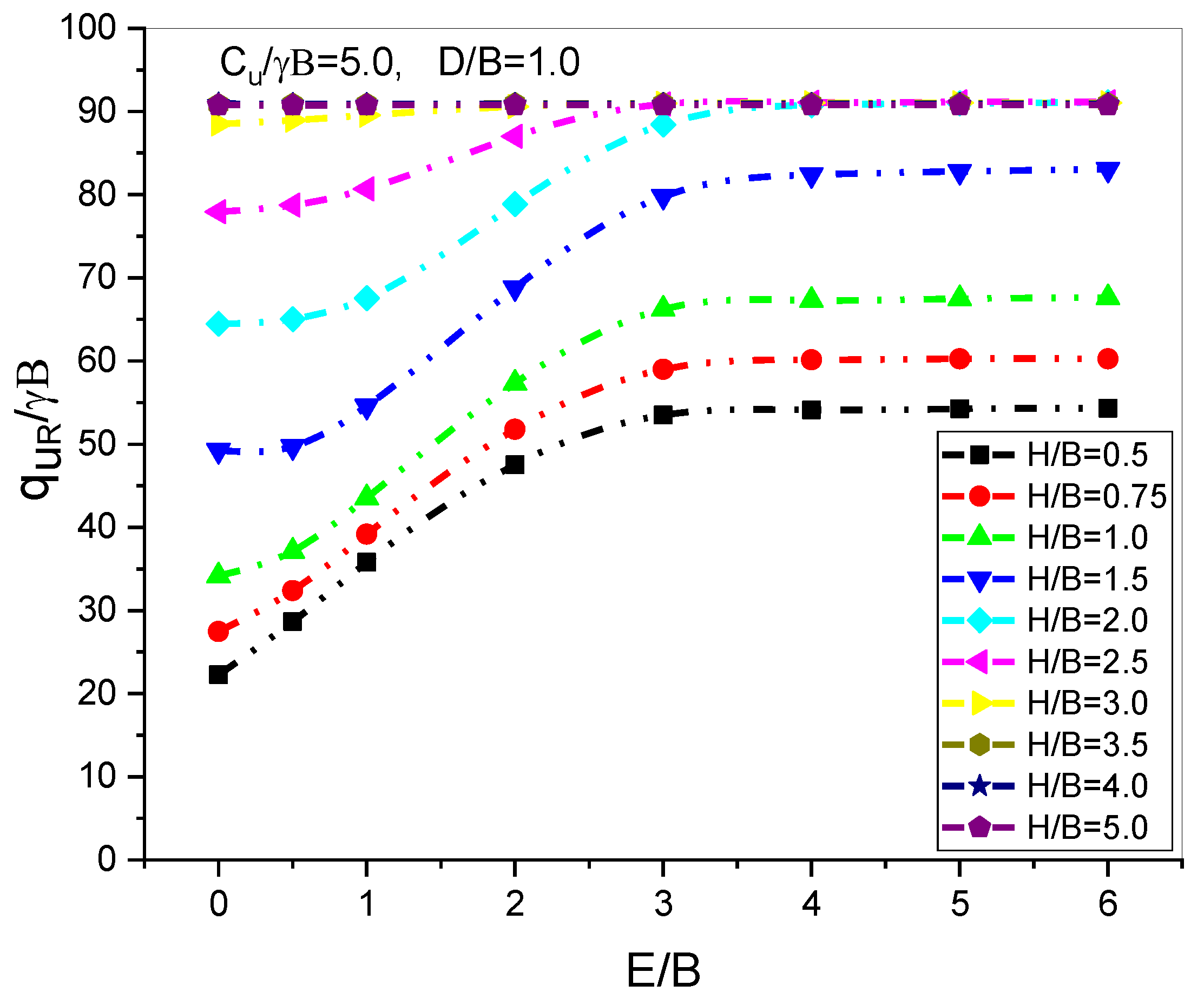
6.4. Effect of the Horizontal Distance (E/B) of the Single Void

The effect of the horizontal distance to a footing width E/B of a single void on the ultimate bearing capacity ratio qu/γB of a strip footing is presented in (Figure 7). Interestingly, the effect of E/B on qu/γB is similar to the effect of D/B. For all values of H/B, the bearing capacity ratio qu/γB increases with increasing E/B up to a certain value. As illustrated in (Figure 7), the qu/γB ratio reaches a steady value at an E/B value = 3.0 for H/B from 0.5 to 2.0, and at about E/B = 2.5 for H/B = 2.5, while at H/B > 3.0, the effect of parameter E/B on the qu/γB ratio is negligible. On the other hand, the value of qu/γB shows a quasi-linear trend for E/B values ranging from 0.0 to 3.0. Comparing these results with a previous study carried out by Yao Xiao et al. [20], it can be concluded that both have the same trend in which the bearing capacity ratio qu/γB decreases with decreasing D/B and E/B, regardless of the number of layers and the size of the voids.

6.5. Effect of the Top Layer Thickness (H/B)

The effect of the thickness of the sand layer over the width of the strip footing ratio, H/B, on the bearing capacity ratio qu/γB has already been considered in previous sections, as presented in (Figure 5, Figure 6 and Figure 7). The effect of H/B on the bearing capacity ratio qu/γB can be divided into four categories: (1) the effect of the H/B parameter on the qu/γB ratio is negligible when Cu/γB = 1.5; (2) for the case of H/B = D/B, the effect of H/B on the qu/γB ratio is small when Cu/γB = 1.5; (3) for the case of H/B > D/B and qu/γB = 1.5, the value bearing capacity ratio qu/γB increases with an increasing H/B value; (4) for the case of H/B ≥ 4.0 and Cu/γB ≥ 3.5, the value of qu/γB does not change (remaining almost constant) with the increase in H/B value.

6.6. Effect of a Single Square Void (H’/B = B’/B)

Figure 8 presents the effect of the presence of a single square void located at the bottom of the footing on the ultimate bearing capacity ratio qu/γB of the strip footing. For the case of Cu/γB = 4.0 and D/B ≤ 3.5, the figure shows that as the value of B’/B increases from 0.25 to 0.75, the value of qu/γB drops linearly and swiftly. However, when the value of (B’/B) (H’/H) ranges from 0.75 to 2.5, the value of qu/γB decreases linearly at a lower reduction rate, revealing that an increase in (B’/B) (H’/H) will reduce the ultimate bearing capacity ratio qu/γB.

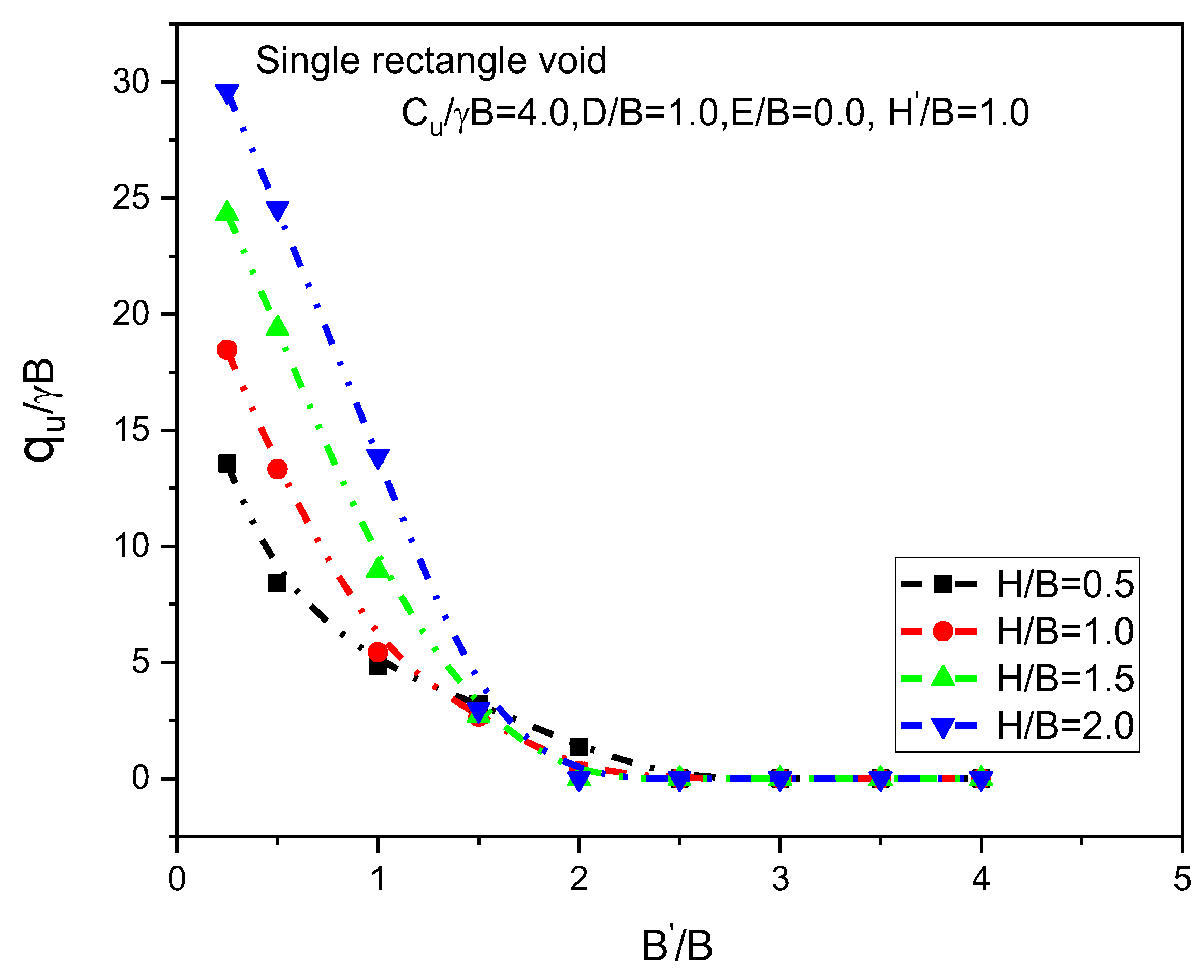
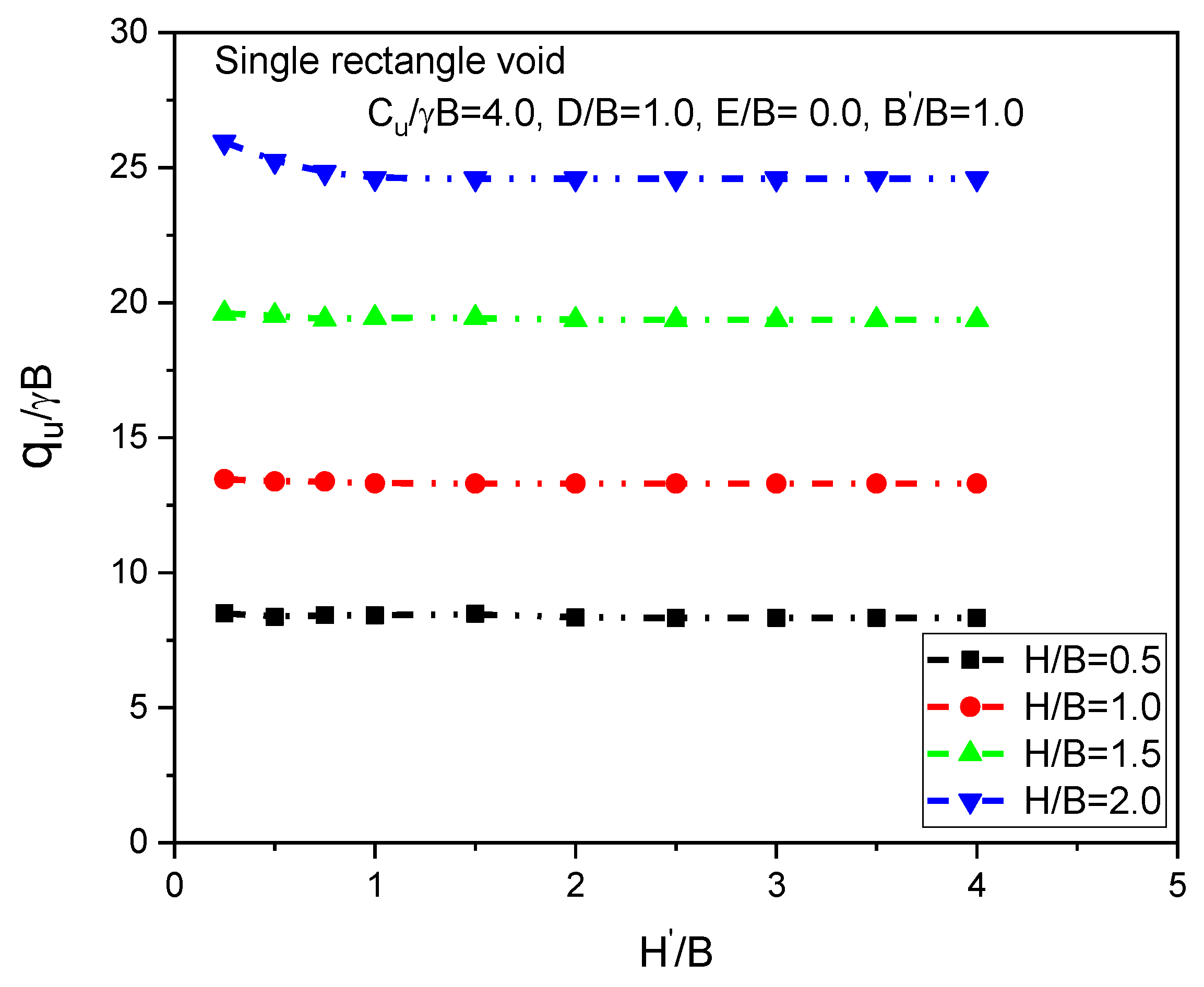
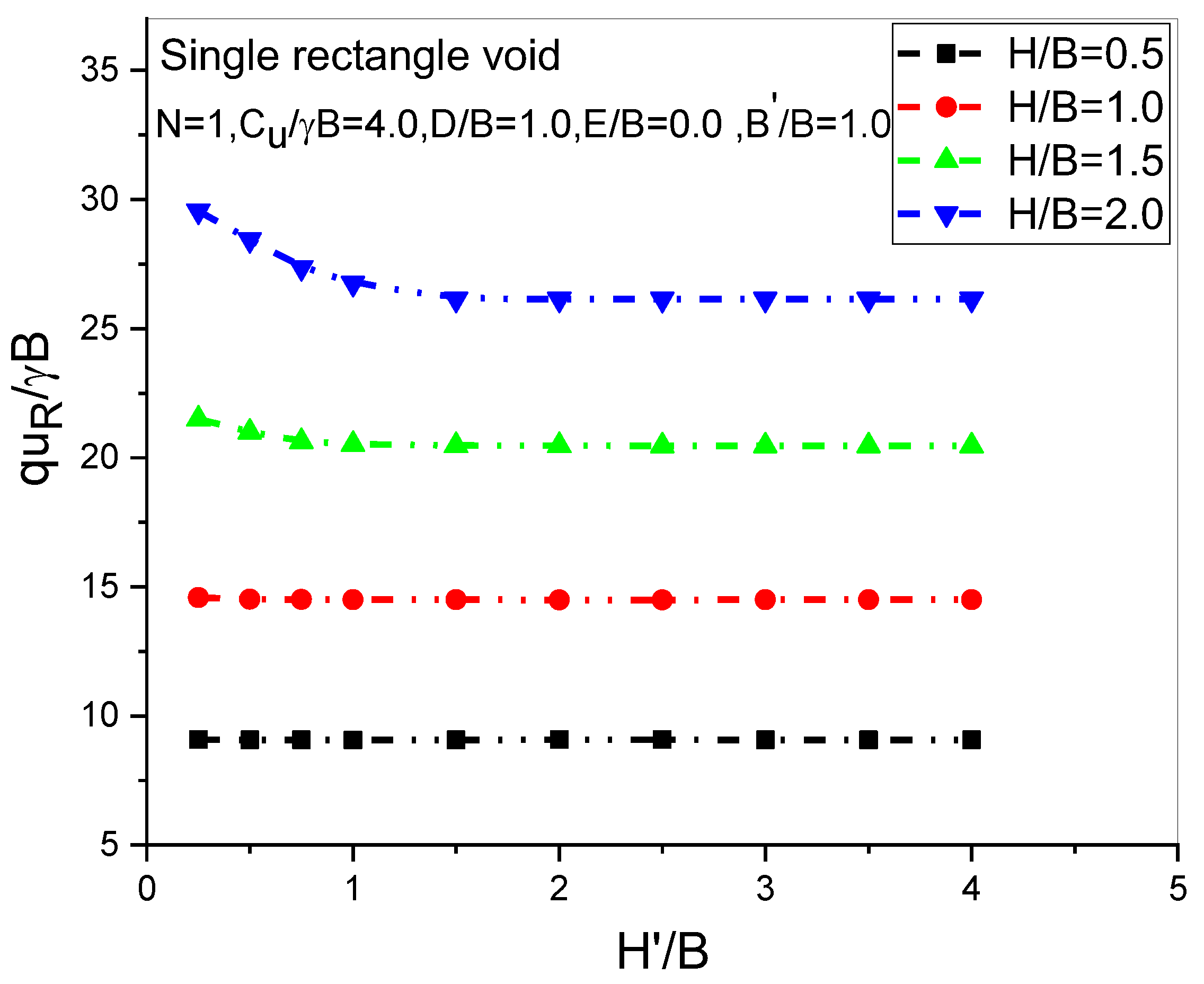
6.7. Effect of a Single Rectangular Void

The influence of void width and void height on the ultimate bearing capacity ratio qu/γB of the strip footing was investigated, and the results are presented in (Figure 9 and Figure 10), respectively. As shown in (Figure 10), it is clear that the void height has a negligible influence on the ultimate bearing capacity. From (Figure 9), it can be observed that the width of the void has a significant influence on the bearing capacity ratio qu/γB as compared to its height. However, when B’/B ≥ 1.5 for H/B ≥ D/B, the influence of H/B on the bearing capacity ratio becomes negligible, while for B’/B ≤ 1.5, the influence of H/B cannot be neglected.

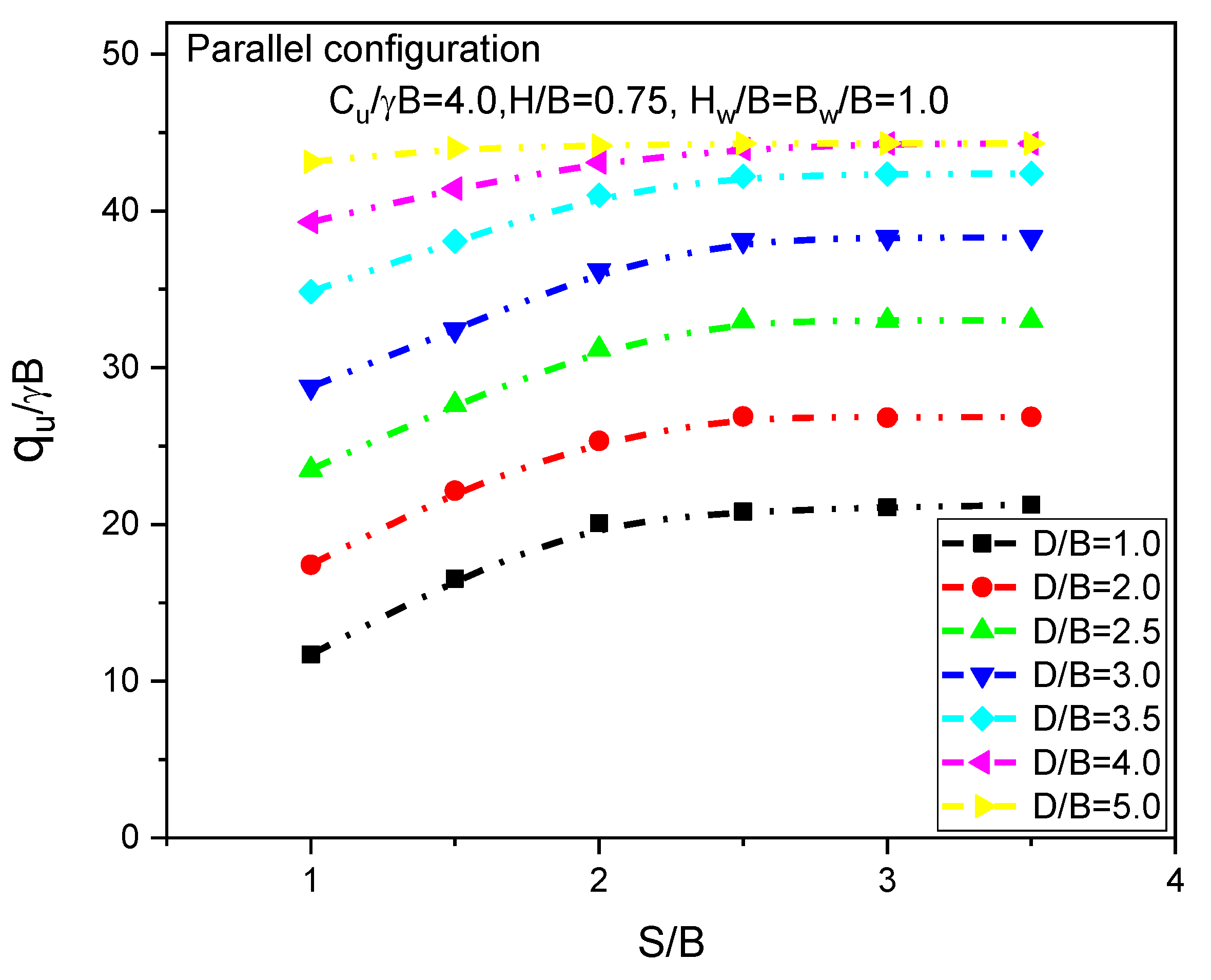
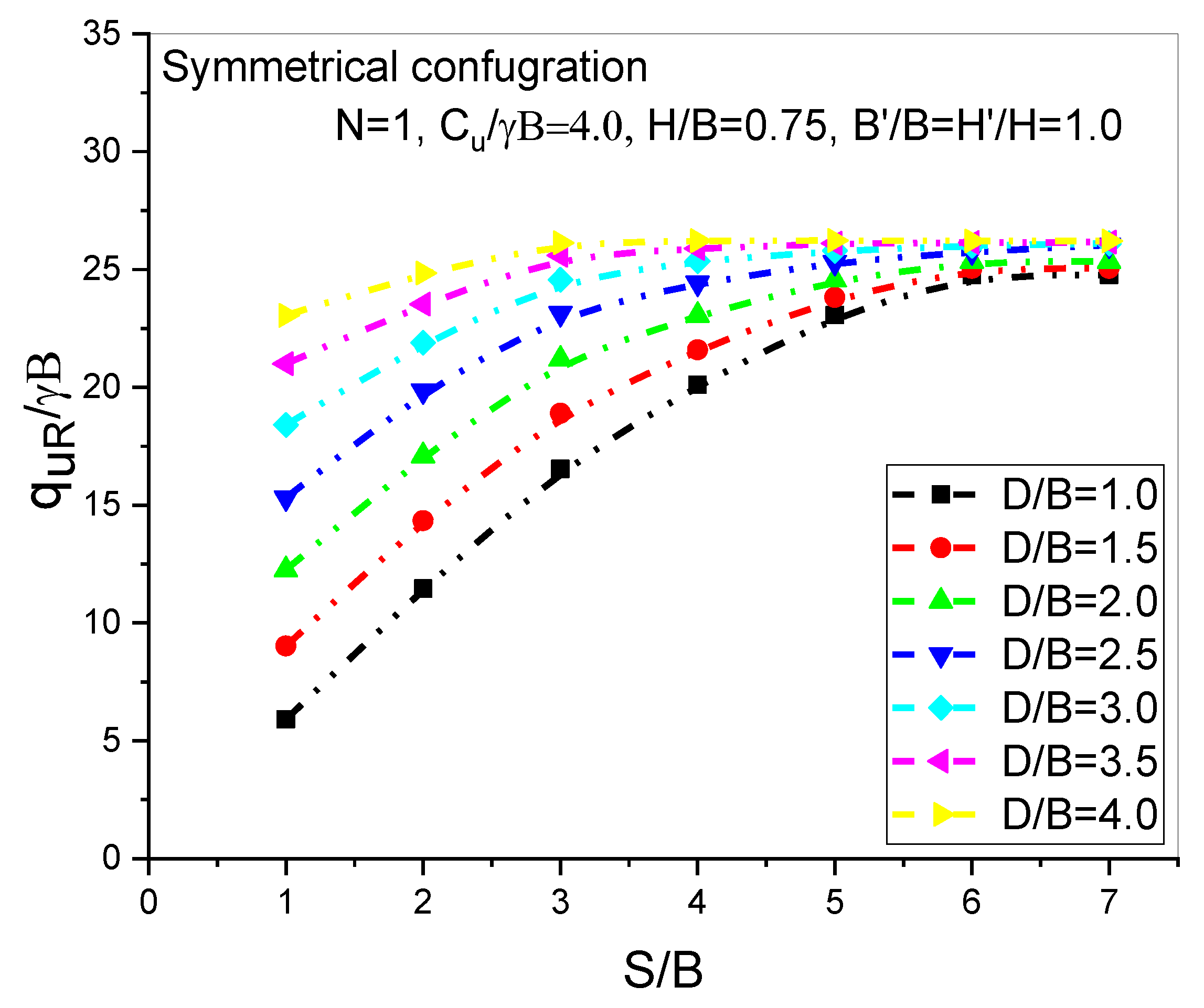
6.8. Effect of Two Voids (Parallel and Symmetrical Configurations)

The effects of the existence of two voids on the ultimate bearing capacity ratio qu/γB of the strip footing are presented in (Figure 11 and Figure 12) for a parallel configuration and a symmetrical configuration with spacing S, respectively. The results indicate that the bearing capacity ratio of the strip footing qu/γB increases with an increasing spacing-to-footing-width ratio S/B, regardless of the pattern of configuration. As shown in (Figure 11), for a parallel configuration with Cu/γB = 4.0, the value of qu/γB increases with increasing S/B, approaching a constant value at about S/B ≥ 2.5. (Figure 12) clearly demonstrates the significant effect of the S/B ratio of the symmetric voids on the bearing capacity ratio qu/γB of the strip footing. With the undrained strength ratio Cu/γB = 4.0, qu/γB reaches a constant value, which corresponds to the bearing capacity ratio without voids after a certain S/B value. This value is approximately at S/B = 2.0 for D/B = 4.0, at S/B = 3.0 for D/B = 3.5, at S/B = 3.5 for D/B = 3.0, at S/B = 4.0 for D/B = 2.5, at S/B = 4.5, for D/B = 2.0, at S/B = 5.0 for D/B = 1.5 and at S/B = 6.0 for D/B = 1.0.

6.9. Effect of Geotextile on the Bearing Capacity Ratio (qu/γB) for Different Cu/γB Values

The effect of one geotextile reinforcement layer on the ultimate bearing capacity ratio qu/γB of the strip footing on a sand layer overlying clay with one void is shown in (Figure 13). The results in (Figure 13) show that the value of qu/γB ratio increases with an increasing value of Cu/γB, regardless of the value of the H/B coefficient and the void location. As compared to the previous cases without reinforcement (Figure 5a) for D/B = 1.0 and E/B = 0, the value of qu/γB increases in the presence of geotextile reinforcement at the sand–clay interface, as shown in (Figure 13a). (Figure 13a) also shows that the geotextile reinforcement has a certain effect on improving the ultimate bearing capacity ratio qu/γB when the value of H/B < 2, while for H/B ≥ 2, the effect is not significant. (Figure 13b,c) present the effect of geotextile reinforcement on the final bearing capacity ratio qu/γB of the strip footing for two different void positions, in the vertical and horizontal directions, for different undrained shear strength ratios and with stability in the thickness of the upper layer. The figures demonstrate an increase in the bearing capacity ratio qu/γB as compared to the results obtained for the case without geotextile reinforcement, as shown in (Figure 5b,c). The results clearly show that the use of reinforcement contributes to the improvement in the bearing capacity of the strip footing, even though the clay layer coefficient and the position of the void have changed.

6.10. Effect of the Geotextile on the Bearing Capacity Ratio (qu/γB) for Different Vertical Distances of the Void

The effect of placing geotextile on the ultimate bearing capacity ratio qu/γB of the strip footing for the case of a single void located at different vertical distances was investigated, and the results are graphically illustrated in (Figure 14). For all H/B values, the qu/γB ratios, in the presence of geotextile reinforcement, increase with increasing normalized depth D/B. Compared to the cases without reinforcement shown in (Figure 6), the bearing capacity values increase in the presence of the reinforcement for certain values of H/B. For the case of H/B = 0.75, wherein D/B = 1.0 and D/B = 5, the ultimate bearing capacity ratio qu/γB increases by 12.19% and 17.62%, respectively. However, for other values of D/B, the values of qu/γB are close with and without reinforcement. As shown in (Figure 6 and Figure 14), when H/B > 2, the reinforcement does not have a significant impact on the carrying bearing capacity of the strip footing, which means that the reinforcement has a limited field effect.

6.11. Effect of the Geotextile on the Bearing Capacity Ratio (qu/γB) for Different Horizontal Distance of Voids

The effect of geotextile reinforcement on the ultimate bearing capacity ratio qu/γB of the strip footing for the case of a single void located at different horizontal distances is presented in (Figure 15). The figure shows that the qu/γB ratio, in the presence of geotextile reinforcement, increases with increasing normalised horizontal distance E/B, similar to the effect of reinforcement for the void with different D/B ratios. The figure also shows that the bearing capacity ratio qu/γB increases due to the presence of the reinforcement for certain values of H/B as compared to the cases without reinforcement (Figure 7). For the case of H/B = 0.75, wherein E/B = 2.0 and E/B = 6.0, the ultimate bearing capacity ratio increases by 7.91% and 18.13%, respectively. However, when the ratio of E/B ≥ 3.0, the value of qu/γB for the two cases, with and without reinforcement, becomes constant and similar.

6.12. Effect of the Geotextile on the Bearing Capacity Ratio (qu/γB) for the Square Void Size (H’/B = B’/B) Case

The effect of geotextile on the ultimate bearing capacity ratio qu/γB of the strip footing on a sand layer overlying clay in the presence of a square void is presented in (Figure 16). The figure shows that the value of the bearing capacity ratio qu/γB increases in the presence of geotextile reinforcement in light of the increase in void size (B’/B) (H’/H) as compared to the case without reinforcement, as shown in (Figure 8). Moreover, the results clearly demonstrate that the placement of geotextile reinforcement at the sand–clay interface reduces the effect of void size.

6.13. Effect of the Geotextile on the Bearing Capacity Ratio (qu/γB) for the Case of Rectangular Void Size

Figure 17 and Figure 18 present the effect of geotextile reinforcement on the ultimate bearing capacity ratio qu/γB of the strip footing on a sand layer overlying clay with one rectangular void for changes in void width and void height, respectively. The results shown in the two figures demonstrate that the placement of geotextile reinforcement at the sand–clay interface affects the ultimate bearing capacity ratio qu/γB of the strip footing in light of changes in both the void width and the void height, as compared to the previous results obtained in the case where no reinforcement is used, as presented in (Figure 9 and Figure 10). As seen in the figures, the effect on the bearing capacity ratio qu/γB is inversely proportional with the shape of the void.

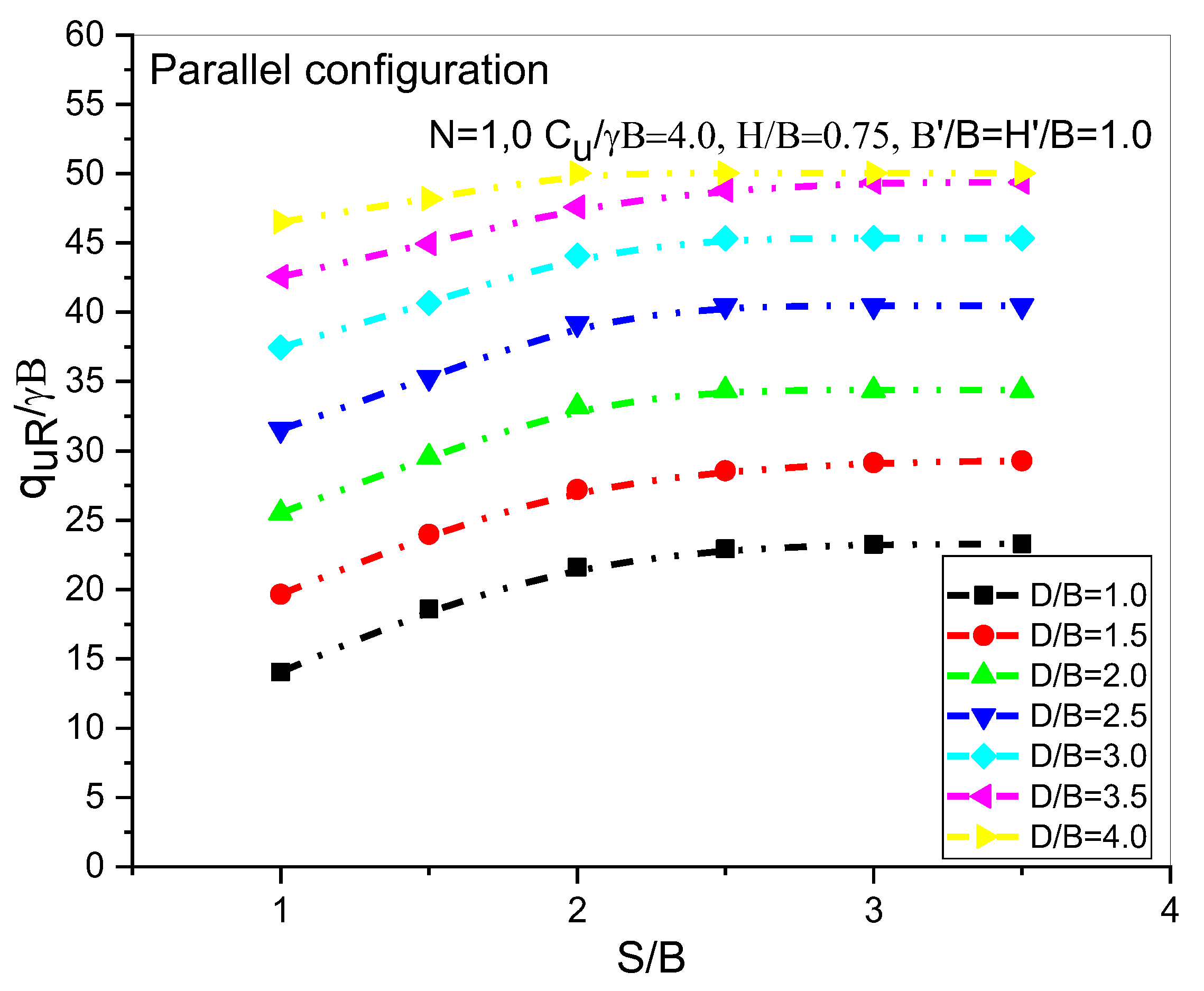
6.14. Effect of the Geotextile on the Bearing Capacity Ratio (qu/γB) for the Parallel and Symmetrical Configuration of Two Voids

The effect of geotextile reinforcement on the ultimate bearing capacity ratio qu/γB of the strip footing on a sand layer overlying clay with two voids was investigated for two different configurations of void, parallel and symmetrical (see Figure 1), and the results are presented in (Figure 19 and Figure 20), respectively. The results obtained indicate that the bearing capacity ratio qu/γB increases in the presence of reinforcement regardless of the increase in the spacing ratio S/B, depth ratio D/B and the void configuration. Comparing the bearing capacity ratio results obtained for the case wherein geotextile reinforcement is used with those obtained for the case wherein reinforcement is not used (Figure 11 and Figure 12), it can be observed that the improvement in qu/γB is due to the presence of the geotextile reinforcement.

7. Conclusions

A detailed numerical study has been carried out on the stability of strip footings on top of a sand layer overlying clay with voids, with and without geotextile reinforcement at the interface between sand and clay. Using the finite difference software FLAC, the bearing capacity ratio qu/γB of the strip footing has been calculated for voids with different depths and horizontal distances for two configurations (parallel and symmetrical). The effects of the thickness of the top layer of sand and the undrained shear stress ratio of the clay layer and geotextile reinforcement on the bearing capacity ratio qu/γB were investigated. Furthermore, several other geometric parameters, such as position, height, distance, size and number of voids, have been studied, alongside an examination of the effect of reinforcement. The results show that the ultimate bearing capacity ratio qu/γB is affected by the above parameters. Based on the results of this study, the following conclusions can be drawn:

(1) The ultimate bearing capacity ratio qu/γB of a strip footing on sand overlying clay without a void is greatly dependent on the significant parameters (H/B, Cu/γB and φ), as shown by the present study. Indeed, the ultimate bearing capacity ratio qu/γB was greatly improved by increasing the three parameters mentioned above.

(2) The presence of a void under the footing reduces the ultimate bearing capacity ratio and the stability of the footing, and the behaviour of the footing is greatly affected by the presence of the void only when the void falls within the region of failure of the footing.

(3) As the embedding depth D/B of the blank increases, the bearing capacity ratio increases, regardless of the ratio of dimensionless soil strength and the number and location of voids. For a given value of H/B, the bearing capacity of sand overlying clay increases when D/B increases until a value of D/B = 3 is reached, whereafter the bearing capacity becomes constant. Furthermore, the bearing capacity increases with increasing H/B until a value of H/B = 2.5 is reached, whereafter the bearing capacity reaches a constant maximum. One can conclude that for D/B ≥ 3 and H/B ≥ 2.5, there is no effect of void D/B depth on the bearing capacity ratio.

(4) For single rectangular voids, the value of qu/γB decreases linearly with increasing values of B’/B from 0.25 to 0.75 at a high reduction rate, and from 0.75 to 2.5 at a low reduction rate. However, it can be seen that void height H’/B has a negligible effect on the ultimate bearing capacity ratio. For single square voids, the value of qu/γB increases with increasing D/B and E/B, until the ratio qu/γB reaches a constant value, indicating that the shape of the void influences the ultimate bearing capacity ratio.

(5) In the case where two voids are present, the value of ratio qu/γB increases with an increase in the value of S/B, regardless of the configuration style, parallel or symmetrical. For the parallel configuration, there are fewer failure modes compared to the symmetrical configuration. Therefore, the value of S/B for the parallel configuration is less than that for the symmetrical configuration when the ratio qu/γB reaches a constant value.

(6) The ultimate bearing capacity ratio increases with decreases in both the B’/B and H’/B ratios to the width of the footing. It turns out that the shape and depth of the void have major effects on the bearing capacity. The width of the void in particular has a great influence, while the height has a small effect in comparison.

(7) The embedding depth of void D/B and its number, size and location, in addition to the optimum depth of soil reinforcement N, greatly affect the bearing capacity of the footing. However, for the thickness of the top layer H/B > 2.0, the contribution of the reinforcement to the improvement in bearing capacity is practically negligible.

(8) On the other hand, the negative effects of the void inherent to the increase in the embedding depth of the void can be reduced by introducing a reinforcement at an optimum depth. Therefore, cost optimisation is essential to determine the economic value of all parameters influencing the bearing capacity.