Capacity Assessment in Freight-Passengers Complex Railway Nodes: Trieste Case Study
Abstract
1. Introduction
2. State of the Art
2.1. Line Capacity
2.2. Node Capacity
2.3. Combined Line-Node Capacity
2.4. Simulation
3. Materials and Methods
- Geometry of the tracks (straight, curves, etc.);
- Characteristics of the signaling system (type of block, number and length of sections, minimum distance between trains, braking distance, etc.;
- Layout of stations.
- Operational models (passengers/goods, short/long-distance traffic, etc.);
- Rolling stock (length of trains, acceleration/deceleration performances, etc.);
- Operational time (day, peak periods, etc.);
- Timetabling (running time, buffer time, dwell time, occupation/interdiction time among trains, etc.).
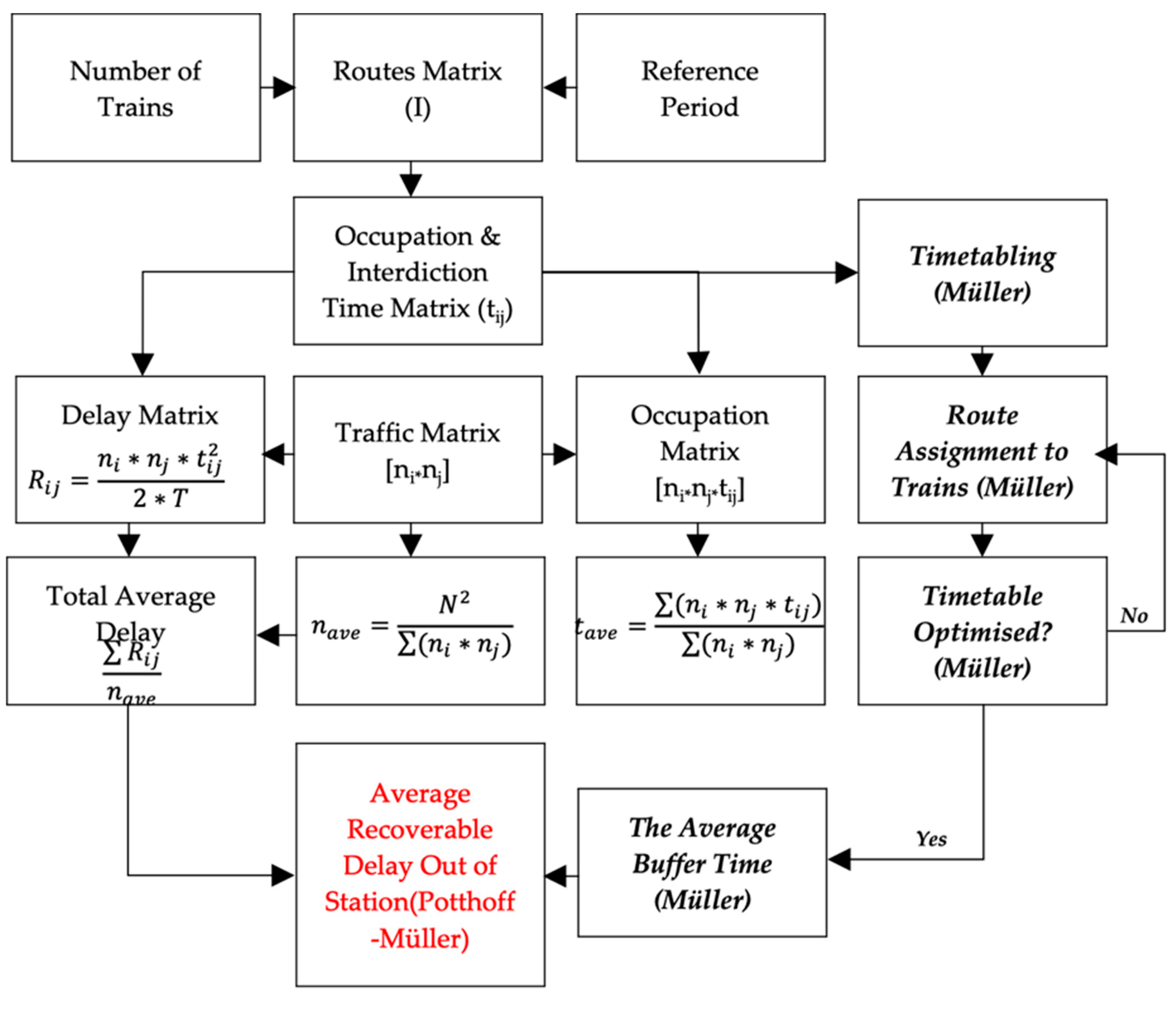
3.1. Analytical Method
- Passenger trains reference time: 18 h;
- Freight trains reference time: 22 h;
- Passenger traffic in both directions for station Trieste Centrale: 106 trains/day;
- Freight traffic in both directions for station Trieste Campo Marzio: 31 trains/day;
- Intermediate dwell time: 1 min for passenger trains, no stops for freight trains;
- Maximum speed along the line: 60 km/h;
- Maximum speed on deviations: 30 km/h.
- Constant density of arrivals probability in T;
- Probability to meet a not permissive signal on the line i.
- R = medium delay that the trains on the line i suffered by waiting on the passing of another train from line j;
- t = waiting time of the train;
- n = number of trains;
- T = reference time.
- Traditional automatic block signalling system;
- Overall buffer time is calculated as the average of entry and exit buffers;
- Paths are categorized according to the destinations usable as alternatives for train dispatching;
- Departure time from the origin station is based on the same original timetable for both Müller method and OpenTrack® simulation.
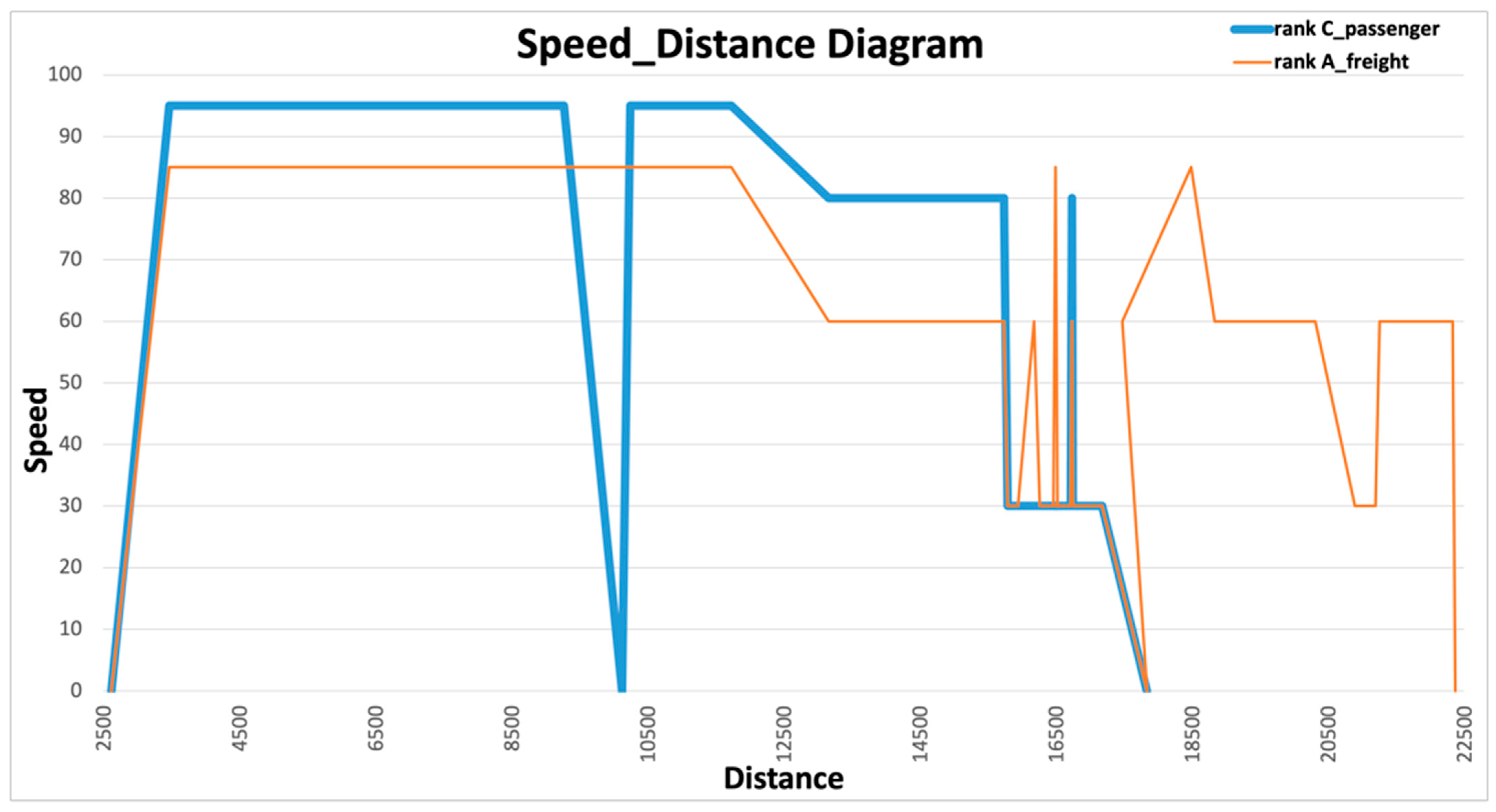
3.2. Simulation Method
- First Train movement is modelled based on a mixed continuous-discrete method. The motion of trains in modelled by the solution of the differential motion equation (continuous) combined with signal information (discrete);
- Second Differential motion equation calculates the train’s forward motion based on the maximum possible acceleration per time step;
- Second Train speed is obtained using integration and the distance covered using reintegration Figure 4;
- Second Type of occupation method is based on the default brake curves setting;
- Second Delay settings are the following: Small delays (minimum value for a train to be on delay, default = 1 s); Medium delays (default = 60 s); Large delays (default = 300 s).
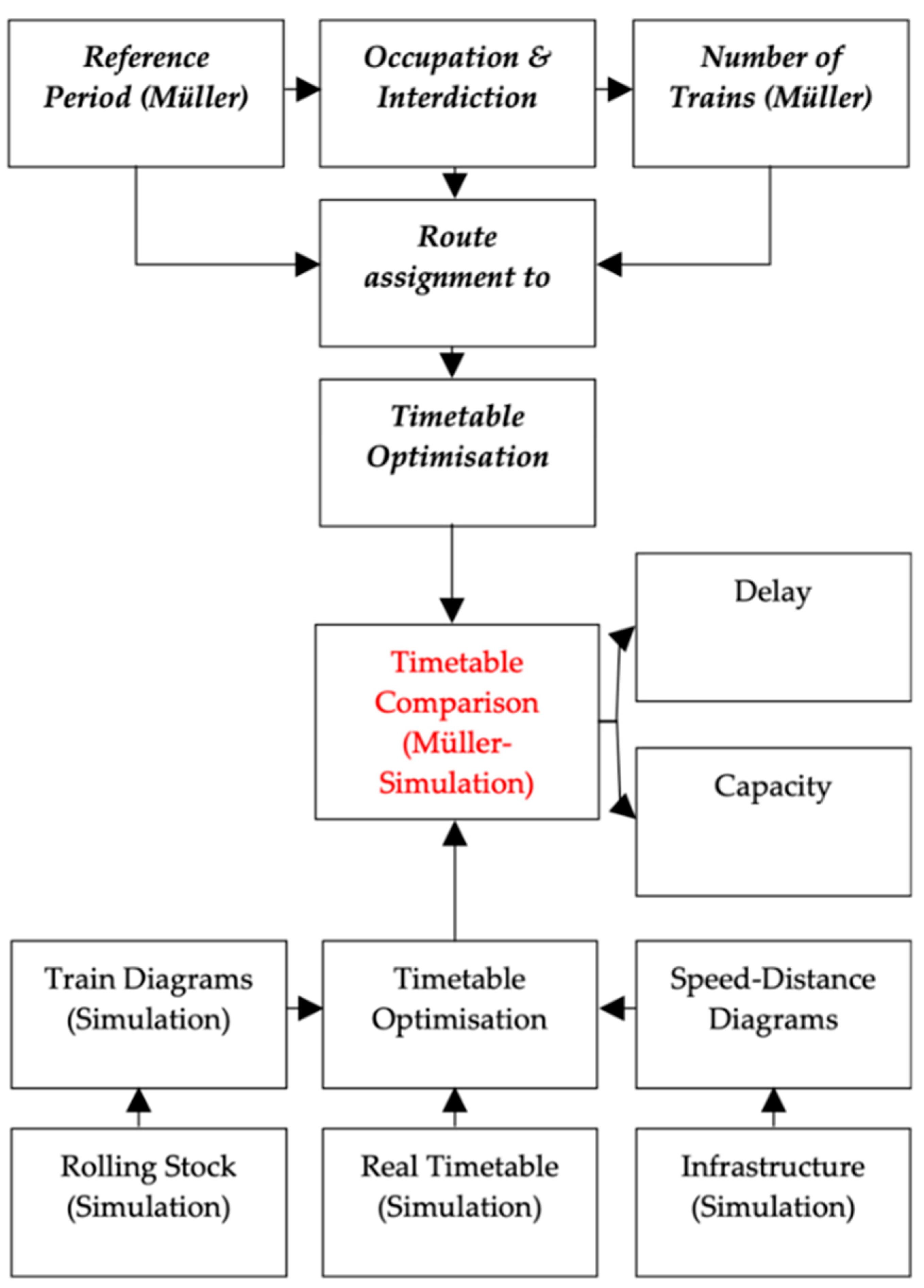
3.3. Comparative Analysis
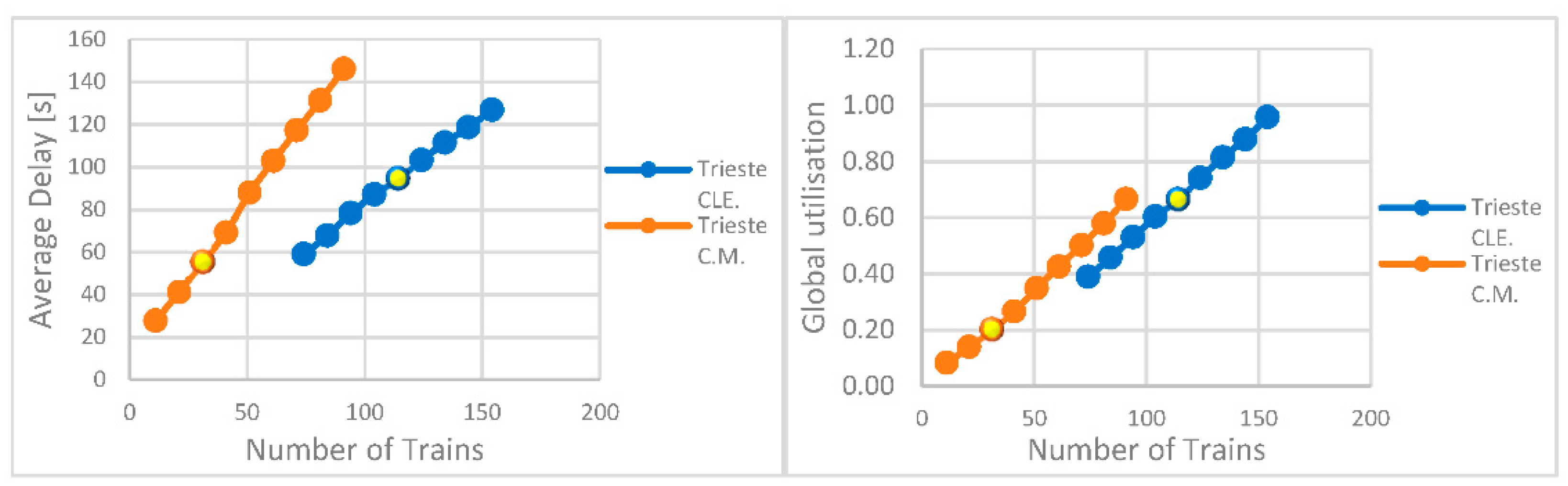
4. Results
- Delay due to conflicts in the station (calculated by the Potthoff method);
- Total buffer time available, according to the planned timetable, respectively, resulting by Müller (on the left) and OpenTrack® simulation (on the right);
- Delay matured out of the station is recoverable by the residual buffer (difference between available buffer and delay matured in the station).
5. Discussion
- ■
- Quantification of effects of timetable compression (e.g., by the UIC 406 method) on capacity and punctuality of both stations and lines;
- ■
- Further tests based on various traffic simulation tools at the network level;
- ■
- The sensitivity of the network capacity to upgrades of the signalling systems.
6. Conclusions
- ■
- The use of the analytical method appears in line with the scope of high-level analyses for the identification of the most appropriate infrastructure layouts and signalling systems to adopt in a long-term perspective, independently upon a specific timetable structure;
- ■
- The implementation of a simulation model is necessary for in-depth analyses aiming at the optimization of the use of capacity and the timetable structure itself.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, P.; Pasha, J.; Moses, R.; Sobanjo, J.; Ozguven, E.E.; Dulebenets, M.A. Development of exact and heuristic optimization methods for safety improvement projects at level crossings under conflicting objectives. Reliab. Eng. Syst. Saf. 2022, 220, 108296. [Google Scholar] [CrossRef]
- Di Marco, G.; Malavasi, G. Affidabilità dei sistemi ferroviari. Analisi e valutazione mediante modelli di simulazione. Ing. Ferrov. 2000, 2, 311. [Google Scholar]
- Li, X.; Martin, U.; Oetting, A.; Nachtigall, K. Methodik zur effizienten marktgeeigneten Trassenbelegung im spurgeführten Verkehr. ETR 2017, 6, 56–64. [Google Scholar]
- Oneto, L.; Fumeo, E.; Clerico, G.; Canepa, R.; Papa, F.; Dambra, C.; Anguita, D. Dynamic delay predictions for large-scale railway networks: Deep and shallow extreme learning machines tuned via threshold out. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2754–2767. [Google Scholar] [CrossRef]
- Tang, L.; Xu, X. Optimisation for operation scheme of express and local trains in suburban rail transit lines based on station classification and bi-level programming. J. Rail Transp. Plan. Manag. 2022, 21, 100283. [Google Scholar]
- Zhang, T.; Li, D.; Qiao, Y. Comprehensive optimization of urban rail transit timetable by minimizing total travel times under time-dependent passenger demand and congested conditions. Appl. Math. Model. 2018, 58, 421–446. [Google Scholar] [CrossRef]
- Solinen, E.; Nicholson, G.; Peterson, A. A microscopic evaluation of railway timetable robustness and critical points. J. Rail Transp. Plan. Manag. 2017, 7, 207–223. [Google Scholar] [CrossRef]
- Gestrelius, S.; Häll, C.H.; Peterson, A. Capacity Utilization, Travel Time, Stability and Heterogeneity-a Linear Programming Analysis for Railway Timetabling. In Proceedings of the RailBeijing Conference, Beijing, China, 3–7 November 2021. [Google Scholar]
- Erlandson, W.; Häll, C.H.; Peterson, A.; Schmidt, C. Meta-Heuristic for Inserting a Robust Train Path in a Non-Cyclic Timetable. In Proceedings of the RailBeijing Conference, Beijing, China, 3–7 November 2021. [Google Scholar]
- Haehn, R.; Ábrahám, E.; Nießen, N. Probabilistic simulation of a railway timetable. In Proceedings of the 20th Symposium on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems. Virtual ATMOS Conference, Pisa, Italy, 7–8 September 2020. [Google Scholar]
- Capacity. UIC Code 406, 2nd ed.; International Union of Railways: Paris, France, 2013. [Google Scholar]
- Corazza, G.R. Il problema del nodo e la verifica degli impianti di stazione. Ing. Ferrov. 1979, 34, 271–283. [Google Scholar]
- Müller, G. Eisenbahnanlagen und Fahrdynamik; Springer: Berlin, Germany, 1960; pp. 1–2. [Google Scholar]
- Cuppi, F. Analysis of Railway Signalling Systems to Increase Line and Node Capacity. Ph.D. Thesis, AMS Dottorato, Bologna, Italy, 2022. [Google Scholar]
- Prokopy, J.C.; Rubin, R.B. Parametric Analysis of Railway Line Capacity; FRA-OPPD-75-1; U.S. Department of Transportation: Washington, DC, USA, 1975.
- Links between Railway Infrastructure Capacity and the Quality of Operations; UIC 405 OR; International Railway Union: Paris, France, 1996.
- Vicuna, G. Organizzazione e Tecnica Ferroviaria, 2nd ed.; CIFI: Rome, Italy, 1986. [Google Scholar]
- Canciani, G. Criteri Progettuali di Rinnovo o Potenziamento Delle Line Ferroviarie: Modello di Calcolo e di Verifica Della Potenzialità di Circolazione. Ph.D. Thesis, University of Trieste, Trieste, Italy, 1991. [Google Scholar]
- RFI. Metodi di Calcolo Della Capacità Delle Line Ferroviarie; RFI: Rome, Italy, 2011. [Google Scholar]
- Bianchi, M. Potenzialità di line ferroviarie. Ing. Ferrov. 1964, 12, 981–994. [Google Scholar]
- Capacity. UIC Code 406, 1st ed.; International Union of Railways: Paris, France, 2004. [Google Scholar]
- Corriere, F. Potenzialità e regolarità di esercizio nelle line ferroviarie. Ing. Ferrov. 1982, 1–2, 38–43. [Google Scholar]
- Genovesi, P.R. Flussi e capacità delle line ferroviarie a doppio binario. Ing. Ferrov. 2006, 7–8, 571–586. [Google Scholar]
- Armstrong, J.; Blainey, S.; Preston, J.; Hood, I. Developing a CUI-based approach to network capacity assessment. In Proceedings of the 4th International Seminar on Rail Operations Modelling and Analysis, Rome, Italy, 16–18 February 2011. [Google Scholar]
- Florio, L.M.G. Principi teorici per la verifica di un impianto complesso e determinazione dei margini di potenzialità. Ing. Ferrov. 1984, 12, 846. [Google Scholar]
- Corazza, G.R.; Florio, L. Gli impianti di stazione e la loro analisi topologica. Ing. Ferrov. 1987, 11, 643. [Google Scholar]
- Malavasi, G.; Molkovà, T.; Ricci, S.; Rotoli, F. A synthetic approach to the evaluation of the carrying capacity of complex railway nodes. J. Rail Transp. Plan. Manag. 2014, 4, 28–42. [Google Scholar] [CrossRef]
- Potthoff, G. Die Zugfolge auf Strecken und in Bahnhöfen; Transpress: Berlin, Germany, 1970; Volume 1. [Google Scholar]
- Mussone, L. An analytical approach to calculate the capacity of a railway system. Eur. J. Oper. Res. 2013, 228, 11–23. [Google Scholar] [CrossRef]
- Jovanović, P.; Pavlović, N.; Belošević, I.; Milinković, S. Graph coloring-based approach for railway station design analysis and capacity determination. Eur. J. Oper. Res. 2020, 287, 348–360. [Google Scholar] [CrossRef]
- Kontaxi, E.; Ricci, S. Techniques and methodologies for carrying capacity evaluation: Comparative analysis and integration perspectives. Ing. Ferrov. 2009, 64, 1051–1080. [Google Scholar]
- Kontaxi, E.; Ricci, S. Calculation of railway network capacity: Comparing methodologies for lines and nodes. In Proceedings of the 4th Intern. Seminar on Railway Operations Modelling and Analysis, Rome, Italy, 16–18 February 2011; Volume 16. [Google Scholar]
- Kontaxi, E.; Ricci, S. Railway capacity handbook: A systematic approach to methodologies. Procedia-Soc. Behav. Sci. 2012, 48, 2689–2696. [Google Scholar] [CrossRef][Green Version]
- Kianinejadoshah, A.; Ricci, S. Comparative application of methods for the combined lines-nodes capacity assessment. Int. J. Transp. Dev. Integr. 2020, 4, 243–251. [Google Scholar] [CrossRef]
- Kianinejadoshah, A.; Ricci, S. Comparative Application of Methods for Nodes Capacity Assessment. Transp. Res. Procedia 2021, 53, 72–79. [Google Scholar] [CrossRef]
- Kianinejadoshah, A.; Ricci, S. Comparative Application of Analytical and Simulation Methods for the Combined Railway Nodes-Lines Capacity Assessment. Transp. Res. Procedia 2021, 55, 103–109. [Google Scholar] [CrossRef]
- Malavasi, G.; Ricci, S. Carrying capacity of railway networks: Interaction of line and node models. WIT Trans. Built Environ. 2000, 50, 10. [Google Scholar]
- Crenca, D.; Malavasi, G.; Ricci, S. Dependence of railway lines carrying capacity by signalling systems and track geometry. In Proceedings of the 1st International Seminar on Railway Operations Modelling and Analysis, Delft, The Netherlands, 8–10 July 2005. [Google Scholar]
- Crenca, D.; Malavasi, G.; Mancini, R. Effects of stations layout on railway lines carrying capacity. In Proceedings of the 14th International Symposium EURNEX-Towards the Competitive Rail System in Europe, Athens, Greece, 27 April–1 May 2006. [Google Scholar]
- Rotoli, F.; Malavasi, G.; Ricci, S. Complex railway systems: Capacity and utilisation of interconnected networks. Name Eur. Transp. Res. Rev. 2016, 8, 1–21. [Google Scholar]
- Ciuffini, F. Orario Ferroviario, Integrazione e Connettività; Collegio Ingegneri Ferroviari Italiani: Rome, Italy, 2019. [Google Scholar]
- Weik, N.; Warg, J.; Johansson, I.; Bohlin, M.; Nießen, N. Extending UIC 406-based capacity analysis. New approaches for railway nodes and network effects. J. Rail Transp. Plan. Manag. 2020, 15, 100–199. [Google Scholar] [CrossRef]
- Johansson, I.; Weik, N. Strategic assessment of railway station capacity. Further development of a UIC 406-based approach considering timetable uncertainty. In Proceedings of the 9th International Conference on Railway Operations Modelling and Analysis (ICROMA), RailBeijing, Beijing, China, 3–7 November 2021. [Google Scholar]
- Robinson, S. Successful Simulation: A Practical Approach to Simulation Projects; McGraw-Hill Book Company Limited: London, UK, 1994. [Google Scholar]
- Gamerman, D.L. Markov Chain Monte Carlo; Chapman and Hall/CRC: New York, NY, USA, 2006. [Google Scholar]
- Kontaxi, E.; Ricci, S. Railway capacity analysis: Methodological framework and harmonization perspectives. In Proceedings of the 12th World Conference on Transportation Research, Surabaya, Indonesia, 22–23 July 2010. [Google Scholar]
- Lindfeldt, A.; Sipilä, H. Simulation of freight train operations with departures ahead of schedule. Trans. Built Environ. 2014, 135, 239–249. [Google Scholar]
- Adamko, N.; Klima, V. Optimisation of railway terminal design and operations using Villon generic simulation model. Transport 2008, 23, 335–340. [Google Scholar] [CrossRef]
- De Fabris, S.; Medeossi, G.; Montanaro, G. Improving the microscopic simulation of railway networks. Comput. Railw. XVI WIT Press 2018, 181, 199–211. [Google Scholar]
- Nash, A.; Huerlimann, D. Railroad simulation using OpenTrack. WIT Trans. Built Environ. 2004, 74, 10. [Google Scholar]
- Singh, P.; Dulebenets, M.A.; Pasha, J.; Gonzalez, E.D.S.; Lau, Y.Y.; Kampmann, R. Deployment of autonomous trains in rail transportation: Current trends and existing challenges. IEEE Access 2021, 9, 91427–91461. [Google Scholar] [CrossRef]
- Krzykowska-Piotrowska, K.; Piotrowski, M.; Organiściak-Krzykowska, A.; Kwiatkowska, E. Maritime or Rail: Which of these will save the planet? EU Macro-Regional strategies and reality. Sustainability 2022, 14, 3555. [Google Scholar] [CrossRef]
- Caramuta, C. A Methodology for the Optimization and Evaluation of Railway Capacity in a Multi-Actor Context: The Case Study of the Port of Trieste; ICAR/05 TRASPORTI; Università Degli Studi di Trieste: Trieste, Italy, 2021. [Google Scholar]
- Malavasi, G.; Rotoli, F. Carrying capacity of complex railway nodes. In Proceedings of the International Conference on Applications of Advanced Technologies in Transportation, Athens, Greece, 27–31 May 2008. [Google Scholar]
- Giuliani, L.; Malavasi, G.; Ricci, S. Analisi di un impianto di stazione sulla base del programma di esercizio. Ing. Ferrov. 1989, 10, 572–582. [Google Scholar]
- Singh, P.; Elmi, Z.; Meriga, V.K.; Pasha, J.; Dulebenets, M.A. Internet of Things for sustainable railway transportation: Past, present, and future. Clean. Logist. Supply Chain. 2022, 4, 100065. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kianinejadoshah, A.; Ricci, S. Capacity Assessment in Freight-Passengers Complex Railway Nodes: Trieste Case Study. Infrastructures 2022, 7, 106. https://doi.org/10.3390/infrastructures7080106
Kianinejadoshah A, Ricci S. Capacity Assessment in Freight-Passengers Complex Railway Nodes: Trieste Case Study. Infrastructures. 2022; 7(8):106. https://doi.org/10.3390/infrastructures7080106
Chicago/Turabian StyleKianinejadoshah, Atieh, and Stefano Ricci. 2022. "Capacity Assessment in Freight-Passengers Complex Railway Nodes: Trieste Case Study" Infrastructures 7, no. 8: 106. https://doi.org/10.3390/infrastructures7080106
APA StyleKianinejadoshah, A., & Ricci, S. (2022). Capacity Assessment in Freight-Passengers Complex Railway Nodes: Trieste Case Study. Infrastructures, 7(8), 106. https://doi.org/10.3390/infrastructures7080106






