A Review of Numerical Models for Slab-Asphalt Track Railways
Abstract
1. Introduction
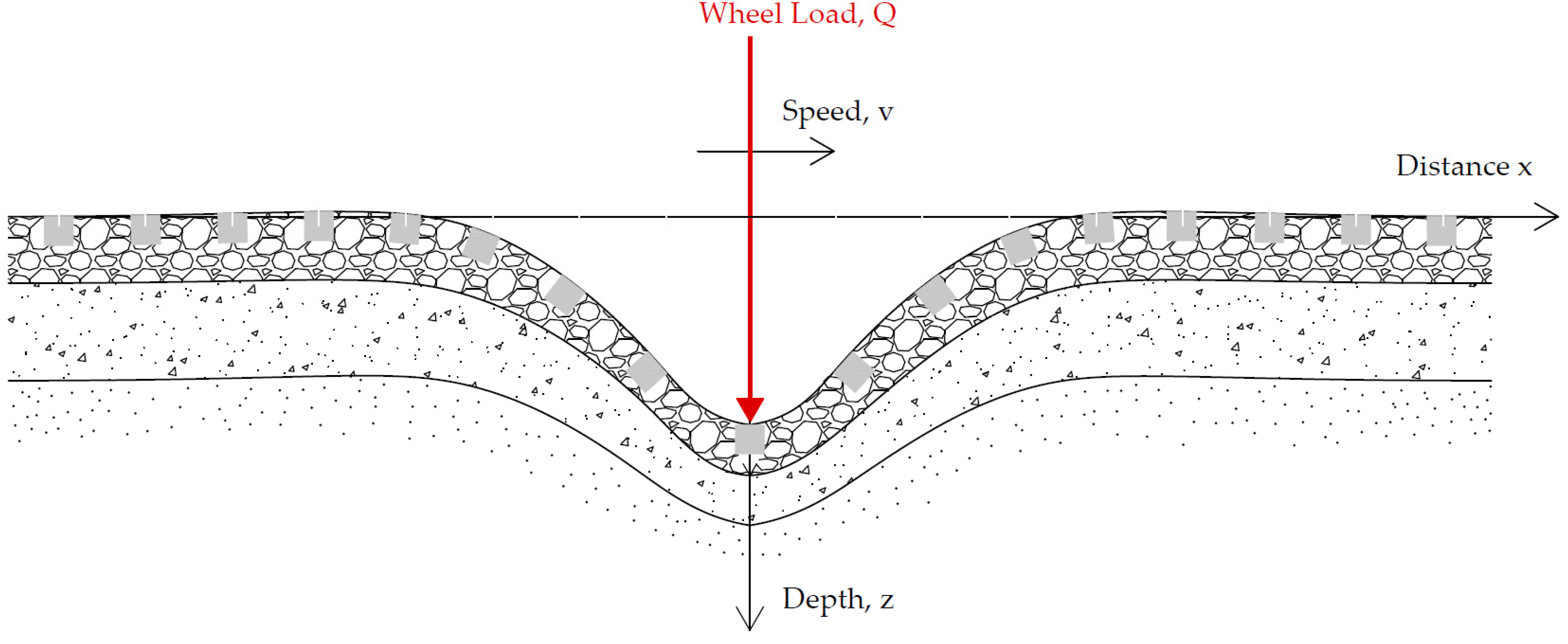
2. Mechanism of Vibration Propagation in Railways
3. The Damping of Vibrations
3.1. Geometrical Damping
3.2. Material Damping
4. Critical Speed and Resonance Effect
5. Background to Railway Modelling
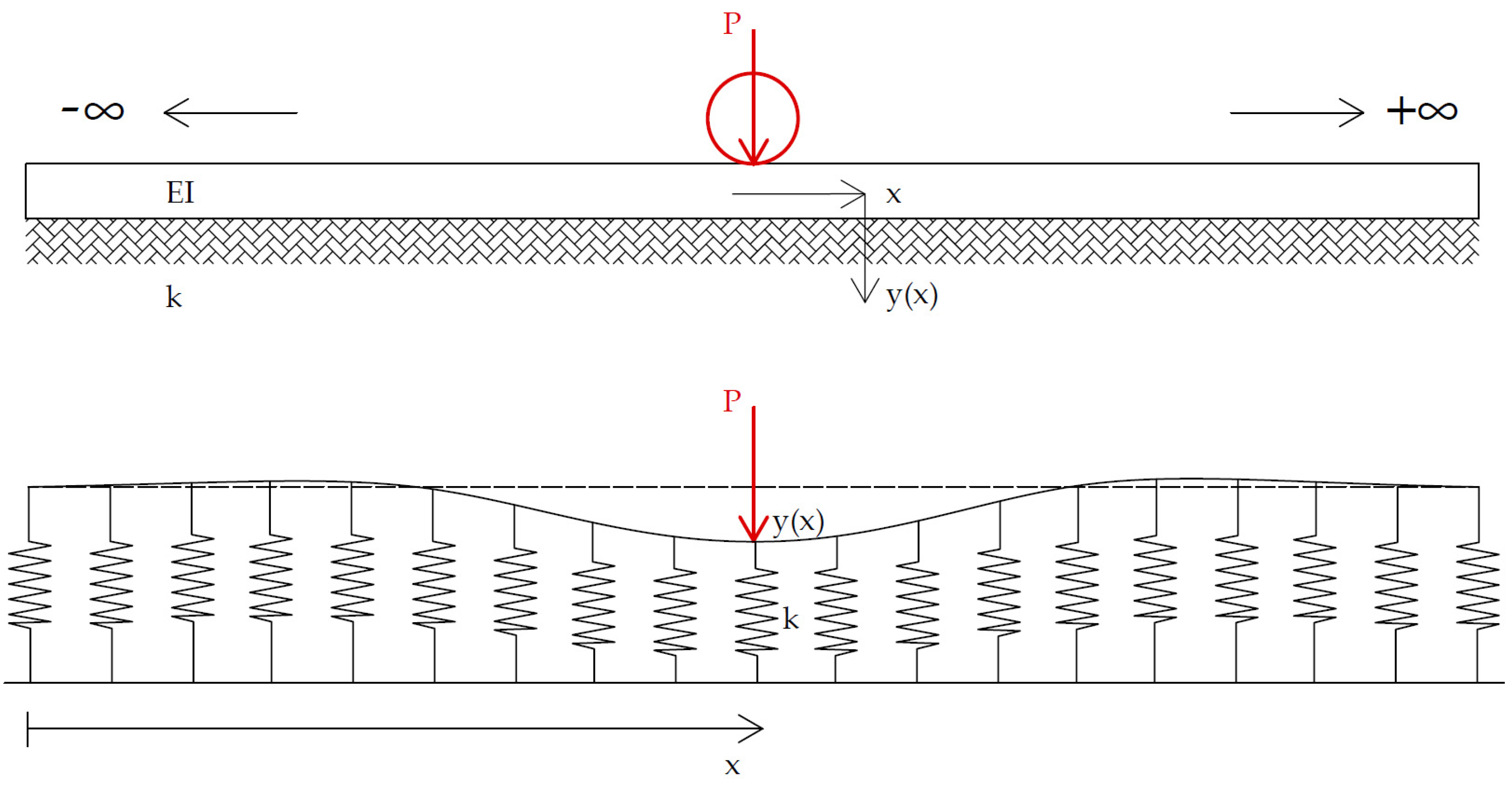
5.1. Analytical Models
5.2. Numerical Models
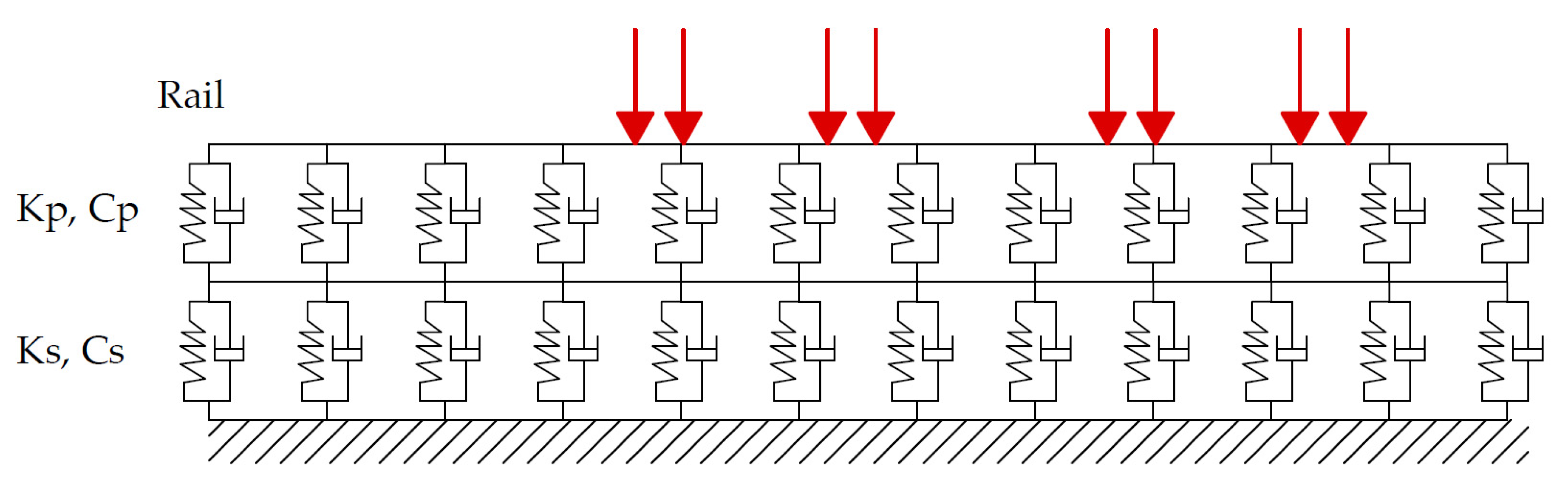
6. The Dynamics of Slab Track Railways
7. Soil Modelling in Train–Track Interaction
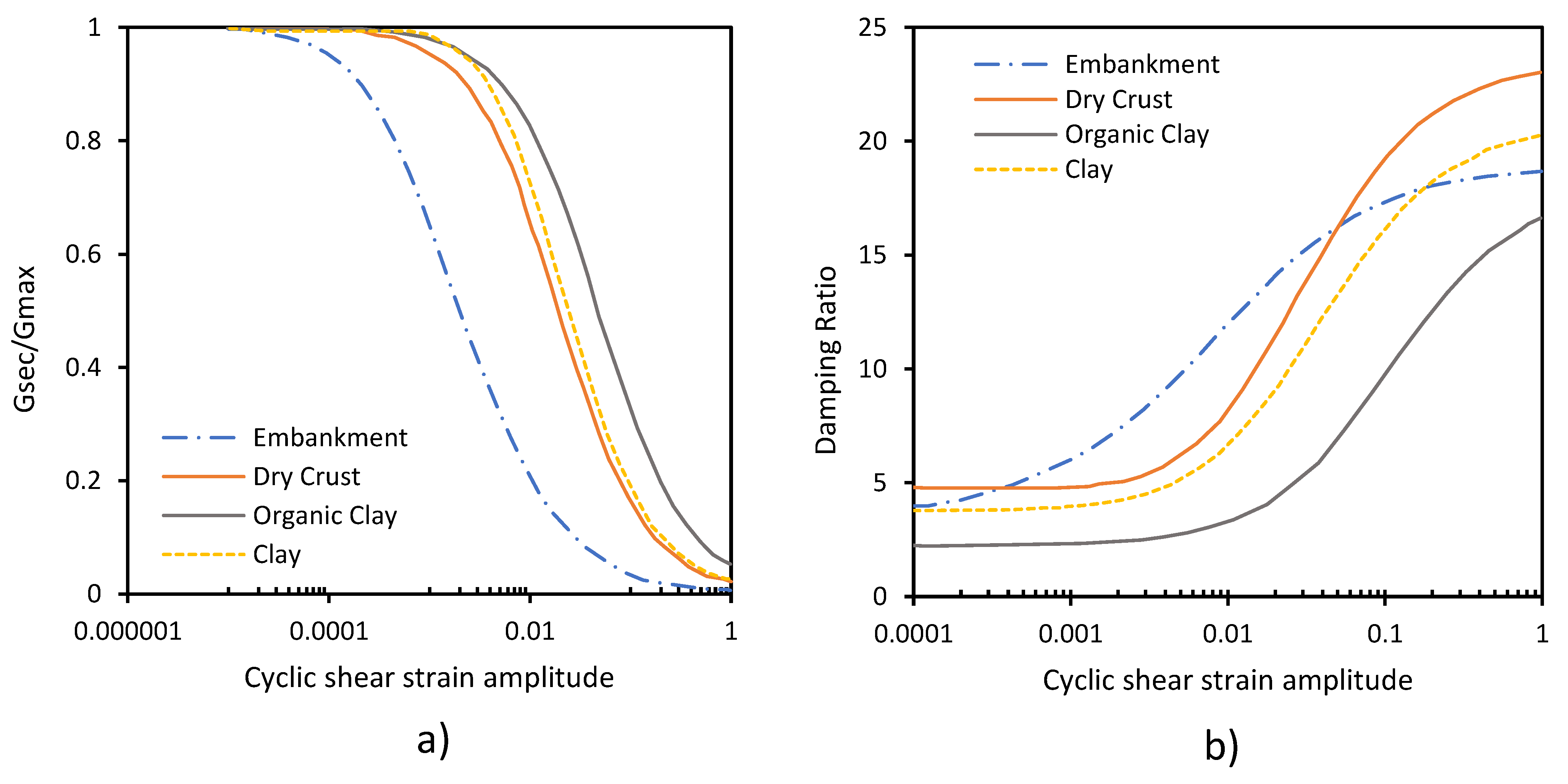
7.1. Equivalent Linear Model
7.2. Constitutive Models
8. Using Asphalt on Railways
9. Discussion and Recommendations
10. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, J.; Bian, X.; Jiang, J. Critical Velocity of High-speed Train Running on Soft Soil and Induced Dynamic Soil Response. Procedia Eng. 2016, 143, 1034–1042. [Google Scholar] [CrossRef]
- Krylov, V.V. Noise and Vibration from High-Speed Trains; ICE Publishing: London, UK, 2001. [Google Scholar] [CrossRef]
- Hu, J.; Bian, X.; Xu, W.; Thompson, D. Investigation into the critical speed of ballastless track. Transp. Geotech. 2019, 18, 142–148. [Google Scholar] [CrossRef]
- Madshus, C.; Kaynia, A.M. High-speed railway lines on soft ground: Dynamic behaviour at critical train speed. J. Sound Vib. 2000, 231, 689–701. [Google Scholar] [CrossRef]
- Costa, P.A.; Colaço, A.; Calçada, R.; Cardoso, A.S. Critical speed of railway tracks. Detailed and simplified approaches. Transp. Geotech. 2015, 2, 30–46. [Google Scholar] [CrossRef]
- Sayeed, M.A.; Shahin, M.A. Three-dimensional numerical modelling of ballasted railway track foundations for high-speed trains with special reference to critical speed. Transp. Geotech. 2016, 6, 55–65. [Google Scholar] [CrossRef]
- Shih, J.Y.; Thompson, D.J.; Zervos, A. The influence of soil nonlinear properties on the track/ground vibration induced by trains running on soft ground. Transp. Geotech. 2017, 11, 1–16. [Google Scholar] [CrossRef]
- Freudenstein, S.; Geisler, K.; Mölter, T.; Mißler, M.; Stolz, C. Ballastless Tracks; John Wiley and Sons: Hoboken, NJ, USA, 2018; ISBN 9783433030738. [Google Scholar]
- Thompson, D. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Hall, L. Simulations and Analyses of Train-induced Ground Vibrations: A Comparative Study of Two-and Three-dimensional Calculations with Actual Measurements. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2000. [Google Scholar]
- Knothe, K.L.; Grassie, S.L. Modelling of Railway Track and Vehicle/Track Interaction at High Frequencies. Int. J. Veh. Mech. Mobil. 1993, 22, 209–262. [Google Scholar] [CrossRef]
- Connolly, D.P. Ground Borne Vibrations from High Speed Trains. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2013. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996; ISBN 0133749436. [Google Scholar]
- Thompson, D. Railway Noise and Vibration; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 9780080451473. [Google Scholar] [CrossRef]
- Kouroussis, G.; Connolly, D.P.; Verlinden, O. Railway-induced ground vibrations—A review of vehicle effects. Int. J. Rail Transp. 2014, 2, 69–110. [Google Scholar] [CrossRef]
- Lombaert, G.; Degrande, G. Ground-borne vibration due to static and dynamic axle loads of InterCity and high-speed trains. J. Sound Vib. 2009, 319, 1036–1066. [Google Scholar] [CrossRef]
- Lamb, H. On Group-Velocity. Proc. Lond. Math. Soc. 1904, 2, 473–479. [Google Scholar] [CrossRef]
- Caughey, T.K. Classical normal modes in damped linear dynamic systems. J. Appl. Mech. Trans. ASME 1960, 27, 269–271. [Google Scholar] [CrossRef]
- Fernández-Ruiz, J.; Miranda, M.; Castro, J.; Medina Rodríguez, L. Improvement of the critical speed in high-speed ballasted railway tracks with stone columns: A numerical study on critical length. Transp. Geotech. 2021, 30, 100628. [Google Scholar] [CrossRef]
- Sunaga, M.; Sekine, E.; Ito, T. Vibration behaviors of roadbed on soft grounds under train load. Q. Rep. Railw. Tech. Res. Inst. 1990, 31, 29–35. [Google Scholar]
- Huang, H.; Chrismer, S. Discrete element modeling of ballast settlement under trains moving at “critical Speeds”. Constr. Build. Mater. 2013, 38, 994–1000. [Google Scholar] [CrossRef]
- Picoux, B.; Le Houédec, D. Diagnosis and prediction of vibration from railway trains. Soil Dyn. Earthq. Eng. 2005, 25, 905–921. [Google Scholar] [CrossRef]
- Krylov, V.V. Generation of ground vibrations by superfast trains. Appl. Acoust. 1995, 44, 149–164. [Google Scholar] [CrossRef]
- Dimitrovová, Z.; Varandas, J.N. Critical velocity of a load moving on a beam with a sudden change of foundation stiffness: Applications to high-speed trains. Comput. Struct. 2009, 87, 1224–1232. [Google Scholar] [CrossRef]
- Auersch, L. The effect of critically moving loads on the vibrations of soft soils and isolated railway tracks. J. Sound Vib. 2008, 310, 587–607. [Google Scholar] [CrossRef]
- Costa, P.A.; Lopes, P.; Cardoso, A.S. Soil shakedown analysis of slab railway tracks: Numerical approach and parametric study. Transp. Geotech. 2018, 16, 85–96. [Google Scholar] [CrossRef]
- Costa, P.A.; Soares, P.; Colaço, A.; Lopes, P.; Connolly, D. Railway critical speed assessment: A simple experimental-analytical approach. Soil Dyn. Earthq. Eng. 2020, 134, 106156. [Google Scholar] [CrossRef]
- Dong, K.; Connolly, D.P.; Laghrouche, O.; Woodward, P.K.; Alves Costa, P. The stiffening of soft soils on railway lines. Transp. Geotech. 2018, 17, 178–191. [Google Scholar] [CrossRef]
- Dong, K.; Connolly, D.P.; Laghrouche, O.; Woodward, P.K.; Alves Costa, P. Non-linear soil behaviour on high speed rail lines. Comput. Geotech. 2019, 112, 302–318. [Google Scholar] [CrossRef]
- El Kacimi, A.; Woodward, P.K.; Laghrouche, O.; Medero, G. Time domain 3D finite element modelling of train-induced vibration at high speed. Comput. Struct. 2013, 118, 66–73. [Google Scholar] [CrossRef]
- Mezher, S.B.; Connolly, D.P.; Woodward, P.K.; Laghrouche, O.; Pombo, J.; Costa, P.A. Railway critical velocity—Analytical prediction and analysis. Transp. Geotech. 2016, 6, 84–96. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Thompson, D.J. A theoretical study on the influence of the track on train-induced ground vibration. J. Sound Vib. 2004, 272, 909–936. [Google Scholar] [CrossRef]
- Takemiya, H. Simulation of track-ground vibrations due to a high-speed train: The case of X-2000 at Ledsgard. J. Sound Vib. 2003, 261, 503–526. [Google Scholar] [CrossRef]
- Kaynia, A.M.; Madshus, C.; Zackrisson, P. Ground Vibration from High-Speed Trains: Prediction and Countermeasure. J. Geotech. Geoenviron. Eng. 2000, 126, 531–537. [Google Scholar] [CrossRef]
- Frýba, L. Vibration of Solids and Structures under Moving Loads; ICE Publishing: London, UK, 1999. [Google Scholar] [CrossRef]
- Timoshenko, S. Method of Analysis of Statical and Dynamical Stresses in Rail. In Proceedings of the 2nd International Congress for Applied Mechanics, Zurich, Switzerland, 12–17 September 1926. [Google Scholar]
- Kenney, J.T. Steady-state vibrations of beam on elastic foundation for moving load. J. Appl. Mech. ASME 1954, 21, 359–364. [Google Scholar] [CrossRef]
- EsveldR, C. Modern Railway Track; MRT-Productions: Zaltbommel, The Netherlands, 2001; ISBN 9080032433. [Google Scholar]
- Krylov, V.V. Effects of Track Properties on Ground Vibrations Generated by High-Speed Trains. Acustica 1998, 84, 78–90. [Google Scholar]
- Massarsch, K.R.; Fellenius, B.H. Ground vibrations induced by impact pile driving. In Proceedings of the Sixth International Conference in Case Histories in Geotechnical Engineering, Arlington, VA, USA, 11–16 August 2008. [Google Scholar]
- Yang, Y.B.; Hung, H.H.; Chang, D.W. Train-induced wave propagation in layered soils using finite/infinite element simulation. Soil Dyn. Earthq. Eng. 2003, 23, 263–278. [Google Scholar] [CrossRef]
- Connolly, D.P.; Dong, K.; Alves Costa, P.; Soares, P.; Woodward, P.K. High speed railway ground dynamics: A multi-model analysis. Int. J. Rail Transp. 2020, 8, 324–346. [Google Scholar] [CrossRef]
- Nguyen, K.; Goicolea, J.M.; Galbadon, F. Dynamic effect of high speed railway traffic loads on the ballast track settlement. In Proceedings of the Conference of Numerical Methods in Engineering, Coimbra, Portugal, 14–17 June 2011. [Google Scholar]
- Bosso, N.; Gugliotta, A.; Zampieri, N. A Comprehensive Strategy to Estimate Track Condition and its Evolution. Int. J. Railw. Technol. 2012, 1, 1–19. [Google Scholar] [CrossRef]
- Indraratna, B.; Nimbalkar, S.; Rujikiatkamjorn, C. Modernisation of Rail Tracks for Higher Speeds and Greater Freight. Int. J. Railw. Technol. 2013, 2, 1–20. [Google Scholar] [CrossRef]
- Fortunato, E.; Paixão, A.; Calçada, R. Railway Track Transition Zones: Design, Construction, Monitoring and Numerical Modelling. Int. J. Railw. Technol. 2013, 2, 33–58. [Google Scholar] [CrossRef]
- Momoya, Y.; Nakamura, T.; Fuchigami, S.; Takahashi, T. Improvement of Degraded Ballasted Track to Reduce Maintenance Work. Int. J. Railw. Technol. 2016, 5, 31–54. [Google Scholar] [CrossRef]
- Woodward, P.K.; Laghrouche, O.; Mezher, S.B.; Connolly, D.P. Application of Coupled Train-Track Modelling of Critical Speeds for High-Speed Trains using Three-Dimensional Non-Linear Finite Elements. Int. J. Railw. Technol. 2015, 4, 1–35. [Google Scholar] [CrossRef]
- Grassie, S.; Gregory, R.; Johnson, K. The dynamic response of railway track to high frequency lateral excitation. J. Mech. Eng. Sci. 1982, 24, 91–95. [Google Scholar] [CrossRef]
- Grassie, S.; Gregory, R.; Johnson, K. The dynamic response of railway track to high frequency longitudinal excitation. J. Mech. Eng. Sci. 1982, 24, 97–102. [Google Scholar] [CrossRef]
- Mathews, P.M. Vibrations of a beam on elastic foundation. Z. Angew. Math. Mech. 1959, 39, 13–19. [Google Scholar] [CrossRef]
- Mathews, P. Vibrations of a beam on elastic foundation II. Z. Angew. Math. Mech. 1958, 38, 105–115. [Google Scholar] [CrossRef]
- Jezequel, L. Response of periodic systems to a moving load. J. Appl. Mech. Trans. ASME 1981, 48, 613–618. [Google Scholar] [CrossRef]
- Timoshenko, S.; Young, D.; Weaver, J. Vibration Problems in Engineering, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Warburton, G. The Dynamical Behavior of Structures, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1976; ISBN 0080203647. [Google Scholar] [CrossRef]
- Cai, C.W.; Cheung, Y.K.; Chan, H.C. Dynamic response of infinite continuous beams subjected to a moving force—An exact method. J. Sound Vib. 1988, 123, 461–472. [Google Scholar] [CrossRef]
- Lei, X. High Speed Railway Track Dynamics: Models, Algorithms and Applications; Springer: Cham, Switzerland, 2016; ISBN 9789811020391. [Google Scholar] [CrossRef]
- Boresi, A.P.; Schmidt, R.J. Advanced Mechanics of Materials, 6th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003; ISBN 9780471438816. [Google Scholar]
- Kerr, A.D. Fundamentals of Railway Track Engineering; Simmons Boardman Publishing Co.: New York, NY, USA, 2003; ISBN 9780911382402. [Google Scholar]
- Hussein, M.F.M.; Hunt, H.E.M. Modelling of floating-slab tracks with continuous slabs under oscillating moving loads. J. Sound Vib. 2006, 297, 37–54. [Google Scholar] [CrossRef]
- Kuo, C.M.; Huang, C.H.; Chen, Y.Y. Vibration characteristics of floating slab track. J. Sound Vib. 2008, 317, 1017–1034. [Google Scholar] [CrossRef]
- Lombaert, G.; Degrande, G.; Vanhauwere, B.; Vandeborght, B.; François, S. The control of ground-borne vibrations from railway traffic by means of continuous floating slabs. J. Sound Vib. 2006, 297, 946–961. [Google Scholar] [CrossRef]
- Kouroussis, G.; Verlinden, O.; Conti, C. Finite-Dynamic Model for Infinite Media: Corrected Solution of Viscous Boundary Efficiency. J. Eng. Mech. 2011, 137, 509–511. [Google Scholar] [CrossRef]
- Shih, J.Y.; Thompson, D.J.; Zervos, A. The effect of boundary conditions, model size and damping models in the finite element modelling of a moving load on a track/ground system. Soil Dyn. Earthq. Eng. 2016, 89, 12–27. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite Dynamic Model for Infinite Media. J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar] [CrossRef]
- Zhai, W.; Cai, Z. Dynamic interaction between a lumped mass vehicle and a discretely supported continuous rail track. Comput. Struct. 1997, 63, 987–997. [Google Scholar] [CrossRef]
- Yang, L.A.; Powrie, W.; Priest, J.A. Dynamic stress analysis of a ballasted railway track bed during train passage. J. Geotech. Geoenviron. Eng. 2009, 135, 680–689. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Hung, H.-H. A 2.5D finite/infinite element approach for modelling visco-elastic bodies subjected to moving loads. Int. J. Numer. Methods Eng. 2001, 51, 1317–1336. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Thompson, D.J. Prediction of ground vibration from trains using the wavenumber finite and boundary element methods. J. Sound Vib. 2006, 293, 575–586. [Google Scholar] [CrossRef]
- Lombaert, G.; Degrande, G.; Kogut, J.; François, S. The experimental validation of a numerical model for the prediction of railway induced vibrations. J. Sound Vib. 2006, 297, 512–535. [Google Scholar] [CrossRef]
- Bian, X.C.; Chen, Y.M.; Hu, T. Numerical simulation of high-speed train induced ground vibrations using 2.5D finite element approach. Sci. China Ser. G Phys. Mech. Astron. 2008, 51, 632. [Google Scholar] [CrossRef]
- Costa, P.A.; Calçada, R.; Cardoso, A.S. Track-ground vibrations induced by railway traffic: In-situ measurements and validation of a 2.5D FEM-BEM model. Soil Dyn. Earthq. Eng. 2012, 32, 111–128. [Google Scholar] [CrossRef]
- De Abreu Corrêa, L.; Quezada, J.C.; Cottereau, R.; d’Aguiar, S.C.; Voivret, C. Randomly-fluctuating heterogeneous continuum model of a ballasted railway track. Comput. Mech. 2017, 60, 845–861. [Google Scholar] [CrossRef]
- Galvín, P.; Romero, A.; Domínguez, J. Fully three-dimensional analysis of high-speed traintracksoil-structure dynamic interaction. J. Sound Vib. 2010, 329, 5147–5163. [Google Scholar] [CrossRef]
- Varandas, J.N.; Hölscher, P.; Silva, M.A.G. Dynamic behaviour of railway tracks on transitions zones. Comput. Struct. 2011, 89, 1468–1479. [Google Scholar] [CrossRef]
- Olivier, B.; Connolly, D.P.; Alves Costa, P.; Kouroussis, G. The effect of embankment on high speed rail ground vibrations. Int. J. Rail Transp. 2016, 4, 229–246. [Google Scholar] [CrossRef]
- Hall, L. Simulations and analyses of train-induced ground vibrations in finite element models. Soil Dyn. Earthq. Eng. 2003, 23, 403–413. [Google Scholar] [CrossRef]
- Cai, Z.; Raymond, G.P. Modelling the dynamic response of railway track to wheel/rail impact loading. Struct. Eng. Mech. 1994, 2, 95–112. [Google Scholar] [CrossRef]
- Kouroussis, G.; Verlinden, O.; Conti, C. Ground propagation of vibrations from railway vehicles using a finite/infinite-element model of the soil. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 405–413. [Google Scholar] [CrossRef]
- Connolly, D.; Giannopoulos, A.; Forde, M.C. Numerical modelling of ground borne vibrations from high speed rail lines on embankments. Soil Dyn. Earthq. Eng. 2013, 46, 13–19. [Google Scholar] [CrossRef]
- Poveda, E.; Yu, R.C.; Lancha, J.C.; Ruiz, G. A numerical study on the fatigue life design of concrete slabs for railway tracks. Eng. Struct. 2015, 100, 455–467. [Google Scholar] [CrossRef]
- Costa, P.A.; Calçada, R.; Cardoso, A.S.; Bodare, A. Influence of soil non-linearity on the dynamic response of high-speed railway tracks. Soil Dyn. Earthq. Eng. 2010, 30, 221–235. [Google Scholar] [CrossRef]
- Di Mascio, P.; Loprencipe, G.; Moretti, L. Competition in rail transport: Methodology to evaluate economic impact of new trains on track. In Proceedings of the 3rd International Conference on Tranportation Infrastructure, ICTI 2014—Sustainability, Eco-Efficiency and Conservation in Transportation Infrastructure Asset Management, Pisa, Italy, 22–25 April 2014. [Google Scholar]
- Ando, K.; Sunaga, M.; Aoki, H.; Haga, O. Development of slab tracks for Hokuriku Shinkansen line. Q. Rep. Railw. Tech. Res. Inst. 2001, 42, 35–41. [Google Scholar] [CrossRef]
- Kece, E.; Reikalas, V.; DeBold, R.; Ho, C.L.; Robertson, I.; Forde, M.C. Evaluating ground vibrations induced by high-speed trains. Transp. Geotech. 2019, 20, 100236. [Google Scholar] [CrossRef]
- Zhao, P.; Ding, C.; Guo, L.; Zhang, Y.; Liu, X. A prototype fatigue test for slab track subjected to the coupling action of wheel load, temperature variation, and water erosion. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 566–579. [Google Scholar] [CrossRef]
- Sainz-Aja, J.; Pombo, J.; Tholken, D.; Carrascal, I.; Polanco, J.; Ferreño, D.; Casado, J.; Diego, S.; Perez, A.; Filho, J.E.A.; et al. Dynamic calibration of slab track models for railway applications using full-scale testing. Comput. Struct. 2020, 228, 106180. [Google Scholar] [CrossRef]
- Wang, M.; Cai, C.; Zhu, S.; Zhai, W. Experimental study on dynamic performance of typical nonballasted track systems using a full-scale test rig. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 470–481. [Google Scholar] [CrossRef]
- Malmborg, J.; Persson, P.; Persson, K. Effects of modeling strategies for a slab track on predicted ground vibrations. Soil Dyn. Earthq. Eng. 2020, 136, 106254. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, S.; Zhai, W. Theoretical modelling of a vehicle-slab track coupled dynamics system considering longitudinal vibrations and interface interactions. Veh. Syst. Dyn. 2020, 59, 1313–1334. [Google Scholar] [CrossRef]
- Lou, P.; Gong, K.; Zhao, C.; Xu, Q.; Luo, R.K. Dynamic Responses of Vehicle-CRTS III Slab Track System and Vehicle Running Safety Subjected to Uniform Seismic Excitation. Shock Vib. 2019, 2019, 5308209. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Yang, W. Dynamics shakedown analysis of slab track substructures with reference to critical speed. Soil Dyn. Earthq. Eng. 2018, 106, 1–13. [Google Scholar] [CrossRef]
- He, Q.; Cai, C.; Zhu, S.; Zhang, J.; Zhai, W. Dynamic performance of low vibration slab track on shared high-speed passenger and freight railway. Transport 2018, 33, 669–678. [Google Scholar] [CrossRef]
- Liu, S.; Chen, X.; Ma, Y.; Yang, J.; Cai, D.; Yang, G. Modelling and in-situ measurement of dynamic behavior of asphalt supporting layer in slab track system. Constr. Build. Mater. 2019, 228, 116776. [Google Scholar] [CrossRef]
- Liu, S.; Chen, X.; Yang, J.; Cai, D.; Yang, G. Numerical study and in-situ measurement of temperature features of asphalt supporting layer in slab track system. Constr. Build. Mater. 2020, 233, 117343. [Google Scholar] [CrossRef]
- Li, T.; Su, Q.; Kaewunruen, S. Influences of piles on the ground vibration considering the train-track-soil dynamic interactions. Comput. Geotech. 2020, 120, 103455. [Google Scholar] [CrossRef]
- Malmborg, J.; Persson, K.; Persson, P. Evaluating the effect of vibration isolation mats on train-induced ground vibrations. In Proceedings of the 7th International Conference on Structural Engineering, Mechanics and Computation—Advances in Engineering Materials, Structures and Systems: Innovations, Mechanics and Applications, Cape Town, South Africa, 2–4 September 2019. [Google Scholar] [CrossRef]
- Xin, T.; Ding, Y.; Wang, P.; Gao, L. Application of rubber mats in transition zone between two different slab tracks in high-speed railway. Constr. Build. Mater. 2020, 243, 118219. [Google Scholar] [CrossRef]
- Real, T.; Zamorano, C.; Hernández, C.; García, J.A.; Real, J.I. Static and dynamic behavior of transitions between different railway track typologies. KSCE J. Civ. Eng. 2016, 20, 1356–1364. [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, Z.; Shi, Z. Vibration Reduction Performance of a Periodic Layered Slab Track. In Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Duong, T.V.; Cui, Y.J.; Tang, A.M.; Dupla, J.C.; Canou, J.; Calon, N.; Robinet, A. Investigating the mud pumping and interlayer creation phenomena in railway sub-structure. Eng. Geol. 2014, 171, 45–58. [Google Scholar] [CrossRef]
- Huang, J.; Su, Q.; Wang, W.; Phong, P.D.; Liu, K. Field investigation and full-scale model testing of mud pumping and its effect on the dynamic properties of the slab track–subgrade interface. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 802–816. [Google Scholar] [CrossRef]
- Nsabimana, E.; Jung, Y.H. Dynamic subsoil responses of a stiff concrete slab track subjected to various train speeds: A critical velocity perspective. Comput. Geotech. 2015, 69, 7–21. [Google Scholar] [CrossRef]
- Beresnev, I.A.; Wen, K.-L. Nonlinear soil response—A reality? Bull. Seismol. Soc. Am. 1996, 86, 964–1978. [Google Scholar]
- Zhang, J.; Andrus, R.D.; Juang, C.H. Normalized Shear Modulus and Material Damping Ratio Relationships. J. Geotech. Geoenviron. Eng. 2005, 131, 453–464. [Google Scholar] [CrossRef]
- Shankar Kumar, S.; Murali Krishna, A.; Dey, A. Parameters Influencing Dynamic Soil Properties: A Review Treatise. Int. J. Innov. Res. Sci. 2014, 3, 47–60. [Google Scholar]
- Thach, P.N.; Liu, H.L.; Kong, G.Q. Vibration analysis of pile-supported embankments under high-speed train passage. Soil Dyn. Earthq. Eng. 2013, 55, 92–99. [Google Scholar] [CrossRef]
- Freitas da Cunha, J.P. Modelling of Ballasted Railway Tracks for High-Speed Trains. Ph.D. Thesis, University of Minho, Braga, Portugal, 2013. [Google Scholar]
- Çelebi, E.; Kirtel, O. Non-linear 2-D FE modeling for prediction of screening performance of thin-walled trench barriers in mitigation of train-induced ground vibrations. Constr. Build. Mater. 2013, 42, 122–131. [Google Scholar] [CrossRef]
- Çelebi, E.; Göktepe, F. Non-linear 2-D FE analysis for the assessment of isolation performance of wave impeding barrier in reduction of railway-induced surface waves. Constr. Build. Mater. 2012, 36, 1–13. [Google Scholar] [CrossRef]
- Ruiz, J.F.; Rodríguez, L.M. Application of an advanced soil constitutive model to the study of railway vibrations in tunnels through 2D numerical models: A real case in Madrid (Spain). Rev. Constr. 2015, 14, 55–63. [Google Scholar] [CrossRef]
- Radampola, S.S.; Gurung, N.; McSweeney, T.; Dhanasekar, M. Evaluation of the properties of railway capping layer soil. Comput. Geotech. 2008, 35, 719–728. [Google Scholar] [CrossRef]
- Sol-Sánchez, M.; Thom, N.H.; Moreno-Navarro, F.; Rubio-Gámez, M.C.; Airey, G.D. A study into the use of crumb rubber in railway ballast. Constr. Build. Mater. 2015, 75, 19–24. [Google Scholar] [CrossRef]
- Indraratna, B.; Salim, W.; Rujikiatkamjorn, C. Advanced Rail Geotechnology—Ballasted Track; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9780203815779. [Google Scholar] [CrossRef]
- Sol-Sánchez, M.; Moreno-Navarro, F.; Rubio-Gámez, M.C. The use of deconstructed tires as elastic elements in railway tracks. Materials 2014, 7, 5903–5919. [Google Scholar] [CrossRef] [PubMed]
- Sol-Sánchez, M.; Pirozzolo, L.; Moreno-Navarro, F.; Rubio-Gámez, M.C. A study into the mechanical performance of different configurations for the railway track section: A laboratory approach. Eng. Struct. 2016, 119, 13–23. [Google Scholar] [CrossRef]
- Rose, J.G. Selected in-track applications and performances of hot-mix asphalt trackbeds. In Proceedings of the 2013 Joint Rail Conference, JRC 2013, Knoxville, TN, USA, 15–18 April 2013. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, J.W.; Park, D.W.; Vo, H.V. Evaluation of asphalt concrete mixtures for railway track. Constr. Build. Mater. 2014, 73, 13–18. [Google Scholar] [CrossRef]
- Di Mino, G.; Di Liberto, M.; Maggiore, C.; Noto, S. A Dynamic Model of Ballasted Rail Track with Bituminous Sub-Ballast Layer. Procedia Soc. Behav. Sci. 2012, 53, 366–378. [Google Scholar] [CrossRef]
- Fang, M.; Cerdas, S.F.; Qiu, Y. Numerical determination for optimal location of sub-track asphalt layer in high-speed rails. J. Mod. Transp. 2013, 21, 103–110. [Google Scholar] [CrossRef][Green Version]
- Rose, J.G.; Souleyrette, R. Hot-mix asphalt (bituminous) railway trackbeds: In-track tests, evaluations, and performances—A global perspective: Part I—Introduction to asphalt trackbeds and international applications and practices. In Proceedings of the 3rd International Conference on Tranportation Infrastructure, ICTI 2014—Sustainability, Eco-Efficiency and Conservation in Transportation Infrastructure Asset Management, Pisa, Italy, 22–25 April 2014. [Google Scholar]
- Rose, J.G.; Bryson, L.S. Hot mix asphalt railway trackbeds: Trackbed materials, performance evaluations ans significant implications. In Proceedings of the International Conference on Perpetual Pavements, Columbus, OH, USA, 30 September–2 October 2009. [Google Scholar]
- Rose, J.; Teixeira, P.; Ridgway, N. Utilization of Asphalt/Bituminous Layers and Coatings in Railway Trackbeds: A Compendium of International Applications. In Proceedings of the 2010 Joint Rail Conference, Urbana, IL, USA, 27–29 April 2010; Volume 1. [Google Scholar] [CrossRef]
- Rose, J.G.; Teixeira, P.F.; Veit, P. International design practices, applications, amd performances pf asphalt/bituminous railway trackbeds. In Proceedings of the International Symposium Railway Geotechnical Engineering (GeoRail 2011), Paris, France, 19–20 May 2011. [Google Scholar]
- Huang, Y.H.; Rose, J.G.; Khoury, C.J. Hot-mix asphalt railroad trackbeds. Transp. Res. Rec. 1986, 1095, 102–110. [Google Scholar]
- Hensley, M.; Rose, J.G. Design, construction and performance of Hot Mix Asphalt for railway trackbeds. In Proceedings of the 1st World of Asphalt Pavements International Conference, Sydney, Australia, 20–24 February 2000. [Google Scholar]
- Yu, Z.; Connolly, D.P.; Woodward, P.K.; Laghrouche, O. Settlement behaviour of hybrid asphalt-ballast railway tracks. Constr. Build. Mater. 2019, 208, 808–817. [Google Scholar] [CrossRef]
- Lee, S.H.; Vo, H.V.; Park, D.W. Investigation of asphalt track behavior under cyclic loading: Full-scale testing and numerical simulation. J. Test. Eval. 2018, 46, 20160554. [Google Scholar] [CrossRef]
- Fang, M.; Qiu, Y.; Rose, J.G.; West, R.C.; Ai, C. Comparative analysis on dynamic behavior of two HMA railway substructures. J. Mod. Transp. 2011, 19, 26–34. [Google Scholar] [CrossRef]
- Fang, M.; Cerdas, S.F. Theoretical analysis on ground vibration attenuation using sub-track asphalt layer in high-speed rails. J. Mod. Transp. 2015, 23, 214–219. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, D.W.; Vo, H.V.; Dessouky, S. Asphalt mixture for the first asphalt concrete directly fastened track in Korea. Adv. Mater. Sci. Eng. 2015, 2015, 701940. [Google Scholar] [CrossRef]
- Lee, S.H.; Choi, Y.T.; Lee, H.M.; Park, D.W. Performance evaluation of directly fastened asphalt track using a full-scale test. Constr. Build. Mater. 2016, 113, 404–414. [Google Scholar] [CrossRef]
- Lee, S.H.; Eum, K.Y.; Ho Minh Le, T.; Park, D.W. Evaluation on mechanical behavior of asphalt concrete trackbed with slab panel using full-scale static and dynamic load test. Constr. Build. Mater. 2021, 276, 122207. [Google Scholar] [CrossRef]
- Roberts, F.L.; Kandhal, P.S.; Braown, E.R. Hot Mix Asphalt Materials, Mixture Design, and Constrution; National Center for Asphalt Technology: Auburn, AL, USA, 1996. [Google Scholar]
- Jadidi, K.; Esmaeili, M.; Kalantari, M.; Khalili, M.; Karakouzian, M. A review of different aspects of applying asphalt and bituminous mixes under a railway track. Materials 2021, 14, 169. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.J.; Zhang, X.L.; Zheng, Q.T.; Wang, L. Simulation and mitigation analysis of ground vibrations induced by high-speed train with three dimensional FEM. Soil Dyn. Earthq. Eng. 2017, 94, 204–214. [Google Scholar] [CrossRef]
- Bian, X.; Jiang, H.; Chang, C.; Hu, J.; Chen, Y. Track and ground vibrations generated by high-speed train running on ballastless railway with excitation of vertical track irregularities. Soil Dyn. Earthq. Eng. 2015, 76, 29–43. [Google Scholar] [CrossRef]
- Indraratna, B.; Ionescu, D.; Christie, H.D. Shear Behavior of Railway Ballast Based on Large-Scale Triaxial Tests. J. Geotech. Geoenviron. Eng. 1998, 124, 439–449. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Y. Dynamic responses of subgrade under double-line high-speed railway. Soil Dyn. Earthq. Eng. 2018, 110, 1–12. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Y. Dynamic vertical displacement for ballastless track-subgrade system under high-speed train moving loads. Soil Dyn. Earthq. Eng. 2020, 129, 105911. [Google Scholar] [CrossRef]
- Tang, Y.; Xiao, S.; Yang, Q. Numerical study of dynamic stress developed in the high speed rail foundation under train loads. Soil Dyn. Earthq. Eng. 2019, 123, 36–47. [Google Scholar] [CrossRef]
- Yang, E.; Wang, K.C.P.; Luo, Q.; Qiu, Y. Asphalt concrete layer to support track slab of high-speed railway. Transp. Res. Rec. 2015, 2505, 6–14. [Google Scholar] [CrossRef]
- Thölken, D.; Abdalla Filho, J.E.; Pombo, J.; Sainz-Aja, J.; Carrascal, I.; Polanco, J.; Esen, A.; Laghrouche, O.; Woodward, P. Three-dimensional modelling of slab-track systems based on dynamic experimental tests. Transp. Geotech. 2021, 31, 100663. [Google Scholar] [CrossRef]
- Ramos, A.; Gomes Correia, A.; Calçada, R.; Alves Costa, P.; Esen, A.; Woodward, P.K.; Connolly, D.P.; Laghrouche, O. Influence of track foundation on the performance of ballast and concrete slab tracks under cyclic loading: Physical modelling and numerical model calibration. Constr. Build. Mater. 2021, 277, 122245. [Google Scholar] [CrossRef]
- Shi, H.; Yu, Z.; Shi, H. An improved method for dynamic modelling of a slab track on a high-speed railway. WIT Trans. Built Environ. 2016, 162, 225–237. [Google Scholar] [CrossRef]
- Ntotsios, E.; Thompson, D.J.; Hussein, M.F.M. A comparison of ground vibration due to ballasted and slab tracks. Transp. Geotech. 2019, 21, 100256. [Google Scholar] [CrossRef]
- Marolt Čebašek, T.; Esen, A.F.; Woodward, P.K.; Laghrouche, O.; Connolly, D.P. Full scale laboratory testing of ballast and concrete slab tracks under phased cyclic loading. Transp. Geotech. 2018, 17, 33–40. [Google Scholar] [CrossRef]
- Esen, A.F.; Woodward, P.K.; Laghrouche, O.; Čebašek, T.M.; Brennan, A.J.; Robinson, S.; Connolly, D.P. Full-scale laboratory testing of a geosynthetically reinforced soil railway structure. Transp. Geotech. 2021, 28, 100526. [Google Scholar] [CrossRef]
- Yao, H.L.; Hu, Z.; Lu, Z.; Zhan, Y.X.; Liu, J. Prediction of Ground Vibration from High Speed Trains Using a Vehicle-Track-Ground Coupling Model. Int. J. Struct. Stab. Dyn. 2016, 16, 1550051. [Google Scholar] [CrossRef]
- Yusupov, B.; Qiu, Y.; Ding, H.; Rahman, A. Temperature and material behaviour effects on dynamic responses of asphalt concrete trackbed. Int. J. Rail Transp. 2020, 8, 66–79. [Google Scholar] [CrossRef]

| Soil Type | P-Wave Velocity (m/s) | S-Wave Velocity (m/s) | Rayleigh-Wave Velocity (m/s) (CR ≈ 0.9 CS) |
|---|---|---|---|
| Water | 1450 | 0 | 0 |
| Glacial till | 600–1800 | 300–600 | 270–540 |
| Dry gravel | 500–1000 | 250–400 | 225–360 |
| Saturated gravel | 1450 | 300–400 | 270–360 |
| Dry sand | 300–600 | 150–200 | 135–180 |
| Saturated sand | 1450 | 150–250 | 135–225 |
| Silts and stiff clays | 1450 | 100–200 | 90–180 |
| Plastic clay | 1450 | 50–100 | 45–90 |
| Organic soils | 1450 | 30–50 | 27–45 |
| Ref. | Ref. | Method Info. | Track Layers | Nonlinear Behaviour | Boundary Conditions | Focus | Model Length | Train Speed (km/h) | Parameters Studied |
|---|---|---|---|---|---|---|---|---|---|
| [3] | (Hu et al., 2019) | 2.5D FEM | R + F + S + CAM +BC + RB + Sub + G | - | - | Critical speed | - | 360 | VerAcc, VerDis, VerStress |
| [85] | (Kece et al., 2019) | 2D FEM | S + CF + E + G | - | IB | The effects of subsoil stiffness, track speed, and track type | - | 150 to 400 | VerDis |
| [87] | (Sainz-Aja et al., 2020) | 3D FEM | R + EVAP + SP + EPDMP + TBS + S + GM + HBL + FPL + Sub | - | FB | Calibration of the slab track model | 2.2 | 160–360 | VerDis, VerAcc |
| [88] | (Wang et al., 2017) | FST | R + RP + S + CAM + SL + Sub | - | - | Dynamic characteristics of different slab tracks | 55.17 | - | VerAcc, VerAcc, TF, TDS, DC |
| [91] | (Lou et al., 2019) | 3D BSDM | R + F + S + SCCL + CL + BL | - | - | Track parameters, seismic intensity, running speed | - | 200 to 350 | VerAcc, VerDis, TStress, DC |
| [93] | (He et al., 2018) | 3D BSDM | R + F + S + GM + RuP + SL + G | - | FB | Optimal modulus of the rubber pad | 5.6 | 160–400 | VerDis, CStress, TStress, VerAcc, |
| [94] | (Liu et al., 2019) | 3D FEM | R + S + SCCL + BP + US + LS + Sub + G | - | VB | In-depth study of asphalt layer | 16.8 | 350 | VerStress, LatStress, LongStress, VerDis, VerAcc |
| [95] | (Liu et al., 2020) | 3D FEM | R + F + S + SCCL + BP + ASL + Sub | - | AB | Temperature features of asphalt layer | 5.6 | - | T, SR, WS |
| [133] | (Lee et al., 2021) | FST | R + RP + S + GT + SB + US + LS | - | - | Effect of different thickness of asphalt layer | 20 | 140 | SP, VerDis, TS, SL, TStrain, Cstrain |
| [136] | (Feng et al., 2017) | 3D FEM | R + S + CAM + BC + SU + LS + G + BB | - | VB | The effects of subgrade treatment and ground vibration | 70 | 300–360–667 | VerDis, LongDis, VerAcc |
| [137] | (Bian et al., 2015) | 2.5D FEM | R + F + S + CAM + BC + RB + Sub + E+ + SCM +SC + Si | - | FB | Track irregularities | - | 100–700 | VerDis, VerAcc |
| [139] | (Chen and Zhou, 2018) | 3D FEM | R + RP + S + CAM + SL + US + LS + E + G | - | VB | Dynamic responses of different train speed and line patterns | - | 250–300–360 | Vertical stress, VerDis, VerAcc, VerAcc |
| [140] | (Chen and Zhou, 2020) | 3D FEM | R + F + S + CAM + SL + US + LS + E + G | - | FB | Effect of subgrade, foundation modulus, and fastener stiffness | 10 | 360 | VerDis |
| [141] | (Tang, Xiao and Yang, 2019) | 3D FEM | R + F + S + CAM + BC + RB + US + LS + Sub + GC | ELM | IB | Geosynthetic-reinforced pile foundation | 58 | 200 to 550 | VerDis, DS, VerAcc |
| [142] | (Yang et al., 2015) | 3D FEM | S + BC + ASL + US + LS + Sub | - | FB | Material composition and mechanical response of asphalt layer | - | - | TransStress, VerStress |
| [143] | (Thölken et al., 2021) | 3D FEM | R + RP + S + GM + HBL + FPL + Sub | - | - | Validation of experimental results | 2.2 | - | VerDis, VerStress |
| [144] | (Ramos et al., 2021) | 3D FEM | R + RP + S + GM + HBL + FPL + Sub | - | FB | Validation of experimental results | 6.2 | - | VerDis, VerAcc |
| [145] | (Shi, Yu and Shi, 2016) | 2D BSDM | R + RP + F + S + CAM + TP + SL+ Sub | - | - | CAM deterioration and vibration responses | - | 300 | VerDis, VerAcc |
| [146] | (Ntotsios, Thompson and Hussein, 2019) | 3D SAM | R + RP + S + HBL + G | - | - | Comparison of ground vibration due to ballasted and slab tracks | - | 120–300 | VerDis, VerVel |
| [147] | (Marolt Čebašek et al., 2018) | FST | R + RP + S + GM + HBL + FPL + Sub | - | - | Long-term settlement performance | 6.2 | - | VerDis, CS |
| [148] | (Esen et al., 2021) | FST | R + RP + S + GM + HBL + FPL + Sub with geogrid | - | - | Geosynthetically reinforced soil performance | 6.2 | - | VerDis, CS |
| [149] | (Yao et al., 2016) | SAM | R + RP + S + US + Sub + G | - | - | Ground vibration | - | 70 to 432 | VerDis, VerAcc, VerStress |
| [150] | (Yusupov et al., 2020) | 3D FEM | R + RP + S + CAM + PCC + US + LS + Sub | - | IB | Effects of different temperatures | 80 | 350 | VerDis, LongDis, TStrain |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atalan, M.; Prendergast, L.J.; Grizi, A.; Thom, N. A Review of Numerical Models for Slab-Asphalt Track Railways. Infrastructures 2022, 7, 59. https://doi.org/10.3390/infrastructures7040059
Atalan M, Prendergast LJ, Grizi A, Thom N. A Review of Numerical Models for Slab-Asphalt Track Railways. Infrastructures. 2022; 7(4):59. https://doi.org/10.3390/infrastructures7040059
Chicago/Turabian StyleAtalan, Mucahit, Luke J. Prendergast, Athina Grizi, and Nick Thom. 2022. "A Review of Numerical Models for Slab-Asphalt Track Railways" Infrastructures 7, no. 4: 59. https://doi.org/10.3390/infrastructures7040059
APA StyleAtalan, M., Prendergast, L. J., Grizi, A., & Thom, N. (2022). A Review of Numerical Models for Slab-Asphalt Track Railways. Infrastructures, 7(4), 59. https://doi.org/10.3390/infrastructures7040059









