BAT Algorithm-Based ANN to Predict the Compressive Strength of Concrete—A Comparative Study
Abstract
1. Introduction
2. Background
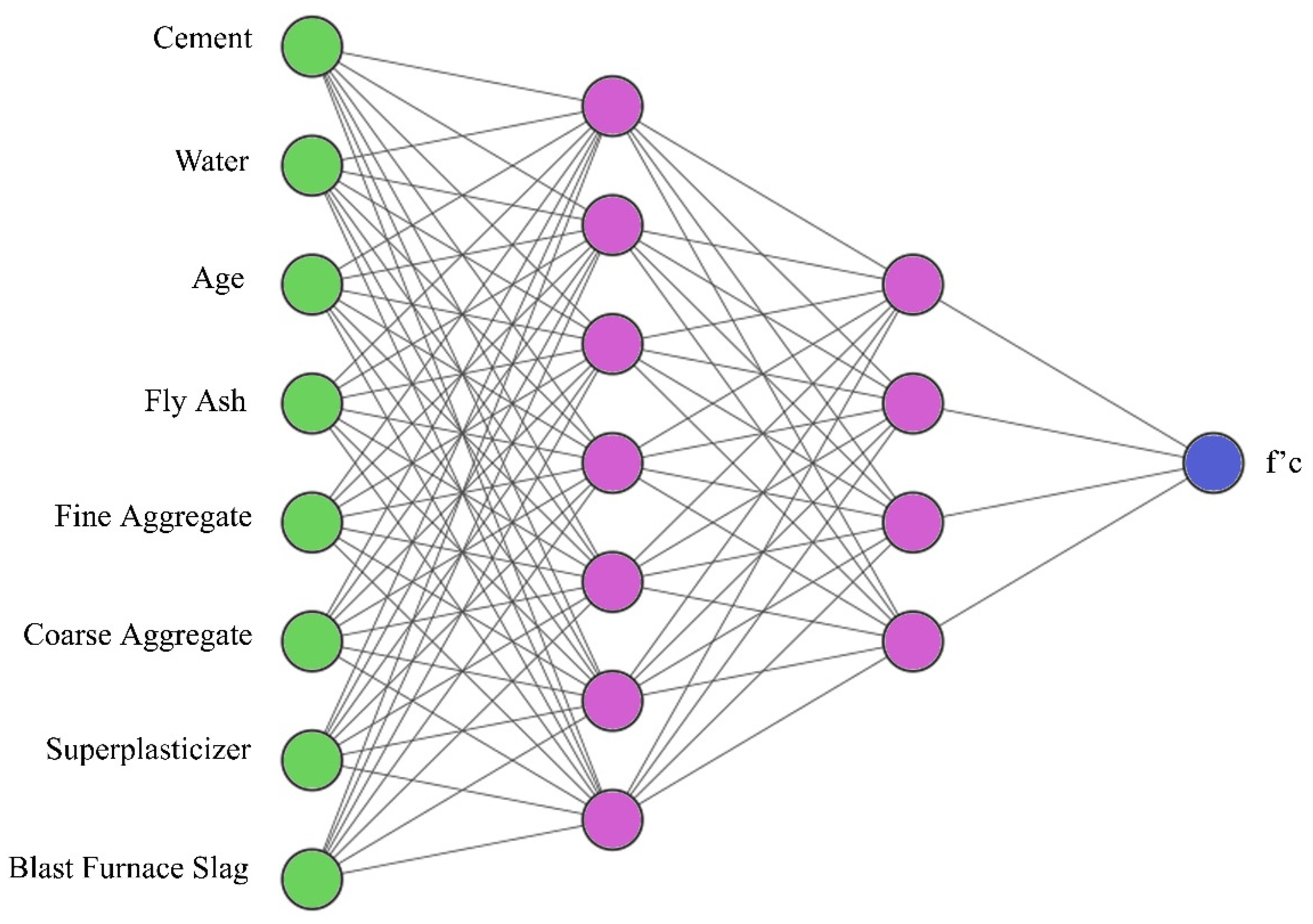
2.1. Artificial Neural Networks
- Data are handled in specific entities called nodes.
- Links relay signals between nodes.
- The weight assigned to each link indicates the strength of that link.
- Nodes calculate their outputs by applying activation functions to input data.
- Training: this subgroup of data is used to train the ANN, and learning occurs through examples, similar to the human brain. The training sessions are repeated until the acceptable precision of the model is achieved.
- Validation: this subset determines the extent of training of the model and estimates model features such as classification errors, mean error for numerical predictions, etc.
- Testing: This subgroup can confirm the performance of the training subset developed in the ANN model.
2.2. BAT Algorithm
- bats use echolocation, and they can discern between prey and surroundings;
- at any given location xi, they fly randomly with velocity vi and contingent upon the location of prey they adjust their rate of pulse emission;
- the loudness of the emitted pulse ranges from A0 to a minimum value of Amin.
3. Methods and Materials
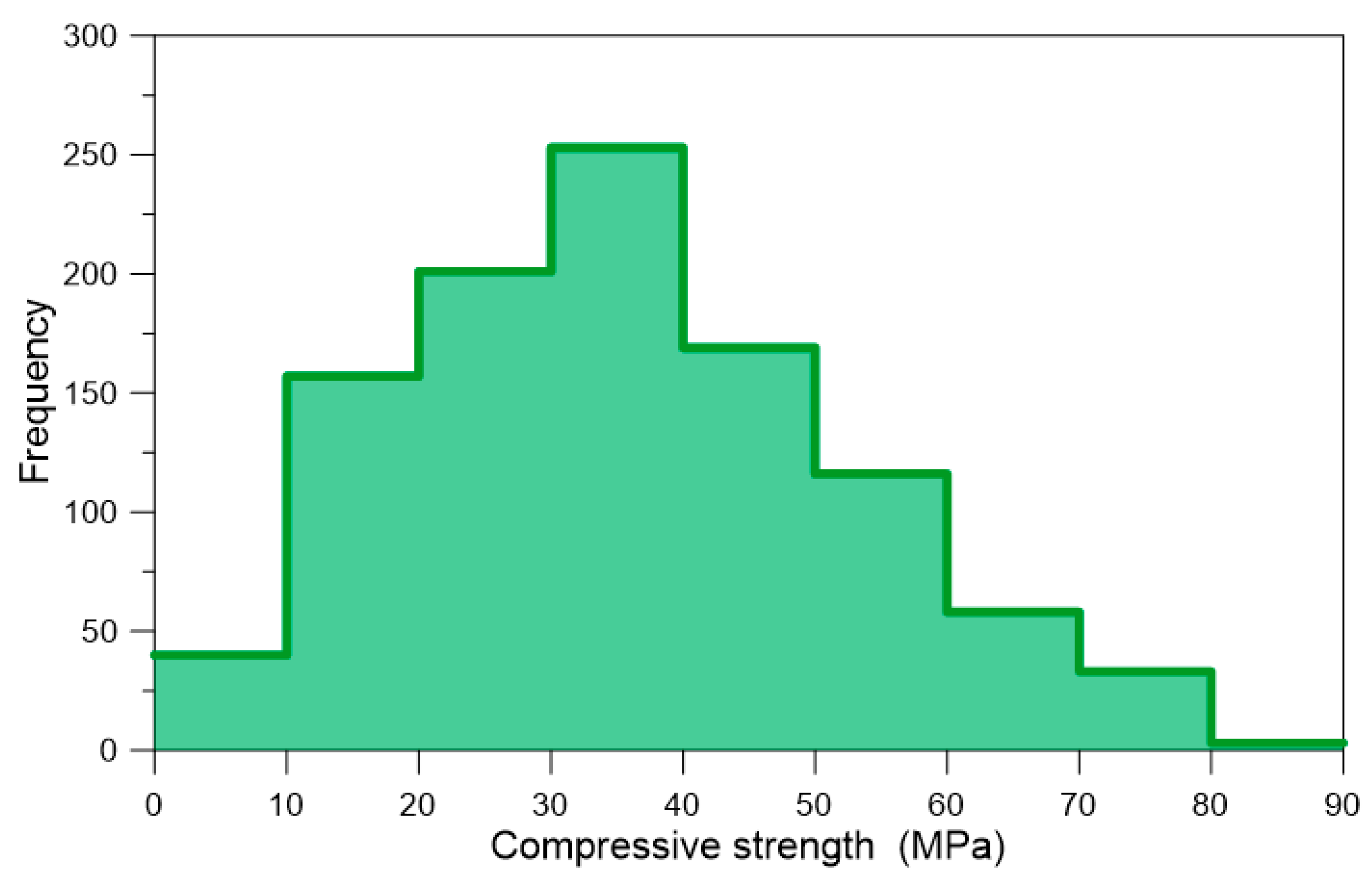
3.1. Dataset
3.2. Performance Measures
3.3. Experimental Model Generation Utilizing ANNs and BAT Algorithm
4. Results
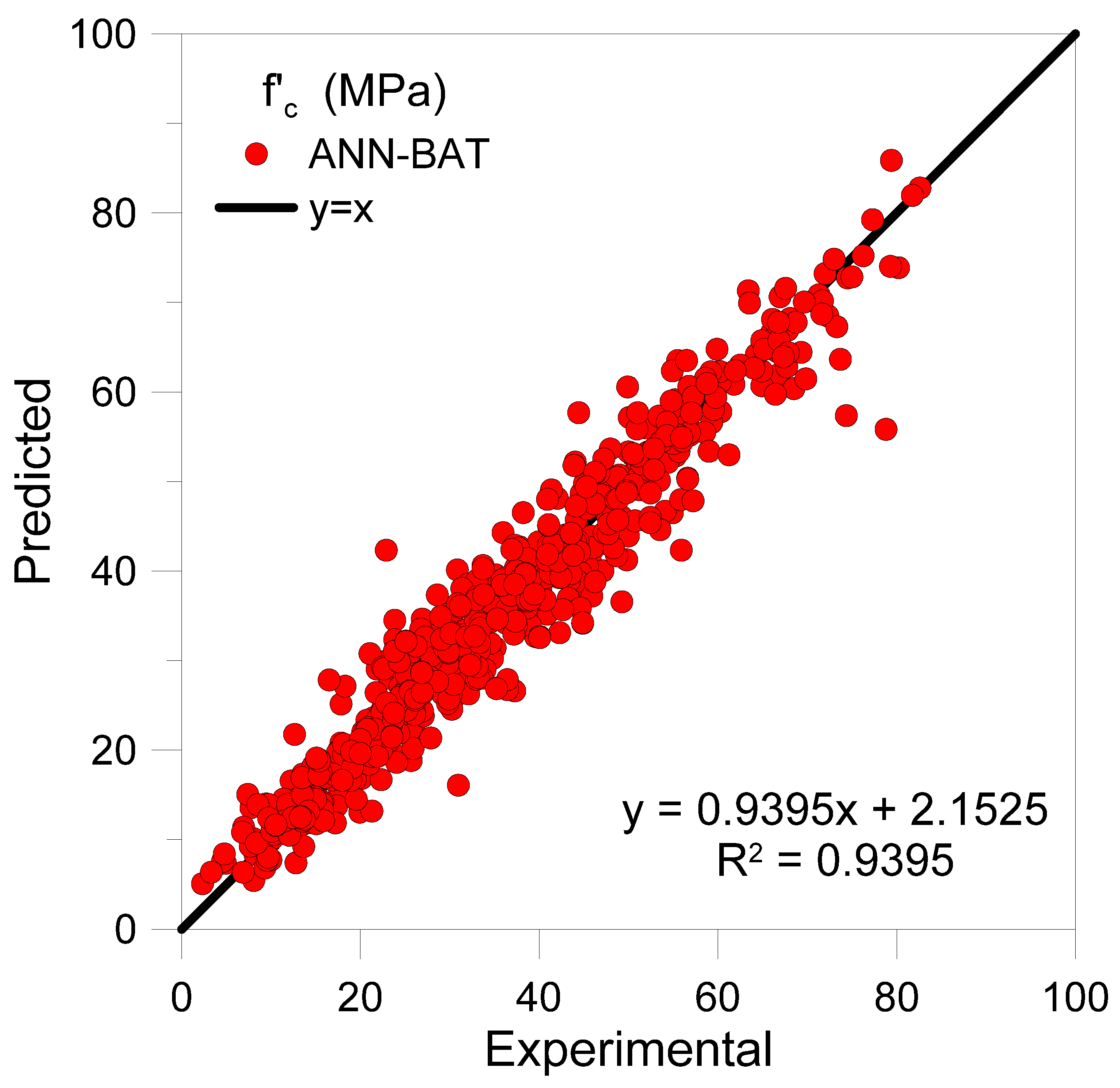
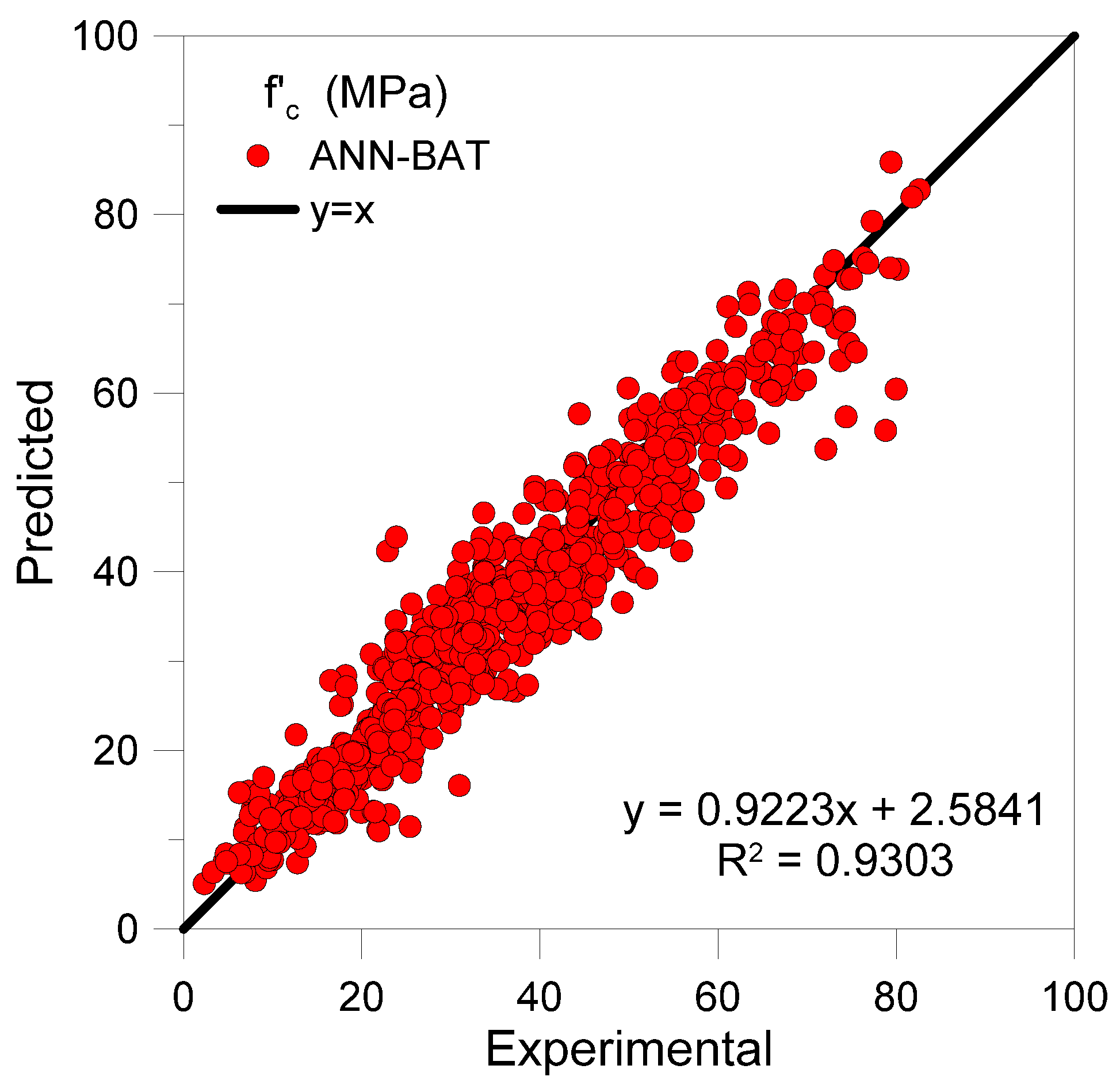
4.1. Experimental Model Assessment
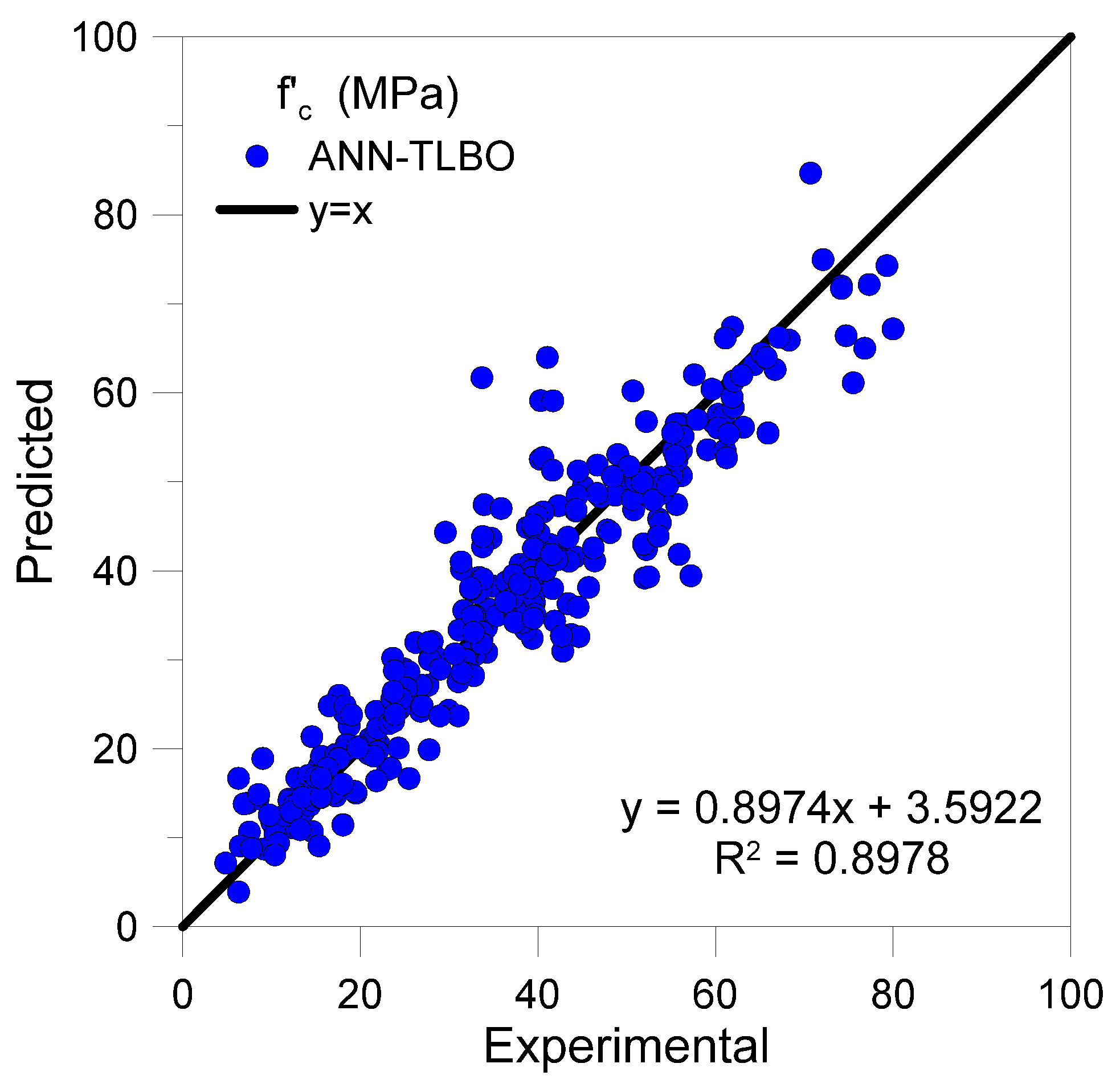
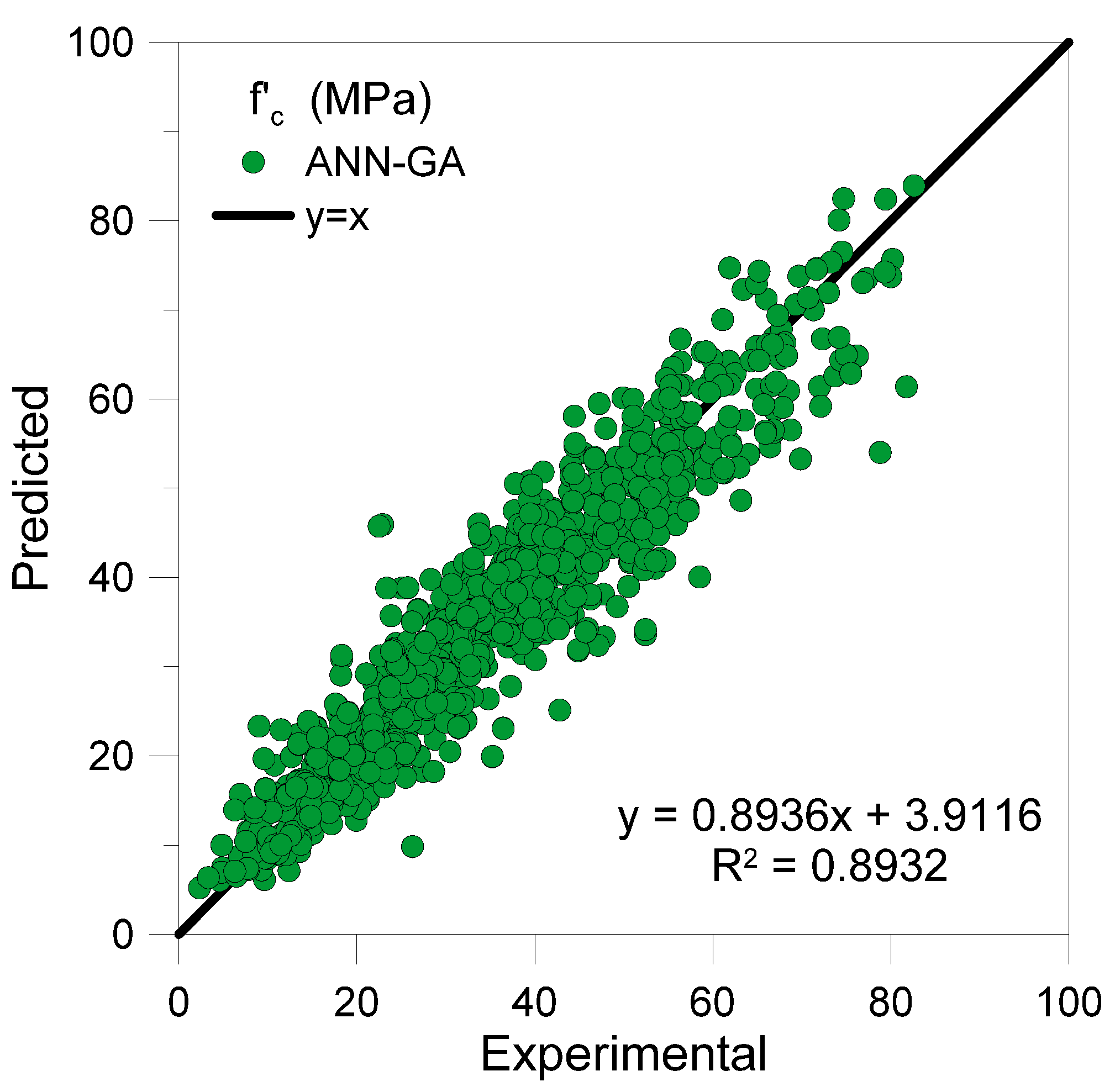
4.2. Comparison with Other Methods
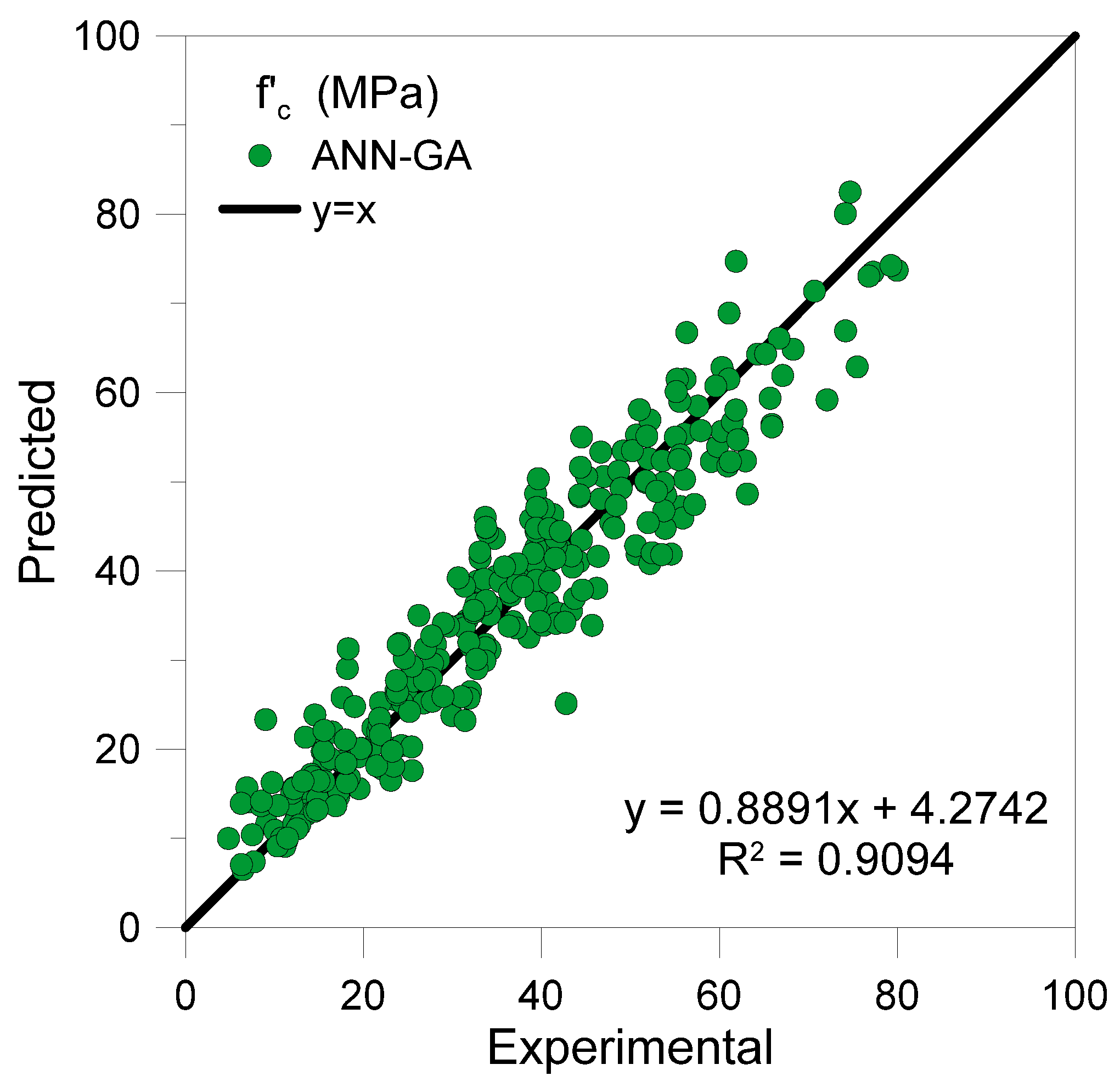
4.2.1. Genetic Algorithm and Teaching-Learning-Based-Optimization Models
4.2.2. Multi Linear Regression Model
| C: Cement | W: Water |
| BFS: Blast Furnace Slag | S: Superplasticizer |
| FA: Fly Ash | CA: Coarse Aggregate |
| Fag: Fine Aggregate | f’c: compressive strength |
| A: Age |
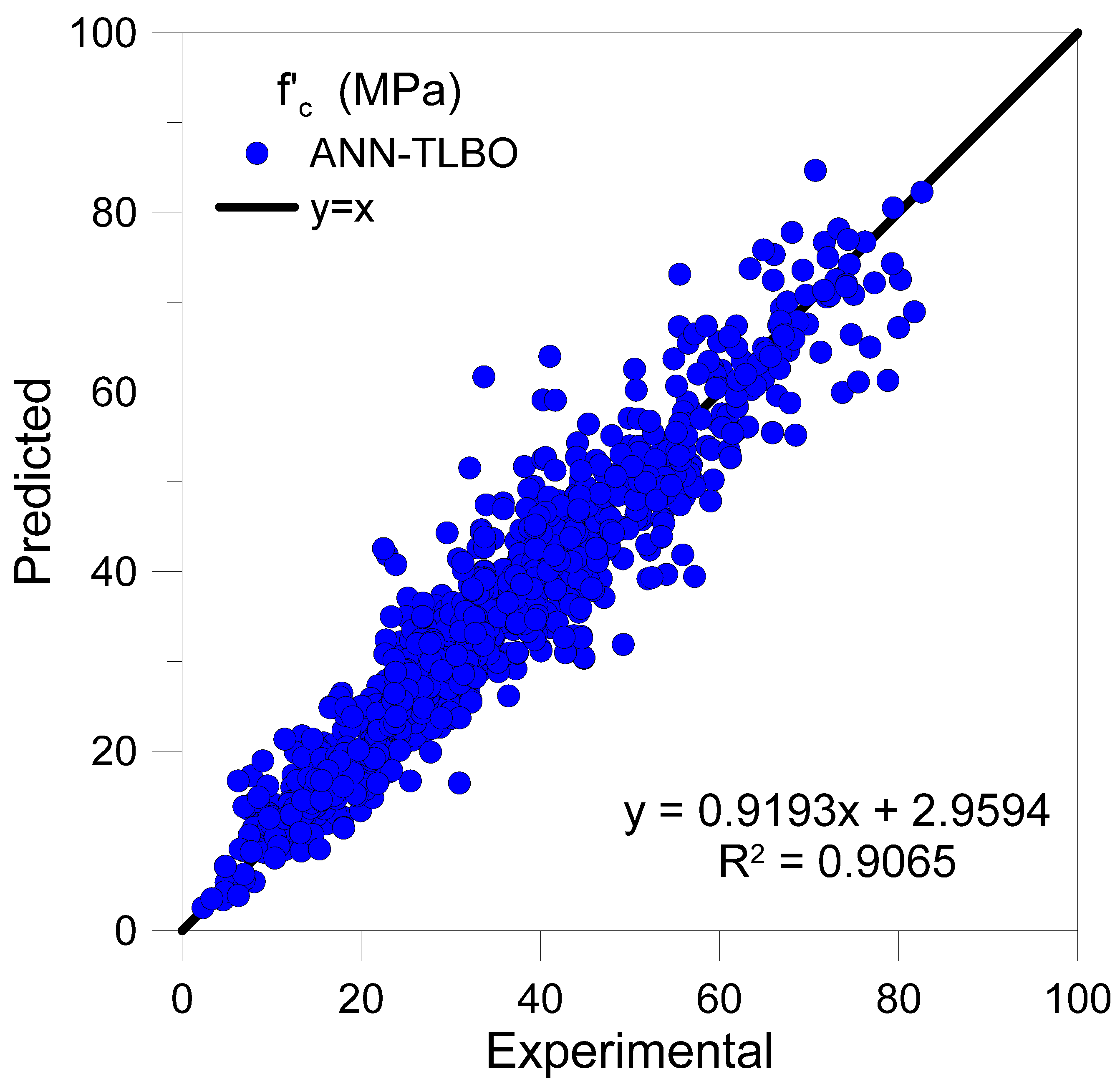
4.2.3. Comparison on All Data
4.2.4. Comparative Analysis with Models Proposed in Literature
4.3. Predictive Model and ANN Weights
5. Conclusions
- The top-performing bat-based ANN model, ANN-BAT-2L (7-4), yielded a mean squared error of 27.624 on testing data.
- Due to its simplicity, a classical MLR model was presented for predicting compressive strength; however, it is less accurate than the proposed ANN-BAT model.
- The top-performing bat algorithm-based ANN was compared with ANNs trained using GA and TLBO algorithms. The top models based on these algorithms were ANN-GA-2L (3-5) and ANN-TLBO 2L (5-6); however, they were less accurate than the ANN-BAT-2L (7-4) model. The next best performing ANN was the TLBO-based, followed by GA-based, and the MLR model.
- The top-performing bat algorithm-based ANN was compared with four predictive models proposed in literature for compressive strength of concrete. The bat-based ANN outperformed all four.
- The network parameters, i.e., weights and biased of the ANN-BAT-2L (7-4) model were provided in tabular format for manual calculation of network prediction. Thus, for desired and new concrete samples, the compressive strength can be estimated by providing the presented formulas with sample inputs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nikoo, M.; Torabian Moghadam, F.; Sadowski, Ł. Prediction of concrete compressive strength by evolutionary artificial neural networks. Adv. Mater. Sci. Eng. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Asteris, P.G.; Mokos, V.G. Concrete compressive strength using artificial neural networks. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Lai, S.; Serra, M. Concrete strength prediction by means of neural network. Constr. Build. Mater. 1997, 11, 93–98. [Google Scholar] [CrossRef]
- Lee, S.-C. Prediction of concrete strength using artificial neural networks. Eng. Struct. 2003, 25, 849–857. [Google Scholar] [CrossRef]
- Diab, A.M.; Elyamany, H.E.; Abd Elmoaty, A.E.M.; Shalan, A.H. Prediction of concrete compressive strength due to long term sulfate attack using neural network. Alex. Eng. J. 2014, 53, 627–642. [Google Scholar] [CrossRef]
- Khashman, A.; Akpinar, P. Non-Destructive Prediction of Concrete Compressive Strength Using Neural Networks. In Proceedings of the Procedia Computer Science, Zurich, Switzerland, 12–14 June 2017; Volume 108, pp. 2358–2362. [Google Scholar]
- Rajeshwari, R.; Mandal, S. Prediction of Compressive Strength of High-Volume Fly Ash Concrete Using Artificial Neural Network. In Sustainable Construction and Building Materials; Springer: Singapore, 2019; pp. 471–483. ISBN 978-981-13-3316-3. [Google Scholar]
- Kewalramani, M.A.; Gupta, R. Concrete compressive strength prediction using ultrasonic pulse velocity through artificial neural networks. Autom. Constr. 2006, 15, 374–379. [Google Scholar] [CrossRef]
- Słoński, M. A comparison of model selection methods for compressive strength prediction of high-performance concrete using neural networks. Comput. Struct. 2010, 88, 1248–1253. [Google Scholar] [CrossRef]
- Atici, U. Prediction of the strength of mineral admixture concrete using multivariable regression analysis and an artificial neural network. Expert Syst. Appl. 2011, 38, 9609–9618. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling Concrete Strength with Augment-Neuron Networks. J. Mater. Civ. Eng. 1998, 10, 263–268. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Öztaş, A.; Pala, M.; Özbay, E.; Kanca, E.; Çagˇlar, N.; Bhatti, M.A. Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Faridmehr, I.; Bedon, C.; Huseien, G.F.; Nikoo, M.; Baghban, M.H. Assessment of Mechanical Properties and Structural Morphology of Alkali-Activated Mortars with Industrial Waste Materials. Sustainability 2021, 13, 2062. [Google Scholar] [CrossRef]
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 10, 1859–1867. [Google Scholar] [CrossRef]
- Nazari, A.; Riahi, S. Prediction split tensile strength and water permeability of high strength concrete containing TiO2 nanoparticles by artificial neural network and genetic programming. Compos. Part B Eng. 2011, 42, 473–488. [Google Scholar] [CrossRef]
- Bui, D.K.; Nguyen, T.; Chou, J.S.; Nguyen-Xuan, H.; Ngo, T.D. A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr. Build. Mater. 2018, 180, 320–333. [Google Scholar] [CrossRef]
- Sadowski, L.; Nikoo, M.; Nikoo, M. Concrete compressive strength prediction using the imperialist competitive algorithm. Comput. Concr. 2018, 22, 355–363. [Google Scholar] [CrossRef]
- Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.-N.; Moayedi, H. A novel artificial intelligence technique to predict compressive strength of recycled aggregate concrete using ICA-XGBoost model. Eng. Comput. 2020, 1–18. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, F.; Zhu, F. Estimation of compressive strength of hollow concrete masonry prisms using artificial neural networks and adaptive neuro-fuzzy inference systems. Constr. Build. Mater. 2016, 125, 417–426. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Asteris, P.G. A comparative study of ANN and ANFIS models for the prediction of cement-based mortar materials compressive strength. Neural Comput. Appl. 2021, 33, 4501–4532. [Google Scholar] [CrossRef]
- Hoła, J.; Schabowicz, K. Application of artificial neural networks to determine concrete compressive strength based on non-destructive tests. J. Civ. Eng. Manag. 2005, 11, 23–32. [Google Scholar] [CrossRef]
- Khademi, F.; Akbari, M.; Jamal, S.M.; Nikoo, M. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 2017, 11, 90–99. [Google Scholar] [CrossRef]
- Fan, M.; Zhang, Z.; Wang, C. Chapter 7—Optimization Method for Load Frequency Feed Forward Control; Academic Press: New York, NY, USA, 2019; pp. 221–282. ISBN 978-0-12-813231-9. [Google Scholar]
- Fan, M.; Zhang, Z.; Wang, C. Optimization Method for Load Frequency Feed Forward Control. In Mathematical Models and Algorithms for Power System Optimization; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Ellis, G. Feed-Forward. In Control System Design Guide; Ellis, G., Ed.; Academic Press: Burlington, NJ, USA, 2004; pp. 151–169. ISBN 978-0-12-237461-6. [Google Scholar]
- Jun, L.; Liheng, L.; Xianyi, W. A double-subpopulation variant of the bat algorithm. Appl. Math. Comput. 2015, 263, 361–377. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 9780124167438. [Google Scholar]
- Dehghani, H.; Bogdanovic, D. Copper price estimation using bat algorithm. Resour. Policy 2018, 55, 55–61. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Pearson: London, UK, 2008; Volume 3, ISBN 9780131471399. [Google Scholar]
- Hasanzade-Inallu, A.; Zarfam, P.; Nikoo, M. Modified imperialist competitive algorithm-based neural network to determine shear strength of concrete beams reinforced with FRP. J. Cent. South Univ. 2019, 26, 3156–3174. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists; Australian Government: Canberra, Australia, 2008; ISBN 9781921498305. [Google Scholar]
- Géron, A. Hands-on Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2017. [Google Scholar]
- Plevris, V.; Asteris, P.G. Modeling of masonry failure surface under biaxial compressive stress using Neural Networks. Constr. Build. Mater. 2014, 55, 447–461. [Google Scholar] [CrossRef]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- MATLAB; The MathWorks: Natick, MA, USA, 2018.
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. CAD Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Nikoo, M.; Sadowski, L.; Khademi, F.; Nikoo, M. Determination of Damage in Reinforced Concrete Frames with Shear Walls Using Self-Organizing Feature Map. Appl. Comput. Intell. Soft Comput. 2017, 2017, 1–10. [Google Scholar] [CrossRef]
- Delozier, M.R.; Orlich, S. Discovering influential cases in linear regression with MINITAB: Peeking into multidimensions with a MINITAB macro. Stat. Methodol. 2005, 2, 71–81. [Google Scholar] [CrossRef]
- Panesar, D.K.; Aqel, M.; Rhead, D.; Schell, H. Effect of cement type and limestone particle size on the durability of steam cured self-consolidating concrete. Cem. Concr. Compos. 2017, 80, 157–159. [Google Scholar] [CrossRef]
- Gevrey, M.; Dimopoulos, I.; Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Model. 2003, 160, 249–264. [Google Scholar] [CrossRef]
- Hasanzade-Inallu, A. Grey Wolf Optimizer-Based ANN to Predict Compressive Strength of AFRP-Confined Concrete Cylinders. Soil Struct. Interact. 2018, 3, 23–32. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H.; Shadmehri, D.M.; Sahab, M.G. An empirical model for shear capacity of RC deep beams using genetic-simulated annealing. Arch. Civ. Mech. Eng. 2013, 13, 354–369. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Chou, J.S.; Chong, W.K.; Bui, D.K. Nature-Inspired Metaheuristic Regression System: Programming and Implementation for Civil Engineering Applications. J. Comput. Civ. Eng. 2016, 30, 4016007. [Google Scholar] [CrossRef]




| Statistical Index | Unit | Min | Min | Average | Standard Deviation | Mode | Median |
|---|---|---|---|---|---|---|---|
| Cement | Kg/m3 | 540 | 102 | 281.17 | 104.51 | 425 | 272.9 |
| Blast Furnace Slag | Kg/m3 | 359.4 | 0 | 73.90 | 86.28 | 0 | 22 |
| Fly Ash | Kg/m3 | 200.1 | 0 | 54.19 | 64.00 | 0 | 0 |
| Water | Kg/m3 | 247 | 121.75 | 181.57 | 21.36 | 192 | 185 |
| Superplasticizer | Kg/m3 | 32.2 | 0 | 6.20 | 5.97 | 0 | 6.35 |
| Coarse Aggregate | Kg/m3 | 1145 | 801 | 972.92 | 77.75 | 932 | 968 |
| Fine Aggregate | Kg/m3 | 992.6 | 594 | 773.58 | 80.18 | 594 | 779.51 |
| Age | day | 365 | 1 | 45.66 | 63.17 | 28 | 28 |
| Concrete compressive strength | MPa | 82.60 | 2.33 | 35.82 | 16.71 | 33.40 | 34.44 |
| Num | Topology | Num | Topology | ... | Num | Topology | Num | Topology |
|---|---|---|---|---|---|---|---|---|
| 1 | 1-1 | 9 | 2-1 | ... | 65 | 9-1 | 73 | 1 |
| 2 | 1-2 | 10 | 2-2 | ... | 66 | 9-2 | 74 | 2 |
| 3 | 1-3 | 11 | 2-3 | ... | 67 | 9-3 | 75 | 3 |
| 4 | 1-4 | 12 | 2-4 | ... | 68 | 9-4 | 76 | 4 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 7 | 1-7 | 15 | 2-7 | ... | 71 | 9-7 | 88 | 16 |
| 8 | 1-8 | 16 | 2-8 | ... | 72 | 9-8 | 89 | 17 |
| Hyperparameter | Value | Hyperparameter | Value |
|---|---|---|---|
| Population Total | 100 | Max Generations | 200 |
| Loudness | 0.9 | Pulse Rate | 0.5 |
| Min Freq. | 0 | Max Freq. | 2 |
| Alpha | 0.99 | Gamma | 0.01 |
| Num | Network Designation | Training | |||
|---|---|---|---|---|---|
| MSE | ME | MAE | RMSE | ||
| 1 | ANN-BAT-1L (4) | 28.471 | 0.000 | 3.989 | 5.336 |
| 2 | ANN-BAT-2L (3-2) | 28.543 | 0.000 | 4.018 | 5.343 |
| 3 | ANN-BAT-2L (8-5) | 10.928 | 0.000 | 2.448 | 3.306 |
| 4 | ANN-BAT-2L (7-4) | 16.001 | 0.000 | 2.895 | 4.000 |
| Num | Network Designation | Testing | |||
|---|---|---|---|---|---|
| MSE | ME | MAE | RMSE | ||
| 1 | ANN-BAT-1L (4) | 37.146 | −0.147 | 4.674 | 6.095 |
| 2 | ANN-BAT-2L (3-2) | 37.496 | 0.148 | 4.739 | 6.123 |
| 3 | ANN-BAT-2L (8-5) | 40.130 | −0.546 | 3.828 | 6.335 |
| 4 | ANN-BAT-2L (7-4) | 27.624 | −0.664 | 3.847 | 5.256 |
| Name | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| Genetic Algorithm | Max generations | 100 | Crossover (%) | 50 |
| Recombination (%) | 15 | Crossover method | single point | |
| Lower Bound | −1 | Selection Mode | 1 | |
| Upper Bound | +1 | Population Size | 150 | |
| Teaching Learning Base Optimization | Lower Bound | −1 | Max Interaction | 50 |
| Upper Bound | +1 | Population Size | 150 |
| Topology | Train | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| ME | MAE | MSE | RMSE | ME | MAE | MSE | RMSE | |
| ANN-GA-2L (3-5) | 0.04 | 4.13 | 30.35 | 5.51 | 0.25 | 4.17 | 28.44 | 5.33 |
| ANN-TLBO-2L (5-6) | 0.16 | 3.59 | 23.68 | 4.87 | −0.14 | 4.02 | 31.87 | 5.65 |
| Topology | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| ME | MAE | MSE | RMSE | ME | MAE | MSE | RMSE | |
| MLR | 0.00 | 8.08 | 106.49 | 10.32 | −0.02 | 8.52 | 108.91 | 10.44 |
| Type | Network Designation | ME | MAE | MSE | RMSE |
|---|---|---|---|---|---|
| All Data | ANN-BAT-2L(7-4) | −0.199 | 3.181 | 19.488 | 4.414 |
| ANN-GA-2L(3-5) | 0.10 | 4.14 | 29.77 | 5.46 | |
| ANN-TLBO-2L(5-6) | 0.07 | 3.72 | 26.13 | 5.11 | |
| MLR | −0.01 | 8.22 | 107.21 | 10.35 |
| Author | Model | Reference |
|---|---|---|
| A.H. Gandomi et al. | Genetic-Simulated Annealing | [43] |
| J.-S. Chou et al. | Support Vector Machines | [44] |
| Jui-Sheng et al. | Least Squares Support Vector Machines | [45] |
| D.-K. Bui et al. | Firefly Algorithm combined Artificial Neural Network | [17] |
| Model | R2 | MAE |
|---|---|---|
| Present (ANN-BAT-2L (7-4)) | 0.93 | 3.18 |
| D.-K. Bui et al. (2018) | 0.90 | 3.41 |
| J.-S. Chou et al. (2013) | 0.88 | 4.24 |
| Jui-Sheng et al. (2016) | 0.88 | 5.62 |
| A.H. Gandomi et al. (2013) | 0.81 | 5.48 |
| −0.8061 | −0.2178 | −0.2297 | −0.4198 | −0.5889 | −0.3034 | −0.2999 | −0.1035 | −0.8156 |
| 0.2371 | −0.6965 | −0.1132 | 1.3410 | 1.5170 | 0.3782 | 0.0238 | 0.1807 | 0.6200 |
| −6.3017 | −2.6506 | −2.4931 | 2.5263 | 2.0438 | −0.8616 | −4.4602 | −1.1676 | −1.1071 |
| 0.0226 | −0.0670 | −0.1191 | 0.0505 | 0.0342 | 0.0304 | −0.0781 | 3.6208 | 4.6903 |
| −6.9203 | −18.4075 | −3.0575 | −27.3813 | −10.0966 | −11.8482 | −7.9640 | −1.1299 | −16.3967 |
| 31.2215 | −7.9121 | −19.6231 | −0.0551 | 14.0536 | −15.0847 | −12.6117 | −2.1349 | −4.3244 |
| 0.6362 | −3.2611 | 4.4076 | −5.9958 | 4.4666 | −4.3309 | −1.5010 | −8.0783 | 1.1720 |
| −1.6512 | −0.7434 | 0.3050 | 0.1381 | 0.1699 | −0.1258 | −0.1164 | −2.0524 | |
| 6.6296 | 2.6327 | −1.7307 | 13.1062 | −0.6463 | −0.0506 | 1.1651 | −9.5413 | |
| 33.0428 | 23.3462 | 3.0604 | −21.0571 | −1.8540 | 0.2323 | −19.2491 | −12.8245 | |
| 1.0129 | 0.6331 | −0.6631 | 9.3516 | −0.7377 | 0.4773 | 0.3696 | −8.0055 | |
| 12.8658 | 0.4640 | 0.2489 | 0.4572 | 11.7091 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aalimahmoody, N.; Bedon, C.; Hasanzadeh-Inanlou, N.; Hasanzade-Inallu, A.; Nikoo, M. BAT Algorithm-Based ANN to Predict the Compressive Strength of Concrete—A Comparative Study. Infrastructures 2021, 6, 80. https://doi.org/10.3390/infrastructures6060080
Aalimahmoody N, Bedon C, Hasanzadeh-Inanlou N, Hasanzade-Inallu A, Nikoo M. BAT Algorithm-Based ANN to Predict the Compressive Strength of Concrete—A Comparative Study. Infrastructures. 2021; 6(6):80. https://doi.org/10.3390/infrastructures6060080
Chicago/Turabian StyleAalimahmoody, Nasrin, Chiara Bedon, Nasim Hasanzadeh-Inanlou, Amir Hasanzade-Inallu, and Mehdi Nikoo. 2021. "BAT Algorithm-Based ANN to Predict the Compressive Strength of Concrete—A Comparative Study" Infrastructures 6, no. 6: 80. https://doi.org/10.3390/infrastructures6060080
APA StyleAalimahmoody, N., Bedon, C., Hasanzadeh-Inanlou, N., Hasanzade-Inallu, A., & Nikoo, M. (2021). BAT Algorithm-Based ANN to Predict the Compressive Strength of Concrete—A Comparative Study. Infrastructures, 6(6), 80. https://doi.org/10.3390/infrastructures6060080









