Explicitly Assessing the Durability of RC Structures Considering Spatial Variability and Correlation
Abstract
:1. Introduction
2. Corrosion-Induced Deterioration of RC Structures
3. Explicit Approach for Durability Performance Assessment
3.1. Material-Level Durability Assessment
3.2. Durability Performance Assessment Considering Spatial Variability and Correlation
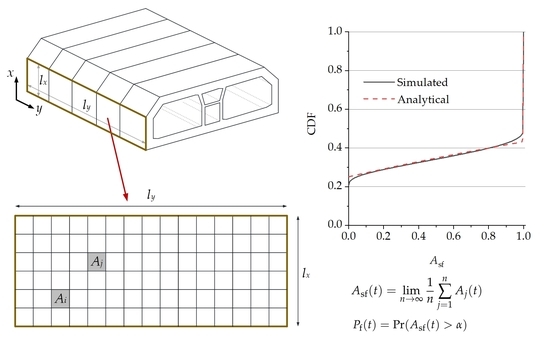
4. Example
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FIB. Model Code for Service Life Design; Bulletin 34; Fédération International du Béton: Lausanne, Switzerland, 2006. [Google Scholar]
- FIB. Model Code 2010—First Complete Draft; Bulletin 55/56; Fédération International du Béton: Lausanne, Switzerland, 2010. [Google Scholar]
- ISO 16204. Durability—Service Life Design of Concrete Structures; International Organization for Standardization: London, UK, 2012. [Google Scholar]
- CEN. EuroCode2: Design of Concrete Structures (prEN 1992-1-1); European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]
- Li, Q.; Ye, X. Surface deterioration analysis for probabilistic durability design of RC structures in marine environment. Struct. Saf. 2018, 75, 13–23. [Google Scholar] [CrossRef]
- Alexander, M.; Beushausen, H. Durability, service life prediction, and modeling for reinforced concrete structures–review and critique. Cem. Concr. Res. 2019, 122, 17–29. [Google Scholar] [CrossRef]
- McGee, R. Modelling of durability performance of Tasmanian bridges. ICASP8 Appl. Stat. Probab. Civ. Eng. 1999, 1, 297–306. [Google Scholar]
- DuraCrete. Probabilistic Performance Based Durability of Concrete Structures: General Guidelines for Durability Design and Redesign; Technical Report, Report No. BE95-1347; CUR: Gouda, The Netherlands, 2000. [Google Scholar]
- Li, K.; Li, Q.; Zhou, X.; Fan, Z. Durability Design of the Hong Kong-Zhuhai-Macau Sea-Link Project: Principle and Procedure. J. Bridge Eng. 2015, 20, 04015001. [Google Scholar] [CrossRef]
- Li, Q.; Li, K.; Zhou, X.; Zhang, Q.; Fan, Z. Model-based durability design of concrete structures in Hong Kong-Zhuhai-Macau sea link project. Struct. Saf. 2015, 53, 1–12. [Google Scholar] [CrossRef]
- Hackl, J.; Kohler, J. Reliability assessment of deteriorating reinforced concrete structures by representing the coupled effect of corrosion initiation and progression by Bayesian networks. Struct. Saf. 2016, 62, 12–23. [Google Scholar] [CrossRef]
- Wang, C. Structural Reliability and Time-Dependent Reliability; Springer Nature: Cham, Switzerland, 2021. [Google Scholar]
- Hong, H. Assessment of reliability of aging reinforced concrete structures. J. Struct. Eng. 2000, 126, 1458–1465. [Google Scholar] [CrossRef]
- Pang, L.; Li, Q. Service life prediction of RC structures in marine environment using long term chloride ingress data: Comparison between exposure trials and real structure surveys. Constr. Build. Mater. 2016, 113, 979–987. [Google Scholar] [CrossRef]
- Wu, L.; Li, W.; Yu, X. Time-dependent chloride penetration in concrete in marine environments. Constr. Build. Mater. 2017, 152, 406–413. [Google Scholar] [CrossRef]
- Stewart, M.G. Spatial variability of pitting corrosion and its influence on structural fragility and reliability of RC beams in flexure. Struct. Saf. 2004, 26, 453–470. [Google Scholar] [CrossRef]
- Li, Y.; Vrouwenvelder, T.; Wijnants, G.; Walraven, J. Spatial variability of concrete deterioration and repair strategies. Struct. Concr. 2004, 5, 121–129. [Google Scholar] [CrossRef]
- Muigai, R.; Moyo, P.; Alexander, M. Durability design of reinforced concrete structures: A comparison of the use of durability indexes in the deemed-to-satisfy approach and the full-probabilistic approach. Mater. Struct. 2012, 45, 1233–1244. [Google Scholar] [CrossRef]
- Stewart, M.G. Spatial and time-dependent reliability modeling of corrosion damage, safety and maintenance for reinforced concrete structures. Struct. Infrastruct. Eng. 2012, 8, 607–619. [Google Scholar] [CrossRef]
- Demis, S.; Papadakis, V.G. Durability design process of reinforced concrete structures-Service life estimation, problems and perspectives. J. Build. Eng. 2019, 26, 100876. [Google Scholar] [CrossRef]
- Vu, K.A.; Stewart, M.G. Predicting the likelihood and extent of reinforced concrete corrosion-induced cracking. J. Struct. Eng. 2005, 131, 1681–1689. [Google Scholar] [CrossRef]
- Akiyama, M.; Frangopol, D.M.; Takenaka, K. Reliability-based durability design and service life assessment of reinforced concrete deck slab of jetty structures. Struct. Infrastruct. Eng. 2017, 13, 468–477. [Google Scholar] [CrossRef]
- Shafei, B.; Alipour, A. Application of large-scale non-Gaussian stochastic fields for the study of corrosion-induced structural deterioration. Eng. Struct. 2015, 88, 262–276. [Google Scholar] [CrossRef]
- Li, C.Q. Life-cycle modeling of corrosion-affected concrete structures: Propagation. J. Struct. Eng. 2003, 129, 753–761. [Google Scholar] [CrossRef]
- Li, C.Q. Life cycle modeling of corrosion affected concrete structures—Initiation. J. Mater. Civ. Eng. 2003, 15, 594–601. [Google Scholar] [CrossRef]
- Yi, Y.; Zhu, D.; Guo, S.; Zhang, Z.; Shi, C. A review on the deterioration and approaches to enhance the durability of concrete in the marine environment. Cem. Concr. Compos. 2020, 113, 103695. [Google Scholar] [CrossRef]
- Bazant, Z.P. Physical model for steel corrosion in concrete sea structures-theory. J. Struct. Div. ASCE 1979, 105, 1137–1153. [Google Scholar] [CrossRef]
- Bamforth, P. The derivation of input data for modeling chloride ingress from eight-year UK coastal exposure trials. Mag. Concr. Res. 1999, 51, 87–96. [Google Scholar] [CrossRef]
- Li, C.Q. Corrosion initiation of reinforcing steel in concrete under natural salt spray and service loading—Results and analysis. Mater. J. 2000, 97, 690–697. [Google Scholar]
- Khan, M.U.; Ahmad, S.; Al-Gahtani, H.J. Chloride-induced corrosion of steel in concrete: An overview on chloride diffusion and prediction of corrosion initiation time. Int. J. Corros. 2017, 2017, 5819202. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Weyers, R.E. Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures. Mater. J. 1998, 95, 675–680. [Google Scholar]
- El Maaddawy, T.; Soudki, K. A model for prediction of time from corrosion initiation to corrosion cracking. Cem. Concr. Compos. 2007, 29, 168–175. [Google Scholar] [CrossRef]
- Mullard, J.A.; Stewart, M.G. Corrosion-induced cover cracking: New test data and predictive models. ACI Struct. J. 2011, 108, 71–79. [Google Scholar]
- Collepardi, M.; Marcialis, A.; Turriziani, R. Penetration of chloride ions into cement pastes and concretes. J. Am. Ceram. Soc. 1972, 55, 534–535. [Google Scholar] [CrossRef]
- Mangat, P.; Molloy, B. Prediction of long term chloride concentration in concrete. Mater. Struct. 1994, 27, 338–346. [Google Scholar] [CrossRef]
- Mangat, P.; Molloy, B. Model for long term chloride penetration in concrete. Mater. Struct. 1994, 25, 404–411. [Google Scholar] [CrossRef]
- Alonso, C.; Andrade, C.; Rodriguez, J.; Diez, J.M. Factors controlling cracking of concrete affected by reinforcement corrosion. Mater. Struct. 1998, 31, 435–441. [Google Scholar] [CrossRef]
- Vidal, T.; Castel, A.; Francois, R. Analyzing crack width to predict corrosion in reinforced concrete. Cem. Concr. Res. 2004, 34, 165–174. [Google Scholar] [CrossRef]
- Gonzalez, J.; Andrade, C.; Alonso, C.; Feliu, S. Comparison of rates of general corrosion and maximum pitting penetration on concrete embedded steel reinforcement. Cem. Concr. Res. 1995, 25, 257–264. [Google Scholar] [CrossRef]
- Engelund, S.; Sørensen, J.D. A probabilistic model for chloride-ingress and initiation of corrosion in reinforced concrete structures. Struct. Saf. 1998, 20, 69–89. [Google Scholar] [CrossRef]
- O’Connor, A.; Kenshel, O. Experimental evaluation of the scale of fluctuation for spatial variability modeling of chloride-induced reinforced concrete corrosion. J. Bridge Eng. 2013, 18, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, C. Explicit Approach for Reliability-Based Design of Lining Structures Subjected to Water Seepage Considering Spatial Correlation and Uncertainty. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021036. [Google Scholar] [CrossRef]
- Mathai, A.; Moschopoulos, P.; Pederzoli, G. Random points associated with rectangles. Rend. Circ. Mat. Palermo 1999, 48, 163–190. [Google Scholar] [CrossRef]
- Fenton, N.; Neil, M. Risk Assessment and Decision Analysis with Bayesian Networks; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Luque, J.; Straub, D. Risk-based optimal inspection strategies for structural systems using dynamic Bayesian networks. Struct. Saf. 2019, 76, 68–80. [Google Scholar] [CrossRef]
- Nakagawa, T.; Seshimo, Y.; Onitsuka, S.; Tsutsumi, T. Assessment of corrosion speed of RC structure under the chloride deterioration environment. In Proceedings of the JCI Symposium on the Analysis Model Supporting the Verification of Longterm Performance of Concrete Structure in Design; Japan Concrete Institute: Tokyo, Japan, 2004; pp. 325–330. [Google Scholar]
- Liu, P.L.; Der Kiureghian, A. Multivariate distribution models with prescribed marginals and covariances. Probabilistic Eng. Mech. 1986, 1, 105–112. [Google Scholar] [CrossRef]
- JTJ 302-2006. Technical Specification for Detection and Assessment of Harbour and Marine Structures; Ministry of Transport of the People’s Republic of China: Beijing, China, 2007. [Google Scholar]
- Zhang, J.; Wang, J.; Kong, D. Chloride diffusivity analysis of existing concrete based on Fick’s second law. J. Wuhan Univ. Technol. Sci. Ed. 2010, 25, 142–146. [Google Scholar] [CrossRef]
- Andrade, C.; Prieto, M.; Tanner, P.; Tavares, F.; d’Andrea, R. Testing and modeling chloride penetration into concrete. Constr. Build. Mater. 2013, 39, 9–18. [Google Scholar] [CrossRef]
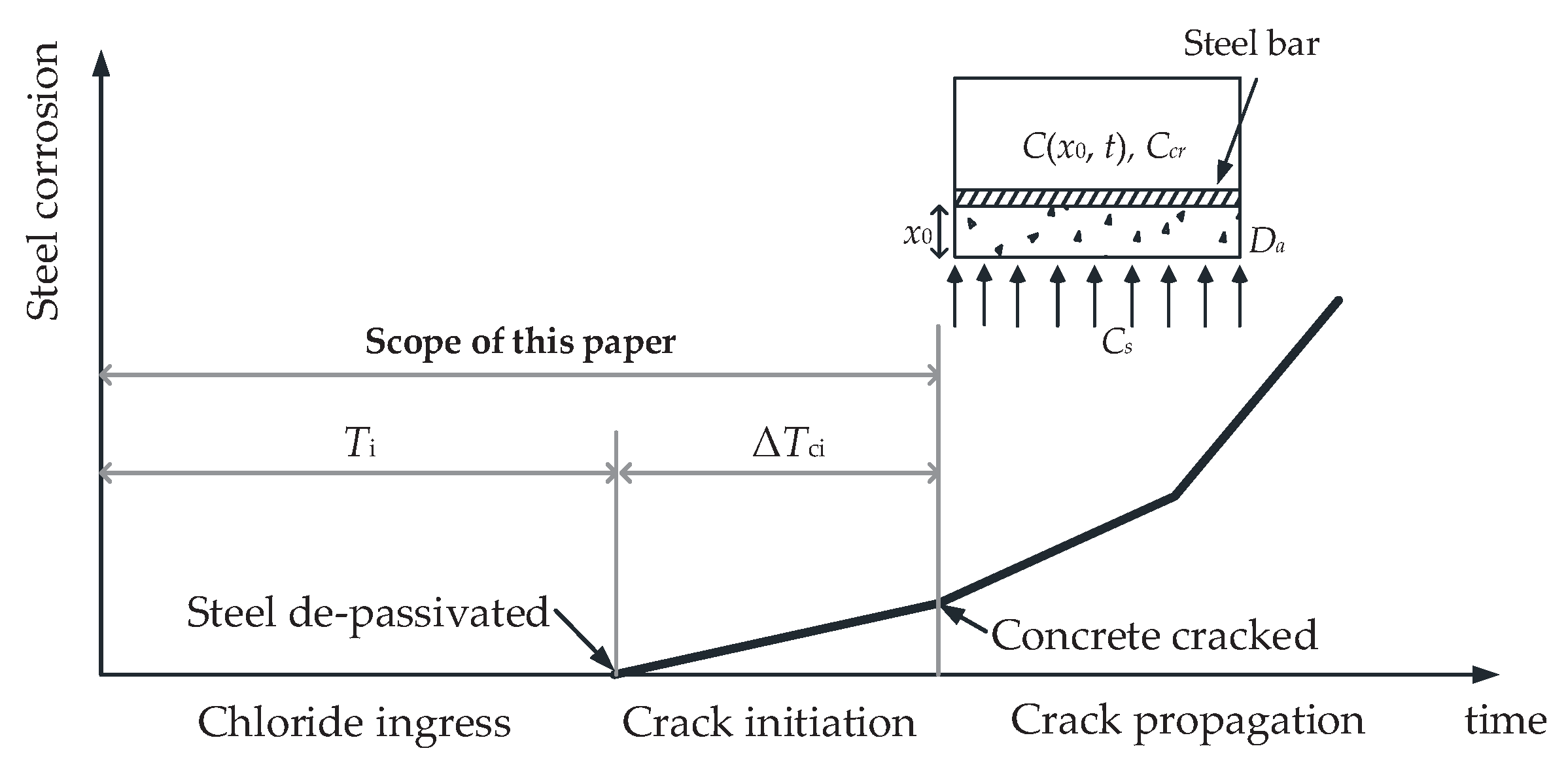
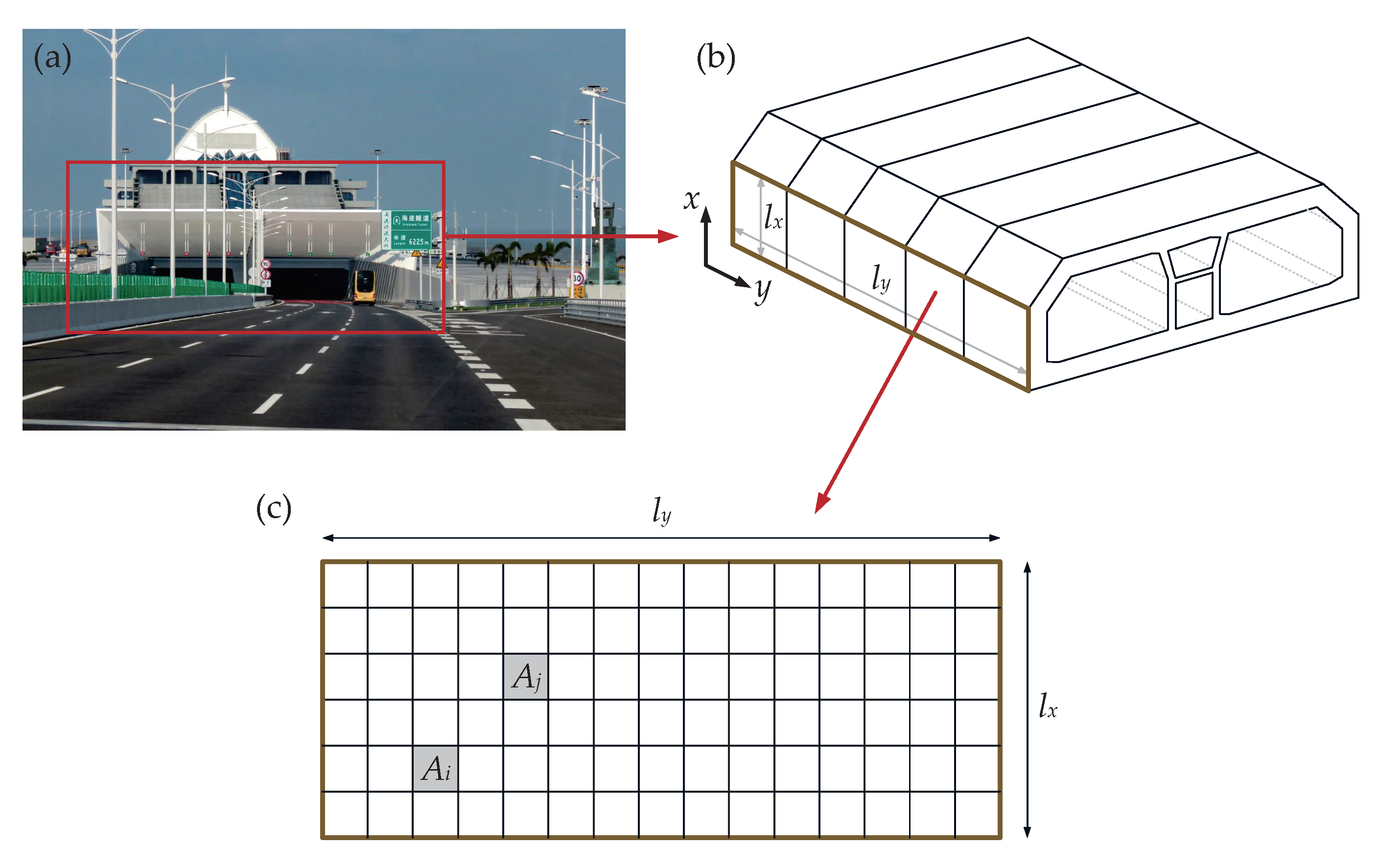
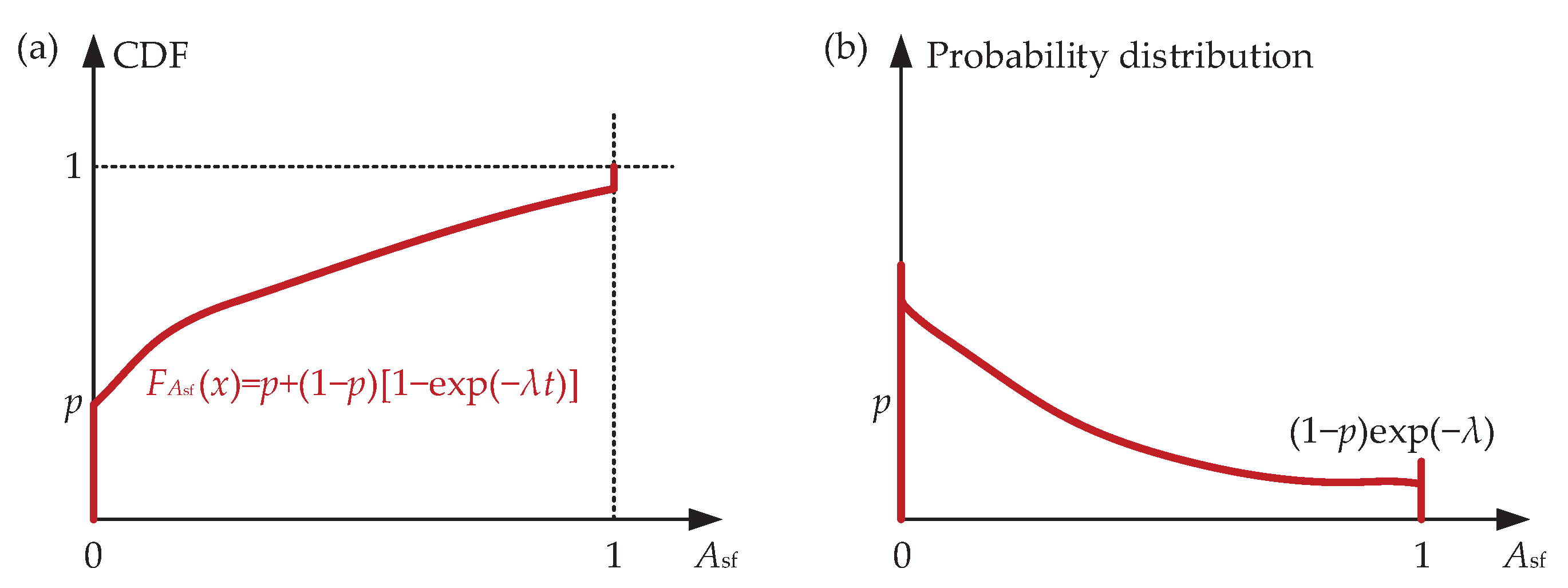
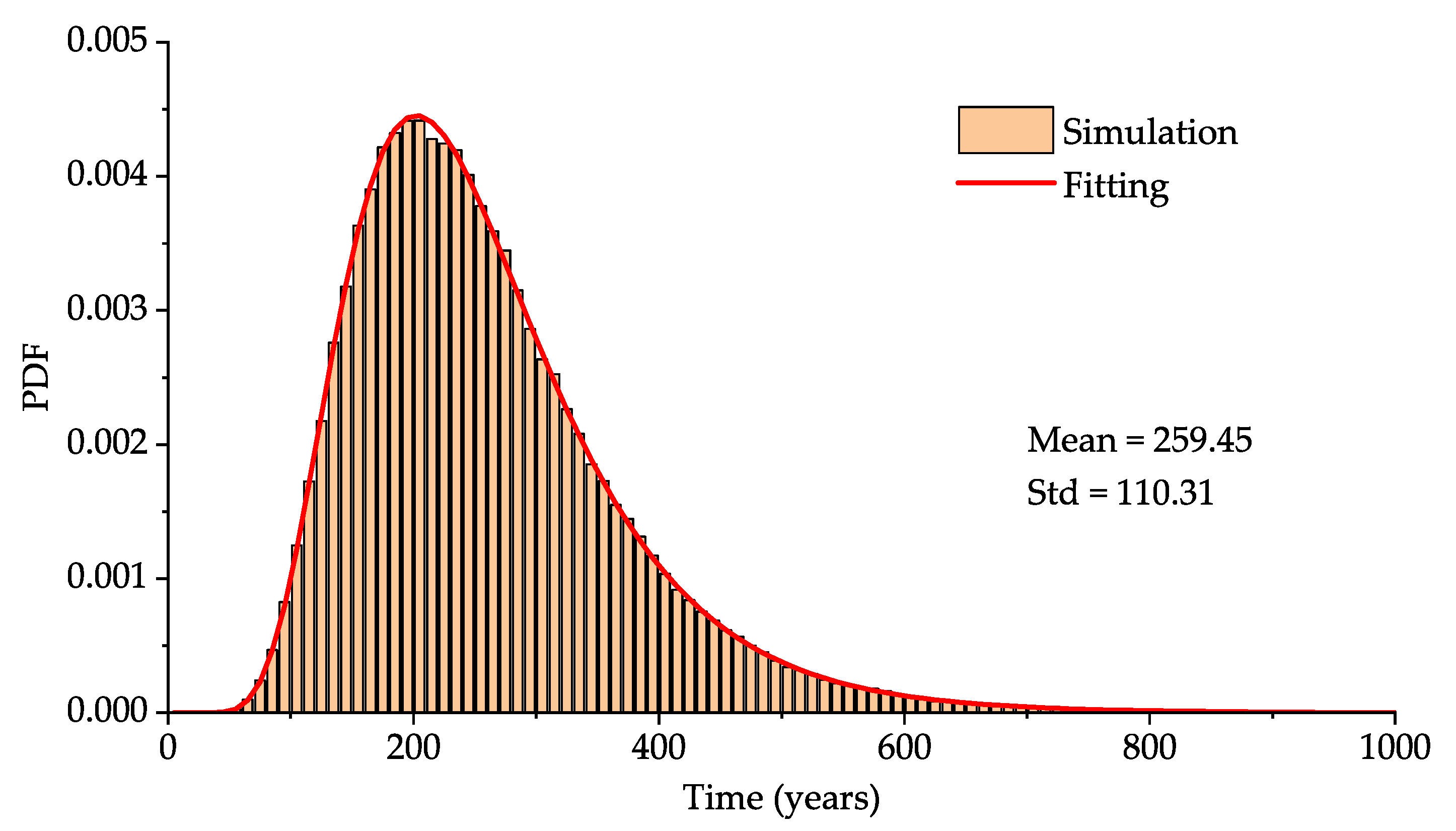
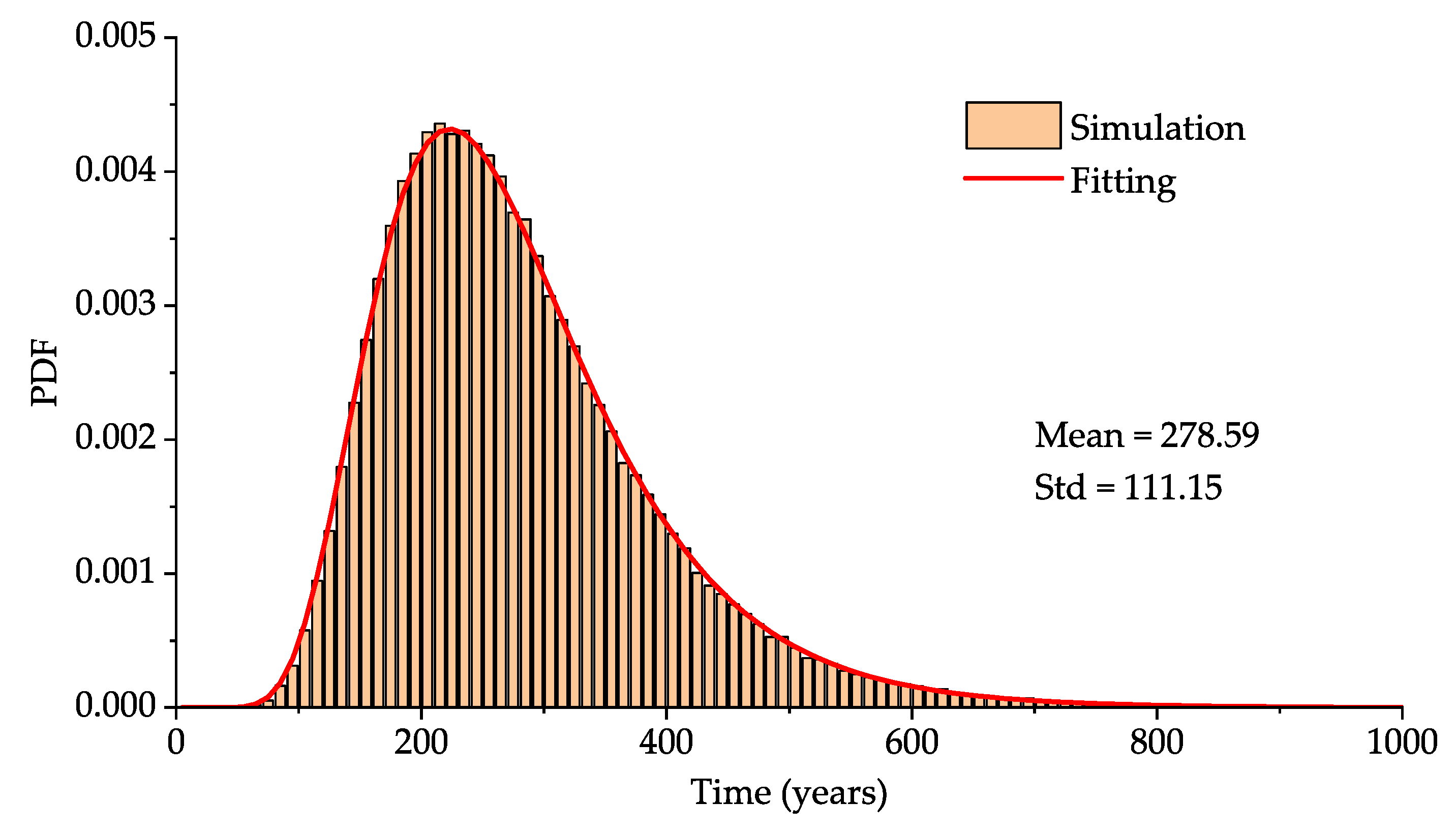

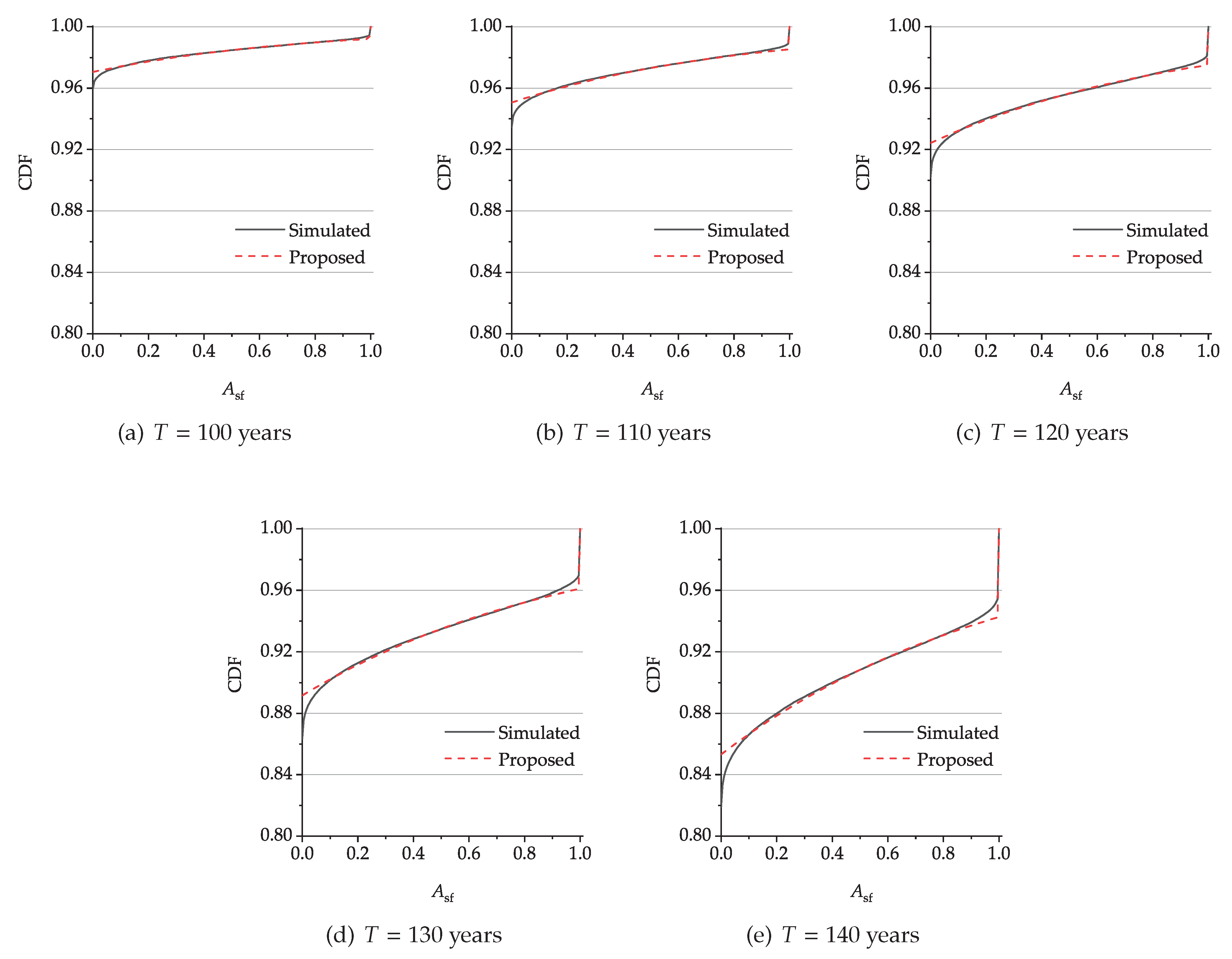
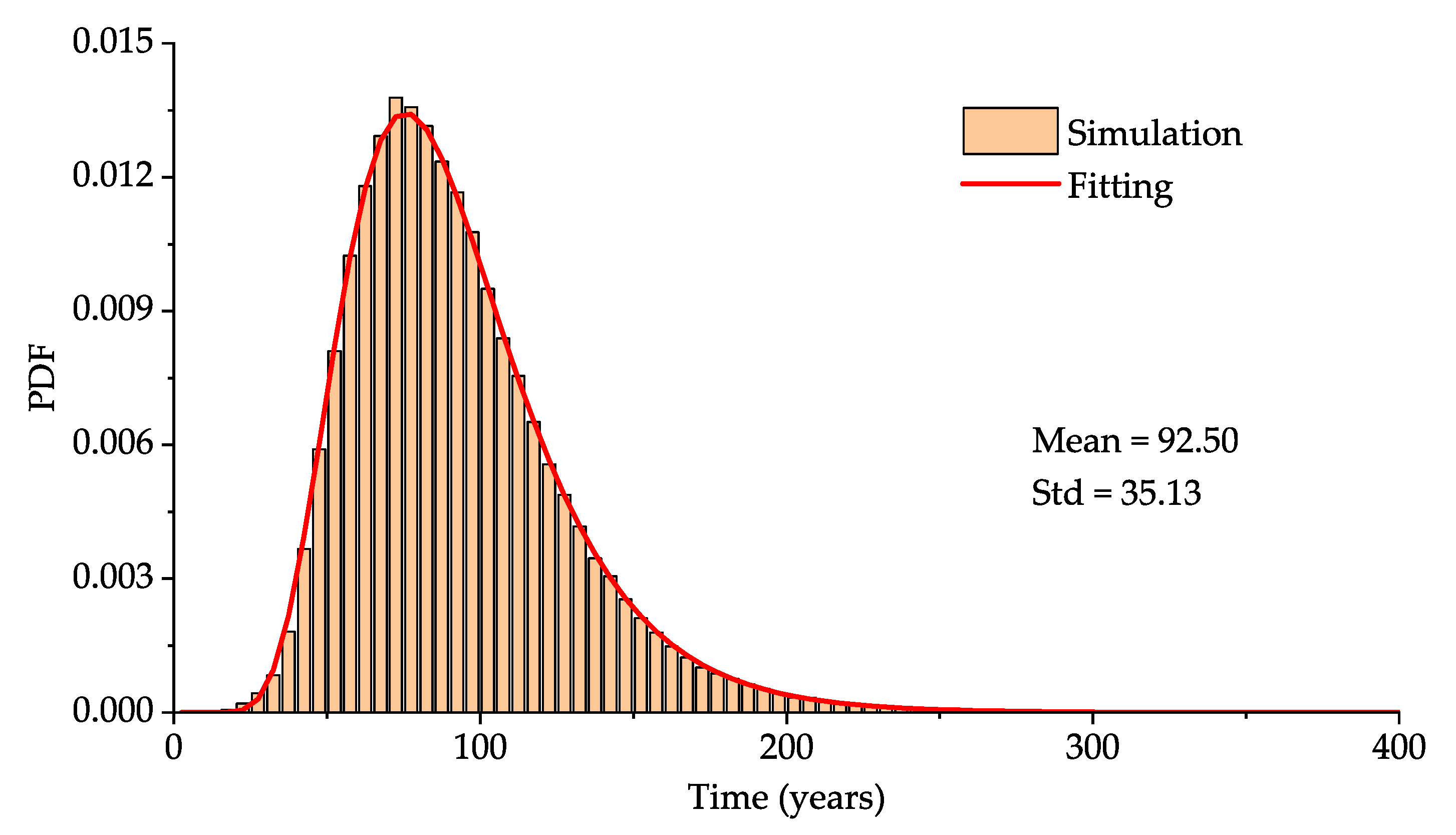
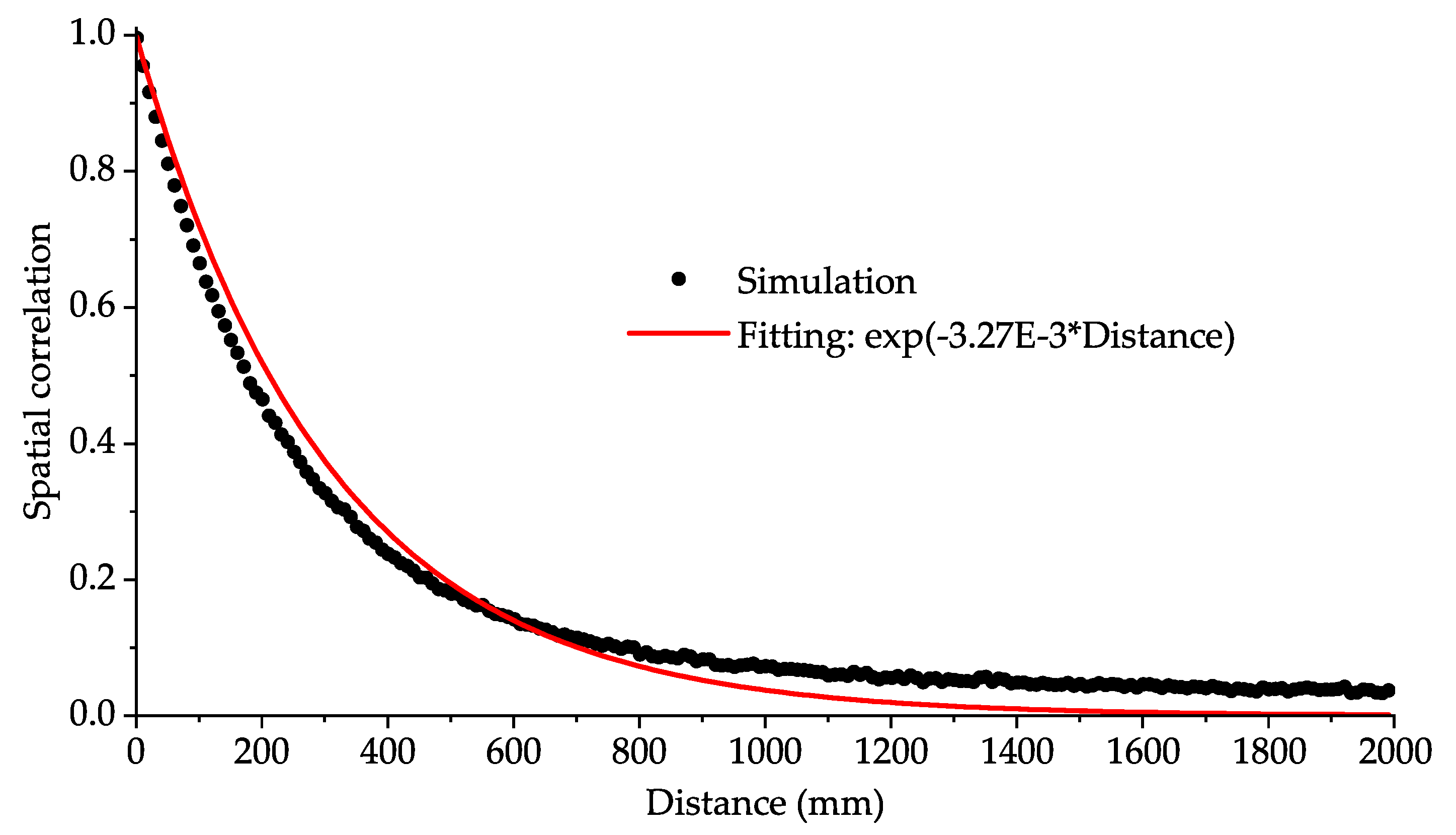
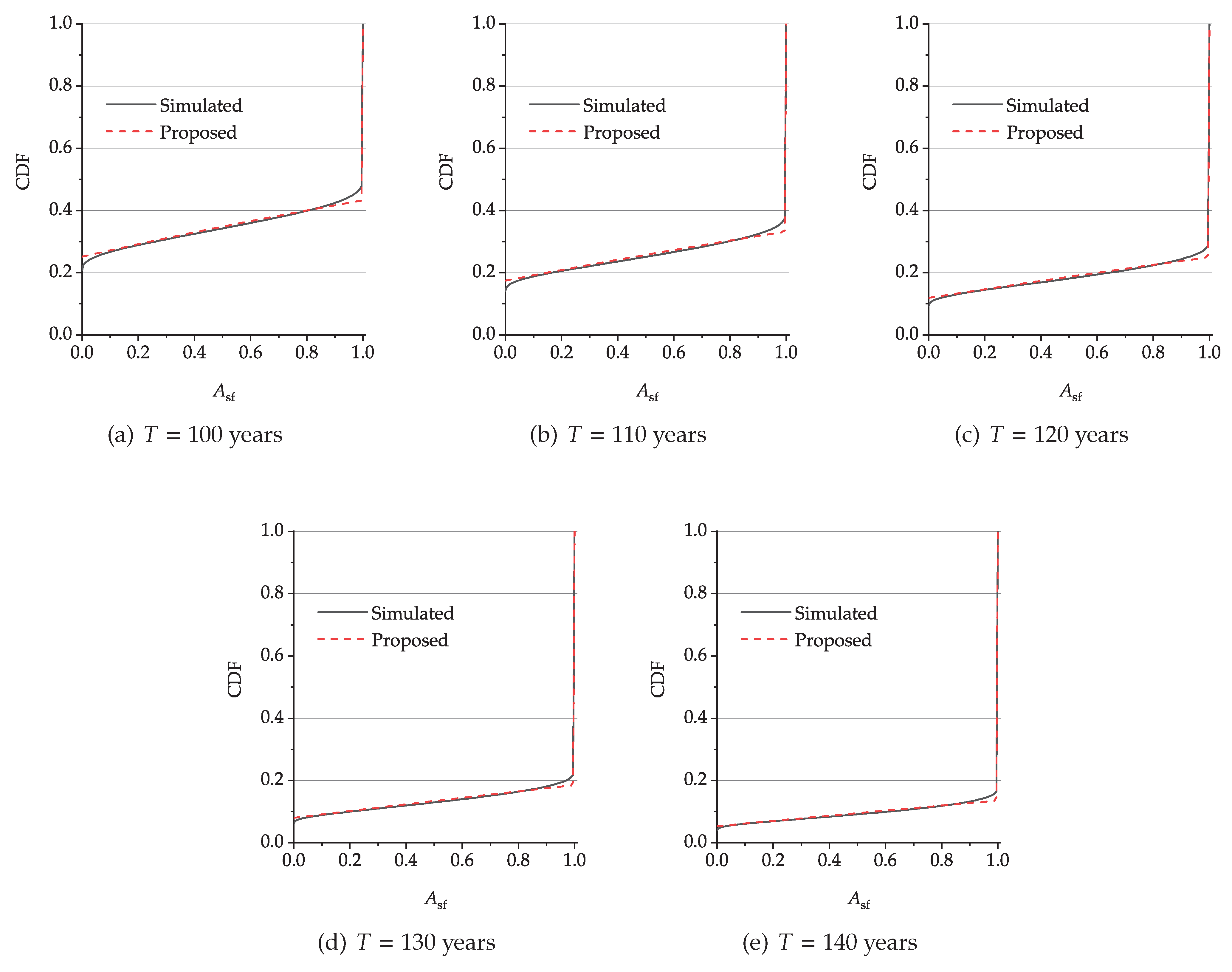
| p |
| Phase | Variable | Distribution Type | Statistics | Correlation Length (mm) | Sources |
|---|---|---|---|---|---|
| Chloride ingress | Lognormal | mean = 4.5%, COV * = 0.15 | 2000 | [5,10] | |
| (mm) | Normal | mean = 90, COV = 0.06 | 130 | [5,10] | |
| () ** | Lognormal | mean = 3.5, COV = 0.35 | 250 | [5,10] | |
| Normal | mean = 0.47, COV = 0.06 | 250 | [10] | ||
| Crack initiation | in Equation (6) | Uniform | lower = 4, upper = 8 | / | [39] |
| K in Equation (7) | Deterministic | / | [5] | ||
| in Equation (7) () | Lognormal | mean = 0.67, COV = 0.58 | 2000 | [5,46] |
| Service Life | Mean | Standard Deviation | ||||
|---|---|---|---|---|---|---|
| Proposed | Simulated | Error (%) | Proposed | Simulated | Error (%) | |
| 100 y | 0.016 | 0.016 | 0.124 | 0.112 | 0.111 | 0.981 |
| 110 y | 0.029 | 0.028 | 0.327 | 0.149 | 0.147 | 1.196 |
| 120 y | 0.046 | 0.046 | 0.035 | 0.188 | 0.186 | 0.899 |
| 130 y | 0.068 | 0.068 | 0.067 | 0.228 | 0.226 | 0.831 |
| 140 y | 0.095 | 0.095 | 0.302 | 0.267 | 0.265 | 0.898 |
| Service Life | Proposed | Simulated | Error (%) |
|---|---|---|---|
| 100 y | 0.029 | 0.034 | 14.647 |
| 110 y | 0.049 | 0.056 | 13.236 |
| 120 y | 0.075 | 0.085 | 12.101 |
| 130 y | 0.107 | 0.120 | 10.841 |
| 140 y | 0.145 | 0.162 | 10.016 |
| Service Life | Mean | Standard Deviation | ||||
|---|---|---|---|---|---|---|
| Proposed | Simulated | Error (%) | Proposed | Simulated | Error (%) | |
| 100 y | 0.654 | 0.656 | 0.306 | 0.443 | 0.438 | 1.084 |
| 110 y | 0.744 | 0.746 | 0.308 | 0.405 | 0.400 | 1.266 |
| 120 y | 0.814 | 0.816 | 0.208 | 0.360 | 0.355 | 1.375 |
| 130 y | 0.867 | 0.868 | 0.125 | 0.313 | 0.308 | 1.531 |
| 140 y | 0.905 | 0.906 | 0.073 | 0.268 | 0.264 | 1.518 |
| Service Life | Proposed | Simulated | Error (%) |
|---|---|---|---|
| 100 y | 0.770 | 0.747 | 3.018 |
| 110 y | 0.841 | 0.824 | 2.048 |
| 120 y | 0.893 | 0.880 | 1.451 |
| 130 y | 0.928 | 0.919 | 0.983 |
| 140 y | 0.952 | 0.946 | 0.601 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C. Explicitly Assessing the Durability of RC Structures Considering Spatial Variability and Correlation. Infrastructures 2021, 6, 156. https://doi.org/10.3390/infrastructures6110156
Wang C. Explicitly Assessing the Durability of RC Structures Considering Spatial Variability and Correlation. Infrastructures. 2021; 6(11):156. https://doi.org/10.3390/infrastructures6110156
Chicago/Turabian StyleWang, Cao. 2021. "Explicitly Assessing the Durability of RC Structures Considering Spatial Variability and Correlation" Infrastructures 6, no. 11: 156. https://doi.org/10.3390/infrastructures6110156
APA StyleWang, C. (2021). Explicitly Assessing the Durability of RC Structures Considering Spatial Variability and Correlation. Infrastructures, 6(11), 156. https://doi.org/10.3390/infrastructures6110156