Vision-Based Vibration Monitoring of Structures and Infrastructures: An Overview of Recent Applications
Abstract
1. Introduction
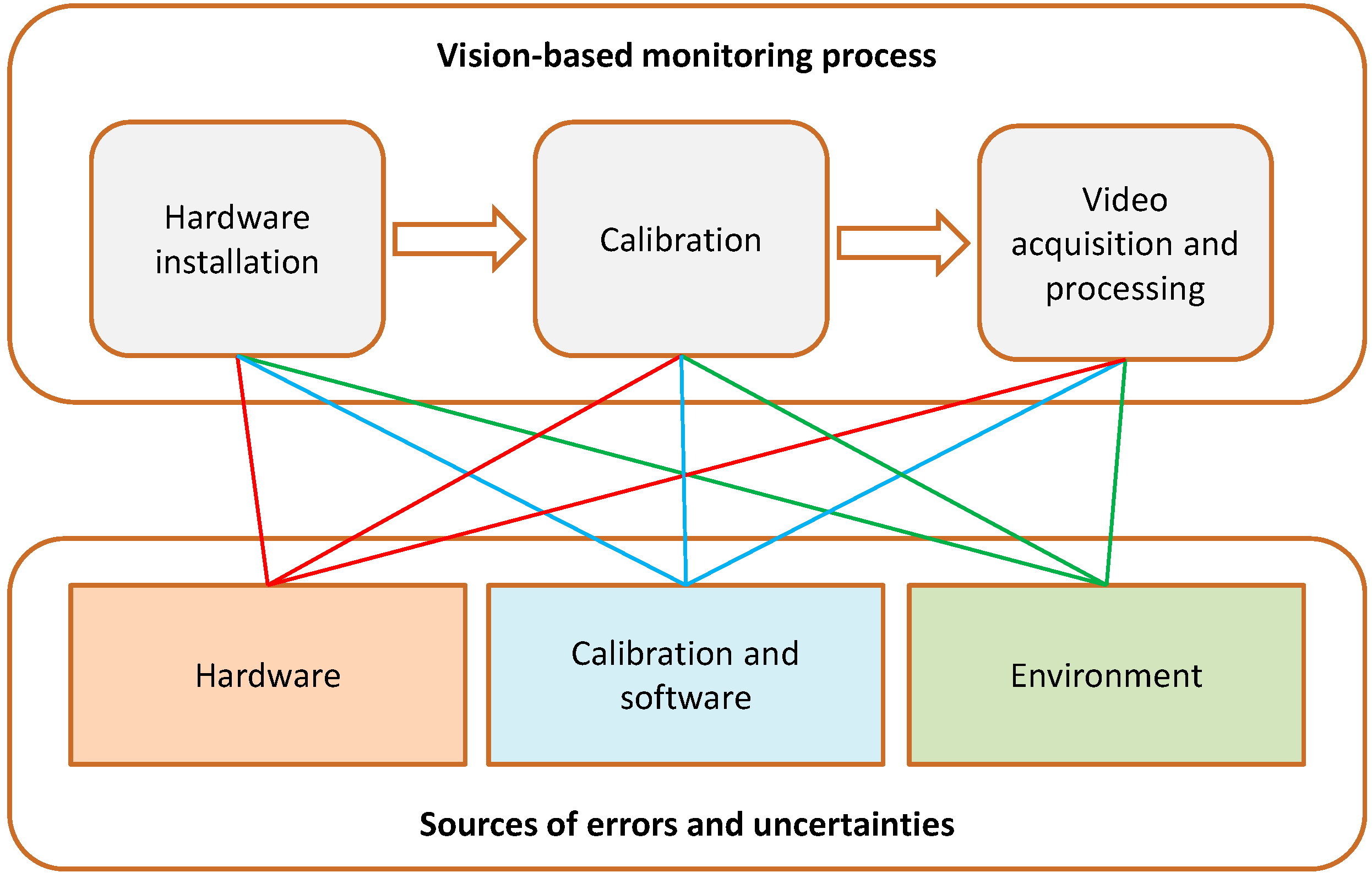
2. Brief Overview of Vision-Based Monitoring Systems
2.1. Monitoring Process
2.2. Errors and Uncertainties
3. Recent Field Applications of Vision-Based Vibration Monitoring in Civil Engineering
3.1. General Overview
3.2. Steel Bridges
3.3. Steel Footbridges
3.4. Steel Structures for Sport Stadiums
3.5. Reinforced Concrete Structures
3.6. Masonry Structures
3.7. Timber Footbridge
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; Wiley: Chichester, UK, 2000; pp. 1–576. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures: An Introduction and Guide for Applications, 1st ed.; Springer: New York, NY, USA, 2014; pp. 1–314. [Google Scholar]
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis, 1st ed.; Wiley: Chichester, UK, 2015; pp. 1–360. [Google Scholar]
- Mottershead, J.E.; Friswell, M.I. Model updating in structural dynamics: A survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Friswell, M.I.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics, 1st ed.; Springer: New York, NY, USA, 1995; pp. 1–286. [Google Scholar]
- Paultre, P.; Proulx, J.; Talbot, M. Dynamic testing procedures for highway bridges using traffic loads. J. Struct. Eng. 1995, 121, 362–376. [Google Scholar] [CrossRef]
- De Callafon, R.A.; Moaveni, B.; Conte, J.P.; He, X.; Udd, E. General realization algorithm for modal identification of linear dynamic systems. J. Eng. Mech. 2008, 134, 712–722. [Google Scholar] [CrossRef]
- Moaveni, B.; He, X.; Conte, J.P.; Restrepo, J.I.; Panagiotou, M. System identification study of a 7-story full-scale building slice tested on the UCSD-NEES shake table. J. Struct. Eng. 2011, 137, 705–717. [Google Scholar] [CrossRef]
- Shahidi, S.G.; Pakzad, S.N. Generalized response surface model updating using time domain data. J. Struct. Eng. 2014, 140, A4014001. [Google Scholar] [CrossRef]
- Asgarieh, E.; Moaveni, B.; Stavridis, A. Nonlinear finite element model updating of an infilled frame based on identified time-varying modal parameters during an earthquake. J. Sound Vib. 2014, 333, 6057–6073. [Google Scholar] [CrossRef]
- Asgarieh, E.; Moaveni, B.; Barbosa, A.R.; Chatzi, E. Nonlinear model calibration of a shear wall building using time and frequency data features. Mech. Syst. Signal Process. 2017, 85, 236–251. [Google Scholar] [CrossRef]
- Meggitt, J.W.R.; Moorhouse, A.T. Finite element model updating using in-situ experimental data. J. Sound Vib. 2020, 489, 115675. [Google Scholar] [CrossRef]
- Rainieri, C.; Notarangelo, M.A.; Fabbrocino, G. Experiences of dynamic identification and monitoring of bridges in serviceability conditions and after hazardous events. Infrastructures 2020, 5, 86. [Google Scholar] [CrossRef]
- Li, Q.; Fan, J.; Nie, J.; Li, Q.; Chen, Y. Crowd-induced random vibration of footbridge and vibration control using multiple tuned mass dampers. J. Sound Vib. 2010, 329, 4068–4092. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Magalhães, F.; Moutinho, C. Studies for controlling human-induced vibration of the Pedro e Inês footbridge, Portugal. Part 1: Assessment of dynamic behavior. Eng. Struct. 2010, 32, 1069–1081. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Magalhães, F.; Moutinho, C. Studies for controlling human-induced vibration of the Pedro e Ines footbridge, Portugal. Part 2: Implementation of tuned mass dampers. Eng. Struct. 2010, 32, 1082–1091. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Ragni, L.; Zona, A.; Nardini, L.; Salvatore, W. Design and experimental analysis of an externally prestressed steel and concrete footbridge equipped with vibration mitigation devices. J. Bridge Eng. 2016, 21, C5015001. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, H.X.; Moaveni, B.; Yang, W.G.; Huang, S.Q. Vibration monitoring of two long-span floors equipped with tuned mass dampers. Int. J. Struct. Stab. Dyn. 2019, 19, 1950101. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Carden, E.P.; Fanning, P. Vibration based condition monitoring: A review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Teughels, A.; De Roeck, G. Damage detection and parameter identification by finite element model updating. Arch. Comput. Methods Eng. 2005, 12, 123–164. [Google Scholar] [CrossRef]
- Farrar, C.; Lieven, N. Damage prognosis: The future of structural health monitoring. Philos. Trans. A Math. Phys. Eng. Sci. 2007, 365, 623–632. [Google Scholar] [CrossRef]
- Fraser, M.; Elgamal, A.; He, X.; Conte, J. Sensor network for structural health monitoring of a highway bridge. J. Comput. Civ. Eng. 2009, 24, 11–24. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective, 1st ed.; Wiley: Chichester, UK, 2012; pp. 1–631. [Google Scholar]
- Limongelli, M.P.; Celebi, M. Seismic Structural Health Monitoring: From Theory to Successful Applications, 1st ed.; Springer: New York, NY, USA, 2019; pp. 1–447. [Google Scholar]
- Lynch, J.; Loh, K. A summary review of wireless sensors and sensor networks for structural health monitoring. Shock Vibrat. Dig. 2006, 38, 91–128. [Google Scholar] [CrossRef]
- Li, J.; Mechitov, K.A.; Kim, R.E.; Spencer, B.F. Efficient time synchronization for structural health monitoring using wireless smart sensor networks. Struct. Control Health Monit. 2016, 23, 470–486. [Google Scholar] [CrossRef]
- Noel, A.B.; Abdaoui, A.; Elfouly, T.; Ahmed, M.H.; Badawy, A.; Shehata, M.S. Structural health monitoring using wireless sensor networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2017, 19, 1403–1423. [Google Scholar] [CrossRef]
- Sabato, A.; Niezrecki, C.; Fortino, G. Wireless MEMS-based accelerometer sensor boards for structural vibration monitoring: A review. IEEE Sens. J. 2017, 17, 226–235. [Google Scholar] [CrossRef]
- Abdulkarem, M.; Samsudin, K.; Rokhani, F.Z.; Rasid, M.F.A. Wireless sensor network for structural health monitoring: A contemporary review of technologies, challenges, and future direction. Struct. Health Monit. 2020, 19, 693–735. [Google Scholar] [CrossRef]
- Bastianini, F.; Matta, F.; Rizzo, A.; Galati, N.; Nanni, A. Overview of recent bridge monitoring applications using distributed Brillouin fiber optic sensors. J. Nondestruct. Test. 2007, 12, 269–276. [Google Scholar]
- Li, S.; Wu, Z. Development of distributed long-gage fiber optic sensing system for structural health monitoring. Struct. Health Monit. 2007, 6, 133–143. [Google Scholar] [CrossRef]
- Kim, D.H.; Feng, M.Q. Real-time structural health monitoring using a novel fiber-optic accelerometer system. IEEE Sens. J. 2007, 7, 536–543. [Google Scholar] [CrossRef]
- Matta, F.; Bastianini, F.; Galati, N.; Casadei, P.; Nanni, A. Distributed strain measurement in steel bridge with fiber optic sensors: Validation through diagnostic load test. J. Perform. Constr. Facil. 2008, 22, 264–273. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef]
- Narasimhan, S.; Wang, Y. Noncontact sensing technologies for bridge structural health assessment. J. Bridge Eng. 2020, 25, 02020001. [Google Scholar] [CrossRef]
- Xia, H.; De Roeck, G.; Zhang, N.; Maeck, J. Experimental analysis of a high-speed railway bridge under Thalys trains. J. Sound Vib. 2003, 268, 103–113. [Google Scholar] [CrossRef]
- Nassif, H.H.; Gindy, M.; Davis, J. Comparison of laser Doppler vibrometer with contact sensors for monitoring bridge deflection and vibration. NDT E Int. 2005, 38, 213–218. [Google Scholar] [CrossRef]
- Rothberg, S.J.; Allen, M.S.; Castellini, P.; Di Maio, D.; Dirckx, J.J.J.; Ewins, D.J.; Halkon, B.J.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt. Lasers Eng. 2017, 99, 11–22. [Google Scholar] [CrossRef]
- Garg, P.; Moreu, F.; Ozdagli, A.; Taha, M.R.; Mascareñas, D. Noncontact dynamic displacement measurement of structures using a moving laser doppler vibrometer. J. Bridge Eng. 2019, 24, 04019089. [Google Scholar] [CrossRef]
- Farrar, C.R.; Darling, T.W.; Migliori, A.; Baker, W.E. Microwave interferometers for non-contact vibration measurements on large structures. Mech. Syst. Signal Process. 1999, 13, 241–253. [Google Scholar] [CrossRef]
- Pieraccini, M.; Parrini, F.; Fratini, M.; Atzeni, C.; Spinelli, P.; Micheloni, M. Static and dynamic testing of bridges through microwave interferometry. NDT E Int. 2007, 40, 208–214. [Google Scholar] [CrossRef]
- Gentile, C.; Bernardini, G. An interferometric radar for noncontact measurement of deflections on civil engineering structures: Laboratory and full-scale tests. Struct. Infrastruct. Eng. 2010, 6, 521–534. [Google Scholar] [CrossRef]
- Gentile, C. Deflection measurement on vibrating stay cables by non-contact microwave interferometer. NDT E Int. 2010, 43, 231–240. [Google Scholar] [CrossRef]
- Gentile, C.; Cabboi, A. Vibration-based structural health monitoring of stay cables by microwave remote sensing. Smart Struct. Syst. 2015, 16, 263–280. [Google Scholar] [CrossRef]
- Whitlow, R.D.; Haskins, R.; McComas, S.L.; Crane, C.K.; Howard, I.L.; McKenna, M.H. Remote bridge monitoring using infrasound. J. Bridge Eng. 2019, 24, 04019023. [Google Scholar] [CrossRef]
- Lobo-Aguilar, S.; Zhang, Z.; Jiang, Z.; Christenson, R. Infrasound-based noncontact sensing for bridge structural health monitoring. J. Bridge Eng. 2019, 24, 04019033. [Google Scholar] [CrossRef]
- Brown, C.J.; Karuna, R.; Ashkenazi, V.; Roberts, G.W.; Evans, R.A. Monitoring of structures using the Global Positioning System. Proc. Inst. Civil Eng. 1999, 134, 97–105. [Google Scholar] [CrossRef]
- Roberts, G.W.; Meng, X.; Dodson, A.H. Integrating a global positioning system and accelerometers to monitor the deflection of bridges. J. Surv. Eng. 2004, 130, 65–72. [Google Scholar] [CrossRef]
- Meng, X.; Dodson, A.H.; Roberts, G.W. Detecting bridge dynamics with GPS and triaxial accelerometers. Eng. Struct. 2007, 29, 3178–3184. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Measurement of the dynamic displacements and of the modal frequencies of a short-span pedestrian bridge using GPS and an accelerometer. Eng. Struct. 2011, 33, 10–17. [Google Scholar] [CrossRef]
- Hoppe, E.; Bruckno, B.; Campbell, E.; Acton, S.; Vaccari, A.; Stuecheli, M.; Bohane, A.; Falorni, G.; Morgan, J. Transportation infrastructure monitoring using satellite remote sensing. In Materials and infrastructures 1; Torrenti, J.M., La Torre, F., Eds.; Wiley: Chichester, UK, 2016; Chapter 14; pp. 185–198. [Google Scholar] [CrossRef]
- Huang, Q.; Monserrat, O.; Crosetto, M.; Crippa, B.; Wang, Y.; Jiang, J.; Ding, Y. Displacement monitoring and health evaluation of two bridges using Sentinel-1 SAR images. Remote Sens. 2018, 10, 1714. [Google Scholar] [CrossRef]
- Lazecky, M.; Hlavacova, I.; Bakon, M.; Sousa, J.J.; Perissin, D.; Patricio, G. Bridge displacements monitoring using space-borne X-band SAR interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 205–210. [Google Scholar] [CrossRef]
- Zhu, M.; Wan, X.; Fei, B.; Qiao, Z.; Ge, C.; Minati, F.; Vecchioli, F.; Li, J.; Costantini, M. Detection of building and infrastructure instabilities by automatic spatiotemporal analysis of satellite SAR interferometry measurements. Remote Sens. 2018, 10, 1816. [Google Scholar] [CrossRef]
- Cavalaglia, N.; Kita, A.; Falco, S.; Trillo, F.; Costantini, M.; Ubertini, F. Satellite radar interferometry and in-situ measurements for static monitoring of historical monuments: The case of Gubbio, Italy. Remote Sens. Environ. 2019, 235, 11453. [Google Scholar] [CrossRef]
- Hoppe, E.J.; Novali, F.; Rucci, A.; Fumagalli, A.; Del Conte, S.; Falorni, G.; Toro, N. Deformation monitoring of posttensioned bridges using high-resolution satellite remote sensing. J. Bridge Eng. 2019, 24, 04019115. [Google Scholar] [CrossRef]
- Psimoulis, P.A.; Stiros, S.C. Measurement of deflections and of oscillation frequencies of engineering structures using Robotic Theodolites (RTS). Eng. Struct. 2007, 29, 3312–3324. [Google Scholar] [CrossRef]
- Psimoulis, P.A.; Stiros, S.C. Measuring deflections of a short-span railway bridge using a robotic total station. J. Bridge Eng. 2013, 18, 182–185. [Google Scholar] [CrossRef]
- Forno, C.; Brown, S.; Hunt, R.A.; Kearney, A.M.; Oldfield, S. The measurement of deformation of a bridge by moirè photography and photogrammetry. Strain 1991, 27, 83–87. [Google Scholar] [CrossRef]
- Ri, S.; Fujigaki, M.; Morimoto, Y. Sampling moiré method for accurate small deformation distribution measurement. Exp. Mech. 2010, 50, 501–508. [Google Scholar] [CrossRef]
- Ri, S.; Muramatsu, T.; Saka, M.; Nanbara, K.; Kobayashi, D. Accuracy of the sampling moiré method and its application to deflection measurements of large-scale structures. Exp. Mech. 2012, 52, 331–340. [Google Scholar] [CrossRef]
- Kulkarni, R.; Gorthi, S.S.; Rastogi, P. Measurement of in-plane and out-of-plane displacements and strains using digital holographic moiré. J. Mod. Opt. 2014, 61, 755–762. [Google Scholar] [CrossRef][Green Version]
- Chen, X.; Chang, C.C. In-plane movement measurement technique using digital sampling moiré method. J. Bridge Eng. 2019, 24, 04019013. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H.W. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications, 1st ed.; Springer: New York, NY, USA, 2009; pp. 1–316. [Google Scholar]
- Kohut, P.; Holak, K. Vision-Based Monitoring System. In Advanced Structural Damage Detection, 1st ed.; Stepinski, T., Uhl, T., Staszewski, W., Eds.; Wiley: Chichester, UK, 2013; pp. 279–320. [Google Scholar]
- Schumacher, T.; Shariati, A. Monitoring of structures and mechanical systems using virtual visual sensors for video analysis: Fundamental concept and proof of feasibility. Sensors 2013, 13, 16551–16564. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z.; Liu, T. A review of machine vision-based structural health monitoring: Methodologies and applications. J. Sens. 2016, 2016, 7103039. [Google Scholar] [CrossRef]
- Ye, X.W.; Yi, T.H.; Dong, C.Z.; Liu, T. Vision-based structural displacement measurement: System performance evaluation and influence factor analysis. Measurement 2016, 88, 372–384. [Google Scholar] [CrossRef]
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and optical methods in structural dynamics—A review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Spencer, B.F.; Hoskere, V.; Narazaki, Y. Advances in computer vision-based civil infrastructure inspection and monitoring. Engineering 2019, 5, 199–222. [Google Scholar] [CrossRef]
- Dong, C.Z.; Catbas, F.N. A review of computer vision–based structural health monitoring at local and global levels. Struct. Health Monit. 2020. in print. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital imaging techniques in experimental stress analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for inplane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Pan, B.; Li, K. A fast digital image correlation method for deformation measurement. Opt. Lasers Eng. 2011, 49, 841–847. [Google Scholar] [CrossRef]
- Pan, B.; Li, K.; Tong, W. Fast, robust and accurate digital image correlation calculation without redundant computations. Exp. Mech. 2013, 53, 1277–1289. [Google Scholar] [CrossRef]
- Pan, B. Bias error reduction of digital image correlation using Gaussian pre-filtering. Opt. Lasers Eng. 2013, 51, 1161–1167. [Google Scholar] [CrossRef]
- Pan, B. An evaluation of convergence criteria for digital image correlation using inverse compositional Gauss–Newton algorithm. Strain 2014, 50, 48–56. [Google Scholar] [CrossRef]
- Wang, Z.; Kieu, H.; Nguyen, H.; Le, M. Digital image correlation in experimental mechanics and image registration in computer vision: Similarities, differences and complements. Opt. Lasers Eng. 2015, 65, 18–27. [Google Scholar] [CrossRef]
- Pan, B.; Wang, B. Digital image correlation with enhanced accuracy and efficiency: A comparison of two subpixel registration algorithms. Exp. Mech. 2016, 56, 1395–1409. [Google Scholar] [CrossRef]
- Zhong, F.; Quan, C. Efficient digital image correlation using gradient orientation. Opt. Laser Technol. 2018, 106, 417–426. [Google Scholar] [CrossRef]
- Mathworks MATLAB Computer Vision Toolbox. Available online: https://mathworks.com/products/computer-vision.html (accessed on 29 October 2020).
- Dantec Dynamics, Laser Optical Measurements Systems and Sensors. Available online: https://www.dantecdynamics.com/ (accessed on 29 October 2020).
- Correlated Solutions, Leaders in Non-Contact Measurements Solutions. Available online: https://www.correlatedsolutions.com/ (accessed on 29 October 2020).
- IMETRUM Non-Contact Precision Measurement. Available online: https://www.imetrum.com/ (accessed on 29 October 2020).
- Liu, C.; Torralba, A.; Freeman, W.T.; Durand, F.; Adelson, E.H. Motion magnification. ACM Trans. Graphics 2005, 24, 519–526. [Google Scholar] [CrossRef]
- Wu, H.Y.; Rubinstein, M.; Shih, E.; Guttag, J.V.; Durand, F.; Freeman, W.T. Eulerian video magnification for revealing subtle changes in the world. ACM Trans. Graphics 2012, 31, 1–8. [Google Scholar] [CrossRef]
- Wadhwa, N.; Rubinstein, M.; Durand, F.; Freeman, W.T. Phase-based video motion processing. ACM Trans. Graphics 2013, 32, 80. [Google Scholar] [CrossRef]
- Davis, A.; Rubinstein, M.; Wadhwa, N.; Mysore, G.; Durand, F.; Freeman, W. The visual microphone: Passive recovery of sound from video. ACM Trans. Graph. 2014, 33, 79. [Google Scholar] [CrossRef]
- Ngo, A.C.L.; Phan, R.C.W. Seeing the invisible: Survey of video motion magnification and small motion analysis. ACM Comput. Surv. 2019, 52, 114. [Google Scholar] [CrossRef]
- Harmanci, Y.E.; Gülan, U.; Holzner, M.; Chatzi, E. A novel approach for 3D-structural identification through video recording: Magnified tracking. Sensors 2019, 19, 1229. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Sutton, M.A.; Bruck, H.A.; Schreier, H.W. Quantitative error assessment in pattern matching: Effects of intensity pattern noise, interpolation, strain and image contrast on motion measurements. Strain 2009, 45, 160–178. [Google Scholar] [CrossRef]
- Bornert, M.; Brémand, F.; Doumalin, P.; Dupré, J.C.; Fazzini, M.; Grédiac, M.; Hild, F.; Mistou, S.; Molimard, J.; Orteu, J.J.; et al. Assessment of digital image correlation measurement errors: Methodology and results. Exp. Mech. 2009, 49, 353–370. [Google Scholar] [CrossRef]
- Amiot, F.; Bornert, M.; Doumalin, P.; Dupré, J.C.; Fazzini, M.; Orteu, J.J.; Poilâne, C.; Robert, L.; Rotinat, R.; Toussaint, E.; et al. Assessment of digital image correlation measurement accuracy in the ultimate error regime: Main results of a collaborative benchmark. Strain 2013, 49, 483–496. [Google Scholar] [CrossRef]
- D’Emilia, G.; Razzè, L.; Zappa, E. Uncertainty analysis of high frequency image-based vibration measurements. Measurement 2013, 46, 2630–2637. [Google Scholar] [CrossRef]
- Zappa, E.; Mazzoleni, P.; Matinmanesh, A. Uncertainty assessment of digital image correlation method in dynamic applications. Opt. Lasers Eng. 2014, 56, 140–151. [Google Scholar] [CrossRef]
- Zappa, E.; Matinmanesh, A.; Mazzoleni, P. Evaluation and improvement of digital image correlation uncertainty in dynamic conditions. Opt. Lasers Eng. 2014, 59, 82–92. [Google Scholar] [CrossRef]
- Mazzoleni, P.; Matta, F.; Zappa, E.; Sutton, M.A.; Cigada, A. Gaussian pre-filtering for uncertainty minimization in digital image correlation using numerically-designed speckle patterns. Opt. Lasers Eng. 2015, 66, 19–33. [Google Scholar] [CrossRef]
- Mazzoleni, P.; Zappa, E.; Matta, F.; Sutton, M.A. Thermo-mechanical toner transfer for high-quality digital image correlation speckle patterns. Opt. Lasers Eng. 2015, 75, 72–80. [Google Scholar] [CrossRef]
- Liu, C.; Yuan, Y.; Zhang, M. Uncertainty analysis of displacement measurement with Imetrum Video Gauge. ISA Trans. 2016, 65, 547–555. [Google Scholar] [CrossRef]
- Gao, Z.; Xu, X.; Su, Y.; Zhang, Q. Experimental analysis of image noise and interpolation bias in digital image correlation. Opt. Lasers Eng. 2016, 81, 46–53. [Google Scholar] [CrossRef]
- Blaysat, B.; Grédiac, M.; Sur, F. On the propagation of camera sensor noise to displacement maps obtained by DIC—An experimental study. Exp. Mech. 2016, 56, 919–944. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, Q.; Su, Y.; Wu, S. Accuracy evaluation of optical distortion calibration by digital image correlation. Opt. Lasers Eng. 2017, 98, 143–152. [Google Scholar] [CrossRef]
- Xu, X.; Su, Y.; Zhang, Q. Theoretical estimation of systematic errors in local deformation measurements using digital image correlation. Opt. Lasers Eng. 2017, 88, 265–279. [Google Scholar] [CrossRef]
- Su, Y.; Gao, Z.; Zhang, Q.; Wu, S. Spatial uncertainty of measurement errors in digital image correlation. Opt. Lasers Eng. 2018, 110, 113–121. [Google Scholar] [CrossRef]
- Sutton, M.A.; Wolters, W.J.; Peters, W.H.; Ranson, W.F.; McNeill, S.R. Determination of displacements using an improved digital correlation method. Image Vision Comput. 1983, 1, 133–139. [Google Scholar] [CrossRef]
- Sutton, M.A.; Cheng, M.; Peters, W.H.; Chao, Y.J.; McNeill, S.R. Application of an optimized digital correlation method to planar deformation analysis. Image Vision Comput. 1986, 4, 143–150. [Google Scholar] [CrossRef]
- Lee, J.J.; Shinozuka, M. Real-time displacement measurement of a flexible bridge using digital image processing techniques. Exp. Mech. 2006, 46, 105–114. [Google Scholar] [CrossRef]
- Yoneyama, S.; Kitagawa, A.; Iwata, S.; Tani, K.; Kikuta, H. Bridge deflection measurement using digital image correlation. Exp. Tech. 2007, 31, 34–40. [Google Scholar] [CrossRef]
- Park, J.W.; Lee, J.J.; Jung, H.J.; Myung, H. Vision-based displacement measurement method for high-rise building structures using partitioning approach. NDT E Int. 2010, 43, 642–647. [Google Scholar] [CrossRef]
- Peddle, J.; Goudreau, A.; Carlson, E.; Santini-Bell, E. Bridge displacement measurement through digital image correlation. Bridge Struct. 2011, 7, 165–173. [Google Scholar] [CrossRef]
- Sładek, J.; Ostrowska, K.; Kohut, P.; Holak, K.; Gaska, A.; Uhl, T. Development of a vision based deflection measurement system and its accuracy assessment. Measurement 2013, 46, 1237–1249. [Google Scholar] [CrossRef]
- Park, S.W.; Park, H.S.; Kim, J.H.; Adeli, H. 3D displacement measurement model for health monitoring of structures using a motion capture system. Measurement 2015, 59, 352–362. [Google Scholar] [CrossRef]
- Quan, C.; Tay, C.J.; Sun, W.; He, X. Determination of three-dimensional displacement using two-dimensional digital image correlation. Appl. Opt. 2008, 47, 583–593. [Google Scholar] [CrossRef] [PubMed]
- Yoneyama, S.; Ueda, H. Bridge deflection measurement using digital image correlation with camera movement correction. Mater. Trans. 2012, 53, 285–290. [Google Scholar] [CrossRef]
- Hoult, N.A.; Take, W.A.; Lee, C.; Dutton, M. Experimental accuracy of two dimensional strain measurements using digital image correlation. Eng. Struct. 2013, 46, 718–726. [Google Scholar] [CrossRef]
- Gencturk, B.; Hossain, K.; Kapadia, A.; Labib, E.; Mo, Y.L. Use of digital image correlation technique in full-scale testing of prestressed concrete structures. Measurement 2014, 7, 505–515. [Google Scholar] [CrossRef]
- Ghorbani, R.; Matta, F.; Sutton, M.A. Full-field deformation measurement and crack mapping on confined masonry walls using digital image correlation. Exp. Mech. 2015, 55, 227–243. [Google Scholar] [CrossRef]
- Almeida Santos, C.; Oliveira Costa, C.; Batista, J. A vision-based system for measuring the displacements of large structures: Simultaneous adaptive calibration and full motion estimation. Mech. Syst. Signal Process. 2016, 72–73, 678–694. [Google Scholar] [CrossRef]
- Shan, B.; Wang, L.; Huo, X.; Yuan, W.; Xue, Z. A bridge deflection monitoring system based on CCD. Adv. Mater. Sci. Eng. 2016, 4857373. [Google Scholar] [CrossRef]
- Pan, B.; Tian, L.; Song, X. Real-time, non-contact and targetless measurement of vertical deflection of bridges using off-axis digital image correlation. NDT E Int. 2016, 79, 73–80. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.C.; Cho, S.; Sim, S.H. Computer vision-based structural displacement measurement robust to light-induced image degradation for in-service bridges. Sensors 2017, 17, 2317. [Google Scholar] [CrossRef] [PubMed]
- Park, J.W.; Moon, D.S.; Yoon, H.; Gomez, F.; Spencer, B.F.; Kim, J.R. Visual-inertial displacement sensing using data fusion of vision-based displacement with acceleration. Struct. Control Health Monit. 2018, 25, e2122. [Google Scholar] [CrossRef]
- Alipour, M.; Washlesky, S.J.; Harris, D.K. Field deployment and laboratory evaluation of 2D digital image correlation for deflection sensing in complex environments. J. Bridge Eng. 2019, 24, 04019010. [Google Scholar] [CrossRef]
- Carmo, R.N.F.; Valença, J.; Bencardino, F.; Cristofaro, S.; Chiera, D. Assessment of plastic rotation and applied load in reinforced concrete, steel and timber beams using image-based analysis. Eng. Struct. 2019, 198, 109519. [Google Scholar] [CrossRef]
- Halding, P.S.; Christensen, C.O.; Schmidt, J.W. Surface rotation correction and strain precision of wide-angle 2D DIC for field use. J. Bridge Eng. 2019, 24, 04019008. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.C.; Jeong, S.; Lee, Y.J.; Sim, S.H. Long-term displacement measurement of full-scale bridges using camera ego-motion compensation. Mech. Syst. Signal Process. 2020, 140, 106651. [Google Scholar] [CrossRef]
- Dong, C.Z.; Celik, O.; Catbas, F.N.; O’Brien, E.J.; Taylor, S. Structural displacement monitoring using deep learning-based full field optical flow methods. Struct. Infrastruct. Eng. 2020, 16, 51–71. [Google Scholar] [CrossRef]
- Schmidt, T.; Tyson, J.; Galanulis, K. Full-field dynamic displacement and strain measurement using advanced 3d image correlation photogrammetry: Part 1. Exp. Tech. 2003, 27, 47–50. [Google Scholar] [CrossRef]
- Chang, C.C.; Ji, Y.F. Flexible videogrammetric technique for three-dimensional structural vibration measurement. J. Eng. Mech. 2007, 133, 656–664. [Google Scholar] [CrossRef]
- Jurjo, D.L.B.R.; Magluta, C.; Roitman, N.; Gonçalves, P.B. Experimental methodology for the dynamic analysis of slender structures based on digital image processing techniques. Mech. Syst. Signal Process. 2010, 24, 1369–1382. [Google Scholar] [CrossRef]
- Choi, H.S.; Cheung, J.H.; Kim, S.H.; Ahn, J.H. Structural dynamic displacement vision system using digital image processing. NDT E Int. 2011, 44, 597–608. [Google Scholar] [CrossRef]
- Yang, Y.S.; Huang, C.W.; Wu, C.L. A simple image-based strain measurement method for measuring the strain fields in an RC-wall experiment. Earthq. Eng. Struct. Dyn. 2012, 41, 1–17. [Google Scholar] [CrossRef]
- Wang, W.; Mottershead, J.E.; Siebert, T.; Pipino, A. Frequency response functions of shape features from full-field vibration measurements using digital image correlation. Mech. Syst. Signal Process. 2012, 28, 333–347. [Google Scholar] [CrossRef]
- Mas, D.; Espinosa, J.; Roig, A.B.; Ferrer, B.; Perez, J.; Illueca, C. Measurement of wide frequency range structural microvibrations with a pocket digital camera and sub-pixel techniques. Appl. Opt. 2012, 51, 2664–2671. [Google Scholar] [CrossRef]
- Wu, L.J.; Casciati, F.; Casciati, S. Dynamic testing of a laboratory model via vision-based sensing. Eng. Struct. 2014, 60, 113–125. [Google Scholar] [CrossRef]
- Feng, D.M.; Feng, M.Q. Vision-based multi-point displacement measurement for structural health monitoring. Struct. Control Health Monit. 2015, 23, 876–890. [Google Scholar] [CrossRef]
- Chen, J.G.; Wadhwa, N.; Cha, Y.J.; Durand, F.; Freeman, W.T.; Buyukozturk, O. Modal identification of simple structures with high-speed video using motion magnification. J. Sound Vib. 2015, 345, 58–71. [Google Scholar] [CrossRef]
- Oh, B.K.; Hwang, J.W.; Kim, Y.; Cho, T.; Park, H.S. Vision-based system identification technique for building structures using a motion capture system. J. Sound Vib. 2015, 356, 72–85. [Google Scholar] [CrossRef]
- Lei, X.; Jin, Y.; Guo, J.; Zhu, C.A. Vibration extraction based on fast NCC algorithm and high-speed camera. Appl. Opt. 2015, 54, 8198–8206. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, L.; Racic, V.; Brownjohn, J. Measuring human-induced vibrations of civil engineering structures via vision-based motion tracking. Measurement 2016, 83, 44–56. [Google Scholar] [CrossRef]
- McCarthy, D.M.J.; Chandler, J.H.; Palmieri, A. Monitoring 3D vibrations in structures using high-resolution blurred imagery. Photogramm. Rec. 2016, 31, 304–324. [Google Scholar] [CrossRef]
- Yoon, H.; Elanwar, H.; Choi, H.; Golparvar-Fard, M.; Spencer, B.F. Target-free approach for vision-based structural system identification using consumer-grade cameras. Struct. Control Health Monit. 2016, 23, 1405–1416. [Google Scholar] [CrossRef]
- Mas, D.; Ferrer, B.; Acevedo, P.; Espinosa, J. Methods and algorithms for video-based multi-point frequency measuring and mapping. Measurement 2016, 85, 164–174. [Google Scholar] [CrossRef]
- Poozesh, P.; Sarrafi, A.; Mao, Z.; Avitabile, P.; Niezrecki, C. Feasibility of extracting operating shapes using phase-based motion magnification technique and stereo-photogrammetry. J. Sound Vib. 2017, 407, 350–366. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Structural identification using computer vision–based bridge health monitoring. J. Struct. Eng. 2018, 144, 04017202. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Nagarajaiah, S.; Kenyon, G.; Farrar, C.; Mascareñas, D. Blind identification of full-field vibration modes of output-only structures from uniformly-sampled, possibly temporally-aliased (sub-Nyquist), video measurements. J. Sound Vib. 2017, 390, 232–256. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Identification of structural stiffness and excitation forces in time domain using noncontact vision-based displacement measurement. J. Sound Vib. 2017, 406, 15–28. [Google Scholar] [CrossRef]
- Cha, Y.J.; Chen, J.G.; Büyüköztürk, O. Output-only computer vision based damage detection using phase-based optical flow and unscented Kalman filters. Eng. Struct. 2017, 132, 300–313. [Google Scholar] [CrossRef]
- Javh, J.; Slavič, J.; Boltežar, M. The subpixel resolution of optical-flow-based modal analysis. Mech. Syst. Signal Process. 2017, 88, 89–99. [Google Scholar] [CrossRef]
- Xu, F. Accurate measurement of structural vibration based on digital image processing technology. Concurr. Comput. Pract. Exp. 2019, 31, e4767. [Google Scholar] [CrossRef]
- Dong, C.Z.; Ye, X.W.; Jin, T. Identification of structural dynamic characteristics based on machine vision technology. Measurement 2018, 126, 405–416. [Google Scholar] [CrossRef]
- Guo, J.; Jiao, J.; Fujita, K.; Takewaki, I. Damage identification for frame structures using vision-based measurement. Eng. Struct. 2019, 199, 109634. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.Z.; Harvey, P.S. Pixel-based operating modes from surveillance videos for structural vibration monitoring: A preliminary experimental study. Measurement 2019, 148, 106911. [Google Scholar] [CrossRef]
- Kuddusa, M.A.; Lia, J.; Hao, H.; Lia, C.; Bi, K. Target-free vision-based technique for vibration measurements of structures subjected to out-of-plane movements. Eng. Struct. 2019, 190, 210–222. [Google Scholar] [CrossRef]
- Durand-Texte, T.; Simonetto, E.; Durand, S.; Melon, M.; Moulet, M.H. Vibration measurement using a pseudo-stereo system, target tracking and vision methods. Mech. Syst. Signal Process. 2019, 118, 30–40. [Google Scholar] [CrossRef]
- Civera, M.; Zanotti, F.L.; Surace, C. An experimental study of the feasibility of phase-based video magnification for damage detection and localisation in operational deflection shapes. Strain 2020, 56, e12336. [Google Scholar] [CrossRef]
- Eick, B.A.; Narazaki, Y.; Smith, M.D.; Spencer, B.F. Vision-based monitoring of post-tensioned diagonals on miter lock gate. J. Struct. Eng. 2020, 146, 04020209. [Google Scholar] [CrossRef]
- Lai, Z.; Alzugaray, I.; Chli, M.; Chatzi, E. Full-field structural monitoring using event cameras and physics-informed sparse identification. Mech. Syst. Signal Process. 2020, 145, 106905. [Google Scholar] [CrossRef]
- Ngeljaratan, L.; Moustafa, M.A. Structural health monitoring and seismic response assessment of bridge structures using target-tracking digital image correlation. Eng. Struct. 2020, 213, 110551. [Google Scholar] [CrossRef]
- Stephen, G.A.; Brownjohn, J.M.W.; Taylor, C.A. Measurements of static and dynamic displacement from visual monitoring of the Humber Bridge. Eng. Struct. 1993, 154, 197–208. [Google Scholar] [CrossRef]
- Olaszek, P. Investigation of the dynamic characteristic of bridge structures using a computer vision method. Measurement 1999, 25, 227–236. [Google Scholar] [CrossRef]
- Wahbeh, A.M.; Caffrey, J.P.; Masri, S.F. A vision-based approach for the direct measurement of displacements in vibrating systems. Smart Mater Struct 2003, 12, 785–794. [Google Scholar] [CrossRef]
- Lee, J.J.; Shinozuka, M. A vision-based system for remote sensing of bridge displacement. NDT E Int. 2006, 39, 425–431. [Google Scholar] [CrossRef]
- Ji, Y.F.; Chang, C.C. Nontarget image-based technique for small cable vibration measurement. J. Bridge Eng. 2008, 13, 34–42. [Google Scholar] [CrossRef]
- Chang, C.C.; Xiao, X.H. An integrated visual-inertial technique for structural displacement and velocity measurement. Smart Struct. Syst. 2010, 6, 1025–1039. [Google Scholar] [CrossRef]
- Fukuda, Y.; Feng, M.Q.; Shinozuka, M. Cost-effective vision-based system for monitoring dynamic response of civil engineering structures. Struct. Control Health Monit. 2010, 17, 918–936. [Google Scholar] [CrossRef]
- Caetano, E.; Silva, S.; Bateira, J. A vision system for vibration monitoring of civil engineering structures. Exp. Tech. 2011, 4, 74–82. [Google Scholar] [CrossRef]
- Mazzoleni, P.; Zappa, E. Vision-based estimation of vertical dynamic loading induced by jumping and bobbing crowds on civil structures. Mech. Syst. Signal Process. 2012, 33, 1–12. [Google Scholar] [CrossRef]
- Ye, X.W.; Ni, Y.Q.; Wai, T.T.; Wong, K.Y.; Zhang, X.M.; Xu, F. A vision-based system for dynamic displacement measurement of long-span bridges: Algorithm and verification. Smart Struct. Syst. 2013, 12, 363–379. [Google Scholar] [CrossRef]
- Kim, S.W.; Kim, N.S. Dynamic characteristics of suspension bridge hanger cables using digital image processing. NDT E Int. 2013, 59, 25–33. [Google Scholar] [CrossRef]
- Kohut, P.; Holak, K.; Uhl, T.; Ortyl, Ł.; Owerko, T.; Kuras, P.; Kocierz, R. Monitoring of a civil structure’s state based on noncontact measurements. Struct. Health Monit. 2013, 12, 411–429. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calcada, R.; Ferreira, J.; Martins, T. Non-contact measurement of the dynamic displacement of railway bridges using an advanced video-based system. Eng. Struct. 2014, 75, 164–180. [Google Scholar] [CrossRef]
- Busca, G.; Cigada, A.; Mazzoleni, P.; Zappa, E. Vibration monitoring of multiple bridge points by means of a unique vision-based measuring system. Exp. Mech. 2014, 54, 255–271. [Google Scholar] [CrossRef]
- Feng, M.Q.; Fukuda, Y.; Feng, D.; Mizuta, M. Nontarget vision sensor for remote measurement of bridge dynamic response. J. Bridge Eng. 2015, 20, 04015023. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M. Model updating of railway bridge using in situ dynamic displacement measurement under trainloads. J. Bridge Eng. 2015, 20, 04015019. [Google Scholar] [CrossRef]
- Bartilson, D.T.; Wieghaus, K.T.; Hurlebaus, S. Target-less computer vision for traffic signal structure vibration studies. Mech Syst Signal Process 2015, 60–61, 571–582. [Google Scholar] [CrossRef]
- Ferrer, B.; Mas, D.; García-Santos, J.I.; Luzi, G. Parametric study of the errors obtained from the measurement of the oscillating movement of a bridge using image processing. J. Nondestruct. Eval. 2016, 35, 53. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, C. Dynamic displacement measurement of large-scale structures based on the Lucas–Kanade template tracking algorithm. Mech. Syst. Signal Process 2016, 66-67, 425–436. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z.; Liu, T. Image-based structural dynamic displacement measurement using different multi-object tracking algorithms. Smart Struct. Syst. 2016, 17, 935–956. [Google Scholar] [CrossRef]
- Shariati, A.; Schumacher, T. Eulerian-based virtual visual sensors to measure dynamic displacements of structures. Struct. Control. Health Monit. 2017, 24, e1977. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Completely contactless structural health monitoring of real-life structures using cameras and computer vision. Struct. Control Health Monit. 2017, 24, e1852. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Computer vision-based displacement and vibration monitoring without using physical target on structures. Struct. Infrastruct. Eng. 2017, 13, 505–516. [Google Scholar] [CrossRef]
- Feng, D.; Scarangello, T.; Feng, M.Q.; Ye, Q. Cable tension force estimate using novel noncontact vision-based sensor. Measurement 2017, 99, 44–52. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Experimental validation of cost-effective vision-based structural health monitoring. Mech. Syst. Signal Process. 2017, 88, 199–211. [Google Scholar] [CrossRef]
- Chen, J.G.; Davis, A.; Wadhwa, N.; Durand, F.; Freeman, W.T.; Büyüköztürk, O. Video camera–based vibration measurement for civil infrastructure applications. J. Infrastruct. Syst. 2017, 23, B4016013-1. [Google Scholar] [CrossRef]
- Chen, J.G.; Adams, T.M.; Sun, H.; Bell, E.S.; Büyüköztürk, O. Camera-based vibration measurement of the World War I Memorial Bridge in Portsmouth, New Hampshire. J. Struct. Eng. 2018, 144, 04018207. [Google Scholar] [CrossRef]
- Harvey, P.S.; Elisha, G. Vision-based vibration monitoring using existing cameras installed within a building. Struct. Control Health Monit. 2018, 25, e2235. [Google Scholar] [CrossRef]
- Fioriti, V.; Roselli, I.; Tatì, A.; Romano, R.; De Canio, G. Motion magnification analysis for structural monitoring of ancient constructions. Measurement 2018, 129, 375–380. [Google Scholar] [CrossRef]
- Acikgoz, S.; DeJong, M.J.; Kechavarzi, C.; Soga, K. Dynamic response of a damaged masonry rail viaduct: Measurement and interpretation. Eng. Struct. 2018, 168, 544–558. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.; Kong, D. A non-contact vision-based system for multipoint displacement monitoring in a cable-stayed footbridge. Struct Control Health Monit. 2018, 25, e2155. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W.; Huseynov, F. Accurate deformation monitoring on bridge structures using a cost-effective sensing system combined with a camera and accelerometers: Case study. J. Bridge Eng. 2019, 24, 05018014. [Google Scholar] [CrossRef]
- Dhanasekar, M.; Prasad, P.; Dorji, J.; Zahra, T. Serviceability assessment of masonry arch bridges using digital image correlation. J. Bridge Eng. 2019, 24, 04018120. [Google Scholar] [CrossRef]
- Lydon, D.; Lydon, M.; Taylor, S.; Martinez Del Rincon, J.; Hester, D.; Brownjohn, J. Development and field testing of a vision-based displacement system using a low cost wireless action camera. Mech. Syst. Signal Process. 2019, 121, 343–358. [Google Scholar] [CrossRef]
- Hoskere, V.; Park, J.W.; Yoon, H.; Spencer, B.F. Vision-based modal survey of civil infrastructure using unmanned aerial vehicles. J. Struct. Eng. 2019, 145, 04019062. [Google Scholar] [CrossRef]
- Dong, C.Z.; Celik, O.; Catbas, F.N. Marker-free monitoring of the grandstand structures and modal identification using computer vision methods. Struct. Health Monit. 2019, 18, 1491–1509. [Google Scholar] [CrossRef]
- Dong, C.Z.; Bas, S.; Catbas, F.N. Investigation of vibration serviceability of a footbridge using computer vision-based methods. Eng. Struct. 2020, 224, 111224. [Google Scholar] [CrossRef]
- Fradelos, Y.; Thalla, O.; Biliani, I.; Stiros, S. Study of lateral displacements and the natural frequency of a pedestrian bridge using low-cost cameras. Sensors 2020, 20, 3217. [Google Scholar] [CrossRef]
- Fukuda, Y.; Feng, M.Q.; Narita, Y.; Kaneko, S.; Tanaka, T. Vision-based displacement sensor for monitoring dynamic response using robust object search algorithm. IEEE Sens. J. 2013, 13, 4725–4732. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q.; Ozer, E.; Fukuda, Y. A vision-based sensor for noncontact structural displacement measurement. Sensors 2015, 15, 16557–16575. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, J.; Lei, X.; Zhu, C. A high-speed vision-based sensor for dynamic vibration analysis using fast motion extraction algorithms. Sensors 2016, 16, 572. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.H.; Kim, D. A target-less vision-based displacement sensor based on image convex hull optimization for measuring the dynamic response of building structures. Sensors 2016, 16, 2085. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; He, S.; Wang, S.; Liu, Y.; Zhang, Z.; He, L.; Wang, F.; Cai, Q.; Shi, R.; Yang, Y. A high-speed target-free vision-based sensor for bus rapid transit viaduct vibration measurements using CMT and ORB algorithms. Sensors 2017, 17, 1305. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Feng, M.Q.; Wu, Z.Y. Robust vision sensor for multi-point displacement monitoring of bridges in the field. Eng. Struct. 2018, 163, 255–266. [Google Scholar] [CrossRef]
- Erdogan, Y.S.; Ada, M. A computer-vision based vibration transducer scheme for structural health monitoring applications. Smart Mater. Struct. 2020, 29, 085007. [Google Scholar] [CrossRef]
- Park, J.H.; Huynh, T.C.; Choi, S.H.; Kim, J.T. Vision-based technique for bolt-loosening detection in wind turbine tower. Wind. Struct. 2015, 21, 709–726. [Google Scholar] [CrossRef]
- Poozesh, P.; Baqersad, J.; Niezrecki, C.; Avitabile, P.; Harvey, E.; Yarala, R. Large-area photogrammetry based testing of wind turbine blades. Mech. Syst. Signal Process. 2017, 86, 98–115. [Google Scholar] [CrossRef]
- Sarrafi, A.; Mao, Z.; Niezrecki, C.; Poozesh, P. Vibration-based damage detection in wind turbine blades using phase-based motion estimation and motion magnification. J. Sound Vib. 2018, 421, 300–318. [Google Scholar] [CrossRef]
- Poozesh, P.; Sabato, A.; Sarrafi, A.; Niezrecki, C.; Avitabile, P.; Yarala, R. Multicamera measurement system to evaluate the dynamic response of utility-scale wind turbine blades. Wind Energy 2020, 23, 1619–1639. [Google Scholar] [CrossRef]
| Group | Structure | Country | Authors and Reference |
|---|---|---|---|
| Steel bridges | Suspension bridge | U.S.A. | Feng and Feng [187] |
| Truss with vertical lift | U.S.A. | Chen et al. [189] | |
| Skew girder | U.K. | Xu et al. [194] | |
| Steel footbridges | Cable-stayed bridge | U.K. | Xu et al. [193] |
| Suspension bridge | North Ireland | Lydon et al. [196] | |
| Suspension bridge | U.S.A. | Hoskere et al. [197] | |
| Vertical truss frames | U.S.A. | Dong et al. [199] | |
| Steel structures for sport stadiums | Grandstands | U.S.A. | Khuc and Catbas [184,185,198] |
| Superstructure cables | U.S.A. | Feng et al. [186] | |
| Reinforced concrete structures | Deck on arch footbridge | U.S.A. | Shariati and Schumacher [183] |
| Five-story building | U.S.A. | Harvey and Elisha [190] | |
| Beam-slab bridge | North Ireland | Lydon et al. [196] | |
| Masonry structures | Heritage ruins and arch bridge | Italy | Fioriti et al. [191] |
| Arch bridge | U.K. | Acikgoz et al. [192] | |
| Arch bridge | Australia | Dhanasekar et al. [195] | |
| Timber footbridge | Deck-stiffened arch | Greece | Fradelos et al. [200] |
| Reference | Camera, Pixel Resolution, and Frame Rate (FPS) | Video Processing Algorithm | Loading Condition during Monitoring | Comparisons with Other Monitoring Technologies |
|---|---|---|---|---|
| [187] | Point Grey, 1280 × 1024, 10 | Template mat. | Passage of subway trains | No direct, GPS, and radar |
| [189] | Point Grey, 800 × 600, 30 | Optical flow | Lift impact, normal traffic | Accelerom., strain gauges |
| [194] | Go Pro, 1920 × 1080, 25 Imetrum, 2048 × 1088, 30 | Template mat. Imetrum [87] | Passage of trains | Low cost and high-end vision-based, accelerometers |
| [193] | Go Pro, 1920 × 1080, 30 | Template mat. | Crowd of pedestrians | Wireless accelerometers |
| [196] | Go Pro, 1920 × 1080, 25 | Template mat. | Crowd of pedestrians | Accelerometers |
| [197] | DJI 3840 × 2160, 30 | Optical flow | Walk, running, jumping | Accelerometers |
| [199] | Low cost, 1920 × 1080, 60 | Feature mat. | Walk, running, jumping | Accelerometers |
| [184,185,198] | Canon, N/A, 30 and 60 | Feature mat. | Crowd during game | Accelerom., displ. transd. |
| [186] | Point Grey, 1280 × 1024, 50 | Template mat. | Operational, shaken | Load cell |
| [183] | Canon, N/A, 60 | Motion magn. | Pedestrian jumping | No direct, vision-based |
| [190] | N/A, 1056 × 720, 25 | Feature mat. | Outdoor shake table | Accelerometers |
| [196] | Go Pro, 1920 × 1080, 25 | Template mat. | Normal vehicular traffic | No direct, integr. fiber optics |
| [191] | N/A | Motion magn. | Tram vibrations, wind | Velocimeters |
| [192] | Imetrum, N/A, 50 | Imetrum [87] | Passage of trains | Fiber optics |
| [195] | Sony, 1936 × 1216, 50 | Dantec [85] | Passage of trains | No direct, numerical |
| [200] | Low cost, 1920 × 1080, 30 | Optical flow | Group of pedestrians | Accelerom., GPS, theodolite |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zona, A. Vision-Based Vibration Monitoring of Structures and Infrastructures: An Overview of Recent Applications. Infrastructures 2021, 6, 4. https://doi.org/10.3390/infrastructures6010004
Zona A. Vision-Based Vibration Monitoring of Structures and Infrastructures: An Overview of Recent Applications. Infrastructures. 2021; 6(1):4. https://doi.org/10.3390/infrastructures6010004
Chicago/Turabian StyleZona, Alessandro. 2021. "Vision-Based Vibration Monitoring of Structures and Infrastructures: An Overview of Recent Applications" Infrastructures 6, no. 1: 4. https://doi.org/10.3390/infrastructures6010004
APA StyleZona, A. (2021). Vision-Based Vibration Monitoring of Structures and Infrastructures: An Overview of Recent Applications. Infrastructures, 6(1), 4. https://doi.org/10.3390/infrastructures6010004





