Abstract
This study examines the relation between maximum seismic displacements and residual displacements for reinforced concrete building structures. In order to achieve a reliable relationship between these critical structural parameters for the seismic performance of concrete buildings, an extensive parametric study is conducted by examining the nonlinear behavior of numerous planar framed structures. In this work, dynamic inelastic analyses are executed to investigate the seismic behavior of two sets of frames. The first group consists of four planar frames which have been designed for seismic and vertical loads according to modern structural codes while the second group also consists of four frames, which have been designed for vertical loads only, in order to examine older structures that have been designed using codes with inadequate seismic provisions. These two sets of buildings are subjected to various earthquakes with different amplitudes in order to develop a large structural response databank. On the basis of this wide-ranging parametric investigation, after an appropriate statistical analysis, simple empirical expressions are proposed for a straightforward and efficient evaluation of maximum seismic displacements of reinforced concrete buildings structures from their permanent deformation. Permanent displacements can be measured in-situ after strong ground motions as a post-earthquake assessment. It can be concluded that the measure of permanent deformation can be efficiently used to estimate the post-seismic performance level of reinforced concrete buildings.
1. Introduction
A vast development of knowledge in earthquake engineering has been obtained during the last three decades [1,2]. In that context, the assessment of post-seismic performance of reinforced concrete buildings has in recent times received substantial interest in terms of evaluation of protection, rehabilitation and maintenance. Consequently, the post-seismic performance level of reinforced concrete buildings gives a very significant basis of information for both feasible maintenance approaches and evaluation of behavior of structures in response to possible future ground motions, e.g., aftershocks [3,4,5]. According to the findings of these studies, the dynamic characteristics of buildings or their response to strong earthquakes can be used to evaluate one of the most significant factors of seismic performance of buildings, i.e., the total building damage level [6,7].
After a strong earthquake, permanent displacements can be measured in-situ by applying a variety of procedures such as applications of robotic theodolites [8], procedures of Global Positioning System (GPS) [9] and methods of digital image correlation [10]. Permanent displacements appear to be a very crucial structural parameter for the evaluation of the earthquake performance of buildings, as concluded in references [11,12,13]. Furthermore, the work of Pampanin et al. [14] and that of Mohsenian and Mortezaei [15] proposed a qualitative categorization of structural damage, which is derived from the permanent inter-story drift ratio (IDR) of buildings. However, the damage index is straightforwardly described by the critical state and existing ductility intensities on buildings. All these recent and pertinent works focused on the quantification or minimization of permanent deformation. Furthermore, maximum displacements are directly used for direct displacement-based design procedures [16,17]. On the other hand, Hatzigeorgiou et al. [18] and Christidis et al. [19] found that permanent deformation can be used to evaluate maximum deformation. Maximum displacements are used by the most of modern seismic codes as a reliable index of damage level for the building structures. The aforementioned works, i.e., references [18,19], are exclusively focused on single-degree-of-freedom systems and steel buildings, respectively; according to the best of the authors’ knowledge, there is no pertinent research study that evaluates maximum deformation from the corresponding permanent deformation, especially for reinforced concrete buildings.
It is worth noticing that when examining the cases of non-ductile and of ductile reinforced concrete framed structures with identical permanent inter-story drifts, the corresponding damage levels can be quite different. Therefore, it seems more appropriate to determine important structural performance properties other than IDR, such as the maximum displacements, which are directly related to damage and lead directly to the total IDR levels and the ductility demands. Furthermore, it is apparent that any procedure for seismic performance evaluation should take into account the available ductilities of structures under consideration or equivalently should take into account the seismic provisions, modern or out-of-date, that have been used for the design of reinforced concrete buildings. For these reasons, this work examines various frames using the Ruaumoko program [20] to create an adequate response databank and then proposes empirical expressions for the assessment of maximum deformation as a function of permanent displacements, which can be quantified in-situ after intense earthquakes.
2. Reinforced Concrete Frames under Consideration
2.1. General Description
Two groups of structures are investigated in this study. The first group consists of eight framed structures, i.e., Frames A1-A4, which is considered to represent low- to mid-rise reinforced concrete buildings which have up to eight stories. Thus, each frame consists exclusively of typical beam-column members, i.e., without concrete shear-walls, positioned at an area of Europe with high-risk seismicity, taking into account both gravity and earthquake actions with peak ground acceleration equal to 0.24 g, while soil class C consistent with European Seismic Code EC8 [21] is assumed. The frames under consideration have been designed for the loading combinations [21,22]:
- (a)
- 1.35G + 1.50Q
- (b)
- 1.00G + ψQ + 1.00E
- (c)
- 1.00G + ψQ – 1.00E
where G, Q and E that have to do with dead, live and seismic loads, respectively. Furthermore, ψ is the combination coefficient for live load, which was assumed to be ψ = 0.80 in this study.
Numerous reinforced concrete buildings have been designed consistent with early seismic provisions or, sometimes, lacking any seismic provision. With the intention of examining such structures designed for inadequate seismic provision or ignoring completely the seismic action, an alternative group of frames, i.e., Frames B1-B4, was also investigated, where all these structures have been designed for the above-mentioned first loading combination only.
Groups A and B have identical external geometry, material properties and vertical (dead and live) loads but they have different reinforcement (amount and arrangement). This study, investigating these groups of frames, did not concentrate on a rigorous comparison between them, but primarily focused on the correlation between maximum and permanent deformation.
All frames under consideration have three equal bays with total lengths equal to 13.5 m (=3 × 4.5 m). Characteristic floor-to-floor height is equal to 3.0 m except for 8-story structures where the first floor height is equal to 4.0 m. Typical interior frames of these buildings are examined here in order to simplify the examined problem, i.e., to investigate two-dimensional models of these structures. The dimensions of beams and columns used in this study are typical frame element proportions in real existing structures. All columns are square with sides of 30–40 cm. All beams had a width equal to 30 cm and a height equal to 40–60 cm. It was expected that the amount of reinforcement for beams and columns of Frames A1–A4 would be higher than that of Frames B1–B4. This dissimilarity mainly has to do with the idea of capacity design of modern seismic codes, where columns are stronger than beams. Thus, the design of vertical members of Group A fulfills the provision of §4.4.2.3 of EC8 [21], for any joint of beams with columns
where ΣMRC and ΣMRB are the sums of the design values for the moments corresponds to the columns and beams framing the joint, respectively. This demand is waived at the top floor of the frames of Group A.
According to provisions of EC8 [21] and satisfying the Ductility Capacity Medium (DCM) criteria, the behavior factor for regular buildings A1 and A3 of Group A is q = 3.9. Furthermore, buildings A2 and A4, which present along-height irregularities, require q = 0.8 × 3.9 = 3.12, taking into account that for structures which are not regular in elevation, the corresponding behavior factor should be decreased by 20%. Finally, in order to consider the cracking of members sections, reduced moments of inertia, Ief, were assumed, i.e., for columns Ief = 90%·Ig and for beams Ief = 50%·Ig where Ig is the gross section moment of inertia [23].
2.2. Nonlinear Modeling
The dynamic equilibrium equation (equation of motion) in incremental form for an inelastic structure, which is modeled by a multi-degree of freedom (MDOF) system with viscously damped force-displacement and moment-rotation relationships, is examined here to evaluate the nonlinear response [24]
where the upper dots denote the derivative of time, M is the mass matrix of, C is the damping matrix according to the Rayleigh approach [24], KT is the tangent stiffness matrix and denotes the ground acceleration. The solution of the dynamic equilibrium equation has been provided by the Ruaumoko program [20]. Beam and column elements were both modeled as nonlinear frame elements with lumped plasticity by defining plastic hinges at both ends. For the beams, axial forces were assumed to be practically zero, since all floor slabs are considered to be rigid in their plan to simulate the diaphragm action. Typical input data for strength that are essential for Ruaumoko [20] are the axial force -bending moment interaction relations for vertical members (columns) and maximum and minimum strength values associated with bending moments for horizontal members (beams). In this research study, a home-made design and analysis program was developed for each reinforced concrete section using the model of fibers. The cyclic behavior of all members was evaluated using the well-known Takeda hysteresis model which is available in Ruaumoko [20] and it is shown in Figure 1. The phenomenological parameters of Takeda’s model are mainly influenced by the end resistances of columns and beams, which are evidently dissimilar for the corresponding structures of Group B. It should be mentioned that due to inadequate seismic design provisions for Group B, all these structures appear to have stiffness and strength degradation after yielding. One can consult the Ruaumoko user manual by Carr [20] for an in-depth description of degradation factors and their effect on the shape of the hysteresis model.
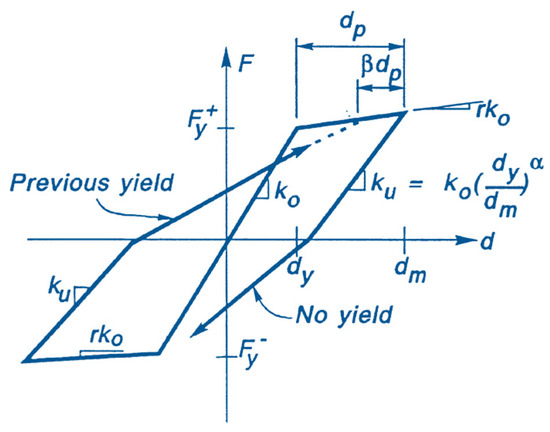
Figure 1.
The modified Takeda model (adopted from reference [20]).
An additional crucial factor, which is required to describe the inelastic response of members with lumped plasticity modeling, is the plastic hinge length. This length associates the rotation values with the corresponding curvatures, and in the past various plastic hinge lengths have been proposed in the pertinent literature. In this study, a very simple model was adopted where the plastic hinge length, lph for each member is equal to half of its section’s height, H:
lph = 0.5·H.
2.3. Description of Structures and their Reinforcement Amount and Arrangement
Frames A1 and B1 (Figure 2 and Figure 3): the selected longitudinal reinforcement amount of the exterior columns of Frame A1 is 8∅18, and is 8∅22 for the interior columns. For all the beams of Frame A1 and Frame B1, the selected reinforcement amount of upper web is 5∅16, while the reinforcement amount of down web is 3∅16. The selected longitudinal reinforcement of all columns of Frame B1 is 8∅14.
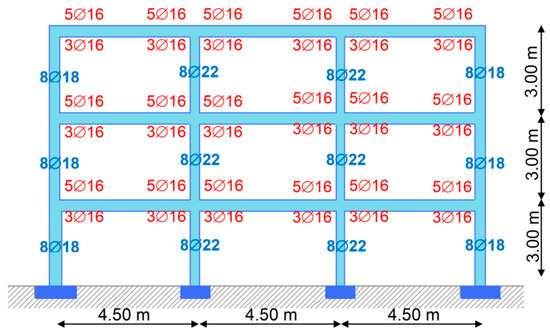
Figure 2.
Frame A1 properties.
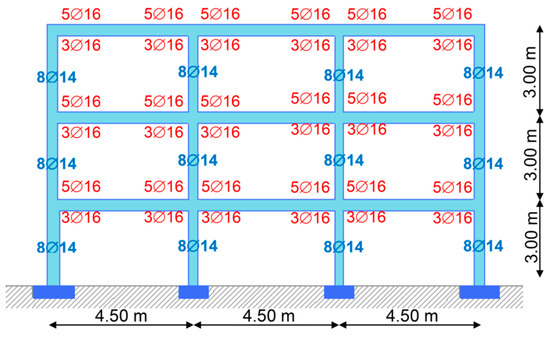
Figure 3.
Frame B1 properties.
Frames A2 and B2 (Figure 4 and Figure 5): the selected longitudinal reinforcement of the exterior columns of Frame A2 is 8∅18, and is 8∅22 for the interior columns. For the beams of Frame A2 and Frame B2, the selected reinforcement amount of down web is 3∅16, however the reinforcement of upper web is different at the left and the right ends. The selected reinforcement amount of all columns of Frame B2 is 8∅14.
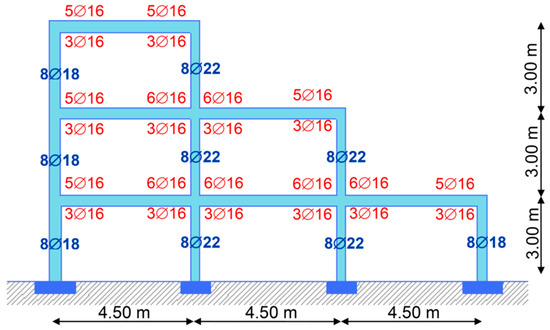
Figure 4.
Frame A2 properties.
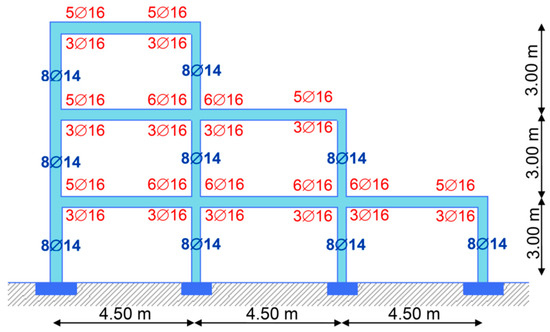
Figure 5.
Frame B2 properties.
Frames A3 and B3 (Figure 6 and Figure 7): the selected longitudinal reinforcement of the exterior columns of Frame A3 is 8∅18, and is 8∅22 for the interior columns. For all the beams of Frame A3 the reinforcement amount is 5∅16/3∅16. For the columns of first and second floor of Frame B3 the selected reinforcement is 8∅16, while for the others is 8∅14. For the beams of first, second, third and fourth floor of Frame B3, the selected reinforcement is 4∅16/3∅14, while for the others the reinforcement is 5∅16/3∅16.
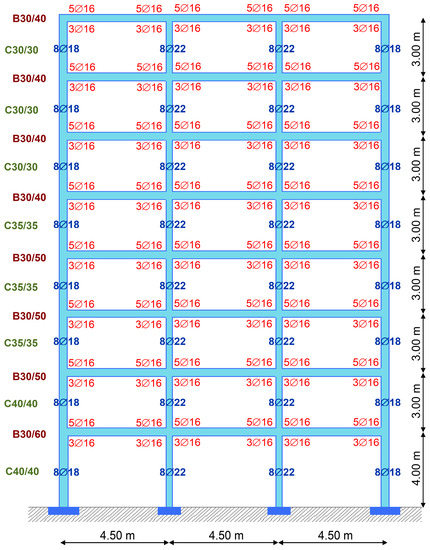
Figure 6.
Frame A3 properties.
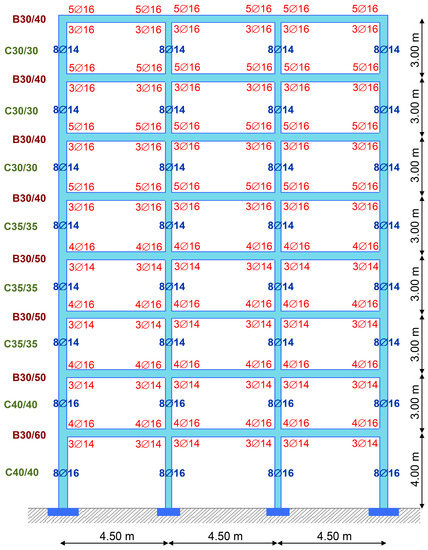
Figure 7.
Frame B3 properties.
Frames A4 and B4 (Figure 8 and Figure 9): the selected longitudinal reinforcement of the columns of Frame A4 is 8∅18. For all the beams of Frame A4 the reinforcement amount is 5∅16/3∅16. For the columns of first and second floor of Frame B4 the selected reinforcement is 8∅16, while for the others, the reinforcement is 8∅14. For the beams of first, second, third and fourth floor of Frame B4 the selected reinforcement is 4∅16/3∅14, while for the other frames, it is 5∅16/3∅16.
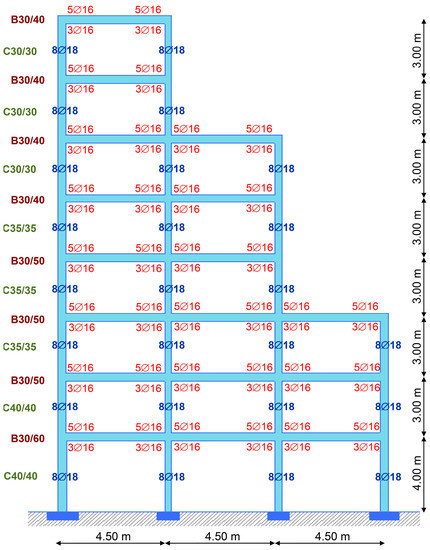
Figure 8.
Frame A4 properties.

Figure 9.
Frame B4 properties.
3. Seismic Input
The strong ground motion database that was used here consists of twenty eight real seismic records. These records have been adopted to have compatibility with the design process, i.e., with Type 1 spectrum of EC8 [21] where the peak ground acceleration is scaled in any case to PGA = 0.24 g. Table 1 provides details associated with these records, which have been downloaded from the PEER database [25].

Table 1.
Strong ground motions examined in this study (downloaded from reference [25]).
4. Results and Discussion
This work suggests a new method to evaluate the post-seismic structural performance of reinforced concrete structures. It concentrates on the evaluation of maximum displacements which are directly related to the IDR values and the ductility damage. The proposed approach evaluates the maximum deformation from the permanent deformation, where the latter can be measured in-situ after an intense earthquake. Two groups of reinforced concrete framed structures (Group A—Frames: A1, A2, A3 and A4) and (Group B—Frames: B1, B2, B3 and B4) are analyzed by using the finite element program Ruaumoko [20]. An in-detail statistical analysis of the created database is employed to derive substantial conclusions. Thus, this work concentrates on the results which are related to permanent and maximum deformation. The eight aforementioned reinforced concrete framed structures are subjected to twenty eight different earthquake records and examined for appropriate ground motions’ scale factors, which are compatible with the design peak ground accelerations. Furthermore, all these scale factors are also multiplied by 1.50 and applied to the whole set of frames in order to examine even more results using a wide-ranging databank. Thus, for each structure, 2 × 28 = 56 dynamic inelastic analyses have been provided and 224 analyses (=4 frames × 28 records × 2 scale factors) have been executed for each group of reinforced concrete structures.
From the created databank of results, the analysis is focused on the maximum horizontal displacement for the top floor of each frame. The vital objective of this work is to give simple and effective empirical equations for the assessment of maximum structural displacements as functions of permanent deformations. The latter can also be measured in-situ after a strong seismic event, as mentioned above. In this study, it is considered that the maximum normalized top displacement (normalization in terms of height) can evaluated from the normalized residual displacement (normalization in terms of height) as
where T and H are the fundamental period and the total height of each frame, respectively, while a1–a3 are appropriate parameters which have been determined numerically to have the best fit for Equation (4). These parameters appear in Table 2, where the correlation coefficient R2 is also provided.

Table 2.
Values of a1, a2 and a3 parameters.
The significance of graphs and the influence of outliers on the statistical elements of a dataset should also be mentioned. For this reasons, Figure 10 and Figure 11 are built to compare the ‘exact’ results from dynamic inelastic analyses of Ruaumoko [20] with the proposed model empirical expressions, for the whole sample of Group A and Group B.
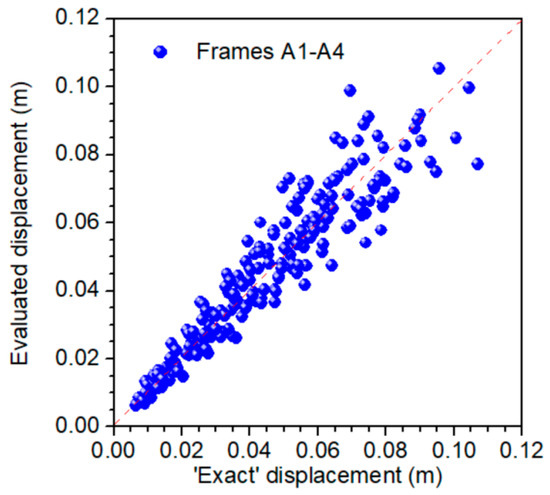
Figure 10.
Evaluation of maximum displacements for well-designed frames—Results from 224 dynamic inelastic analyses.
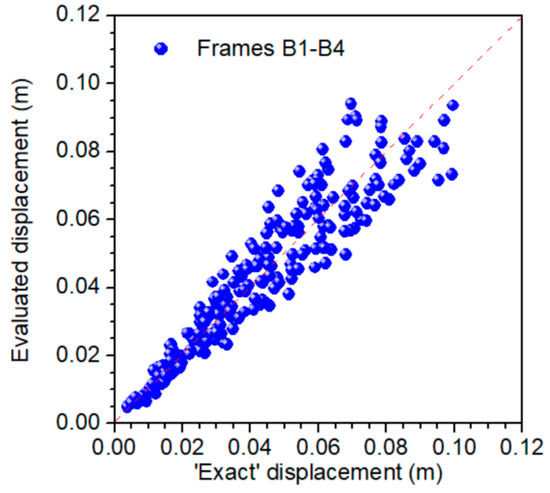
Figure 11.
Evaluation of maximum displacements for poor-designed frames—Results from 224 dynamic inelastic analyses.
It is apparent that the empirical expressions results obtained from this study (Equation (4)) are in acceptable agreement with those obtained from the ‘exact’ dynamic analyses, thus confirming the validity of the proposed method.
Finally, in order to further verify the proposed method, two additional applications are investigated. For the sake of fair treatment, the ground motions for these two examples are not belong to the list in Table 1. Investigating the first verification example, the 8-story Frame A4 (see Figure 8) is subjected to Bam earthquake (Bam, Iran, 26/12/2003). The time-history of ground acceleration for this strong ground motion is shown in Figure 12.
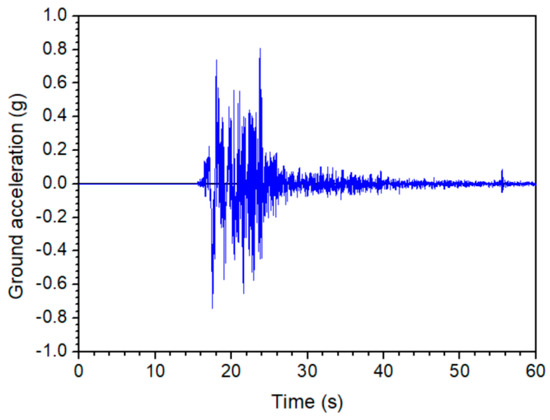
Figure 12.
Time history of ground acceleration (Bam earthquake, Iran, 26/12/2003).
Figure 13 depicts the response of the structure, i.e., the time-history of the horizontal top displacement. For comparison reasons, the application of Equation (4) for Frame A4 (height H = 25 m, fundamental period T = 0.97 s) is also shown. It is evident that the proposed method can reliably evaluate the maximum top displacement, i.e., umax,Eq.4 = 149 mm since this value is very close to that from dynamic inelastic analysis, i.e., umax,analysis = 148 mm. Thus, the relative error is r.e. = 100%|148 − 149|/148 = 0.68%.
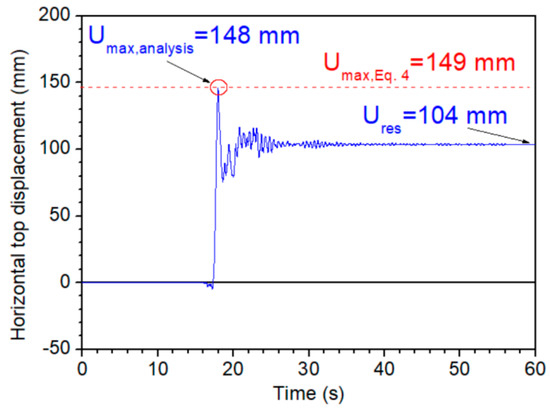
Figure 13.
Time history of top displacement of Frame A4 under the Bam (26/12/2003) earthquake.
Examining the second verification example, the 3-story Frame B1 (see Figure 3) is subjected to Loma Prieta earthquake (E-W component, Gilroy Station, Loma Prieta/California, 18/10/1989). The time-history of ground acceleration for this strong ground motion is shown in Figure 14.
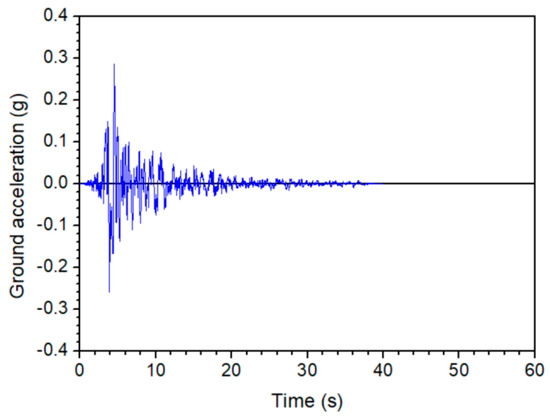
Figure 14.
Time history of ground acceleration (Loma Prieta earthquake, 18/10/1989).
Figure 15 shows the response of the structure, i.e., the time-history of the horizontal top displacement. For comparison reasons, the application of Equation (4) for Frame B1 (height H = 9m, fundamental period T = 0.49 s) is also shown. It is evident that the proposed method can reliably evaluate the maximum top displacement, i.e., umax,Eq.4 = 61 mm since this value is very close to that from dynamic inelastic analysis, i.e., umax,analysis = 60 mm. Thus, the relative error in this case is r.e. = 100%|61 − 60|/61 = 1.64%.
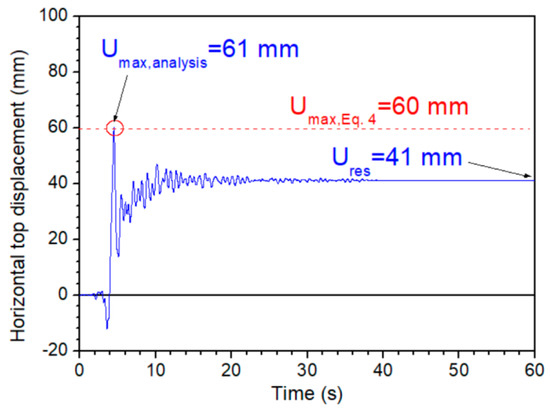
Figure 15.
Time history of top displacement of Frame B1 under the Loma Prieta (18/10/1989) earthquake.
It should be mentioned that the performance levels examined by the provisions of modern seismic codes, such as those of Eurocode 8 [21] and FEMA P-58 [26], are related to normalized drifts and mainly to the maximum relative horizontal displacement of two adjacent floors normalized to the story height, which is called the interstory drift ratio (IDR). Furthermore, the maximum roof drift (maximum roof displacement for a building normalized to its total height) is another crucial structural response parameter. More specifically, maximum roof drift which can be used to assess not only the global performance level of a structure but also to interrelate this drift with IDR [27]. The proposed empirical expression (Equation (4)) focuses on the normalized roof displacement, i.e., it relates the maximum roof drift (umax/H) with the residual roof drift (ures/H) and therefore can be used to assess the global performance level of a reinforced concrete frame system.
5. Conclusions
This work proposes a new method for the evaluation of maximum seismic displacements of planar reinforced concrete framed structures directly from their residual deformation. Two groups of regular and irregular buildings, which have been designed either for vertical and seismic loads or for vertical loads only, are investigated. A comprehensive analysis has been conducted and the following conclusions can be drawn:
- The maximum seismic deformation of reinforced concrete structures can be successfully assessed using the pertinent residual deformation. The new method proposed herein can be applied for both regular and irregular (with setbacks) reinforced concrete buildings. Additionally, this new approach can be used for both well-designed and under-designed structures.
- The correlation coefficient between the ‘exact’ results from dynamic inelastic analyses and those produced by the proposed empirical relation is equal to 95.9% for the case of well-design reinforced concrete structures, and 95.1% for the set of under-designed structures. Therefore, the proposed empirical relation appears to be reliable for a direct and rapid evaluation of the maximum response.
- The effectiveness and the accuracy of the proposed method are additionally confirmed using two verification examples. It is found that the maximum displacements evaluated by the proposed approach are very close to those computed by dynamic inelastic analysis. Thus, the relative error between these methods for the first verification example is 0.68%, and for the second example is equal to 1.64%.
- In order to apply this method in 3-D structures, an extension of the proposed methodology is required in order to also consider deformation due to vertically (torsional) rotations. Furthermore, more analyses are required for reinforced concrete systems with shear walls.
Author Contributions
Conceptualization, G.H.; methodology, F.K. and G.H.; formal analysis, F.K.; resources, F.K., K.E., T.T. and I.N.; data curation, F.K., G.H.; writing—original draft preparation, All; writing—review and editing, F.K., G.H.; visualization, F.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Muho, E.V.; Papagiannopoulos, G.A.; Beskos, D.E. A seismic design method for reinforced concrete moment resisting frames using modal strength reduction factors. Bull. Earthq. Eng. 2019, 17, 337–390. [Google Scholar] [CrossRef]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Seismic behavior of composite steel/concrete MRFs: Deformation assessment and behavior factors. Bull. Earthq. Eng. 2015, 13, 3871–3896. [Google Scholar] [CrossRef]
- Faisal, A.; Majid, T.A.; Hatzigeorgiou, G.D. Investigation of story ductility demands of inelastic concrete frames subjected to repeated earthquakes. Soil Dyn. Earthq. Eng. 2013, 44, 42–53. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D. Ductility demands control under repeated earthquakes using appropriate force reduction factors. J. Earthq. Tsunami 2010, 4, 231–250. [Google Scholar] [CrossRef]
- Hatzivassiliou, M.; Hatzigeorgiou, G.D. Seismic sequence effects on three-dimensional reinforced concrete buildings. Soil Dyn. Earthq. Eng. 2015, 72, 77–88. [Google Scholar] [CrossRef]
- Yue, J.; Qian, J.; Beskos, D.E. A generalized multi-level seismic damage model for RC framed structures. Soil Dyn. Earthq. Eng. 2016, 80, 25–39. [Google Scholar] [CrossRef]
- Diaz, S.A.; Pujades, L.G.; Barbat, A.H.; Vargas, Y.F.; Hidalgo-Leiva, D.A. Energy damage index based on capacity and response spectra. Eng. Struct. 2017, 152, 424–436. [Google Scholar] [CrossRef]
- Dos Santos, R.C.; Larocca, A.P.; de Araújo Neto, J.O.; Barbosa, A.C.; Oliveira, J.V. Detection of a curved bridge deck vibration using robotic total stations for structural health monitoring. J. Civ. Struct. Health Monitor. 2019, 9, 63–76. [Google Scholar] [CrossRef]
- Li, X.; Huang, G.; Zhang, Q.; Zhao, Q. A new GPS/BDS tropospheric delay resolution approach for monitoring deformation in super high-rise buildings. GPS Solut. 2018, 22, 90. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X. Real-time subtraction-based calibration methods for deformation measurement using structured light techniques. Appl. Opt. 2019, 58, 7727–7732. [Google Scholar] [CrossRef] [PubMed]
- Bravo-Haro, M.A.; Elghazouli, A.Y. Permanent seismic drifts in steel moment frames. J. Constr. Steel Res. 2018, 148, 589–610. [Google Scholar] [CrossRef]
- Dai, K.; Wang, J.; Li, B.; Hong, H.P. Use of residual drift for post-earthquake damage assessment of RC Buildings. Eng. Struct. 2017, 147, 242–255. [Google Scholar] [CrossRef]
- Gou, H.; Leng, D.; Yang, L.; Jia, H. Modeling the cumulative residual deformation of high-speed railway bridge pier subjected to multiple earthquakes. Earthq. Struct. 2019, 17, 317–327. [Google Scholar]
- Pampanin, S.; Christopoulos, C.; Priestley, M.J. Performance-based seismic response of frame structures including residual deformations part II: Multi-degree of freedom systems. J. Earthq. Eng. 2003, 7, 119–147. [Google Scholar] [CrossRef]
- Mohsenian, V.; Mortezaei, A. New proposed drift limit states for box-type structural systems considering local and global damage indices. Adv. Struct. Eng. 2019, 22, 3352–3366. [Google Scholar] [CrossRef]
- Moehle, J.P. Displacement-based design of RC structures subjected to earthquakes. Earth. Spectra 1992, 8, 403–428. [Google Scholar] [CrossRef]
- Calvi, G.M.; Priestley, M.J.; Kowalsky, M.J. Displacement Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007. [Google Scholar]
- Hatzigeorgiou, G.D.; Papagiannopoulos, G.A.; Beskos, D.E. Evaluation of maximum seismic displacements of SDOF systems from their residual deformation. Eng. Struct. 2011, 33, 3422–3431. [Google Scholar] [CrossRef]
- Christidis, A.A.; Dimitroudi, E.G.; Hatzigeorgiou, G.D.; Beskos, D.E. Maximum seismic displacements evaluation of steel frames from their post-earthquake residual deformation. Bull. Earthq. Eng. 2013, 11, 2233–2248. [Google Scholar] [CrossRef]
- Carr, A.J. RUAUMOKO—Inelastic Dynamic Analysis Program; Department of Civil Engineering, University of Canterbury: Christchurch, New Zealand, 2008. [Google Scholar]
- EN 1998 Eurocode 8. Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- EN 1991 Eurocode 1. Actions on Structures, Part 1-1: General Actions- Densities, Self-Weight, Imposed Loads for Buildings; European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]
- Hatzigeorgiou, G.D.; Liolios, A.A. Nonlinear behaviour of RC frames under repeated strong ground motions. Soil Dyn. Earthq. Eng. 2010, 30, 1010–1025. [Google Scholar] [CrossRef]
- Chopra, A. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 3rd ed.; Prentice Hall Inc.: New York, NJ, USA, 2006. [Google Scholar]
- Pacific Earthquake Engineering Research Center. PEER Strong Motion Database. Available online: https://ngawest2.berkeley.edu/ (accessed on 13 December 2019).
- ATC - Applied Technology Council. FEMA P-58 Next-Generation Seismic Performance Assessment for Buildings, Volume 1 – Methodology; Federal Emergency Management Agency: Washington, DC, USA, 2012. [Google Scholar]
- Ghobarah, A.; Abou-Elfath, H.; Biddah, A. Response-based damage assessment of structures. Earthq. Eng. Struct. Dyn. 1999, 28, 79–104. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).