Toward the Development of Load Transfer Efficiency Evaluation of Rigid Pavements by a Rolling Wheel Deflectometer

Abstract

The jointed rigid pavement is currently evaluated by the Falling weight deflectometer which is rather slow for the testing of the jointed pavements. Continuous nondestructive evaluation of rigid pavements with a rolling wheel deflectometer can be used to measure the load transfer and is investigated. Load transfer is an important indicator of the rigid pavement’s condition and this is the primary factor which is studied. Continuous data from experimental measurements across a joint allows for the determination of not only the load transfer efficiency provided parameters characterizing the pavement is known. A three-dimensional semi-analytical model was implemented for simulating the pavement response near a joint and used for interpretation and verification of the experimental data. Results show that this development is promising for the use of a rolling wheel deflectometer for rapid evaluation of joints.

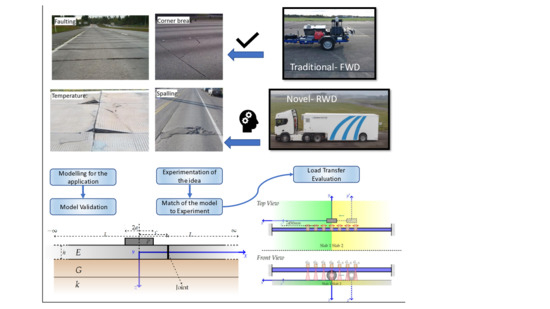
1. Introduction

Airports and highways have a huge network of rigid pavement infrastructures. To maintain these infrastructures, their structural assessment is a routine activity by infrastructure owners. The study of the structural condition of the rigid jointed pavement is traditionally achieved by the use of Falling weight deflectometer(FWD). Given that there have been few developments on the efficiency of structural assessment, new technology must be developed or applied to benefit the network owners. This will help the owners to do maintenance cost-effectively by reducing the time required to do such assessments and thus allowing the infrastructure to be more available to its users. In this study, the potential of a novel application of Rolling wheel Deflectometer(RWD) technology for rigid pavement is developed. The aim is to develop the analysis which will help to understand the measurements.

Continuous pavement structural measurement devices operate at the traffic speed and require no traffic disruption. Devices such as the RWD has been developed with the potential to reveal the structural information on a routine basis. For example a continuous, contact-based sensor device such as the rolling dynamic deflectometer(RDD) has been shown to be effective for jointed pavement rehabilitation [1]. A project based research study by using RDD deflection data interpretation and its application on evaluating existing concrete pavement has been carried out in [2]. The RDD is a truck-mounted system that dynamically loads the pavement and simultaneously monitors the pavement response while continuously moving at about 1.6 km/hr. The major components include an electro-hydraulic dynamic loading system, a force measurement system, an array of 4 rolling sensors that are located underneath the RDD, and a distance measurement system as described in [3]. RDD measures at the center of the vehicle at a position 0.6 m far from the tire loads, capturing the influence from both wheels. The positioning of sensors is very far and the magnitude of signals decreases with distance and it is challenging to be capture signals accurately. In a project-level study, measurement speed was limited by pavement contact nature of the sensors. Recent developments indicate a new generation of devices with non-contact continuous measurement technology which has increasingly started to show its capability [4,5]. Recently, Dynatest developed a new RWD device called the Rapid Pavement Tester (Raptor) for rapid evaluation of pavements. The research presented in this study shows its potential for evaluation of rigid pavements, where it has already been demonstrated for flexible pavements [6]. Given that it is a very new technology and there may be developments required on the technology itself, but it is evident that this can be applied to rigid pavements. In contrast to the RDD, this device is faster, the senors are closer to the loads and numbers of sensors are significantly more in RWD.

It is a challenge to understand and draw conclusions from these devices since the measurements themselves are taken in different locations relative to the load. This happens due to the device-specific geometries which are different compared to FWD. In studies with a RDD, the conclusions on joint conditions and load transfer efficiency were formed by setting threshold values for the project and thus they cannot be applied to a different maintenance project [7]. RDD uses rolling geophones with limited sensor capabilities demonstrating the potential of continuous deflection measurements for jointed pavements. However, there have been no significant studies done to investigate the response of jointed rigid pavement with an array of non-contact sensors with a continuously moving load. Therefore, deflections obtained from a continuous deflection measurement device cannot be used to conclude about structural conditions of joints until more investigations are done.

The first step to a back-calculation is a mechanistic model which can accurately and rapidly predict the response under a moving wheel. Historically, FWD measurements use different mechanistic models to do back-calculations, but these same models cannot be applied to the RWD in case of the jointed pavements. Several FEM models of rigid pavements have been able to predict deflections under all types of environmental and design loads [8]. To include and characterize the load transfer mechanisms, advanced modelling strategies e.g., Enrichment of Finite elements to include discontinuities has been shown to work [9,10]. Such advanced modelling strategies are challenging for a practical back-calculation method.

The study aims to develop and test the analysis for the use of RWD technology. A three dimensional analytical model of the rigid pavement joint is developed. This model is then used to analyze the experimental data. The experimental data is gathered by performing a reference beam experiment. This experiment aims to show the potential of the use of non-destructive testing across a rigid pavement discontinuity.

2. Methods

To assess the rigid pavements, different methods exist based on type of assessment and maintenance activity under consideration. In the structural assessment category, the strength of slabs and the subgrade along with joints condition are checked for their performance. Most failures arise from the failure of joints and corners as they fail to perform as a rigid pavement structure, as it ages over its use. From structural assessment point of view, jointed pavements are tested for load transfer capability by measuring deflection ratios at the edges. Where as from modelling point of view, this ability to transfer load can be defined based on definitions based on stresses, strains and deflections induced under the loads. A vertical deflection-based definition of load transfer is classical and most used, as it is easy to calculate.

2.1. Mathematical Model

Various modelling methods exists that can provide deflections. Methods such as Empirical-mechanistic methods and Mechanistic methods have been used in pavement engineering for decades. Such equations were developed from experience and modelling. These models were used for back-calculation. Though accurate but these equations provide deflection values for fewer predefined positions of the load. Intending to predict vertical deflections at positions surrounding the load and the joint, based on a structural formulation as close as possible to a physical problem, a mechanical model simulating the jointed rigid pavement is set up.

From a purely modelling perspective, numerical and analytical methods are two categories where the numerical methods are more popular and handle any geometry. Analytical methods can only handle simple and idealized geometry as for complicated geometries, an analytical solution might not exist. A model of two jointed semi-infinite slabs resting on a Pasternak foundation is a geometrically simplified model to handle a single joint. Therefore, a 3D semi-analytical formulation that already existed in the literature has been implemented here. This formulation has been solved in this study. Thus, a method to predict the deflections all over the slab irrespective of the load’s position is developed.

2.1.1. Formulation

To predict the response of a jointed concrete pavement, a static 3D semi-analytical solution is developed. This forward model aims to be a sufficiently good approximation to real rigid pavements while being fast to calculate, e.g., in comparison with more numerically intensive approaches like finite element modelling. An efficient forward model is a foundation for the development of efficient back-calculation methods. 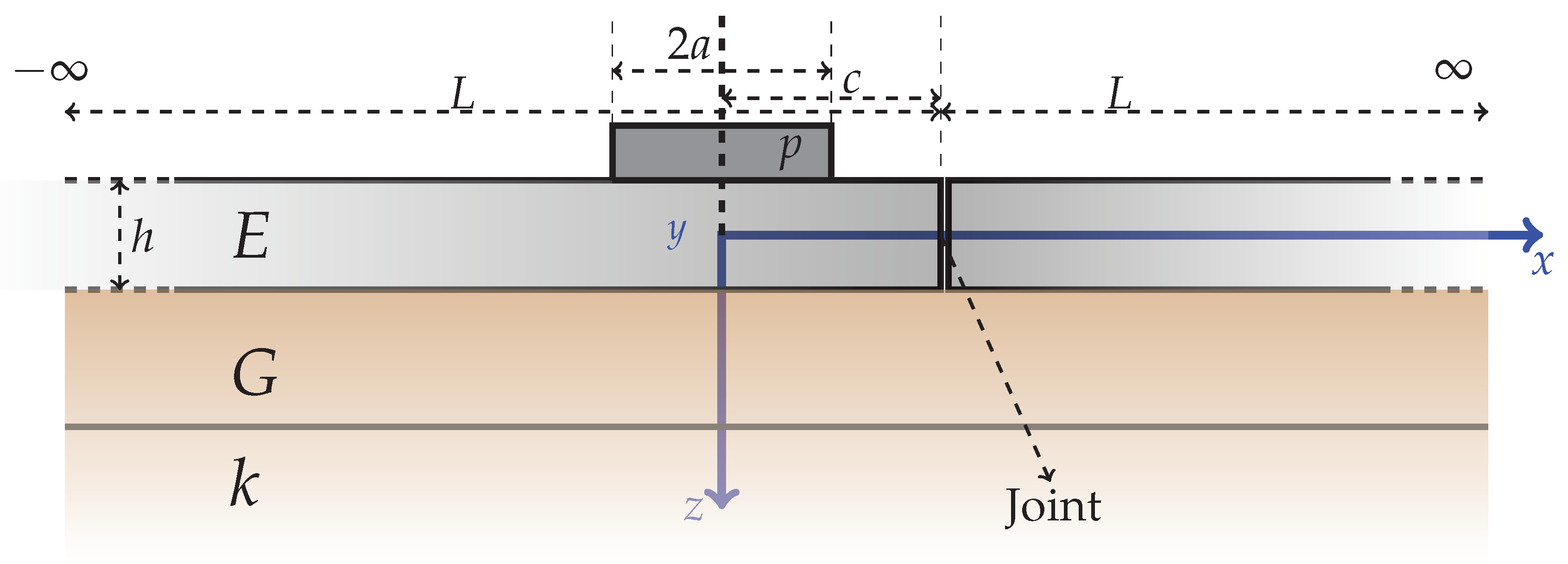Figure 1 presents a schematic of the model. The origin of the coordinate system is at the position of the load and x is the driving direction, y is the transverse direction and z is the vertical direction. The formulation is based on two semi-infinite jointed concrete slabs resting on a Pasternak foundation with subgrade reaction k and independent spring modulus G. The load transfer efficiency $\delta$ in Equation (1) is the ratio of the vertical deflection on the unloaded ($w_{UL}$) and loaded ($w_L$) slab right next to the joint at $x=c$.

$$\delta =\frac{w_{UL}}{w_L}$$

(1)

This formulation has a vertical load of pressure p with a rectangular contact area $2a$ by $2b$ at a distance c from the joint. The slab is of thickness h with Young’s Modulus E. The model is derived from the equilibrium equation of the system. The boundary conditions imply zero vertical displacements at infinity in both x and y directions. The load pressure is assumed uniform and shear loads are not included in the model. The solution method is presented in [11], but the numerically challenging implementation is done in this study.

The model follows linear elasticity and a small strain framework. Static loading is assumed and thermal effects are ignored. The load transfer in the y-direction is assumed constant here.

2.1.2. Two Semi-Infinite Slabs Resting on a Pasternak Foundation

The equilibrium equation in terms of the vertical deflection w can be written as in Equation (2), where D is the flexural rigidity of the slab in Equation (3). The relation between the radius of relative stiffness l and the flexural rigidity is expressed in Equation (4).

$$\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}\right)-\frac{G}{D}\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}\right)+\frac{kw}{D}=\frac{p}{D}$$

(2)

$$D=\frac{E{h}^3}{12\left(1-v^2\right)}$$

(3)

$$\frac{G}{D}=\frac{2g}{l^2}\mathrm{and}\frac{k}{D}=\frac{1}{l^4}$$

(4)

To solve Equation (2), both the load and deflection are expressed as double Fourier integrals, which is shown in Equation (6) for deflection. The ratio between the deflection on both sides of the joint is given by the definition of the load transfer efficiency in Equation (1). On each side of the joint, the solution is expressed as a linear combination of a particular solution w to the inhomogeneous equation as in Equation (5).

$$w_L=\left(w+A\left(s\right)w_a+B\left(s\right)w_b\right);w_{UL}=w+C\left(s\right)w_c+D\left(s\right)w_d$$

(5)

$$\begin{array}{c}\hfill w=\frac{p}{\pi k}\frac{1}{\sqrt{1-g^2}}{\int }_0^{\infty }\frac{cos(sy/l)sin(sb/l)}{s\left(s^4+2g{s}^2+1\right)}\\ \hfill \left\{e^{-(x-a)\alpha /l}\left[\sqrt{1-g^2}cos[(x-a)\beta /l]+\left(s^2+g\right)sin[(x-a)\beta /l]\right]\right.\\ \hfill \left.-e^{-(x+a)\alpha /l}\left[\sqrt{1-g^2}cos[(x+a)\beta /l]+\left(s^2+g\right)sin[(x+a)\beta /l]\right]\right\}ds\end{array}$$

(6)

And the two solutions to the homogeneous equation $w_a$ and $w_b$ for the loaded slab and $w_c$ and $w_d$ for unloaded slab are shown in Equation (7).

$$\begin{array}{c}{w}_a=\frac{p}{\pi k}\frac{1}{\sqrt{1-g^2}}{\int }_0^{\infty }[A\left(s\right)cos(\beta x/l)]e^{\alpha x/l}\frac{cos(sy/l)sin(sb/l)}{s}ds\hfill \\ w_b=\frac{p}{\pi k}\frac{1}{\sqrt{1-g^2}}{\int }_0^{\infty }[B\left(s\right)sin(\beta x/l)]e^{\alpha x/l}\frac{cos(sy/l)sin(sb/l)}{s}ds\hfill \\ w_c=\frac{p}{\pi k}\frac{1}{\sqrt{1-g^2}}{\int }_0^{\infty }[C\left(s\right)cos(\beta x/l)]e^{-\alpha x/l}\frac{cos(sy/l)sin(sb/l)}{s}ds\hfill \\ w_d=\frac{p}{\pi k}\frac{1}{\sqrt{1-g^2}}{\int }_0^{\infty }[D\left(s\right)sin(\beta x/l)]e^{-\alpha x/l}\frac{cos(sy/l)sin(sb/l)}{s}ds\hfill \end{array}$$

(7)

Where two new auxiliary parameters have been introduced in Equation (8).

$$\begin{array}{c}{\alpha }^2=\frac{1}{2}\left[\sqrt{{\left(s^2+g\right)}^2+1-g^2}+\left(s^2+g\right)\right]\hfill \\ {\beta }^2=\frac{1}{2}\left[\sqrt{{\left(s^2+g\right)}^2+1-g^2}-\left(s^2+g\right)\right]\hfill \end{array}$$

(8)

By the fourth-order partial differential equation, four conditions are required to couple the solution across the discontinuity at the joint. By relating deflections, forces and moments, Equations (9)–(12), can be written at the joint at $x=c$ in Figure 1. Equation (9) is relating the deflections between unloaded and loaded slabs. Equations (10) and (11) are the cancellation of the moment at the edge of the loaded slab and unloaded slab respectively. Equation (12) is equality of the shear forces at the the joint.

$$\delta \left(w+A\left(s\right)w_a+B\left(s\right)w_b\right)=w+C\left(s\right)w_c+D\left(s\right)w_d$$

(9)

$$\left(\frac{{\partial }^2}{\partial x^2}+v\frac{{\partial }^2}{\partial y^2}\right)\left(w+A\left(s\right)w_a+B\left(s\right)w_b\right)=0$$

(10)

$$\left(\frac{{\partial }^2}{\partial x^2}+v\frac{{\partial }^2}{\partial y^2}\right)\left(w+C\left(s\right)w_c+D\left(s\right)w_d\right)=0$$

(11)

$$\begin{array}{c}\hfill \left(\frac{{\partial }^3}{\partial x^3}+(2-v)\frac{{\partial }^3}{\partial x\partial y^2}-\frac{2g}{l^2}\right)\left(w+A\left(s\right)w_a+B\left(s\right)w_b\right)\\ \hfill =\left(\frac{{\partial }^3}{\partial x^3}+(2-v)\frac{{\partial }^3}{\partial x\partial y^2}-\frac{2g}{l^2}\right)\left(w+C\left(s\right)w_c+D\left(s\right)w_d\right)\end{array}$$

(12)

2.2. Model Validation

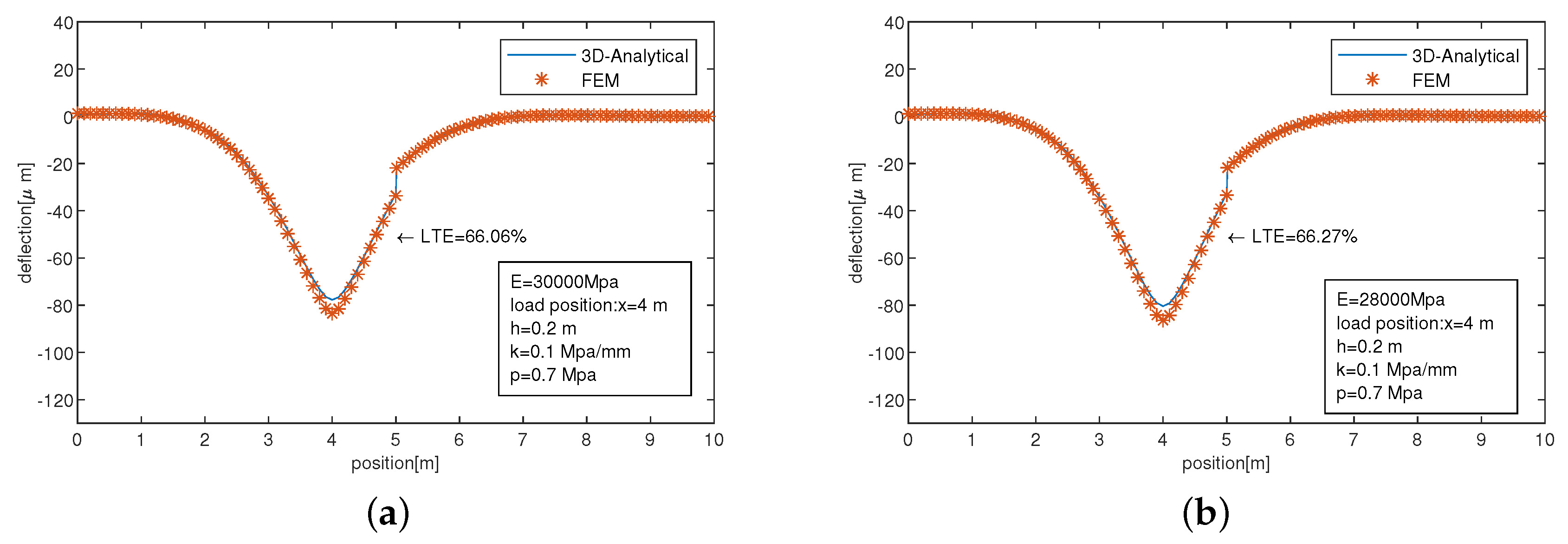
The response from the semi-analytical model is compared to the result of a FEM solution from EverFE. EverFE is a free FEM tool that models the response of jointed slab systems due to various load configurations [12]. EverFE considers load transfer [13] and effects such as aggregate interlock and dowel properties [8]. Figure 2 shows a comparison of the modelled responses from the semi-analytical model and EverFE for two different slab moduli. Note how the semi-analytical model is very close to the FEM solution except immediately under the load (which is due to discretization error in the FEM solution). The deflection in Figure 2 is in the plane passing through the centre of the load. The comparison in Figure 2 validates the 3D semi-analytical model.

With the mechanical model ready, it is aimed that accurately measured deflections with a rolling wheel can be used to back-calculate load transfer efficiency. That will then indicate the condition of joints and predict the state of rigid pavements. With the trust in being able to predict vertical deflections, an experiment needs to be set up to test the viability of this idea. The simplest way to measure vertical deflections by using a rolling wheel is by using a reference beam set up across the joint.

2.3. A Reference Experiment

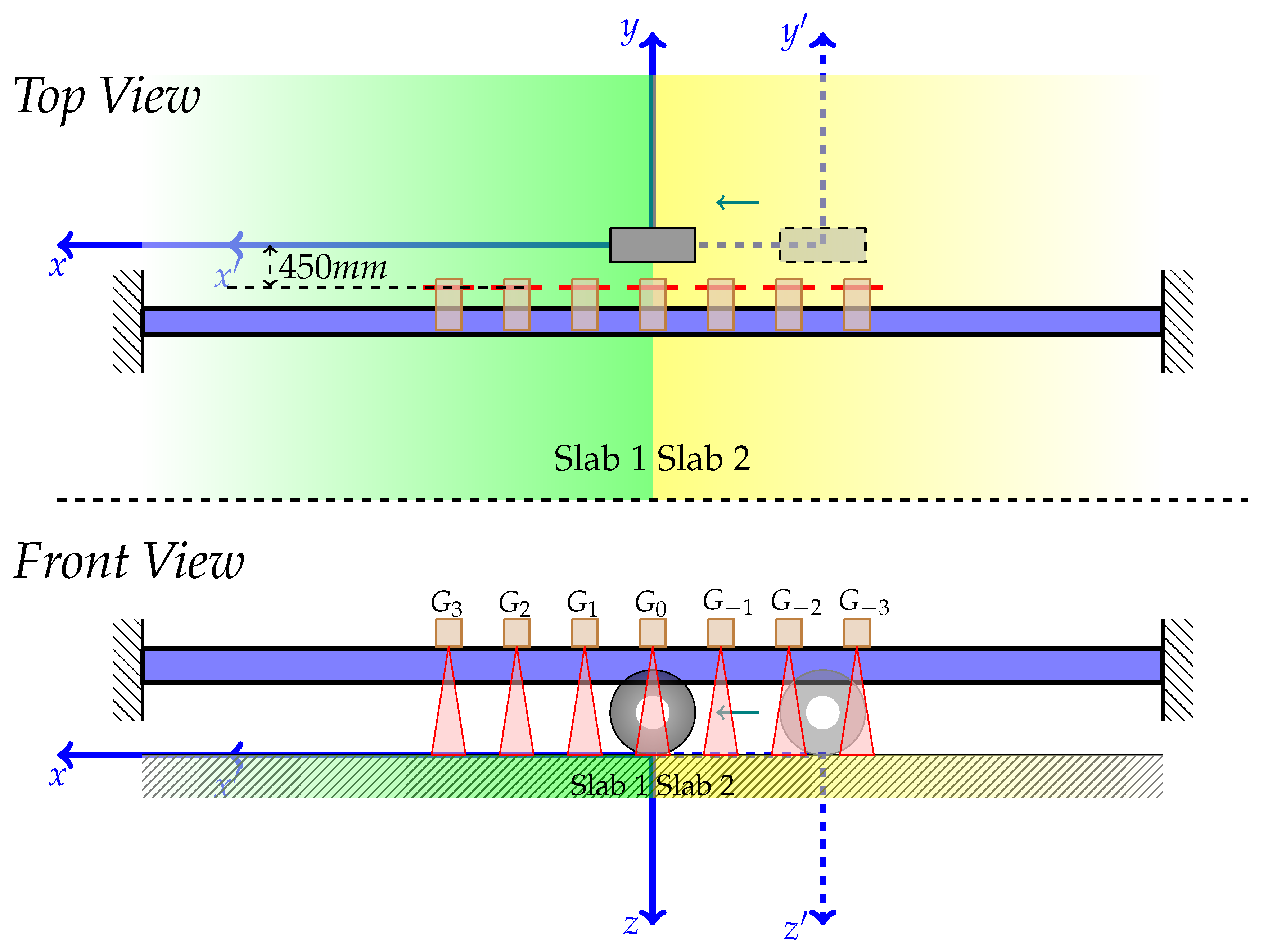
The whole measurement system comprises of the lasers, odometer(encoder), a reference beam, an ethernet switch, a power supply, a moving load and a recording application (Figure 3).

To measure the edge deflection response of jointed slabs under the influence of a moving wheel load, a beam mounted with distance lasers is setup. This beam is placed across the joints in the centre of two jointed slabs. The beam is mounted with 7 distances lasers such that the middle laser is placed across the joint formed by both the slabs. It is a symmetric setup across the joints. The beam is 6 m in length and mounted on two supports, one at each end. The beam has a rectangular cross-section with channels for mounting brackets and supports.

The load consists of a moving wheel load carrying 5 tons. The loading wheel is a part of a trailer which has an independent suspension in the rear axle. The trailer is attached to a truck and driven at a slow and controlled speed for the experiment. There are other axles and their influence is observable but ignored for this study. Initially, the trailer is moved to a far location from the joint considered for measurement. During the experiment, the load is moved parallel to the beam. The aim is to get as close as possible to the beam in the longitudinal direction to get a good signal.

An accurate odometer device, which measures the moving position of the wheel load at all times is used. This device is known as ‘encoder’ and is attached to the moving wheel. The signal from this sensor comes from a cable attached to it. On the other end, it is connected to the whole measurement setup via a cable. The output from this device is saved via the recording application and is linked in time to all the lasers.

2.3.1. Experiment at the Vaerlose Airbase

To begin with, the site with joints is selected after visual inspection. After inspection of selected slabs forming the joint, the setup is placed across it symmetrically. The distance of the beam is measured from parallel edges of the slabs to make sure it is in the centre. Then, coloured markings on the slabs at incremental distances parallel to the laser signal are done to help the person driving the truck for visual guidance.

After all the verifications, the measurement starts. The truck is at least 4 slabs distance away from the joint in consideration with its front axle on the edge of the 4th slab. With a slow and constant driving speed of 10 km/h, the truck is carefully driven to avoid vibrations and maintain parallel distance to the laser signal, when it arrives closer to the beam. It is shown in Figure 4. After the loaded wheel axle of the trailer carrying the 5 tons has passed in front of beam and slabs onto the other site, measurement is stopped, and the collected data is saved. This sequence of process is repeated for several joints at the site.

2.3.2. Modelling the Experiment

The 3D semi-analytical model predicts deflection field over the jointed slabs for one position of the load. Though this model solves a static case, it can be used to compare a moving load as they are not impact loads. During the experiment, a moving wheel is generating deflections all over slabs in space, so a total of 18 realizations of the model with incremental load positions of 0.4 m toward the joint are considered. When the load is over the joint, then linear combinations of realizations with fine increments of 0.05 m load positions are used. This generates a set of deflection response to form a modelled signal which can be compared to the measurements ultimately. The distance between the centre of the load wheel and the laser signal is estimated and used in generating deflections from the model. To account for the influence of sinking of the beam’s end support, a linear combination of deflections from cases when the load is in front of the beam’s support and near the edge is implemented. In the end, the deflection at the edges of the slab containing the joint is modelled, which is equivalent to experimentally measured deflection by the laser at the centre of the beam.

3. Results

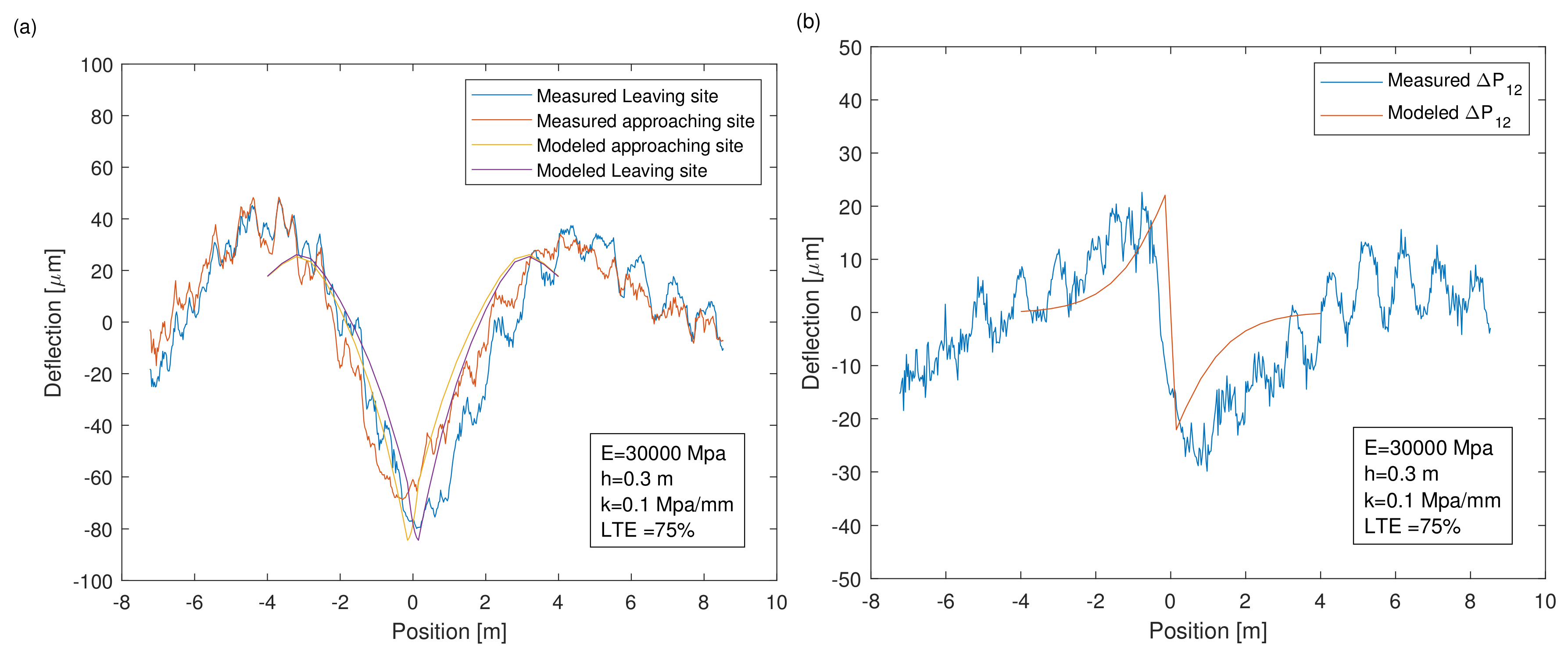
Deflections from two different sites are presented. Each of these sites was measured three times for repetition. In Figure 5a, x axis represents the position of the load and y axis represents deflections measured by the laser over the joint in microns. The deflection is measured on the slab under $G^0$ from the negative axis is the approaching side, while the other part of the laser $G^0$ after the joint is marked as leaving side. The joint is approximately positioned at $x=0$ m in all cases. In plots, selected load positions to range from −8 m to 8 m which includes the effect of the loaded wheel. Measured deflections range approximately over −100 microns to 50 microns. The symmetric peaks in the deflection signal at x = −4 m and 4 m appear due to contribution from the load crossing the other edge and then approach the beam’s support. Deflection values at the edge of the slab as a function of the load position is ultimately measured. In Figure 5b, the deflection difference of the signal shown in Figure 5a, is shown with respect to the load position and it can be observed that the model compares well to this difference as inherent noise is canceled.

As the information about the moduli, structure, subgrade and load transfer is unknown. By assuming a set of realistic values of these parameters as shown in the Figure 5a, the model can generate deflections. This set of parameters is kept constant for the repetitions while comparing modelled deflections to measurements for the same site. A comparison of the measured signal to the modelled signal shows the match of the peaks. Modelled deflections to the left and right of the joint match the trend in the measured data with a load transfer efficiency of 75%.

This comparison demonstrates that the model can predict the response due to a moving load closer to the edge. Given some structural information of the pavement, it is obvious that this model can be used to back-calculate the properties of the slabs from the measurements and eventually the load transfer capability of the slabs. This experiment also demonstrates the capability of the measurement system and associated sensors to capture deflection in order of microns without embedding the sensors inside the structure. It’s a simple demonstration of nondestructive evaluation by a slow-moving load. A more advanced measurement system based on the setup used in this study forms the Dynatest Rolling wheel Deflectometer technology platform.

4. Discussion

To use a novel measurement technique based on an RWD technology, a model predicting the deflection outside of load plane is required. To obtain a vertical deflection field for jointed rigid pavements with a deflection-based load transfer mechanism, a simple 3D semi-analytical solution is obtained. The model is reliable in predicting deflections as good as a FEM based model solution. It solves for deflection with a static loading condition in load’s vicinity and across joint on slabs forming it. Due to its simple and yet accurate formulation, it requires a smaller number of inputs compared to a FEM solution. In a back-calculation process, these advantages will help to calculate the load transfer adequately. Next steps were to build the understanding of the measurements and how it can be used. Measurements are based on a simple beam setup where the measuring device is fixed, and the load is a rolling wheel. This technique relies on measuring equipment with its accuracy and precision. It also requires data processing which is tailored to the measurement technique. After processing of the high-frequency raw measurements, a comparison to deflections from the model is done. The trends in comparison of measured deflection to the modelled deflections mean that it is possible to measure the deflections with a moving load on a rigid pavement with some uncertainty. If the layer and subgrade properties are known, then model can be used to fit the measured data leading to calculation of load transfer efficiency. However further research is required as at this time there are still some improvements that could be potentially achieved. The deflection values decrease sharply further out of the load plane and if the measurement system could be closer to the load, the measured signal would be larger. Variation in the moving load speed could be used to understand how this affects the experiment. Additional steps to reduce the noise in the data by putting additional weights on the beam could be one idea. The aim is to have a large signal to noise ratio.

Overall results from this experiment support the objectives that were set up. This development is foundational and preliminary for the use of RWD technology on jointed pavement. It has been demonstrated that the load transfer efficiency can be calculated and given the layer and subgrade properties by a moving load, where the measuring instrument is stationary. However, there are limitations in the sense that the load transfer mechanism such as dowels and other types of jointed structures are not modelled separately. These separate jointed structures influence the shape of the deflection profile and thus will pose challenge in load transfer evaluation. Improvements in the modelling with these ideas need to be researched in future.

With this built up understanding, next steps would require using the model to simulate the Rolling wheel, where measurement setup mounting lasers on a beam is fixed inside the trailer with the loading wheel with RWD technology. Further development of this setup in the modelling and the resulting deflection needs to be investigated.

5. Conclusions

The study demonstrates that by using an analytical model, a faster prediction of the rigid pavement response across joints can be done. The model is a three-dimensional model and analytical in its formulation. Use of this model will be effective in the development of analysis for RWD based measurement technologies for a static load. Along with the model being faster, it uses more structural parameters than a simple analytical model, thus can provide more information than a traditional back-calculation. Thus, by analyzing high-frequency measurements from RWD technology, information about the pavement can be inferred and understood better. This application of a three-dimensional analytical formulation for a discontinuity in rigid pavements combined with an experimental demonstration by use of RWD technology is a novel development.