1. Introduction
Railways are used to transport large numbers of passengers and large amounts of goods at specified speeds. As railway infrastructure networks deteriorate over time, interventions have to be executed in order to be able to provide an adequate level of service over time. When executed, these interventions cost owners a considerable amount of money and they normally result in disruptions to service. If they are not executed, failures will eventually occur, which will also result in intervention costs and disruptions to service. The determination of the optimal combination of interventions to execute in an upcoming planning period is challenging due to the need of considering all objects,
the costs of the interventions for both the owner and the users of the network, which vary depending on the time of execution (e.g., night, day) and the possibility to group interventions together, and
the benefits of the interventions in terms of risk reduction for both the owner and the user, i.e., the probability and consequence of failures.
Although railway infrastructure managers are using computer systems to help them determine intervention programs, there are none that result in the highest net benefits take into consideration all of these aspects. Most of these systems, and research done to support the development of these systems, have predominantly either, (1) considered only the costs and benefits of executing interventions on objects of one type, e.g., tracks; (2) neglected the variations in the costs and disruptions to the service of grouping interventions of different types; or (3) both. Without an appropriate model, railway managers are unable to determine the optimal intervention programs.
This paper proposes a network flow model approach that overcomes this problem as it allows determining optimal intervention programs for railway infrastructure networks while taking into consideration;
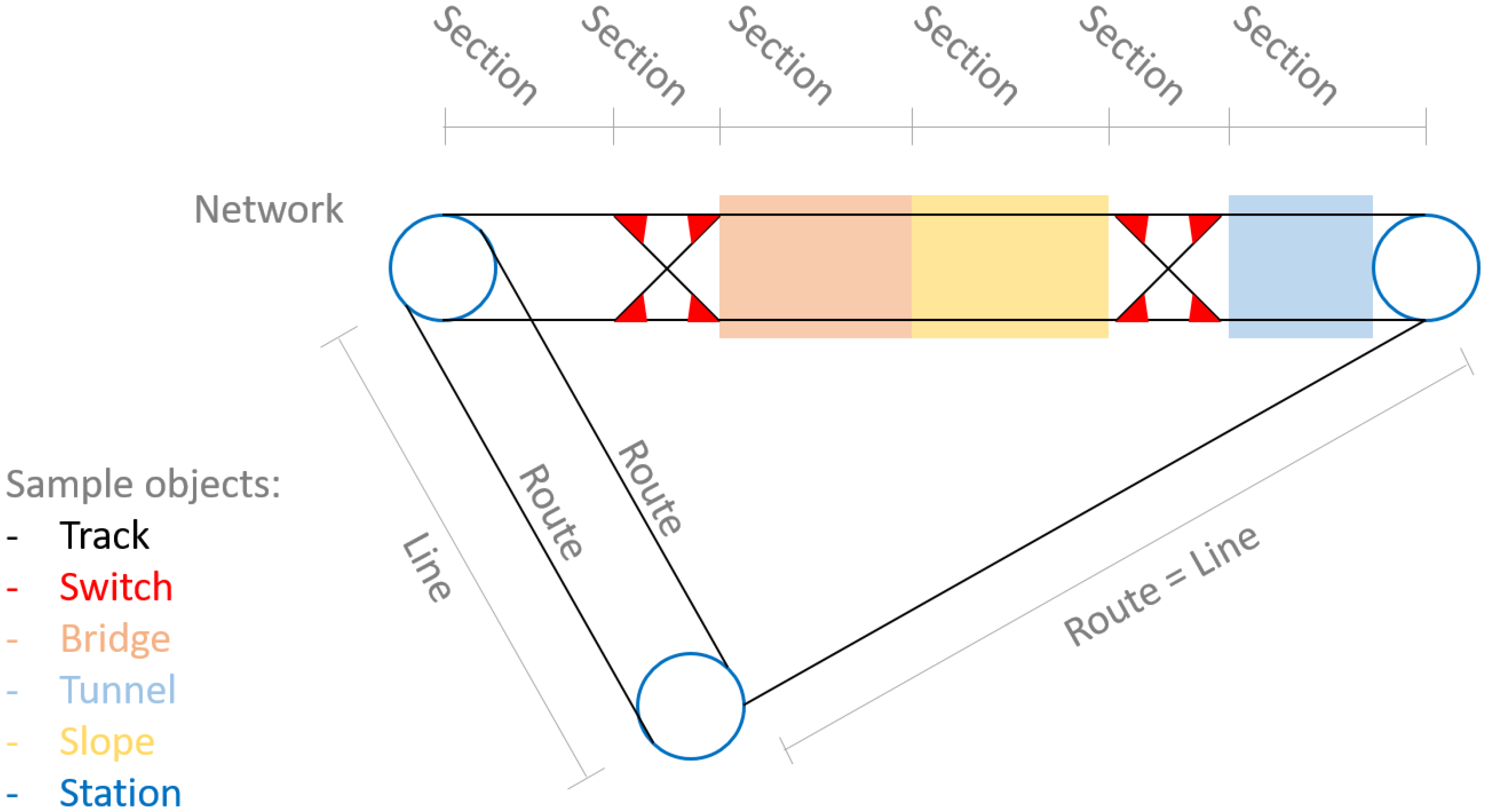
different types of objects,
how the objects work together to provide service,
dependencies between objects, and
object-traffic dependencies.
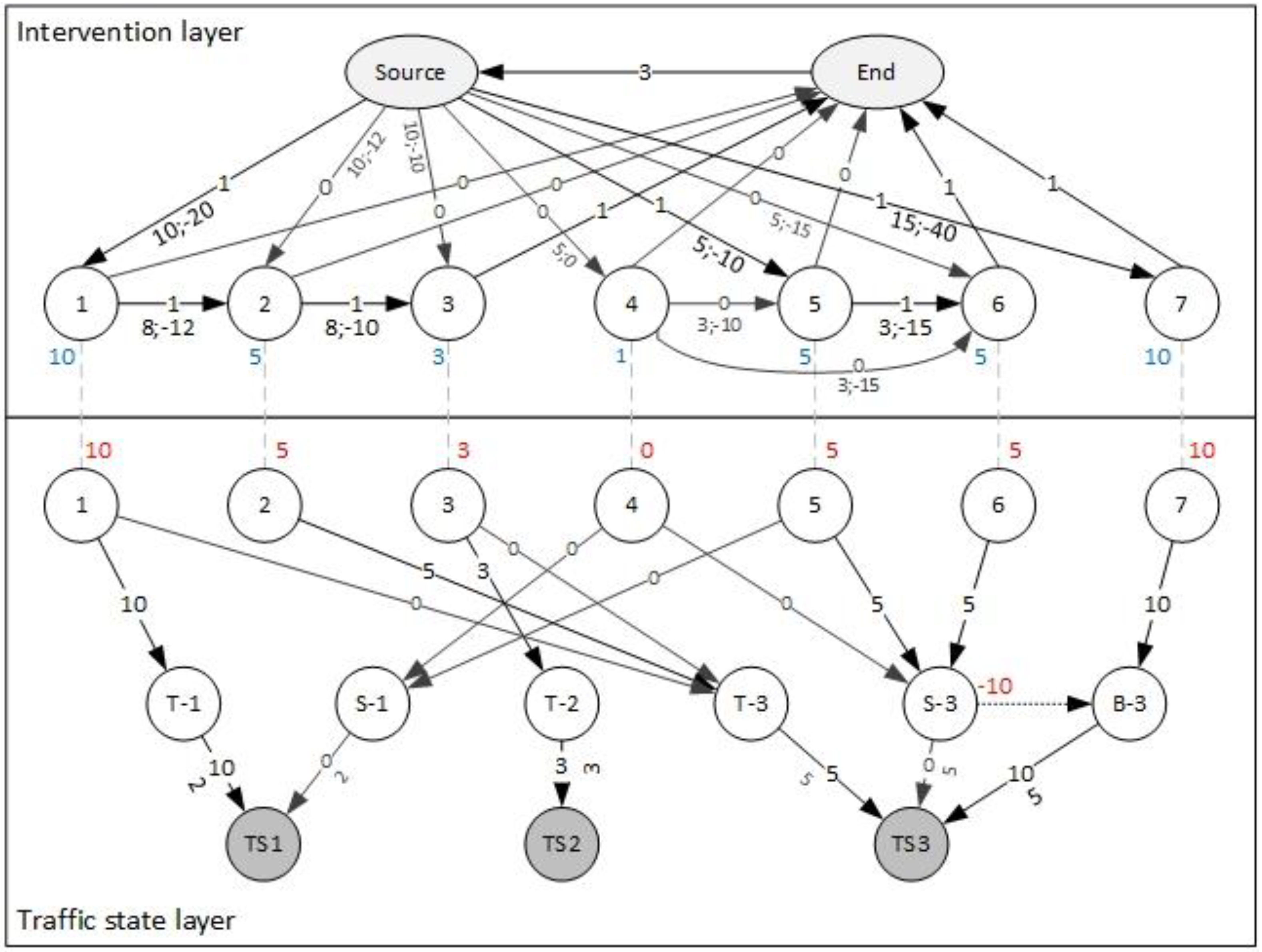
Using constrained network flow models as proposed in this paper overcomes this problem. They allow for the determination of the optimal intervention programs for railway infrastructure networks while taking into considerations different types of objects, how the objects work together to provide service, and object and object-traffic dependencies. The optimal intervention program is the one that has the maximum net benefit, i.e., the difference between the reductions in risks due to the execution of interventions minus the costs. The models consist of an intervention layer, which enables the selection of the interventions and consideration of the object dependencies, and a traffic state layer, which enables the modelling of how the network provides service and the object-traffic dependencies. To ensure the models work constraints are required. They include flow conservation constraints to ensure consistency in the model and side constraints, which ensure that the real world is realistically modelled. The side constraints include (1) source flow constraints to enable modelling the durations of interventions; (2) topological constraints to enable the introduction of topological dependencies; (3) exclusivity constraints to ensure that multiple interventions are not executed on the same object in the same time period; (4) organisational constraints to ensure that external limitations, e.g., budget are not exceeded; and (5) structural constraints to ensure that mandatory interventions are executed if required. The network flow models are formulated as mixed integer linear problems. They are solved while using the simplex method and the branch and bound algorithm.
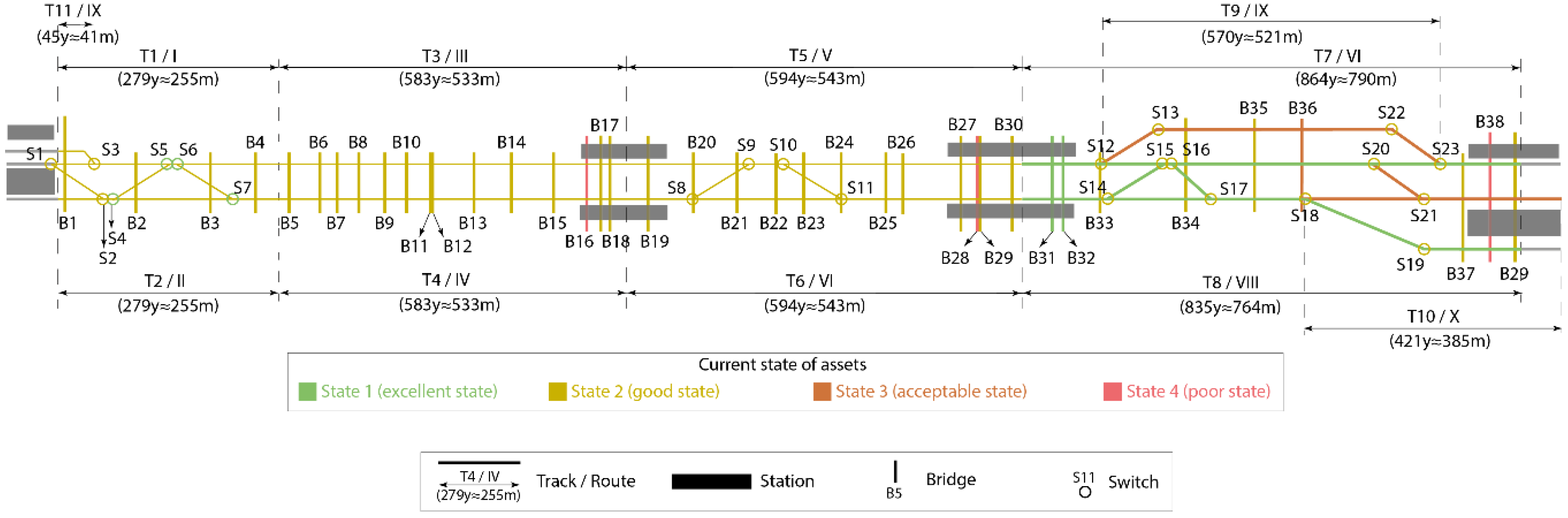
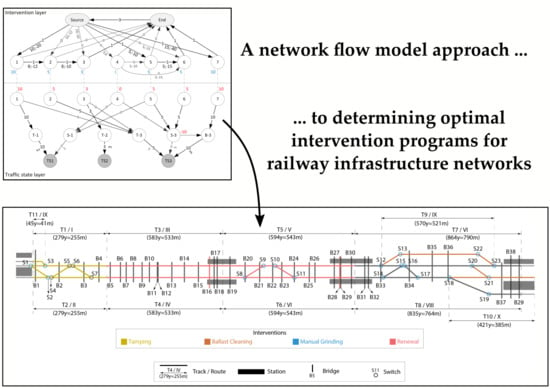
The modelling approach is illustrated by using it to determine the optimal intervention program for a 2200 m multi-track railway line, which consists in addition to the 11 track sections of 23 switches and 39 bridges. The efficiency and effectiveness of the model are demonstrated by comparing the determination of this intervention program with the ones determined while using a reduced exhaustive search algorithm and an algorithm based on simplified decision rules. It is shown that the proposed constrained network flow model and search algorithm can be used to determine the optimal intervention program within a reasonable amount of time.
The remainder of this paper is structured as follows:
Section 2 includes a literature review.
Section 3 includes a description of the problem and its components.
Section 4 includes a description of the constrained network flow models in both general terms and mathematically.
Section 5 includes the example.
Section 6 includes the comparisons of the optimal intervention programs determined while using the three different approaches.
Section 7 includes a discussion and the conclusions of the work.
2. Literature Review
Research focused on the best ways to plan interventions has increased in recent years. The research can be grouped into three general categories. In category 1, researchers have focused on determining optimal intervention strategies, i.e., the determination of the optimal interventions to be executed on specific objects over their life cycles if there are no external constraints [
1,
2,
3,
4]. In category 2, researchers have focused on determining optimal intervention programs, i.e., the determination of the optimal interventions to execute on many objects taking into consideration the current state of the objects, the optimal intervention strategies of all objects, and external constraints, e.g., [
5,
6,
7,
8,
9,
10,
11,
12,
13]. In category 3, researchers have focused on how to group interventions on objects once it is known the work that needs to be executed, e.g., [
14,
15,
16]. Although categories 1 and 3 are interesting, they are not directly related to the work that is presented in this article, and are, therefore, not followed further.
The research conducted in category 2 can be further divided into research using a bottom-up approach, a top-down approach and using an integrated approach. Using the bottom-up approach, researchers determine the interventions to be executed for each object individually, i.e., without consideration of other objects or constraints on the development of intervention programs, and then modify these interventions to take into consideration reductions in cost and service disruptions of executing interventions on multiple objects of the same type simultaneously. Using the top-down approach, researchers determine where track occupancy schedules are required without detailed consideration of individual objects and then determine the interventions that should be executed on the objects within the affected area. Using an integrated approach, researchers directly determine the interventions to be executed on objects of different types while taking into consideration the possible reductions in costs and disruptions to service of executing multiple interventions simultaneously.
Of the researchers that have used a bottom-up approach, which is more common, most have focused on the determination of the optimal intervention programs for tracks, e.g., [
5,
6,
7,
8,
9]. Caetano & Teixeira [
6] determined optimal and near-optimal interventions to be executed for each object individually, before developing the intervention program for multiple adjoined railway segments while using penalty costs for moving away from the optimal point in time for the execution of interventions. The interventions to be executed were determined using a mixed integer linear program. Furuya & Madanat [
8] incorporated economies of scale and capacity constraints in order to consider economical, functional, and stochastic dependencies between different objects in the network in order to determine the interventions to be executed with a two-stage approach. Zhao et al. [
5] developed a genetic algorithm-based approach for synchronising the interventions of different components within a track section. They simplified the combinatorial complexity by using three standard combinations. Fecarotti & Andrews [
7] developed intervention programs for an entire network by selecting the intervention strategy to follow for each object out of different strategies evaluated using Petri-Net simulations. Pargar [
9] used a linear integer program to determine the optimal time point for executing interventions on different track components considering dependencies between different components through component and location specific setup costs, and between different track sections through a system dependent setup cost. An area of improvement on this research, however, is the consideration of the reduction in costs and service disruptions of executing interventions on multiple objects of different types (e.g., track, switches, level crossing, and bridges).
The researchers that have used a top-down approach have all focused on the grouping of interventions on different types of objects within time-free periods, which are determined by the models [
10,
11,
12,
13]. Den Hertog et al. [
10], extended by Van Zante-De Fokkert et al. [
13], used a maximum work zone length and a time of the day constraint to develop optimal intervention work zones for railway infrastructure networks in order to minimise the service disturbance and costs. In the second step, the work zones were assigned to particular nights when considering the possible combinations of work zones over the network. Jenema [
11] developed a train-free period planning approach that is based on a linear integer program for minimising the required track capacity for executing interventions. They considered the trade-off between higher intervention costs and lower possession costs for a night execution compared with a day execution. Lethanh & Adey [
12] assumed that managers of a railway line passing through different countries would need to agree on fixed windows of intervention time in the future without knowing which intervention that they would need to execute exactly, and used a real options approach to determine the optimal window for each rail manager.
The researchers that have used an integrated approach have all focused on directly estimating the owner costs of interventions and the user costs of service disruption while taking into consideration the reductions in costs and service disruptions by executing interventions simultaneously. For example, Burkhalter et al. [
17] estimated the object level owner costs together with the network level user costs without the requirement of an iterative process or a multi-step model, by using faults to connect the owner costs of interventions with the user costs that are related to states of the network. An integer non-linear program was used to determine the optimal intervention program. Hajdin & Adey [
18], extended by Eicher et al. [
19] and Lethanh et al. [
20], developed a network model for developing optimal intervention programs for road networks while taking into account cost variations by executing intervention on neighbouring objects, spatial constraints, and a budget limitation. Their network model searched for the path with the lowest cost along a network, and was formulated as an integer linear program. The approach that is presented in this paper, is based on this work. The approach to modelling enables the development of similar models that are capable of determining optimal intervention programs for railway infrastructure networks. The adaptations have also enabled the mathematical models to be linear, instead of non-linear, as the one presented in [
17].
6. Comparison
When there was no budget limit, the optimal intervention program determined while using the network flow model was compared with those determined using, (1) an exhaustive search approach and (2) a decision rule approach (
Table 10). Both approaches were used to evaluate a subset of the total number of intervention programs since the 3 × 10
82 possible programs could not be evaluated in a reasonable time. When there was a budget limit, the optimal intervention program that was determined using the network flow model was compared with the one determined using the decision rule approach. The exhaustive search approach could not be used, as a budget constraint imposed on interventions on all objects cannot be evaluated by investigating object groups one at a time.
The owner costs, user costs, risk reduction and the net benefit of the intervention programs determined using the three approaches are shown in
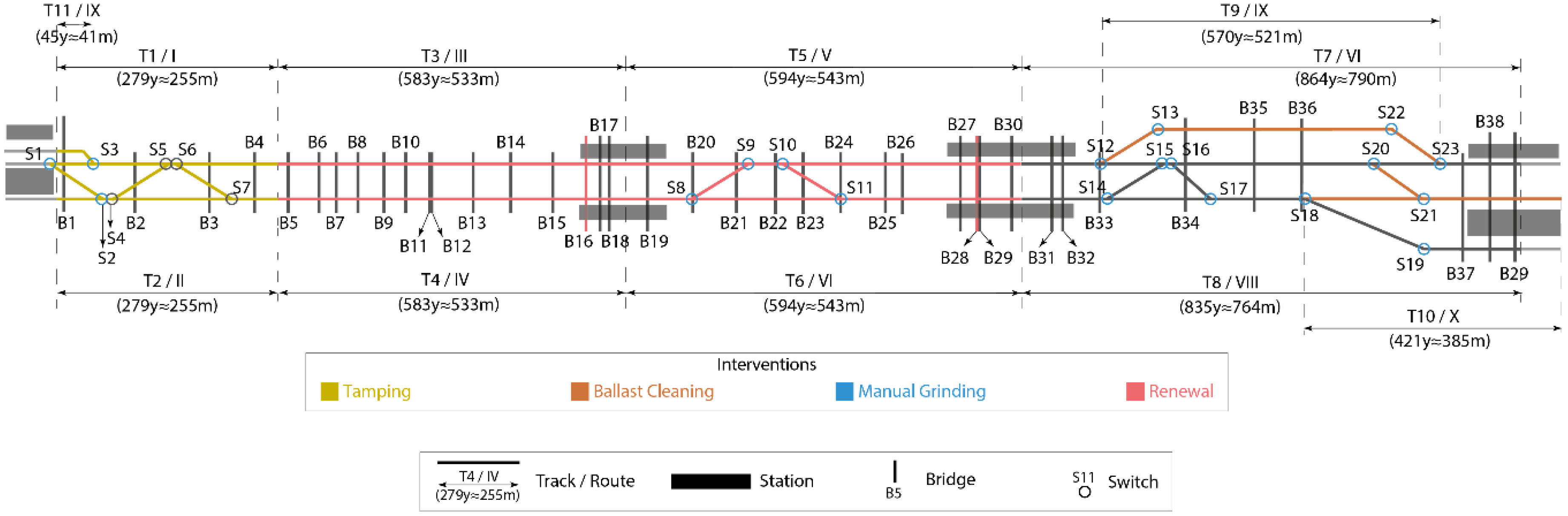
Table 11. As the network flow model and the exhaustive search find the same optimal intervention program all numbers are the same. The decision rules approach yields a near optimal intervention program, but not the optimal one, therefore there are slight differences in the owner and user costs and the risk reduction. One of the differences in the intervention programs is that the interventions on switches
S21 and
S22 are executed during the night with the near optimal intervention program, whereas they are executed during the weekend with the optimal intervention program.
The computation time of each approach is also shown in
Table 11. It can be seen that the network flow model determines the optimal intervention program considerably faster than the exhaustive search, but that it was not as fast as the decision rules. Of course, the even faster time that is required by the decision rule approach comes at the expense of lost optimality, or in other words lost net-benefit. At least for the example this does not seem to be worth it. One cannot, however, forget that there are many approximations that have gone into the development of the models of the railway network and the possible interventions. These assumptions reduce the significance of the difference between the theoretically optimal intervention program and the near optimal intervention program.
7. Summary and Conclusions
An approach to develop models to determine optimal intervention programs for railway infrastructure networks was presented, i.e., the one with the maximal difference between the benefit in terms of risk reduction and the costs to the owner and user of executing interventions. The developed models are network flow models formulated as mixed integer linear programs and are constructed as constrained minimum cost flow problems, which search for the flow with the minimum cost within a given network under the consideration of flow conservation in each node, budget constraint and constraints that ensure that the times required to execute multiple intervention simultaneously are correctly considered. It enables the consideration of
economical dependencies (i.e., those between similar interventions allowing to reduce intervention costs),
structural dependencies (i.e., those that mean that an intervention on one necessitates an intervention on another), and
topological dependencies (i.e., those between objects in terms of the system functionality).
The approach was used to develop a model to determine the optimal intervention program for a network with 73 objects, i.e., 11 tracks, 23 switches, and 39 bridges. The optimal intervention program was determined for the situations with and without a budget limitation.
It was shown that the developed model was able to determine the optimal intervention program in much faster computational time than using an exhaustive search, even with a reduced search space. It was also shown that the developed model was slower, but more accurate than a more simplified approach that is based on straightforward decision rules. The significance of the trade-off between speed and accuracy depends on the accuracy of the underlying models of infrastructure and the possible interventions, as well as the amount of time available for analysis.