A Novel Application of Photogrammetry for Retaining Wall Assessment
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Image Collection and Processing
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Clayton, C.R.; Woods, R.I.; Bond, A.J.; Milititsky, J. Earth Pressure and Earth-Retaining Structures; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Wendland, S. When Retaining Walls Fail. Civil Engineering News, 2011. Available online: http://www.cenews.com (accessed on 5 October 2015).
- DeMarco, M.J.; Anderson, S.A.; Armstrong, A. Retaining Walls Are Assets Too! Publ. Roads 2009, 73, 30–37. [Google Scholar]
- Goh, A.T.C.; Kulhawy, F.H. Reliability assessment of serviceability performance of braced retaining walls using a neural network approach. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 627–642. [Google Scholar] [CrossRef]
- Duncan, C. Soils and Foundations for Architects and Engineers; Springer Science and Business Media: Norwell, MA, USA, 1992. [Google Scholar]
- Budhu, M. Soil Mechanics & Foundations; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Anderson, S.A.; Rivers, B.S. Capturing the Impacts of Geotechnical Features on Transportation System Performance. In Proceedings of the Geo-Congress, San Diego, CA, USA, 28 March 2013; pp. 1633–1642. [Google Scholar]
- Mohammad, T. Failure of a Ten-Storey Reinforced Concrete Building Tied To Retaining Wall: Evaluation, Causes, and Lessons Learned. Struct. Congr. 2005. [Google Scholar] [CrossRef]
- Bernhardt, K.L.S.; Loehr, J.E.; Huaco, D. Asset Management Framework for Geotechnical Infrastructure. J. Infrastruct. Syst. 2003, 9. [Google Scholar] [CrossRef]
- Anderson, S.A.; Alzamora, D.; DeMarco, M.J. Asset Management Systems for Retaining Walls. In Proceedings of the Biennial Geotechnical Seminar Conference, ASCE, Denver, CO, USA, 7 November 2008; pp. 162–177. [Google Scholar]
- Butler, C.J.; Gabr, M.A.; Rasdorf, W.; Findley, D.J.; Chang, J.C.; Hammit, B.E. Retaining Wall Field Condition Inspection, Rating Analysis, and Condition Assessment. J. Perform. Constr. Facil. 2015, 30, 04015039. [Google Scholar] [CrossRef]
- Chouinard, L.; Andersen, G.; Torrey, V., III. Ranking Models Used for Condition Assessment of Civil Infrastructure Systems. J. Infrastruct. Syst. 1996. [Google Scholar] [CrossRef]
- AASHTO Transportation Asset Management Guide: A Focus on Implementation; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2013.
- Kimmerling, R.E.; Thompson, P.D. Assessment of Retaining Wall Inventories for Geotechnical Asset Management. Transp. Res. Rec. 2015, 2510, 1–6. [Google Scholar] [CrossRef]
- Brutus, O.; Tauber, G. Guide to Asset Management of Earth Retaining STRUCTURES; US Department of Transportation, Federal Highway Administration, Office of Asset Management: Washington, DC, USA, 2009.
- Han, J.; Hong, K.; Kim, S. Application of a Photogrammetric System for Monitoring Civil Engineering Structures; InTech.: Rijeka, Croatia, 2012. [Google Scholar]
- Wyllie, D.; Mah, C. Rock Slope Engineering Civil and Mining, 4th ed.; Spon Press: New York, NY, USA, 2004. [Google Scholar]
- Scaioni, M.; Alba, M.; Roncoroni, F.; Giussani, A. Monitoring of a SFRC retaining structure during placement. Eur. J. Environ. Civ. Eng. 2010, 14, 467–493. [Google Scholar] [CrossRef]
- Wang, G.; Philips, D.; Joyce, J.; Rivera, F. The integration of TLS and continuous GPS to study landslide deformation: A case study in Puerto Rico. J. Geod. Sci. 2011, 1, 25–34. [Google Scholar] [CrossRef]
- Vaghefi, K.; Oats, R.; Harris, D.; Ahlborn, T.; Brooks, C.; Endsley, K.; Roussi, C.; Shuchman, R.; Burns, J.; Dobson, R. Evaluation of Commercially Available Remote Sensors for Highway Bridge Condition Assessment. J. Bridge Eng. 2012, 17. [Google Scholar] [CrossRef]
- Escobar-Wolf, R.; Oommen, T.; Brooks, C.; Dobson, R.; Ahlborn, T. Unmanned Aerial Vehicle (UAV)-based Assessment of Concrete Bridge Deck Delamination Using Thermal and Visible Camera Sensors: A Preliminary Analysis. Res. Nondestr. Eval. 2017. [Google Scholar] [CrossRef]
- Jauregui, D.V.; White, K.R.; Woodward, C.B.; Leitch, K.R. Noncontact Photogrammetric Measurements of Vertical Bridge Deflection. J. Bridge Eng. 2003, 212. [Google Scholar] [CrossRef]
- Jiang, R.; Jauregui, D.V.; White, K.R. Close-Range Photogrammetry Applications in Bridge Measurement: Literature Review. Measurement 2008, 41, 823–834. [Google Scholar] [CrossRef]
- Bouali, E.; Oommen, T.; Escobar-Wolf, R. Interferometric Stacking toward Geohazard Identification and Geotechnical Asset Monitoring. J. Infrastruct. Syst. 2016, 22. [Google Scholar] [CrossRef]
- Oskouie, P.; Becerik-Gerber, B.; Soibelman, L. Automated Cleaning of Point Clouds for Highway Retaining Wall Condition Assessment. In Proceedings of the 2014 International Conference on Computing in Civil and Building Engineering, Orlando, FL, USA, 23–25 June 2014. [Google Scholar]
- Gong, J.; Zhou, H.; Gordon, C.; Jalayer, M. Mobile Terrestrial Laser Scanning for Highway Inventory Data Collection. Comp. Civ. Eng. 2012. [Google Scholar] [CrossRef]
- Laefer, D.; Lennon, D. Viability Assessment of Terrestrial LiDAR for Retaining Wall Monitoring. GeoCongress 2008, 310. [Google Scholar] [CrossRef]
- Olsen, M.J.; Butcher, S.; Silvia, E.P. Real-Time Change and Damage Detection of Landslides and Other Earth Movements Threatening Public Infrastructure; Transportation Research and Education Center (TREC): Portland, OR, USA, 2012; OTREC-RR-11-23. [Google Scholar]
- Xiao, R.; He, X. GPS and InSAR Time Series Analysis: Deformation Monitoring Application in a Hydraulic Engineering Resettlement Zone, Southwest China. Math. Prob. Eng. 2013, 2013, 601209. [Google Scholar] [CrossRef]
- Vosselman, G.; Maas, H.G. (Eds.) Airborne and Terrestrial Laser Scanning; Whittles Publishing: Dunbeath, Scotland, 2010. [Google Scholar]
- Casagli, N.; Cigna, F.; Bianchini, S.; Hölbling, D.; Füreder, P.; Righini, G.; Vlcko, J. Landslide mapping and monitoring by using radar and optical remote sensing: Examples from the EC-FP7 project SAFER. Remote Sens. Appl. Soc. Environ. 2016, 4, 92–108. [Google Scholar] [CrossRef]
- Golparvar-Fard, M.; Balali, V.; de la Garza, J.M. Segmentation and recognition of highway assets using image-based 3D point clouds and semantic Texton forests. J. Comp. Civ. Eng. 2012, 29. [Google Scholar] [CrossRef]
- Cleveland, L.; Wartman, J. Principles and Applications of Digital Photogrammetry for Geotechnical Engineering. Proc. Site Geomat. Charact. 2006, 16, 128–135. [Google Scholar]
- Remondino, F.; El-Hakim, S. Image-based 3D modelling: A review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. Structure-for-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Ellenberg, A.; Branco, L.; Krick, A.; Bartoli, I.; Kontsos, A. Use of Unmanned Aerial Vehicle for Quantitative Infrastructure Evaluation. J. Infrastruct. Syst. 2014, 21. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A. Elements of Photogrammetry: With Applications in GIS, 3rd ed.; McGraw-Hill Co. Inc.: New York, NY, USA, 2000. [Google Scholar]
- Scaioni, M.; Barazzetti, L.; Giussani, A.; Previtali, M.; Roncoroni, F.; Alba, I.M. Photogrammetric techniques for monitoring tunnel deformation. Earth Sci. Inf. 2014, 7, 83–95. [Google Scholar] [CrossRef]
- Lindenbergh, R.; Pietrzyk, P. Change detection and deformation analysis using static and mobile laser scanning. Appl. Geomat. 2015, 7, 65–74. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, L.; Yang, B.; Wu, L. Applications of Structure from Motion: A Survey. J. Zhejiang Univ.-Sci. C 2013, 14, 486–494. [Google Scholar] [CrossRef]
- Khaloo, A.; Lattanzi, D. Hierarchical Dense Structure-from-Motion Reconstructions for Infrastructure Condition Assessment. J. Comput. Civ. Eng. 2016, 31. [Google Scholar] [CrossRef]
- Dai, F.; Rashidi, A.; Brilakis, I.; Vela, P. Comparison of image-based and time-of-flight-based technologies for three-dimensional reconstruction of infrastructure. J. Constr. Eng. Manag. 2012, 139. [Google Scholar] [CrossRef]
- Golparvar-Fard, M.; Bohn, J.; Teizer, J.; Savarese, S.; Peña-Mora, F. Evaluation of image-based modeling and laser scanning accuracy for emerging automated performance monitoring techniques. Autom. Constr. 2011, 20, 1143–1155. [Google Scholar] [CrossRef]
- Zhu, Z.; Brilakis, I. Comparison of optical sensor-based spatial data collection techniques for civil infrastructure modeling. J. Comput. Civ. Eng. 2009, 23. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wöhler, C. 3D Computer Vision: Efficient Methods and Applications; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Faugeras, O.; Luong, Q.T.; Papadopoulo, T. The Geometry of Multiple images: The Laws that Govern the Formation of Multiple Images of a Scene and Some of Their Applications; MIT Press: Cambridge, MI, USA, 2004. [Google Scholar]
- Scaioni, M.; Feng, T.; Barazzetti, L.; Previtali, M.; Roncella, R. Image-Based Deformation Measurement. Appl. Geomat. 2015, 7, 75–90. [Google Scholar] [CrossRef]
- Federal Highway Administration (FHWA). Seismic Retrofitting Manual for Highway Structures: Part 2—Retaining Structure, Slopes, Tunnels, Culverts, and Roadways; U.S. Department of Transportation: Washington, DC, USA, 2004.
- Federal Highway Administration (FHWA). Mechanically Stabilized Earth Walls and Reinforced Soil Slopes Design & Construction Guidelines; Publication No. FHWA-NHI-00-043; U.S. Department of Transportation National Highway Institute (NHI) Office of Bridge Technology: Arlington, VA, USA, 2001.
- Nikon D510 Digital Camera Reference Manual. 2011. Available online: http://cdn-10.nikon-cdn.com/pdf/manuals/noprint/D5100_ENnoprint.pdf (accessed on 25 June 2017).
- Forlani, G.; Pinto, L.; Roncella, R.; Pagliari, D. Terrestrial photogrammetry without ground control points. Earth Sci. Inform. 2014, 7, 71–81. [Google Scholar] [CrossRef]
- Pix4D Support. Offline Getting Started and Manual. 2016. Available online: https://support.pix4d.com/hc/en-us/articles/204272989-Offline-Getting-Started-and-Manual-pdf-#gsc.tab=0 (accessed on 25 June 2017).
- Freund, R.J.; Wilson, W.J. Statistical Methods, 2nd ed.; Elsevier: Burlington, MA, USA, 2003; p. 673. [Google Scholar]
- Su, Y.Y.; Hashash, Y.M.A.; Liu, L.Y. Integration of construction as-built data via laser scanning with geotechnical monitoring of urban excavation. J. Constr. Eng. Manag. 2006, 132. [Google Scholar] [CrossRef]
- Oskouie, P.; Becerik-Gerber, B.; Soibelman, L. Automated measurement of highway retaining wall displacements using terrestrial laser scanners. Autom. Constr. 2016, 65, 86–101. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; Walter de Gruyter: Berlin, Germany, 2014. [Google Scholar]
- Chen, L. What Is the Accuracy I Can Achieve with Pix4Dmapper Pro? Pix4D 2017. Available online: https://pix4d.com/getting-expected-accuracy-pix4dmapper-pro/ (accessed on 25 June 2017).
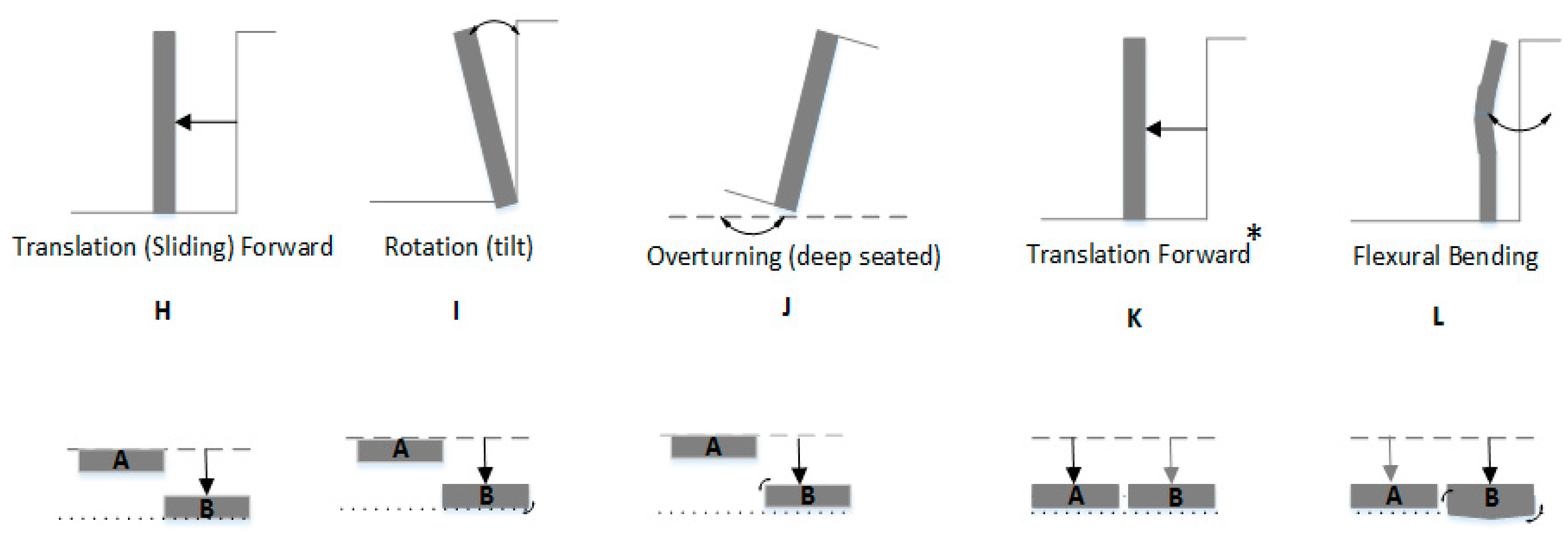

| Scenario | Observed Failure Mode of Wall Section A | Observed Failure Mode of Wall Section B | Avg. Displacement of Control Points (cm) |
|---|---|---|---|
| G | None | None | -- |
| H | None | Translation Forward | 3.13 |
| I | None | Rotation (tilt forward) | 5.75 |
| J | None | Overturning (deep seated) | 9.23 |
| K | Translation Forward | Overturning (deep seated) * | 1.45 |
| L | Translation Forward * | Bending (flexural bend forward) | 6.07 |
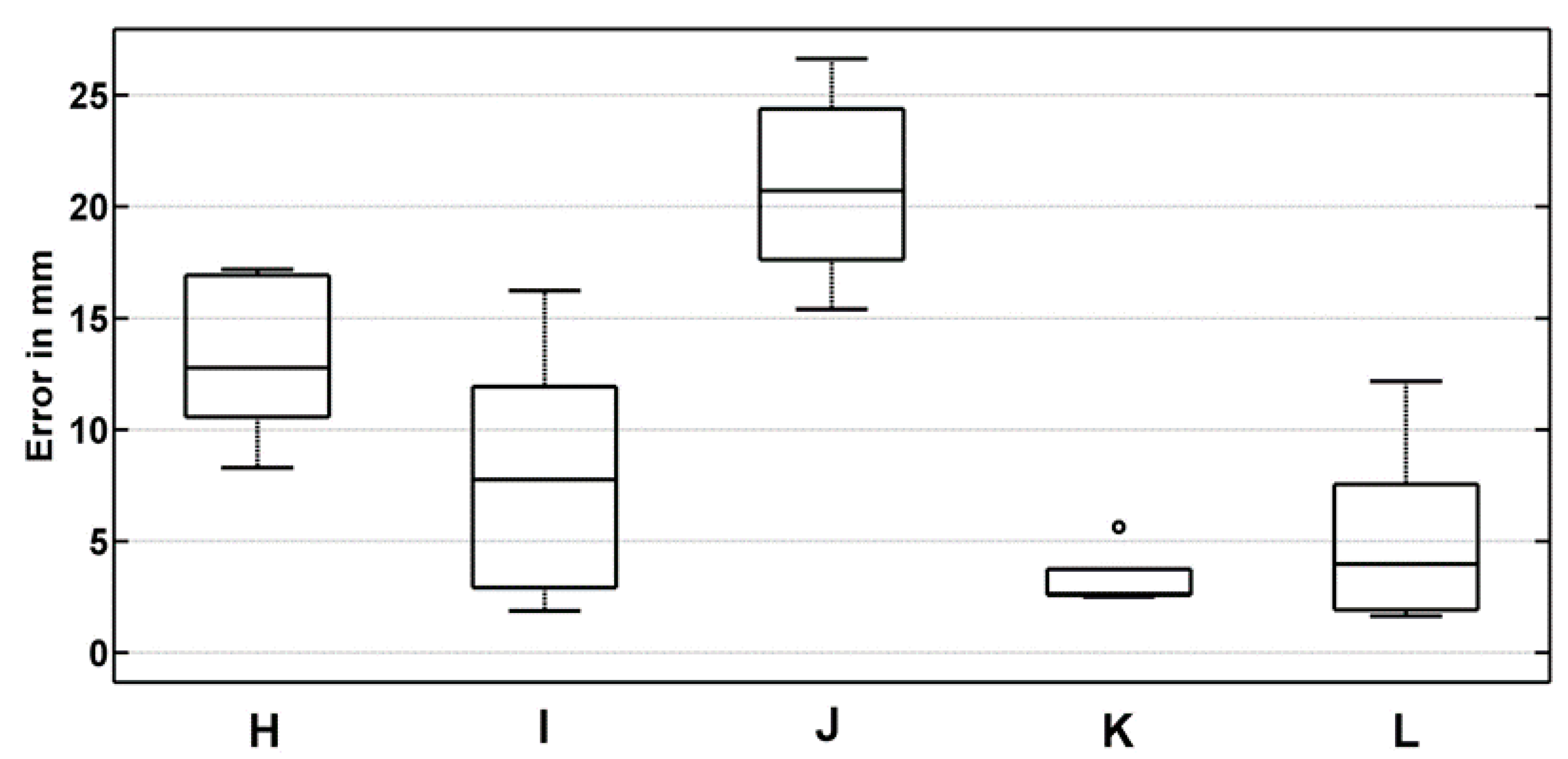
| Scenario | Control Point | Differences between Coordinates (mm) | Total 3D Error (mm) | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| H | B1 | 7.0 | 8.5 | 6.5 | 12.7 |
| B2 | 15.2 | 6.2 | −3.8 | 16.8 | |
| B3 | 9.8 | 1.9 | −5.5 | 11.4 | |
| B4 | 5.3 | −5.3 | −3.6 | 8.3 | |
| B5 | 12.2 | −7.0 | −9.9 | 17.2 | |
| I | B1 | 6.7 | 2.0 | 3.5 | 7.8 |
| B2 | 8.3 | −2.1 | 6.1 | 10.5 | |
| B3 | 6.8 | 0.5 | 14.8 | 16.2 | |
| B4 | 1.5 | −0.9 | 0.7 | 1.9 | |
| B5 | 2.1 | −1.7 | 1.9 | 3.3 | |
| J | B1 | −7.8 | −2.6 | 19.0 | 20.7 |
| B2 | 10.9 | −3.2 | 24.1 | 26.6 | |
| B3 | −9.1 | −0.1 | 15.9 | 18.3 | |
| B4 | −7.8 | 2.5 | 13.0 | 15.3 | |
| B5 | 10.4 | 2.4 | 21.1 | 23.6 | |
| K | A1 | 1.5 | −0.2 | −5.4 | 5.6 |
| A2 | 2.2 | −0.3 | 1.4 | 2.6 | |
| A3 | 1.2 | 0.8 | −2.1 | 2.5 | |
| A4 | 1.7 | −0.4 | −1.9 | 2.5 | |
| A5 | 1.8 | 0.8 | −2.4 | 3.1 | |
| L | B1 | 0.5 | 0.6 | −2.2 | 2.3 |
| B2 | 1.0 | 1.4 | 3.5 | 3.9 | |
| B3 | 1.1 | 1.0 | −2.2 | 2.6 | |
| B4 | 1.0 | −0.1 | −3.0 | 3.1 | |
| B5 | 2.4 | −0.3 | 2.4 | 3.4 | |
| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Square Value | F Statistic | p-Value (Probability of F > Fcritical) |
|---|---|---|---|---|---|
| Scenarios | 1015.99 | 4 | 253.997 | 14.64 | 9.68 × 10−6 |
| Error | 347.05 | 20 | 17.353 | -- | -- |
| Total | 1363.04 | 24 | -- | -- | -- |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oats, R.C.; Escobar-Wolf, R.; Oommen, T. A Novel Application of Photogrammetry for Retaining Wall Assessment. Infrastructures 2017, 2, 10. https://doi.org/10.3390/infrastructures2030010
Oats RC, Escobar-Wolf R, Oommen T. A Novel Application of Photogrammetry for Retaining Wall Assessment. Infrastructures. 2017; 2(3):10. https://doi.org/10.3390/infrastructures2030010
Chicago/Turabian StyleOats, Renee C., Rudiger Escobar-Wolf, and Thomas Oommen. 2017. "A Novel Application of Photogrammetry for Retaining Wall Assessment" Infrastructures 2, no. 3: 10. https://doi.org/10.3390/infrastructures2030010
APA StyleOats, R. C., Escobar-Wolf, R., & Oommen, T. (2017). A Novel Application of Photogrammetry for Retaining Wall Assessment. Infrastructures, 2(3), 10. https://doi.org/10.3390/infrastructures2030010








