Abstract
Retaining walls are critical geotechnical assets and their performance needs to be monitored in accordance to transportation asset management principles. Current practices for retaining wall monitoring consist mostly of qualitative approaches that provide limited engineering information or the methods include traditional geodetic surveying, which may provide high accuracy and reliability, but is costly and time-consuming. This study focuses on evaluating failure modes of a 2.43 m × 2.43 m retaining wall model using three-dimensional (3D) photogrammetry as a cost-effective quantitative alternative for retaining wall monitoring. As a remote sensing technique, photogrammetry integrates images collected from a camera and creates a 3D model from the measured data points commonly referred to as a point cloud. The results from this photogrammetric approach were compared to ground control points surveyed with a total station. The analysis indicates that the accuracy of the displacement measurements between the traditional total station survey and photogrammetry were within 1–3 cm. The results are encouraging for the adoption of photogrammetry as a cost-effective monitoring tool for the observation of spatial changes and failure modes for retaining wall condition assessment.
1. Introduction
Retaining walls, such as rigid cantilever structures stabilizing earth pressure along highways or roadways, are an indispensable geotechnical asset and a critical part of transportation infrastructure corridors [1,2,3,4]. Different factors can lead to retaining wall failure, including deterioration of materials, unregulated backfill specifications, or poor drainage systems [5,6,7,8]. These different failure mechanisms include many types of behaviors, such as a deep-seated movement, overturning motion or a sliding translation [6,9].
Monitoring of retaining wall displacement can be a tool for diagnosing the wall’s performance, as part of a larger asset management system. Asset management is receiving greater attention in geotechnical infrastructure to improve operations, enhance safety, and minimize costs with the inclusion of innovative assessment methods by incorporating a performance-based approach [10,11,12,13]. However, challenges, such as inadequacies of the current methods to effectively assess the condition of retaining walls and identifying the needs for preservation of physical transportation assets, have been acknowledged [13,14].
Current methods for retaining wall condition assessment includes mostly qualitative field inspections to evaluate wall elements, which is subjective and could incur defective documentation and result in overlooking critical safety problems [7,11,15]. Various in-contact devices, such as global positioning systems (GPS), tiltmeters, and total station surveying devices, have been used to measure deformation or slope movement of structures, such as retaining walls, but can be expensive, time-consuming, limited by physical or traffic accessibilities, or have poor accuracy in capturing real-time movements [16,17,18,19].
Remote sensing technologies have become increasingly popular for the assessment of infrastructure systems [20,21,22,23]. Advancements in remote sensing technologies for condition assessment present potential for unique applications, including for geotechnical infrastructure [24,25]. Decreased costs and high spatial resolution of remote sensing tools, such as Light Detection and Ranging (LiDAR), laser scanning (terrestrial), and Synthetic Aperture Radar (SAR), have shown promising results for detecting structure changes [17,26,27,28,29,30,31]. On the other hand, there are some limitations, including attaining suitable atmospheric conditions, acquiring target setups for measurements, and accessing satellite availability for devices, which can become a significant challenge [17,26,27,28,29,30,31].
Recent advancements in lower-cost optical cameras, image processing, and three-dimensional (3D) modeling have enabled photogrammetry to three-dimensionally reconstruct objects from digital images, for civil or transportation structure applications [16,32,33,34,35,36]. Photogrammetry provides the ability to obtain quantitative measurements from 3D models created from quality easily documented two-dimensional (2D) images, and has been used for assessing the condition of transportation assets [21,37]. Research has been documented in which photogrammetry or Structure from Motion (SfM) techniques and terrestrial laser scanning (TLS) were applied for 3D reconstruction for civil infrastructure systems [38,39,40,41,42,43,44]. Very few efforts have been conducted to investigate the application of photogrammetry for retaining wall infrastructure systems providing a more budget-friendly evaluation for geotechnical assets. Integrating non-contact photogrammetry techniques is advantageous with widely available quality digital single lens reflex (DSLR) cameras and advancing computer processing capabilities with open source software options [16,34,35,36,37,38,39]. Applying this to the vast geotechnical infrastructure to not only provide automatic easy data-logged qualitative documentation of condition, but also quantitative changes, can further advance retaining wall asset management [10,13,14,16]. The objective of this study is to evaluate the applicability of digital photogrammetry to provide a quantitative assessment of retaining walls compared to a traditional surveying measuring approach. In addition, deploying photogrammetric-based techniques without the need for extensive additional calibration processing will further promote its use for in-field retaining wall assessment.
2. Materials and Methods
Photogrammetric methods to generate three-dimensional representations of surfaces have been used for over a century [37]. Recently, improvements in computational power and efficient processing algorithms have allowed digital photogrammetric methods to be of extensive practical use [21,37,38,39].
This study promotes using photogrammetry principles within the processing software that incorporates overlapping images (including bundle adjustment) and intrinsic calibration for optimal model reconstruction. Supplementary details on such processes and algorithms are beyond the aim of this paper, and the reader should review the standard references for more on the topic, e.g., [38,39,45,46,47,48]. Digital photogrammetry can provide 3D coordinates of points on a surface, and by comparing the locations of the surface, represented by the points in 3D space, at different times, it is possible to infer surface movements. A more detailed description of image-based deformation measurements can be found in Scaioni et al. [48]. In the case of the retaining walls, this would be equivalent to tracking the wall’s position through time. From such movement tracking, it may be possible to infer whether the wall is stable or not, which could indicate failure.
2.1. Experimental Setup
To evaluate failure behavior on retaining wall structures, a 2.43 m × 2.43 m (8 ft × 8 ft) cantilevered-style retaining wall model was deployed for analysis. The 8 ft × 8 ft model was constructed using two individual 1.22 m × 2.43 m (4 ft × 8 ft), sections simulating different sections of the retaining wall. The sections were placed on a strandboard frame, which is covered with sheets of insulating foam boards. The foam sections are fixed at the bottom by two hinges, which enables a tilting motion to simulate wall failure by tilting. The sections are held in place by a cord attached to the back of the plywood board structure with a screw to simulate tilting deflection. Fourteen reference or control points were placed in the test setup to infer ground locations for georeferencing and surveyed using a total station. Ten of these markers were placed on the wall model itself, five on each section and four were placed on neighboring static objects positioned at different elevations and depths from the wall model.
Retaining walls can exhibit different movements associated with their failure. Four failure modes were selected due to their common occurrence: translation (sliding forward), tilting (forward rotation), deep-seated rotation (backward or overturning), and a flexural bending (forward bend) [6,49,50]. Five scenarios were tested for different failure modes separately and in combination. Table 1 summarizes the failure configurations along with the Trimble (Sunnyvale, California, USA) S3 Robotic total station average measured displacements for the control points.

Table 1.
Testing scenarios for retaining wall failure observations.
All wall displacements were measured with respect to a references position, referred to as scenario G. Figure 1 presents a visual illustration for the failure mode scenarios explored in this study along with the plan view diagrams.
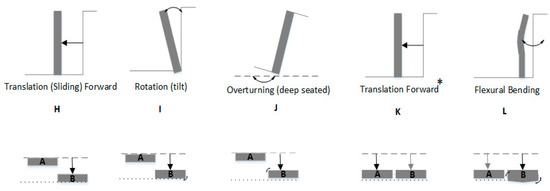
Figure 1.
Visual of retaining wall failure modes with an accompanying plan view illustration. * Repeated failure mode on wall section B.
Figure 2a shows the retaining wall setup with the five reference markers or control points labeled as either A1–A5 or B1–B5, depending on the wall section on which they are located. The four remaining reference markers were labeled C1–C4, placed on the nearby building wall and two stationary stools, which are also shown on Figure 2b.

Figure 2.
(a) Image of the retaining wall model and surrounding control points during data collection; (b) point cloud creation for the model with the reference control points (highlighted as flagged points on wall A); and (c) visualization of the point cloud (with referenced control points) and camera positions during image collection.
2.2. Image Collection and Processing
Images were taken along a 7.62 m (25 ft) line perpendicular (at 90 degrees) to the wall model of sight from at least ten different positions. The base (distance between camera positions) ranged from 0.8 to 1.2 m, resulting in overlaps between adjacent frames of 70% to 85%. At each position, two images were collected from the wall, one standing and one kneeling, to produce some vertical parallax view of the wall, in addition to the horizontal parallax. The collection of the images were nearly 1 m apart along the line of sight. A Nikon (Minato, Tokyo, Japan) D5100 DSLR camera was used to collect images, with a 55 mm focal length lens. The Nikon D5100 contains a 16.2 megapixel resolution (4928 × 3264 pixels) and 23.6 mm × 15.6 mm CMOS sensor size [51]. Enough overlap between adjacent photographs ensured that no data gaps would occur in the photogrammetric processing. The photogrammetry methodology obtains accurate sensor calibration within the coordinate measurement processing methods for gathering spatial information [44,52].
Photogrammetric processing of the images was done using Pix4D® (Lausanne, Vaud, Switzerland) commercial software. Pix4D software processing includes a calibration optimization step in which the external and internal parameters (including radial and tangential lens distortion) are optimized for optimal reconstruction [53]. After acquiring the images for each scenario configuration as noted, a Trimble total station surveying device was used to capture the location of the control point markers with a 0.91 mm (0.04 in) precision.
The Pix4D software builds three-dimensional models of the surfaces captured in the photographs using digital photogrammetry methods. The models consist of a large set of points in three-dimensional space, i.e., point clouds. The numbers of points are commonly on the order of several million, which results in point densities of tens to hundreds of thousands of points per m2 at the scales at which the tests were performed. Figure 2b provides an illustration of the 3D point cloud model including the control point markers. Figure 2c reveals the model point cloud visualization (including setup of control points) with the corresponding images captured at the 7.62 m line of sight parallel camera positions.
Pix4D processing involves feature matching in building the dense point cloud reconstruction which allows details along the object’s image surface [53]. Surface displacement calculations were done by comparing the positions of common points representing the surfaces for different scenarios. Co-registration of the point clouds in a common coordinate system for the different scenarios was achieved using control points that did not move between scenarios. Control points on the moving panels were compared between scenarios, but also with the total station measurements. After obtaining the point clouds from Pix4D, we manually identified the location of the control point in the point cloud, to extract their 3D coordinates and compare them with the coordinates obtained from the total station measurements. The point closest to the center of the control point target was selected, and we estimate that the error induced by this procedure is on the order of 1–2 mm.
3. Results
Photogrammetric processing of the digital images from the experimental setup produced high-quality three-dimensional point clouds (shown on Figure 2b). The visual inspection of these models shows a good correspondence with the actual shape and appearance of the setup. Table 2 lists the differences between the coordinates of the control points measured by the total station and extracted from the digital photogrammetry. The differences are usually within a few mm. The control point differences for each test scenario is shown, as well as the total 3D error for that control point location. Comparisons between the digital photogrammetry and total station (TS) measurements produced small errors for most of the scenarios.

Table 2.
Differences in mm between the coordinates of the control points obtained from the total station and the coordinates of the same control points extracted from the digital photogrammetry point cloud.
Scenarios H–J contained slightly larger error differences than both K and L scenarios. This error is defined as the differences between the TS recorded locations of the control points and the center of the control point locations identified from the Pix4D point cloud model. The center of the control point locations in the point cloud was manually selected to ensure true comparison with the TS center measured location. Scenario H–J incurred additional directional movement of failure mode behavior than the latter two scenarios. Figure 3 also expands on this analysis with a box plot of scenario control errors determined from the difference between TS results and 3D model control point locations. These represent the mean error for the individual control points processed with Pix4D compared to the total station in each scenario.
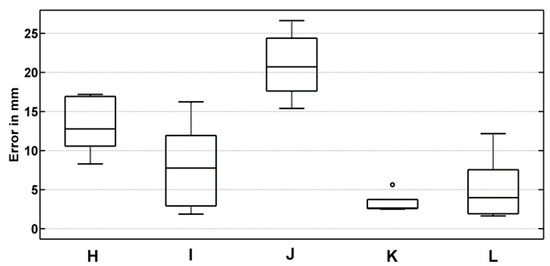
Figure 3.
Box plot of mean errors between total station and photogrammetric 3D model using Pix4D for testing scenarios H-L.
Errors in all cases are less than 2.1 cm, and in several scenarios are less than 1 cm, most being less than 1.5 cm, with the exception of scenario J, which produced the largest error. Standard deviations are quite small indicating under a 0.5 cm deviation for all the simulated scenarios, and as small as 0.013 cm for scenario K. The 95% confidence intervals are less than 8 mm for all scenarios (even less than 4 mm for both K and L) excluding the outlier scenario J. Scenario J reveals the largest errors across the five control points, while scenario I indicates the largest distribution similar to the greatest deviation.
To test that the mean error values between the different experiments are statistically different, a simple one-way balanced analysis of variance (ANOVA) test was performed. The ANOVA is a standardized statistical procedure [54] that can be used for testing the hypothesis that mean values, in this case errors for different scenarios, are not equal at a given level of statistical significance. The ANOVA procedure relies on the F-test, such that an F statistic is calculated using the ratio of the between-group variability (the differences in errors between scenarios, for our case) to the within-group variability (the error levels within each scenario, in our case). The F statistic is then compared with the values of the F distribution that would be expected if the null hypothesis was true (the Fcritical value), and if it is larger, the null hypothesis can be rejected at the given confidence level. This can also be shown as a statistical p-value from which the significance of the test can also be assessed. The results are usually shown in a standard ANOVA table, which details the test parameters. Further details and background information on this test can be found on standard statistical references [54] and the reader is referred to such texts for a more in depth discussion. An ANOVA test was done on the error values for the different scenarios to test for statistically significant differences; Table 3 summarizes the ANOVA results and shows that a very small value (9.68 × 10−6) is obtained for the p-value. Considering a significance level of 0.01, the corresponding critical value for the F statistic (for between-group and within-group degrees of freedom of 4 and 20, respectively) would be 4.431, and the F value obtained from the ANOVA test is 14.64, which means that the differences are significant at that level.

Table 3.
Standard ANOVA results for the comparison of mean errors from the different scenarios.
Measurements of displacements perpendicular to the wall were obtained by interpolating the point clouds into raster datasets (their values being the distance perpendicular to the wall plane) and subtracting their pixel values, on a pixel-by-pixel basis. Figure 4 shows a 3D mesh plot of the displacements perpendicular to the wall plane corresponding to scenarios J and L. The left panel in both cases remained stationary, and this is shown by the near zero displacement (note the zero displacement along the vertical axis). The right panel shows tilt displacements of up to 0.12 m or 12 cm, in the case of scenario J experiencing deep-seated failure, and −0.06 m or −6 cm, in the case of scenario L under flexural bending (scale legend indicating deformation change along the surface).
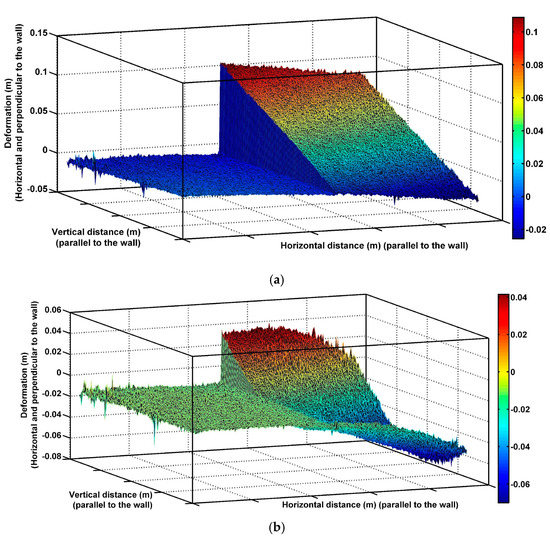
Figure 4.
3D Illustration of retaining wall displacement contours (with color scale) in m for (a) Scenario J and (b) Scenario L.
4. Discussion
Generally, errors were within 1.5 cm for the majority of testing scenarios. Scenarios I, K, and L present the smallest average or mean error producing more accurate 3D model reconstructions. Scenario J experienced the greatest error, with a mean value of 21 mm. The variability of the errors between different scenarios presents striking results. Individual error sources are difficult to pinpoint, but can be separated into several categories. These errors are small enough for the technique to be useful in monitoring retaining walls, as wall movements of less than 1 or 2 cm in most cases will not be critical, but movements of more than a few centimeters would be problematic.
The algorithm used in digital photography software can introduce errors and noise (such as acquisition or image grain compatibility). For the initial solution of the bundle adjustment, the algorithm has to match features between different images, and the quality of the matching will impact the final quality of the point cloud. Further point densification will increase the number of points, but not the overall accuracy of the point cloud positions. Therefore, the quality and density of the initial bundle adjustment solution is critical for the overall point cloud accuracy. Reconstruction errors or modeling noise could have been influenced by the quality of surface features (or, rather, detection of features) as the model walls may not have contained sufficient texture for the matching process.
The large number of points obtained from the digital photogrammetry method allows for a very detailed representation of the three-dimensional geometry of the surface. This certainly presents an advantage over the sparse point representation obtained from other surveying methods, e.g., total station or GPS surveying of only a few points. Small details, especially local deformations certain sections or features (within the full scale or global movements) of the retaining walls, could easily be identified and measured with the high density point clouds, but could easily be missed when only a few points were measured with a total station or GPS. Figure 4 illustrates this, as the full reconstruction of the retaining wall flexural bending deformation would not be possible from a sparse set of points.
Finally, the number and precision of control points can also have an impact on the overall quality of the output dataset. It should be acknowledged that the digital photogrammetry requires a minimum set of control points to correctly scale the three dimensional point cloud models, setting up such control points will usually require using high-precision measurement techniques (e.g., total station surveying, as in our case). Alternatively, the dimensions of known objects could be used to scale the three dimensional point clouds, if such dimensions are known with enough precision, and are well-defined in the point cloud.
Point clouds generated from digital photogrammetry are very similar to LiDAR generated point clouds, although they may be less precise. The average errors in this study were relatively close to the errors and even near accuracies found in other studies in which LiDAR laser scanning was used for geotechnical applications [26,55]. Su et al. [55] mentioned root mean square errors within the range of 4–19 mm, whereas this study presented a mean error range of 3.3–20.9 mm for the tested scenarios. Gong et al. [26] noted accuracies below 10 mm, as this study had an average range minimum value near 10 mm, but also acknowledges the different setups and displacement scales that were used. Similar results were noted in comparing Oskouie et al.’s [56] results of maximum displacement errors near 2.4 mm, but encompassed different collection distance and a single panel subjected to simulated movement.
The relatively simple operation and portability of photographic cameras also make this technique attractive. Since the photogrammetry-based monitoring requires little or no calibration, other than acquiring control points, it is easy to apply the technique to retaining walls and similar structures. Depending on the testing setup, additional calibration modeling procedures can be deployed for the camera system [35,36,52]. Ultimately, these advantages translate as cost reductions in the geotechnical asset management process. Furthermore, the quality of point cloud measurements can be improved with higher-grade DSLR cameras and even change in camera collection distance for more comparability with other sensing tools.
In this study, the images were collected along a distance parallel to the wall with from a camera pointed perpendicular to the wall surface. In general, the results of close range photogrammetry can be improved by using a variety of viewing angles, i.e., a larger number of converging camera poses [48,57]. Having converging camera poses could particularly increase the accuracy in the depth direction (perpendicular distance to retaining wall). Acquiring photographs from other viewing angles would also increase the computational load and the imagery storage needs. For instance, acquiring three images (one oblique forward-looking, one perpendicular, and one oblique backward-looking) at each position along the retaining wall would increase by a factor of three the processing and file storage needs. The additional costs of such an extended image acquisition plan would have to be weighed against the benefits of a higher accuracy. Such alternative viewing geometries are not further explored in this work, but should be addressed by future work in this field.
For this investigation, image collection was limited to one line of sight distance of 7.62 m. With the near 1 m baseline and the minimal image position of 10, the images were able to obtain an average of 80% base overlap. Some of the overlap may have been lower around 66% and obtaining more would produce more information for image matching. Understanding the influence of increasing baseline image position, altering the camera to object distance, as well as the camera specifications, could provide improvements for increasing accuracy. It was noted that potential improvement in model accuracy by increasing the focal length or by decreasing the distance between the object and the camera still needs investigation. Generally, Pix4D software and the known image setup accuracies were in the range of several millimeters [58]. A comparison of the software used in this study with an alternative software was also conducted, the overlap in result accuracies are reported elsewhere to further illustrate the reliability of photogrammetry processing (Oats et al., manuscript in preparation, 2017).
The results of this study illustrates that digital photogrammetry can be a suitable method to monitor displacements of retaining walls. This study also presents the ability of photogrammetry to capture these crucial displacements and changes of the wall, but does not limit the measurement to allowable displacement before failure, as that would vary for each retaining wall structure, depending on its design. Moreover, the results presented here are preliminary and more extensive testing, including an actual field test on real retaining walls, is necessary. These tests should include high-precision control methods (e.g., total station surveying of control points), varied camera collection distances, and should cover more extensive time periods, to assess how well the technique can track multiple changes through time.
5. Conclusions
Effective assessment methods are critical for the analysis of failure modes of retaining walls. Photogrammetric principles were employed to create 3D models of the retaining wall model under different failure conditions. This study investigates photogrammetry’s ability to provide retaining wall displacement measurements. Comparison of the digital photogrammetry results with total station measurements show a correspondence of both methods to within 2–3 cm and, in some cases, as low as a few millimeters. The results were obtained from an experimental setup that simulates two adjacent retaining wall sections that experience differential movement and wall element deformation. These results suggest that the method would be adequate to measure spatial changes and retaining wall displacements over time, but more extensive testing, including experiments on real retaining walls is necessary to confirm the results. A better characterization of the error sources and the influence of control point density, distribution, and precision would also clarify the capabilities of the method.
Photogrammetry would provide output products similar to the point clouds generated from LiDAR scanners, but the equipment and operation of digital, consumer grade, photographic cameras is much less expensive compared with LiDAR equipment and operation. The need for precise ground control points, or some other method of precisely scaling the digital photogrammetric point clouds, imposes some additional restrictions on the method, but future technological developments, including real-time kinematic (RTK) GPS integration with the camera [52], may reduce the demands on such external control points. Our results show the feasibility of digital photogrammetry for monitoring retaining walls, potentially as part of a wider geotechnical asset system.
Acknowledgments
This project was partially funded by the U.S. Department of Transportation (USDOT) through the Office of the Assistant Secretary for Research and Technology (Cooperative Agreement No. RITARS-14-H-MTU).
Author Contributions
Renee C. Oats, Rudiger Escobar-Wolf, and Thomas Oommen conceived and designed the experiments; Renee C. Oats, Rudiger Escobar-Wolf and Thomas Oommen performed the experiments; Renee C. Oats and Rudiger Escobar-Wolf analyzed the data; and Renee C. Oats, Rudiger Escobar-Wolf, and Thomas Oommen wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clayton, C.R.; Woods, R.I.; Bond, A.J.; Milititsky, J. Earth Pressure and Earth-Retaining Structures; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Wendland, S. When Retaining Walls Fail. Civil Engineering News, 2011. Available online: http://www.cenews.com (accessed on 5 October 2015).
- DeMarco, M.J.; Anderson, S.A.; Armstrong, A. Retaining Walls Are Assets Too! Publ. Roads 2009, 73, 30–37. [Google Scholar]
- Goh, A.T.C.; Kulhawy, F.H. Reliability assessment of serviceability performance of braced retaining walls using a neural network approach. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 627–642. [Google Scholar] [CrossRef]
- Duncan, C. Soils and Foundations for Architects and Engineers; Springer Science and Business Media: Norwell, MA, USA, 1992. [Google Scholar]
- Budhu, M. Soil Mechanics & Foundations; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Anderson, S.A.; Rivers, B.S. Capturing the Impacts of Geotechnical Features on Transportation System Performance. In Proceedings of the Geo-Congress, San Diego, CA, USA, 28 March 2013; pp. 1633–1642. [Google Scholar]
- Mohammad, T. Failure of a Ten-Storey Reinforced Concrete Building Tied To Retaining Wall: Evaluation, Causes, and Lessons Learned. Struct. Congr. 2005. [Google Scholar] [CrossRef]
- Bernhardt, K.L.S.; Loehr, J.E.; Huaco, D. Asset Management Framework for Geotechnical Infrastructure. J. Infrastruct. Syst. 2003, 9. [Google Scholar] [CrossRef]
- Anderson, S.A.; Alzamora, D.; DeMarco, M.J. Asset Management Systems for Retaining Walls. In Proceedings of the Biennial Geotechnical Seminar Conference, ASCE, Denver, CO, USA, 7 November 2008; pp. 162–177. [Google Scholar]
- Butler, C.J.; Gabr, M.A.; Rasdorf, W.; Findley, D.J.; Chang, J.C.; Hammit, B.E. Retaining Wall Field Condition Inspection, Rating Analysis, and Condition Assessment. J. Perform. Constr. Facil. 2015, 30, 04015039. [Google Scholar] [CrossRef]
- Chouinard, L.; Andersen, G.; Torrey, V., III. Ranking Models Used for Condition Assessment of Civil Infrastructure Systems. J. Infrastruct. Syst. 1996. [Google Scholar] [CrossRef]
- AASHTO Transportation Asset Management Guide: A Focus on Implementation; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2013.
- Kimmerling, R.E.; Thompson, P.D. Assessment of Retaining Wall Inventories for Geotechnical Asset Management. Transp. Res. Rec. 2015, 2510, 1–6. [Google Scholar] [CrossRef]
- Brutus, O.; Tauber, G. Guide to Asset Management of Earth Retaining STRUCTURES; US Department of Transportation, Federal Highway Administration, Office of Asset Management: Washington, DC, USA, 2009.
- Han, J.; Hong, K.; Kim, S. Application of a Photogrammetric System for Monitoring Civil Engineering Structures; InTech.: Rijeka, Croatia, 2012. [Google Scholar]
- Wyllie, D.; Mah, C. Rock Slope Engineering Civil and Mining, 4th ed.; Spon Press: New York, NY, USA, 2004. [Google Scholar]
- Scaioni, M.; Alba, M.; Roncoroni, F.; Giussani, A. Monitoring of a SFRC retaining structure during placement. Eur. J. Environ. Civ. Eng. 2010, 14, 467–493. [Google Scholar] [CrossRef]
- Wang, G.; Philips, D.; Joyce, J.; Rivera, F. The integration of TLS and continuous GPS to study landslide deformation: A case study in Puerto Rico. J. Geod. Sci. 2011, 1, 25–34. [Google Scholar] [CrossRef]
- Vaghefi, K.; Oats, R.; Harris, D.; Ahlborn, T.; Brooks, C.; Endsley, K.; Roussi, C.; Shuchman, R.; Burns, J.; Dobson, R. Evaluation of Commercially Available Remote Sensors for Highway Bridge Condition Assessment. J. Bridge Eng. 2012, 17. [Google Scholar] [CrossRef]
- Escobar-Wolf, R.; Oommen, T.; Brooks, C.; Dobson, R.; Ahlborn, T. Unmanned Aerial Vehicle (UAV)-based Assessment of Concrete Bridge Deck Delamination Using Thermal and Visible Camera Sensors: A Preliminary Analysis. Res. Nondestr. Eval. 2017. [Google Scholar] [CrossRef]
- Jauregui, D.V.; White, K.R.; Woodward, C.B.; Leitch, K.R. Noncontact Photogrammetric Measurements of Vertical Bridge Deflection. J. Bridge Eng. 2003, 212. [Google Scholar] [CrossRef]
- Jiang, R.; Jauregui, D.V.; White, K.R. Close-Range Photogrammetry Applications in Bridge Measurement: Literature Review. Measurement 2008, 41, 823–834. [Google Scholar] [CrossRef]
- Bouali, E.; Oommen, T.; Escobar-Wolf, R. Interferometric Stacking toward Geohazard Identification and Geotechnical Asset Monitoring. J. Infrastruct. Syst. 2016, 22. [Google Scholar] [CrossRef]
- Oskouie, P.; Becerik-Gerber, B.; Soibelman, L. Automated Cleaning of Point Clouds for Highway Retaining Wall Condition Assessment. In Proceedings of the 2014 International Conference on Computing in Civil and Building Engineering, Orlando, FL, USA, 23–25 June 2014. [Google Scholar]
- Gong, J.; Zhou, H.; Gordon, C.; Jalayer, M. Mobile Terrestrial Laser Scanning for Highway Inventory Data Collection. Comp. Civ. Eng. 2012. [Google Scholar] [CrossRef]
- Laefer, D.; Lennon, D. Viability Assessment of Terrestrial LiDAR for Retaining Wall Monitoring. GeoCongress 2008, 310. [Google Scholar] [CrossRef]
- Olsen, M.J.; Butcher, S.; Silvia, E.P. Real-Time Change and Damage Detection of Landslides and Other Earth Movements Threatening Public Infrastructure; Transportation Research and Education Center (TREC): Portland, OR, USA, 2012; OTREC-RR-11-23. [Google Scholar]
- Xiao, R.; He, X. GPS and InSAR Time Series Analysis: Deformation Monitoring Application in a Hydraulic Engineering Resettlement Zone, Southwest China. Math. Prob. Eng. 2013, 2013, 601209. [Google Scholar] [CrossRef]
- Vosselman, G.; Maas, H.G. (Eds.) Airborne and Terrestrial Laser Scanning; Whittles Publishing: Dunbeath, Scotland, 2010. [Google Scholar]
- Casagli, N.; Cigna, F.; Bianchini, S.; Hölbling, D.; Füreder, P.; Righini, G.; Vlcko, J. Landslide mapping and monitoring by using radar and optical remote sensing: Examples from the EC-FP7 project SAFER. Remote Sens. Appl. Soc. Environ. 2016, 4, 92–108. [Google Scholar] [CrossRef]
- Golparvar-Fard, M.; Balali, V.; de la Garza, J.M. Segmentation and recognition of highway assets using image-based 3D point clouds and semantic Texton forests. J. Comp. Civ. Eng. 2012, 29. [Google Scholar] [CrossRef]
- Cleveland, L.; Wartman, J. Principles and Applications of Digital Photogrammetry for Geotechnical Engineering. Proc. Site Geomat. Charact. 2006, 16, 128–135. [Google Scholar]
- Remondino, F.; El-Hakim, S. Image-based 3D modelling: A review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. Structure-for-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Ellenberg, A.; Branco, L.; Krick, A.; Bartoli, I.; Kontsos, A. Use of Unmanned Aerial Vehicle for Quantitative Infrastructure Evaluation. J. Infrastruct. Syst. 2014, 21. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A. Elements of Photogrammetry: With Applications in GIS, 3rd ed.; McGraw-Hill Co. Inc.: New York, NY, USA, 2000. [Google Scholar]
- Scaioni, M.; Barazzetti, L.; Giussani, A.; Previtali, M.; Roncoroni, F.; Alba, I.M. Photogrammetric techniques for monitoring tunnel deformation. Earth Sci. Inf. 2014, 7, 83–95. [Google Scholar] [CrossRef]
- Lindenbergh, R.; Pietrzyk, P. Change detection and deformation analysis using static and mobile laser scanning. Appl. Geomat. 2015, 7, 65–74. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, L.; Yang, B.; Wu, L. Applications of Structure from Motion: A Survey. J. Zhejiang Univ.-Sci. C 2013, 14, 486–494. [Google Scholar] [CrossRef]
- Khaloo, A.; Lattanzi, D. Hierarchical Dense Structure-from-Motion Reconstructions for Infrastructure Condition Assessment. J. Comput. Civ. Eng. 2016, 31. [Google Scholar] [CrossRef]
- Dai, F.; Rashidi, A.; Brilakis, I.; Vela, P. Comparison of image-based and time-of-flight-based technologies for three-dimensional reconstruction of infrastructure. J. Constr. Eng. Manag. 2012, 139. [Google Scholar] [CrossRef]
- Golparvar-Fard, M.; Bohn, J.; Teizer, J.; Savarese, S.; Peña-Mora, F. Evaluation of image-based modeling and laser scanning accuracy for emerging automated performance monitoring techniques. Autom. Constr. 2011, 20, 1143–1155. [Google Scholar] [CrossRef]
- Zhu, Z.; Brilakis, I. Comparison of optical sensor-based spatial data collection techniques for civil infrastructure modeling. J. Comput. Civ. Eng. 2009, 23. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wöhler, C. 3D Computer Vision: Efficient Methods and Applications; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Faugeras, O.; Luong, Q.T.; Papadopoulo, T. The Geometry of Multiple images: The Laws that Govern the Formation of Multiple Images of a Scene and Some of Their Applications; MIT Press: Cambridge, MI, USA, 2004. [Google Scholar]
- Scaioni, M.; Feng, T.; Barazzetti, L.; Previtali, M.; Roncella, R. Image-Based Deformation Measurement. Appl. Geomat. 2015, 7, 75–90. [Google Scholar] [CrossRef]
- Federal Highway Administration (FHWA). Seismic Retrofitting Manual for Highway Structures: Part 2—Retaining Structure, Slopes, Tunnels, Culverts, and Roadways; U.S. Department of Transportation: Washington, DC, USA, 2004.
- Federal Highway Administration (FHWA). Mechanically Stabilized Earth Walls and Reinforced Soil Slopes Design & Construction Guidelines; Publication No. FHWA-NHI-00-043; U.S. Department of Transportation National Highway Institute (NHI) Office of Bridge Technology: Arlington, VA, USA, 2001.
- Nikon D510 Digital Camera Reference Manual. 2011. Available online: http://cdn-10.nikon-cdn.com/pdf/manuals/noprint/D5100_ENnoprint.pdf (accessed on 25 June 2017).
- Forlani, G.; Pinto, L.; Roncella, R.; Pagliari, D. Terrestrial photogrammetry without ground control points. Earth Sci. Inform. 2014, 7, 71–81. [Google Scholar] [CrossRef]
- Pix4D Support. Offline Getting Started and Manual. 2016. Available online: https://support.pix4d.com/hc/en-us/articles/204272989-Offline-Getting-Started-and-Manual-pdf-#gsc.tab=0 (accessed on 25 June 2017).
- Freund, R.J.; Wilson, W.J. Statistical Methods, 2nd ed.; Elsevier: Burlington, MA, USA, 2003; p. 673. [Google Scholar]
- Su, Y.Y.; Hashash, Y.M.A.; Liu, L.Y. Integration of construction as-built data via laser scanning with geotechnical monitoring of urban excavation. J. Constr. Eng. Manag. 2006, 132. [Google Scholar] [CrossRef]
- Oskouie, P.; Becerik-Gerber, B.; Soibelman, L. Automated measurement of highway retaining wall displacements using terrestrial laser scanners. Autom. Constr. 2016, 65, 86–101. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; Walter de Gruyter: Berlin, Germany, 2014. [Google Scholar]
- Chen, L. What Is the Accuracy I Can Achieve with Pix4Dmapper Pro? Pix4D 2017. Available online: https://pix4d.com/getting-expected-accuracy-pix4dmapper-pro/ (accessed on 25 June 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).