Machine Learning and Optimality in Multi Storey Reinforced Concrete Frames

Abstract

The present study investigates the potential of the implementation of machine learning techniques in optimized multi storey reinforced concrete frames. The variables that are taken into account in the objective function of the optimization problem are the following: the frame type (frame bay length optimality) and dimensioning of the cross sections. The objective function has the goal of attaining a minimum cost design based on market data, after a structural analysis of the frames. A number of optimized examples with widely encountered cases of total lengths of frames and with various loadings are presented. Modeling is based on Eurocode 2. Optimization takes place with the use of evolutionary algorithms. The optimized results are subjected to predictive modeling based on neural networks. The objective of the study is to create predictive models with the aim of minimizing the usage of scarce resources.

1. Introduction

1.1. Initial Considerations

In the structural design of frames used in buildings, a structural analysis first takes place for the determination of the axial, shear forces, and moments of every member (beams and columns) [1]. Following this, the beams and columns are dimensioned to resist the axial, shear forces, and moments that arise. The total cost of a frame is therefore a sum that is dependent on its form and on the sizes of its beams and columns [2].

In reinforced concrete buildings, a very common formula used to evaluate the cost of each component is the following:

$$C_{member}=C_{concrete}+C_{steelreinforcement}+C_{formwork}$$

(1)

where: C_concrete, C_steel reinforcement, and C_formwork, respectively, are the costs of concrete, steel reinforcement, and formwork in RC elements [2].

From an overview of the relevant literature, the following conclusions can be drawn:

• A difference in the cost coefficients for concrete and steel reinforcement leads to different optimal results in RC prestressed beams and slabs [2,3].
• The stirrup costs are generally ignored as they do not have a significant impact on the optimized results [2,4].
• The compressive strength of reinforced concrete also has a negligible influence on the optimized results, as previous studies have shown [2,5].

Well-known examples regarding the optimization of RC structures include the works of: Krishnamurthy and Munro [6] (where linear programming was employed for the optimization of RC frames), Lee and Ahn [7] and Camp, Pezeshk & Hansson [8] (where genetic algorithms and discrete optimization were used for the optimization of RC frames), and Guerra and Kiousis [9] (where Sequential Quadratic Programming was implemented for the same purposes). As far as the implementation of Artificial Neural Networks is concerned, Yousif et al. [10] have proposed ANN-based techniques for the purpose of forecasting the resistance of a structure, by using critical structural variables such as the material strength and loading conditions as predictors.

One of the main concerns of structural designers when using frames with multiple bays is to opt for economic solutions. Since such designs depend on the number of bays of the frames, the length of the bays, and the sizes of the beam and column cross sections, optimization techniques can be implemented to effectively deal with the computational difficulties which arise when assessing the large number of potential design solutions.

In light of this, the objective of the present study is to demonstrate a method to construct a predictive model based on machine learning to predict optimality in reinforced concrete frames with multiple storeys. The potential benefits of constructing a machine learning model deal with the minimization of the time required to predict optimality. The study focuses on presenting a method for the attainment of optimality from a cost standpoint, emphasizing the structural capacity of RC frames. With respect to the optimization of the frame structural costs, the present study faces this issue as a discrete optimization problem [11].

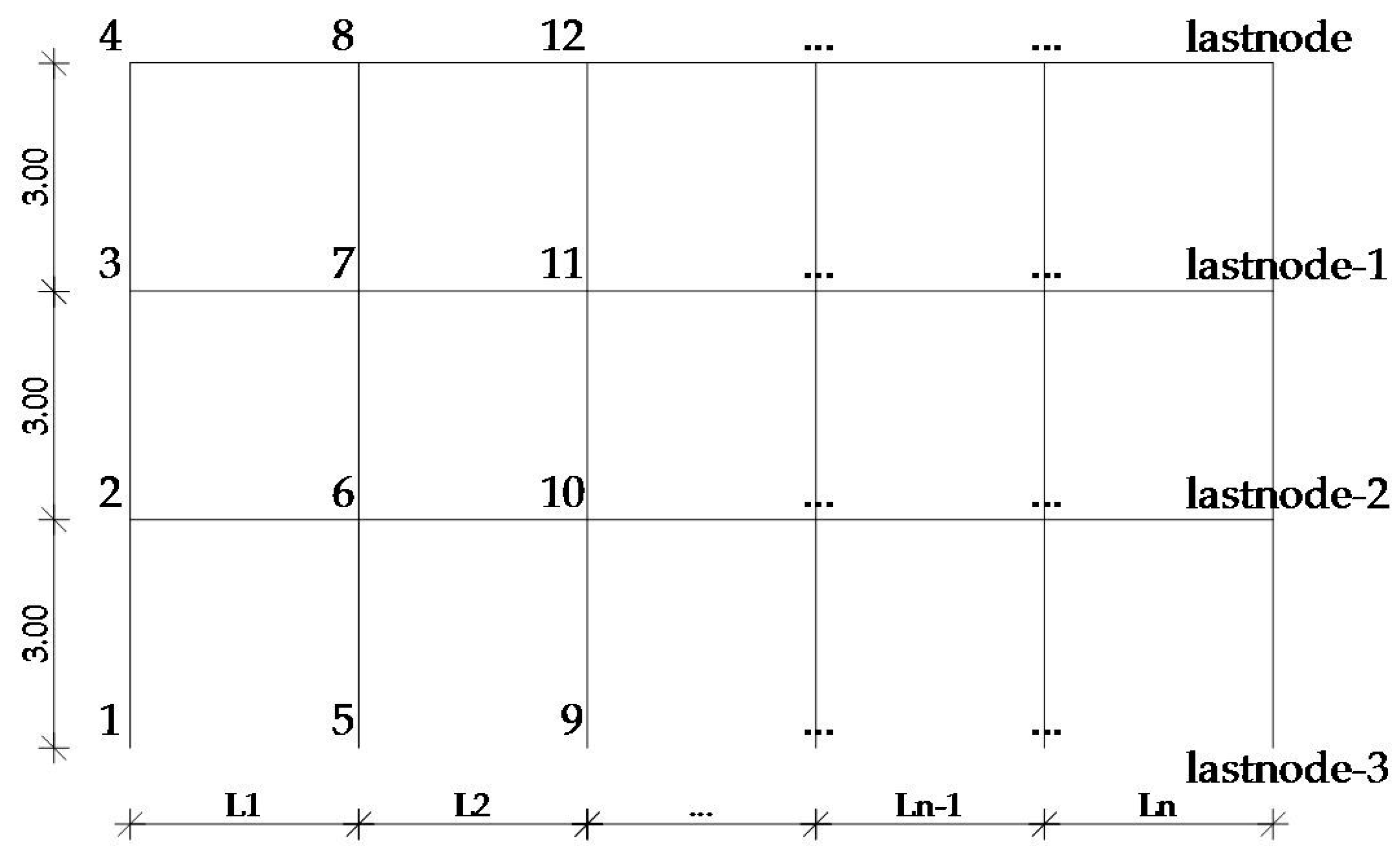
1.2. Programming Logic Followed for the Construction of the FEM Algorithm

A 2D finite element frame analysis framework has been followed for the construction of an algorithm in MATLAB [12,13]. A uniformly distributed load is assumed to be applied on the frame. This is a loading case that is commonly encountered in real life building structures. Initially, an estimation of the number of structural elements needed (beams and columns) was made according to empirical criteria (preliminary sizing) [14]. It was therefore considered that the number of elements would be five at a minimum and 19 at a maximum. As a result of this, eight different scenarios were included in the algorithm. Since the algorithm conducts the structural analysis through the finite element method, it is meaningful to mention several details about the procedure. The algorithm has been developed in MATLAB [12,13] in a way that makes it possible to solve a frame regardless of its total number of elements and by having observed the repeated patterns of the nodes -and accordingly the degrees of freedom- of every beam and column, the applied fixed end moments and shear forces to every start and end beam element node, the applied axial loads on the end or on the intermediate columns, and of the prescribed degrees of freedom. The reader should pay attention to the fact that the number of columns is always odd and the number of beams is always even, and the following relationship is always true [11]:

$$numberofcolumns=numberofbeams+1$$

(2)

This consideration has critically influenced the programming logic. Furthermore, the number of elements has a constant relationship with the number of nodes (number of nodes = number of elements + 1) and the number of degrees of freedom (number of degrees of freedom = 3 × number of nodes).

Even though there are also other possible programming approaches, for reasons of predictability, the numbering logic of the degrees of freedom in the finite element algorithm that was constructed in MATLAB and the programming logic is as follows [12]:

elementDof = [indice indice + numberNodes indice + 2*numberNodes]

(3)

where: the term elementDof stands for the degrees of freedom of each element; indice is the start or end index of a node; and numberNodes is a parameter equal to the total number of nodes of a frame, assisting in the arrangement of the global stiffness matrix and the identification of each degree of freedom.

The first term of the above matrix stands for the axial displacements’ degrees of freedom, the second for the shear displacements’ degrees of freedom, and the last for the degrees of freedom that concern the elements’ moments [12,13].

The degrees of freedom are used in the construction of the global stiffness matrix, as well as in the start and end nodes of every frame element, regardless of the number of bays, following the node numbering logic shown in the figure below. This consideration has critically influenced the programming logic. The effect that this relationship has on the node numbering logic is demonstrated below (Figure 1).

It is evident that the repeated pattern of the numbering logic renders the nodes -and accordingly the degrees of freedom- of every beam and column quite easy to predict. Therefore, for a frame with three storeys, the beams have the indices that are displayed below:

Beam nodes first floor: [2:numberofstoreys + 1):(lastnode − (numberofstoreys − 1))]
Beam nodes second floor: [3:(numberofstoreys + 1):(lastnode − (numberofstoreys − 2))]
Beam nodes third floor: [4:(numberofstoreys + 1):(lastnode)]

(4)

where: the colon punctuation (:) represents the increment measured in an integer number of nodes, with a start point at the bottom left column node. The logic shown above is similar to the one used in the MATLAB algorithm that was constructed. The term numberofstoreys represents the number of storeys of the examined frame and the term lastnode represents the node that concerns the last node according to the numbering logic displayed in Figure 1.

Apart from this, since the lower end of all columns at the lowest storey is considered to be fixed, the repeatability of the prescribed degrees of freedom is shown in the following pseudocode [12], demonstrating the programming logic that has been followed:

prescribedDof1 = [1:(numberofstoreys + 1):(lastnode − (numberofstoreys))]

(5)

prescribedDof2 = [1:(numberofstoreys + 1):(lastnode − (numberofstoreys))] + numberofelements

(6)

prescribedDof3 = [1:(numberofstoreys + 1):(lastnode − (numberofstoreys))] + 2*numberofelements

(7)

prescribedDof = [prescribedDof1,prescribedDof2,prescribedDof3]

(8)

where: the term prescribedDof represents the prescribed degrees of freedom that are the bottom end nodes of each column element at the lowest storey and the term numberofelements represents the number of elements that are dependent on the form of the frames.

It is also meaningful to note that the connectivities among the elements were expressed in the algorithm as preset options, following the aforementioned numbering logic and corresponding to the number of bays of each frame type. After the solution of a frame, it becomes possible for the design moments, axial forces, and shear forces to be calculated and used for the dimensioning of the cross sections.

2. Optimization Procedure and Variables

The optimization procedure aimed to simulate as variables all of the parameters that a structural designer takes into consideration when opting for a frame. Specifically, these are: the number of bays of a frame, the cross sections of all the columns that constitute the frame, the cross sections of all the beams that constitute the frame, and the length of each separate beam. As is mentioned above, the selection of the range of the potential options for each variable is also based on empirical criteria [14]. After the completion of the finite element analysis that is conducted in MATLAB [12], the frame components are optimized by taking into account the following variables:

• Variable related to the form of the frames whose change influences the number of bays (eight possible choices leading to a total number of beam-column elements between five and 19).
• Variables related to the lengths of the beams. Each front beam length is considered to have a value between 3 and 7.5 m, with a step size of 0.5 m.
• Variables related to the cross sections of the beams of each storey that compose the structural frames. For all the frame scenarios, the following beam cross sections were considered: b = 350 mm h = 550 mm ρ = 1%, b = 350 mm h = 550 mm ρ = 2%, b = 350 mm h = 550 mm ρ = 3%, b = 350 mm h = 550 mm ρ = 4%, b = 350 mm h = 550 mm ρ = 5%, b = 350 mm h = 550 mm ρ = 6%, b = 350 mm h = 600 mm ρ = 1%, b = 350 mm h = 600 mm ρ = 2%, b = 350 mm h = 600 mm ρ = 3%, b = 350 mm h = 600 mm ρ = 4%, b = 350 mm h = 600 mm ρ = 5%, and b = 350 mm h = 600 mm ρ = 6% (where: b is the smaller dimension of the cross section, h is the larger dimension of the cross section, and ρ is the steel reinforcement ratio of the cross section).
• Variables related to the cross sections of the columns (each storey is examined separately) that compose the structural frames. For all the frame scenarios, the following column cross sections were considered: b = 350 mm h = 350 mm ρ = 1%, b = 350 mm h = 350 mm ρ = 2%, b = 350 mm h = 350 mm ρ = 3%, b = 350 mm h = 400 mm ρ = 1%, b = 350 mm h = 400 mm ρ = 2%, b = 350 mm h = 400 mm ρ = 3%, b = 400 mm h = 400 mm ρ = 1%, b = 400 mm h = 400 mm ρ = 2%, b = 400 mm h = 400 mm ρ = 3%, b = 400 mm h = 450 mm ρ = 1%, b = 400 mm h = 450 mm ρ = 2%, b = 400 mm h = 450 mm ρ = 3%, b = 450 mm h = 450 mm ρ = 1%, b = 450 mm h = 450 mm ρ = 2%, b = 450 mm h = 450 mm ρ = 3%, b = 450 mm h = 500 mm ρ = 1%, b = 500 mm h = 500 mm ρ = 1%, and b = 500 mm h = 550 mm ρ = 1%.

3. Reinforced Concrete Design Constraints

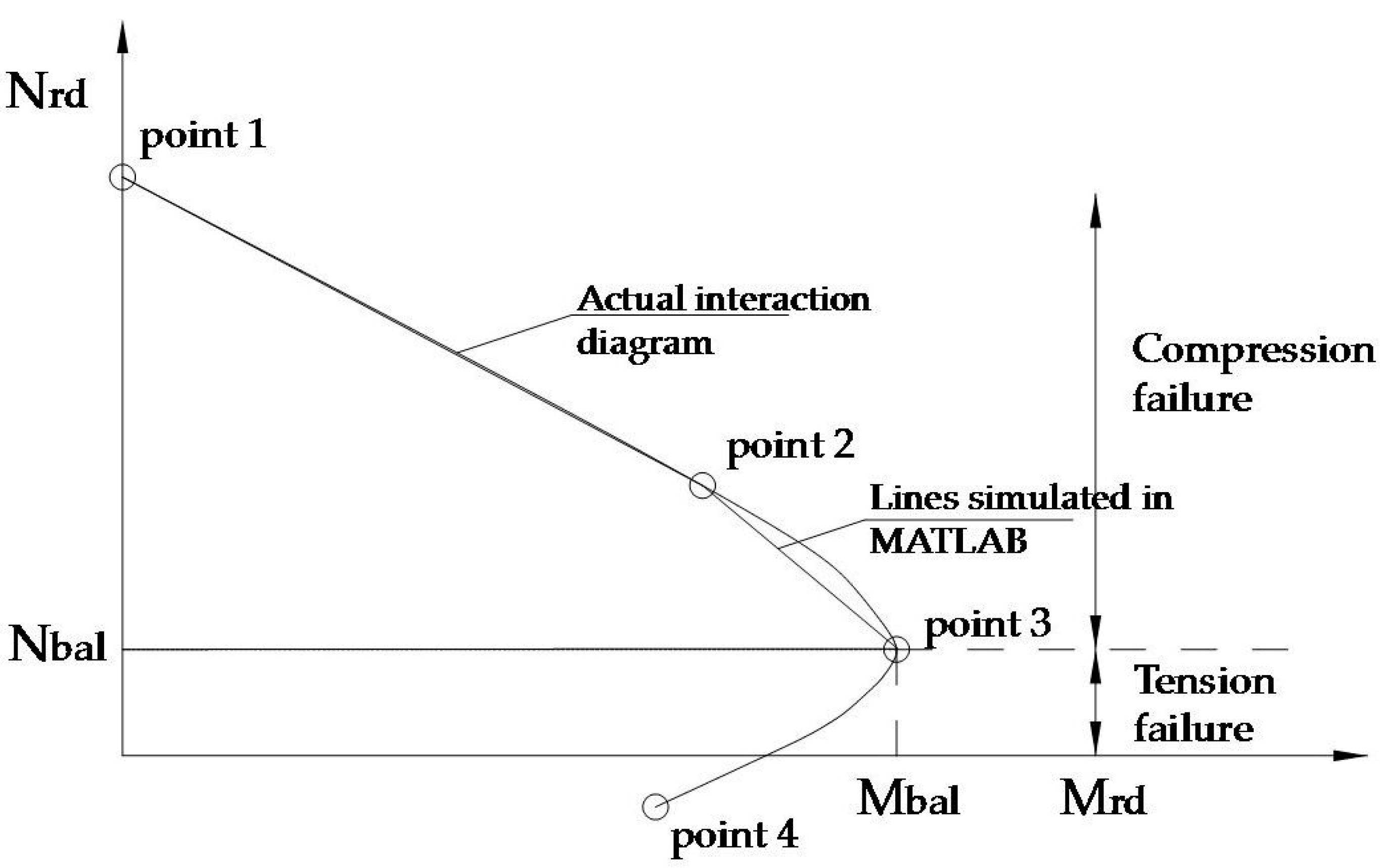
3.1. Modeling the RC Interaction Diagrams as a Separate Constraint

An interaction diagram of an RC element is used to assess its capacity in an axial load and bending moment. The simulation approach that has been followed in the study generates the advantage of points with constant values, to allow for a quick estimation of the interaction diagram. The coordinates of the points are as follows: (x,y) = point 1: (0, N_rd,max), point 2: (N₂, M₂), and point 3: (M_bal, N_bal) (Where: N_rd is the ultimate axial resistance of the RC cross section, N_bal is the axial resistance value at the point of balanced failure, M_bal is the moment resistance value at the point of balanced failure, and M_rd is the moment of resistance of the RC cross section) [15,16,17,18,19]. The points are connected to each other in a consecutive order and this results in the creation of three lines (Figure 2), which are modelled as constraints representing bounds that must not be exceeded by any combination of N_sd and M_sd (Where: M_sd is the design moment of the cross section and N_sd is the design axial load of the cross section).

The first line derives from the points 1 & 2, the second from the points 2 & 3, and the third from point 3. If d is the cover of the cross section, point 2 represents a predictable condition, where the following relationship is true for the neutral axis x [16,17,18,19]:

$$x=h-d\Rightarrow f_s=0$$

(9)

$$\mathrm{And}: f_{sc}=f_{yd}$$

(10)

where: x is the neutral axis depth of the cross section, d is the cover of the cross section, f_sc is the inner force generated by the reinforcement at the compression zone, f_s is the steel reinforcement stress, f_y is the characteristic yield strength of the reinforcement, and f_yd is the design yield strength of the reinforcement (f_yd = f_y/1.15).

Since the values of x, f_s, and f_sc are known, the axial and moment resistance of the cross section can easily be computed by the following generalized formulae [9,11,16,17,18,19]:

$$N_{rd}=k_1{f}_{cu}bx+f_{sc}As{}_1+f_{st}As{}_2$$

(11)

$$M_{rd}=F_c\left(\frac{h}{2}-k_{2}x\right)+F_{sc}\left(\frac{h}{2}-d\right)+F_{st}\left(d-\frac{h}{2}\right)$$

(12)

where: k₁, k₂ are the characteristic ratios of the stress block, F_c is the inner force generated by the concrete section, F_sc is the inner force generated by the reinforcement at the compression zone, F_st is the inner force generated by the reinforcement at the tension zone, A_s1 is the cross sectional area of the steel reinforcement at the compression zone, and A_s2 is the cross sectional area of the steel reinforcement at the tension zone [16,17,18,19]: Moreover:

$$\mathrm{Moreover}:N_{rd}=F_c+F_{sc}+F_{st}\Rightarrow N_{rd}=k_1{f}_{cu}bh+f_{yd}As{}_1-f_{yd}As{}_2$$

(13)

As regards the values of N_bal and M_bal [11,16,17,18,19]:

$$\begin{array}{l}{N}_{bal}=k_1{f}_{cu}b{x}_{bal}+f_{sc}As{}_1+f_{st}As{}_2\\ \Rightarrow N_{bal}=k_1{f}_{cu}b{x}_{bal}+f_{sc}As{}_1-f_{yd}As{}_2\end{array}$$

(14)

Moreover [9,15,16,17,18,19]:

$$M_{bal}=F_c\left(\frac{h}{2}-k_2{x}_{bal}\right)+F_{sc}\left(\frac{h}{2}-d\right)+F_{st}\left(d-\frac{h}{2}\right)$$

(15)

If f(x) is the function describing the first line, g(x) is the function describing the second line, and h(x) is that describing the third line, the following constraints must be satisfied in order for an RC cross section to resist a particular combination of N_sd and M_sd:

$$N_{sd}-f(M_{sd})\le 0$$

(16)

$$N_{sd}-g(M_{sd})\le 0$$

(17)

$$N_{sd}-h(M_{sd})\ge 0$$

(18)

3.2. Other Constraints Considered for the Reinforced Concrete Elements

The other constraints on which the design of RC elements are subjected to, reflect the requirements of Eurocode 2 and the necessary provisions taken to avoid geometrically or functionally unacceptable conditions. The constraints that were included in the algorithms are mentioned below:

The amount of reinforcement must not exceed the permissible limits. Therefore, the minimum permissible amount of reinforcement has been modeled as follows [16]:

$$As{}_1+As{}_2\ge 0.10N_{sd}/f_{yd}$$

(19)

$$\mathrm{And}:As{}_1+As{}_2\ge 0.002*\left(b*h-As{}_1-As{}_2\right)$$

(20)

Moreover, as regards the maximum permissible amount of reinforcement [16]:

$$\frac{As{}_1}{b*h}+\frac{A{s}_2}{b*h}\le {\rho }_{\max }(\%)$$

(21)

where: ρ_max = 8%.

For the RC columns, the algorithm considers that:

$${As}_1={As}_2$$

(22)

It is important to note that the design moment derives from the combination of moments that are applied on each column from their adjacent beam’s moment, also taking into account a nominal eccentricity which is multiplied by the axial load and generates an extra moment [16].

Moreover, another check applies for the reinforced concrete beams: after the evaluation of the upper and lower reinforcement areas, the total required amount of reinforcement is compared with the acceptable reinforcement limits of the beam [16]. In all cases, if a specific cross section fails a check, a conditional penalty function generates very high cost values, resulting in undesirable total costs. It must be clarified that the design optimization procedure displayed in the present study is merely based on the structural capacity of RC frames, without considering other factors (especially those related to the serviceability limit state, such as cracking, creep, etc.).

4. Objective Function

The study assumes that the main concern of the structural designer is to opt for the most economic, albeit structurally feasible, design. Each element’s cost is computed taking into account the volume of its concrete area, the volume of its rebar reinforcement, and the total area of the formwork perimeter required for its construction. It is evident that this perimeter is equal to b + 2h for each beam element and equal to 2*(b + h) for each column element [2]. Since each frame consists of a number of beam and column elements, the objective function is therefore the sum of the cost of the elements that are its components:

$$\text{total RC frame cost}=\text{cost of all the constituting structural elements}+{\sum }_{i=1}^i{p}_i$$

(23)

For the computation of the cost of the constituting structural elements, two generic data structures based on functional programming that correspond to the cost of an RC beam or an RC column have been created. The cost is therefore expressed as a function of the axial loads, shear forces, and bending moments applied to them. The term p_i represents all the constraints that concern the structural checks of the beam and column elements according to Eurocode 2 [16]. These checks are inside the two aforementioned generic data structures. The value of the factors p_i is conditional. Whenever a constraint is satisfied, the value of the factor p_i that relates to a particular constraint is equal to zero, whereas, whenever a constraint is violated, the factor p_i that relates to a particular constraint has a very high value, exceeding the highest possible cost of the frame. Through this methodology, they function as conditional penalties and this leads to the evolutionary exclusion of undesired solutions.

5. Discussion

5.1. Optimization Scenarios

The frames that were used in the simulation concern 24 scenarios with different loadings, storeys, and total lengths. The relevant cost data derive from the market of Athens, Greece. The models follow a discrete optimization philosophy, where an initial estimation [11] of the number of structural elements needed (beams and columns), and the types of cross sections for the beam and the column elements, was made according to empirical criteria [14]. In a similar manner (discrete optimization), 10 cases of variable-dependent beam lengths were introduced in the algorithm (all possible beam lengths from 3 to 7.5 m for every 0.5 m). Through the use of an adjustment/multiplication coefficient that enforces the total length of the frame at each iteration to be equal to a desired total length, all the lengths of the beam elements are recalculated, in order for the sum of their lengths to be equal to the desired length. Furthermore, different cases of variable-dependent beam and column cross sections were also introduced in the algorithm [11].

Other assumptions that were made in the model frames are as follows:

• Clear column height: 3 m.
• RC forming cost: €75 per m².
• Concrete cost (concrete grade C 25/30): €60 per m³.
• RC reinforcement cost per kg (rebar steel grade S500): €4708.2.
• RC cover: 35 mm.

The following tables (

Table 1. Loading and number of storeys considered for the first frame with a length equal to 15 m.

Number of Storeys	Loading	Loading	Loading	Loading	Length of Frame
2	15 kN/m	35 kN/m	55 kN/m	75 kN/m	15 m
3	15 kN/m	35 kN/m	55 kN/m	75 kN/m

,

Table 2. Loading and number of storeys considered for the second frame with a length equal to 25 m.

Number of Storeys	Loading	Loading	Loading	Loading	Length of Frame
2	15 kN/m	35 kN/m	55 kN/m	75 kN/m	25 m
3	15 kN/m	35 kN/m	55 kN/m	75 kN/m

and

Table 3. Loading and number of storeys considered for the third frame with a length equal to 35 m.

Number of Storeys	Loading	Loading	Loading	Loading	Length of Frame
2	15 kN/m	35 kN/m	55 kN/m	75 kN/m	35 m
3	15 kN/m	35 kN/m	55 kN/m	75 kN/m

) synopsize the optimization scenarios that have been considered:

It is meaningful to note that so far in the relevant literature, there is lack of similar examples—taking into account the number of parameters that the present study takes- and in this sense, the study aims to make an addition to the field.

5.2. Optimization Results and Conclusions

The method of genetic algorithms has been used in the present study for the optimization calculations. The approach that has been followed made use of the optimization toolbox of MATLAB. The authors have generally preferred the preset options of the optimization toolbox and some critical details about the optimization procedure are as follows: Fitness scaling is based on rank, the initial population can iteratively have any size from 300 to 350, the function selection is stochastic and uniform, a scattered crossover function is used, and the mutation function is constraint-dependent. Each optimization scenario necessitates at least 10 trials to ensure that the optimum found at each trial constitutes a good global solution.

The results of the trials were compared and the best solution among the optima generated by each trial was selected. The optimization results (

Table A1. First set of optimized variables for the scenarios 1–24.

Scenario	Number of Storeys	Load (kN/m)	Frame Length	Column 1 1st Storey	Beam 1 1st Storey	Column 2 1st Storey	Beam 2 1st Storey	Column 3 1st Storey	Beam 3 1st Storey	Column 4 1st Storey	Beam 4 1st Storey	Column 5 1st Storey	Beam 5 1st Storey	Column 6 1st Storey	Beam 1 6st Storey	Column 7 1st Storey	Number of Bays	Beam Length 1	Beam Length 2	Beam Length 3	Beam Length 4	Beam Length 5	Beam Length 6
1	2	15	15	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	8.077	6.923	0.000	0.000	0.000	0.000
2	2	35	15	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	7.500	7.500	0.000	0.000	0.000	0.000
3	2	55	15	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	6.923	8.077	0.000	0.000	0.000	0.000
4	2	75	15	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	7.826	7.174	0.000	0.000	0.000	0.000
5	2	15	25	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	12.500	12.500	0.000	0.000	0.000	0.000
6	2	35	25	0.129	1.000	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	8.721	7.558	8.721	0.000	0.000	0.000
7	2	55	25	0.129	1.000	0.169	1.000	0.169	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	8.523	7.950	8.520	0.000	0.000	0.000
8	2	75	25	0.129	1.000	0.226	1.000	0.190	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	8.784	7.433	8.784	0.000	0.000	0.000
9	2	15	35	0.129	1.000	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	11.667	10.000	13.333	0.000	0.000	0.000
10	2	35	35	0.129	2.000	0.129	2.000	0.129	2.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	12.000	11.000	12.000	0.000	0.000	0.000
11	2	55	35	0.129	1.000	0.169	1.000	0.190	1.000	0.148	1.000	0.130	0.000	0.000	0.000	0.000	4	8.750	9.375	9.375	7.500	0.000	0.000
12	2	75	35	0.129	2.000	0.237	2.000	0.237	2.000	0.226	2.000	0.148	0.000	0.000	0.000	0.000	4	7.955	9.545	9.545	7.955	0.000	0.000
13	3	15	15	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	7.500	7.500	0.000	0.000	0.000	0.000
14	3	35	15	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	8.077	6.923	0.000	0.000	0.000	0.000
15	3	55	15	0.129	1.000	0.226	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	7.800	7.200	0.000	0.000	0.000	0.000
16	3	75	15	0.169	1.000	0.290	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	8.125	6.875	0.000	0.000	0.000	0.000
17	3	15	25	0.129	2.000	0.129	2.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	2	12.964	12.038	0.000	0.000	0.000	0.000
18	3	35	25	0.129	1.000	0.148	1.000	0.148	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	8.553	7.895	8.553	0.000	0.000	0.000
19	3	55	25	0.136	1.000	0.237	1.000	0.226	1.000	0.148	0.000	0.000	0.000	0.000	0.000	0.000	3	8.523	7.950	8.523	0.000	0.000	0.000
20	3	75	25	0.148	2.000	0.290	2.000	0.263	2.000	0.237	0.000	0.000	0.000	0.000	0.000	0.000	3	8.333	7.639	9.028	0.000	0.000	0.000
21	3	15	35	0.129	1.000	0.129	1.000	0.129	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	11.667	11.667	11.667	0.000	0.000	0.000
22	3	35	35	0.129	1.000	0.190	1.000	0.190	1.000	0.129	0.000	0.000	0.000	0.000	0.000	0.000	3	12.209	10.581	12.209	0.000	0.000	0.000
23	3	55	35	0.169	1.000	0.190	1.000	0.226	1.000	0.226	1.000	0.190	1.000	0.130	0.000	0.000	5	7.609	6.594	7.609	6.594	6.594	0.000
24	3	75	35	0.148	2.000	0.226	2.000	0.226	2.000	0.226	2.000	0.237	2.000	0.237	2.000	0.226	6	5.904	4.639	5.904	6.326	6.326	5.904

and

Table A2. Second set of optimized variables for the scenarios 1–24.

Scenario	Column 1 2nd Storey	Column 2 2nd Storey	Column 3 2nd Storey	Column 4 2nd Storey	Column 5 2nd Storey	Column 6 2nd Storey	Column 7 2nd Storey	Column 1 3rd Storey	Column 2 3rd Storey	Column 3 3rd Storey	Column 4 3rd Storey	Column 5 3rd Storey	Column 6 3rd Storey	Column 7 3rd Storey	Cost (€)
1	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	4564.126
2	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	4671.232
3	0.129	0.148	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	4797.345
4	0.129	0.190	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	5039.027
5	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	6665.498
6	0.129	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	7192.480
7	0.129	0.129	0.129	0.136	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	7435.705
8	0.129	0.148	0.129	0.169	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	7869.759
9	0.129	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	9021.519
10	0.129	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	9589.716
11	0.129	0.129	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	10,244.155
12	0.129	0.148	0.169	0.129	0.129	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	11,055.325
13	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.129	0.129	0.129	0.000	0.000	0.000	0.000	6847.017
14	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.129	0.129	0.129	0.000	0.000	0.000	0.000	7004.584
15	0.129	0.148	0.129	0.000	0.000	0.000	0.000	0.129	0.129	0.129	0.000	0.000	0.000	0.000	7284.292
16	0.129	0.190	0.129	0.000	0.000	0.000	0.000	0.129	0.129	0.129	0.000	0.000	0.000	0.000	7758.18
17	0.129	0.129	0.129	0.000	0.000	0.000	0.000	0.129	0.129	0.129	0.000	0.000	0.000	0.000	9993.10
18	0.129	0.129	0.129	0.129	0.000	0.000	0.000	0.129	0.129	0.129	0.129	0.000	0.000	0.000	10,806.77
19	0.129	0.190	0.148	0.129	0.000	0.000	0.000	0.129	0.129	0.129	0.129	0.000	0.000	0.000	11,389.19
20	0.148	0.237	0.226	0.169	0.000	0.000	0.000	0.129	0.148	0.148	0.129	0.000	0.000	0.000	12,307.80
21	0.129	0.129	0.129	0.129	0.000	0.000	0.000	0.129	0.129	0.129	0.129	0.000	0.000	0.000	13,544.88
22	0.148	0.169	0.129	0.148	0.000	0.000	0.000	0.148	0.129	0.129	0.148	0.000	0.000	0.000	14,623.87
23	0.129	0.129	0.190	0.129	0.129	0.148	0.000	0.129	0.148	0.130	0.130	0.129	0.148	0.000	16,036.79
24	0.129	0.129	0.136	0.169	0.187	0.187	0.148	0.129	0.129	0.136	0.129	0.148	0.129	0.129	17,457.05

) are shown in the appendix. When looking at the optimization results, the reader should consider that the uncracked equivalent concrete area of the optimized RC elements is displayed in the results, since it was used for the algorithm during the finite element analysis; that the RC elements are demonstrated following a left to right logic; and that, when considering the beam, the indicator 1 stands for a beam with b = 350 mm and h = 550 mm, whereas the indicator 2 for stands for a beam with b = 350 mm and h = 600 mm.

It is meaningful to note that the RC beam costs do not reflect the initial reinforcement area assumption made by the discrete optimization (e.g., a beam with b = 350 mm, h = 550 mm, has a reinforcement area equal to: 1%), because their reinforcement area is recalculated according to what is suggested by Eurocode 2. Nevertheless, the algorithm contains a constraint that requires that the initially assumed reinforcement area by the discrete modeling must not be exceeded.

5.3. Machine Learning Applied on the Optima

After the optimization calculations, the optimal number of bays, as well as the optimal uncracked area of the columns, are the considered independent variables that are subjected to predictive modelling with the use of artificial neural networks [20]. The following predictors are used: loading, total number of storeys, total length of the frame in order for the optimal number of bays to be predicted. Similarly, the following predictors are used: loading, total number of storeys, total length of frame, length of beam on the left side of the column and length of beam on the right side of the column, and total number of storeys above the column in order for the optimal uncracked area of column to be predicted. Even though it is not necessary, statistical significance tests were used to assess the predictors [21]. Specifically, the p values of the following predictors were found to be below 0.05: loading, total length of frame, length of beam on the left side of the column, length of beam on the right side of the column, and total number of storeys above the column. This indicates a low probability that the sampling process was inadequate [21]. A larger sample would also take into account the following predictors: cost of materials, minimum and maximum allowable cross sectional area of the beams and the columns, minimum and maximum allowable lengths of the beams, column lengths, and cross sectional area/moment of inertia of the adjacent elements (for the prediction of the optimal column cross sectional area).

The neural network toolbox of MATLAB is used and the data are automatically partitioned into a training set, a validation set, and a test set to attain statistical independence for the neural networks [20]. The overall performance graphs are used to evaluate the prediction results for all the data (a union of all the sets) attaining very high R values (above R = 0.90 in both cases). The neural networks have the following characteristics:

• Optimal column area prediction network: network train ratio = 50%, network validation ratio = 25%, network test ratio = 25%, number of neurons = 900, number of hidden layers = 2, and transfer function = tan-sigmoid.
• Optimal number of bays prediction network: network train ratio = 50%, network validation ratio = 25%, network test ratio = 25%, number of neurons = 600, number of hidden layers = 2, and transfer function = log-sigmoid.

6. Further Discussion on the Results

A robust framework for the cost optimization of RC frames has been developed, based on relevant data from the Greek market. The procedure that has been shown mainly focuses on their structural capacity. A series of optimized frames have been derived with the use of a discrete optimization modeling approach. The study aimed to simulate the logic followed by structural designers when opting for a frame, and to create an indicative database in order to check if it is possible that the optimality can be predicted with the aid of machine learning and neural networks. The very high R values of the final predictive model indicate that such a purpose is feasible and it ultimately allows for quicker decision-making in the optimal structural design of reinforced concrete frames. Using a bigger and richer database in the future will allow us to test the method for more realistic engineering projects.