Comment on: Toughness of Railroad Concrete Crossties with Holes and Web Openings. Infrastructures 2017, 2, 3
Conflicts of Interest
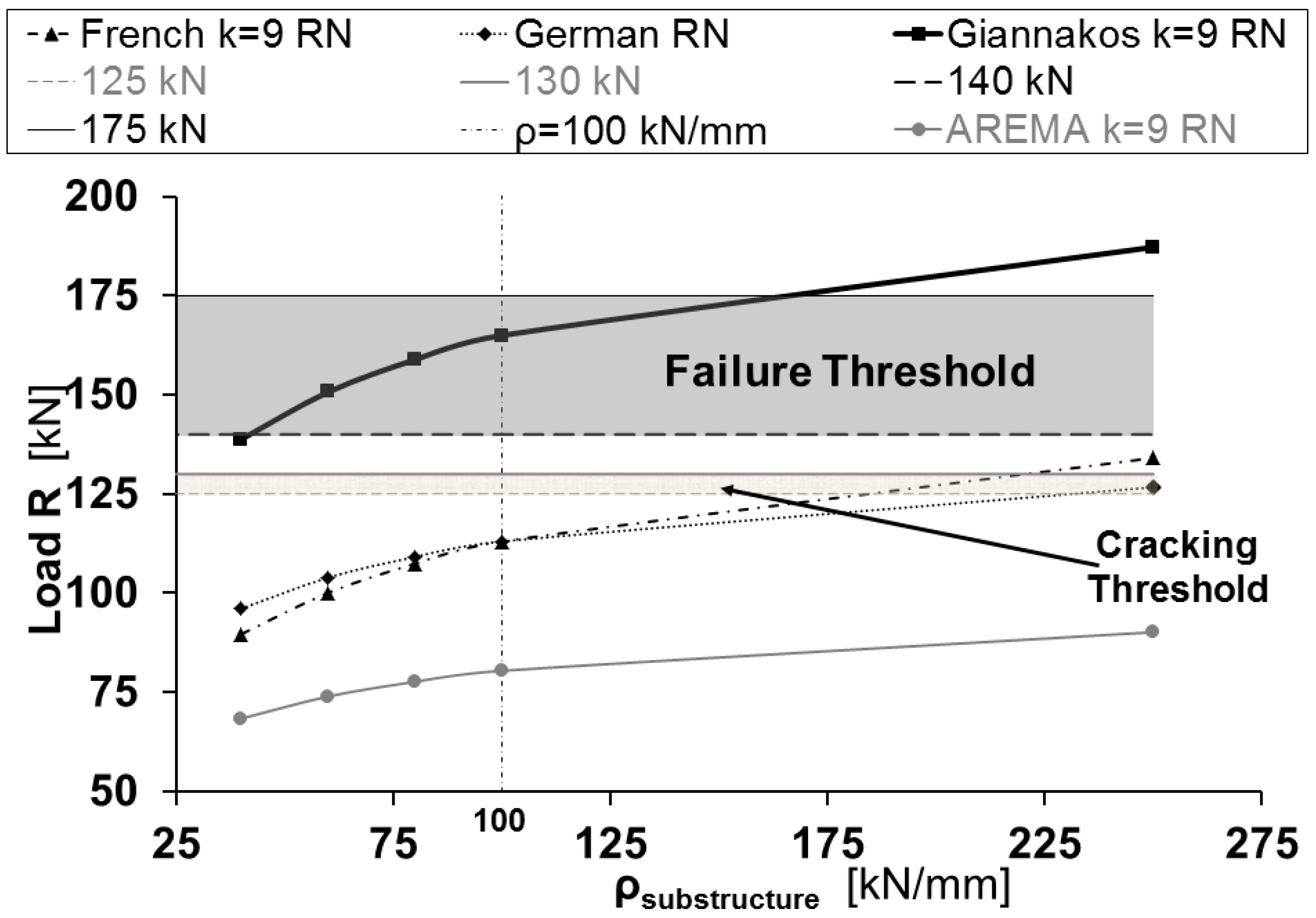
Appendix A. Tests for Concrete Sleepers—Acceptance Criteria (Excerpt of [6])
References and Notes
- Gamage, E.K.; Kaewunruen, S.; Remennikov, A.M.; Ishida, T. Toughness of railroad concrete crossties with holes and web openings. Infrastructures 2017, 2, 3. [Google Scholar] [CrossRef]
- Giannakos, K.; Loizos, A. Ballast stressing on a railway track and the behavior of limestone ballast. In Advances in Transportation Geotechnics; CRC Press and Taylor & Francis Group: Boca Raton, FL, USA, 2008; pp. 577–584. [Google Scholar]
- Giannakos, K.; Tsoukantas, S. Design methodology of slab track systems. In Advances in Transportation Geotechnics; CRC Press and Taylor & Francis Group: Boca Raton, FL, USA, 2008; pp. 585–592. [Google Scholar]
- Giannakos, K.; Loizos, A. Actions on railway track panel and ballast—Behavior of the Hellenic limestone ballast. In Bearing Capacity of Roads, Railways and Airfields; Taylor & Francis Group: Boca Raton, FL, USA, 2009; pp. 1263–1272. [Google Scholar]
- Giannakos, K. Theoretical calculation of the track-mass in the motion of unsprung masses in relation to track dynamic stiffness and damping. Int. J. Pavement Eng. 2010, 11, 319–330. [Google Scholar] [CrossRef]
- Giannakos, K.; Loizos, A. Evaluation of actions on concrete sleepers as design loads–Influence of fastenings. Int. J. Pavement Eng. 2010, 11, 197–213. [Google Scholar] [CrossRef]
- Giannakos, K. Loads on track, ballast fouling and life-cycle under dynamic loading in railways. J. Transp. Eng. 2010, 136, 1075–1084. [Google Scholar] [CrossRef]
- Giannakos, K. Reduced service life of concrete sleepers due to inadequate design. In Concrete under Severe Conditions; Taylor & Francis Group: Boca Raton, FL, USA, 2010; pp. 1281–1288. [Google Scholar]
- Giannakos, K. Comparison of magnitude of actions on track in high-speed and heavy-haul railroads—Influence of fastenings. Transp. Res. Rec. 2012, 2289, 70–77. [Google Scholar] [CrossRef]
- Giannakos, K. Influence of the Track’s Damping on the Track-Mass that Participates in the Motion of the Non-Suspended Masses of the Railway Vehicles; Volume in Honour of the professor George A. Giannopoulos; Aristotle University of Thessaloniki: Thessaloniki, Greece, 2012; pp. 81–94. (In Greek) [Google Scholar]
- Giannakos, K. Track defects and the dynamic loads due to non-suspended masses of railway vehicles. Int. J. Mech. 2013, 7, 180–191. [Google Scholar]
- Giannakos, K. Actions on a railway track, due to an isolated defect. Int. J. Control Autom. 2014, 7, 195–212. [Google Scholar] [CrossRef]
- Giannakos, K. Design loads on railway substructure: Sensitivity analysis of the influence of the fastening stiffness. Int. J. Railw. 2014, 7, 46–56. [Google Scholar] [CrossRef]
- Giannakos, K. Influence of a bent or battered joint or welding on the dynamic loads due to the non-suspended masses of railway vehicles. Int. J. Mech. 2014, 8, 307–318. [Google Scholar]
- Giannakos, K. Mathematical analysis of the transient loads for a deformed joint or welding in a railway Track. Int. J. Eng. Math. Model. 2015, 2, 51–62. [Google Scholar]
- Giannakos, K. Deflection of a railway reinforced concrete slab track: Comparing the theoretical results with experimental measurements. Eng. Struct. J. 2016, 122, 296–309. [Google Scholar] [CrossRef]
- Giannakos, K. Modeling the influence of short wavelength defects in a railway track on the dynamic behavior of the non-suspended masses. J. Mech. Syst. Signal Process. 2016, 68–69, 68–83. [Google Scholar] [CrossRef]
- Giannakos, K. Second order differential equation of motion in railways: The variance of the dynamic component of actions due to the sprung masses of the vehicles. Int. J. Theor. Appl. Mech. 2016, 1, 30–37. [Google Scholar]
- Prud’homme, A.; Erieau, J. Les Nouvelles Traverses en Beton de la SNCF; RGCF 2/1976; Revue Generale des Chemins de Fer/RGCF: Paris, France, 1976. [Google Scholar]
- Giannakos, K. Selected Topics in Railway Engineering, revised 4th version; Department of Civil Engineering, University of Thessaly: Volos, France, 2012; Chapter 14. [Google Scholar]
- Tasios, T.P.; Trezos, K. Laboratory Tests and Measurements on OSE Sleepers; National Technical University of Athens (NTUA)/Reinforced Concrete Laboratory, Research Program: Athens, Greece, 1989. [Google Scholar]
- OSE(Greek Railway Organization)/SNCF, Cooperation: 3/1989. Programme d’ essais realize au centre d’ essais de la Direction de l’ Equipement, OSE’s archives. 1989.
- OSE/SNCF, Cooperation: 6/1988. Comportment des traverses en relation avec les charges dynamiques, OSE’s archives. 1988.
- Giannakos, K.; Iordanidis, P.; Vlassopoulou, I. OSE Committee of Experts Report on their visit to SNCF from 15.5.1988/11.6.1988; OSE/Track Directorate: Athens, Greece, 1988. [Google Scholar]
- Giannakos, K.; Iordanidis, P.; Vlassopoulou, I. Summary Report of the Committee for the Issue of Twin-Block Sleepers after the Second Visit to SNCF in March 1989; OSE/Track Directorate: Athens, Greece, 1989. [Google Scholar]
- SNCF—Direction de l’ Equipement. Specification Technique VRE 2321 80-06 (B), Pour la Fourniture de traveRses Mixtes en Beton Arme, June 1980.
- Giannakos, K. Actions on the Railway Track; Papazissis Publicatios: Athens, Greece, 2004. [Google Scholar]
- fib/Federation Internationale du beton/International Federation of Concrete. Precast Concrete Railway Track Systems, with the participation of Giannakos, K., as railway expert. 2006.
- Giannakos, K. Ties’ design in high-speed and heavy haul railroads: Ultimum strength vs. actions on track. In Proceedings of the TRB Annual Meeting, Washington, DC, USA, 13–17 January 2013.
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannakos, K. Comment on: Toughness of Railroad Concrete Crossties with Holes and Web Openings. Infrastructures 2017, 2, 3. Infrastructures 2017, 2, 4. https://doi.org/10.3390/infrastructures2010004
Giannakos K. Comment on: Toughness of Railroad Concrete Crossties with Holes and Web Openings. Infrastructures 2017, 2, 3. Infrastructures. 2017; 2(1):4. https://doi.org/10.3390/infrastructures2010004
Chicago/Turabian StyleGiannakos, Konstantinos. 2017. "Comment on: Toughness of Railroad Concrete Crossties with Holes and Web Openings. Infrastructures 2017, 2, 3" Infrastructures 2, no. 1: 4. https://doi.org/10.3390/infrastructures2010004
APA StyleGiannakos, K. (2017). Comment on: Toughness of Railroad Concrete Crossties with Holes and Web Openings. Infrastructures 2017, 2, 3. Infrastructures, 2(1), 4. https://doi.org/10.3390/infrastructures2010004





