Maintenance Budget Allocation Models of Existing Bridge Structures: Systematic Literature and Scientometric Reviews of the Last Three Decades
Abstract
1. Introduction
2. Research Methodology
3. Scientometric Review Analysis
3.1. Publication Trend
3.2. Document Analysis
3.3. Co-Authorship Analysis
3.4. Co-Citation Analysis
3.5. Keyword Co-Occurrence Analysis
4. Systematic Review Analysis
4.1. Multi-Criteria Decision-Making (MCDM)-Based Models
| Reference | Year | MCDM Approach | Data Analysis Techniques | Application | Data Type | |
|---|---|---|---|---|---|---|
| Crisp | Fuzzy | |||||
| [78] | 2025 | Hybrid | FBWM + FCE | Condition evaluation of bridges | ✔ | |
| [64] | 2025 | Single | TOPSIS/COPRAS/SAW | Assessment of corrosion control methods | ✔ | |
| [63] | 2024 | Hybrid | GIS + SAW | Prioritization of bridge rehabilitation projects | ✔ | |
| [62] | 2024 | Hybrid | Delphi + WSM | Maintenance ranking of pedestrian bridges | ✔ | |
| [50] | 2025 | Hybrid | AHP + MAUT | Allocation of bridge maintenance funds | ✔ | |
| [58] | 2024 | Hybrid | CRITIC + VIKOR/TOPSIS/COPRAS/ARAS/MOORA | Sequencing bridges for resilience improvement | ✔ | |
| [65] | 2023 | Hybrid | EV + EW + ELECTRE I + SAW | Determining the best repair method of river bridge columns | ✔ | |
| [57] | 2023 | Single | TOPSIS | Socio-technical-based maintenance ranking | ✔ | |
| [42] | 2023 | Single | AHP | Bridge repair following natural disasters | ✔ | |
| [79] | 2023 | Hybrid | SMART + AHP + TLS + BrIM | Prioritizing bridge elements and remediation alternatives | ✔ | |
| [56] | 2023 | Hybrid | AHP + TOPSIS + Sensitivity analysis | Defining the optimum construction techniques of piers | ✔ | |
| [55] | 2022 | Hybrid | T2NN + fuzzy WASPAS + TOPSIS | Carbon footprint-driven planning of bridge repair | ✔ | |
| [45] | 2022 | Single | ANP | Life cycle sustainability analysis of concrete bridges in coastal environments | ✔ | |
| [61] | 2022 | Hybrid | IFT + GRD + EDAS + ILP-ACO | Sorting of bridge reconstruction priorities | ✔ | |
| [80] | 2021 | Hybrid | Rough neutrosophic symmetric cross entropy + Tangent function | Remediation planning of historic pedestrian bridges | ✔ | |
| Reference | Year | MCDM Approach | Data Analysis Techniques | Application | Data Type | |
|---|---|---|---|---|---|---|
| Crisp | Fuzzy | |||||
| [81] | 2021 | Hybrid | AHP + WSM | Determination of bridge condition index | ✔ | |
| [82] | 2021 | Single | Optimization index | Formulation of highway bridge maintenance | ✔ | |
| [60] | 2021 | Hybrid | FAHP + GRA | Optimal identification of reinforcement schemes | ✔ | |
| [66] | 2021 | Single | CNN-LSTM + WSM | Selecting optimal intervention action | ✔ | |
| [83] | 2020 | Hybrid | FANP + IWO + GPR + TOPSIS + GRA | Maintenance ranking of bridge decks | ✔ | |
| [54] | 2020 | Hybrid | Neutrosophic AHP + TOPSIS | Sustainability-based evaluation of designs of prestressed bridges | ✔ | |
| [59] | 2019 | Hybrid | Target-based standard deviation + VIKOR | Sorting of concrete bridge rehabilitation projects | ✔ | |
| [46] | 2019 | Single | AHP + GIS + Fusion tables | Ranking of bridge maintenance systems | ✔ | |
| [48] | 2019 | Hybrid | AHP + WSM | Condition assessment of suspension bridges | ✔ | |
| [84] | 2019 | Single | MAUT | Maintenance Planning for Network-Level Bridges | ✔ | |
| [85] | 2018 | Single | MAUT + Sensitivity analysis | Maintenance management of bridge inventory | ✔ | |
| [86] | 2018 | Hybrid | FL + SE + TOPSIS | Planning MR&R actions of bridge components | ✔ | |
| [51] | 2017 | Hybrid | SMART + S-AHP + WSM | Modeling of remediation actions of steel bridges | ✔ | |
| [43] | 2016 | Single | S-AHP | Assessing key factors of bridge repair | ✔ | |
| Reference | Year | MCDM Approach | Data Analysis Techniques | Application | Data Type | |
|---|---|---|---|---|---|---|
| Crisp | Fuzzy | |||||
| [87] | 2015 | Hybrid | GA + MAUT | Sustainability-based planning of highway bridge maintenance | ✔ | |
| [88] | 2014 | Single | Dominance-based rough set | Network-scale bridge maintenance management | ✔ | |
| [89] | 2013 | Hybrid | ε—Constraint Method + WSM | Strategic management of bridge inventory | ✔ | |
| [47] | 2013 | Single | AHP + Sensitivity analysis | Optimizing factors of bridge rehabilitation/reconstruction | ✔ | |
| [90] | 2011 | Single | DEA | Prioritization of bridge maintenance needs” | ✔ | |
| [52] | 2011 | Hybrid | AHP + MAUT | Optimizing bridge infrastructure management with limited budgets | ✔ | |
| [53] | 2010 | Hybrid | AHP + MAUT | Allocation of bridge maintenance funds | ✔ | |
| [49] | 2012 | Hybrid | AHP + WSM | Analysis of bridge health index | ✔ | |
| [91] | 2008 | Single | AHP + Fuzzy synthetic evaluation | Condition assessment of reinforced concrete bridges | ✔ | |
| [44] | 2008 | Single | AHP | Ranking of bridge rehabilitation plans | ✔ | |
| MCDM Technique | Acronym | Description | Reference |
|---|---|---|---|
| Analytical Hierarchy process | AHP | A structured tool for deriving priority scales from experts’ judgments | [44] |
| Analytical Network Process | ANP | It is a network-structured MCDM method that generalizes AHP by emulating the interdependencies among criteria and alternatives, using pairwise comparisons | [92] |
| Criteria Importance Through Intercriteria Correlation | CRITIC | A weight interpretation method through quantifying statistical contrast and intercriteria correlation | [93] |
| Shannon Entropy | SE | An information-theoretic MCDM technique that calculates objective criteria weights by measuring data dispersion | [94] |
| Best-worst Method | BWM | A pairwise comparison-based MCDM technique for deriving criteria weights systematically by comparing the best and worst indicators | [95] |
| Technique for Order Preference by Similarity to Ideal Solution | TOPSIS | A selection method for the best alternative by identifying the ideal and negative ideal solutions | [96] |
| Complex Proportional Assessment | COPRAS | A ranking method of alternatives based on their utility degrees in relation to the ideal best and worst solutions | [97] |
| Grey Relational Analysis | GRA | A ranking method by measuring the similarities between data sequences using the grey relational grade | [98] |
| Weighted Aggregated Sum Product Assessment | WASPAS | A unified ranking method stepping on balancing additive and multiplicative aggregation approaches | [99] |
| ÉLimination Et Choix Traduisant la RÉalité | ELECTRE | An outranking method that is based on determining the concordance and discordance sets through pairwise comparisons | [100] |
| Preference Ranking Organization Method for Enrichment Evaluation | PROMETHEE | A family of outranking methods based on positive and negative preference flows for each alternative | [101] |
| Evaluation based on Distance from Average Solution | EDAS | A distance-based MCDM technique of alternatives through quantifying their negative and positive deviations from the average solution | [102] |
| Multi-attribute Utility Theory | MAUT | A utility-based MCDM technique that assesses alternatives by aggregating single-attribute utility functions | [103] |
| Vlsekriterijumska Optimizacija I Kompromisno Resenje | VIKOR | A compromise ranking method that accommodates group utility and individual target values | [104] |
| Data Envelopment Analysis | DEA | A non-parametric linear programming technique that develops the efficiency frontier through optimizing weighted outputs to weighted inputs | [105] |
| Dominance-based Rough Set Approach | DRSA | A rough set-based MCDM method that uses dominance relations and collective decision rules for analyzing preference-ordered data | [106] |
| List of Factors | References | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [78] | [50] | [82] | [65] | [108] | [81] | [46] | [51] | [47] | [79] | [84] | [85] | [44] | [62] | [53] | [58] | |
| Climate event vulnerability | ✔ | ✔ | ||||||||||||||
| Climate load vulnerability | ✔ | |||||||||||||||
| Maintenance cost/agency cost | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||
| Safety | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||
| Durability | ✔ | ✔ | ✔ | ✔ | ||||||||||||
| Suitability | ✔ | |||||||||||||||
| Reinforcement economy | ✔ | |||||||||||||||
| Condition/reliability | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| Age | ✔ | ✔ | ||||||||||||||
| Location | ✔ | |||||||||||||||
| Maintenance history | ✔ | |||||||||||||||
| Scheduled maintenance | ✔ | |||||||||||||||
| Traffic volume/traffic disruption | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| Duration | ✔ | |||||||||||||||
| Scouring depth | ✔ | |||||||||||||||
| Geometry consistency | ✔ | |||||||||||||||
| Ease of construction | ✔ | |||||||||||||||
| Embodied carbon/environmental impact | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||
| Hydrology and climate | ✔ | |||||||||||||||
| Load impact | ✔ | |||||||||||||||
| Geotechnics and seismicity | ✔ | |||||||||||||||
| Strategic importance | ✔ | |||||||||||||||
| Facilities index | ✔ | |||||||||||||||
| Serviceability/useful life | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| Riding comfort | ✔ | |||||||||||||||
| Resilience | ✔ | ✔ | ||||||||||||||
| Aesthetic value | ✔ | |||||||||||||||
| Regional economic impact | ✔ | |||||||||||||||
| Effect on surrounding communities/societal impact/user cost | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||||
| Area | ✔ | |||||||||||||||
| High flood level | ✔ | |||||||||||||||
| Finish road level | ✔ | |||||||||||||||
4.2. Life Cycle Assessment (LCA)-Based Models
| Ref. | Application | Analytical Methods | Findings |
|---|---|---|---|
| [126] | Financial evaluation of Weigh-In-Motion (WIM) sensor installation for fatigue monitoring in steel bridge girders. | Probabilistic life-cycle cost analysis using the Hasofer–Lind reliability method. | Continuous WIM data reduces load uncertainty, enables optimal repair scheduling, enhances safety and yields net savings. |
| [127] | Long-term financial assessment of seismic structural health monitoring (SHM) installation on highway bridges. | Time-dependent LCCA via Monte Carlo simulation of seismic damage and repair scenarios. | Seismic SHM achieves cost break-even by lowering expected post-quake repair costs. |
| [110] | Comparative life-cycle cost analysis of fiber-reinforced polymer (FRP) vs. traditional steel stay cables on long spans. | Deterministic LCCA with scenario and sensitivity analysis on discount rate and service life. | A mixed FRP/steel arrangement is identified as the most cost-effective option among those analyzed. |
| [128] | Life-cycle cost comparison of corrosion mitigation: painted carbon steel, weathering steel, and stainless-steel girders. | Probabilistic LCCA via Monte Carlo corrosion-progression simulation. | Stainless steel can minimize total LCC in aggressive environments; the optimal choice depends on coating life, discount rate. |
| [112] | Optimal intervention timing for reinforced concrete bridges in seismic zones using renewal-theory LCCA. | Renewal-theory-based LCCA with analytical expressions for expected cost and downtime. | Accumulated seismic damage drives life-cycle cost; renewal theory provides closed-form insights into optimal schemes. |
| [113] | LCCA of selected concrete repair methods for chloride-contaminated columns. | Probabilistic event-based simulation of damage progression and Weibull-modeled service-life distributions. | Patch repair + hydrophobic impregnation and Ti-mesh cathodic protection deliver the lowest total LCC. |
| [129] | LCCA framework for maintenance strategies on concrete and steel railway bridges. | Probabilistic LCCA via Monte Carlo coupled with a maintenance-optimization algorithm. | Element-level cost modeling accelerates budgeting and improves repair prioritization |
| [130] | Deck replacement scheduling under strength and serviceability constraints | Probabilistic LCCA based on limit-state reliability indices. | Serviceability-based criteria lead to higher LCC than strength-only; reliability-constrained optimization yields realistic, safety-aware timing. |
| [131] | Expected LCC comparison of single vs. multiple maintenance interventions for aging RC bridges. | Probabilistic LCCA with time-dependent reliability modeling. | Multiple smaller interventions smooth cost and risk profiles and outperform single-action strategies. |
| [132] | LCCA of maintenance profiles for various superstructure types (steel vs. concrete). | Probabilistic LCCA via Monte Carlo and stochastic dominance. | Preventive-maintenance profiles consistently outperform rehabilitation-heavy profiles. |
| [109] | Long-term LCA of all-aluminum bridge vs. hypothetical aluminum-deck replacement (100-year span). | Deterministic cradle-to-grave LCA based on historical and projected cost data. | The aluminum deck option extends service life and minimizes disruptions despite a higher initial investment. |
| [133] | Preventive-maintenance scheduling for reinforced concrete bridges based on life-cycle cost minimization. | Monte Carlo simulation of random damage (Weibull) and repair events; expected-cost LCCA. | The optimal maintenance interval balances rising repair costs against escalating damage costs; Weibull-modeled damage/repair times drive the minimum expected LCC. |
| [111] | Life-cycle costing framework development for Myanmar highway bridges. | Deterministic component-based LCCA per ISO 15686-5; present-value analysis over a 40-year horizon. | Even a basic preventive maintenance plan can reduce 30-year LCC by ~20% versus reactive repairs; framework guides budgeting under limited funds. |
| [114] | Expected LCC evaluation for deteriorating reinforced concrete bridge elements. | Analytical probabilistic LCCA using a Markov/deterioration process and closed-form expected-cost equations. | Provides expected maintenance cost and intervention count over the service life; supports optimal allocation of resources under uncertainty. |
| Ref. | Application | Analytical Methods | Findings |
|---|---|---|---|
| [115] | Environmental impact assessment of bridge life-cycle stages (design, construction, operation, end-of-life). | Probabilistic life-cycle LCA with Bayesian network for data gaps and fuzzy-mathematics aggregation. | >53% of impacts arise from material production and O&M; optimized traffic management reduces CO2 by ~330 t/year. |
| [116] | Integrated environmental and cost LCA across design, construction and O&M phases for bridges. | Probabilistic life-cycle sustainability analysis using Monte Carlo propagation and surrogate modeling. | Modeling phase interactions alters sustainability rankings; single-stage expected values can mislead decision-making. |
| [117] | Stage-by-stage environmental LCA (manufacturing, use, EoL) of two optimal concrete box-girder bridge designs. | ISO 14040 life-cycle inventory and impact assessment. | Manufacturing and maintenance stages dominate; the durability-oriented design yields lower total impacts despite higher initial footprint. |
| [118] | LCA and LCCA of rehab vs. rebuild options for long-span cable-stayed bridges (30-year horizon). | Cradle-to-grave LCA with dynamic energy-mix factors; deterministic LCCA. | Material production is the largest emitter; construction is smallest; dynamic energy modeling shifts the optimal renewal schedule. |
| [119] | LCA of epoxy-asphalt vs. GA + SMA pavement systems on steel bridge decks. | Cradle-to-grave LCA with Monte Carlo–based uncertainty assessment of inventory and impact factors. | Epoxy-asphalt systems consume ~2.5× less energy and emit ~3.4× fewer GHGs than GA + SMA mixtures; raw-material production dominates impacts. |
| Ref. | LCA Type | Application | Analytical Methods | Findings |
|---|---|---|---|---|
| [120] | Social and cost LCA | Combined financial and social-cost evaluation of design/maintenance strategies for reinforced-concrete bridges. | Stochastic social-cost LCCA: ranking by integrating quantified social factors into the life-cycle cost. | Social costs (e.g., user delays, business losses) dominate total LCC; including them shifts optimal maintenance timing. |
| [121] | Social and cost LCA | Financial and social-cost appraisal of preventive measures (increased concrete cover, SS rebar, cathodic protection) for prestressed concrete bridges in chloride environments. | Deterministic social-cost LCCA: ranking by discounted total cost. | A well-chosen preventive strategy can reduce total LCC by up to ~58%; user-delay costs dominate for frequent major works. |
| [124] | Cost and environmental LCA | Financial and environmental LCA of painted steel vs. corrosion-resistant steel for bridges. | Probabilistic LCCA combined with life cycle GHG LCA via Monte Carlo. | Corrosion-resistant steel reduces total LCC and CO2 emissions in chloride environments, offsetting its higher first cost. |
| [122] | Cost and social LCA | Bridge design/maintenance decisions incorporating user and social costs. | Multi-level stochastic cost-benefit LCCA with discounting and life-quality indices. | User-related costs (delays, closures) often exceed agency costs by a factor of 10 or more; therefore, total societal cost minimization is recommended. |
| [123] | Cost and social LCA | Optimal deck replacement timing for highway bridges, including user and social cost penalties. | Analytical cost-benefit optimization integrating failure probability and user/social costs. | The inclusion of user and societal costs raises optimal reliability targets and justifies earlier interventions. |
| [125] | Environmental and cost LCA | Comparative LCA and LCCA of conventional vs. UHPC overlays for bridge decks. | Parameterized life-cycle inventory and cost model; eco-efficiency scenario comparison. | Ultra-High Performance Concrete overlays—despite higher initial cost—yield lower total LCC and embodied carbon when service life ≥ ~2× that of conventional overlays. |
4.3. Digital Twin (DT)-Based Models
4.4. Bridge Inspection Models
| Study | Application | Inspection Technique | Approach | Optimization | Key Contribution | |
|---|---|---|---|---|---|---|
| Concrete bridges | Abdelkhalek et al. [138] | Bridge deck inspections | Camera, IRT, IE, USW, UPE, GPR, HCP, ER, PR | Multi-NDT integration with simulation | Multi-objective PSO + DES | Combines multiple NDTs to optimize scheduling, reduce cost/time, and enhance accuracy |
| Abdelkhalek & Zayed [3] | Bridge networks over large areas | Simulation-based adaptation * | Crew routing with distance/work constraints | DES + GA | Reduces travel, idle time, and crew cost | |
| Kwon et al. [140] | Deteriorating bridges | Failure probability extrapolation | KDE | Improves timing accuracy for inspections using KDE-based prediction | ||
| Mohamad & Tran [139] | Highway construction QA | Fuzzy logic + expert risk input | Fuzzy sets + Bayesian networks | Prioritizes inspection using quantified uncertainty and expert judgment | ||
| Sein et al. [156] | Bridge management in Estonia | Stochastic degradation model | MCMC stochastic simulation | Reduces uncertainty in scheduling by optimizing with degradation forecasts | ||
| Su et al. [157] | Concrete beam bridge | Logic-based optimization with linkages | C5.0 Boosting Decision Tree | Enhances efficiency via asset screening and coordination | ||
| Vereecken et al. [141] | RC structures under corrosion (bridge girders) | Spatial Bayesian decision updating | VoI + Bayesian | Minimizes cost/risk by incorporating outcome-based updates | ||
| Oyegbile & Chorzepa [142] | Concrete bridge (Georgia) | Co-active prioritization model | Heuristic logic | Boosts BHI by targeting critical elements with inspection timing adjustments | ||
| Huang et al. [158] | Bridge routing and lodging | Vehicle routing optimization | ACO + local search | Minimizes cost via optimized routes/accommodation for multi-teams | ||
| Washer et al. [143] | General bridge structures | Risk matrix–based interval planning | Simple risk matrix | Converts fixed intervals to adaptive risk-based timing | ||
| Kim & Frangopol [144] | RC highway bridge | Damage detectability–driven timing | Monte Carlo simulation | Minimizes delay in detection and lifecycle cost |
| Study | Application | Inspection Technique | Approach | Optimization | Key Contribution | |
|---|---|---|---|---|---|---|
| Steel bridge | Sun & Vatn [145] | Steel road bridge | Simulation-Based Adaptation * | Markov deterioration with inspection delay | Phase-type multi-state Markov | Optimizes cost with fewer inspections and postponed repairs |
| Jiang et al. [146] | Fatigue in steel bridges | Digital Twin + probabilistic fatigue model | Bayesian inference + surrogate optimization | Enables real-time repair sizing and inspection updates to extend fatigue life | ||
| Cheng & Frangopol [147] | Corroded steel girders | Load rating + inspection planning | MDP with state augmentation | Reduces lifecycle cost with adaptive inspection/replacement rules | ||
| Crémona & Lukić [152] | Welded joints in steel bridges | Fracture mechanics + reliability | Probabilistic fatigue model | Updates reliability and costs to determine inspection interval | ||
| Sommer et al. [148] | Highway steel-girder bridges | Reliability index for time-based intervals | Probabilistic reliability analysis | Recommends constant 5–10 year intervals based on corrosion/load degradation | ||
| Soliman et al. [151] | Fatigue-prone steel bridges | LPI, UI, ECI | Multi-objective NDT selection | Probabilistic optimization | Chooses best NDT + schedule under uncertainty and cost limits | |
| Orcesi & Frangopol [149] | Steel bridges | UI, VI, MPI | Lifetime functions + event tree | Probabilistic + cost optimization | Balances NDT strategy, failure, and maintenance costs under uncertainty | |
| Others | Wu et al. [153] | UAV inspection of infrastructure | UAV | Model-based prognostics | Physics-based probabilistic analysis | Optimizes UAV flight parameters and inspection update rules |
| Phung et al. [34] | Surface inspection (e.g., buildings) | CCD camera attached to a controllable gimbal | Vision-based robotic inspection | PSO on GPU | Reduces path computation time and improves controllable gimbal inspection efficiency | |
| Yang & Frangopol [154] | Civil and marine structures | Simulation-Based Adaptation * | Static vs. adaptive RBI | Bayesian + Monte Carlo | Adaptive plans lower costs and preserve safety better than fixed methods | |
| Sheils et al. [155] | Infrastructure maintenance | Two-stage Markov inspection planning | Markov modeling | Optimizes cost-effective technique combinations and intervals |
4.5. Artificial Intelligence-Based Models

4.6. Optimization-Based Models
| Reference | Year | Employed Algorithms | Application | Optimization Type | Objective Functions | Design Constraints |
|---|---|---|---|---|---|---|
| [207] | 2024 | Modified NSGA-II (NDX crossover operator + adaptive hybrid mutation operator) | Resource-driven maintenance optimization of in-service bridges | Multi-objective | a. Minimize the cumulative structural safety loss b. Minimize the entire duration of planned maintenance | a. Structural reliability of bridge component b. Cumulative number of construction labors for bridge repairing |
| [208] | 2022 | NSGA-II | Maintenance programming at the bridge element level, bridge-level, and network-level | Multi-objective | a. Maximize the network health index b. Minimize the network LCC | a. Total budget b. Network health index |
| [199] | 2021 | AHP + HCWOA | Supporting bridge expansion and contraction installation | Single-objective | Minimize the inconsistent comparison matrix | N/A |
| [12] | 2021 | QFD + GA | Short-term and long-term MRR optimization for bridge decks under performance-based contracting | Multi-objective | a. Minimize the total rehabilitation actions cost b. Maximize the average condition | a. Total available budget b. Performance at each year c. Level of service threshold |
| Reference | Year | Employed Algorithms | Application | Optimization Type | Objective Functions | Design Constraints |
|---|---|---|---|---|---|---|
| [209] | 2025 | NSGA-II | Dynamic maintenance optimization of regional transportation network | Multi-objective | a. Maximize the condition benefits of the bridge network b. Minimize the maintenance expenses | a. Maintenance funding of bridge network |
| [203] | 2022 | Xgboost + MAUT + NSGA-II | Formulating bridge network maintenance plans that maximize performance within financial limitations | Multi-objective | a. Minimize the total maintenance cost b. Maximize the performance condition rating | a. Condition level of bridges b. Available estimated budget |
| [14] | 2020 | MAUT + NSGA-II | Multi-year maintenance planning optimization for road bridge networks | Multi-objective | a. Minimize the total maintenance expenditures b. Maximize the bridge performance level | a. Bridge network condition index b. Budget limit |
| [205] | 2012 | MOPSO + MCS + parrallel computing | Maintenance planning of deteriorated bridges | Multi-objective | a. Minimize the discounted present worth of maintenance costs b. Maximize the lowest condition index c. Maximize the lowest safety index | a. Condition index b. Safety index c. Budget limit |
| Reference | Year | Employed Algorithms | Application | Optimization Type | Objective Functions | Design Constraints |
|---|---|---|---|---|---|---|
| [210] | 2024 | FST + AHP + PSO | Optimizing MR&R strategies of bridges | Multi-objective | a. Minimize the user and maintenance costs b. Maximize the reliability of bridge maintenance | a. Allocated budget limit for each bridge |
| [10] | 2024 | IEFO | Reliability-driven maintenance optimization of bridges | Single-objective | a. Minimize the equivalent annual maintenance costs | N/A |
| [204] | 2023 | NSGA-II + Disease transmission concept | Maintenance fund assignment of bridge networks | Multi-objective | a. Maximize the total economic benefits of bridge repair b. Maximize the total technical benefits of bridge repair c. Minimize the total maintenance costs of bridge repair | a. Available maintenance budget |
| [198] | 2006 | GA/SFL | Optimization of bridge deck rehabilitation | Single-objective | a. Minimize the total life cycle costs of bridge repairs | a. Annual budget limits b. Condition level of bridges c. Entire condition rating of bridge network |
| Reference | Year | Employed Algorithms | Application | Optimization Type | Objective Functions | Design Constraints |
|---|---|---|---|---|---|---|
| [211] | 2022 | NSGA-II | Condition-driven maintenance of corroded RC columns in seismic zones | Multi-objective | a. Minimize the seismic risk of columns b. Minimize the life cycle cost of maintenance | a. Time interval between successive maintenance actions b. Maintenance period c. Maximum permissible risk threshold |
| [206] | 2019 | MOPSO-II + LHS | Stochastic optimization of life-cycle maintenance actions to enhance bridge superstructure durability | Multi-objective | a. Maximize the life cycle performance b. Minimize the life cycle maintenance costs | a. Available maintenance funding b. Time interval between subsequent maintenance actions |
| [212] | 2013 | GA + LHS | Optimized maintenance scheduling of bridge networks | Multi-objective | a. Maximize the bridge network connectivity b. Minimize the total maintenance costs | a. Available maintenance fund b. Number of travels originated and attracted by each node |
| [201] | 2005 | MOGA + MCS | Annual optimization of limited maintenance funding for deteriorating bridge elements | Multi-objective | a. Maximize the lowest lifetime condition b. Maximize the lowest safety index c. Minimize the lifecycle maintenance costs | a. Condition index of bridge element b. Safety index of bridge element c. Limit of life cycle cost |
| Reference | Year | Employed Algorithms | Application | Optimization Type | Objective Functions | Design Constraints |
|---|---|---|---|---|---|---|
| [200] | 2022 | GA + MCS | Risk-cost optimization of maintenance programs of steel bridges | Single-objective | Minimize the total risk of steel bridge failure | a. Allowable probability of each failure mode b. Allowable failure probability of steel bridges |
| [11] | 2022 | ECDE + CRITIC + COPRAS + GRA | Optimizing bridge maintenance plans of bridge elements | Multi-objective | a. Maximize the performance status of bridge elements b. Minimize the total life cycle maintenance expenditures c. Minimize the traffic disruption duration d. Minimize the environmental footprint | a. Minimum condition of bridge elements b. Estimated total budget c. Available annual funding d. Maximum permissible standard deviation of repair actions e. Number of intervention actions of bridges |
| [213] | 2021 | GA + DES | Simulation-based bridge maintenance planning | Single-objective | Minimize the crew and user costs | Available annual budget of repair activities |
| [214] | 2020 | GA + MCS | Optimizing maintenance schedules for enhanced disaster resilience | Multi-objective | a. Minimize the total annual maintenance cost b. Maximize the safety performance of each bridge element c. Maximize the resilience against natural disasters | a. Safety performance threshold b. Maximum number of bridges to be repaired |
| Reference | Year | Employed Algorithms | Application | Optimization Type | Objective Functions | Design Constraints |
|---|---|---|---|---|---|---|
| [215] | 2020 | DES + ENN + DE + PROMETHEE II | Simulation and planning of bridge deck replacement projects | Multi-objective | a. Minimize the duration of bridge deck replacement b. Minimize the cost of bridge deck replacement c. Minimize the greenhouse gases of bridge deck replacement | Thresholds for managing the utilization of resources |
| [216] | 2018 | GA + MCS | Time dependent reliability-based optimization of bridges | Multi-objective | a. Minimize the cumulative probability of failure of bridges b. Minimize the life cycle cost of repair actions c. Minimize the life cycle environmental footprint of repair actions | a. Target failure probability b. Preventive maintenance timeframe c. Timing of application of initial preventive maintenance |
| [217] | 2018 | GA | Maintenance cost optimization of reinforced concrete bridge superstructure | Single-objective | Minimize the uniform equivalent annual expenditures of maintenance | Allocated funding limits |
| [202] | 2012 | GA + MCS | Safety-focused maintenance optimization of steel box girder bridges | Multi-objective | a. Minimize the total life-cycle maintenance expenditures b. Maximize the life-cycle condition index c. Maximize the life-cycle reliability index | a. Given budget limit b. Performance condition threshold |
4.7. Critical Discussion
4.8. Summary of Case Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Description | Acronym | Description |
| ASCE | American Society of Civil Engineers | FHWA | Federal Highway Administration |
| BMS | Bridge Management System | MR & R | Maintenance, repair and rehabilitation |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses | TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| GRA | Grey Relational Analysis | CWM | Constant Weight Model |
| FVWM | Factor-based Variable Weight Model | FAVWM | Factor and Age-based Variable Weight Model |
| MAUT | Multi Attribute Utility Theory | WASPAS | Weighted Aggregated Sum Product Assessment |
| T2NN | Type-2 neutrosophic number | SMART | Specific, Measurable, Achievable, Relevant, and Time-bound |
| VIKOR | VIseKriterijumska Optimizacija i Kompromisno Rešenje | WSM | Weighted Sum Model |
| ARAS | Additive Ratio Assessment | COPRAS | Complex Proportional Assessment |
| MOORA | Multi-Objective Optimization on the Ratio Analysis | EDAS | Evaluation Based on Distance from Average Solution |
| SAW | Simple Additive Weighting | ELECTRE | ELimination Et Choix Traduisant la REalité |
| DEMATEL | Decision Making Trial and Evaluation Laboratory | BWM | Best-Worst Method |
| CRITIC | Criteria Importance Through Intercriteria Correlation | SWARA | Step-wise Weight Assessment Ratio Analysis |
| FUCOM | Full Consistency Method | MEREC | Method based on the Removal Effects of Criteria |
| SDV | Standard Deviation | CILOS | Criterion Impact Loss |
| LOPCOW | Logarithmic Percentage Change-driven O Weighting | PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluations |
| TLS | Terrestrial Laser Scanning | EV | Eigenvector |
| BrIM | Bridge Information Modeling | ILP | Integer Linear Programming |
| EW | Entropy Weighting | GRD | Grey Relational Degree |
| CODAS | Combinative Distance-based Assessment | SE | Shannon Entropy |
| FL | Fuzzy Logic | DEA | Data Envelopment Analysis |
| IWO | Invasive Weed Optimization | SHM | Structural Health Monitoring |
| LCCA | Life Cycle Cost Analysis | UAV | Unmanned Aerial Vehicle |
| ACO | Ant Colony Optimization | MPI | Magnetic Particle Inspection |
| AI | Artificial Intelligence | NDI | Non-destructive Inspection |
| BHI | Bridge Health Index | NDT | Non-destructive Testing |
| C5.0 | Boosting Decision Tree algorithm | PI | Penetrant Inspection |
| DES | Discrete Event Simulation | PoD | Probability of Detection |
| ECI | Eddy Current Inspection | PR | Polarization Resistance |
| ER | Electrical Resistivity | PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm | RC | Reinforced Concrete |
| GPR | Ground-Penetrating Radar | RBI | Risk-Based Inspection |
| HCP | Half-Cell Potential | UI | Ultrasonic Inspection |
| IE | Impact Echo | BIM | Building Information Modeling |
| IRT | Infrared Thermography | USW | Ultrasonic Surface Wave |
| LPI | Liquid Penetrant Inspection | UPE | Ultrasonic Pulse Echo |
| MDP | Markov Decision Process | VI | Visual Inspection |
| MCMC | Markov Chain Monte Carlo | VoI | Value of Information |
| ML | Machine Learning | DL | Deep Learning |
| BriMai_all | Maintenance fund allocation models of bridges | AHP | Analytica Hierarchy Process |
| ANP | Analytical Network Process | LCA | Life Cycle Assessment |
| MCDM | Multi-criteria decision making | DRL | Deep Reinforcement Learning |
| PNN | Probabilistic Neural Network | PCA | Principal Component Analysis |
| RBFN | Radial Basis Function Network | SVM | Support Vector Machines |
| CNN | Convolutional Neural Network | LSTM | Long Short-Term Memory |
| DNN | Deep Neural Network | RL | Reinforcement Learning |
| SOMCM | and Self-Organizing Map-based Cluster Merging | DT | Decision Tree |
| NN-EE | Neural Networks with Entity Embeddings | DQN | Deep Q-Network |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II | MAR-PPO | Proximal Policy Optimization and its multi-agent variants |
| DP | Dynamic programming | ARIMA | Autoregressive Integrated Moving Average |
| DCMA2C | Double-Critic Multi-Agent A2C | ConvAE-DQN | Convolutional Autoencoder–Structured Deep Q-Network |
| HCWOA | Hybrid Chaotic Whale Optimization Algorithm | MOPSO | Multi-objective Particle Swarm Optimization |
| QFD | Quality Function Deployment | FST | Fuzzy Set Theory |
| MCS | Monte Carlo Simulation | MOGA | Multi-objective Genetic Algorithm |
Appendix A
| Selection and Topic | Item Number | Checklist Item | Location Where Item Is Reported |
|---|---|---|---|
| TITLE | |||
| Title | 1 | Identify the report as a systematic review | Title |
| ABSTRACT | |||
| Abstract | 2 | See the PRISMA 2020 for Abstracts checklist | Abstract |
| INTRODUCTION | |||
| Rationale | 3 | Describe the rationale for the review in the context of existing knowledge. | Introduction |
| Objectives | 4 | Provide an explicit statement of the objective(s) or question(s) the review addresses | Introduction |
| METHODS | |||
| Eligibility criteria | 5 | Specify the inclusion and exclusion criteria for the review and how studies were grouped for the syntheses | Research Methodology |
| Information sources | 6 | Specify all databases, registers, websites, organizations, reference lists and other sources searched or consulted to identify studies. Specify the date when each source was last searched or consulted | Research Methodology |
| Search strategy | 7 | Present the full search strategies for all databases, registers and websites, including any filters and limits used | Research Methodology |
| Selection process | 8 | Specify the methods used to decide whether a study met the inclusion criteria of the review, including how many reviewers screened each record and each report retrieved, whether they worked independently, and if applicable, details of automation tools used in the process | Research Methodology |
| Data collection process | 9 | Specify the methods used to collect data from reports, including how many reviewers collected data from each report, whether they worked independently, any processes for obtaining or confirming data from study investigators, and if applicable, details of automation tools used in the process | Research Methodology |
| Data items | 10.a | List and define all outcomes for which data were sought. Specify whether all results that were compatible with each outcome domain in each study were sought (e.g., for all measures, time points, analyses), and if not, the methods used to decide which results to collect | Research Methodology |
| 10.b | List and define all other variables for which data were sought (e.g., participant and intervention characteristics, funding sources). Describe any assumptions made about any missing or unclear information | Research Methodology | |
| Study risk of bias assessment | 11 | Specify the methods used to assess risk of bias in the included studies, including details of the tool(s) used, how many reviewers assessed each study and whether they worked independently, and if applicable, details of automation tools used in the process | Not Applicable |
| Effect measures | 12 | Specify for each outcome the effect measure(s) (e.g., risk ratio, mean difference) used in the synthesis or presentation of results | Not Applicable |
| Synthesis methods | 13.a | Describe the processes used to decide which studies were eligible for each synthesis (e.g., tabulating the study intervention characteristics and comparing against the planned groups for each synthesis (item #5)) | Research Methodology |
| 13.b | Describe any methods required to prepare the data for presentation or synthesis, such as handling of missing summary statistics, or data conversions | Research Methodology | |
| 13.c | Describe any methods used to tabulate or visually display results of individual studies and syntheses | Research Methodology | |
| 13.d | Describe any methods used to synthesize results and provide a rationale for the choice(s). If meta-analysis was performed, describe the model(s), method(s) to identify the presence and extent of statistical heterogeneity, and software package(s) used. | Research Methodology | |
| 13.e | Describe any methods used to explore possible causes of heterogeneity among study results (e.g., subgroup analysis, meta-regression) | Not Applicable | |
| 13.f | Describe any sensitivity analyses conducted to assess robustness of the synthesized results | Not Applicable | |
| Reporting bias assessment | 14 | Describe any methods used to assess risk of bias due to missing results in a synthesis (arising from reporting biases) | Not Applicable |
| Certainty assessment | 15 | Describe any methods used to assess certainty (or confidence) in the body of evidence for an outcome | Not Applicable |
| RESULTS | |||
| Study selection | 16.a | Describe the results of the search and selection process, from the number of records identified in the search to the number of studies included in the review, ideally using a flow diagram | Scientometric Review Analysis and Systematic Review Analysis |
| 16.b | Cite studies that might appear to meet the inclusion criteria, but which were excluded, and explain why they were excluded | Scientometric Review Analysis and Systematic Review Analysis | |
| Study characteristics | 17 | Cite each included study and present its characteristics. | Scientometric Review Analysis and Systematic Review Analysis |
| Risk of bias in studies | 18 | Present assessments of risk of bias for each included study. | Not Applicable |
| Results of individual studies | 19 | For all outcomes, present, for each study: (a) summary statistics for each group (where appropriate) and (b) an effect estimate and its precision (e.g., confidence/credible interval), ideally using structured tables or plots. | Scientometric Review Analysis and Systematic Review Analysis |
| Results of syntheses | 20.a | For each synthesis, briefly summarize the characteristics and risk of bias among contributing studies. | Not Applicable |
| 20.b | Present results of all statistical syntheses conducted. If meta-analysis was done, present for each the summary estimate and its precision (e.g., confidence/credible interval) and measures of statistical heterogeneity. If comparing groups, describe the direction of the effect. | Scientometric Review Analysis and Systematic Review Analysis | |
| 20.c | Present results of all investigations of possible causes of heterogeneity among study results. | Scientometric Review Analysis and Systematic Review Analysis | |
| 20.d | Present results of all sensitivity analyses conducted to assess the robustness of the synthesized results | Not Applicable | |
| Reporting biases | 21 | Present assessments of risk of bias due to missing results (arising from reporting biases) for each synthesis assessed | Not Applicable |
| Certainty of evidence | 22 | Present assessments of certainty (or confidence) in the body of evidence for each outcome assessed | Not Applicable |
| DISCUSSION | |||
| Discussion | 23.a | Provide a general interpretation of the results in the context of other evidence | Critical Discussion |
| 23.b | Discuss any limitations of the evidence included in the review | Conclusions | |
| 23.c | Discuss any limitations of the review processes used | Conclusions | |
| 23.d | Discuss implications of the results for practice, policy, and future research | Conclusions | |
| OTHER INFORMATION | |||
| Registration and protocol | 24.a | Provide registration information for the review, including register name and registration number, or state that the review was not registered. | Not applicable |
| 24.b | Indicate where the review protocol can be accessed, or state that a protocol was not prepared. | Not applicable | |
| 24.c | Describe and explain any amendments to information provided at registration or in the protocol. | Not applicable | |
| Support | 25 | Describe sources of financial or non-financial support for the review, and the role of the funders or sponsors in the review. | Funding statement (p. 69) |
| Competing interests | 26 | Declare any competing interests of review authors. | Conflict of Interest statement (p. 69) |
| Availability of data, code and other materials | 27 | Report which of the following are publicly available and where they can be found: template data collection forms; data extracted from included studies; data used for all analyses; analytic code; any other materials used in the review. | Data Availability Statements (p. 69) |

References
- Durango-Cohen, P.L.; Madanat, S.M. Introduction to Special Issue on Transportation Infrastructure Management. EURO J. Transp. Logist. 2015, 4, 1–4. [Google Scholar] [CrossRef]
- Abdelkader, E.M.; Zayed, T.; Faris, N. Synthesized Evaluation of Reinforced Concrete Bridge Defects, Their Non-Destructive Inspection and Analysis Methods: A Systematic Review and Bibliometric Analysis of the Past Three Decades. Buildings 2023, 13, 800. [Google Scholar] [CrossRef]
- Abdelkhalek, S.; Zayed, T. Optimizing the Inspection Schedule for Bridge Networks. Can. J. Civil. Eng. 2023, 50, 721–736. [Google Scholar] [CrossRef]
- Mahdi, I.M.; Khalil, A.H.; Mahdi, H.A.; Mansour, D.M.M. Decision Support System for Optimal Bridge’ Maintenance. Int. J. Constr. Manag. 2022, 22, 342–356. [Google Scholar] [CrossRef]
- Ibrahim, A.; Abdelkhalek, S.; Zayed, T.; Qureshi, A.H.; Mohammed Abdelkader, E. A Comprehensive Review of the Key Deterioration Factors of Concrete Bridge Decks. Buildings 2024, 14, 3425. [Google Scholar] [CrossRef]
- Taherkhani, A.; Mo, W.; Bell, E.; Han, F. Towards Equitable Infrastructure Asset Management: Scour Maintenance Strategy for Aging Bridge Systems in Flood-Prone Zones Using Deep Reinforcement Learning. Sustain. Cities Soc. 2024, 114, 105792. [Google Scholar] [CrossRef]
- Federal Highway Administration (FHWA) Bridges & Structures. Bridge Condition by Highway System 2020. Available online: https://www.fhwa.dot.gov/bridge/nbi/no10/condition19.cfm (accessed on 2 May 2025).
- American Society of Civil Engineers (ASCE) 2025 Report Card for America’s Infrastructure. Available online: https://infrastructurereportcard.org/wp-content/uploads/2025/03/Bridges.pdf (accessed on 2 June 2025).
- Federation of Canadian Municipalities (FCM) The 2019 Canada Infrastructure Report Card. Available online: https://cnam.ca/2019-canadian-infrastructure-report-card/ (accessed on 2 May 2025).
- Wang, Y.; Wang, Y.; Ni, J.; Zhang, H. Reliability-Centric Maintenance Planning for Bridge Infrastructure: A Novel Method Based on Improved Electric Fish Optimization. Buildings 2024, 14, 3583. [Google Scholar] [CrossRef]
- Abdelkader, E.M.; Moselhi, O.; Marzouk, M.; Zayed, T. An Exponential Chaotic Differential Evolution Algorithm for Optimizing Bridge Maintenance Plans. Autom. Constr. 2022, 134, 104107. [Google Scholar] [CrossRef]
- Alsharqawi, M.; Abu Dabous, S.; Zayed, T.; Hamdan, S. Budget Optimization of Concrete Bridge Decks under Performance-Based Contract Settings. J. Constr. Eng. Manag. 2021, 147, 04021040. [Google Scholar] [CrossRef]
- Miyamoto, A.; Kawamura, K.; Nakamura, H. Development of a Bridge Management System for Existing Bridges. Adv. Eng. Softw. 2001, 32, 821–833. [Google Scholar] [CrossRef]
- Allah, B.Z.; Stipanovic, I.; Doree, A.G. Multi-Year Maintenance Planning Using Multi-Attribute Utility Theory and Genetic Algorithms. Eur. Transp. Res. Rev. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Miyamoto, A.; Kawamura, K.; Nakamura, H. Bridge Management System and Maintenance Optimization for Existing Bridges. Comput. Aided Civil. Infrastruct. Eng. 2000, 15, 45–55. [Google Scholar] [CrossRef]
- Orcesia, A.D.; Cremona, C.F. Optimal Maintenance Strategies for Bridge Networks Using the Supply and Demand Approach. Struct. Infrastruct. Eng. 2011, 7, 765–781. [Google Scholar] [CrossRef]
- van Eck, N.J.; Waltman, L. Software Survey: VOSviewer, a Computer Program for Bibliometric Mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 Statement: An Updated Guideline for Reporting Systematic Reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Moher, D. Updating Guidance for Reporting Systematic Reviews: Development of the PRISMA 2020 Statement. J. Clin. Epidemiol. 2021, 134, 103–112. [Google Scholar] [CrossRef] [PubMed]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. BMJ 2009, 339, 332–336. [Google Scholar] [CrossRef]
- Al-Ashmori, A.; Basri, S.B.; Dominic, P.D.D.; Capretz, L.F.; Muneer, A.; Balogun, A.O.; Gilal, A.R.; Ali, R.F. Classifications of Sustainable Factors in Blockchain Adoption: A Literature Review and Bibliometric Analysis. Sustainability 2022, 14, 5176. [Google Scholar] [CrossRef]
- Liu, Y.; He, H. Scientometrics of Scientometrics Based on Web of Science Core Collection Data between 1992 and 2020. Information 2023, 14, 637. [Google Scholar] [CrossRef]
- Cretu, D.M.; Grosseck, G. A Bibliometric Analysis of Romanian Educational Research in Web of Science: Trends, Challenges, and Opportunities for Global Integration. Educ. Sci. 2025, 15, 358. [Google Scholar] [CrossRef]
- Kalogeraki, M.; Antoniou, F. Claim Management and Dispute Resolution in the Construction Industry: Current Research Trends Using Novel Technologies. Buildings 2024, 14, 967. [Google Scholar] [CrossRef]
- Lancho-Barrantes, B.S.; Cantu-Ortiz, F.J. Quantifying the Publication Preferences of Leading Research Universities. Scientometrics 2021, 126, 2269–2310. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, A.; Zayed, T.; Lafhaj, Z. Enhancing Construction Performance: A Critical Review of Performance Measurement Practices at the Project Level. Buildings 2024, 14, 1988. [Google Scholar] [CrossRef]
- Farouk, A.M.; Rahman, R.A. Integrated Applications of Building Information Modeling in Project Cost Management: A Systematic Review. J. Eng. Des. Technol. 2025, 23, 287–305. [Google Scholar] [CrossRef]
- Prabhakaran, A.; Mahamadu, A.M.; Mahdjoubi, L. Understanding the Challenges of Immersive Technology Use in the Architecture and Construction Industry: A Systematic Review. Autom. Constr. 2022, 137, 104228. [Google Scholar] [CrossRef]
- Masood, R.; Lim, J.B.P.; González, V.A.; Roy, K.; Khan, K.I.A. A Systematic Review on Supply Chain Management in Prefabricated House-Building Research. Buildings 2022, 12, 40. [Google Scholar] [CrossRef]
- Aria, M.; Cuccurullo, C. Bibliometrix: An R-Tool for Comprehensive Science Mapping Analysis. J. Informetr. 2017, 11, 959–975. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Liu, M. Maintenance and Management of Civil Infrastructure Based on Condition, Safety, Optimization, and Life-Cycle Cost. Struct. Infrastruct. Eng. 2007, 18, 96–108. [Google Scholar] [CrossRef]
- Dan Frangopol, B.M.; Lin, K.-Y.; Estes, A.C. Life-Cycle Cost Design Of Deteriorating Structures. J. Struct. Eng. 1997, 123, 1390–1401. [Google Scholar] [CrossRef]
- Allen Estes, B.C.; Frangopol, D.M. Repair Optimization of Highway Bridges Using System Reliability Approach. J. Struct. Eng. 1999, 125, 766–775. [Google Scholar] [CrossRef]
- Phung, M.D.; Quach, C.H.; Dinh, T.H.; Ha, Q. Enhanced Discrete Particle Swarm Optimization Path Planning for UAV Vision-Based Surface Inspection. Autom. Constr. 2017, 81, 25–33. [Google Scholar] [CrossRef]
- Kong, J.S.; Frangopol, D.M. Life-Cycle Reliability-Based Maintenance Cost Optimization of Deteriorating Structures with Emphasis on Bridges. J. Struct. Eng. 2003, 129, 818–828. [Google Scholar] [CrossRef]
- Bocchini, P.; Frangopol, D.M. Optimal Resilience- and Cost-Based Postdisaster Intervention Prioritization for Bridges along a Highway Segment. J. Bridge Eng. 2012, 17, 117–129. [Google Scholar] [CrossRef]
- Morcous, G.; Lounis, Z. Maintenance Optimization of Infrastructure Networks Using Genetic Algorithms. Autom. Constr. 2005, 14, 129–142. [Google Scholar] [CrossRef]
- Okasha, N.M.; Frangopol, D.M. Lifetime-Oriented Multi-Objective Optimization of Structural Maintenance Considering System Reliability, Redundancy and Life-Cycle Cost Using GA. Struct. Saf. 2009, 31, 460–474. [Google Scholar] [CrossRef]
- Van Noortwijk, J.M.; Frangopol, D.M. Two Probabilistic Life-Cycle Maintenance Models for Deteriorating Civil Infrastructures. Probabilistic Eng. Mech. 2004, 19, 345–359. [Google Scholar] [CrossRef]
- Lounis, Z.; McAllister, T.P. Risk-Based Decision Making for Sustainable and Resilient Infrastructure Systems. J. Struct. Eng. 2016, 142, F4016005. [Google Scholar] [CrossRef]
- Bradford, S.C. Sources of Information on Specific Subjects. Engineering 1934, 137, 85–86. [Google Scholar] [CrossRef]
- Yau, N.J.; Liao, H.K.; Tabor, J.M.M.; Jallow, M. An AHP-Based Prioritization Model for Bridge Maintenance after Natural Disasters. J. Chin. Inst. Eng. Trans. Chin. Inst. Eng. Ser. A 2023, 46, 255–266. [Google Scholar] [CrossRef]
- Rashidi, M.; Samali, B.; Sharafi, P. A New Model for Bridge Management: Part B: Decision Support System for Remediation Planning. Aust. J. Civil. Eng. 2016, 14, 46–53. [Google Scholar] [CrossRef]
- Abu Dabous, S.; Alkass, S. Decision Support Method for Multi-Criteria Selection of Bridge Rehabilitation Strategy. Constr. Manag. Econ. 2008, 26, 883–893. [Google Scholar] [CrossRef]
- Navarro, I.J.; Martí, J.V.; Yepes, V. Analytic Network Process-Based Sustainability Life Cycle Assessment of Concrete Bridges in Coastal Regions. Sustainability 2022, 14, 688. [Google Scholar] [CrossRef]
- Contreras-Nieto, C.; Shan, Y.; Lewis, P.; Hartell, J.A. Bridge Maintenance Prioritization Using Analytic Hierarchy Process and Fusion Tables. Autom. Constr. 2019, 101, 99–110. [Google Scholar] [CrossRef]
- Salem, O.M.; Miller, R.A.; Deshpande, A.S.; Arurkar, T.P. Multi-Criteria Decision-Making System for Selecting an Effective Plan for Bridge Rehabilitation. Struct. Infrastruct. Eng. 2013, 9, 806–816. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q.; Ren, Y.; Zhao, D.Y.; Zhang, D.Y.; Sun, H. Bin Condition Evaluation of Suspension Bridges for Maintenance, Repair and Rehabilitation: A Comprehensive Framework. Struct. Infrastruct. Eng. 2019, 15, 555–567. [Google Scholar] [CrossRef]
- Wakchaure, S.S.; Jha, K.N. Determination of Bridge Health Index Using Analytical Hierarchy Process. Constr. Manag. Econ. 2012, 30, 133–149. [Google Scholar] [CrossRef]
- Alshibani, A.; Abu Saa, A.S.; Hassanain, M.A.; Bubshait, A.; Shash, A. Decision Support Model for Allocating Maintenance Budgets for Bridges. Appl. Sci. 2023, 13, 9679. [Google Scholar] [CrossRef]
- Rashidi, M.; Ghodrat, M.; Samali, B.; Kendall, B.; Zhang, C. Remedial Modelling of Steel Bridges through Application of Analytical Hierarchy Process (AHP). Appl. Sci. 2017, 7, 168. [Google Scholar] [CrossRef]
- Dabous, S.A.; Alkass, S. Managing Bridge Infrastructure under Budget Constraints: A Decision Support Methodology. Can. J. Civil. Eng. 2011, 38, 1227–1237. [Google Scholar] [CrossRef]
- Dabous, S.A.; Alkass, S. A Multi-Attribute Ranking Method for Bridge Management. Eng. Constr. Archit. Manag. 2010, 17, 282–291. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Sustainability Assessment of Concrete Bridge Deck Designs in Coastal Environments Using Neutrosophic Criteria Weights. Struct. Infrastruct. Eng. 2020, 16, 949–967. [Google Scholar] [CrossRef]
- Gokasar, I.; Deveci, M.; Kalan, O. CO2 Emission Based Prioritization of Bridge Maintenance Projects Using Neutrosophic Fuzzy Sets Based Decision Making Approach. Res. Transp. Econ. 2022, 91, 101029. [Google Scholar] [CrossRef]
- Ors, D.M.; Ebid, A.M.; Mahdi, I.M.; Mahdi, H.A. Decision Support System to Select the Optimum Construction Techniques for Bridge Piers. Ain Shams Eng. J. 2023, 14, 102152. [Google Scholar] [CrossRef]
- Das, R.; Nakano, M. A Multi-Criteria Decision-Making Model Using Socio-Technical Attributes for Transportation Bridge Maintenance Prioritisation. Int. J. Constr. Manag. 2023, 23, 579–585. [Google Scholar] [CrossRef]
- Lad, V.H.; Patel, D.A.; Chauhan, K.A.; Patel, K.A. Prioritisation of Bridge for Improving Its Resilience Using Multi-Criteria Decision-Making Techniques. Eng. Constr. Archit. Manag. 2024, 31, 2952–2976. [Google Scholar] [CrossRef]
- Gao, Z.; Liang, R.Y.; Xuan, T. VIKOR Method for Ranking Concrete Bridge Repair Projects with Target-Based Criteria. Results Eng. 2019, 3, 100018. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, Z.; Wang, H.; Zhou, S. Gray Relation Analysis for Optimal Selection of Bridge Reinforcement Scheme Based on Fuzzy-AHP Weights. Math. Probl. Eng. 2021, 2021, 8813940. [Google Scholar] [CrossRef]
- Rogulj, K.; Pamuković, J.K.; Antucheviciene, J.; Zavadskas, E.K. Intuitionistic Fuzzy Decision Support Based on EDAS and Grey Relational Degree for Historic Bridges Reconstruction Priority. Soft Comput. 2022, 26, 9419–9444. [Google Scholar] [CrossRef]
- Tabor, J.M.M.; Yau, N.J.; Liao, H.K. Maintenance Prioritisation Framework for Taiwan’s Pedestrian Bridges. Struct. Infrastruct. Eng. 2024, 20, 1500–1514. [Google Scholar] [CrossRef]
- Mohamadiazar, N.; Ebrahimian, A.; Azizinamini, A. Equitable Prioritization of Bridge Rehabilitation Projects Using a Spatial Multi-Criteria Decision Support Framework. Transp. Res. Rec. 2024, 2678, 2069–2076. [Google Scholar] [CrossRef]
- Seçer, M.; Saylan, A.A. Evaluation of Corrosion Management Strategies for Steel Truss Bridges Based on Ultimate Load Capacity and Lifetime Direct Cost. Struct. Infrastruct. Eng. 2025, 21, 675–694. [Google Scholar] [CrossRef]
- Salmaninezhad, M.; Jazayeri Moghaddas, S.M. A Multi-Attribute Approach to Select the Best Method for Repairing River Bridge Columns. Eng. Constr. Archit. Manag. 2023, 30, 1–18. [Google Scholar] [CrossRef]
- Karaaslan, E.; Bagci, U.; Catbas, N. A Novel Decision Support System for Long-term Management of Bridge Networks. Appl. Sci. 2021, 11, 5928. [Google Scholar] [CrossRef]
- Chakraborty, S.; Datta, H.N.; Kalita, K.; Chakraborty, S. A Narrative Review of Multi-Objective Optimization on the Basis of Ratio Analysis (MOORA) Method in Decision Making. Opsearch 2023, 60, 1844–1887. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of Objective Weights Using a New Method Based on the Removal Effects of Criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M. Assessment of Distribution Center Locations Using a Multi-Expert Subjective–Objective Decision-Making Approach. Sci. Rep. 2021, 11, 19461. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Tomczyk, T.; Gandor, M.; Sałabun, W. Subjective Weight Determination Methods in Multi-Criteria Decision-Making: A Systematic Review. Procedia Comput. Sci. 2024, 246, 5396–5407. [Google Scholar] [CrossRef]
- Zakeri, S.; Chatterjee, P.; Konstantas, D.; Ecer, F. A Decision Analysis Model for Material Selection Using Simple Ranking Process. Sci. Rep. 2023, 13, 8631. [Google Scholar] [CrossRef]
- Altıntaş, F.F. A Novel Approach To Measuring Criterion Weights In Multiple Criteria Decision Making: Cubic Effect-Based Measurement (CEBM). Nicel Bilim. Derg. 2023, 5, 151–195. [Google Scholar] [CrossRef]
- Ayan, B.; Abacıoğlu, S.; Basilio, M.P. A Comprehensive Review of the Novel Weighting Methods for Multi-Criteria Decision-Making. Information 2023, 14, 285. [Google Scholar] [CrossRef]
- Stoilova, S. A New Aggregated Multi-Criteria Approach for Evaluation of the Autonomous Metro Systems’ Performance in the European Countries. Symmetry 2022, 14, 2025. [Google Scholar] [CrossRef]
- Torbacki, W. Achieving Sustainable Mobility in the Szczecin Metropolitan Area in the Post-COVID-19 Era: The DEMATEL and PROMETHEE II Approach. Sustainability 2021, 13, 2672. [Google Scholar] [CrossRef]
- Machado, R.H.C.; Conceição, S.V.; Pelissari, R.; Amor, S.B.; Resende, T.L. A Multiple Criteria Framework to Assess Learning Methodologies. Think. Ski. Creat. 2023, 48, 101290. [Google Scholar] [CrossRef]
- Cinelli, M.; Kadziński, M.; Gonzalez, M.; Słowiński, R. How to Support the Application of Multiple Criteria Decision Analysis? Let Us Start with a Comprehensive Taxonomy. Omega 2020, 96, 102261. [Google Scholar] [CrossRef]
- Li, Y.; Deng, J.; Wang, Y.; Liu, H.; Peng, L.; Zhang, H.; Liang, Y.; Feng, Q. The Condition Evaluation of Bridges Based on Fuzzy BWM and Fuzzy Comprehensive Evaluation. Appl. Sci. 2025, 15, 2904. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rashidi, M.; Yu, Y.; Samali, B. Integration of TLS-Derived Bridge Information Modeling (BrIM) with a Decision Support System (DSS) for Digital Twinning and Asset Management of Bridge Infrastructures. Comput. Ind. 2023, 147, 103881. [Google Scholar] [CrossRef]
- Rogulj, K.; Pamuković, J.K.; Ivić, M. Hybrid Mcdm Based on Vikor and Cross Entropy under Rough Neutrosophic Set Theory. Mathematics 2021, 9, 1334. [Google Scholar] [CrossRef]
- Darban, S.; Tehrani, H.G.; Karballaeezadeh, N.; Mosavi, A. Application of Analytical Hierarchy Process for Structural Health Monitoring and Prioritizing Concrete Bridges in Iran. Appl. Sci. 2021, 11, 8060. [Google Scholar] [CrossRef]
- Ikpong, A.; Chandra, A.; Bagchi, A. Alternative to Ahp Approach to Criteria Weight Estimation in Highway Bridge Management. Can. J. Civil. Eng. 2021, 48, 1181–1191. [Google Scholar] [CrossRef]
- Abdelkader, E.M.; Marzouk, M.; Zayed, T. An Invasive Weed Optimization-Based Fuzzy Decision-Making Framework for Bridge Intervention Prioritization in Element and Network Levels. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 1189–1246. [Google Scholar] [CrossRef]
- Allah Bukhsh, Z.; Stipanovic, I.; Klanker, G.; O’ Connor, A.; Doree, A.G. Network Level Bridges Maintenance Planning Using Multi-Attribute Utility Theory. Struct. Infrastruct. Eng. 2019, 15, 872–885. [Google Scholar] [CrossRef]
- Bukhsh, Z.A.; Stipanovic, I.; Palic, S.S.; Klanker, G. Robustness of the Multi-Attribute Utility Model for Bridge Maintenance Planning. Balt. J. Road Bridge Eng. 2018, 13, 404–415. [Google Scholar] [CrossRef]
- Markiz, N.; Jrade, A.; Professor, A. Integrating Fuzzy-Logic Decision Support With A Bridge Information Management System (Brims) At The Conceptual Stage Of Bridge Design. J. Inf. Technol. Constr. 2018, 23, 92–121. [Google Scholar]
- Sabatino, S.; Frangopol, D.M.; Dong, Y. Sustainability-Informed Maintenance Optimization of Highway Bridges Considering Multi-Attribute Utility and Risk Attitude. Eng. Struct. 2015, 102, 310–321. [Google Scholar] [CrossRef]
- Augeri, M.G.; Colombrita, R.; Greco, S.; Sapienza, P. Dominance-Based Rough Set Approach To Network Bridge Management. Balt. J. Road Bridge Eng. 2014, 9, 31–42. [Google Scholar] [CrossRef]
- Sahrapeyma, A.; Hosseini, A. Strategic Planning for the National Bridge Stock of Iran. Civil. Eng. Infrastruct. J. 2013, 46, 51–68. [Google Scholar] [CrossRef]
- Wakchaure, S.S.; Jha, K.N. Prioritization of Bridges for Maintenance Planning Using Data Envelopment Analysis. Constr. Manag. Econ. 2011, 29, 957–968. [Google Scholar] [CrossRef]
- Sasmal, S.; Ramanjaneyulu, K. Condition Evaluation of Existing Reinforced Concrete Bridges Using Fuzzy Based Analytic Hierarchy Approach. Expert. Syst. Appl. 2008, 35, 1430–1443. [Google Scholar] [CrossRef]
- Saaty, T.L. Making and Validating Complex Decisions with the AHP/ANP. J. Syst. Sci. Syst. Eng. 2005, 14, 1–36. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining Objective Weights in Multiple Criteria Problems: The Critic Method. Comput. Ops Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. A Math. Theory Commun. 1948, 27, 623–656. [Google Scholar]
- Rezaei, J. Best-Worst Multi-Criteria Decision-Making Method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Zavadskas, E.; Kaklauskas, A. Determination of an Efficient Contractor by Using the New Method of Multicriteria Assessment. In The Organization and Management of Construction; Routledge: Oxfordshire, UK, 1996. [Google Scholar]
- Deng, J. Control Problems of Grey Systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of Weighted Aggregated Sum Product Assessment. Elektron. Ir Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Bernard, R. The Outranking Approach and the Foundations of ELECTRE Methods. Theory Decis. 1991, 31, 49–73. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincke, P. Note—A Preference Ranking Organisation Method: (The PROMETHEE Method for Multiple Criteria Decision-Making). Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs. IEEE Trans. Syst. Man. Cybern. 1979, 9, 403. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Multicriteria Planning of Post-Earthquake Sustainable Reconstruction. Comput. Aided Civil. Infrastruct. Eng. 2002, 17, 211–220. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the Efficiency of Decision Making Units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Greco, S.; Matarazzo, B.; Slowinski, R. Rough Approximation by Dominance Relations. Int. J. Intell. Syst. 2002, 17, 153–171. [Google Scholar] [CrossRef]
- Alsharqawi, M.; Zayed, T.; Abu Dabous, S. Integrated Condition Rating and Forecasting Method for Bridge Decks Using Visual Inspection and Ground Penetrating Radar. Autom. Constr. 2018, 89, 135–145. [Google Scholar] [CrossRef]
- Pipinato, A.; Rebelo, C.; Pedrosa, B.; Gervásio, H. Assessment Procedure and Rehabilitation Criteria for Riveted Road Bridges. Struct. Eng. Int. 2020, 30, 109–118. [Google Scholar] [CrossRef]
- Fortin, T.; Dey, P.; Boissonnade, N.; Fafard, M. Life Cycle Cost Assessment of an Existing All-Aluminum Bridge: Comparison of Two Deck Options. Eng. Proc. 2023, 43, 3038. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Wu, Z. Life Cycle Cost Analysis of FRP Cables for Long-Span Cable Supported Bridges. Structures 2020, 25, 24–34. [Google Scholar] [CrossRef]
- Singh, D.; Tiong, R.L.K. Development of Life Cycle Costing Framework for Highway Bridges in Myanmar. Int. J. Proj. Manag. 2005, 23, 37–44. [Google Scholar] [CrossRef]
- Kumar, R.; Gardoni, P. Renewal Theory-Based Life-Cycle Analysis of Deteriorating Engineering Systems. Struct. Saf. 2014, 50, 94–102. [Google Scholar] [CrossRef]
- Binder, F. Life Cycle Costs of Selected Concrete Repair Methods Demonstrated on Chloride Contaminated Columns. In Proceedings of the 11th International Probabilistic Workshop, Brno, Czech Republic, 6–8 November 2013. [Google Scholar]
- Kong, J.S.; Asce, M.; Frangopol, D.M.; Asce, F. Evaluation of Expected Life-Cycle Maintenance Cost of Deteriorating Structures. J. Struct. Eng. 2003, 129, 682–691. [Google Scholar] [CrossRef]
- Zhou, Z.; Alcalá, J.; Kripka, M.; Yepes, V. Life Cycle Assessment of Bridges Using Bayesian Networks and Fuzzy Mathematics. Appl. Sci. 2021, 11, 4916. [Google Scholar] [CrossRef]
- Padgett, J.E.; Vishnu, N. Interaction of Life-Cycle Phases in a Probabilistic Life-Cycle Framework for Civil Infrastructure System Sustainability. Sustain. Resilient Infrastruct. 2020, 5, 289–310. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Martí, J.V.; García-Segura, T.; Yepes, V. Life-Cycle Assessment: A Comparison between Two Optimal Post-Tensioned Concrete Box-Girder Road Bridges. Sustainability 2017, 9, 1864. [Google Scholar] [CrossRef]
- Xia, B.; Xiao, J.; Ding, T.; Guan, X.; Chen, J. Life Cycle Assessment of Carbon Emissions for Bridge Renewal Decision and Its Application for Maogang Bridge in Shanghai. J. Clean. Prod. 2024, 448, 141724. [Google Scholar] [CrossRef]
- Zhang, X.F.; Qian, Z.D.; Gao, H. Life-Cycle Environmental Impact Assessment of Steel Bridge Deck Pavement. In Developments in International Bridge Engineering. Springer Tracts on Transportation and Traffic; Springer: Cham, Switzerland, 2021; Volume 17. [Google Scholar]
- Wang, Z.; Dong, Y.; Asce, A.M.; Jin, W. Life-Cycle Cost Analysis of Deteriorating Civil Infrastructures Incorporating Social Sustainability. J. Infrastruct. Syst. 2021, 27, 04018102. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Life Cycle Cost Assessment of Preventive Strategies Applied to Prestressed Concrete Bridges Exposed to Chlorides. Sustainability 2018, 10, 845. [Google Scholar] [CrossRef]
- Thoft-Christensen, P. Infrastructures and Life-Cycle Cost-Benefit Analysis. Struct. Infrastruct. Eng. 2012, 8, 507–516. [Google Scholar] [CrossRef]
- Thoft-Christensen, P. Life-Cycle Cost-Benefit (LCCB) Analysis of Bridges from a User and Social Point of View. Struct. Infrastruct. Eng. 2009, 5, 49–57. [Google Scholar] [CrossRef]
- Soliman, M.; Frangopol, D.M. Life-Cycle Cost Evaluation of Conventional and Corrosion-Resistant Steel for Bridges. J. Bridge Eng. 2015, 20, 06014005. [Google Scholar] [CrossRef]
- Malik, M.; Amor, B. Optimizing Bridge Rehabilitation: A Life Cycle Assessment and Cost Analysis of Conventional and UHPC Overlays. In Smart & Sustainable Infrastructure: Building a Greener Tomorrow; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Sacconi, S.; Venanzi, I.; Ierimonti, L.; Torti, M.; Laflamme, S.; Ubertini, F. Fatigue Reliability Assessment and Life-Cycle Cost Analysis of Roadway Bridges Equipped with Weigh-in-Motion Systems. Struct. Infrastruct. Eng. 2023, 19, 1317–1333. [Google Scholar] [CrossRef]
- Torti, M.; Venanzi, I.; Laflamme, S.; Ubertini, F. Life-Cycle Management Cost Analysis of Transportation Bridges Equipped with Seismic Structural Health Monitoring Systems. Struct. Health Monit. 2022, 21, 100–117. [Google Scholar] [CrossRef]
- Kere, K.J.; Huang, Q. Life-Cycle Cost Comparison of Corrosion Management Strategies for Steel Bridges. J. Bridge Eng. 2019, 24, 04019007. [Google Scholar] [CrossRef]
- Nielsen, D.; Raman, D.; Chattopadhyay, G. Life Cycle Management for Railway Bridge Assets. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2013, 227, 570–581. [Google Scholar] [CrossRef]
- Stewart, M.G.; Estes, A.C.; Frangopol, D.M. Bridge Deck Replacement for Minimum Expected Cost Under Multiple Reliability Constraints. J. Struct. Eng. 2004, 130, 1414–1419. [Google Scholar] [CrossRef]
- Petcherdchoo, A. Probabilistic Model for Single and Multiple Action Costs in Maintaining Both Condition and Safety of Deteriorating Reinforced Concrete Bridges. Case Stud. Constr. Mater. 2023, 19, e02613. [Google Scholar] [CrossRef]
- Leiva-Maldonado, S.; Bowman, M.D.; Gomez, D. Life-Cycle Cost Profiles Selection for Different Superstructure Bridge Types. Structures 2023, 54, 1–13. [Google Scholar] [CrossRef]
- Escobedo, D.D.L.; Torres-Acosta, A. Bridge Preventive Maintenance Based on Life-Cycle Assessment. Rev. Técnica Fac. Ing Univ. Zulia 2010, 33, 3–10. [Google Scholar]
- Crisan, A.; Juravle, A.; Bancila, R. A BIM-Enabled Workflow for the Rehabilitation of Heritage Steel Bridges. Appl. Sci. 2025, 15, 677. [Google Scholar] [CrossRef]
- Gao, Y.; Xiong, G.; Hu, Z.; Chai, C.; Li, H. Bridge Digital Twin for Practical Bridge Operation and Maintenance by Integrating GIS and BIM. Buildings 2024, 14, 3731. [Google Scholar] [CrossRef]
- Franciosi, M.; Kasser, M.; Viviani, M. Digital Twins in Bridge Engineering for Streamlined Maintenance and Enhanced Sustainability. Autom. Constr. 2024, 168, 105834. [Google Scholar] [CrossRef]
- Heng, J.; Dong, Y.; Lai, L.; Zhou, Z.; Frangopol, D.M. Digital Twins-Boosted Intelligent Maintenance of Ageing Bridge Hangers Exposed to Coupled Corrosion–Fatigue Deterioration. Autom. Constr. 2024, 167, 105697. [Google Scholar] [CrossRef]
- Abdelkhalek, S.; Zayed, T.; Eltoukhy, A.E.E. Multifaceted Optimization for Bridge Inspection Process. J. Constr. Eng. Manag. 2025, 151, 04025034. [Google Scholar] [CrossRef]
- Mohamad, M.; Tran, D.Q. Risk-Based Prioritization Approach to Construction Inspections for Transportation Projects. J. Constr. Eng. Manag. 2021, 147, 04020150. [Google Scholar] [CrossRef]
- Kwon, K.; Park, K.T.; Jung, K.S.; Kim, S. Efficient Reliability-Based Inspection Planning for Deteriorating Bridges Using Extrapolation Approaches. Appl. Sci. 2022, 12, 744. [Google Scholar] [CrossRef]
- Vereecken, E.; Botte, W.; Lombaert, G.; Caspeele, R. Bayesian Decision Analysis for the Optimization of Inspection and Repair of Spatially Degrading Concrete Structures. Eng. Struct. 2020, 220, 111028. [Google Scholar] [CrossRef]
- Oyegbile, O.B.; Chorzepa, M.G. Co-Active Prioritization by Means of Contingency Tables for Analyzing Element-Level Bridge Inspection Results and Optimizing Returns. Infrastructures 2020, 5, 13. [Google Scholar] [CrossRef]
- Washer, G.; Connor, R.; Nasrollahi, M.; Provines, J. New Framework for Risk-Based Inspection of Highway Bridges. J. Bridge Eng. 2016, 21, 04015077. [Google Scholar] [CrossRef]
- Kim, S.; Frangopol, D.M. Inspection and Monitoring Planning for RC Structures Based on Minimization of Expected Damage Detection Delay. Probabilistic Eng. Mech. 2011, 26, 308–320. [Google Scholar] [CrossRef]
- Sun, T.; Vatn, J. A Phase-Type Maintenance Model Considering Condition-Based Inspections and Maintenance Delays. Reliab. Eng. Syst. Saf. 2024, 243, 109836. [Google Scholar] [CrossRef]
- Jiang, F.; Ding, Y.; Song, Y.; Geng, F.; Wang, Z. Digital Twin-Driven Framework for Fatigue Lifecycle Management of Steel Bridges. Struct. Infrastruct. Eng. 2023, 19, 1826–1846. [Google Scholar] [CrossRef]
- Cheng, M.; Frangopol, D.M. Optimal Load Rating-Based Inspection Planning of Corroded Steel Girders Using Markov Decision Process. Probabilistic Eng. Mech. 2021, 66, 103160. [Google Scholar] [CrossRef]
- Anne Mette Sommerfl Andrzej Nowak, B.S.; Thoft-Christensen, P. Probability-Based Bridge Inspection Strategy. J. Struct. Eng. 1993, 119, 3520–3536. [Google Scholar]
- Orcesi, A.D.; Frangopol, D.M. Use of Lifetime Functions in the Optimization of Nondestructive Inspection Strategies for Bridges. J. Struct. Eng. 2011, 137, 531–539. [Google Scholar] [CrossRef]
- Chung, H.-Y.; Manuel, L.; Frank, K.H. Optimal Inspection Scheduling of Steel Bridges Using Nondestructive Testing Techniques. J. Bridge Eng. 2006, 11, 305–319. [Google Scholar] [CrossRef]
- Soliman, M.; Frangopol, D.M.; Kim, S. Probabilistic Optimum Inspection Planning of Steel Bridges with Multiple Fatigue Sensitive Details. Eng. Struct. 2013, 49, 996–1006. [Google Scholar] [CrossRef]
- Crémona, C.; Lukic’, M.L. Probability-Based Assessment and Maintenance of Welded Joints Damaged by Fatigue. Nucl. Eng. Des. 1998, 182, 253–266. [Google Scholar] [CrossRef]
- Wu, Z.; Zeng, J.; Hu, Z.; Todd, M.D. Optimization of Unmanned Aerial Vehicle Inspection Strategy for Infrastructure Based on Model-Enabled Diagnostics and Prognostics. Mech. Syst. Signal Process 2023, 204, 110841. [Google Scholar] [CrossRef]
- Yang, D.Y.; Frangopol, D.M. Risk-Based Inspection Planning of Deteriorating Structures. Struct. Infrastruct. Eng. 2021, 18, 109–128. [Google Scholar] [CrossRef]
- Sheils, E.; O’Connor, A.; Schoefs, F.; Breysse, D. Investigation of the Effect of the Quality of Inspection Techniques on the Optimal Inspection Interval for Structures. Struct. Infrastruct. Eng. 2012, 8, 557–568. [Google Scholar] [CrossRef]
- Sein, S.; Matos, J.C.; Idnurm, J.; Kiisa, M.; Coelho, M. Rc Bridge Management Optimisation Considering Condition Assessment Uncertainties. Proc. Est. Acad. Sci. 2021, 70, 172–189. [Google Scholar] [CrossRef]
- Su, D.; Liu, Y.; Li, X.; Cao, Z. Study on Optimization of Inspection Mechanism of Concrete Beam Bridge. PLoS ONE 2021, 16, e0256028. [Google Scholar] [CrossRef]
- Huang, S.H.; Huang, Y.H.; Blazquez, C.A.; Paredes-Belmar, G. Application of the Ant Colony Optimization in the Resolution of the Bridge Inspection Routing Problem. Appl. Soft Comput. J. 2018, 65, 443–461. [Google Scholar] [CrossRef]
- Shi, X.; Zhao, B.; Yao, Y.; Wang, F. Prediction Methods for Routine Maintenance Costs of a Reinforced Concrete Beam Bridge Based on Panel Data. Adv. Civil. Eng. 2019, 2019, 5409802. [Google Scholar] [CrossRef]
- Gui, C.; Zhang, J.; Lei, J.; Hou, Y.; Zhang, Y.; Qian, Z. A Comprehensive Evaluation Algorithm for Project-Level Bridge Maintenance Decision-Making. J. Clean. Prod. 2021, 289, 125713. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Chiu, Y.F.; Chiu, C.K.; Prayogo, D.; Wu, Y.W.; Hsu, Z.L.; Lin, C.H. Risk-Based Maintenance Strategy for Deteriorating Bridges Using a Hybrid Computational Intelligence Technique: A Case Study. Struct. Infrastruct. Eng. 2019, 15, 334–350. [Google Scholar] [CrossRef]
- Asghari, V.; Hsu, S.-C.; Wei, H.-H. Expediting Life Cycle Cost Analysis of Infrastructure Assets Under Multiple Uncertainties by Deep Neural Networks. J. Manag. Eng. 2021, 37, 04021059. [Google Scholar] [CrossRef]
- Allah Bukhsh, Z.; Stipanovic, I.; Saeed, A.; Doree, A.G. Maintenance Intervention Predictions Using Entity-Embedding Neural Networks. Autom. Constr. 2020, 116, 103202. [Google Scholar] [CrossRef]
- Chen, J.H.; Su, M.C.; Lin, S.K.; Lin, W.J.; Gheisari, M. Smart Bridge Maintenance Using Cluster Merging Algorithm Based on Self-Organizing Map Optimization. Autom. Constr. 2023, 152, 104913. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, B. Performance Life Cost-Based Maintenance Strategy Optimization for Reinforced Concrete Girder Bridges. J. Bridge Eng. 2013, 18, 172–178. [Google Scholar] [CrossRef]
- Estes, A.C.; Frangopol, D.M. Minimum Expected Cost-Oriented Optimal Maintenance Planning for Deteriorating Structures: Application to Concrete Bridge Decks. Reliab. Eng. Syst. Saf. 2001, 73, 281–291. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Abd, A.O.; Halim, E.; Mohamed, H.A. Bridge Management by Dynamic Programming and Neural Networks. Can. J. Civil. Eng. 1996, 23, 1064–1069. [Google Scholar] [CrossRef]
- Moghaddam, K.S.; Usher, J.S. Preventive maintenance and replacement scheduling for repairable and maintainable systems using dynamic programming. Comput. Ind. Eng. 2011, 60, 654–665. [Google Scholar] [CrossRef]
- Xu, G.; Guo, F. Sustainability-Oriented Maintenance Management of Highway Bridge Networks Based on Q-Learning. Sustain. Cities Soc. 2022, 81, 103855. [Google Scholar] [CrossRef]
- Wei, S.; Bao, Y.; Li, H. Optimal Policy for Structure Maintenance: A Deep Reinforcement Learning Framework. Struct. Saf. 2020, 83, 101906. [Google Scholar] [CrossRef]
- Lei, X.; Xia, Y.; Deng, L.; Sun, L. A Deep Reinforcement Learning Framework for Life-Cycle Maintenance Planning of Regional Deteriorating Bridges Using Inspection Data. Struct. Multidiscip. Optim. 2022, 65, 149. [Google Scholar] [CrossRef]
- Lai, L.; Dong, Y.; Andriotis, C.P.; Wang, A.; Lei, X. Synergetic-Informed Deep Reinforcement Learning for Sustainable Management of Transportation Networks with Large Action Spaces. Autom. Constr. 2024, 160, 105302. [Google Scholar] [CrossRef]
- Yang, D.Y. Adaptive Risk-Based Life-Cycle Management for Large-Scale Structures Using Deep Reinforcement Learning and Surrogate Modeling. J. Eng. Mech. 2022, 148, 04021126. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Yuan, Y.; Yang, D.; Xu, P.; Au, F.T.K. A Multi-Agent Ranking Proximal Policy Optimization Framework for Bridge Network Life-Cycle Maintenance Decision-Making. Struct. Multidiscip. Optim. 2024, 67, 194. [Google Scholar] [CrossRef]
- Zhou, Q.N.; Yuan, Y.; Yang, D.; Zhang, J. An Advanced Multi-Agent Reinforcement Learning Framework of Bridge Maintenance Policy Formulation. Sustainability 2022, 14, 50. [Google Scholar] [CrossRef]
- Asghari, V.; Biglari, A.J.; Hsu, S.-C. Multiagent Reinforcement Learning for Project-Level Intervention Planning under Multiple Uncertainties. J. Manag. Eng. 2023, 39, 04022075. [Google Scholar] [CrossRef]
- Alekseev, A.; Kozhemyakin, L.; Nikitin, V.; Bolshakova, J. Data Preprocessing and Neural Network Architecture Selection Algorithms in Cases of Limited Training Sets—On an Example of Diagnosing Alzheimer’s Disease. Algorithms 2023, 16, 219. [Google Scholar] [CrossRef]
- Ebrahim, K.M.P.; Fares, A.; Faris, N.; Zayed, T. Exploring Time Series Models for Landslide Prediction: A Literature Review. Geoenviron. Disasters 2024, 11, 25. [Google Scholar] [CrossRef]
- Liu, Y.; Pang, B.; Wang, Y.; Shi, C.; Zhang, B.; Guo, X.; Zhou, S.; Wang, J. Life-Cycle Maintenance Strategy of Bridges Considering Reliability, Environment, Cost and Failure Probability CO2 Emission Reduction: A Bridge Study with Climate Scenarios. J. Clean. Prod. 2022, 379, 134740. [Google Scholar] [CrossRef]
- Lei, X.; Dong, Y.; Frangopol, D.M. Sustainable Life-Cycle Maintenance Policymaking for Network-Level Deteriorating Bridges with a Convolutional Autoencoder–Structured Reinforcement Learning Agent. J. Bridge Eng. 2023, 28, 04023063. [Google Scholar] [CrossRef]
- Abedinpourshotorban, H.; Hasan, S.; Shamsuddin, S.M.; As’Sahra, N.F. A Differential-Based Harmony Search Algorithm for the Optimization of Continuous Problems. Expert. Syst. Appl. 2016, 62, 317–332. [Google Scholar] [CrossRef]
- Chatterjee, A.; Kim, E.; Reza, H. Adaptive Dynamic Probabilistic Elitist Ant Colony Optimization in Traveling Salesman Problem. SN Comput. Sci. 2020, 1, 95. [Google Scholar] [CrossRef][Green Version]
- Ribeiro, C.C.; Aloise, D.; Noronha, T.F.; Rocha, C.; Urrutia, S. A Hybrid Heuristic for a Multi-Objective Real-Life Car Sequencing Problem with Painting and Assembly Line Constraints. Eur. J. Oper. Res. 2008, 191, 981–992. [Google Scholar] [CrossRef]
- Dhal, K.G.; Das, A.; Sasmal, B.; Ghosh, T.K.; Sarkar, K. Eagle Strategy in Nature-Inspired Optimization: Theory, Analysis, Applications, and Comparative Study. Arch. Comput. Methods Eng. 2024, 31, 1213–1232. [Google Scholar] [CrossRef]
- Thakur, K.; Kumar, G. Nature Inspired Techniques and Applications in Intrusion Detection Systems: Recent Progress and Updated Perspective. Arch. Comput. Methods Eng. 2021, 28, 2897–2919. [Google Scholar] [CrossRef]
- John, H. Holland Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Storn, R.M.; Price, K. Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yilmaz, S.; Sen, S. Electric Fish Optimization: A New Heuristic Algorithm Inspired by Electrolocation. Neural Comput. Appl. 2020, 32, 11543–11578. [Google Scholar] [CrossRef]
- Mehrabian, A.R.; Lucas, C. A Novel Numerical Optimization Algorithm Inspired from Weed Colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled Frog-Leaping Algorithm: A Memetic Meta-Heuristic for Discrete Optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Woo Geem, Z.; Hoon Kim, J.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 201. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- de Oliveira, M.C.; Delgado, M.R.; Britto, A. A Hybrid Greedy Indicator- and Pareto-Based Many-Objective Evolutionary Algorithm. Appl. Intell. 2021, 51, 4330–4352. [Google Scholar] [CrossRef]
- Herzel, A.; Ruzika, S.; Thielen, C. Approximation Methods for Multiobjective Optimization Problems: A Survey. Inf. J. Comput. 2021, 33, 1284–1299. [Google Scholar] [CrossRef]
- Elbehairy, H.; Elbeltagi, E.; Hegazy, T.; Soudki, K. Comparison of Two Evolutionary Algorithms for Optimization of Bridge Deck Repairs. Comput. Aided Civil. Infrastruct. Eng. 2006, 21, 561–572. [Google Scholar] [CrossRef]
- Xu, Z.; Huang, M. Improving Bridge Expansion and Contraction Installation Replacement Decision System Using Hybrid Chaotic Whale Optimization Algorithm. Appl. Sci. 2021, 11, 6222. [Google Scholar] [CrossRef]
- Li, L.; Mahmoodian, M.; Khaloo, A.; Sun, Z. Risk-Cost Optimized Maintenance Strategy for Steel Bridge Subjected to Deterioration. Sustainability 2022, 14, 436. [Google Scholar] [CrossRef]
- Liu, M.; Frangopol, D.M. Bridge Annual Maintenance Prioritization under Uncertainty by Multiobjective Combinatorial Optimization. Comput. Aided Civil. Infrastruct. Eng. 2005, 20, 343–353. [Google Scholar] [CrossRef]
- Park, K.H.; Lee, S.Y.; Park, C.; Cho, H.N.; Kong, J.S. Safety-Based Multi-Objective Life-Cycle Management System for Steel Box Girder Bridges. Struct. Infrastruct. Eng. 2012, 8, 211–225. [Google Scholar] [CrossRef]
- Jaafaru, H.; Agbelie, B. Bridge Maintenance Planning Framework Using Machine Learning, Multi-Attribute Utility Theory and Evolutionary Optimization Models. Autom. Constr. 2022, 141, 104460. [Google Scholar] [CrossRef]
- Shen, Z.; Liu, Y.; Liu, J.; Liu, Z.; Han, S.; Lan, S. A Decision-Making Method for Bridge Network Maintenance Based on Disease Transmission and NSGA-II. Sustainability 2023, 15, 5007. [Google Scholar] [CrossRef]
- Yang, I.-T.; Hsieh, Y.-M.; Kung, L.-O. Parallel Computing Platform for Multiobjective Simulation Optimization of Bridge Maintenance Planning. J. Constr. Eng. Manag. 2012, 138, 215–226. [Google Scholar] [CrossRef]
- Yang, D.Y.; Frangopol, D.M.; Teng, J.G. Probabilistic Life-Cycle Optimization of Durability-Enhancing Maintenance Actions: Application to FRP Strengthening Planning. Eng. Struct. 2019, 188, 340–349. [Google Scholar] [CrossRef]
- Wei, J.; Chen, G.; Huang, J.; Shou, W.; Wang, J. Resource-Constrained Bridge Maintenance Optimization by Harmonizing Structural Safety and Maintenance Duration. Eng. Struct. 2024, 308, 118024. [Google Scholar] [CrossRef]
- Naji, K.; Santini-Bell, E.; Kwiatkowski, K. Element-Based Multi-Objective Optimization Methodology Supporting a Transportation Asset Management Framework for Bridge Planning and Programming. Transp. Res. Rec. 2022, 2676, 222–241. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Sun, Z.; Wang, B.; Zhao, Y. Dynamic Optimization of Maintenance Strategy for Bridges in Regional Transportation Network through Semi-Markov Processes. Autom. Constr. 2025, 174, 106175. [Google Scholar] [CrossRef]
- Shojaei, F.; Naserabadi, H.D.; Taheri Amiri, M.J. Developing a Fuzzy Bi-Objective Programming and MCDM Model for Bridge Maintenance Strategy Optimization. Sci. Rep. 2024, 14, 13336. [Google Scholar] [CrossRef]
- Katikala, S.; Banerjee, S.; Arora, R.K. Optimized Preventive Maintenance Strategies for Corroded Bridge Columns in Earthquake-Prone Regions. Pract. Period. Struct. Des. Constr. 2022, 27, 04022030. [Google Scholar] [CrossRef]
- Bocchini, P.; Frangopol, D.M. Connectivity-Based Optimal Scheduling for Maintenance of Bridge Networks. J. Eng. Mech. 2013, 139, 760–769. [Google Scholar] [CrossRef]
- Nili, M.H.; Taghaddos, H.; Zahraie, B. Integrating Discrete Event Simulation and Genetic Algorithm Optimization for Bridge Maintenance Planning. Autom. Constr. 2021, 122, 103513. [Google Scholar] [CrossRef]
- Ishibashi, K.; Furuta, H.; Nakatsu, K. Bridge Maintenance Scheduling in Consideration of Resilience Against Natural Disasters. Front. Built Environ. 2020, 6, 4467. [Google Scholar] [CrossRef]
- Abdelkader, E.M.; Moselhi, O.; Marzouk, M.; Zayed, T. Integrative Evolutionary-Based Method for Modeling and Optimizing Budget Assignment of Bridge Maintenance Priorities. J. Constr. Eng. Manag. 2021, 147, 04021100. [Google Scholar] [CrossRef]
- Xie, H.B.; Wu, W.J.; Wang, Y.F. Life-Time Reliability Based Optimization of Bridge Maintenance Strategy Considering LCA and LCC. J. Clean. Prod. 2018, 176, 36–45. [Google Scholar] [CrossRef]
- Ghodoosi, F.; Abu-Samra, S.; Zeynalian, M.; Zayed, T. Maintenance Cost Optimization for Bridge Structures Using System Reliability Analysis and Genetic Algorithms. J. Constr. Eng. Manag. 2018, 144, 04017116. [Google Scholar] [CrossRef]
- Ghafoori, M.; Abdallah, M.; Ozbek, M.E. Machine Learning–Based Bridge Maintenance Optimization Model for Maximizing Performance within Available Annual Budgets. J. Bridge Eng. 2024, 29, 04024011. [Google Scholar] [CrossRef]
- Mao, X.; Jiang, X.; Yuan, C.; Zhou, J. Modeling the Optimal Maintenance Scheduling Strategy for Bridge Networks. Appl. Sci. 2020, 10, 498. [Google Scholar] [CrossRef]
- Kim, S.; Ge, B.; Frangopol, D.M. Probabilistic Optimum Bridge System Maintenance Management Considering Correlations of Deteriorating Components and Service Life Extensions. ASCE ASME J. Risk Uncertain. Eng. Syst. Civ. Eng. 2022, 8, 04022023. [Google Scholar] [CrossRef]
- Nicolai, R.P.; Frenk, J.B.G.; Dekker, R. Modelling and Optimizing Imperfect Maintenance of Coatings on Steel Structures. Struct. Saf. 2009, 31, 234–244. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Liu, M. Bridge Network Maintenance Optimization Using Stochastic Dynamic Programming. J. Struct. Eng. 2007, 133, 1772–1782. [Google Scholar] [CrossRef]

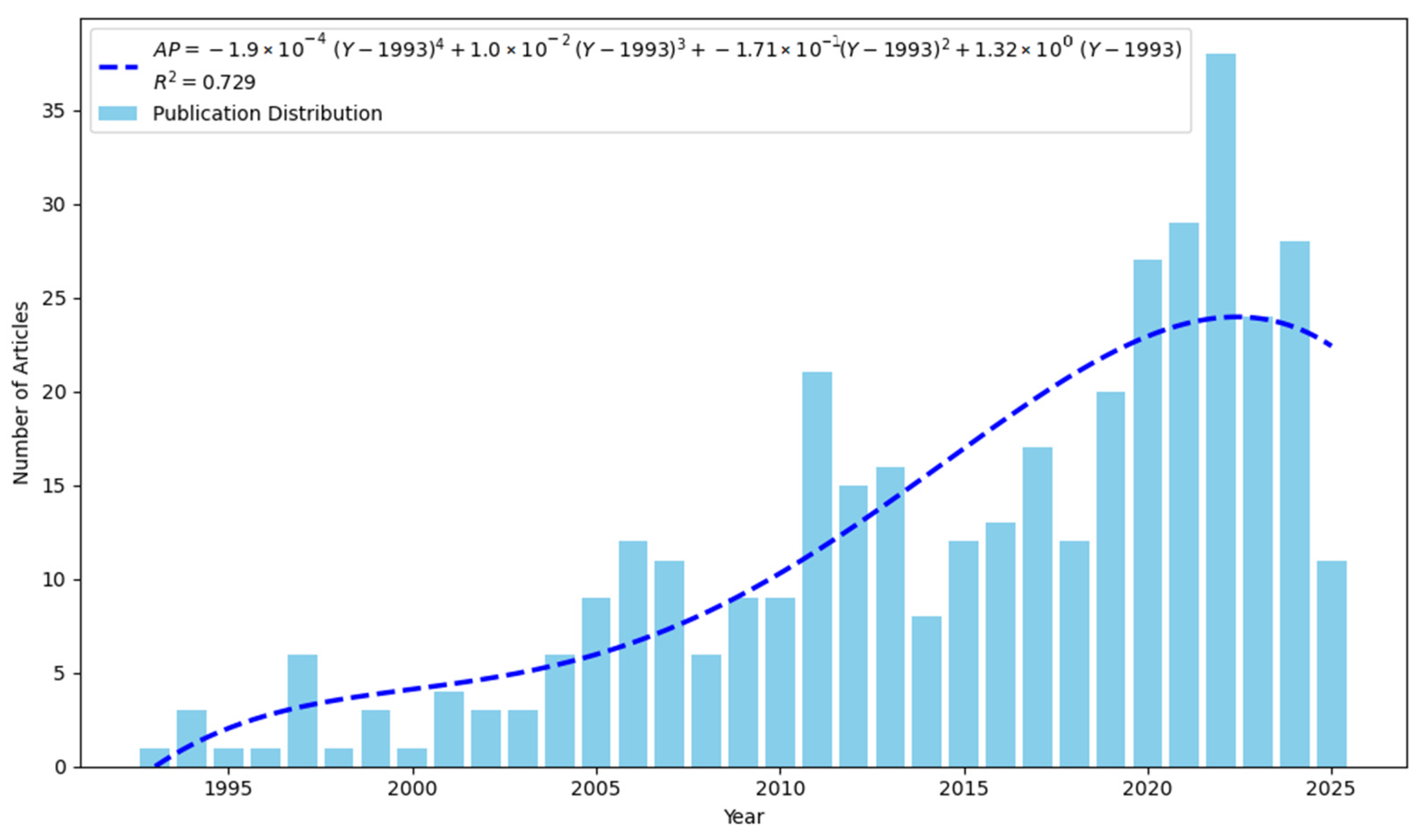
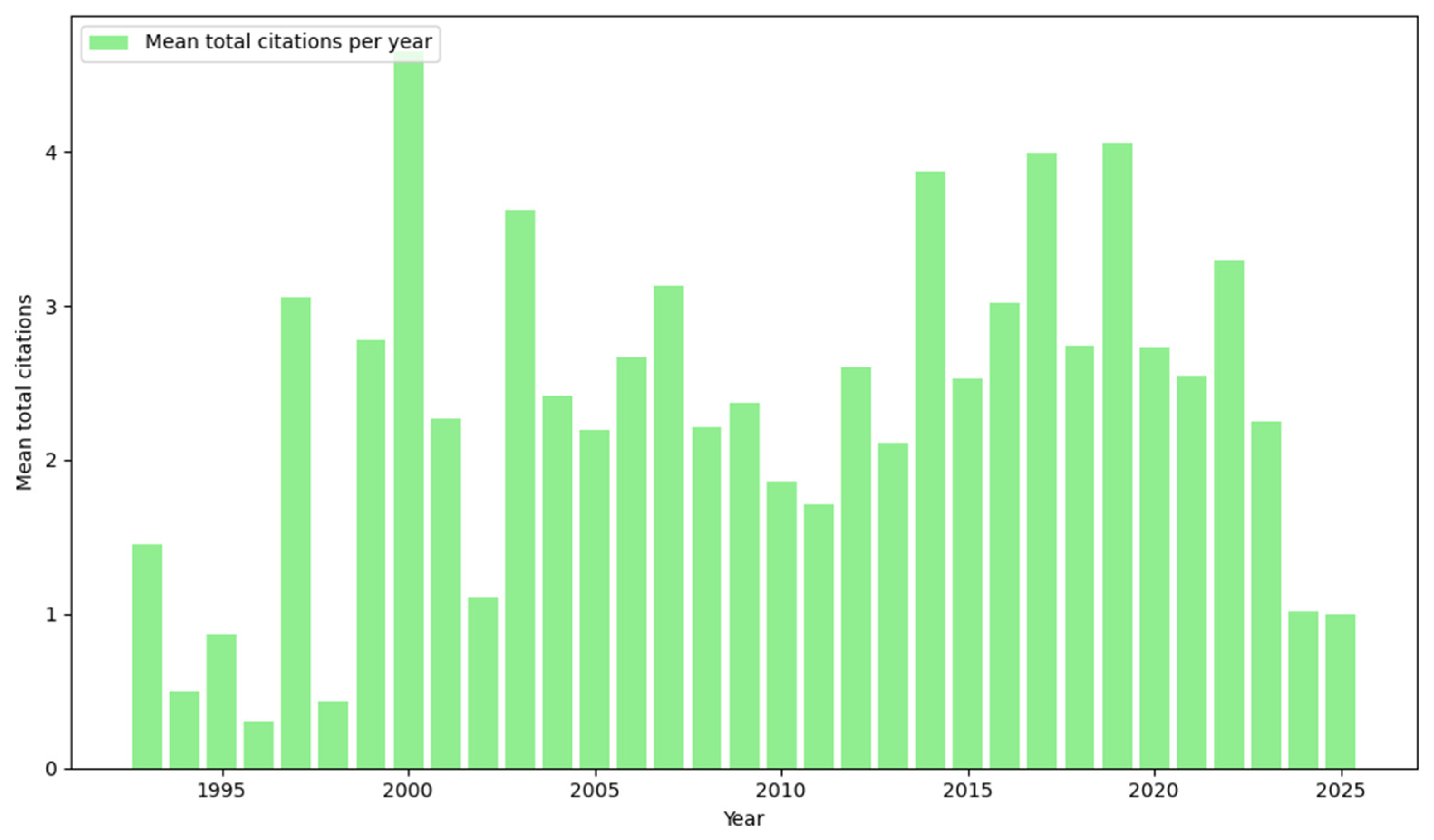
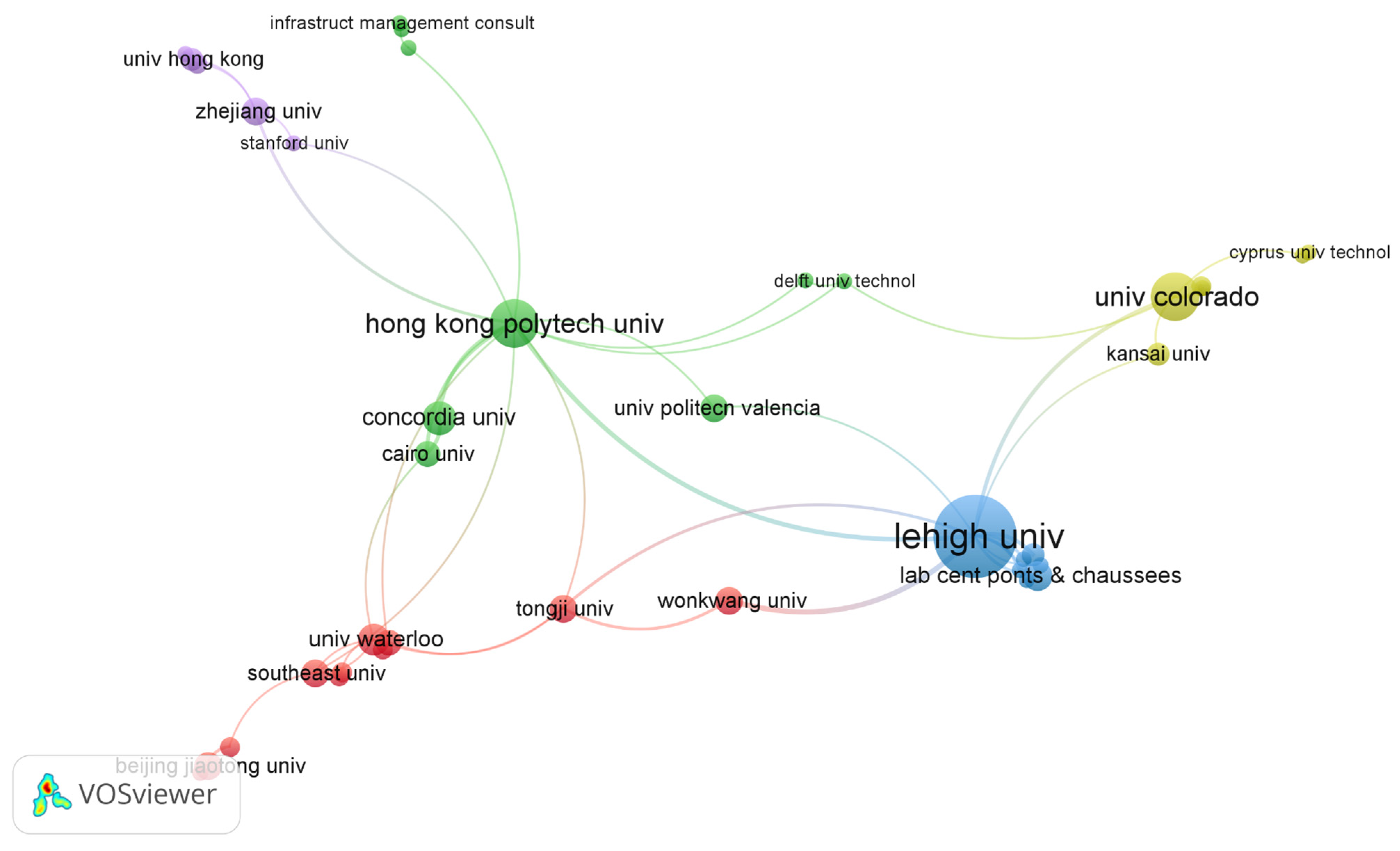
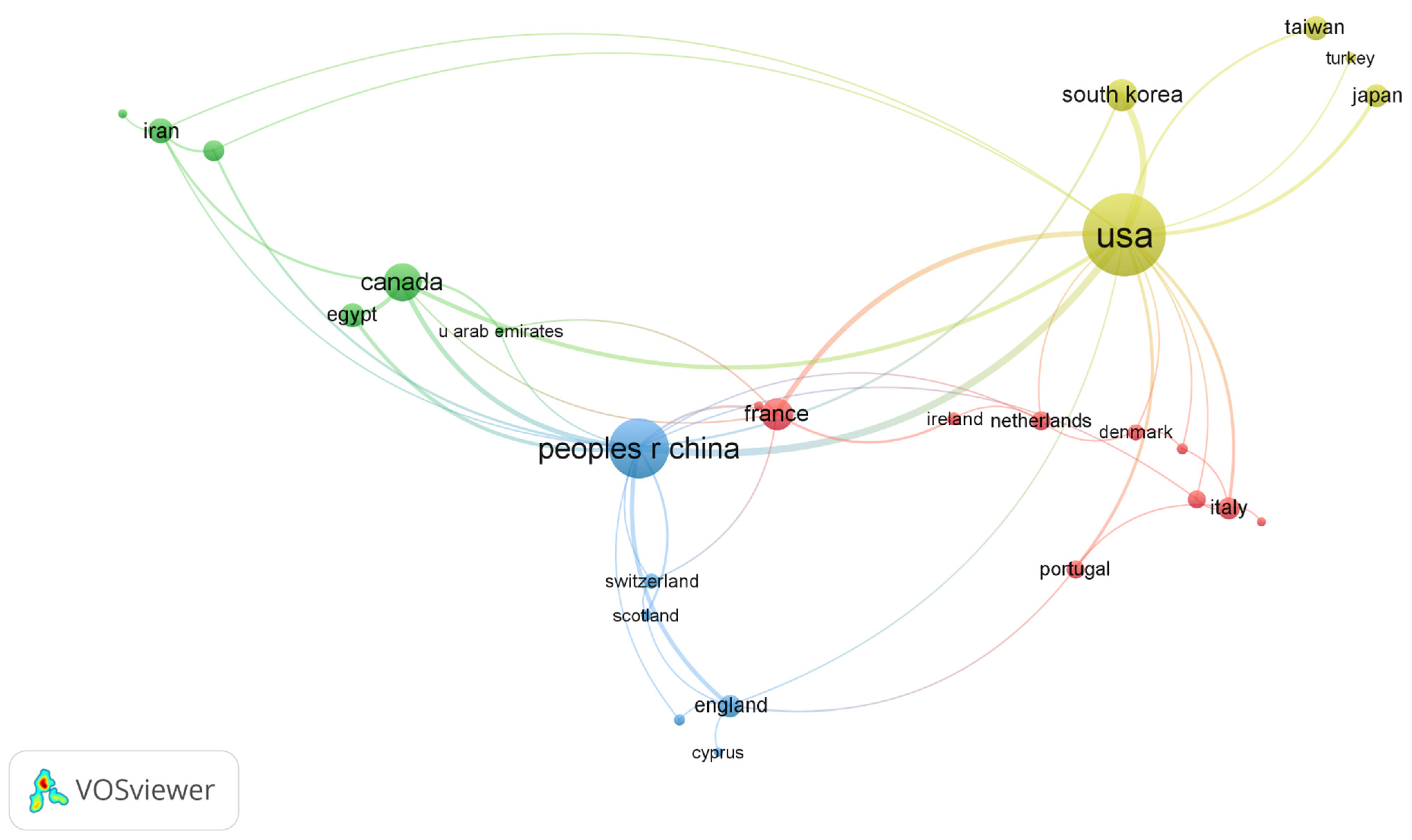
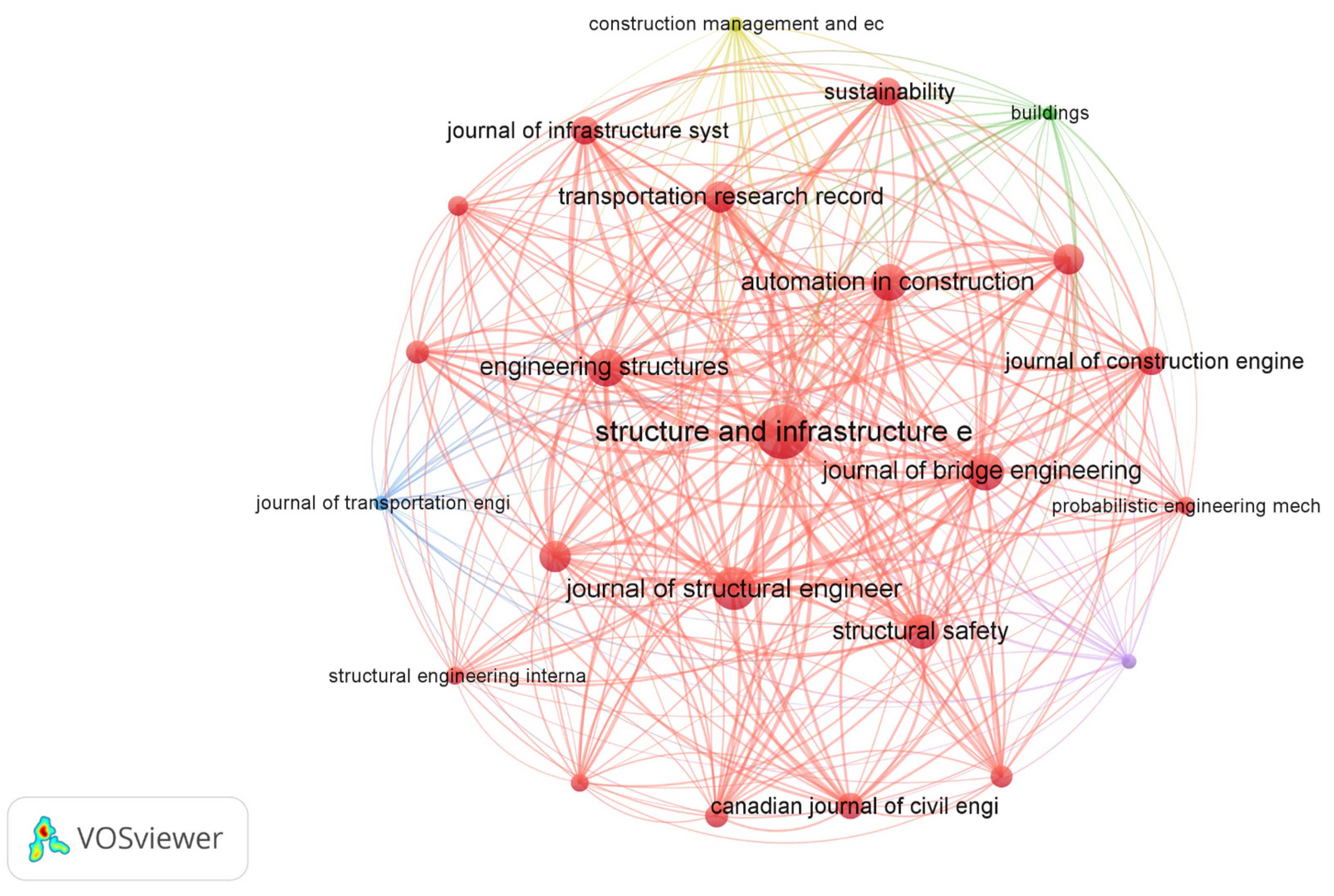
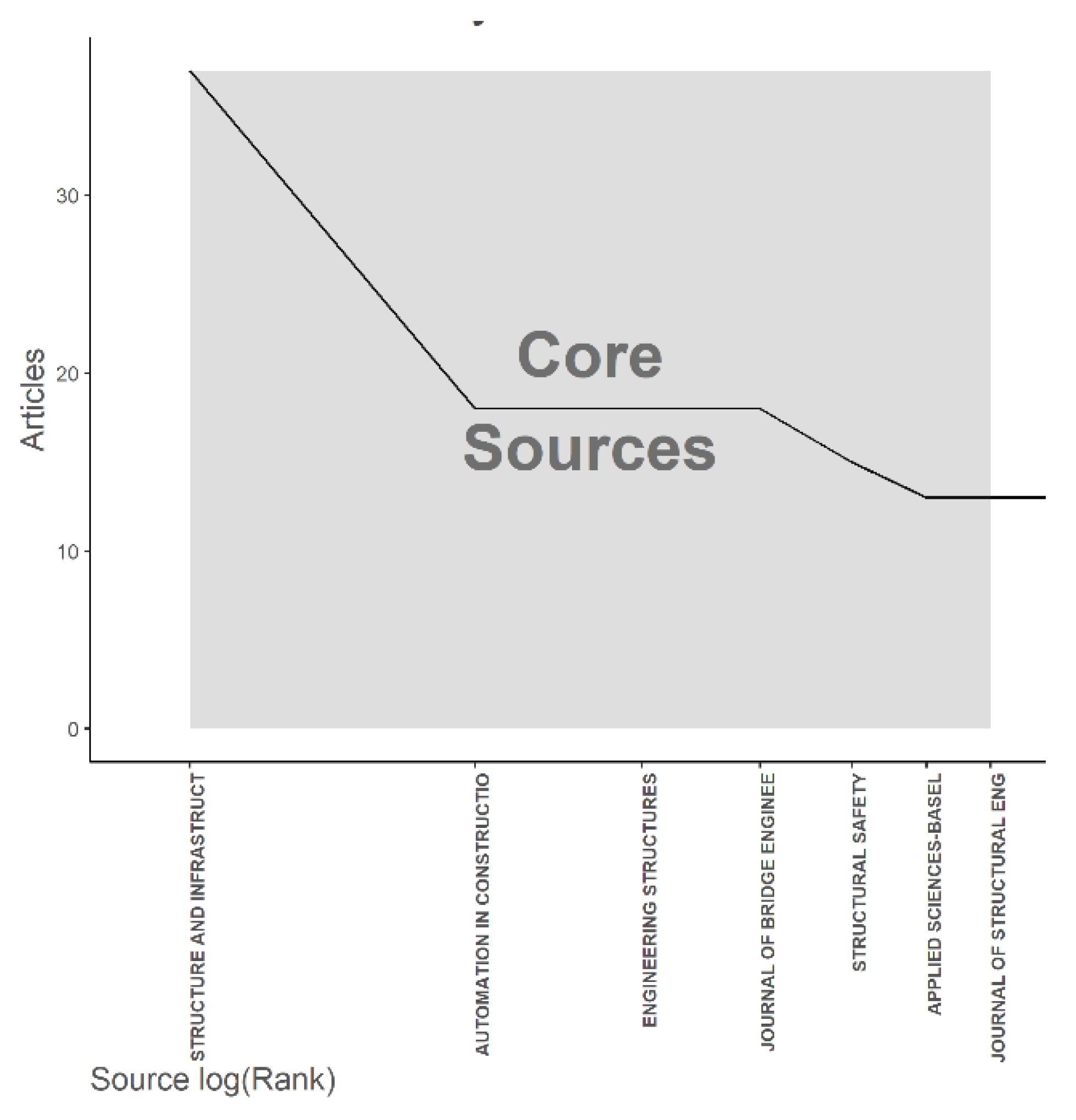
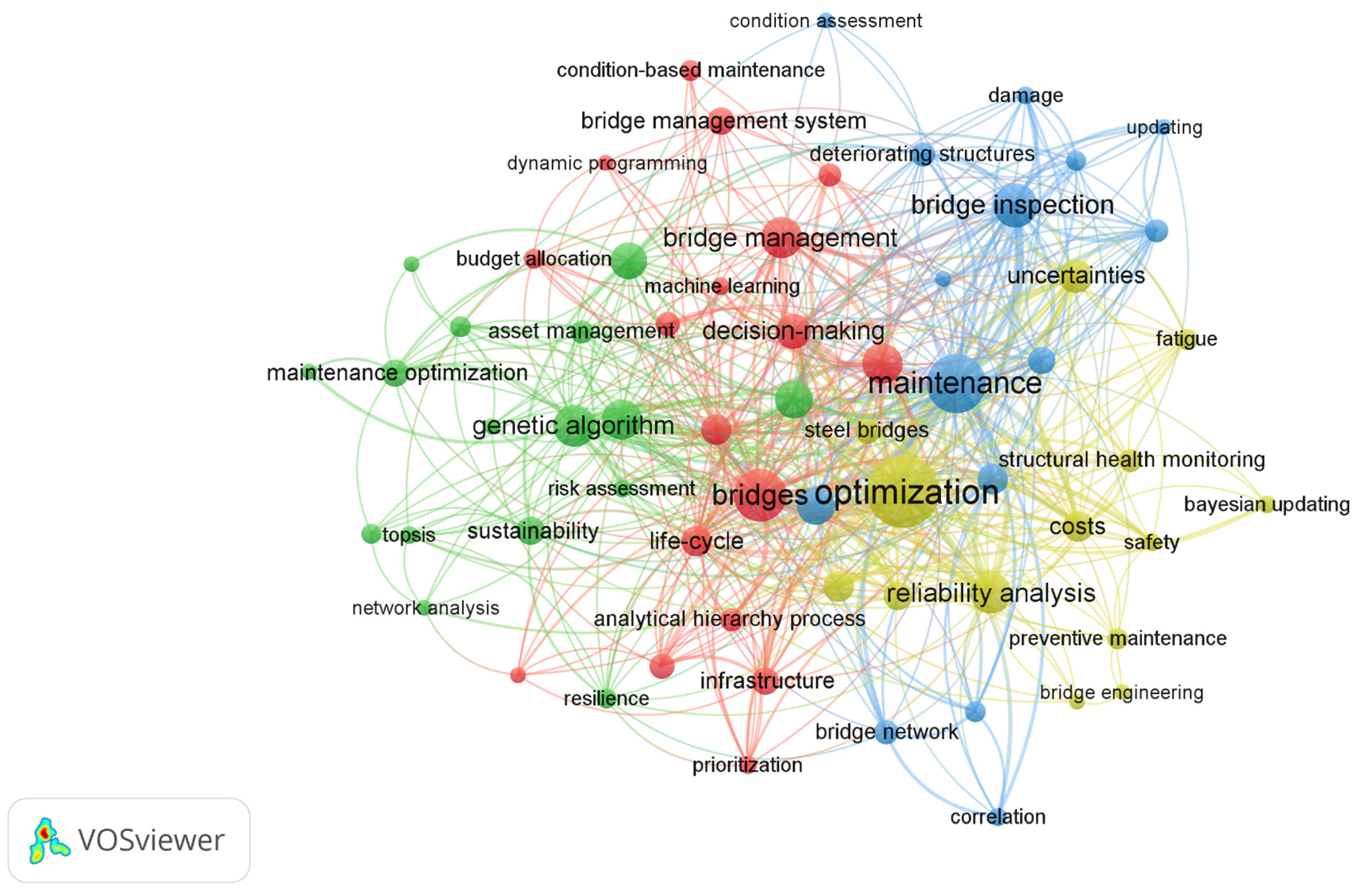

| Database | Search String |
|---|---|
| Web of Science | ((TS = (“bridge*”))) AND ((TS = (“remedia*”)) OR (TS = (“rehabilitation”)) OR (TS = (“repair”)) OR (TS = (“maintenance”)) OR (TS = (“budget”)) OR (TS = (“fund”)) OR (TS = (“decision support system”)) OR (TS = (“prioritiz*”)) OR (TS = (“inspection”))) AND ((TS = (“optimiz*”)) OR (TS = (“Pareto”)) OR (TS = (“multi criteria decision making”)) OR (TS = (“mcdm”)) OR (TS = (“madm”))) |
| Scopus | ((TITLE-ABS-KEY (“bridge*”))) AND ((TITLE-ABS-KEY (“remedia*”)) OR (TITLE-ABS-KEY (“rehabilitation”)) OR (TITLE-ABS-KEY (“repair”)) OR (TITLE-ABS-KEY (“maintenance”)) OR (TITLE-ABS-KEY (“budget”)) OR (TITLE-ABS-KEY (“fund”)) OR (TITLE-ABS-KEY (“decision support system”)) OR (TITLE-ABS-KEY (“prioritiz*”)) OR (TITLE-ABS-KEY (“inspection”))) AND ((TITLE-ABS-KEY(“optimiz*”)) OR (TITLE-ABS-KEY (“Pareto”)) OR (TITLE-ABS-KEY (“multi criteria decision making”)) OR (TITLE-ABS-KEY (“mcdm”)) OR (TITLE-ABS-KEY (“madm”))) |
| Rank | Reference | Title | Publication Year | Total Citations | Normalized Citations | Key Findings |
|---|---|---|---|---|---|---|
| 1 | [31] | Maintenance and management of civil infrastructure based on condition, safety, optimization, and life-cycle cost | 2007 | 362 | 6.08 | Multi-objective optimization using genetic algorithms produces a range of maintenance strategies that balance structure performance, safety, and life-cycle cost, thereby enabling more informed decision-making. |
| 2 | [32] | Life-Cycle Cost Design of Deteriorating Structures | 1997 | 299 | 3.37 | A reliability-based life-cycle cost optimization approach, especially via non-uniform inspection intervals, can substantially reduce maintenance costs while ensuring structural reliability, with the optimal strategy being susceptible to corrosion rates and failure costs. |
| 3 | [33] | Repair Optimization of Highway Bridges Using System Reliability Approach | 1999 | 182 | 2.43 | A system reliability approach to lifetime repair planning for highway bridges can minimize life-cycle costs while ensuring overall structural reliability; however, its effectiveness depends on regular updates through inspection and improved quantification of uncertainties. |
| 4 | [34] | Enhanced discrete particle swarm optimization path planning for UAV vision-based surface inspection | 2017 | 174 | 4.84 | A new method quickly computes efficient inspection routes that cover all areas and avoid obstacles, significantly reducing travel distance and processing time. |
| 5 | [35] | Life-Cycle Reliability-Based Maintenance Cost Optimization of Deteriorating Structures with Emphasis on Bridges | 2003 | 168 | 2.02 | A reliability-based methodology integrates random variable modeling, Monte Carlo simulation, and reliability index profile superposition to predict life-cycle performance and cost, enabling optimal maintenance strategies that balance long-term reliability with minimized cumulative costs under uncertainty. |
| Rank | Reference | Title | Publication Year | Total Citations | Normalized Citations | Key Findings |
|---|---|---|---|---|---|---|
| 6 | [36] | Optimal Resilience- and Cost-Based Postdisaster Intervention Prioritization for Bridges along a Highway Segment | 2012 | 157 | 4.31 | Integrating genetic algorithms with advanced traffic flow analysis, the framework automatically produces optimal bridge intervention schedules that balance resilience and cost after disruptive events. |
| 7 | [37] | Maintenance optimization of infrastructure networks using genetic algorithms | 2004 | 148 | 3.22 | By integrating genetic algorithms with Markov-chain models, the methodology was successfully applied to the maintenance programming of Quebec’s concrete bridge decks, resulting in an optimal mix of maintenance actions that minimize costs while keeping network conditions above acceptable thresholds. |
| 8 | [38] | Lifetime-oriented multi-objective optimization of structural maintenance considering system reliability, redundancy, and life-cycle cost using GA | 2009 | 145 | 3.60 | An automated genetic algorithm framework was developed to optimize maintenance strategies by balancing reliability, redundancy, and life-cycle cost. Its application to truss and bridge structures demonstrated that focusing on critical components yields more cost-effective and robust results. |
| 9 | [39] | Two probabilistic life-cycle maintenance models for deteriorating civil infrastructures | 2004 | 143 | 2.68 | A Monte Carlo–based reliability model was developed to optimize infrastructure maintenance by simulating multiple failure modes and uncertainties. Compared with an analytic model from the Netherlands, comprehensive reliability data yield more cost-effective, robust bridge maintenance. |
| 10 | [40] | Risk-Based Decision Making for Sustainable and Resilient Infrastructure Systems | 2016 | 143 | 4.73 | A risk-informed decision-making framework applied to highway bridge decks revealed that using high-performance concrete significantly reduces life-cycle costs and environmental impacts while minimizing damage and recovery times compared to conventional concrete designs. |
| Rank | Country | Number of Documents | Total Citations | Normalized Citations | Average Publication Year | Average Citations | Average Normalized Citations | Total Link Strength |
|---|---|---|---|---|---|---|---|---|
| Publication count | ||||||||
| 1 | Lehigh University | 52 | 2663 | 95.02 | 2015.19 | 51.21 | 1.83 | 28 |
| 2 | The Hong Kong Polytechnic University | 18 | 274 | 29.06 | 2020.89 | 15.22 | 1.61 | 20 |
| 3 | University of Colorado | 18 | 1773 | 32.12 | 2004.44 | 98.50 | 1.78 | 10 |
| 4 | Concordia University | 9 | 202 | 9.41 | 2015.44 | 22.44 | 1.05 | 6 |
| 5 | University of Waterloo | 8 | 185 | 6.4511 | 2012.75 | 23.13 | 0.81 | 5 |
| Total citations | ||||||||
| 1 | Lehigh University | 52 | 2663 | 95.02 | 2015.19 | 51.21 | 1.83 | 28 |
| 2 | University of Colorado | 18 | 1773 | 32.12 | 2004.44 | 98.50 | 1.78 | 10 |
| 3 | The Hong Kong Polytechnic University | 18 | 274 | 29.06 | 2020.89 | 15.22 | 1.61 | 20 |
| 4 | Concordia University | 9 | 202 | 9.41 | 2015.44 | 22.44 | 1.05 | 6 |
| 5 | Valencia Polytechnic University | 6 | 192 | 7.80 | 2019.17 | 32.00 | 1.30 | 2 |
| Average normalized citations | ||||||||
| 1 | Delft University of Technology | 2 | 151 | 6.61 | 2014 | 75.50 | 3.31 | 3 |
| 2 | Harbin Institute of Technology | 2 | 76 | 5.07 | 2022 | 38 | 2.54 | 0 |
| 3 | University of Perugia | 4 | 40 | 8.25 | 2023 | 10 | 2.06 | 2 |
| 4 | Paris-Saclay University | 2 | 106 | 4.07 | 2020 | 53 | 2.04 | 2 |
| 5 | Wuhan University of Technology | 2 | 8 | 3.93 | 2024.5 | 4 | 1.96 | 2 |
| Rank | Country | Number of Documents | Total Citations | Normalized Citations | Average Publication Year | Average Citations | Average Normalized Citations | Total Link Strength |
|---|---|---|---|---|---|---|---|---|
| Publication count | ||||||||
| 1 | United States of America | 150 | 5769 | 191.29 | 2013.72 | 38.46 | 1.28 | 54 |
| 2 | People’s Republic of China | 78 | 1112 | 81.5 | 2020.54 | 14.256 | 1.04 | 41 |
| 3 | Canada | 32 | 706 | 28.61 | 2015.9 | 22.06 | 0.89 | 21 |
| 4 | France | 23 | 631 | 24.44 | 2012.13 | 27.43 | 1.06 | 15 |
| 5 | South Korea | 22 | 377 | 12.96 | 2016.5 | 17.14 | 0.59 | 12 |
| Total citations | ||||||||
| 1 | United States of America | 150 | 5769 | 191.29 | 2013.72 | 38.46 | 1.28 | 54 |
| 2 | People’s Republic of China | 78 | 1112 | 81.5 | 2020.54 | 14.26 | 1.04 | 41 |
| 3 | Canada | 32 | 706 | 28.61 | 2015.9 | 22.06 | 0.89 | 21 |
| 4 | France | 23 | 631 | 24.44 | 2012.13 | 27.43 | 1.06 | 15 |
| 5 | Taiwan | 13 | 480 | 9.74 | 2013.38 | 36.92 | 0.75 | 2 |
| Average normalized citations | ||||||||
| 1 | Norway | 2 | 23 | 4.28 | 2022.50 | 11.5 | 2.14 | 1 |
| 2 | Spain | 7 | 198 | 13.25 | 2020.00 | 28.29 | 1.89 | 3 |
| 3 | Australia | 10 | 357 | 17.01 | 2017.60 | 35.7 | 1.7 | 5 |
| 4 | Netherlands | 8 | 321 | 13.24 | 2017.13 | 40.13 | 1.65 | 4 |
| 5 | Belgium | 3 | 79 | 4.93 | 2019.33 | 26.33 | 1.64 | 3 |
| Rank | Journal | Number of Documents | Total Citations | Normalized Citations | Average Publication Year | Average Citations | Average Normalized Citations | Total Link Strength |
|---|---|---|---|---|---|---|---|---|
| Publication count | ||||||||
| 1 | Structure and infrastructure engineering | 37 | 1119 | 42.59 | 2015.95 | 30.24 | 1.15 | 8029 |
| 2 | Journal of structural engineering | 23 | 1712 | 36.97 | 2008 | 74.43 | 1.61 | 5313 |
| 3 | Engineering structures | 18 | 782 | 24.84 | 2013.06 | 43.44 | 1.38 | 4248 |
| 4 | Journal of Bridge Engineering | 18 | 701 | 25.62 | 2014.28 | 38.94 | 1.42 | 4248 |
| 5 | Automation in Construction | 17 | 616 | 36.62 | 2018.65 | 36.24 | 2.15 | 4029 |
| Total citations | ||||||||
| 1 | Journal of structural engineering | 23 | 1712 | 36.97 | 2008 | 74.43 | 1.61 | 5313 |
| 2 | Structure and infrastructure engineering | 37 | 1119 | 42.59 | 2015.95 | 30.24 | 1.15 | 8029 |
| 3 | Structural safety | 15 | 845 | 31.25 | 2013.33 | 56.33 | 2.08 | 3585 |
| 4 | Engineering structures | 18 | 782 | 24.84 | 2013.06 | 43.44 | 1.38 | 4248 |
| 5 | Journal of Bridge Engineering | 18 | 701 | 25.62 | 2014.28 | 38.94 | 1.42 | 4248 |
| Average normalized citations | ||||||||
| 1 | Automation in Construction | 17 | 616 | 36.62 | 2018.65 | 36.24 | 2.15 | 4029 |
| 2 | Structural safety | 15 | 845 | 31.25 | 2013.33 | 56.33 | 2.08 | 3585 |
| 3 | Reliability engineering and system safety | 12 | 621 | 20.47 | 2012.67 | 51.75 | 1.71 | 2904 |
| 4 | Journal of structural engineering | 23 | 1712 | 36.97 | 2008 | 74.43 | 1.61 | 5313 |
| 5 | Journal of cleaner production | 5 | 87 | 7.54 | 2021.40 | 17.40 | 1.51 | 1245 |
| Keyword | Occurrences | Average Publication Year | Average Citations | Average Normalized Citations | Links | Total Link Strength |
|---|---|---|---|---|---|---|
| Optimization | 78 | 2014.21 | 31.51 | 1.09 | 53 | 216 |
| Maintenance | 51 | 2014.00 | 36.84 | 1.13 | 45 | 159 |
| Bridges | 41 | 2014.00 | 32.39 | 1.13 | 47 | 113 |
| Bridge inspection | 29 | 2015.31 | 29.55 | 1.03 | 30 | 91 |
| Genetic algorithm | 26 | 2015.50 | 29.15 | 0.97 | 29 | 60 |
| Bridge management | 25 | 2012.32 | 19.88 | 0.68 | 34 | 61 |
| Reliability analysis | 25 | 2014.48 | 31.96 | 1.12 | 31 | 70 |
| Bridge maintenance | 24 | 2015.17 | 24.75 | 0.89 | 34 | 53 |
| Life-cycle cost | 24 | 2014.04 | 40.92 | 0.98 | 32 | 63 |
| Deterioration | 21 | 2013.81 | 40.05 | 1.12 | 28 | 60 |
| Multi-objective optimization | 21 | 2016.33 | 39.57 | 1.20 | 29 | 53 |
| Life-cycle analysis | 20 | 2018.55 | 28.65 | 1.34 | 24 | 36 |
| Decision-making | 18 | 2016.83 | 24.06 | 0.90 | 25 | 48 |
| Uncertainties | 17 | 2015.00 | 51.53 | 1.52 | 29 | 58 |
| Corrosion | 14 | 2016.00 | 32.00 | 1.22 | 18 | 38 |
| costs | 14 | 2010.00 | 45.07 | 1.24 | 24 | 55 |
| Highway bridges | 14 | 2014.14 | 36.64 | 1.22 | 24 | 39 |
| Life-cycle | 14 | 2013.86 | 44.14 | 1.22 | 30 | 49 |
| Markov decision process | 14 | 2012.07 | 34.93 | 1.06 | 24 | 38 |
| Maintenance management | 12 | 2015.75 | 15.75 | 0.68 | 21 | 30 |
| Sustainability | 12 | 2018.00 | 43.92 | 1.57 | 18 | 23 |
| Bridge management system | 11 | 2014.82 | 16.27 | 0.51 | 14 | 14 |
| Infrastructure | 11 | 2014.27 | 38.82 | 0.85 | 15 | 26 |
| Maintenance optimization | 11 | 2018.64 | 41.18 | 2.06 | 15 | 21 |
| Repair | 11 | 2014.73 | 25.45 | 0.81 | 21 | 34 |
| Rehabilitation | 10 | 2011.60 | 20.90 | 0.47 | 15 | 24 |
| Steel bridges | 10 | 2015.30 | 23.60 | 0.97 | 18 | 24 |
| Bridge network | 9 | 2018.44 | 21.89 | 1.21 | 12 | 24 |
| Decision support system | 9 | 2020.44 | 10.11 | 0.59 | 12 | 13 |
| Deteriorating structures | 9 | 2012.78 | 41.22 | 1.17 | 18 | 25 |
| Analytical hierarchy process | 8 | 2014.50 | 23.25 | 0.95 | 9 | 16 |
| Asset management | 8 | 2019.25 | 15.50 | 0.56 | 16 | 18 |
| Probability | 8 | 2008.25 | 49.75 | 1.56 | 22 | 35 |
| Structural health monitoring | 8 | 2016.88 | 24.25 | 1.42 | 13 | 22 |
| User costs | 8 | 2012.13 | 24.25 | 0.67 | 8 | 14 |
| Ref. | Data Type | Core Techs and Tools | Data-Analysis Techniques | Function/Service |
|---|---|---|---|---|
| [134] | Terrestrial LiDAR geometry + periodic strain/vibration records. | Revit; Solibri; Navisworks. | Scan-to-BIM segmentation; FE import and “what-if” rehab simulation. | Predictive rehab planning; heritage asset archiving. |
| [135] | UAV imagery, LiDAR, IoT strain gauges, Met-Office weather; GIS layers. | Xeokit; CesiumJS. | Mask R-CNN defect vision; Graph-based traffic rerouting; GraphSAGE logistics; optional FEA. | Traffic diversion, O&M scheduling, logistics optimization. |
| [136] | LiDAR point cloud; GNSS and total-station control; inspection docs. | Rhino; SketchUp; SCIA Engineer. | Template-matching segmentation; mesh remeshing; differential-evolution FE calibration. | Scenario simulation and life-cycle sustainability planning. |
| [137] | SHM stress/ambient data; visual inspections. | Python Tensorflow library; OpenSees. | Multi-physics corrosion-fatigue model; RL-based maintenance optimizer. | Dynamic inspection and maintenance optimization; hanger replacement timing. |
| Category | Methods | Strengths | Limitations | Scalability |
|---|---|---|---|---|
| Statistical Models | Linear Regression, Time-Series | Simple, interpretable; captures trends | Limited to linear or stationary patterns | Moderate |
| Shallow ML | SVM, PNN, RBFN, PCA | Captures nonlinearity; good for classification | Requires tuning; sensitive to hyperparameters | Moderate |
| DL | DNN, NN-EE, SOMCM | Handles complex, high-dimensional data | Requires large data and computational resources | High |
| Optimization Techniques | NSGA-II, DP, DT | Solves multi-objective problems; interpretable | Computationally intensive; poor for large-scale problems | Moderate |
| DRL Techniques | DQN, PPO, MAR-PPO | Learns optimal policies; scalable to complex systems | Needs extensive training and tuning | High |
| Hybrid DRL + DL | DRL + CNN, DRL + surrogate models | Captures spatio-temporal dynamics; robust to uncertainty | High computational cost | High |
| Ref. | Application | Analytical Methods | AI Techniques and Tools | Performance Indicators |
|---|---|---|---|---|
| [165] | Optimize maintenance schedule of an RC girder bridge for safety, service life and cost | Multi-objective optimization; stochastic deterioration curves | Improved NSGA-II genetic algorithm | Condition index, reliability index, maintenance cost, service life |
| [171] | Plan 100-year life-cycle maintenance for a region of deteriorating bridges | Probabilistic deterioration modeling; life-cycle cost analysis | Deep Q-Network with encoder–decoder CNN | Life-cycle cost-effectiveness of maintenance actions. |
| [160] | Rank project-level bridge interventions under multiple criteria | Probabilistic modeling; multi-criteria decision analysis; degradation-rate factor; LCC estimate | Probabilistic Neural Network; Radial-Basis-Function NN | Accuracy of condition state, reliability index, degradation-rate prediction, LCC error, optimal timing |
| [174] | Derive cost-effective, risk-aware policies for a bridge network | Markov Decision Process; stochastic cost model | Multi-agent Ranking PPO (MAR-PPO) | Network maintenance cost-effectiveness; excessive-risk cost |
| [173] | Manage a steel-girder bridge under risk-based life-cycle criteria | Probabilistic LCC; reliability analysis | Double-Critic Multi-Agent A2C (DCMA2C) RL | Expected LCC; annual reliability index; annual failure risk |
| [175] | Formulate network-wide maintenance policies | Markov-chain deterioration; Bayesian updating; LCC analysis | Multi-agent Q-learning RL | Cost-effectiveness, condition distribution, mean annual maintenance cost |
| [167] | Allocate annual budget and schedule works across a bridge network | Dynamic programming optimizer | Hopfield neural-network search | Annual budget utilization rate |
| [162] | Speed up life-cycle cost analysis under multiple uncertainties | Monte-Carlo LCC; Markov deterioration; Poisson hazard and cost volatility | Deep fully-connected neural network as surrogate model | Agency cost; user cost; composite utility |
| [179] | Devise bridge maintenance strategy under climate-change scenarios | Hybrid LCA + LCC; reliability-index modeling; multi-objective optimization | Decision-tree classification framework | Environmental cost; economic cost; probability of CO2-reduction failure |
| [163] | Predict condition state, risk level and maintenance advice for bridges from routine inspection records | Supervised multi-task classification; cost-sensitive learning to handle class imbalance | Entity-embedding multi-task neural network plus comparative logistic-regression and tree-based learners | Predicted condition state, risk level and maintenance advice classes for each bridge element |
| Ref. | Application | Analytical Methods | AI Techniques and Tools | Performance Indicators |
|---|---|---|---|---|
| [166] | Minimize expected life-cycle cost by optimally timing inspections and repairs of corrosion-damaged steel bridges | Probabilistic optimization with Bayesian updating; event-tree life-cycle simulation | Event-tree search routine (model-based optimizer) | Minimum expected life-cycle cost, optimal inspection/repair schedule, network-level failure probability |
| [176] | Plan project-level maintenance interventions under multiple uncertainties to maximize stakeholder utility | Markov decision process; life-cycle cost and utility evaluation | Multi-agent DeepQ-Network with Advantage Actor–Critic (MARL) | Convergence of expected reward, agency-cost change, user-cost change, stakeholder-utility gain |
| [170] | Derive the optimal maintenance policy for a deck system and cable-stayed bridge across its life-cycle | Markov decision process with reward-based life-cycle-cost evaluation; Monte-Carlo state simulation | Deep Q-Network optimizer | Long-term life-cycle cost compared with benchmark time-based and condition-based policies |
| [159] | Forecast routine maintenance cost of reinforced-concrete beam bridges | Hierarchical multivariate regression; autoregressive time-series forecasting | Cost-age regression model combined with AR forecast module (statistical ML) | Annual routine-maintenance cost profile for budgeting |
| [161] | Select risk-based maintenance timing and budget for deteriorating bridges | Monte-Carlo life-cycle simulation; expectancy–value theory for risk attitude modeling | Evolutionary Support-Vector-Machine with Symbiotic-Organisms-Search meta-heuristic | Expected life-cycle cost, optimal intervention years and annual budget envelope |
| [164] | Prioritize bridge maintenance using unsupervised patterns in historic inspection data | Self-organizing-map clustering; association-rule mining for attribute correlation | SOM neural network with cluster-merging algorithm | Targeted maintenance strategy list ranked by cluster risk profiles |
| [169] | Minimize total annual carbon emissions for a highway bridge network under budget limits | Two-dimensional Markov-chain deterioration; integer-programming budget allocation | Q-learning reinforcement learning for single-bridge policies | Network-level annual CO2 emissions and budget utilization curve |
| [180] | Produce sustainable life-cycle maintenance policies balancing cost, emissions and safety for a bridge network | Probabilistic deterioration and life-cycle carbon/safety evaluation; multi-attribute utility theory | Convolutional Autoencoder–Structured Deep Q-Network (ConvAE-DQN) | Maintenance-policy utility scores for cost, environmental and safety metrics across budget scenarios |
| [172] | Balance agency cost, CO2 and traffic-mobility delay over 100 years for a road-bridge network | Partially observable MDP with traffic-flow redistribution; Monte-Carlo roll-outs and multi-attribute reward | Hierarchical Branching-Dueling Q-Network with multi-reward back-propagation | Long-run reductions in life-cycle cost, carbon emissions, and congestion versus engineer-designed plans |
| Metaheuristic | Acronym | Type | Description | Reference |
|---|---|---|---|---|
| GA | Genetic algorithm | Biological-inspired | It is inspired by Darwin’s theory of biological evolution, and mimics the principles of natural selection and survival of the fittest | [186] |
| NSGA-II | Non-dominated sorting genetic algorithm-II | Biological-inspired | It emulates natural selection by ranking solutions into Pareto fronts and preserving diversity using the crowding distance | [187] |
| DE | Differential evolution | Biological-inspired | It simulates Darwinian evolution through three key operations: mutation, crossover, and selection | [188] |
| EFO | Electric fish optimization | Nature-inspired | It is modeled after the electrolocation and electrocommunication behaviors of weakly electric fish | [189] |
| IWO | Invasive weed optimization | Nature-inspired | It draws inspiration from the colonization behavior of weeds, and combines the basics of reproduction, spatial distribution, and competitive selection | [190] |
| WOA | Whale optimization algorithm | Nature-inspired | It imitates the hunting behavior of humpback whales, particularly their bubble-net feeding strategy | [191] |
| PSO | Particle swarm optimization | Nature-inspired | It models the social behavior of birds or individual particles flocking and adjusting their positions based on their own experience and the best-known position of the group | [192] |
| SFLA | Shuffled frog leaping algorithm | Nature-inspired | It is influenced by the foraging behavior of frogs, combining local search with global exploration | [193] |
| HS | Harmony search | Music-inspired | It is sparked by the improvisation process of musicians who adjust their notes or melodies to achieve the best harmony | [194] |
| SA | Simulated annealing | Physics-based | It is motivated by the metallurgical process of annealing, where a material is heated and slowly cooled to remove defects | [195] |
| Reference | Year | Employed Algorithms | Application | Optimization Type | Objective Functions | Design Constraints |
|---|---|---|---|---|---|---|
| [218] | 2024 | Binary linear programming + DT/RF/GB/SVM | Optimizing long-term maintenance plans of bridge components | Single-objective | Maximize the average bridge performance index | a. Annual maintenance budget b. Selection of maintenance strategy c. Minimum permissible condition of bridge components |
| [220] | 2022 | Constrained nonlinear minimization | Optimal rehabilitation management of bridge girders | Single-objective | Maximize the time until specified failure probability of bridge is reached | a. Initial maintenance should not be conducted until at least two years of service have passed b. Maintenance intervals must be between 2 and 20 years |
| [219] | 2020 | Nonlinear programming + sensitivity analysis | Optimal maintenance scheduling of bridges, including time and job sequences | Multi-objective | a. Minimize the total traffic delays in the network b. Maximize the number of bridges to be repaired | a. Budget limit b. Number of maintenance operations handled by a crew c. Amount of simultaneous maintenance activities |
| [221] | 2009 | Dynamic programming | Optimizing maintenance of deteriorated coatings in steel bridges | Single-objective | Minimize discounted maintenance expenditures over a defined planning period | N/A |
| [222] | 2007 | DP + MCS | Optimizing maintenance works of highway bridge networks | Single-objective | Minimize the life-cycle maintenance expenses | Yearly maintenance budget |
| Reference | Location | Description |
|---|---|---|
| [12] | Quebec, Canada | A real reinforced concrete bridge with its inspection reports available from the Ministère des Transports du Québec. The bridge deck was scanned using the ground-penetrating radar technology |
| [44] | Montreal, Canada | A 2.7-km Jacques Cartier bridge connecting Montreal and Longueuil over the St. Lawrence River. It underwent major rehabilitation in 2001–2002 to rebuild its aging deck |
| [48] | China | A suspension bridge with a 1385-m main span, which was opened to traffic in 1999 |
| [58] | India | Twelve bridges across the river Tapi in Surat city |
| [65] | Iran | Zohreh river bridge in the southwestern region. The flowing water under the bridge causes erosion and scour to the columns |
| [62] | Taoyuan, Taiwan | Six types of pedestrian bridges: (1) suspension, (2) truss, (3) tied arch, (4) open spandrel arch, (5) cable-stayed, and (6) girder |
| [199] | China | In-service Guo bridge that has a total length of 20.6 m and a width of 8.6 m. It incorporates a modular expansion joint with a capacity of 60 mm |
| [200] | Australia | A railway bridge, which had recently undergone maintenance, with a remaining service life of 60 years. It is a single-span bridge of 12-m length that incorporates two supported girders. The girder flanges have a width of 229 mm and a thickness of 19.6 mm |
| [209] | China | A regional transportation network within the southern region that is characterized by a humid subtropical climate. The study area consists of 22 rivers and 144 girder and reinforced concrete slab bridges in total. |
| [217] | Canada | A 17 m bridge superstructure comprising four T-beams spaced 2.3 m and a 200-mm-thick deck slab. The total deck area is 514.5 m2 subjected to the application of deicing materials |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkader, E.M.; Al-Sakkaf, A.; Ebrahim, K.; Elkabalawy, M. Maintenance Budget Allocation Models of Existing Bridge Structures: Systematic Literature and Scientometric Reviews of the Last Three Decades. Infrastructures 2025, 10, 252. https://doi.org/10.3390/infrastructures10090252
Abdelkader EM, Al-Sakkaf A, Ebrahim K, Elkabalawy M. Maintenance Budget Allocation Models of Existing Bridge Structures: Systematic Literature and Scientometric Reviews of the Last Three Decades. Infrastructures. 2025; 10(9):252. https://doi.org/10.3390/infrastructures10090252
Chicago/Turabian StyleAbdelkader, Eslam Mohammed, Abobakr Al-Sakkaf, Kyrillos Ebrahim, and Moaaz Elkabalawy. 2025. "Maintenance Budget Allocation Models of Existing Bridge Structures: Systematic Literature and Scientometric Reviews of the Last Three Decades" Infrastructures 10, no. 9: 252. https://doi.org/10.3390/infrastructures10090252
APA StyleAbdelkader, E. M., Al-Sakkaf, A., Ebrahim, K., & Elkabalawy, M. (2025). Maintenance Budget Allocation Models of Existing Bridge Structures: Systematic Literature and Scientometric Reviews of the Last Three Decades. Infrastructures, 10(9), 252. https://doi.org/10.3390/infrastructures10090252









