Structural Characteristics and Damage Analysis of Beijing Wanning Bridge Under the Coupling Effect of Dynamic Traffic and Subway Vibrations
Abstract
1. Introduction
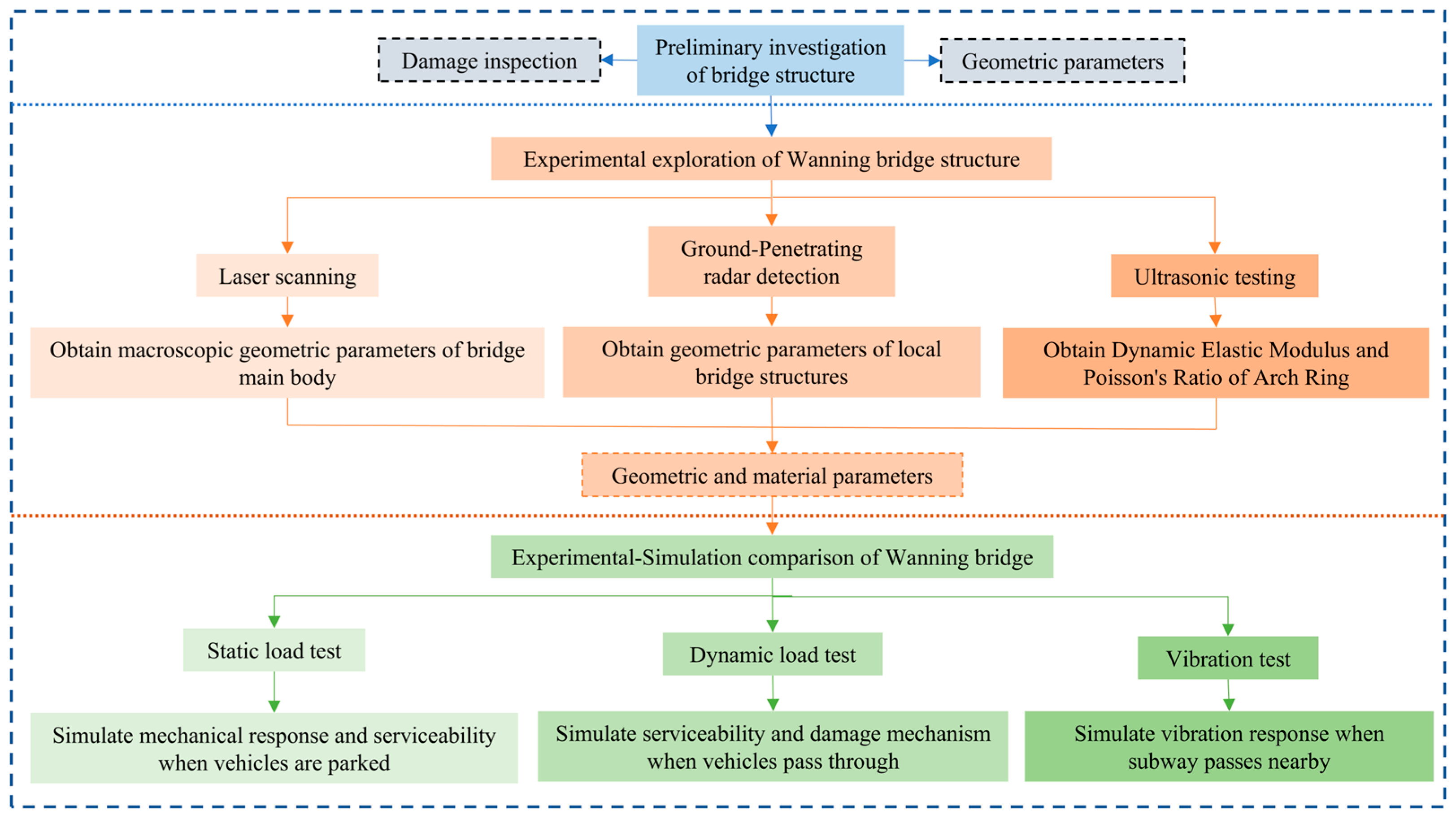
2. Damage Detection of Bridge Structure
2.1. Damage Detection of Bridge Deck System and Buildings on Arch
2.2. Damage Detection of Superstructure and Substructure
3. Bridge Structure Detection
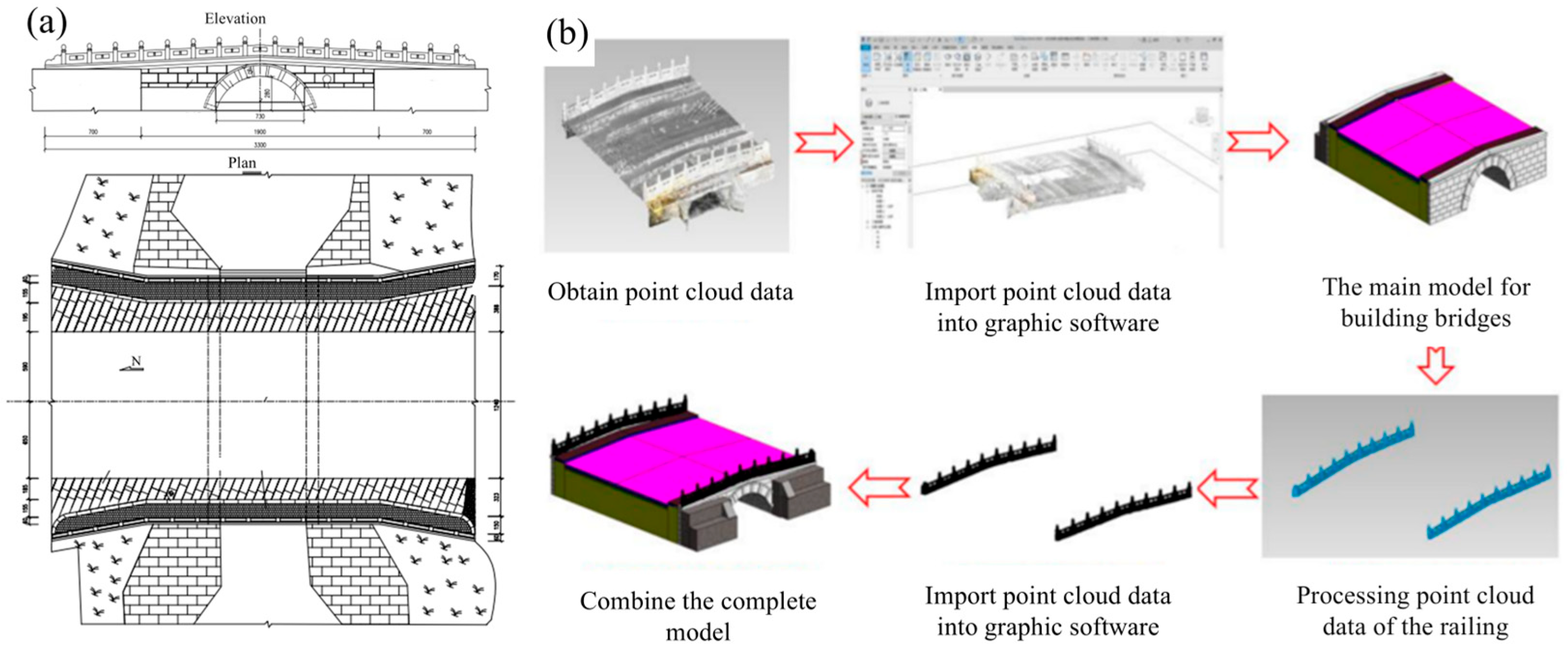
3.1. Three-Dimensional Laser Scanning
3.2. Geological Radar Detection
3.3. Detection of Elastic Modulus of Arch Ring Stone
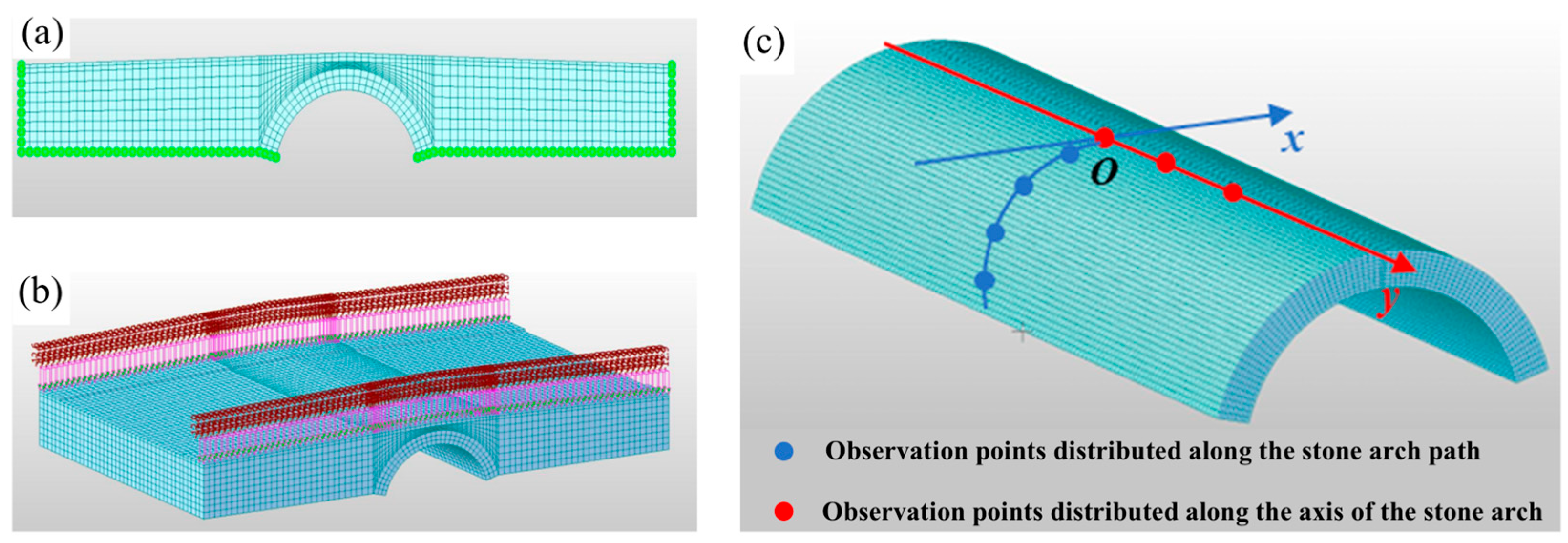
4. Structural Characteristics of Wanning Bridge
4.1. Static Load Test
4.2. Dynamic Load Test
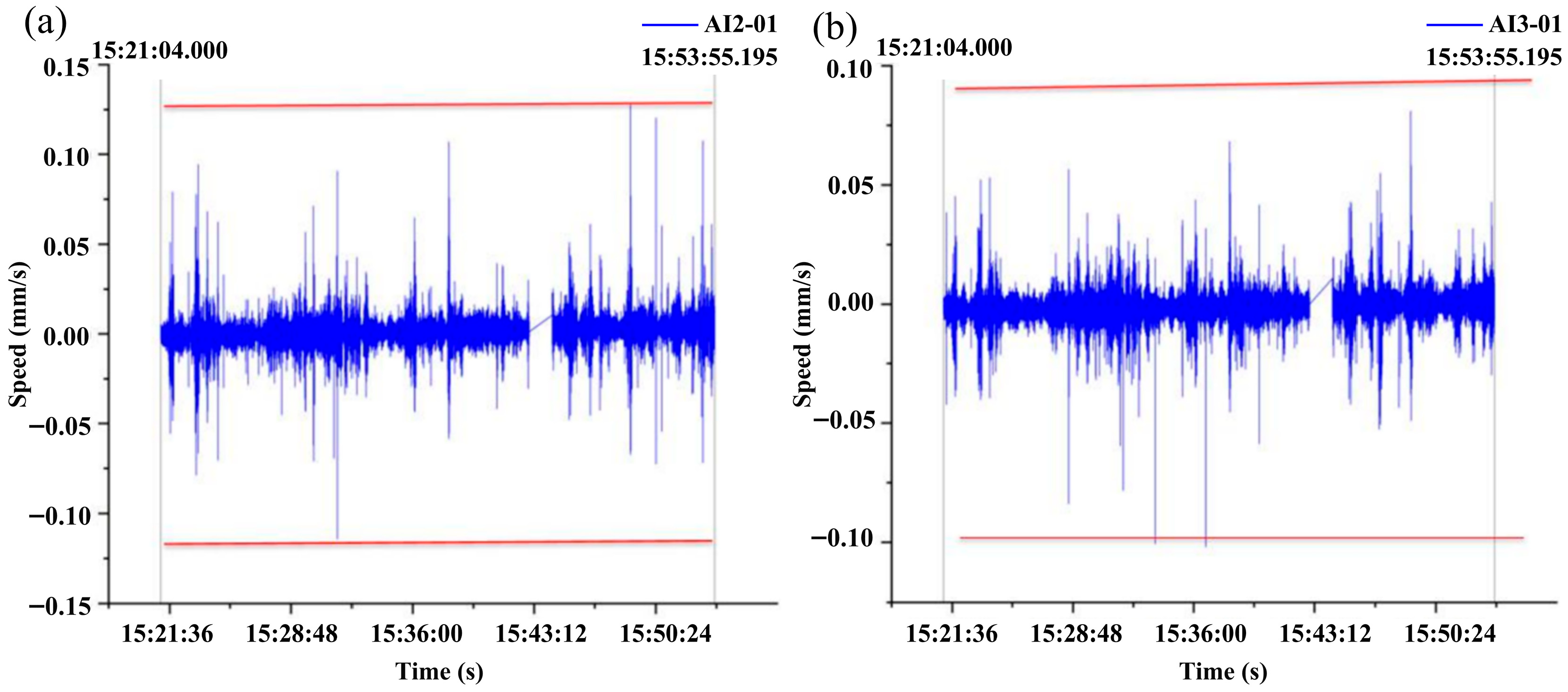
4.3. Vibration Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fraser, D. American bridges in New South Wales. Aust. J. Multi-Discip. Eng. 2010, 8, 23–31. [Google Scholar] [CrossRef]
- Miles, O. The Rolt Memorial Lecture 2013: The Public Benefit of Industrial Heritage-Taking a Positive View. Ind. Archaeol. Rev. 2014, 36, 85–96. [Google Scholar]
- Frank, G. Building on Historical Significance. Lane Rep. 2014, 29, 26–29. [Google Scholar]
- Kim, H.N.; Moo, K.H.; Gul, H.S.; Sun, B.B.; Kyu, Y.W. Towarda Balanced Heritage Management Plan for Old Stone Bridges Considering the Embedded Cultural Significance. Int. J. Archit. Herit. 2009, 3, 195–211. [Google Scholar]
- North, M. Spreading the load: The management of heritage timber truss bridges in the NSW road network. Aust. J. Multi-Discip. Eng. 2012, 9, 79–86. [Google Scholar] [CrossRef]
- Mort, M. A Bridge Worth Saving: A Community Guide to Historic Bridge Preservation; Michigan State University Press: East Lansing, MI, USA, 2008. [Google Scholar]
- Xiao, F.; Mao, Y.; Tian, G.; Chen, G.S.; Shi, X. Partial-model-based damage identification of long-span steel truss bridge based on stiffness separation method. Struct. Control. Health Monit. 2024, 2024, 5530300. [Google Scholar] [CrossRef]
- Xiao, F.; Mao, Y.; Sun, H.; Chen, G.S.; Tian, G.; Chang, C.M. Stiffness separation method for reducing calculation time of truss structure damage identification. Struct. Control. Health Monit. 2024, 2024, 5171542. [Google Scholar] [CrossRef]
- Ma, Y.K.; Chun, Q.; Hua, Q.J. Structural health monitoring and quantitative safety evaluation methods for ancient stone arch bridges. J. Cult. Herit. 2024, 70, 366–380. [Google Scholar] [CrossRef]
- Han, Y.D.; Chun, Q.; Wang, H.Y. Quantitative safety evaluation of ancient Chinese timber arch lounge bridges. J. Wood Sci. 2022, 68, 4. [Google Scholar] [CrossRef]
- Mai, K.Q.; Lee, S.M.; Lee, K. Assessment of historic stone arch bridge characterisation: Experiments and numerical model. P. I Civ. Eng-Str. B 2019, 172, 480–489. [Google Scholar] [CrossRef]
- Aytulun, E.; Soyoz, S.; Karcioglu, E. System Identification and Seismic Performance Assessment of a Stone Arch Bridge. J. Earthq. Eng. 2022, 26, 723–743. [Google Scholar] [CrossRef]
- Zhao, L. The Measurement Analysis of Solid Stone Arch Bridge Considering Arch Construction Stress. Shanxi Sci. Technol. Commun. 2014, 3, 59–64. [Google Scholar]
- Feng, C.; Wang, W.; Liu, C.; Zhao, X. Technical condition and bearing capacity evaluation of stone arch bridges based on appearance and experimental testing. Eng. Constr. 2024, 56, 76–83. [Google Scholar]
- Gong, Z.C.; Wang, Y.Z.; Duan, K.Y. Reliability evaluation of historic stone-arch bridge structure based on non-destructive testing and probability. Saf. Environ. Eng. 2024, 31, 120–128. [Google Scholar]
- León-robles, C.A.; Reinoso-gordo, J.F.; González-quiñones, J.J. Heritage Building Information Modeling (H-BIM) Applied to A Stone Bridge. ISPRS Int. J. Geo-Inf. 2019, 8, 121. [Google Scholar] [CrossRef]
- Deng, Y.; Jia, Y.G.; Li, A.Q. Structural Parameter Identification of Ancient Stone Arch Bridge via Three-Dimensional Laser Ranger Scanning. J. Perform. Constr. Facil. 2022, 36, 04022041. [Google Scholar] [CrossRef]
- Roselli, I.; Malena, M.; De felice, G. Health assessment and ambient vibration testing of the “Ponte delle Torri” of Spoleto during the 2016-2017 Central Italy seismic sequence. J. Civ. Struct. Health Monit. 2018, 8, 199–216. [Google Scholar] [CrossRef]
- Borlenghi, P.; Saisi, A.; Gentile, C. ND testing and establishing models of a multi-span masonry arch bridge. J. Civ. Struct. Health Monit. 2023, 13, 1595–1611. [Google Scholar] [CrossRef]
- Wang, T.C.; Ruan, Z.H.; Jiang, M.J. Shaking-Table Tests for Seismic Response of Arch Foot of a Long-Span Arch Bridge on Sand-Gravel Soil Sites Considering SSI Effect. J. Earthq. Eng. 2024, 28, 2066–2092. [Google Scholar] [CrossRef]
- Karalar, M.; Cufali, G. Structural Assessment of Historical Stone Bridges with the Finite Element Method under Dynamic Effects of Arch Shape: The Antik Iscehisar Bridge. Appl. Sci. 2023, 13, 10740. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, S.; Zhang, P.; Xu, T.; Zhuo, J. Application of Nondestructive Testing Technology in Quality Evaluation of Plain Concrete and RC Structures in Bridge Engineering: A Review. Buildings 2022, 12, 843. [Google Scholar] [CrossRef]
- Cao, W.; Shi, Y.; Mei, D.; Li, M.; Liu, D. Reconstruction of Ancient Stone Arch Bridge Via Terrestrial LiDAR Technology. IOP Conf. Ser. Mater. Sci. Eng. 2020, 960, 042063. [Google Scholar] [CrossRef]
- Eissa, E.A.; Kazi, A. Relation between static and dynamic Young’s moduli of rocks. Int. J. Rock. Mech. Mm Sci. Geomech. Abstr. 1988, 25, 479–482. [Google Scholar] [CrossRef]
- JTG/T D61-2005; Code for Design of Highway Masonry Bridges and Culverts. Ministry of Transport of the People’s Republic of China: Beijing, China, 2005.
- Grazzini, A.; Lacidogna, G. Mechanical Properties of Historic Masonry Stones Obtained by In Situ Non-Destructive Tests on the St. Agostino Church in Amatrice (Italy). Appl. Sci. 2021, 11, 6352. [Google Scholar] [CrossRef]
- JTG/T J21-2011; Specification for Inspection and Evaluation of Load-Bearing Capacity of Highway Bridges. Ministry of Transport of the People’s Republic of China: Beijing, China, 2011.
- Zhong, W.; Lin, Y. Identification of stone materials used in Wanning Bridge, a Beijing municipal cultural relics protection unit. Stone 2021, 9, 53–55. [Google Scholar]
- Liu, G.; Shi, C.; Liu, Y. Analyses of the Elastic Modulus Values of Masonry. J. Hunan Univ. Nat. Sci. 2008, 35, 29–32. [Google Scholar]
- Borlenghi, P.; Saisi, A.; Gentile, C. Determining structural models of a masonry tower from Architectural research and operational modal analysis. J. Build. Eng. 2025, 111, 113347. [Google Scholar] [CrossRef]
- GB/T 50452-2008; Technical Code for Protection of Historic Buildings Against Industrial Vibration. Ministry of Housing and Urban-Rural Development of the People's Republic of China, General Administration of Quality Supervision; China Architecture & Building Press: Beijing, China, 2008.




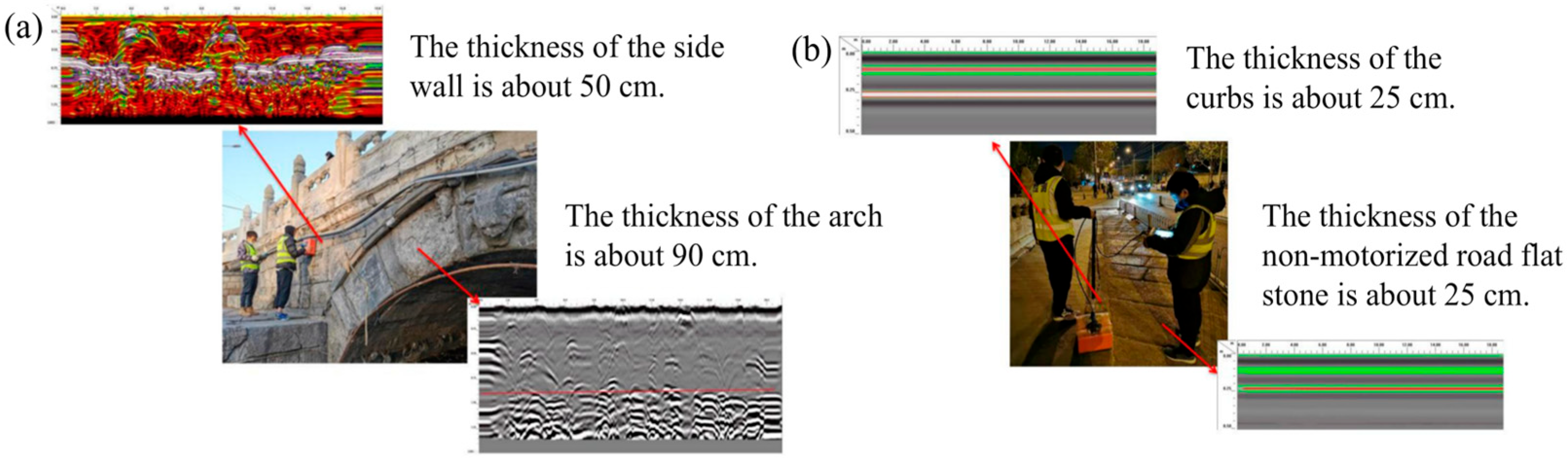

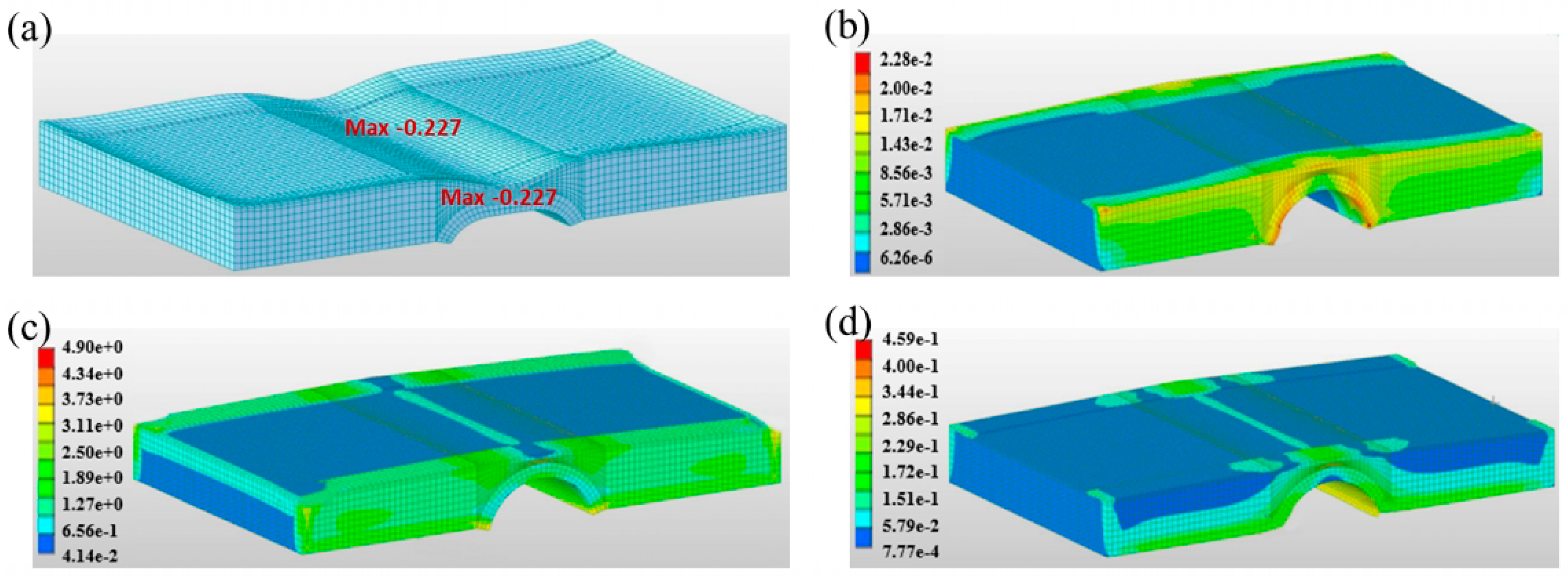



| Structures | Thickness (cm) |
|---|---|
| Arch ring | ≈90 |
| side walls | ≈50 |
| Trail bricks | ≈1.5 |
| Curbs | ≈25 |
| Non-motorized road flat stone | ≈25 |
| Flat stone at the vault of the non-motorized roadway | ≈10 |
| Longitudinal Wave Propagation Time (μs) | Transverse Wave Propagation Time (μs) |
|---|---|
| 35.6 | 73.8 |
| 35.2 | 73.6 |
| 36.4 | 85.2 |
| 36.4 | 77.6 |
| 34.8 | 75.2 |
| 42 | 80.4 |
| 43.2 | 79.6 |
| Longitudinal Wave Velocity Vp (m/s) | Transverse Wave Velocity Vs (m/s) | Dynamic Modulus of Elastic Ed (GPa) | Poisson’s Ratio ν | Dynamic Shear Modulus Gd (GPa) |
|---|---|---|---|---|
| 2489.62 | 1198.82 | 10.08 | 0.35 | 3.74 |
| Arch Ring and Side Walls | Backfill | Trail Bricks | |
|---|---|---|---|
| Young’s Modulus (GPa) | 5.08 | 1.25 | 5.65 |
| Poisson’s ratio | 0.35 | 0.28 | 0.3 |
| Density (kg/m3) | 2600 | 1400 | 2400 |
| Load Case | Vehicle Type and Quantity | Total Mass (t) | Loading Position | Number of Sensors |
|---|---|---|---|---|
| 1 | Two cars with two axles | 39.82 | Front axle in midspan | 29 |
| 2 | Rear axle is located in midspan |
| Monitoring Points | Coordinate | Initial Value | Measured Value | Calculate the Value | Residual Value | Verification Coefficient |
|---|---|---|---|---|---|---|
| 1 | −6.05 | 0.00 | 0.01 | 0.012 | 0.00 | 0.833 |
| 2 | −4.25 | 0.00 | 0.01 | 0.017 | 0.00 | 0.588 |
| 3 | −2.45 | 0.00 | 0.04 | 0.041 | 0.00 | 0.976 |
| 4 | −0.65 | 0.00 | 0.05 | 0.055 | 0.00 | 0.909 |
| 5 | 0.65 | 0.00 | 0.05 | 0.053 | 0.00 | 0.943 |
| 6 | 2.45 | 0.00 | 0.03 | 0.039 | 0.00 | 0.769 |
| 7 | 4.25 | 0.00 | 0.02 | 0.023 | 0.00 | 0.870 |
| 8 | 6.05 | 0.00 | 0.01 | 0.013 | 0.00 | 0.769 |
| Monitoring Points | Coordinate | Initial Value | Measured Value | Calculate the Value | Residual Value | Verification Coefficient |
|---|---|---|---|---|---|---|
| 1 | −6.05 | 0.00 | 0.02 | 0.023 | 0.00 | 0.870 |
| 2 | −4.25 | 0.00 | 0.03 | 0.038 | 0.00 | 0.789 |
| 3 | −2.45 | 0.00 | 0.06 | 0.085 | 0.00 | 0.706 |
| 4 | −0.65 | 0.00 | 0.09 | 0.106 | 0.01 | 0.849 |
| 5 | 0.65 | 0.00 | 0.09 | 0.105 | 0.01 | 0.857 |
| 6 | 2.45 | 0.00 | 0.07 | 0.083 | 0.00 | 0.843 |
| 7 | 4.25 | 0.00 | 0.03 | 0.036 | 0.00 | 0.833 |
| 8 | 6.05 | 0.00 | 0.01 | 0.019 | 0.00 | 0.526 |
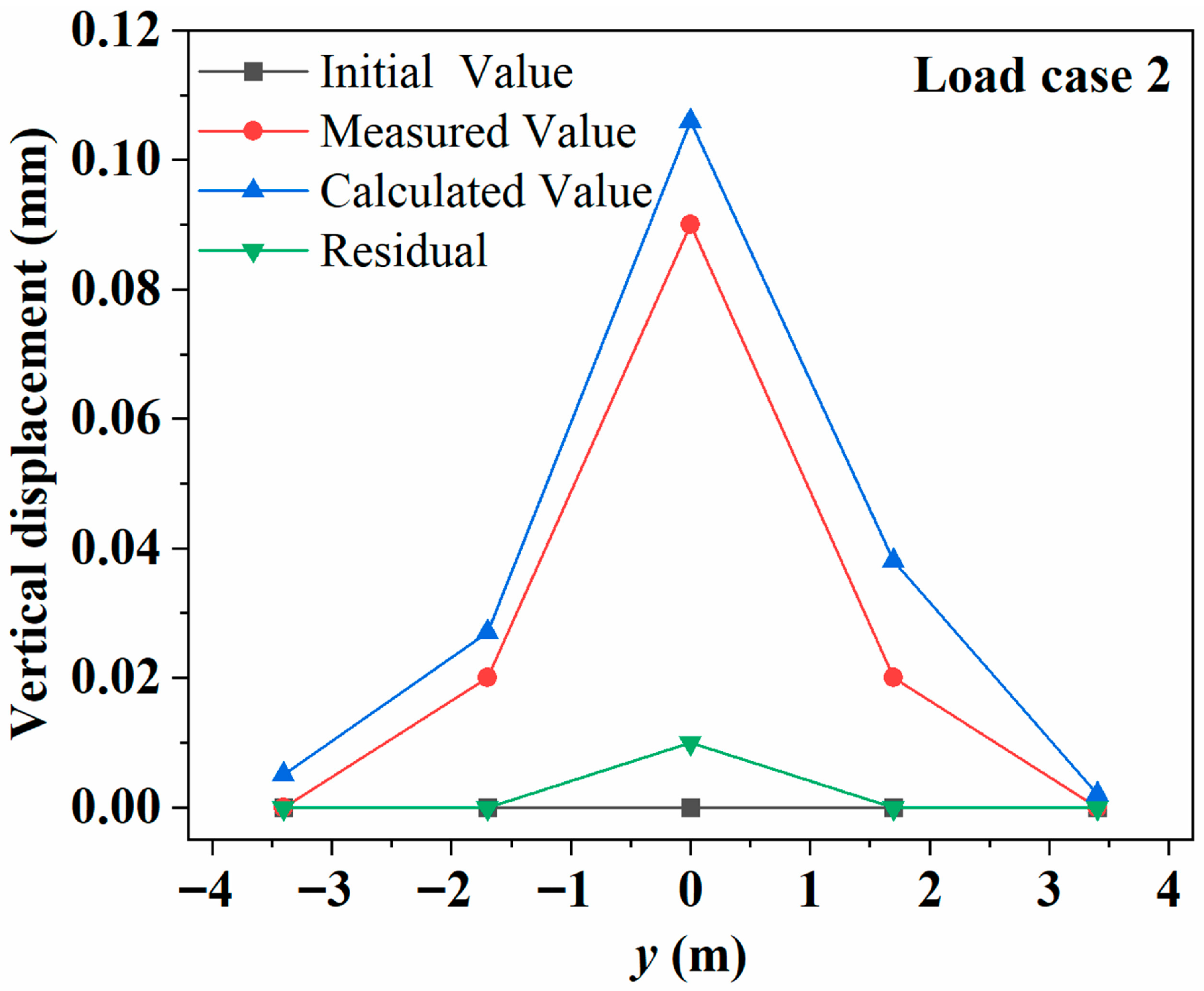
| Monitoring Points | Coordinate | Initial Value | Measured Value | Calculate the Value | Residual Value | Verification Coefficient |
|---|---|---|---|---|---|---|
| 1 | −3.4 | 0.00 | 0.00 | 0.005 | 0.00 | - |
| 2 | −1.7 | 0.00 | 0.02 | 0.027 | 0.00 | 0.741 |
| 3 | 0 | 0.00 | 0.09 | 0.106 | 0.01 | 0.849 |
| 4 | 1.7 | 0.00 | 0.02 | 0.038 | 0.00 | 0.526 |
| 5 | 3.4 | 0.00 | 0.00 | 0.002 | 0.00 | - |
| Load Type | Group 1 | Group 2 |
|---|---|---|
| Maximum deformation under dynamic load (mm) | 0.14 | −0.12 |
| Maximum deformation under static load (mm) | −0.09 | −0.09 |
| Young’s Modulus (GPa) | First-Order Natural Frequency (Hz) | Second-Order Natural Frequency (Hz) | Third-Order Natural Frequency (Hz) |
|---|---|---|---|
| 5.94 | 10.21 | 14.22 | 14.96 |
| 5.65 | 9.84 | 13.75 | 14.38 |
| 5.37 | 9.37 | 12.93 | 13.41 |
| 5.08 | 9.13 | 11.41 | 12.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Guo, Y. Structural Characteristics and Damage Analysis of Beijing Wanning Bridge Under the Coupling Effect of Dynamic Traffic and Subway Vibrations. Infrastructures 2025, 10, 251. https://doi.org/10.3390/infrastructures10090251
Zhu Y, Guo Y. Structural Characteristics and Damage Analysis of Beijing Wanning Bridge Under the Coupling Effect of Dynamic Traffic and Subway Vibrations. Infrastructures. 2025; 10(9):251. https://doi.org/10.3390/infrastructures10090251
Chicago/Turabian StyleZhu, Yuhua, and Yingmei Guo. 2025. "Structural Characteristics and Damage Analysis of Beijing Wanning Bridge Under the Coupling Effect of Dynamic Traffic and Subway Vibrations" Infrastructures 10, no. 9: 251. https://doi.org/10.3390/infrastructures10090251
APA StyleZhu, Y., & Guo, Y. (2025). Structural Characteristics and Damage Analysis of Beijing Wanning Bridge Under the Coupling Effect of Dynamic Traffic and Subway Vibrations. Infrastructures, 10(9), 251. https://doi.org/10.3390/infrastructures10090251




