Connecting Cities: Solving Optimal-Resource-Distribution Problem Using Critical Range Radius

Abstract

Navigating and planning optimal paths for resource delivery algorithms poses significant physical and technical challenges in urban areas, primarily due to the limitations of existing infrastructure. As smart cities continue to develop, the importance of these algorithms becomes increasingly evident. The saturation of current urban landscapes exacerbates the complexity of navigating essential resources. Navigating densely connected networks can be intricate and often requires substantial computational resources or additional algorithms, as it can easily transform into an NP problem. Unfortunately, there is a lack of explicit algorithms designed for navigating these networks, resulting in a dependence on heuristic approaches and previous network systems. This reliance can create computational challenges, as navigation in this context typically involves a combinatorial search space. Current advances in Morphological Mathematics (MM) help to model everyday tasks as processes in discrete spaces, which take advantage of the properties offered by the morphological operators. Morphological Shortest-Path-Planning (MSPP) is a recent solution that effectively calculates the optimal trajectory within complex graphs. By utilizing morphological operators, this approach takes into account discrete properties and maps the process as a complete implementation algorithm using integer logic. In larger cities, determining the optimal delivery route and time from a resource center is a common task. This process is influenced by factors such as average speed, travel time, and distance, which generate a complex graph representation of the town, complicating its analysis. This paper presents a strategy for computing and analyzing delivery times by determining the accessibility of reliable paths from a delivery center to potential destinations in dense urban areas. The strategy presented and the use of the MSPP approach are suitable for calculating the time spent delivering and the distance traveled in working journeys. The MSPP approach is found to be nearly $60\%$ more efficient than the reference approach for computing the optimal path in the case study presented.

1. Introduction

The nature, magnitude, and complexity of the road environment pose significant challenges for intelligent navigation systems [1,2]. One of the primary tasks in this context is selecting the most efficient route for logistical transfer management between two points of interest [3].

In this context, road infrastructure analysis is a critical component of urban and rural resources that support the livelihoods of the population. The infrastructure of transport routes is an indispensable part of the good development and economic growth of a region, reflecting its economic condition [4,5]. Transport and distribution logistics represent the final stage of the traditional product- and service-development life cycle [6]. This phase involves the effective, efficient, and safe transfer of goods and services from distribution centers to multiple delivery points, in order to meet the needs of the end customer. Companies need to reduce the variable costs and fixed costs associated with the processes of distributing goods, since these directly impact the final cost of the products. Specifically, variable costs usually include, among others, fuel costs when traveling a route or the time spent on each transfer. Therefore, these costs are directly influenced by the distance and duration of the trip. In a real-world context, it is necessary to consider various restrictions and parameters that depend on the route, length, and travel time [7,8,9].

Communication infrastructure is conceived as a complex network of interconnected networks that integrate land, rail, port, and air routes, whose function is to guarantee mobility and the efficient exchange of goods, services, and information. These elements are essential for facilitating communication between populated areas. Effective road communication is crucial, as it ensures that people, services, and supplies can reach their destinations quickly and safely, significantly enhancing the quality of life and driving socioeconomic growth in the population [10].

Currently, the literature defines an urban road network as a complex interconnected system, due to the large number of spatial components with intricate structures that interact with each other, which can be represented as a dense graph [11]. Roads in a city/town/country can be represented as a graph of interconnections, and finding the best route with minimum cost in a graph is a challenging task that requires NP-algorithms [12,13,14]. One of the most complex challenges arises when any position in an urban center does not rise with the road infrastructure due to the urban conditions.

An avenue network can be accurately modeled as a graph, and navigating this graph-based structure is a critical focus within graph theory. One of the primary objectives in this field is to identify the most efficient path. The literature offers numerous approaches to tackle this challenge, often constrained by the specific context in which they are applied. Nevertheless, these constraints enable the practical computation of solutions under certain conditions [15,16,17].

The main challenge we face is finding a suitable solution to the problem of finding the most efficient path. The network complexity of road infrastructures transforms the computation task for delivering the optimal solution into an NP-complete problem, as the working space is caused by combinatorial states that represent a complex network resulting from a large city. In the worst cases, the different approaches become undecidable [18]. Therefore, our study aims to develop a practical approach that identifies reliable solutions that closely approximate the optimal ones within a given timeframe and are suitable in terms of the computational resources needed. Finding the shortest path in a dense graph is considered an NP-complete problem [19]. Fortunately, the literature offers several methodologies that provide various efficient algorithms. These approaches use contextual information and operational experience to introduce a set of constraints, ensuring that the problem remains manageable within certain limits.

In this context, Morphological Mathematics (MM) offers a theoretical foundation for expressing and modeling systems as complex graph spaces through a set of structural operators. These operators create order relations that facilitate navigation and represent the modeling process as a discrete, enumerated space. This characteristic is crucial because it allows for a bijection with natural number spaces, enabling the expression of all morphological operators as integer operators. This approach optimally utilizes the computation capabilities of various CPU and GPU architectures, making it an ideal way of representing information.

MM introduces two fundamental operators: dilation and erosion. By combining these operators, we derive several filters, including opening, closing, and the morphological gradient. These operations modify input data based on a neighborhood constraint defined by a structural element, which acts as a vicinity criterion [20,21,22]. In most applications, MM serves as a generalized reference framework primarily used in grid structures. However, it is less frequently applied in graph spaces associated with a lattice through morphological operators [23,24].

In graph theory, the introduction of morphological operators enables the establishment of an order relation, which serves as a criterion for navigating and organizing complex graphs. These morphological operators function as predecessor and successor operators, creating a structured order relation and providing a theoretical mechanism for traversing complex graphs.

This work implements a generalized framework for identifying the minimum path between two designated points based on morphological operators, and a mechanism for traveling along these paths. The morphological approach begins with a minimally connected subgraph, and the total search space is referred to as the supremum. Morphological operators then define a travel mechanism based on the structural vicinity, which helps analyze possible paths and discover the optimal solution. The use of morphological operators creates an order relation that serves as a mechanism for detecting suitable paths in a directed graph. The Minimal Spanning Subgraph Problem (MSSP) represents one of the most recent morphological processes that utilize the properties of MM and provides an approach to computing the optimal path in directed grid spaces [25].

In the context of crowded cities, the delivery of goods and services presents a significant challenge due to the complex road infrastructure and varying operational conditions. Factors such as traffic lights, intersections, roundabouts, and traffic flow velocity—which can change depending on the time of day—make current planning methodologies increasingly complex. This complexity affects both response times and the efficient use of road infrastructure.

These factors have led to the development of new and efficient algorithms for computing path trajectories in dense networks. The Morphological Shortest-Path-Planning (MSPP) approach allows us to model the system as a discrete working space, utilizing a set of operators based on set theory. By integrating these elements, we can create efficient implementations using integer logic operators, which are well-suited for current processor architectures.

By referencing the MSPP algorithm alongside the physical locations of delivery centers, it becomes possible to devise effective strategies for analyzing local neighborhoods. This analysis aids in calculating delivery distance and time, thereby facilitating the implementation of planning strategies that take into account external factors such as time of day and average traffic flow velocity.

The proposed method involves sampling potential delivery destinations near the physical delivery center to assess the local vehicular infrastructure. This assessment aims to calculate the expected response times and travel speeds at various times of the day. The information collected will help identify reliable routes and trajectories throughout the week. These delivery strategies aim to enhance services, as the rapid delivery of goods—enabled by e-commerce and urban logistics—can significantly reduce response times in large cities and optimize the use of urban resources.

This work presents a case study analyzing the applicability of the MSPP algorithm, which was previously proposed and validated by [25]. The aim of this study is to develop a strategy for planning the most reliable paths to optimize resource distribution by calculating optimal routes based on the concept of critical impact range. This concept defines the range of trajectories generated from a distribution center and their effects when navigating through a graphical representation of a dense urban network of manageable complexity. The optimal routes are computed using the MSPP algorithm, which provides an efficient framework for navigation in dense graphs.

The proposed strategy is validated through an experimental process that identifies the most efficient routes, using a geographic image layer of the avenues in Mexico’s largest and most representative city as a foundation. This study focuses on distribution centers located in economically significant and densely populated areas, characterized by complex road networks and numerous interconnected avenues. These regions experience considerable variations in traffic speeds throughout the day. To analyze this, the MSPP algorithm is implemented in the case study. The results obtained demonstrate the effectiveness and applicability of the proposed methodology in real, dynamic, and complex urban environments.

MSPP, a contemporary method for urban path planning, offers several advantages when navigating crowded cities. Its primary characteristic is the use of grid–graph scenarios, which provide an efficient representation of large, densely populated urban areas with complex vehicular infrastructures. The basic algorithm ensures that all networks are connected. However, a modified version [26] enhances this capability by detecting disconnected networks and determining whether there is no connection between two locations within the urban infrastructure.

The main contributions of this paper are as follows:

• A full mathematical morphological strategy for analyzing reliable path trajectories from a delivery center.
• The calculation of reliable paths under the local neighborhood for delivering goods.
• The computation of the delivery response time during the daytime and on working days for different delivery centers.
• A proposed methodological framework to inspect the local neighborhood from a delivery center, aimed at computing the average response time for delivering goods.

The rest of the article is organized into sections. Section 2 presents a literature review of works considered relevant to the subject of this study. Then, Section 3 describes the details of the proposed method. Section 4 presents the experimental analysis and the results obtained, and discusses the findings. Finally, Section 5 presents the conclusions, discusses the limitations of the proposed case study, and describes any future work that may arise.

2. Literature Review

Since the beginning of the COVID-19 pandemic, the world has experienced significant changes in its consumption dynamics, highlighting a notable growth in demand for goods and services. This increase has generated significant opportunities in urban freight distribution. The task of distribution plays a fundamental role as the basis for commercial activities that support the economy and the dynamics of growing cities. However, indirect problems related to increased traffic flow and the quality of services have also been detected [27].

The fundamental problem of vehicle routing initially arises as an optimization task that complements the classic routing problem used in maritime oil transport between refineries. In this sense, a specific set of customers with potentially variable product demands is defined, and a centralized distribution center manages the delivery of goods to these customers through a predefined transport fleet that allows for efficient organization of distribution routes. The main objective is for the distribution of products to reach their destinations, covering the distance with the lowest possible cumulative cost, which in turn implies the minimization of operating resource costs and operating times. Various constraints defined by this use case are also considered [28].

Moutaoukil [29] classifies the problems associated with urban freight distribution into three large groups: the first, related to economic impact, covers problems of operational inefficiency and high service costs, among others; the second, focused on environmental impact, considers aspects such as ${\mathrm{CO}}_2$ emissions, global warming, and excessive consumption of fossil fuels; finally, the third is related to social impact, which is reflected in issues of public health, traffic accidents, noise pollution, and customer satisfaction.

Based on this evidence, two key components can be identified that contribute to addressing these areas of opportunity. The first component generally focuses on the analysis of optimal routes, intending to reduce the calculation of discretized geodesic distances along avenues that must be traveled efficiently, minimizing costs and delivery times, and improving the customer experience. The second component focuses on analyzing the impact radius of distribution centers and the town topology, particularly in complex cities, to enable greater efficiency in delivery planning through parameters such as optimal routes and average traffic speeds. In complex cities, greater efficiency in delivery planning can be achieved through the use of parameters such as the best routes and average traffic speeds.

2.1. Distribution Center Location Logistics

The literature describes a hub as a unified distribution center where key tasks such as receiving, sorting, storing, and processing goods of various types are performed. These centers are essential for logistics management, as they allow for the implementation of more efficient distribution strategies, significantly contributing to cost reduction. Furthermore, each transport unit that departs from the distribution center can be considered a mobile mini-hub, as it transports various quantities of goods that are delivered along a pre-planned route, serving multiple customers located in the same area. The problem of hub location consists of determining the optimal locations for these centers, ensuring an efficient flow of goods. To achieve this, it is necessary to consider the operational scope of the fleet, avoiding areas with high overlap in delivery routes that could hinder or impede the logistics process [30].

Considering the aforementioned challenges and areas of opportunity, a disproportionate growth in demand is identified, along with urban management and logistics problems. Therefore, analyzing the impact radius based on distribution centers located in densely populated areas represents a promising strategy to reduce these problems [31,32].

Some works have proposed models based on the optimal location of micro-hub networks that allow the largest possible area in urban delivery services to be covered, as in [33]. These models are based on optimization algorithms for agile routing, which have proven effective in cities with high logistical complexity, such as the case study of Barcelona, where a large number of distribution centers with variable impact radii are required [10].

Bard and Nananukul [34] propose an integrated framework that includes production, inventory, and distribution planning, with the objective of satisfying customer demand by minimizing total costs. This type of model focuses on clearly defined objective functions, which include (i) minimization of logistics costs, considering the number of vehicles, their types, and load capacities; (ii) minimizing the total distance traveled; (iii) determining the minimum fleet necessary to complete deliveries; (iv) minimizing downtime or empty-vehicle runs; and (v) reducing penalty costs associated with non-compliance with customer service levels.

To address this problem, the model presented in [35] proposes a single hub as a unified distribution center with time-varying demand, a finite planning horizon, and a homogeneous fleet of vehicles for deliveries. The routing problem is solved using reactive tabu search, which allows for finding feasible solutions to the entire problem. However, the model faces significant challenges as the amount of information analyzed increases, due to the high computational complexity of the proposed approach.

2.2. Optimal Routes Approach

In the context of intelligent navigation, route planning represents one of the most relevant areas to consider. Some works introduce the concept of symmetry through bidirectional search techniques, thus optimizing the route calculation process. In practical scenarios, where complex real-world environments are represented as densely connected graphs, planning algorithms such as ${\mathrm{A}}^{*}$ have established themselves as fundamental tools for determining the route with the lowest cumulative cost, according to a metric defined based on the analysis case.

To address this task, there are various approaches aimed at obtaining optimal routes. One of the most classic approaches is based on graph search techniques, among which the most notable are Dijkstra’s algorithm [36]—which has been improved and adapted with use-case-specific restrictions, expanding its applicability—and the ${\mathrm{A}}^{*}$ algorithm, which uses a heuristic function to estimate the minimum cost required to reach the target node [37].

On the other hand, sampling-based algorithms, such as Rapidly Exploring Random Tree (RRT) [38] and Branch and Bound (B&B) [39], build random trees from samples of the search space, discarding trajectories that are not viable for achieving the objective.

However, there are strategies based on optimization functions, among which genetic algorithms [40], particle swarm optimization (PSO) [41], and ant colony optimization (ACO) [42] stand out, among others.

In [43], a model is proposed that addresses the problem of vehicle routing under delivery-time-window constraints. The total distribution radius is calculated using the ${\mathrm{A}}^{*}$ algorithm, considering objective functions that incorporate penalties for delivery overtime, as well as customer satisfaction. This process is optimized using a hybrid algorithm based on ant colonies. Along these lines, various approaches are compared in

Table 1. Approaches to computing the best path trajectory.

Work	Method Category	Working Space	Remarks	Advantages/Disadvantages
Graph Search Methods
Dynamic programming and Lagrangian heuristics algorithms [9]	Graph Search	Graph	This approach uses a new mathematical model that incorporates numerous complex constraints of classical routing problems. A dynamic programming solution is offered, dividing the general problem into subproblems, which are solved repeatedly and stored to avoid unnecessary recalculations.	-Guarantees optimal solutions to the search problem. -Limited application for dynamic constraints.
Optimal traffic allocation approach [44]	Graph Search	Grid	This approach employs an optimal traffic allocation technique aimed at minimizing average travel time. This methodology has proven effective in practical contexts, particularly in traffic management during disaster evacuation scenarios where densely populated areas generate increased traffic congestion on major arterial roads, increasing travel time to safe areas.	-High computational cost for large networks. -Efficient for route planning with reduced cumulative cost (short distances).
Optimization approach
Adaptive genetic algorithm [17]	Optimization	Graph	An adaptive genetic algorithm is introduced that improves local optimization capabilities by exploring large neighborhoods. This algorithm is applied to an urban logistics distribution model with variable constraints and time windows. The objective function considers both total cost minimization and customer satisfaction maximization.	-Efficient in cases where there are complex restrictions. -Slow convergence process.
The tabu search algorithm [35]	Optimization	Graph	An approach to supply chain optimization is presented, focusing on the coordination of production, inventory, and delivery planning, with the goal of minimizing logistics costs. The model considers a single production point, variable customer demand, and a fleet of delivery vehicles. To solve the problem efficiently, a reactive tabu search procedure is implemented.	-Low susceptibility to stagnation in local optima. -The results are affected by parameter tuning.
Heuristic approach with Integer Programming [5]	Optimization	Graph	This heuristic incorporates fairness and dispersion criteria as auxiliary metrics in solving the delivery problem. It also considers multiple variables associated with the loading, unloading, and transfer processes, among other factors that can influence the estimated delivery time. Given that this is a dynamic stochastic problem, an integer programming-based formulation is proposed, allowing for an approximate static–deterministic solution.	-Robust approach to path planning. -Only an approximation of the global solution is obtained.
Hybrid Approach
Improved ${\mathrm{A}}^{*}$ algorithm and Ant colony algorithm [43]	Hybrid	Graph	This method proposes a logistics route optimization model based on the relationship between maximum customer satisfaction and minimum total distribution costs. The model considers two objective functions: the first focuses on minimizing costs associated with ${\mathrm{CO}}_2$ emissions, overload, and distribution, while the second seeks to maximize customer satisfaction. To solve the problem, improved ${\mathrm{A}}^{*}$ algorithms and ant-colony-based optimization techniques are implemented.	-Balance between exploration and objective functions. -Approach with high computational cost.
Agile routing algorithms [10]	Hybrid	Graph	An adaptive algorithm is proposed that efficiently determines the optimal number and ideal location of micro-distribution centers, optimizing urban freight logistics using heuristic methods and machine learning. This approach considers minimizing the total distance, associated costs, and ${\mathrm{CO}}_2$ emissions throughout the distribution network.	-Flexible, adaptable, and scalable strategy. -Susceptible to the quality of the input data.
Alternative approach
Morphological Shortest-Path-Planning Approach [25]	Morphological	Graph and Grid	An innovative approach is proposed that defines a general framework based on operators from Morphological Mathematics, from which two new operators are generated. These operators establish an incremental natural-order relationship, determined by the optimal least-cost path between two points of interest, with a computational complexity comparable to that of state-of-the-art methods.	-Computational complexity competitive with other techniques. -Being a recent algorithm, it has weak validation.

, considering the search space addressed in each study, as well as the constraints and key factors included in the proposed models.

On the other hand, graph-based search approaches that determine the best possible route have proven to be a robust framework for this type of study [25,26]. This approach focuses on analyzing and predicting maximum reach ranges based on the geodesic distance, defined by the distribution environment and strategic location of centers in areas with dense commercial traffic, such as Mexico City. In addition to considering the geodesic distance as a relevant factor, the average traffic speed is incorporated into the analysis according to the time of day at which the delivery is simulated, as well as the delivery area in which it is carried out.

3. The Proposal

In this section, the main contribution of this paper is described: an efficient strategy to analyze starting from a distribution center, the capability to access all possible distribution zones, and computing the most feasible routes. This strategy employs the MSPP approach, proposed by Perez-Ramos et al. [25], which offers better balance in terms of computational complexity and computational resources than other well-accepted methods.

3.1. Search Criterion

The MSPP method employs morphological operators to evaluate the spatial neighborhood to identify potential path trajectories. This technique involves executing a series of dilation operations initiated from the origin node. Upon reaching the destination node, the frequency of dilation for each node generates a new topological surface. On this surface, the paths connecting the origin to the destination nodes represent the shortest trajectories, adhering to a semi-order relation. The semi-order relation is defined by the number of times each node was dilated. The main advantage of this approach is that it can be considered a hybrid search approach. While other approaches analyze the working space first by width or first by depth, this approach combines both methods, resulting in the first-depth–width approach. It takes advantage of the search-width criterion, which helps to create a small hypothesis that searches simultaneously over the working space, reducing the number of iterations required to reach the destination.

The MSSP algorithm starts with an initial graph denoted by $x_0 \subset G$, where G is the working space. In our case, we refer to G as a power set of the grid space of connected zones from the grid, i.e, all possible connected subsets that serve as the initial state. After defining the initial position, $x_0$, it undergoes a dilation process that iterates through all connected zones to $x_0$ and $x_i$ from the i-th iteration. Notationally, the destination is represented by D. The algorithm iterates until $x_i$ becomes intersected over its vicinity with the D subset. Then, the natural-order relation built from the number of times each node was dilated is used in reverse order to determine all possible path trajectories that correspond to the optimal solution.

The details of the algorithm are as follows: It uses the dilation operator ${\delta }_{\lambda }$ iteratively, where each iteration reaches the neighborhood zones with the $\lambda$ criterion of connectivity. Each dilation performed in the graph represents a step in the direction of all connected zones of the working space. Eventually, under the assumption that the destination becomes connected, it reaches it. This iterative process is encapsulated in a covering operator, which, in addition to dilating the graph, computes the number of times each node becomes dilated. Under this operation, we observe that the first node (reference) is eventually dilated n times. If the destination is reached at n times, the dilation frequency of the vicinity decays to unity until it reaches the destination, which has 1 dilation. Using a reverse operation, the path node that represents this step denotes the optimal path. The algorithm has the advantage that this consideration is not limited to one solution, i.e., the set of paths that follow these considerations represents the set of solutions with the minimum path.

This approach demonstrates computational efficiency by exploring both width and depth, thereby enabling the effective elimination of node regions that do not contribute to the optimal solution. The algorithm works on the assumption that solutions can be accessed through dilation, which may lead to a non-decidable state. However, as discussed in [25], this issue is addressed by implementing a conditional test that verifies whether the solution remains within a non-connected graph structure.

This characteristic makes it feasible to use the algorithm for work purposes, which necessitates an efficient algorithm that is decidable over the best path trajectory to be applied in the infrastructure of dense towns. The pseudo-code of MSPP is presented in Algorithm 1. However, in real scenarios, this algorithm might be given a high amount of consideration. The working space must be fulfilled to ensure connection and provide a nearly complete solution. If a destination place is not connected, the algorithm cannot be decidable.

Algorithm 1 Pseudo-code of Non-MSPP based from [25]

1: procedure MSPP ($x_0, D, x^{*}, G, \lambda$)   2:    $M \leftarrow {\delta }_{\lambda }·\underset{\mathrm{n}-\mathrm{times}}{\underbrace{\dots }}·{\delta }_{\lambda }·x_0$ until reach D with the neighborhood $\lambda$   3: ▹ Adopting as origin the starting point in the graph, through dilation the destination is reached.   4:    if D will not reach then   5:    return null path, the destination does not belong to the graph.   6:    end if   7:    $M^{ - 1} \leftarrow {\delta }_{\lambda }·\underset{n-\mathrm{times}}{\underbrace{\dots }}·{\delta }_{\lambda }·D$ until reach $x_o$ with the neighborhood $\lambda$   8:  ▹ From destination D build a list with all possible paths that follow the step-by-step relation semi-order.   9:    $P \leftarrow DetermineOptimalPath$ 10:    $C \leftarrow ComputeCost\left(P\right)$ 11:    return P, C 12: end procedure

The above limitation is improved in the second implementation of the algorithm given in [26]. The second implementation adds a restriction on the covering operator, which makes it decidable. This implementation adds an extra halting condition without increasing complexity, adding robustness. The implementation of the enhanced MSPP is presented in Algorithm 2, which introduces this algorithm and provides an in-depth explanation of the algorithm’s functionality, evaluating all theoretical capabilities and proving why the final lattice computed becomes the shortest path over the workspace.

Algorithm 2 Pseudo-code of decidable MSPP based on [26] and $D \subseteq x^{*}$

1: procedure SearchProcess($x_0, D, x^{*}, G, \lambda$)   2:    $M \leftarrow {\delta }_{\lambda }(x_0, D)$  ▹ Iterates over the initial node until it reaches the destination.   3:    $Mn \leftarrow$ Associate the matrix cost   4:    From the reference position $s_i \in S_0$   5:    $C \leftarrow$ Initializated with $M{n}_{x_0}$   6:    $P \leftarrow$ Initialized with $\{\varnothing \}$   7:    while until find a solution. do   8:    Compute the best step $n_{i+1} \leftarrow C\left(n_i\right)$ according c   9:    Adds current traveling node $\left\{(n_i,n_{i+1})\right\}$ to P 10:    Advance to the follow step $n_{i+1}$ 11:    Update path cost C width $M{n}_{n_i}$ 12:    end while 13: return The path trajectory P and associated cost for traveling C 14: end procedure

3.2. Implementation Issues

To summarize the concepts introduced in this chapter, the proposed methodology focuses on selecting a distribution center and evaluating its surroundings to estimate delivery routes. This process involves considering the size of the access area based on the chosen location, the distribution of vehicles, and the maximum distance that needs to be covered. This distance depends on the delivery infrastructure and can vary; larger zones tend to be more beneficial, as they reduce complexity in the analysis.

Next, the local neighborhood is analyzed to understand the topology (road infrastructure) surrounding the distribution center. The topology is crucial because the complexity and constraints of access can affect the actual distance that needs to be traveled to deliver goods. The distance traveled is referred to as the geodesic distance, as it represents the real adjacency of the roads that form the sequence of routes for delivering the goods. The Euclidean distances (the distance from the delivery center to the location in a direct line) are used to determine the complexity of delivering to each destination zone.

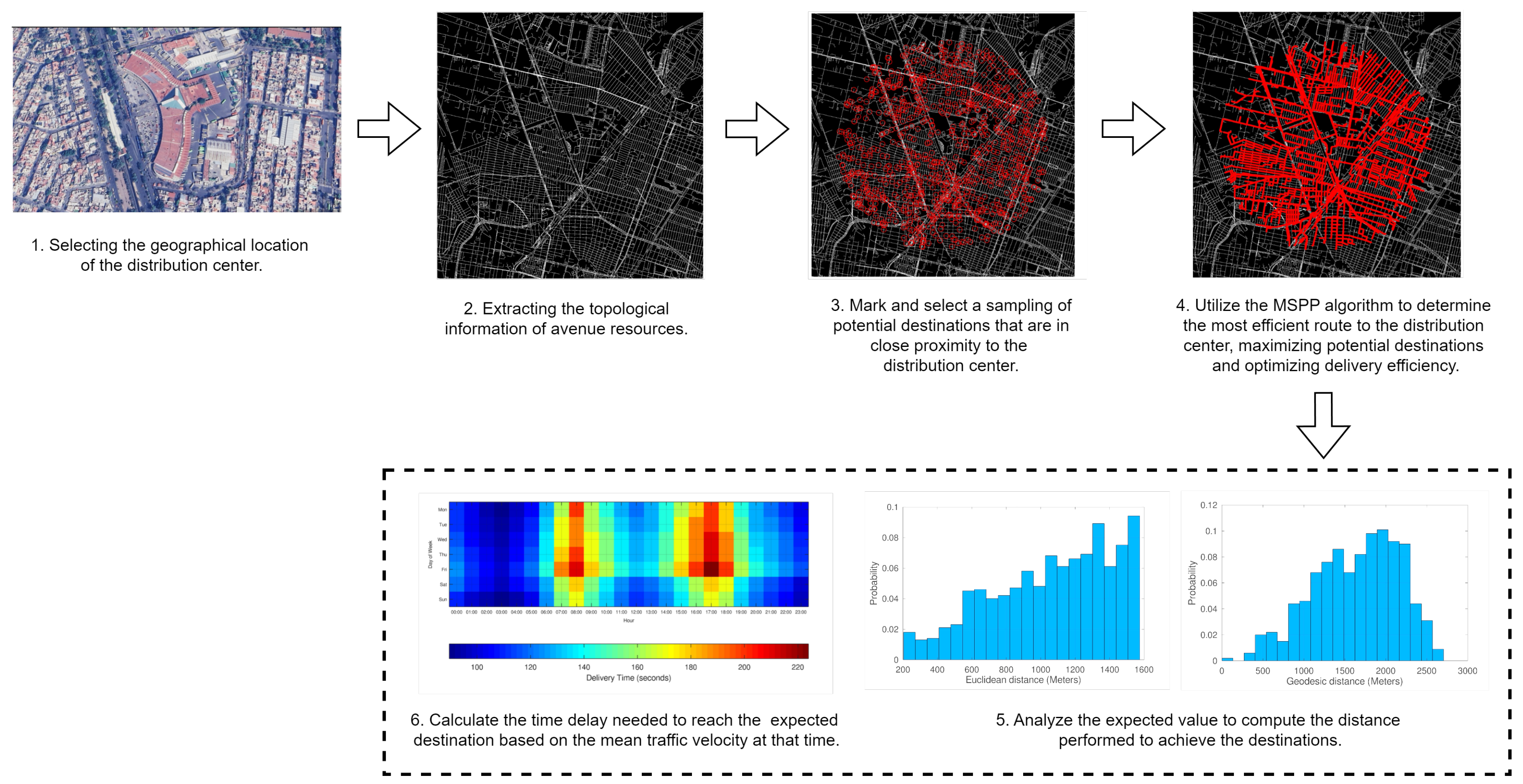
Following this, we used the neighborhood topology along with prior information about common destinations and potential delivery locations to assess neighborhood accessibility. Figure 1 and

Table 2. Step 1: Table of distribution center location.

No	Place	Town Area	Reference (Figure 1)
1	Churubusco	South of town	(a)
2	San Lázaro	Center–east of town	(b)
3	Santa Anita	Center–south of town	(c)
4	Terminal Norte	North of town	(d)
5	Zócalo	Center of town	(e)

illustrate the destination zones; these zones are used as a reference to understand the topology, establish the best criteria for delivering goods, and evaluate the best response time. Formally, the delivery center is denoted by a tuple $D = (x_1, x_2)$, which indexes the physical location in the geographical grid and the list of possible destinations $\mathrm{\Theta } = \{(x_1, x_2)\dots \}$ that represent geographical delivery locations. The maps were taken from Google Maps [45].

Based on this data, we computed a list of optimal delivery paths using the MSSP algorithm described in Algorithm 1. The optimal routes computed denote the geodesic shortest path and represent the most suitable routes to be taken. This list produced a set of optimal routes for deliveries in the area.

The previously visited places, combined with a sampling process, form a list of destinations. The first step involves determining their geographical locations. Once a map of the vitality structure is obtained, the next task is to compute potential and probable destinations within a proximity radius using the MSPP algorithm. This process is illustrated in Figure 2 for the Terminal Norte location. The geographical zone indicates the location of the distribution center. In this context, the proximity area is defined as approximately 2 km, the distance an operator can cover on a motorcycle. Using a motorcycle is preferred because it offers a dynamic mode of transport that is more effective in crowded scenarios.

The MSPP approach offers a good balance in terms of complexity and computer resources used. Its capability to work as a morphological process enables its implementation with integer logic, allowing for its efficient execution on most processor architectures. In [25], the authors conduct an in-depth analysis of the computational complexity of the approach based at three different algorithm stages, where all complexity measures are given with Big O notation in the worst case: (I) the analysis of morphological operators used; (II) the total of computational complexity required in the worst case to compute the best path; and (III) the complexity required to select the best choice at each step in the traveling process.

The complexity of the algorithm is expressed by Equation (1), where the principal expression parameters are given by a connected subgraph of $x^{*}$ from the working space G; the parameter $\lambda$ represents a subset and denotes the neighborhood criterion named structural element; and the degree connection in the nodes $x^{*}$ is expressed by $o^{*} = \left|\lambda \right|$. Finally, two extra parameters are defined by a constant value $\tau$, which takes the value 2 or 3, depending on whether the process is weighted or not, and a k factor that denotes the maximum dilation required to reach a destination and avoid the algorithm becoming undecidable. Finally, to conduct a detailed complexity analysis, we need to determine the covering operator’s complexity, which is expressed as

$$O\left(\tau \right|x^{*}| \times o^{*} \times |\lambda | \times k)$$

(1)

The complexity required to build the best trajectory after reaching the destination D is given by $|M_{x_0}|$ and the C criterion, resulting in

$$O\left(\right|M_{x_0}\left|\right) \times O\left(\right|N\left|\right)$$

(2)

Finally, the total complexity is the result of adding Equations (1) and (2) resulting in (3):

$$O\left(\tau \right|x^{*}| \times o^{*} \times \left|\lambda \right| \times k)+O(|M_{x_0}\left|\right) \times O\left(\right|N\left|\right)$$

(3)

4. Experimental Analysis and Results

A case study was conducted to determine the delivery time on different days of the week and during daytime hours for Mexico City. The case study consists of an analysis of the setup of different delivery centers. Each delivery center aims to deploy various goods using motorized vehicles. The delivery centers are located in different city zones, resulting in varying local conditions in each case. The topology and complexity of vital resources, constraints, and behavior differ significantly. Despite the close similarity in the distance to be covered, the response times and distances are distinct. The delivery task starts from a delivery center and considers the locally accessible destinations surrounding it. Then, the proposed strategy aims to analyze the average distance and time required to reach a destination. This strategy aims to demonstrate and calculate the response along the most reliable and efficient paths to communicate with various destinations from the delivery center. With this information, a plan that takes into account the best times and distances will be generated. The local complexity of urban infrastructure poses a challenge in terms of efficiently determining city topology and zone connections. This kind of analysis helps establish better communication criteria, especially in dense urban towns like Mexico City. The applicability of the proposed approach is described in the cases presented in this study for further analysis.

4.1. The Context of Applying the Proposed Strategy

Planning and estimating deliveries from a distribution point in a large town represents a significant opportunity, as it directly impacts customer satisfaction and can make delivery planning more cost-effective, depending on the town’s local dynamics. To address this challenge, a strategy focused on delivery locations around a store was proposed. This strategy leverages potential delivery areas and sub-sampling locations to optimize the delivery process, enabling a better understanding of the local topology around a delivery center and the potential for proposing efficient deployment that manages delivery and distribution more efficiently.

By using this information, we can define a maximum delivery distance based on the physical distance from the store or delivery center. A list resulting from available locations enables us to determine the optimal delivery path using the MSPP approach, which constructs a dense graph based on the city’s layout. This graph is created to show the center of the average distribution within the maximum proximity radius. The computation considers the town’s structure and direction within this proximity perimeter.

The continuous evaluation of the best delivery path yields insights into the optimal physical delivery route. As a result, the distance distribution across all delivery routes provides valuable data, enabling us to calculate the expected distance that will need to be covered.

While physical distance is an essential factor, it only accounts for part of the task. Traffic flow throughout the day significantly influences the average speed of navigation within the town, which can be represented as a delay in arriving at each destination in our graph. By combining the average traffic flow with the expected delivery distances from the store throughout the day, we can anticipate the delivery times to various locations. This information serves as the basis for creating a delivery planning strategy, which is the primary objective of this work.

4.2. The Case Study

Mexico City, the capital of Mexico, is divided into five main zones: south, north, east, central, and west. It is the most densely populated city in Mexico, with the highest population density found in the central–northern zone. Consequently, certain densely populated areas have been identified where delivery services often incur high costs due to the time and distance needed for deliveries. The choice of location for establishing a delivery center directly impacts response times, delivery distances, and the local complexity of the viaduct infrastructure. These factors are context-dependent and influenced by vehicle flow at different times of the day and varying workdays throughout the week. Figure 3 illustrates the location of Mexico City and the candidate zones chosen for analysis, labeled as 1 to 5, representing strategic zones for installing delivery centers. The maps in Figure 3 were obtained from Google Earth and are used as a general reference to locate the areas analyzed in Mexico City [45]. In particular, Table 2 summarizes the specific candidate zones considered, indicating in a small map the geographical places that correspond to each center set up to deliver supplies.

The implementation of the proposed approach involves using the current town topology while adhering to existing flow restrictions and directions. In this analysis, the proximity radius is approximately 2 km (which represents a coverage area of around 12 km²), which is a manageable distance for a motorcycle. To illustrate the case study, we focus on one of the selected locations, Terminal Norte, and present the complete results for all locations in Section 4.4.

The experimental process requires the use of the MSPP (2024) algorithm [25], which offers a balance of complexity and computational resources. Please note that the analysis should be adjusted slightly according to the base algorithm used to compute the optimal path. The experimental process is conducted using the following steps, which are described in detail.

• Selecting the geographic location of the distribution center: In this process, well-known distribution centers in the city are selected, located in central, high-traffic areas of Mexico City (see Table 2). This selection aims to evaluate the efficiency of the proposed approach in representative environments with high demand for this type of service. The selection of a particular zone is dependent on the delivery requirements to provide goods in the geographical zone.
• Extracting topological information on avenue resources: This process involves encoding cities as a connected graph and creating nodes through this encoding process by modeling the map as a graph space with a 2D grid topology. In this topology, connected nodes represent sub-sampling from an area that constitutes a map. Intersections between avenues, which represent vital infrastructure, are used in a section of the map of the densely populated and complexly structured city of Mexico City. The graph is weighted based on the distance in a defined metric space to represent the connections between nodes accurately. The vertex detection method is used to segment the road and identify the maximum values of the distance transformation, which serve as nodes. The interconnection between the avenues generates arcs that serve to connect each pair of nodes.
• Marking potential destinations near the distribution center: This step involves the previously known delivery points and those that will eventually become candidate destination zones. The working space will be considerably ample for analysis; random sampling is conducted to simulate the final delivery or distribution locations and the demand for goods. This sampling become equiprobable with a uniform random distribution. These delivery points will serve as a reference for calculating the optimal route, considering the average speed variables defined for the area being analyzed.
• Application of the MSPP algorithm to determine the most efficient distribution route: This process defines route reach areas from a central distribution point and the maximum reach. This critical radius is defined under a Euclidean metric and geodesic distance. The Euclidean distance represents the physical neighborhood to be covered, and the geodesic distance represents the real distance covered after performing the deployments, considering the topology of the map. The structure of the avenues, streets, and highways defines the trajectories with a radius based on the geodesy of the scenario, calculating the maximum-reach radius of a service.
• Analyzing the expected value to calculate the distance traveled to reach the destinations: In this stage, the impact is analyzed in multiple representative areas of the main distribution points in Mexico City. The objective is to evaluate the distance traveled to reach any target point, starting from the distribution center, which is considered the center of the affected area, considering both the expected Euclidean distance and the geodesic distance. The computed optimal paths help us determine the actual distances traveled during the delivery process, thereby enabling the computation of delivery times.
• Calculating the time delay required to reach the expected destination based on the average traffic speed: Finally, a complementary analysis is carried out by comparing the length of the maximum-range geodesic routes with the estimated time it takes to travel in an average week, based on average traffic speed values in Mexico City for urban area.

4.3. Implementation Details and Computational Resources

For computational analysis, simulations were performed using GNU Octave 10.2.0, a free software environment compatible with MATLAB R2025a and using the M-language. This tool was used to implement algorithms for data processing and numerical analysis, ensuring the reproducibility of the experiments and facilitating access thanks to its open-source nature. The OpenBLAS Library supports specific Octave implementations as of version 0.3.30, which enables the use of multicore processing in certain matrix transformations. This library enables the use of morphological operations that support the use of Integer graph representation, which helps to improve the speed and efficiency of implementation. The use of Octave ensures transparency and reproducibility in the methods employed, facilitating the replicability of the results by the scientific community.

This strategy is implemented using the shortest-path approach, known as MSPP. The choice of the MSPP algorithm over other widely accepted algorithms is due to its lower computational resource requirements, especially when developing implementations based on integer logic. This feasibility arises from the properties of Mathematical Morphology. Suppose a weighted version of the algorithm is used. In that case, the discrete steps for processing data can be easily implemented by applying a minimum $\delta$ approach, which renormalizes the data in discrete increments. In terms of understanding the advantages of implementing MSPP, a comparison is made of the number of integer operations required to compute the best path in a satellite image. This comparison illustrates the efficiency of algorithms by comparing the brute-force counting of integer operations required to analyze the shortest path using different algorithms. The comparison illustrates the performance of the proposed approach compared to other well-accepted algorithms in performing the same task. As a remark, the performance of the other algorithms, in certain circumstances, is not measured in Integer Ops, because they implement float operations, which might decrease the performance of the system considerably.

Table 3. Comparison of the number of integer operations needed to compute an optimal path.

Approach	IntOps (Giga) ↓	Proportion to MSPP
MSPP	6900	0
Djistra	11,0267	0.598
Three ${\mathrm{A}}^{*}$	29,614	3.291

summarizes the total number of integer operations (IntOps) needed to compute a satellite map with 3,450,132 million edges and 383,348 Mill vertices required to calculate and analyze a single satellite map with the MSPP Algorithm, Dijkstra Algorithm, and ${\mathrm{A}}^{*}$ Algorithm. Dijkstra’s algorithms and Three ${\mathrm{A}}^{*}$ have slightly worse values because they include an operation to compute a priority list, which adds an extra step to complete the task. The MSPP approach will not explicitly require a priority list, due to the covering operator, which measures the number of times a specific node becomes dilated. The resulting discrete surface is traversed in the reverse direction once the destination is reached, building the optimal path. The difference in computation reflects a gain of 59.8% with Dijkstra and more than 300% in Three ${\mathrm{A}}^{*}$, which shows a considerable advantage. In general terms, this gain will improve the priority list, which, in the case of this study and the current implementation of MSPP, becomes more reliable, particularly when there is a need to compute several optimal paths for a given delivery center in scenarios involving transporting resources to dense urban towns, and the coding and representation are expressed in terms of integer operations.

4.4. Results Analysis

Figure 2 shows satellite images comprising binary representations of vital resources and traffic flow within the city. The images encode all vehicular communication roads, expressed as marked zones. The information about the city’s avenues is represented as a graph space. The binary map is an effective navigable map, as it represent a graph of adjacent roads to navigate among the zones. The digital images were the result of binarizing a vector image with all urban infrastructure. The dimensions of these images were $20.000\times 20.000$ pixels.

The algorithm’s input image is derived from candidate locations designated as distribution centers and available distribution destinations, while also considering the surrounding areas for goods delivery. We employ feasible destination zones, complemented by random sampling from these candidate zones, to ensure a uniform probability distribution that accurately captures local neighborhood behavior. Together with the destination list, the computational process analyzes and processes all candidate delivery zones and the candidate delivery center by calculating the shortest routes using MSPP. The optimal path serves as a basis to identify those roads used for delivering.

After identifying all the shortest paths, the Euclidean distance is calculated, representing a direct line between the origin and destination. This measure provides information on the physical distance to the candidate zones. Then, to truly quantify the distance traveled, the geodesic distance is introduced, which reflects the actual distance based on the graph’s topology, i.e., attending to the current urban infrastructure of the roads. These calculations are highly relevant for estimating the travel distance of each delivery vehicle from the distribution center to the destination. The results of the shortest-path distribution are illustrated in the fifth step of Figure 2, which shows the distances calculated from the areas defined as sampling points. The expected-value calculation provides information about the actual distance traveled during the distribution process.

Like distance, the average speed at which vehicles can move in these areas of Mexico City plays a crucial role in calculating the time required for deliveries. The INEGI (Instituto Nacional de Estadística y Geografía) and SEMOVI (Secretaría de Movilidad del Distrito Federal) are departments that currently actively measure urban information. We analyzed data for the last year (2024) based on studies conducted by INEGI and SEMOVI [46,47].

As is known, the time required for delivering goods is not constant; it varies over time due to differences in the average speed of vehicles in each local neighborhood. This speed reflects the density of communication resource usage at different times, affecting delivery timelines. In step 6, we will detail the computation of average velocity and its adjustment to varying hours of the day to provide further clarity on this matter.

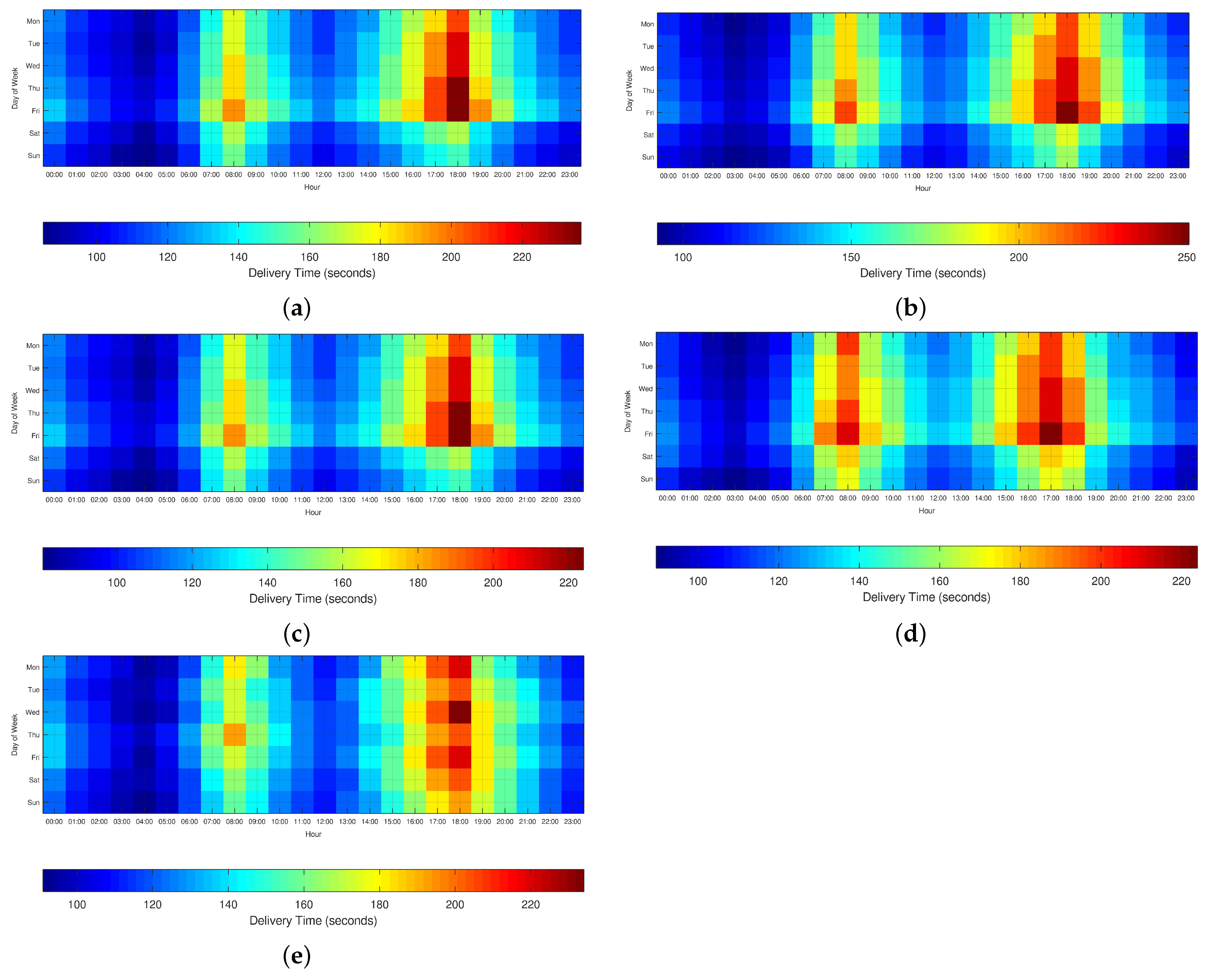
The complete data analysis regarding delivery times is illustrated in Figure 4. The results show the average time delay for completing deliveries in different city zones. Notably, delivery times are influenced by both the hour and the location. For instance, in Churubusco, on a Saturday at 8:00 a.m., the delivery time is approximately 160 s. However, if a delivery is made at the exact same location and time but on a Friday, the time increases to about 190 s. A similar effect is observed on Saturdays in the Santa Anita area, where the difference between making a delivery at 7:00 a.m. and 8:00 a.m. increases from 130 to 160 s, due to the variation in average speed and well-known peak hours in the city.

As is known, the shortest of the previously calculated paths is always the most efficient path to deliver goods. The implication of always computing the most efficient trajectory is that uniform sampling of the local neighborhood delivers local information on the distances that will be traveled for real deliveries. Ideally, the Euclidean distance represents the shortest rectilinear distance (upper right graph from Figure 5a–e). It is observed that the Euclidean distribution is approximated by an incremental distribution in all cases. The surface is sampled as a circle, making it more likely to select zones in external areas, as the sampling is uniform. With respect to geodesic distance (upper right graph from Figure 5a–e), the range of actual distance to be traveled for delivering goods increases. Since there is no direct path between different locations, the candidate path depends on connections between local avenues and the topology. This might cause physically near locations to have higher geodesic distances due to the topology of the infrastructure, which affects the available routes to the destination.

Grouping all measures of distance that the PDF distribution might be approximating indicates a maximum value before the most distant location, suggesting that delivery distances become uniformly distributed. In the locality, a certain degree of connection determines the most probable distances to cover. Once the real distance that must be traveled to each locality, with the average velocity over time, is known, the time response can be estimated. The advantage of this computation is that it reflects the most probable and accurate time delay due to the physical distance that must be covered in the delivery process, which is shown in Figure 4. The delivery-time figure is now used to determine the time elapsed, which is more suitable for providing the best responses or the exact delivery time at a specific hour.

As mentioned in the previous paragraphs, the proposed methodology serves as the basis for creating delivery plans and criteria linked to well-established variables, such as cost, response time, and scheduling, while excluding the impact of traffic. Our results confirm that the proposed approach is a highly reliable framework for developing search algorithms in a graph-based space. Additionally, it establishes a robust framework for path searching, providing a strong and concise theoretical foundation for defining the search process in any given environment. This method effectively simplifies the general approach to searching in discrete spaces.

5. Conclusions

In dense urban networks, determining the most efficient route for delivery vehicles is critical to ensuring the timely distribution of goods and services. This paper focuses on a real-life case study that seeks to calculate the critical distribution radius, considering real-life variables such as average traffic speed, in five dynamically active zones in dense urban areas.

The article presented a reliable strategy based on the MSPP algorithm and mathematical morphology to analyze the complex local topology around a distribution center and calculate the most appropriate delivery routes at different times of day and on weekdays for mass merchandise distribution plans. The proposed strategy was validated using a Mexico City case study, which analyzed the configuration of a set of distribution centers in various locations throughout the city. The strategy calculated feasible destinations considering the delivery times at different times of day.

Our results are satisfactory and demonstrate that the MSPP-based approach outperforms classical methods such as Dijkstra or Tree ${\mathrm{A}}^{*}$, achieving an improvement of nearly 60% compared to the second-best approach in this case study in terms of the number of integer operations performed to analyze a satellite map.

Fusing the proposed strategy with the MSPP algorithm leverages the advantages of Mathematical Morphology. The proposed approach offers a fully implemented strategy based on these foundations, enabling its efficient implementation through an integer logic approach that is compatible with most computer architectures.

The strategy enables the calculation of feasible delivery destinations by considering delivery times at various times of the day. The results are promising, as it allows for the estimation of delivery times to specific locations and provides insight into the urban connectivity surrounding the delivery centers.

Even though the proposed strategy yields positive results, several important issues need to be addressed in future work. The primary concerns stem from the method’s ability to adapt to real-life scenarios, particularly variables such as altitude variations, traffic dependences, and irregular surfaces, which are common in densely populated cities. These limitations highlight a critical opportunity for large-scale applications.

Further Works

Ideas for further work include analyzing other densely populated towns to propose strategies for the optimal deployment of goods and to reduce response times.

Similarly, we propose the inclusion of other urban networks, where latency becomes vital for communication or routing technologies, as well as the inclusion of more urban variables that express locality, such as elevation, temperature, events, or weather behavior, which would help to better plan strategies for road delivery.

With regard to the MSPP algorithm, its implementation is achieved based on Mathematical Morphology, which opens an opportunity whereby the algorithm can be rewritten with theoretical properties to simplify and improve the efficiency of the MSPP’s implementation.

We also propose using more generalized operators such as Morphological Geodesic or Viscous operators, which have properties complementary to graphs with multiple variables.

The proposed strategy utilizes an optimal-path-computing approach. Currently, it employs the Multi-Source Path Planning (MSPP) algorithm to determine the optimal path. However, this strategy is limited by the shortcomings of the MSPP algorithm. It cannot adequately analyze and weigh altitude variations in urban corridors with non-uniform surfaces. Furthermore, in densely populated areas with overlapping urban corridors at different altitude levels, the MSPP algorithm fails to account for these complexities. Therefore, incorporating complex graphs that encapsulate these variables, using morphological concepts, presents a valuable opportunity for further research.