Abstract
Airport-bound access and egress trips comprise a significant portion of total ground transportation trips, especially in regions served by large airports. Connecting urban areas with airports under minimal travel delays can be challenging, with traffic congestion along busy connecting corridors being a common phenomenon. Urban Air Mobility (UAM) is a new transportation mode envisioned to reduce travel times using specific aircraft, such as electric (and non-electric) Vertical or Short Take-off and Landing aircraft (e/VTOLs and STOLs, respectively). The operation of these aircraft requires take-off and landing infrastructure known as vertiports. A strategic infrastructure placement framework was introduced, utilizing and adapting the Capacitated Facility Location Problem (a-CFLP) and the Maximal Covering Location Problem (a-MCLP) with capacity constraints. An adapted capacitated k-means algorithm and a greedy heuristic were considered for the solution of the a-CFLP, while the a-MCLP was formulated as a mixed-integer linear programming problem. The proposed framework was applied in the Chicago Metropolitan Area, revealing that various trade-offs regarding coverage and accessibility, versus operational costs (number of facilities, facility capacity, and service radius), exist. The results showed that, depending on vertiport capacity and service radius capabilities, a range of 5 to 12 vertiports can sufficiently address the demand (above 95% demand coverage) and, with respect to accessibility, serve a moderate UAM demand scenario of 6124 daily requests, as identified for this region.
1. Introduction
Urban Air Mobility (UAM) is a key component of the broader Advanced Air Mobility (AAM) vision (using Vertical or Short Take-off and Landing aircraft—e/VTOLs and STOLs—for intra- and inter-city transportation of passengers and cargo), specifically focusing on the integration of aerial transportation systems within urban environments. Airport shuttle services are one of the envisioned UAM use cases. The vertiport (or skyport [1]) location problem aims to identify strategic sites for these facilities, which serve as take-off and landing stations and as refueling/recharging stations [1].
Connecting urban areas with airports efficiently is an important and rather difficult problem. While public transportation is an option in many urban areas, only a small portion of airport inbound and outbound travelers consider it [2,3]. Travelers show higher travel time sensitivity regarding airport access trips than egress trips, while the opposite was found to be the case regarding the cost [4,5]. Therefore, a transportation mode that offers reduced travel times while increasing reliability by avoiding delays from ground congestion could be attractive, especially considering the significant portion of total daily ground transportation trips that correspond to airport-bound travel [6].
A vertiport location identification framework was introduced, focusing on airport-bound trips to optimize vertiport locations under accessibility and coverage maximization objectives. A potential UAM demand profile can be identified from personal vehicles, public transit (bus and rail), taxi, and ride-hailing (TNC) trips, which have certain ground travel time and distance thresholds [7,8], such that the transition from ground transportation modes will be meaningful and attractive to passengers, mostly through travel time savings. A modified (capacitated) k-means clustering algorithm [9,10] and a greedy heuristic algorithm were considered for the solution of the adapted Capacitated Facility Location Problem (a-CFLP), and mixed-integer linear programming was considered for the solution of the adapted Maximal Coverage Location Problem (a-MCLP).
In this study, the analysis is narrowly focused on vertiports that support airport access operations, rather than broader services and UAM networks. The operational scenario under consideration envisions vertiports strategically located to connect urban areas with major airports, facilitating efficient and faster passenger transfers and potentially relieving ground transportation congestion. This scope is chosen because airport access trips represent one of the most time-sensitive and demand-concentrated use cases for early UAM deployment, making them a practical starting point for evaluating infrastructure placement strategies.
The goal of this study is to formulate and evaluate solution methods for the Facility Location Problem, specifically targeting UAM operations. The proposed framework aims to address potential operational and decision-making challenges associated with infrastructure placement decisions introduced by this new transportation mode. The main research questions that this study is attempting to answer are the following:
- How can infrastructure placement be guided efficiently through spatial considerations of the demand it is destined to serve?
- Are there solution methods that are able to retain an accessible service under conflicting objectives of minimizing infrastructure costs and maximizing demand coverage?
- What are the trade-offs between accessibility and demand coverage, versus operational costs?
The problem scope is defined with some key assumptions: (i) one type of vertiport, (ii) uniform demand distribution and hourly demand requests, (iii) uniform vertiport capacity/service rate, (iv) continuous operations during study hours, and (v) spatial and regulatory restrictions on identified locations for vertiport placement, which were not considered. The main contributions of this study are the following:
- Introducing a strategic facility placement framework for UAM infrastructure, based on the adapted formulations of existing Facility Location Problems (the Capacitated Facility Location Problem and the Maximal Covering Location Problem).
- Developing and evaluating different solution methods that can be used on FLPs, based on existing formulations (k-means clustering, heuristics, and MILP).
- Providing insights into the spatial distribution of a potential airport-bound UAM demand and the role of infrastructure constraints in balancing service efficiency with facility investment.
The remainder of this paper is structured as follows. Section 2 reviews the relevant background and related work. Section 3 presents the methodological framework and problem formulations. Section 4 applies the framework to a case study of airport-bound trips and discusses the results. Section 5 concludes with a discussion, limitations, and future research directions.
2. Background Review
This section refers to key studies and developments in the field of infrastructure location problems in the UAM realm. It also includes a review of solution methods proposed for the problems under consideration and applications that utilize similar solution methods to those introduced in this study.
2.1. Previous Work on the Vertiport Location Identification Problem
Identifying locations and infrastructure requirements for AAM and UAM operations has been examined by several groups, including Wu and Zhang [7], Sinha and Rajendran [11], Brühl et al. [12], and Arellano [13]. A large body of work has applied clustering approaches to this problem: Holden and Goel [14] first outlined a vision for on-demand air transportation, while Lim and Hwang [15], Rajendran and Zack [16], Jeong et al. [17], and Peng et al. [18] used k-means and other clustering techniques to identify candidate vertiport sites based on demand concentration and spatial coherence. Optimization-based approaches have also been developed, with Rajendran [19], Kai et al. [20], and Rath and Chow [21] formulating models to maximize ridership and revenue. Other methods expand beyond clustering and optimization, such as suitability analysis using GIS [22], location queuing formulations for emergency response networks [23], hub-based p-median models for vertiport networks [24], which connect to multi-objective facility location formulations beyond the scope of UAM operations [25], and the comparison between heuristics and exact solution methods for the vertiport Facility Location Problem [26]. More advanced techniques have also emerged, including mathematical programs with equilibrium constraints for hybrid air–ground systems [27] and spatial analyses of repurposed infrastructure, such as rooftops and parking facilities, for UAM integration [28].
Building on the latter, repurposing existing infrastructure and the integration of vertiports within existing urban infrastructure, rather than constructing completely new infrastructure (i.e., “network design from scratch”), is a key consideration for AAM and UAM deployment, particularly in dense urban areas. Much of the literature to date has focused on conceptual discussions or simulation-based analyses, with vertiport networks emerging as a central theme [29]. Ensuring accessibility and connectivity is crucial, requiring an evaluation of how vertiports link to road networks, public transit, and pedestrian pathways [30,31]. Beyond travel time and costs, studies have emphasized the importance of accessibility, environmental impacts, and societal considerations, as well as land use compatibility with surrounding environments, zoning policies, and potential neighborhood effects [31]. To accelerate deployment and reduce costs, several works propose repurposing existing facilities, such as rooftops, parking structures, helipads, and underutilized transport hubs, although challenges include local opposition, regulatory hurdles, and spatial constraints [32,33,34]. Other studies highlight that while existing helipads may support early operations, dedicated new facilities will eventually be needed [35]. Approaches incorporating existing infrastructure—such as airports and heliports—into location models have also been developed, accounting for factors like potential demand, socioeconomic characteristics, and time savings [36,37]. Finally, comparative analyses of operational costs between new and existing facilities underscore the trade-offs between financial feasibility, service accessibility, and community impacts [38].
This work shares methodological similarities with previous studies that employ clustering and facility location formulations to identify vertiport sites (e.g., k-means approaches [17]; mixed-integer programming for capacitated facility location [39]; and constrained demand-based clustering for air taxi demand). However, unlike those studies, this study focuses explicitly on airport-bound UAM travel, targeting the unique dynamics of airport access trips. In this vein, a few recent studies align more closely with airport contexts: Kotwicz Herniczek and German analyzed airspace constraints and energy feasibility for airport shuttle vertiport placement near major U.S. airports [40], while other studies conducted research on airport demand estimation and the impact of mode choice, specifically for airport access UAM configurations [41,42]. One of the main differentiation points of the proposed framework in this study is the application, comparison, and evaluation of different classes of solution methods for vertiport location, specifically for airport-bound demand. The main focus is on the solution of the Facility Location Problem through different solution methods, attempting to locate facilities that can efficiently serve airport-related demand patterns.
2.2. Facility Location Problem
The Facility Location Problem (FLP) represents a fundamental class of optimization problems in logistics, operations research, and supply chain management. Foundational theories and models were introduced by Larson and Odoni [43] and Daskin [44]. One of the earliest analytical formulations, the plant location problem, was developed by Balinski [45]. At its core, the FLP seeks optimal facility locations—such as emergency centers [46], warehouses [47], factories, or service centers—to minimize overall costs or maximize efficiency. Over time, the family of FLP models has expanded to include specific variants such as the single- and multi-facility problems, covering, center, and median models [48], the Uncapacitated FLP [49], and the Capacitated FLP [50], among other formulations.
2.3. Capacitated Facility Location Problem
The objective of the CFLP is to locate facilities and assign customers to minimize the total cost, which comprises the fixed facility setup costs and variable costs associated with operations corresponding to the demand of these facilities. Each facility has a limited capacity, restricting the number of customers that can be served by a given facility. Exact methods, such as integer [51] and mixed-integer programming [52,53,54,55,56], have been used, along with solution approaches such as branch-and-bound [57,58,59,60,61,62], Lagrangian relaxation [63,64,65,66,67,68,69,70], branch-and-cut-and-price [71,72], and cross decomposition methods [73]. Approximation algorithms [74,75] based on various heuristics [76,77,78,79,80], metaheuristics, such as tabu search and search algorithms [81,82,83,84,85] have also been used.
2.4. k-Means Algorithm with Capacity Constraints
Clustering algorithms for CFLPs offer approximately optimal solutions for determining facility locations. Such methods allocate demand points to facilities while considering their varying capacities, which may collectively be insufficient to meet the total demand [86]. Modified versions of the k-means algorithm have been used, either as an individual model [87,88] or as part of a heuristic or solution algorithm [89,90]. Applications of such models range from CFLPs [91,92] to the capacitated p-median problem [90], among others.
2.5. Greedy Heuristics for the Solution of FLPs
Greedy heuristics can obtain sufficient approximation guarantees [91] for FLPs, among other approximation algorithms [92]. The Uncapacitated FLP is one of the main problems of the FLP family that greedy heuristics have been applied to [93,94,95,96,97,98,99,100], in which there is no upper bound on the number of demand requests a facility can serve. Approaches based on greedy algorithms regarding the CFLP have an additional complexity stemming from the introduction of the capacity constraint [101,102,103,104]. Greedy algorithms have also been used for the solution of the p-median problem [105,106,107] and the MCLP [108]. Greedy heuristics have also been used to complement exact and/or other approximation algorithms in settings where the dimensions of the problem are significantly high [109].
2.6. Maximal Coverage Location Problem
According to Church and ReVelle, the Maximal Covering Location Problem (MCLP) seeks to maximize the population served within a given service distance or time while considering a limited number of facilities [110]. Coverage is typically defined in terms of a specified distance or other relevant criteria. The MCLP inherently involves a trade-off between the number of facilities to be opened and their strategic locations, aiming to balance operational efficiency and cost-effectiveness while meeting coverage requirements. This approach has been applied to various planning purposes, including the siting of emergency vehicles [111,112,113], control facilities [114], service centers [115], emergency response units [116], fire prevention facilities [117,118], and charging stations [119] for electric vehicles, among other applications [119,120]. A variant of the MCLP is the capacitated MCLP, in which each facility has a capacity limit, restricting the number of demand points that can be served [113].
3. Methodology
This section presents the existing Facility Location Problem (CFLP and MCLP) formulations, which served as the basis for the adapted formulations introduced in this study, along with the various existing and newly introduced solution methods considered. The overall methodological process followed in this study consists of four main steps: (i) define the adapted facility location formulations (CFLP and MCLP); (ii) design and implement solution approaches, including the capacitated k-means algorithm and the greedy heuristic; (iii) generate candidate facility locations through clustering; and (iv) evaluate the resulting facility configurations with respect to demand coverage, capacity utilization, and operational feasibility. Each of these steps is explained in detail in the subsections below.
3.1. Capacitated Facility Location Problem Formulation
Starting from the UFLP, a set of facilities, , aim to serve a set of demand requests, , [120,121,122,123,124,125]. Each facility has a capital opening cost and a cost to serve the demand request . The objective is the minimization of the total cost to find the optimal number of facilities that satisfy Equation (1).
which is subject to
Equation (2) ensures that all demand requests will be served by an available facility. Equation (3) states that if a facility is serving a demand request, it must be open, where , and . The formulation of the CFLP is similar to the UFLP, with the main difference being the capacity constraint. The minimization of total cost (Equation (4)) is also the objective, subject to Equations (2), (3), (5), and (6), with an emphasis on serving demand requests located within congested regions ( is a weighting factor for each demand request , defined based on the area where demand request is located, and the corresponding congestion levels).
which is subject to
Equation (5) states that the service provided by a facility cannot go beyond its capacity (). A pessimistic threshold of 32 flights/hour can be considered (both landings and take-offs), corresponding to the initial years of operation of a UAM service (based on [14,126,127,128,129,130]). A threshold of 60 to 70 operations/hour can be considered a moderate case. Additionally, a budget constraint (Equation (6)) operates as an upper bound () on the number of facilities that can be opened, where .
3.2. Solution Methods
3.2.1. Capacitated k-Means
This subsection outlines the adapted k-means algorithm (based on [91]), which incorporates capacity constraints (Figure 1). Beginning with an initial (random) set of facility locations, the process iterates through a capacity-constrained assignment of demand points and optimization of facility locations. The overall capacity may either sufficiently or insufficiently accommodate all demands. In the case of a sufficient capacity, the priority measure for demand point assignment to a facility is based on the difference in distances to the first and second closest facilities to that demand point. For cases of insufficient capacity, a load-balancing approach is considered, where demand points are assigned to facilities by considering both the distance and the current load of the facilities. Specifically, a demand point is assigned to the facility that minimizes a weighted sum of the distance to the facility and the ratio of the current load to the facility’s capacity. The objective is the minimization of the squared distances from each demand point to its assigned cluster centroid (Equation (7)), where .
which is subject to
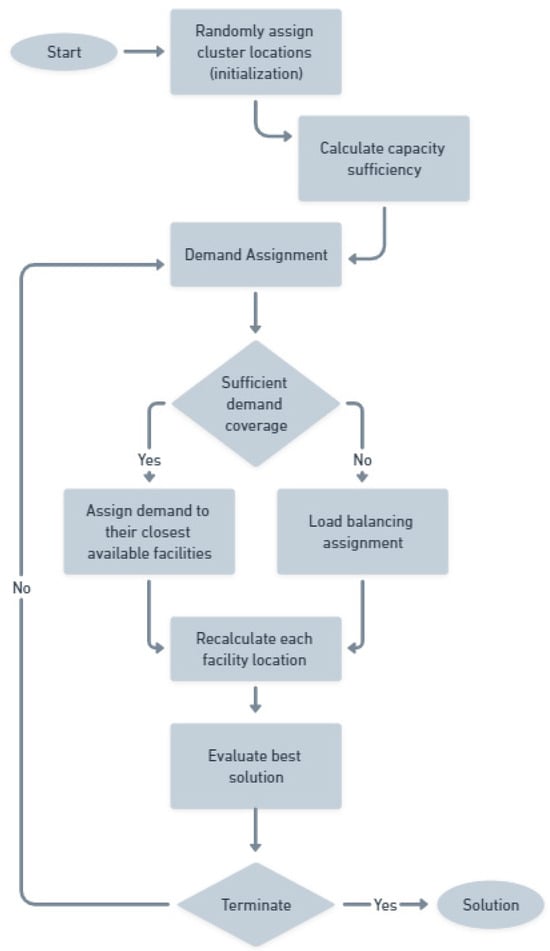
Figure 1.
Capacitated k-means algorithm.
Equation (8) ensures that each demand point is assigned to one cluster, and Equation (9) ensures that each cluster has up to assigned demand points, where indicates whether the demand point is assigned to the cluster ( set of clusters and set of demand points). Equation (9) is a capacity constraint, with being defined by the analyst.
Figure 1 provides a schematic overview of the capacitated k-means procedure, showing the iterative cycle of (a) initializing facility locations, (b) assigning demand points under capacity constraints, (c) updating facility locations, and (d) repeating until convergence. This figure is intended to clarify how the algorithm adapts traditional k-means clustering to account for the operational limitations of UAM vertiports.
3.2.2. Greedy Heuristic Algorithm
The heuristic approach presented in this section was based on Carlo et al. [101], with the algorithm iteratively solving the CFLP introduced earlier, with the difference being that it accounts for a fixed number of facilities, i.e., Equation (6) will be modified as shown in Equation (10).
The algorithm begins by initializing the lower and upper bounds of the number of facilities that will be considered. As a lower bound, facilities that can provide demand coverage of 75% of the total requests were considered based on the capacity of each facility, and an upper bound () of facilities providing full demand coverage was considered, given that respects a budget constraint () for all facilities considered in the network regarding the fixed capital () and yearly operational costs () of each facility (where planning horizon, in years, and ). If the total cost of the facilities needed to cover the demand requests fully is higher than the budget constraint, then the next closest to that number that is below is considered as the . A set of candidate facility locations is given based on the k-means algorithm introduced previously.
Let ; the CFLP described in this subsection is solved, and its objective function is considered as the best () for this given iteration. Let and solve the CFLP again. If the resulting value of the objective function () is greater than , then terminate the algorithm and return as the solution. Otherwise, if , update , set , and repeat the process. If , instead of directly terminating the algorithm, the CFLP solved for , and if the percentage of unserved demand requests () is higher than a certain threshold , along with the total requests () being higher than a fixed number of demand points , i.e., factors that would justify relaxing the upper bound and essentially relaxing the budget constraint, set , and solve the CFLP. If and is reduced by a factor of compared to , set , keep , and terminate; otherwise, keep and as the solution and terminate. Algorithm 1 summarizes the heuristic approach.
| Algorithm 1: Greedy heuristic |
| 1 Run k – means (initialization) |
| 2 Set , , |
| 3 If |
| 4 while |
| 5 Set |
| 6 Set , and solve the CFLP |
| 7 Let |
| 8 while is |
| 9 Set , and solve the CFLP |
| 10 If |
| 11 Set |
| 12 Set |
| 13 Else |
| 14 If |
| 15 Let |
| 16 Else |
| 17 If |
| 18 Set , and solve the CFLP |
| 19 If |
| 20 Set |
| 21 Set |
| 22 Else |
| 23 Set |
| 24 Set |
| 25 Else |
| 26 Set |
| 27 Set |
| 28 Terminate |
In summary, Algorithm 1 is tightly connected to the mathematical formulation described earlier in this section. The initialization of lower and upper bounds for the number of facilities corresponds directly to the cost–capacity balance expressed in Equations (6) and (10). The iterative updates and comparisons of the objective function reflect repeated solutions of the CFLP under these constraints, while the conditions involving unmet demand (), budget feasibility (), and demand thresholds (,) ensure that each step of the heuristic remains consistent with the model’s feasibility and optimality requirements.
3.2.3. Adapted Maximal Covering Location Problem Formulation
The objective reflects the maximization of demand requests (set of demand nodes ) assigned to a facility (Equation (11)), relating to the MCLP. The following problem definition is an adapted formulation of the MCLP, considering capacity constraints on each facility. Also, it does not have a fixed number of facilities, but rather, an upper bound of facilities (), which can be opened based on a set of candidate locations, . Similar to the CFLP formulation, demand nodes in regions susceptible to traffic congestion are prioritized based on their weights . The problem is formulated and solved as a mixed-integer linear programming problem (MILP).
which is subject to
Equation (12) ensures that the number of facilities to be opened is within the upper bound , with , being the number of demand requests on the node , and . A demand request can be served from the facility only if its distance from facility is within the service radius . is an indicator function, where , (Equation (13)).
Equation (14) corresponds to the capacity constraint, i.e., the upper bound () in hourly demand requests that a facility at node can satisfy.
The set of candidate facilities, , is constructed with the use of the adapted k-means clustering algorithm.
4. Applications and Results
The proposed framework was applied in the Chicago Metropolitan Area for an estimated UAM demand profile to identify potential locations and infrastructure needs that the region would have to consider for the UAM service to be capable of operating. This study area was selected as a case study due to its large and diverse population base, high concentration of airport-bound trips, and multimodal ground access challenges to its two major airports, O’Hare and Midway. Chicago also provides rich and publicly available datasets for transit, TNC, and taxi trips, making it a suitable and data-rich environment for testing the proposed framework.
4.1. Cost Function Framework for UAM Airport Access Trips
Candidate UAM trips are defined as those with origins throughout the region and destinations to the major airports, completed via taxi, ride-hailing, bus, or rail, within certain distance and travel time thresholds. The framework compares the total generalized cost of a ground trip with that of a multimodal UAM trip (including access legs), assuming a traveler chooses UAM if it offers generalized cost benefits over the available ground modes (assuming that these are transit and TNC/taxi). The summary of the notation is presented in Table 1.

Table 1.
Notation summary.
The total generalized cost of a UAM trip is given in Equation (15):
where
Equation (16) provides the travel time of a UAM trip:
where and from the Spherical Law of Cosines, with latitudes and longitudes of departure and arrival (at airport) vertiports, and R is the earth’s radius. The total ground travel time () for trip from origin to airport is calculated based on the two assumed available modes for the completion of the total trip through taxi/TNC or transit. Transit is assumed to be calculated based on a mean transit speed value ( and the traveled distance , and the TNC/taxi is calculated based on a mean speed with an addition of extra time (based on a factor ), accounting for potential congestion, and the traveled distance . The choice rule is simply defined as , where UAM will be chosen over TNC/taxi or transit in the case that the generalized cost of UAM is lower than the cost of either TNC/taxi or transit for the full trip to the considered airport.
4.2. Data
Data used to construct the UAM demand profile were based on trips with destinations to the two major airports in the Chicago area (O’Hare International Airport and Midway Airport), completed via bus, rail, taxi, or ride-hailing services. Regarding public transit modes, data from different transit agencies were used [131,132,133,134,135,136,137], in terms of ridership and network structure (routes and stops), for bus and rail routes that have either of the two major airports as their destination, along with routes that operate as feeder/connecting routes. A total of 7% to 12% of travelers will typically select public transit for such trips [2,3], which is in line with what Foote et al. [138] reported based on survey data regarding O’Hare International Airport (5.8% of travelers used bus or rail for access and 4.9% for egress trips) and Midway Airport (7.7% of travelers used bus or rail for access and 9.5% for egress trips) in the Chicago area. However, these percentages correspond to data from 1988 to 1995. So, based on a recent survey conducted by the Chicago Transit Authority [139], suggesting that 31% of the 5121 respondents of the survey designated travel to or from the airport as their trip purpose, 8.5% of the total trips done via public transit were considered as airport-bound trips. The Chicago Data Portal was used for taxi and TNC trip data [140,141].
A trip that fulfils certain criteria (trip duration and distance) is assumed to be eligible for a UAM trip (similar approach as [142,143]). A lower travel time bound of 40 min and a distance threshold of 17.5 miles were considered for a trip to be a UAM trip candidate (based on [7,8,143]). A total of 6124 daily trips were found to be UAM trip candidates, with 214 taxi, 3346 ride-hailing, 503 bus, and 2061 rail trips. To include a reliability metric in the analysis, regions with ground congestion were identified based on congestion estimates by segments and by regions in Chicago [144,145]. Finally, the capital cost per vertiport was estimated at $7.6 million, and the annual operating costs were estimated at $2.4 million (adjusted in 2023 U.S. dollar values, based on [146,147,148,149]).
4.3. Numerical Analysis
Each solution method was applied to identify optimal vertiport locations in the Chicago Metropolitan Area, with the results presented in the following subsections. Scenarios were defined by systematically varying three key parameters: (i) the vertiport capacity (hourly operations), (ii) the maximum service radius, and (iii) the number of facilities allowed in the system. Each parameter was tested under low, moderate, and high values to capture a wide range of operational conditions. The total number of simulations resulted from the full factorial combination of these parameter levels, ensuring coverage of all meaningful configurations. Sensitivity analyses were performed to assess the robustness of the results and to identify the Pareto-efficient solutions.
4.3.1. Capacitated k-Means Results
Figure 2 presents a sensitivity analysis regarding the average and maximum travel distances, along with the demand coverage, to study how each component changes the others and to assess the quality of the corresponding solution. The Pareto optimal solutions are presented as red dots in the figure, with a few of them having their corresponding scenario identification number in a black and white box. Figure 3 presents each solution of the algorithm in a three-dimensional space, with each axis corresponding to the average travel distance, the number of facilities/clusters, and the demand coverage, respectively, to enable the Pareto frontier to be revealed. Each of the Pareto frontier solutions is shown with a black circle around the corresponding circle shape. Based on these figures, most of the Pareto frontier solutions, with respect to the average travel distance, the number of clusters, and the demand coverage, while having average travel distances within reasonable limits, present relatively high maximum distances (i.e., the number of miles one must travel from the furthest demand request point to access the facility). The algorithm generates cluster center locations based on the spatial distribution of the demand, and by assigning a capacity constraint to each cluster center, certain clusters may not serve all the demand points in their vicinity. These unserved demand points are then assigned to the next available facility or cluster center. Since k-means lacks a service radius constraint, a cluster can potentially serve demand points at an unreasonable distance due to the capacity constraint.
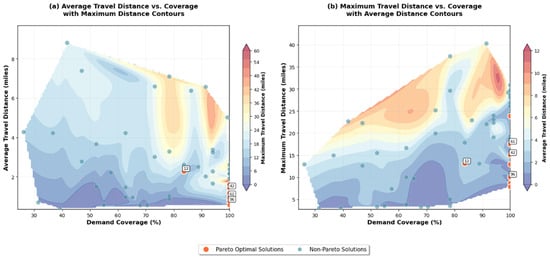
Figure 2.
k-means sensitivity analysis.
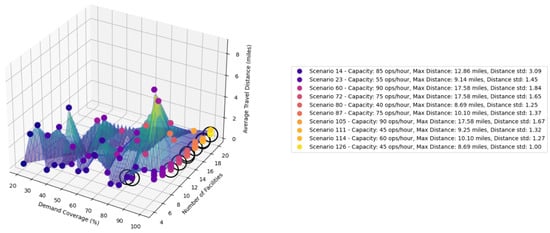
Figure 3.
Representation of k-means solutions (legend includes only Pareto frontier solutions).
4.3.2. Greedy Heuristic Algorithm
Scenarios with different capacities were considered for the greedy algorithm. While the capacity increases, the number of facilities decreases since an individual vertiport can serve more demand requests. Most solutions have an average travel distance that is lower than an acceptable threshold of 2.5 miles, while a portion of these solutions have relatively high maximum travel distances. However, for full coverage (100%) to be achieved, a relatively large number of vertiports or a high vertiport capacity was needed.
Figure 4 presents different solutions with respect to the demand coverage and travel distance of a demand node to a facility and shows how different capacities (i.e., service rates) can alter the quality of the solution. In Figure (4a), the bubble size indicates the number of facilities required, while the color gradient shows capacity levels. Higher-capacity vertiports (warmer colors and smaller bubbles) achieve better coverage with fewer facilities while maintaining acceptable average travel distances below the 2.5-mile threshold. This demonstrates that capacity expansion is an effective strategy for improving network efficiency without compromising service quality. Figure (4b) complements this analysis by examining infrastructure efficiency from an investment perspective. The blue line shows how facility requirements decrease as capacity increases, following an inverse relationship that reflects economies of scale. Simultaneously, the red line tracks coverage efficiency (coverage percentage per facility deployed), revealing a peak efficiency point where the marginal benefit of additional capacity is maximized. Figure 5 presents, in a three-dimensional space, the different scenarios considered in this case, with respect to the demand coverage, number of facilities, and average travel distance. Therefore, the Pareto frontier (shown with black circles around the corresponding solutions) with respect to the demand coverage, number of facilities, and average travel distance can be obtained, with certain solutions presenting demand coverage percentages above 90%, with relatively low average and maximum travel distances. However, there are solutions that can achieve coverage up to 98%, but with either an increased number of facilities with a low capacity or a higher capacity with a lower number of facilities.
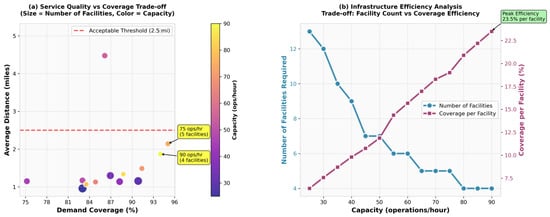
Figure 4.
Greedy heuristic sensitivity analysis.
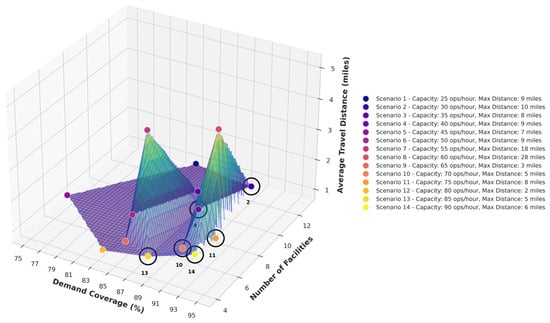
Figure 5.
Representation of greedy heuristic 3D solutions.
To obtain the importance of the size of the set (candidate location set obtained by the k-means algorithm), a sensitivity analysis was performed based on the Pareto frontier solutions. Each of these problems was solved again under varying numbers of clusters/candidate locations to identify significant changes in coverage and accessibility. It was found that 22 to 30 candidate locations are sufficient to provide good solutions. Increased coverage and/or higher accessibility was not obtained by increasing the size of the set beyond that range.
4.3.3. Adapted MCLP
Between the three solution methods presented in this study, the MILP formulation for the a-MCLP presented the highest flexibility in terms of scenario testing, with different values for the capacity, service radius (i.e., the distance within a demand request can be served by a facility if the capacity allows this), and upper bound of the number of facilities that can be opened. The results included solutions having relatively low average and maximum travel distances, i.e., prioritizing accessibility of service, while demand coverage was kept at the higher ends. Figure 6, Figure 7 and Figure 8 present different scenarios with respect to the average distance and demand coverage, with each scenario considering the three elements of the service radius, capacity, and number of facilities. In each figure, one of these elements is variable, and the rest are fixed (based on moderate/average values), generating certain scenarios that show the trade-offs between these components and the metrics under consideration. A service radius of 2 miles was sufficient to achieve coverage higher than 90%, with the average travel distance remaining below 2 miles. Total coverage can be achieved while considering high service radius values (8 miles and above); however, a radius of 4 miles was found to achieve more than 97% coverage. In Figure 6, panel (a) reveals trade-offs between coverage expansion and service accessibility; as the service radius increases, coverage grows, but average travel distances may also increase, with the point size and color both encoding the radius values to show progression. Panel (b) directly illustrates the coverage saturation curve, demonstrating how coverage gains diminish as the service radius expands beyond optimal thresholds, helping identify the minimum radius needed to achieve target coverage levels efficiently.
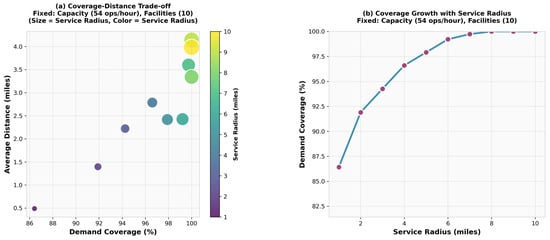
Figure 6.
a-MCLP: Service radius.
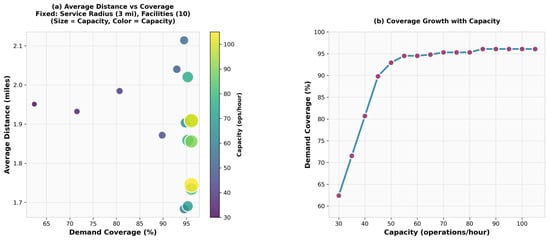
Figure 7.
a-MCLP: Capacity.
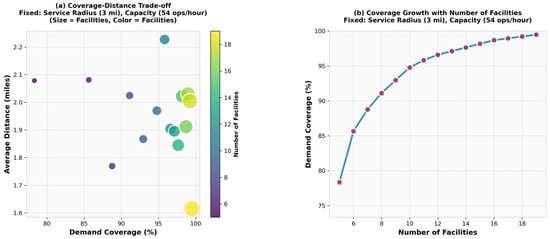
Figure 8.
a-MCLP: Number of facilities.
Capacity is an important parameter, since by going from 30 to 40 hourly operations, coverage can increase more than 25%, and from 40 to 50, an increase of more than 10% can be observed, leading to a coverage of more than 90%, with the average travel distance remaining below 2.5 miles. Panel (a) in Figure 8 presents a trade-off analysis between demand coverage and average travel distance, where each point represents a different capacity scenario. The point size and color both encode capacity levels, with larger and warmer-colored points indicating higher-capacity operations. This visualization reveals the tension between accessibility (shorter distances) and coverage extent while demonstrating how increased capacity can achieve better performance for both metrics simultaneously. Panel (b) shows the direct relationship between the operational capacity and demand coverage percentage, illustrating the growth curve and potential saturation points.
The number of vertiports can have a significant impact on demand coverage (e.g., going from five to seven facilities, coverage increases by approximately 10%, going beyond 90%), and from 10 facilities and beyond, a coverage of more than 95% can be achieved. In Figure 8, panel (a) shows the coverage–distance trade-off across different facility counts, where larger networks (represented by bigger and brighter points) typically achieve a higher coverage with potentially shorter average distances due to better spatial distribution. Figure 8b presents the relationship between the number of facilities and the demand coverage, revealing the marginal benefit of each additional facility and identifying inflection points where adding more facilities yields diminishing coverage returns, which is crucial for optimal network sizing decisions.
Figure 9 presents a three-dimensional view of a holistic analysis, where the Pareto frontier can be obtained. From that holistic analysis, the Pareto frontier was extracted and is presented in Figure 10, showing the considered values of different attributes for each of these scenarios. A coverage between 90% and 96% can be achieved with a relatively low service radius (3 miles), moderate capacity thresholds (in the order of 65 and 70 hourly operations), and a low number of facilities (between 8 and 10), with average travel distance remaining below 3 miles. It is important to note that maximum travel distances were kept at the low ends (below 3 miles).
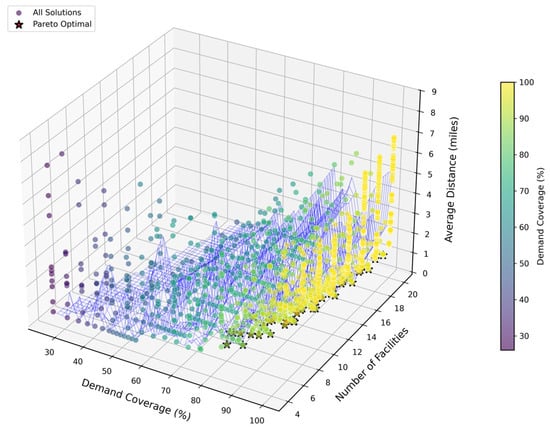
Figure 9.
MCLP: 3D holistic analysis.
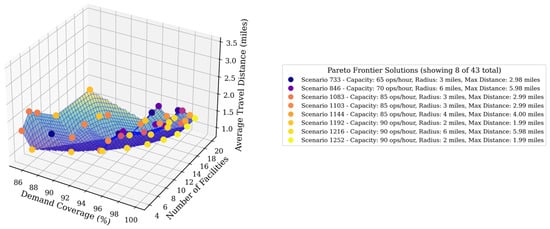
Figure 10.
MCLP—Pareto frontier solutions.
The various trade-offs between coverage and accessibility (average and maximum travel distances), versus operational costs (number of facilities, capacity, and service radius), are evident, with the MCLP formulation being able to offer relatively lower operational costs for sufficient accessibility and coverage in return. Similar to the greedy algorithm, it was found that 20 candidate facilities are sufficient to provide good solutions, with numbers above 30 not offering a significant change or change at all in the solutions.
To provide a form of validation, the proposed framework was cross-checked against baseline ground access patterns. Specifically, the modeled airport access demand shares by mode were compared to transit ridership data for O’Hare and Midway. While not a full behavioral validation, this consistency check confirmed that the generalized cost framework produces results aligned with observed trends, supporting the credibility of the methodology.
5. Conclusions
This section concludes this study by discussing the findings and corresponding limitations, as well as potential ways of addressing these limitations, along with additional future steps for this research direction.
5.1. Discussion
Urban Air Mobility aims to integrate electric Vertical and Short Take-off and Landing aircraft into metropolitan environments. The successful implementation of UAM, however, is contingent upon the strategic placement and efficient operation of the supporting infrastructure, most notably vertiports. This study developed and applied a strategic infrastructure placement framework to address this need, focusing on optimizing vertiport locations through classical facility location models, namely the Capacitated Facility Location Problem and the Maximal Covering Location Problem, while considering key operational variables, such as the capacity, service radius, and number of facilities.
The methodological approach encompassed three solution strategies: a capacitated k-means clustering algorithm, a greedy heuristic algorithm, and a mixed-integer linear programming formulation of the a-MCLP. These approaches were tested in a real-world case study within the Chicago Metropolitan Area. The results illustrated the trade-offs between the infrastructure cost and service levels, as measured by the demand coverage and user accessibility (in terms of average and maximum travel distances).
The capacitated k-means algorithm demonstrated efficiency in identifying spatially distributed facility locations based on demand patterns; yet, it exhibited limitations in controlling service accessibility, particularly in scenarios where capacity constraints resulted in demand assignments over larger distances. The lack of an explicit service radius constraint occasionally allowed for suboptimal assignments, leading to elevated maximum travel distances, despite achieving high average coverage.
The greedy heuristic algorithm proved to be a computationally efficient alternative that is capable of producing solutions with a high demand coverage and low average travel distances, especially under moderate-to-high-capacity scenarios. Nonetheless, ensuring full demand coverage often required either a higher number of facilities or significantly increased individual facility capacity. A sensitivity analysis revealed that a candidate location set size ranging from 22 to 30 was generally sufficient to yield robust solutions, with diminishing returns beyond this range.
Among the evaluated methods, the MILP-based a-MCLP provided the most flexible and analytically rich framework. It enabled precise control over the service radius, capacity thresholds, and facility limits, allowing for comprehensive scenario testing. The a-MCLP approach yielded solutions capable of achieving over 90% coverage with relatively low average and maximum travel distances, often within 2 to 3 miles. Furthermore, Pareto-optimal configurations were identified, demonstrating that a high service performance can be attained with a moderate number of facilities (typically between 8 and 10), moderate service radii (2 to 4 miles), and realistic capacity assumptions (around 65–70 hourly operations per facility). The model also showed that increasing the service radius and facility capacity beyond certain thresholds led to diminishing improvements in coverage and accessibility, underlining the importance of identifying optimal operating ranges.
5.2. Limitations
Despite the robustness of the proposed framework and the promising results obtained through a combination of classical optimization models and heuristics, this study has several limitations that should be acknowledged. These limitations highlight the trade-offs made for tractability and generalizability, and they point toward fruitful avenues for future research. First, the analysis assumed a homogeneous vertiport infrastructure, neglecting variability in site-specific features such as land availability, development costs, power supply, and construction feasibility. Real-world deployment of UAM infrastructure will likely require vertiports of varying sizes, capacities, and operational characteristics, influenced by their urban, peri-urban, or suburban context. Accounting for such heterogeneity would make the model more reflective of actual implementation challenges. Second, the model abstracted away regulatory, institutional, and physical constraints, such as zoning laws, FAA regulations, airspace restrictions, building height limitations, and noise-sensitive areas. These factors can significantly constrain the feasibility of the facility location and may even override optimal model outputs in practice. The absence of these real-world constraints limits the direct translatability of the proposed solutions into actionable policy recommendations. Additionally, the temporal dimension of demand was not considered. This study used static demand assumptions, which may not capture peak-hour variations, daily cycles, or long-term demand shifts due to demographic, economic, or technological changes. Incorporating time-of-day dynamics and stochastic demand modeling would allow for more realistic assessments of vertiport performance, queuing issues, and fleet utilization.
Also, this study did not incorporate cost structures beyond capacity and facility count. Key economic factors such as land value, construction costs, operational expenses, and maintenance were omitted. These components are vital for cost–benefit analysis and investment planning. Integrating comprehensive cost models would support more grounded policy and private-sector decision-making. Of importance is also the fact that travel behavior assumptions were limited to aggregate demand profiles derived from public transit and shared mobility patterns. As UAM adoption may draw from a broader user base, including private vehicle users and new demand segments, excluding these groups could bias the coverage and accessibility assessments. Furthermore, the model assumes deterministic and rational mode choices, overlooking behavioral aspects such as price sensitivity, safety perception, or trust in autonomy. Also, environmental and equity considerations were not explicitly integrated. Planning for UAM infrastructure in cities requires evaluating environmental impacts such as noise, emissions, and land use change, as well as distributional impacts across different population groups. Addressing spatial and social equity is essential for ensuring inclusive mobility outcomes and avoiding disproportionate burdens or benefits. Finally, this study was focused on public transit and shared mobility demand, omitting potential UAM users currently relying on private vehicles.
5.3. Future Steps
Future research should extend the proposed framework by incorporating temporal dynamics, heterogeneous facility types, multimodal integration, and detailed cost structures. Expanding the demand profile to include a broader range of travel behaviors and integrating equity-based metrics can further enrich planning outcomes. More specifically, future research should address the aforementioned limitations by:
- Incorporating heterogeneous vertiport types and infrastructure profiles, allowing site-specific customization.
- Embedding regulatory and spatial constraints into the optimization model, using GIS-based exclusion zones and legal data layers.
- Modeling time-dependent demand and vehicle availability, possibly using agent-based or discrete-event simulation.
- Developing full-cost models to analyze trade-offs between infrastructure investment, operational performance, and user pricing.
- Expanding the demand base and behavioral modeling to include private vehicle users, new market segments, and uncertainty in adoption.
- Integrating environmental and equity metrics, including noise impact zones, environmental justice indicators, and the spatial distribution of benefits.
Author Contributions
All authors contributed to the study design, analysis, and interpretation of the results, as well as the preparation of the manuscript. All authors reviewed the results and approved the submission of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data and sources used in this study are cited in the text, and references can be found for each data source in the References section.
Acknowledgments
The author would like to dedicate this paper to the memory of my co-author, friend, and mentor, Hani S. Mahmassani, whose guidance was instrumental in the conception and execution of this research. Special gratitude to Alireza Talebpour for his guidance and advice on this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Reiche, C.; Goyal, R.; Cohen, A.; Serrao, J.; Kimmel, S.; Fernando, C.; Shaheen, S. Urban Air Mobility Market Study; NASA: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Coogan, M.A. Ground Access to Major Airports by Public Transportation; Transportation Research Board: Washington, DC, USA, 2008. [Google Scholar]
- Mohammed, A.; Roisman, R. Washington-Baltimore Regional Air Passenger Survey; Metropolitan Washington Council of Governments: Washington, DC, USA, 2013. [Google Scholar]
- Harvey, G. Study of Airport Access Mode Choice. J. Transp. Eng. 1986, 112, 525–545. [Google Scholar] [CrossRef]
- Gokasar, I.; Gunay, G. Modeling and Implications of Airport Ground Egress Mode Choice. KSCE J. Civ. Eng. 2021, 25, 669–679. [Google Scholar] [CrossRef]
- FAA. Air Traffic by the Numbers; Federal Aviation Agency: Washington, DC, USA, 2024. [Google Scholar]
- Wu, Z.; Zhang, Y. Integrated Network Design and Demand Forecast for On-Demand Urban Air Mobility. Engineering 2021, 7, 473–487. [Google Scholar] [CrossRef]
- Rimjha, M.; Trani, A. Urban Air Mobility: Factors Affecting Vertiport Capacity. In Proceedings of the 2021 Integrated Communications Navigation and Surveillance Conference (ICNS), Dulles, VA, USA, 19–23 April 2021. [Google Scholar]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; The Regents of the University of California: Oakland, CA, USA, 1967. [Google Scholar]
- Anderberg, M.R. Cluster Analysis for Applications: Probability and Mathematical Statistics: A Series of Monographs and Textbooks; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Sinha, A.A.; Rajendran, S. A Novel Two-Phase Location Analytics Model for Determining Operating Station Locations of Emerging Air Taxi Services. Decis. Anal. J. 2022, 2, 100013. [Google Scholar] [CrossRef]
- Brühl, R.; Lindner, M.; Fricke, H. Locating Air Taxi Infrastructure in Regional Areas—The Saxony Use Case; Technische Universität Dresden: Dresden, Germany, 2022. [Google Scholar]
- Arellano, S. A Data-and Demand-Based Approach at Identifying; Department of Civil, Geo, and Environmental Engineering, Technical University of Munich: Munich, Germany, 2020. [Google Scholar]
- Holden Jeff Goel, N. Fast-Forwarding to a Future of On-Demand Urban Air Transportation; Uber Elevate: Los Angeles, CA, USA, 2016. [Google Scholar]
- Lim, E.; Hwang, H. The Selection of Vertiport Location for On-Demand Mobility and Its Application to Seoul Metro Area. Int. J. Aeronaut. Space Sci. 2019, 20, 260–272. [Google Scholar] [CrossRef]
- Rajendran, S.; Zack, J. Insights on Strategic Air Taxi Network Infrastructure Locations Using an Iterative Constrained Clustering Approach. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 470–505. [Google Scholar] [CrossRef]
- Jeong, J.; So, M.; Hwang, H.-Y. Selection of Vertiports Using K-Means Algorithm and Noise Analyses for Urban Air Mobility (UAM) in the Seoul Metropolitan Area. Appl. Sci. 2021, 11, 5729. [Google Scholar] [CrossRef]
- Peng, X.; Bulusu, V.; Sengupta, R. Hierarchical Vertiport Network Design for On-Demand Multi-Modal Urban Air Mobility. In Proceedings of the 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022. [Google Scholar]
- Rajendran, S. Study on Facility Location of Air Taxi Skyports Using a Prescriptive Analytics Approach. SSRN Electron. J. 2021, 18, 100761. [Google Scholar] [CrossRef]
- Kai, W.; Jacquillat, A.; Vaze, V. Vertiport Planning for Urban Aerial Mobility: An Adaptive Discretization Approach. Manuf. Serv. Oper. Manag. 2022, 24, 3215–3235. [Google Scholar] [CrossRef]
- Rath, S.; Chow, J.Y.J. Air Taxi Skyport Location Problem with Single-Allocation Choice-Constrained Elastic Demand for Airport Access. J. Air Transp. Manag. 2022, 105, 102294. [Google Scholar] [CrossRef]
- Fadhil, D.N. A GIS-Based Analysis for Selecting Ground Infrastructure Locations for Urban Air Mobility; Technical University of Munich: Munich, Germany, 2018. [Google Scholar]
- Boutilier, J.J.; Chan, T.C.Y. Drone Network Design for Cardiac Arrest Response. Manuf. Serv. Oper. Manag. 2022, 24, 2407–2424. [Google Scholar] [CrossRef]
- Willey, L.C.; Salmon, J.L. A Method for Urban Air Mobility Network Design Using Hub Location and Subgraph Isomorphism. Transp. Res. Part C Emerg. Technol. 2021, 125, 102997. [Google Scholar] [CrossRef]
- Karatas, M.; Yakıcı, E. An Iterative Solution Approach to a Multi-Objective Facility Location Problem. Appl. Soft Comput. 2018, 62, 272–287. [Google Scholar] [CrossRef]
- Volakakis, V.; Mahmassani, H.S. Vertiport infrastructure location optimization for equitable access to urban air mobility. Infrastructures 2024, 9, 239. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, M.; Mesbahi, M.; Topcu, U. Vertiport Selection in Hybrid Air-Ground Transportation Networks via Mathematical Programs with Equilibrium Constraints. IEEE Trans. Control. Netw. Syst. 2023, 10, 21082119. [Google Scholar] [CrossRef]
- Ribeiro, J.K.; Borille, G.M.R.; Caetano, M.; da Silva, E.J. Repurposing Urban Air Mobility Infrastructure for Sustainable Transportation in Metropolitan Cities: A Case Study of Vertiports in São Paulo, Brazil. Sustain. Cities Soc. 2023, 98, 104797. [Google Scholar] [CrossRef]
- Mavraj, G.; Eltgen, J.; Fraske, T.; Swaid, M.; Berling, J.; Röntgen, O.; Fu, Y.; Schulz, D. A Systematic Review of Ground-Based Infrastructure for the Innovative Urban Air Mobility. Trans. AerosRes. 2022, 2022, 1–17. [Google Scholar] [CrossRef]
- Rahman, B.; Bridgelall, R.; Habib, M.F.; Motuba, D. Integrating Urban Air Mobility into a Public Transit System: A GIS-Based Approach to Identify Candidate Locations for Vertiports. Vehicles 2023, 1803, 5–1817. [Google Scholar] [CrossRef]
- Rothfeld, R.; Fu, M.; Balać, M.; Antoniou, C. Potential Urban Air Mobility Travel Time Savings: An Exploratory Analysis of Munich, Paris, and San Francisco. Sustainability 2021, 2217, 13. [Google Scholar] [CrossRef]
- Li, X. Repurposing Existing Infrastructure for Urban Air Mobility: A Scenario Analysis in Southern California. Drones 2023, 7, 37. [Google Scholar] [CrossRef]
- Rajendran, S.; Srinivas, S. Air taxi service for urban mobility: A critical review of recent developments, future challenges, and opportunities. TransRes. Part E Logist. TransRev. 2020, 1020, 14390. [Google Scholar] [CrossRef]
- Patel, S.R. Urban Air Mobility Network Asset Acquisition Optimization. Ph.D. Thesis, Purdue University Graduate School, West Lafayette, IN, USA, 2023. [Google Scholar]
- Maheshwari, A.; Mudumba, S.; Sells, B.E.; DeLaurentis, D.A.; Crossley, W.A. Identifying and analyzing operations limits for passenger-carrying urban air mobility missions. In Proceeding of the 2020 AIAA Aviation and Aeronautics Forum and Expo-sition, Virtual, 15–19 June 2020; p. 2913. [Google Scholar]
- Li, S.; Lee, S. Prediction of Urban Air Mobility Multirotor VTOL Broadband Noise Using UCD-QuietFly. J. Am. Helicopter Soc. 2021, 66, 1–13. [Google Scholar] [CrossRef]
- Glaab, P.; Wieland, F.; Santos, M.; Sharma, R.; Tamburro, R.; Lee, P.U. Simulating fleet noise for notional uam vehicles and operations in New York. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Clarke, M.A. Towards a Regional and Urban Air Mobility Future: The Development of Computational Approaches for Quantifying Trade-offs in Electric Aircraft Design; Stanford University: Stanford, CA, USA, 2022. [Google Scholar]
- Venkatesh, N.; Payan, A.P.; Justin, C.Y.; Kee, E.; Mavris, D. Optimal Siting of Sub-Urban Air Mobility (sUAM) Ground Archi-tectures Using Network Flow Formulation. In Proceedings of the AIAA AVIATION 2020 FORUM, Reno, NV, USA, 15–19 June 2020; p. 2921. [Google Scholar]
- Kotwicz Herniczek, M.T.; German, B.J. Impact of airspace restrictions on urban air mobility airport shuttle service route feasibility. Transp. Res. Rec. 2022, 2676, 689–706. [Google Scholar] [CrossRef]
- Sells, B.E.; Maheshwari, A.; Chao, H.; Wright, E.; Crossley, W.; Sun, D. Evaluating the impact of urban air mobility aerodrome siting on mode choice. In AIAA AVIATION 2021 FORUM; Aerospace Research Center: Columbus, OH, USA, 2021; p. 2371. [Google Scholar]
- Rimjha, M.; Hotle, S.; Trani, A.; Hinze, N.; Smith, J.; Dollyhigh, S. Urban air mobility: Airport ground access demand estimation. In AIAA Aviation 2021 Forum; Aerospace Research Center: Columbus, OH, USA, 2021; p. 3209. [Google Scholar]
- Larson, R.C.; Odoni, A.R. Urban Operations Research; Prentice-Hall: Upper Saddle River, NJ, USA, 1981. [Google Scholar]
- Daskin, M.S. Network and Discrete Location: Models, Algorithms, and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Balinski, M.L. Integer Programming: Methods, Uses, Computations. Manag. Sci. 1965, 12, 253–313. [Google Scholar] [CrossRef]
- Larson, R.C. A hypercube queuing model for facility location and redistricting in urban emergency services. Comput. Oper. Res. 1974, 1, 67–95. [Google Scholar] [CrossRef]
- Kuehn, A.A.; Hamburger, M.J. A Heuristic Program for Locating Warehouses. Manag. Sci. 1963, 9, 643–666. [Google Scholar] [CrossRef]
- Zanjirani Farahani, R.; Hekmatfar, M. (Eds.) Facility Location: Concepts, Models, Algorithms and Case Studies; Physica-Verlag HD: Heidelberg, Germany, 2009. [Google Scholar]
- Cornuéjols, G.; Wolsey, L. The Uncapicitated Facility Location Problem; Cornell University Operations Research and Industrial Engineering: Ithaca, NY, USA, 1983. [Google Scholar]
- Sridharan, R. The capacitated plant location problem. Eur. J. Oper. Res. 1995, 87, 203–213. [Google Scholar] [CrossRef]
- Raghavan, S.; Sahin, M.; Salman, F.S. The Capacitated Mobile Facility Location Problem. Eur. J. Oper. Res. 2019, 277, 507–520. [Google Scholar] [CrossRef]
- Melkote, S.; Daskin, M.S. Capacitated Facility Location/Network Design Problems. Eur. J. Oper. Res. 2001, 129, 481–495. [Google Scholar] [CrossRef]
- Wu, L.-Y.; Zhang, X.-S.; Zhang, J.-L. Capacitated Facility Location Problem with General Setup Cost. Comput. Oper. Res. 2006, 33, 1226–1241. [Google Scholar] [CrossRef]
- Papadimitriou, D.; Colle, D. Demeester, Mixed Integer Optimization for the Combined Capacitated Facility Location-Routing Problem. Ann. Telecommun. 2018, 73, 37–62. [Google Scholar] [CrossRef]
- Canel, C.; Khumawala, B.M. A Mixed-integer Programming Approach for the International Facilities Location Problem. Int. J. Oper. Prod. Manag. 1996, 16, 49–68. [Google Scholar] [CrossRef]
- Pirkul, H.; Jayaraman, V. A Multi-Commodity, Multi-Plant, Capacitated Facility Location Problem: Formulation and Efficient Heuristic Solution. Comput. Oper. Res. 1998, 25, 869–878. [Google Scholar] [CrossRef]
- Davis, P.S.; Ray, T.L. A Branch-bound Algorithm for the Capacitated Facilities Location Problem. Nav. Res. Logist. Q. 1969, 16, 331–344. [Google Scholar] [CrossRef]
- Sá, G. Branch-and-Bound and Approximate Solutions to the Capacitated Plant-Location Problem. Oper. Res. 1969, 17, 1005–1016. [Google Scholar] [CrossRef]
- Akinc, U.; Khumawala, B.M. An Efficient Branch and Bound Algorithm for the Capacitated Warehouse Location Problem. Manag. Sci. 1977, 23, 585–594. [Google Scholar] [CrossRef]
- Charikar, M.; Guha, S. Improved Combinatorial Algorithms for the Facility Location and K-Median Problems. In Proceedings of the 40th Annual Symposium on Foundations of Computer Science, New York City, NY, USA, 17–19 October 1999. [Google Scholar]
- Canel, C.; Khumawala, B.M.; Law, J.; Loh, A. An Algorithm for the Capacitated, Multi-Commodity Multi-Period Facility Location Problem. Comput. Oper. Res. 2001, 28, 411–427. [Google Scholar] [CrossRef]
- An, H.-C.; Singh, M.; Svensson, O. LP-Based Algorithms for Capacitated Facility Location. Available online: http://arxiv.org/abs/1407.3263 (accessed on 1 December 2023).
- Christofides, N.; Beasley, J.E. Extensions to a Lagrangean Relaxation Approach for the Capacitated Warehouse Location Problem. Eur. J. Oper. Res. 1983, 12, 19–28. [Google Scholar] [CrossRef]
- Klincewicz, J.G.; Luss, H. A Lagrangian Relaxation Heuristic for Capacitated Facility Location with Single-Source Constraints. J. Oper. Res. Soc. 1986, 37, 495–500. [Google Scholar] [CrossRef]
- Tragantalerngsak, S.; Holt, J.; Ronnqvist, M. Lagrangian Heuristics for the Two-Echelon, Single-Source, Capacitated Facility Location Problem. Eur. J. Oper. Res. 1997, 102, 611–625. [Google Scholar] [CrossRef]
- Holmberg, K.; Rönnqvist, M.; Yuan, D. An Exact Algorithm for the Capacitated Facility Location Problems with Single Sourcing. Eur. J. Oper. Res. 1999, 113, 544–559. [Google Scholar] [CrossRef]
- Klose, A. A Lagrangean Relax-and-Cut Approach for the Two-Stage Capacitated Facility Location Problem. Eur. J. Oper. Res. 2000, 126, 408–421. [Google Scholar] [CrossRef]
- Avella, P.; Boccia, M.; Sforza, A.; Vasil’ev, I. An Effective Heuristic for Large-Scale Capacitated Facility Location Problems. J. Heuristics 2009, 15, 597–615. [Google Scholar] [CrossRef]
- Torres-Soto, J.E.; Üster, H. Dynamic-Demand Capacitated Facility Location Problems with and without Relocation. Int. J. Prod. Res. 2011, 49, 3979–4005. [Google Scholar] [CrossRef]
- Aardal, K. Capacitated Facility Location: Separation Algorithms and Computational Experience. Math. Program. 1998, 81, 149–175. [Google Scholar] [CrossRef]
- Avella, P.; Boccia, M. A Cutting Plane Algorithm for the Capacitated Facility Location Problem. Comput. Optim. Appl. 2009, 43, 39–65. [Google Scholar] [CrossRef]
- Ryu, J.; Park, S. A Branch-and-Price Algorithm for the Robust Single-Source Capacitated Facility Location Problem under Demand Uncertainty. EURO J. Transp. Logist. 2022, 11, 100069. [Google Scholar] [CrossRef]
- Van Roy, T.J. A Cross Decomposition Algorithm for Capacitated Facility Location. Oper. Res. 1986, 34, 145–163. [Google Scholar] [CrossRef]
- Chudak, F.A.; Shmoys, D.B. Improved Approximation Algorithms for the Uncapacitated Facility Location Problem. SIAM J. Comput. 2003, 33, 1–25. [Google Scholar] [CrossRef]
- Levi, R.; Shmoys, D.B.; Swamy, C. LP-Based Approximation Algorithms for Capacitated Facility Location. Math. Program. 2012, 131, 365–379. [Google Scholar] [CrossRef]
- Domschke, W.; Drexl, A. ADD-Heuristics’ Starting Procedures for Capacitated Plant Location Models. Eur. J. Oper. Res. 1985, 21, 47–53. [Google Scholar] [CrossRef]
- Cornuejols, G.; Sridharan, R.; Thizy, J.M. A Comparison of Heuristics and Relaxations for the Capacitated Plant Location Problem. Eur. J. Oper. Res. 1991, 50, 280–297. [Google Scholar] [CrossRef]
- Khumawala, B.M. An Efficient Heuristic Procedure for the Capacitated Warehouse Location Problem. Nav. Res. Logist. Q. 1994, 21, 609–623. [Google Scholar] [CrossRef]
- Feldman, E.; Lehrer, F.A.; Ray, T.L. Warehouse Location Under Continuous Economies of Scale. Manag. Sci. 1966, 12, 670–684. [Google Scholar] [CrossRef]
- Souto, G.; Morais, I.; Mauri, G.R.; Ribeiro, G.M.; González, P.H. A Hybrid Matheuristic for the Two-Stage Capacitated Facility Location Problem. Expert Syst. Appl. 2021, 185, 115501. [Google Scholar] [CrossRef]
- Mauri, G.R.; Biajoli, F.L.; Rabello, R.L.; Chaves, A.A.; Ribeiro, G.M.; Lorena, L.A.N. Hybrid Metaheuristics to Solve a Multiproduct Two-stage Capacitated Facility Location Problem. Int. Trans. Oper. Res. 2021, 28, 3069–3093. [Google Scholar] [CrossRef]
- Delmaire, H.; Díaz, J.A.; Fernández, E.; Ortega, M. Reactive GRASP and Tabu Search Based Heuristics for the Single Source Capacitated Plant Location Problem. INFOR: Inf. Syst. Oper. Res. 1999, 37, 194–225. [Google Scholar] [CrossRef]
- Sun, M. A Tabu Search Heuristic Procedure for the Capacitated Facility Location Problem. J. Heuristics 2012, 18, 91–118. [Google Scholar] [CrossRef]
- Ho, S.C. An Iterated Tabu Search Heuristic for the Single Source Capacitated Facility Location Problem. Appl. Soft Comput. 2015, 27, 169–178. [Google Scholar] [CrossRef]
- Ahuja, R.K.; Orlin, J.B.; Pallotino, S.; Scappara, M.P.; Scutellà, M.G. A Multi-Exchange Heuristic for the Single-Source Capacitated Facility Location Problem. Manag. Sci. 2004, 50, 749–760. [Google Scholar] [CrossRef]
- Lam, M.; Mittenthal, J. Capacitated Hierarchical Clustering Heuristic for Multi Depot Location-Routing Problems. Int. J. Logist. Res. Appl. 2013, 16, 433–444. [Google Scholar] [CrossRef]
- Xu, Y.; Möhring, R.H.; Xu, D.; Zhang, Y.; Zou, Y. A Constant FPT Approximation Algorithm for Hard-Capacitated k-Means. Optim. Eng. 2020, 21, 709–722. [Google Scholar] [CrossRef]
- Geetha, S.; Poonthalir, G.; Vanathi, P.T. Improved K-Means Algorithm for Capacitated Clustering Problem. J. Comput. Sci. 2009, 8, 52–59. [Google Scholar]
- Küçükdeniz, T.; Baray, A.; Ecerkale, K.; Esnaf, Ş. Integrated Use of Fuzzy C-Means and Convex Programming for Capacitated Multi-Facility Location Problem. Expert Syst. Appl. 2012, 39, 4306–4314. [Google Scholar] [CrossRef]
- Mostafa, N.; Eltawil, A. Solving the Heterogeneous Capacitated Vehicle Routing Problem Using K-Means Clustering and Valid Inequalities. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Rabat, Morocco, 11–13 April 2017. [Google Scholar]
- Liao, K.; Guo, D. A Clustering-based Approach to the Capacitated Facility Location Problem. Trans. GIS 2008, 12, 323–339. [Google Scholar] [CrossRef]
- Caballero-Morales, S.O.; Barojas-Payan, E.; Sanchez-Partida, D.; Martinez-Flores, J.L.; Caballero-Morales, S.O.; Barojas-Payan, E.; Sanchez-Partida, D.; Martinez-Flores, J.L. Extended GRASP-Capacitated K-Means Clustering Algorithm to Establish Humanitarian Support Centers in Large Regions at Risk in Mexico. J. Optim. 2018, 2018, 3605298. [Google Scholar] [CrossRef]
- Guha, S.; Khuller, S. Greedy Strikes Back: Improved Facility Location Algorithms. J. Algorithms 1999, 31, 228–248. [Google Scholar] [CrossRef]
- Wang, Q.; Batta, R.; Rump, C.M. Algorithms for a Facility Location Problem with Stochastic Customer Demand and Immobile Servers. Ann. Oper. Res. 2002, 111, 17–34. [Google Scholar] [CrossRef]
- Xu, G.; Xu, J. An Improved Approximation Algorithm for Uncapacitated Facility Location Problem with Penalties. J. Comb. Optim. 2009, 17, 424–436. [Google Scholar] [CrossRef]
- Zhang, J. Approximating the Two-Level Facility Location Problem via a Quasi-Greedy Approach. Math. Program. 2006, 108, 159–176. [Google Scholar] [CrossRef]
- Shen, Z.-J.M.; Zhan, R.L.; Zhang, J. The Reliable Facility Location Problem: Formulations, Heuristics, and Approximation Algorithms. Inf. J. Comput. 2011, 23, 470–482. [Google Scholar] [CrossRef]
- Jain, K.; Mahdian, M.; Markakis, E.; Saberi, A.; Vazirani, V.V. Greedy Facility Location Algorithms Analyzed Using Dual Fitting with Factor-Revealing LP. J. ACM 2003, 50, 795–824. [Google Scholar] [CrossRef]
- Ghosh, D. Neighborhood Search Heuristics for the Uncapacitated Facility Location Problem. Eur. J. Oper. Res. 2003, 150, 150–162. [Google Scholar] [CrossRef]
- Mahdian, M.; Markakis, E.; Saberi, A.; Vazirani, V. A Greedy Facility Location Algorithm Analyzed Using Dual Fitting. In Approximation, Randomization, and Combinatorial Optimization: Algorithms and Techniques; Goemans, M., Jansen, K., Rolim, J.D., Trevisan, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 127–137. [Google Scholar]
- Carlo, H.J.; Aldarondo, F.; Saavedra, P.M.; Torres, S.N. Capacitated Continuous Facility Location Problem with Unknown Number of Facilities. Eng. Manag. J. 2012, 24, 24–31. [Google Scholar] [CrossRef]
- Zare Mehrjerdi, Y.; Nadizadeh, A. Using Greedy Clustering Method to Solve Capacitated Location-Routing Problem with Fuzzy Demands. Eur. J. Oper. Res. 2013, 229, 75–84. [Google Scholar] [CrossRef]
- Korupolu, M.R.; Plaxton, C.G.; Rajaraman, R. Analysis of a Local Search Heuristic for Facility Location Problems. J. Algorithms 2000, 37, 146–188. [Google Scholar] [CrossRef]
- Luis, M.; Ramli, M.F.; Lin, A. A Greedy Heuristic Algorithm for Solving the Capacitated Planar Multi-Facility Location-Allocation Problem. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; p. 1782. [Google Scholar]
- Jain, K.; Mahdian, M.; Saberi, A. A New Greedy Approach for Facility Location Problems. In Proceedings of the Thiry-Fourth Annual ACM Symposium on Theory of Computing, Montreal, QC, Canada, 19–21 May 2002; pp. 731–740. [Google Scholar]
- Hochbaum, D.S. Heuristics for the Fixed Cost Median Problem. Math. Program. 1982, 22, 148–162. [Google Scholar] [CrossRef]
- Zhang, A. New Approximation Algorithm for the k -Facility Location Problem. Theor. Comput. Sci. 2007, 384, 126–135. [Google Scholar] [CrossRef]
- Rodriguez, F.J.; Blum, C.; Lozano, M.; García-Martínez, C. Iterated Greedy Algorithms for the Maximal Covering Location Problem. In Evolutionary Computation in Combinatorial Optimization; Hao, J.-K., Middendorf, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 172–181. [Google Scholar]
- Lim, S.; Kuby, M. Heuristic Algorithms for Siting Alternative-Fuel Stations Using the Flow-Refueling Location Model. Eur. J. Oper. Res. 2010, 204, 51–61. [Google Scholar] [CrossRef]
- Church, R.; ReVelle, C. The Maximal Covering Location Problem. In Papers of the Regional Science Association; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Eaton, D.J.; Daskin, M.S.; Simmons, D.; Bulloch, B.; Jansma, G. Determining Emergency Medical Service Vehicle Deployment in Austin, Texas. Interfaces 1985, 15, 96–108. [Google Scholar] [CrossRef]
- Marianov, V.; ReVelle, C. The Queueing Maximal Availability Location Problem: A Model for the Siting of Emergency Vehicles. Eur. J. Oper. Res. 1996, 93, 110–120. [Google Scholar] [CrossRef]
- Yin, P.; Mu, L. Modular Capacitated Maximal Covering Location Problem for the Optimal Siting of Emergency Vehicles. Appl. Geogr. 2012, 34, 247–254. [Google Scholar] [CrossRef]
- Hougland, E.S.; Stephens, N.T. Air Pollutant Monitor Siting by Analytical Techniques. J. Air Pollut. Control Assoc. 1976, 26, 51–53. [Google Scholar] [CrossRef]
- Megiddo, N.; Zemel, E.; Hakimi, S.L. The Maximum Coverage Location Problem. SIAM J. Algebr. Discret. Methods 1983, 4, 253–261. [Google Scholar] [CrossRef]
- Murray, A.T.; Tong, D.; Grubesic, T.H. Spatial Optimization: Expanding Emergency Services to Address Regional Growth and Development. In Studies in Applied Geography and Spatial Analysis: Addressing Real World Issues; Edward Elgar Publishing: Cheltenham, UK, 2012; p. 109. [Google Scholar]
- Goodchild, M.F.; Lee, J. Coverage Problems and Visibility Regions on Topographic Surfaces. Ann. Oper. Res. 1989, 18, 175–186. [Google Scholar] [CrossRef]
- Bao, S.; Xiao, N.; Lai, Z.; Zhang, H.; Kim, C. Optimizing Watchtower Locations for Forest Fire Monitoring Using Location Models. Fire Saf. J. 2015, 71, 100–109. [Google Scholar] [CrossRef]
- Yi, Z.; Liu, X.C.; Wei, R. Electric Vehicle Demand Estimation and Charging Station Allocation Using Urban Informatics. Transp. Res. Part D Transp. Environ. 2022, 106, 103264. [Google Scholar] [CrossRef]
- Murray, A.T. Maximal Coverage Location Problem: Impacts, Significance, and Evolution. Int. Reg. Sci. Rev. 2016, 39, 5–27. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.J.; Ozuna, L.; López-Piñón, D. The Maximal Covering Location Problem with Accessibility Indicators. Socio-Econ. Plan. Sci. 2020, 71, 100758. [Google Scholar] [CrossRef]
- Cornuejols, G.; Fisher, M.L. Exceptional Paper—Location of Bank Accounts to Optimize Float: An Analytic Study of Exact and Approximate Algorithms. Manag. Sci. 1977, 23, 789–810. [Google Scholar] [CrossRef]
- Galvão, R.D.; Raggi, L.A. A Method for Solving to Optimality Uncapacitated Location Problems. Ann. Oper. Res. 1989, 18, 225–244. [Google Scholar] [CrossRef]
- Daskin, M.S.; Hunter, A.P.; Van Buer, M.G. Toward an Integrated Model of Facility Location and Transportation Network Design. The Transportation Center; Northwestern University: Evanston, IL, USA, 1993. [Google Scholar]
- Magnanti, T.L.; Wong, R. Decomposition Methods for Facility Location Problems. In Discrete Location Theory; Mirchandani, P.B., Francis, R.L., Eds.; Wiley: New York, NY, USA, 1990; pp. 209–262. [Google Scholar]
- Syed, N.; Rye, M.; Ade, M.; Trani, A.; Hinze, N.; Swingle, H.; Smith, J.; Marien, T.; Dollyhigh, S. Preliminary Considerations for ODM Air Traffic Management Based on Analysis of Commuter Passenger Demand and Travel Patterns for the Silicon Valley Region of California. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, AIAA, Denver, CO, USA, 5–9 June 2017; p. 3082. [Google Scholar]
- Goodrich, K.H.; Barmore, B. Exploratory Analysis of the Airspace Throughput and Sensitivities of an Urban Air Mobility System. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Kohlman, L.W.; Patterson, M.D. System-Level Urban Air Mobility Transportation Modeling and Determination of Energy-Related Constraints. In Proceedings of the Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Gentry, J.; Duffy, K.; Swedish, W.J. Airport Capacity Profiles; Federal Aviation Administration: Washington, DC, USA, 2014. [Google Scholar]
- Vascik, P.D.; Hansman, R.J. Evaluation of Key Operational Constraints Affecting On-Demand Mobility for Aviation in the Los Angeles Basin: Ground Infrastructure, Air Traffic Control and Noise. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Chicago Transit Authority. (n.d.). CTA—“L” (rail) lines [Shapefile]. City of Chicago Data Portal. Available online: https://data.cityofchicago.org/Transportation/CTA-L-Rail-Lines-Shapefile/53r7-y88m/about_data (accessed on 6 May 2024).
- Chicago Transit Authority. CTA—“L” Rail Stations [Shapefile]. Data.gov. 2023. Available online: https://catalog.data.gov/dataset/cta-l-rail-stations-shapefile (accessed on 6 May 2024).
- SSMA (n.d.). Pace Bus Routes, Schedules, and Maps. Pace. Available online: https://www.pacebus.com/routes-schedules-and-maps (accessed on 6 May 2024).
- Regional Transportation Authority Mapping and Statistics (RTAMS). Pace Bus Ridership by Route. 2024. Available online: https://www.rtams.org/ridership/pace/routes (accessed on 7 May 2024).
- Regional Transportation Authority Mapping and Statistics (RTAMS). Pace Ridership. 2024. Available online: https://rtams.org/ridership (accessed on 6 May 2024).
- Chicago Transit Authority. Monthly Ridership Report: March 2024 [PDF]. 2024. Available online: https://www.transitchicago.com/assets/1/6/Monthly_Ridership_2024-3.pdf (accessed on 6 May 2024).
- Regional Transportation Authority Mapping and Statistics (RTAMS). CTA Rail Ridership by Station. 2024. Available online: https://www.rtams.org/ridership/cta/stations (accessed on 7 May 2024).
- Foote Peter, J.; LaBelle, S.J.; Stuart, D.G. Increasing rail transit access to airports in Chicago. Transp. Res. Rec. 1997, 1600, 1–9. [Google Scholar] [CrossRef]
- Chicago Transit Authority. Return to Transit Survey Results Overview. 2022. Available online: https://www.transitchicago.com/assets/1/6/2021_Return_to_Transit_Survey_Results.pdf (accessed on 6 May 2024).
- City of Chicago. Transportation Network Providers (Trips 2018–2022) [Dataset]. Chicago Data Portal. 2022. Available online: https://data.cityofchicago.org/Transportation/Transportation-Network-Providers-Trips-2018-2022-/m6dm-c72p/about_data (accessed on 6 May 2024).
- City of Chicago. Taxi Trips (2013–2023) [Dataset]. Chicago Data Portal. 2022. Available online: https://data.cityofchicago.org/Transportation/Taxi-Trips-2013-2023-/wrvz-psew/about_data (accessed on 6 May 2024).
- Guo, Y.; Hu, M.; Zou, B.; Hansen, M.; Zhang, Y.; Xie, H. Air Traffic Flow Management Integrating Separation Management and Ground Holding: An Efficiency-Equity Bi-Objective Perspective. Transp. Res. Part B: Methodol. 2022, 155, 394–423. [Google Scholar] [CrossRef]
- Cohen, A.P.; Shaheen, S.A.; Farrar, E.M. Urban Air Mobility: History, Ecosystem, Market Potential, and Challenges. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6074–6087. [Google Scholar] [CrossRef]
- City of Chicago. Chicago Traffic Tracker—Historical Congestion Estimates by Segment. Data.gov. 2024. Available online: https://catalog.data.gov/dataset/chicago-traffic-tracker-historical-congestion-estimates-by-segment-2024-current (accessed on 6 May 2024).
- City of Chicago. Chicago Traffic Tracker—Congestion estimates by region. City of Chicago Data Portal. 2024. Available online: https://data.cityofchicago.org/Transportation/Chicago-Traffic-Tracker-Congestion-Estimates-by-Re/t2qc-9pjd/about_data (accessed on 6 May 2024).
- Yedavalli, P.; Cohen, A. Planning Land Use Constrained Networks of Urban Air Mobility Infrastructure in the San Francisco Bay Area. Transp. Res. Rec. J. Transp. Res. Board 2022, 2676, 106–116. [Google Scholar] [CrossRef]
- Mallela, J.; Wheeler, P.; Le Bris, G.; Nguyen, L.G. Urban Air Mobility: An Airport Perspective; Transportation Research Board: Washington, DC, USA, 2023. [Google Scholar]
- Black & Veatch. Powered for Take Off: NIA-NASA Urban Air Mobility Electric Infrastructure Study; Black & Veatch: Overland Park, KS, USA, 2018. [Google Scholar]
- Lilium, GmBH. Designing a Scalable Vertiport; Lilium: Wessling, Germany, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).