Dynamic Simulation and Seismic Analysis of Hillside RC Buildings Isolated by High-Damping Rubber Bearings
Abstract
1. Introduction
2. High-Damping Rubber Bearing Constitutive Model
3. Numerical Modeling
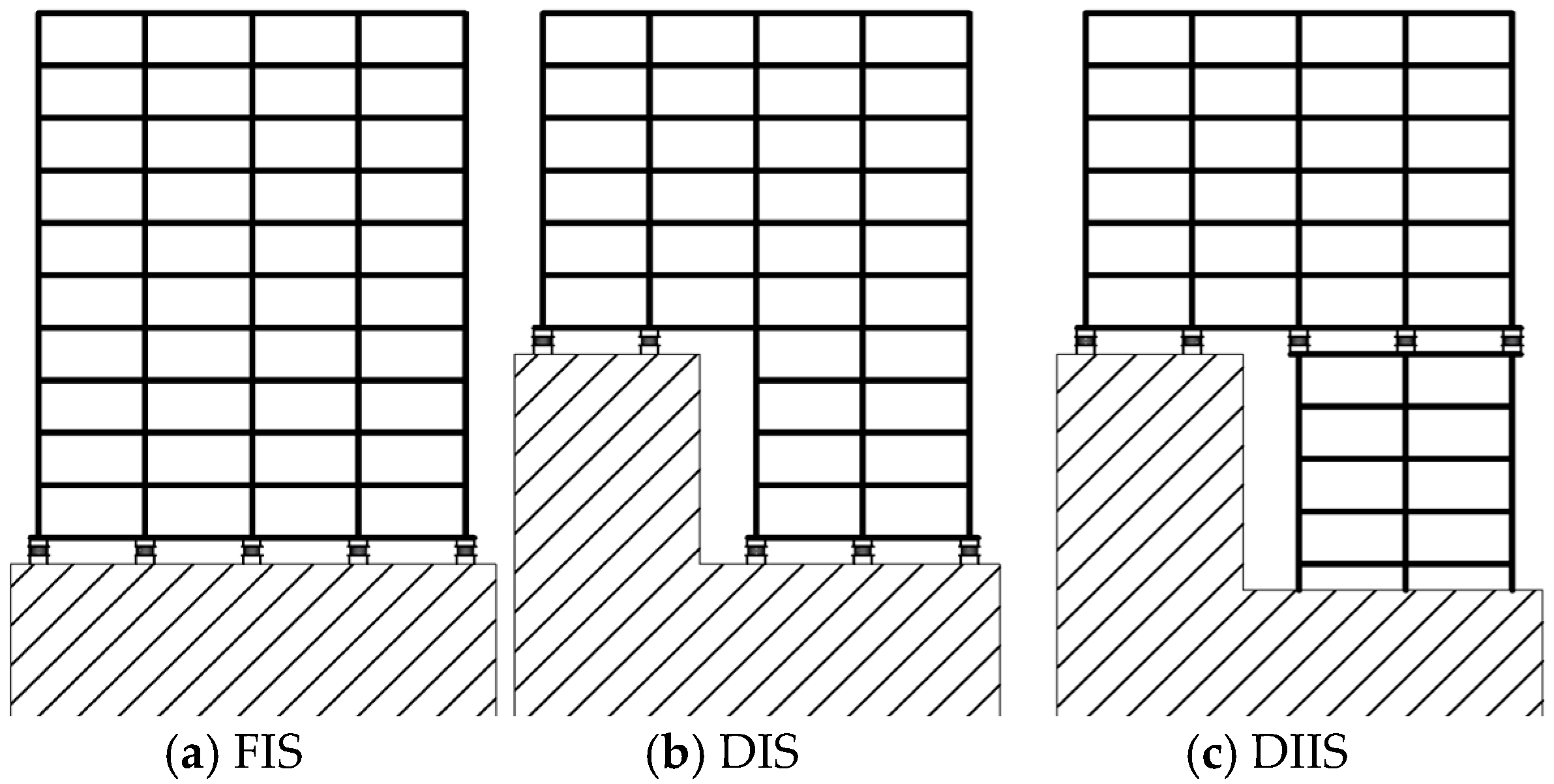
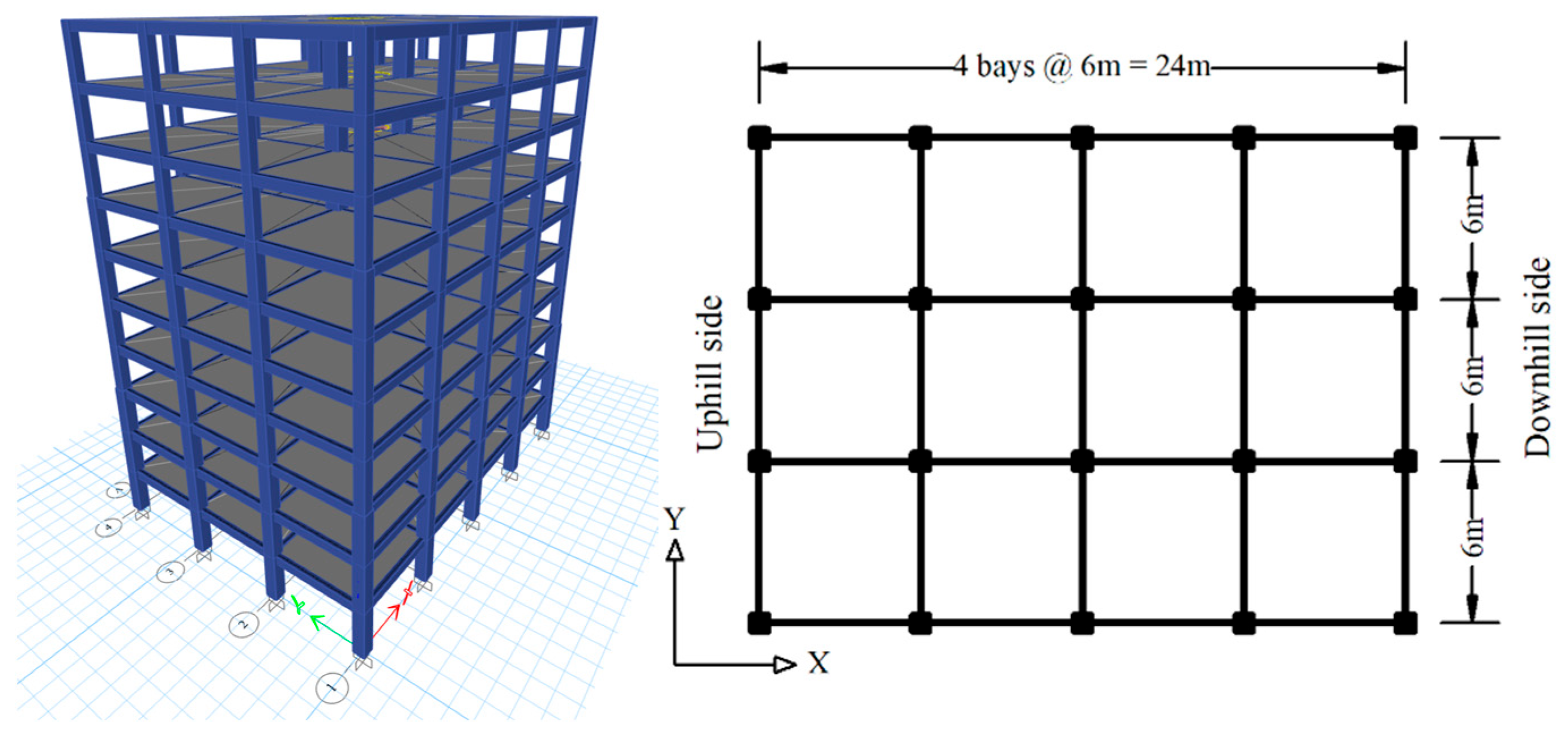
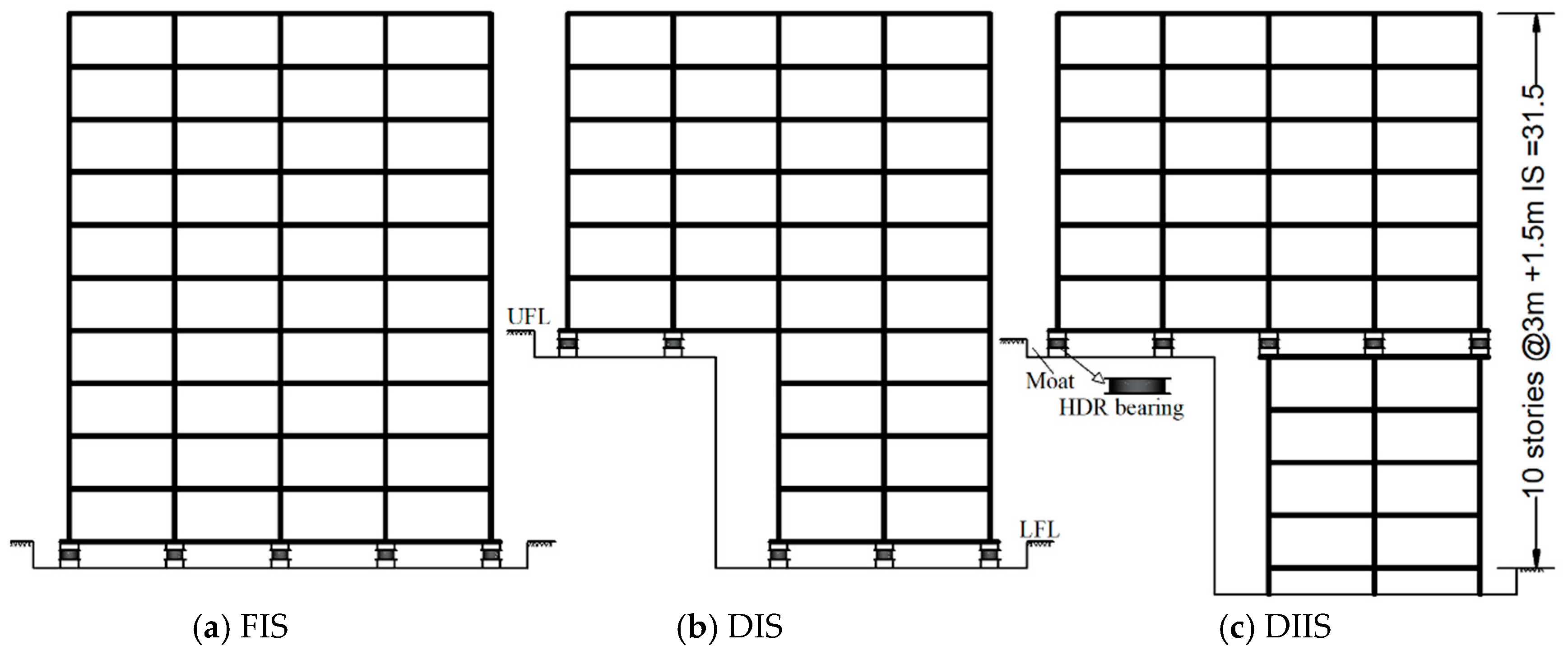
3.1. Structural Modeling of Hilly Buildings
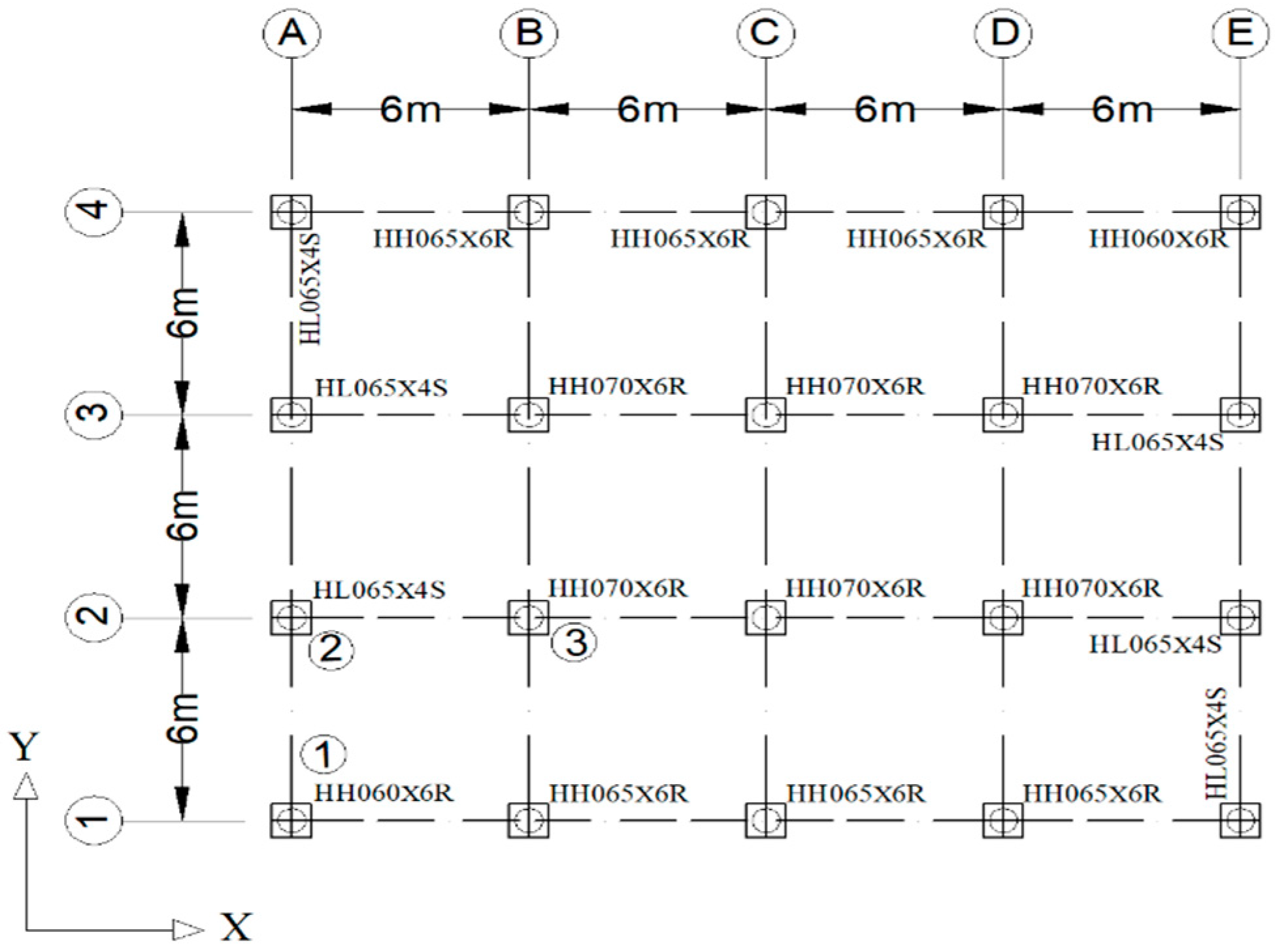
3.2. Design of High-Damping Rubber Bearings
3.3. Modal Analysis
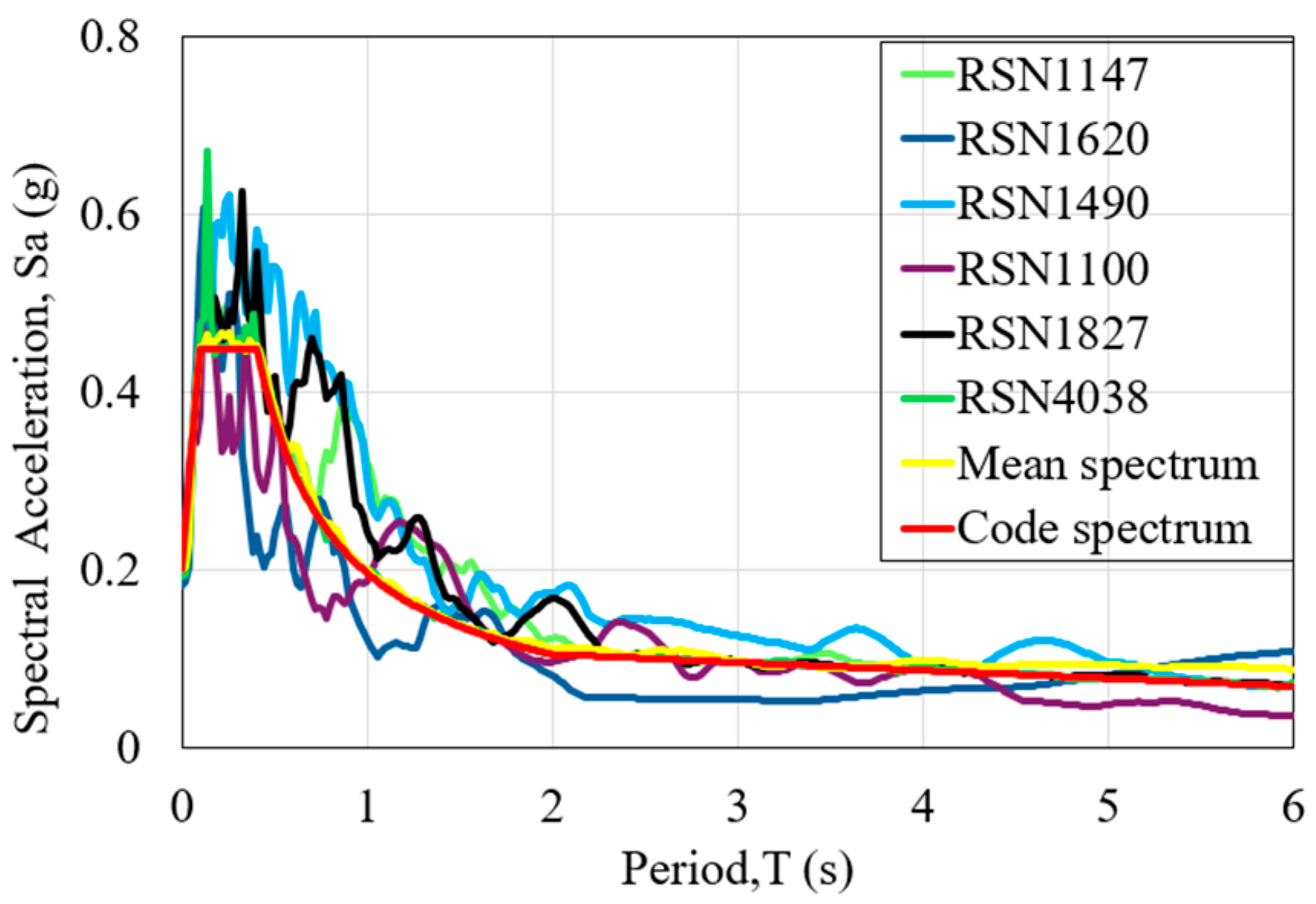
3.4. Ground Motion Selection and Scaling
4. Results and Discussion
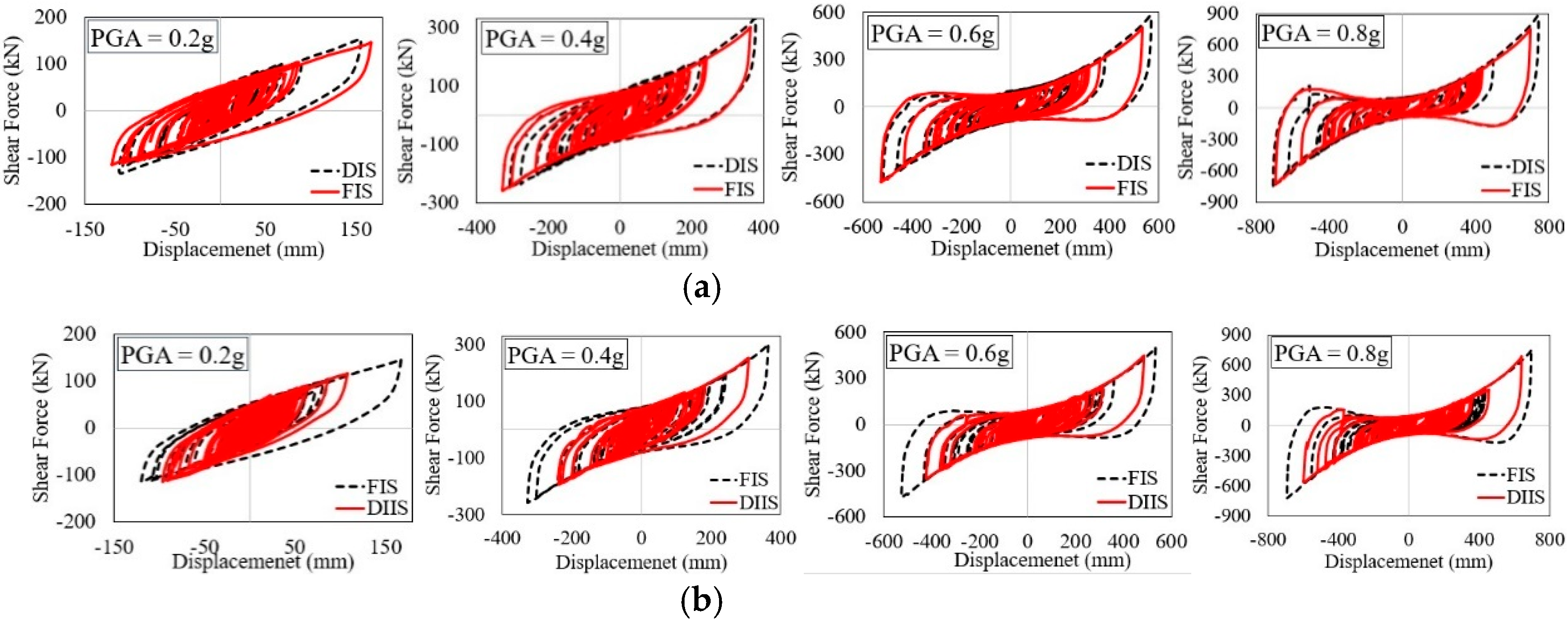
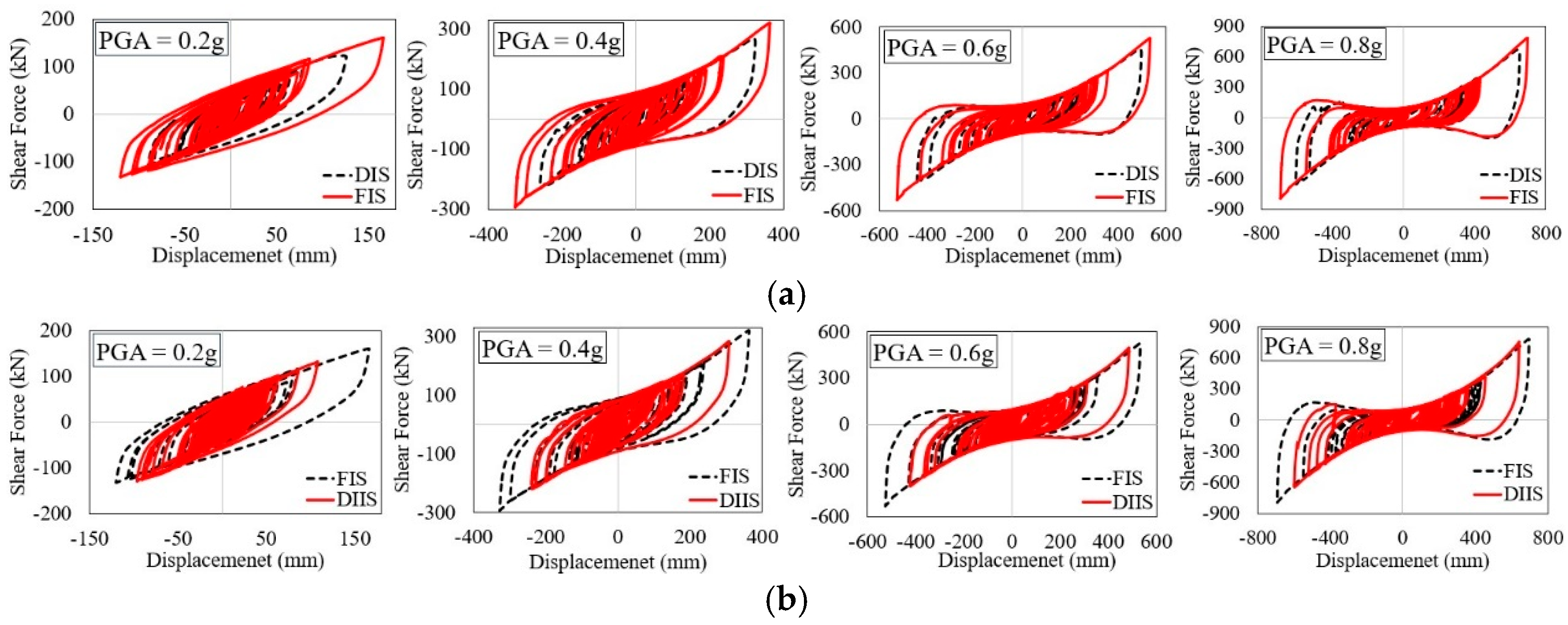
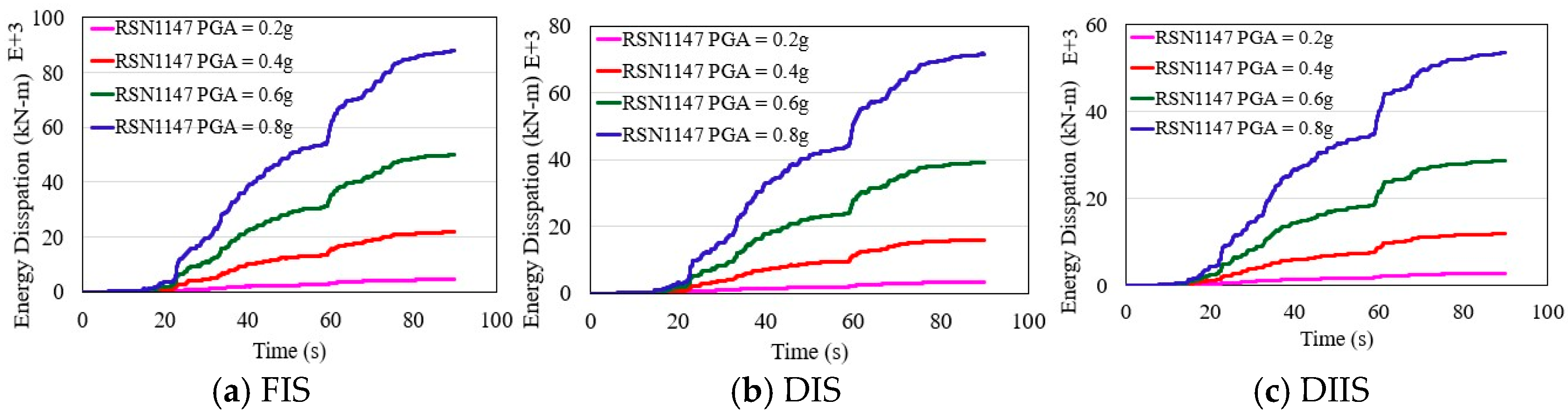
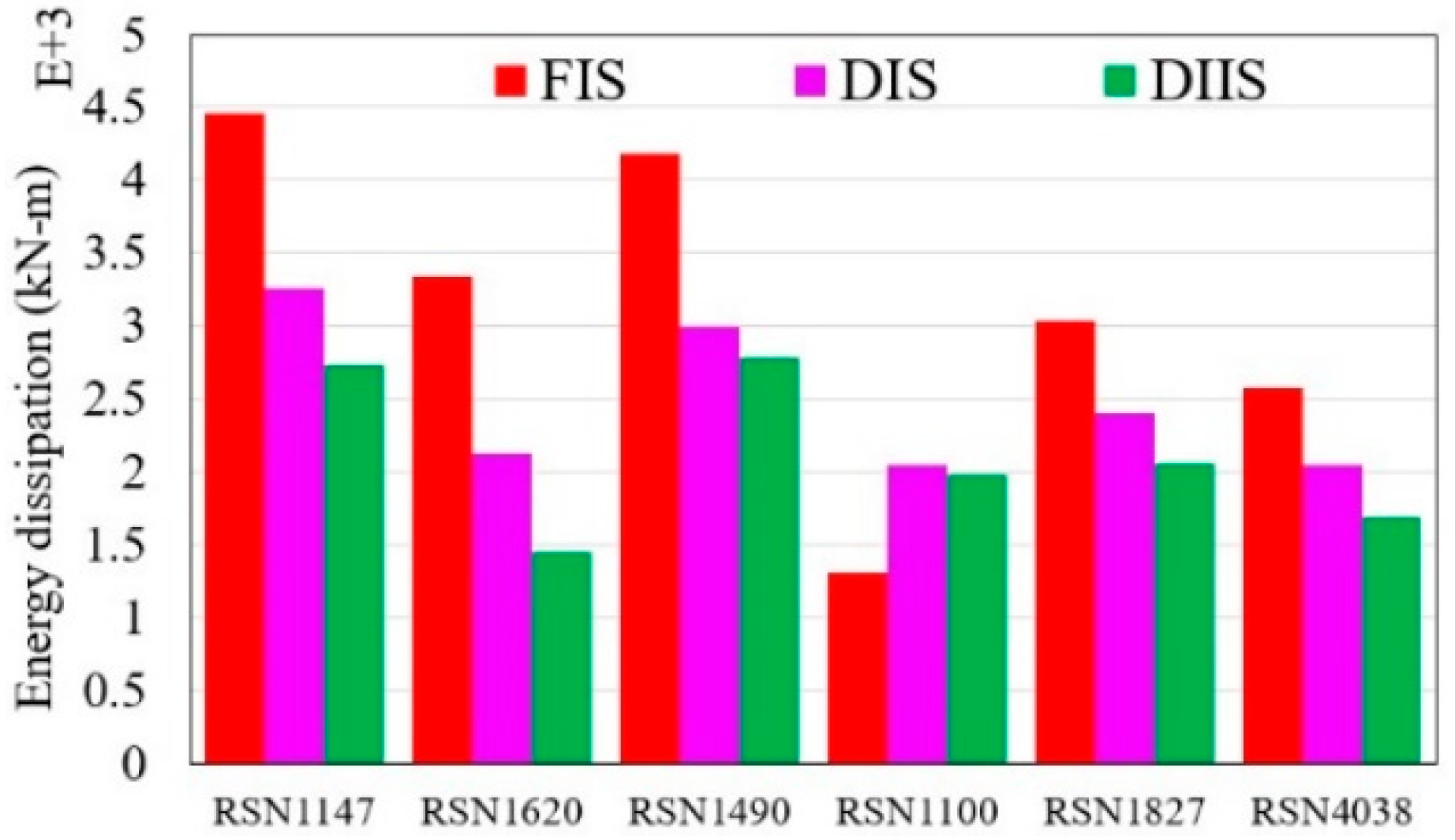
4.1. Hysteresis and Energy Dissipation of the Bearings
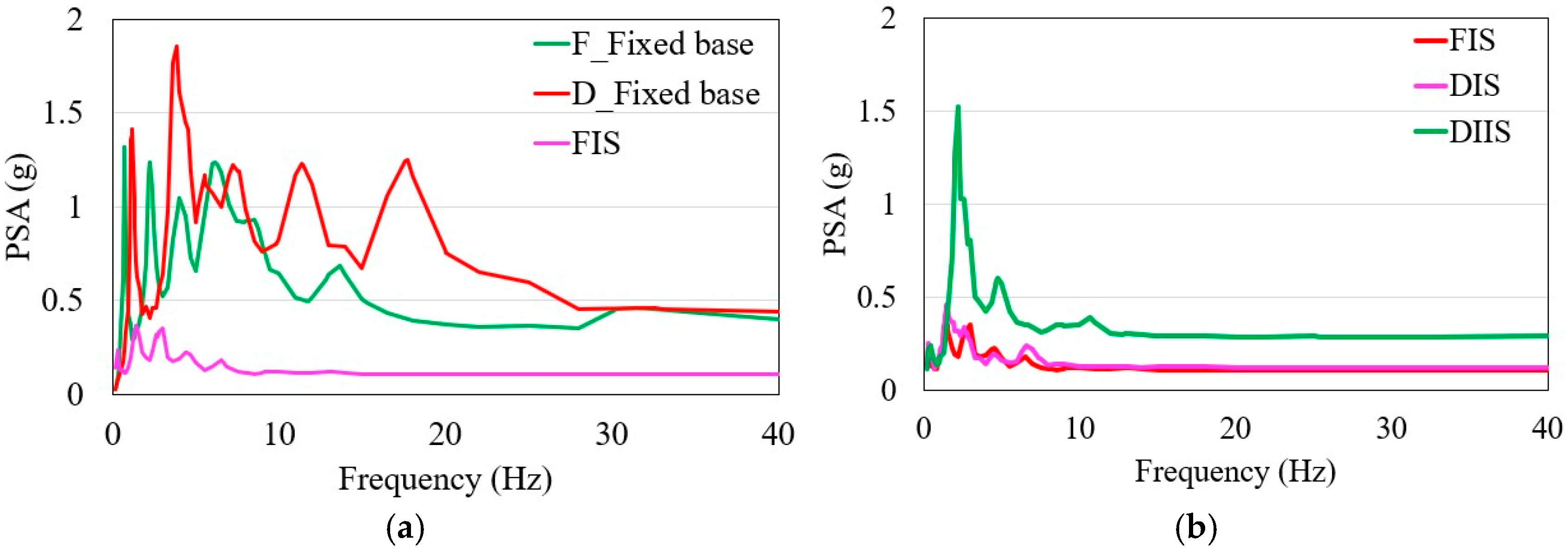
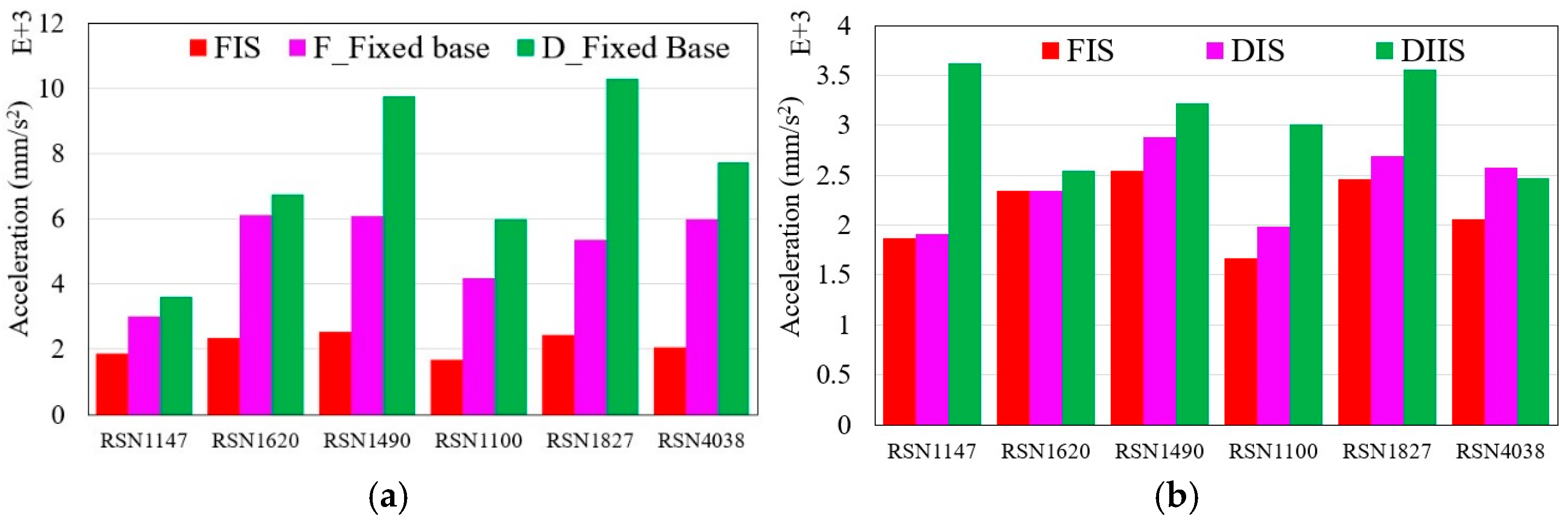
4.2. Peak Acceleration of the Superstructures
4.3. Maximum Inter-Story Drift
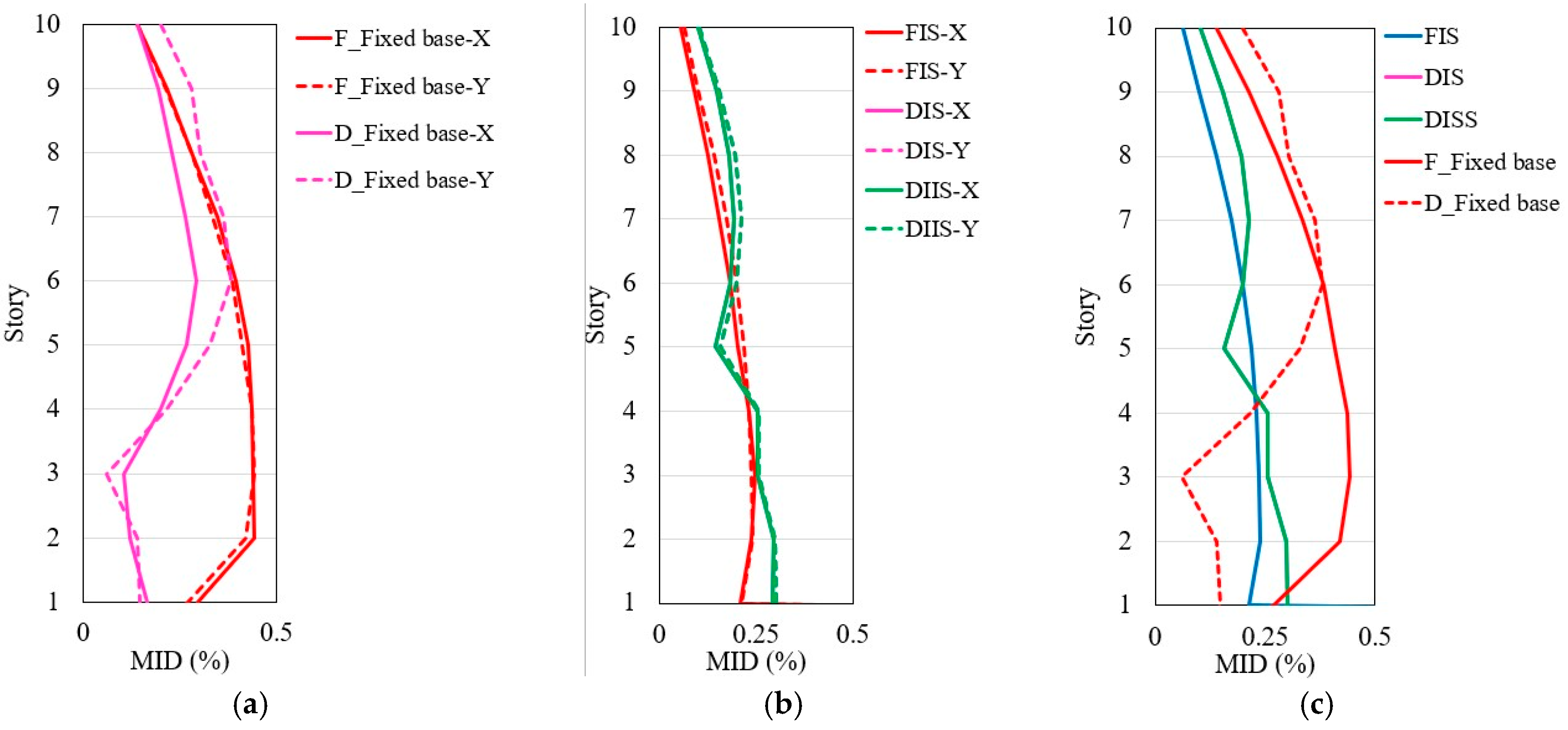
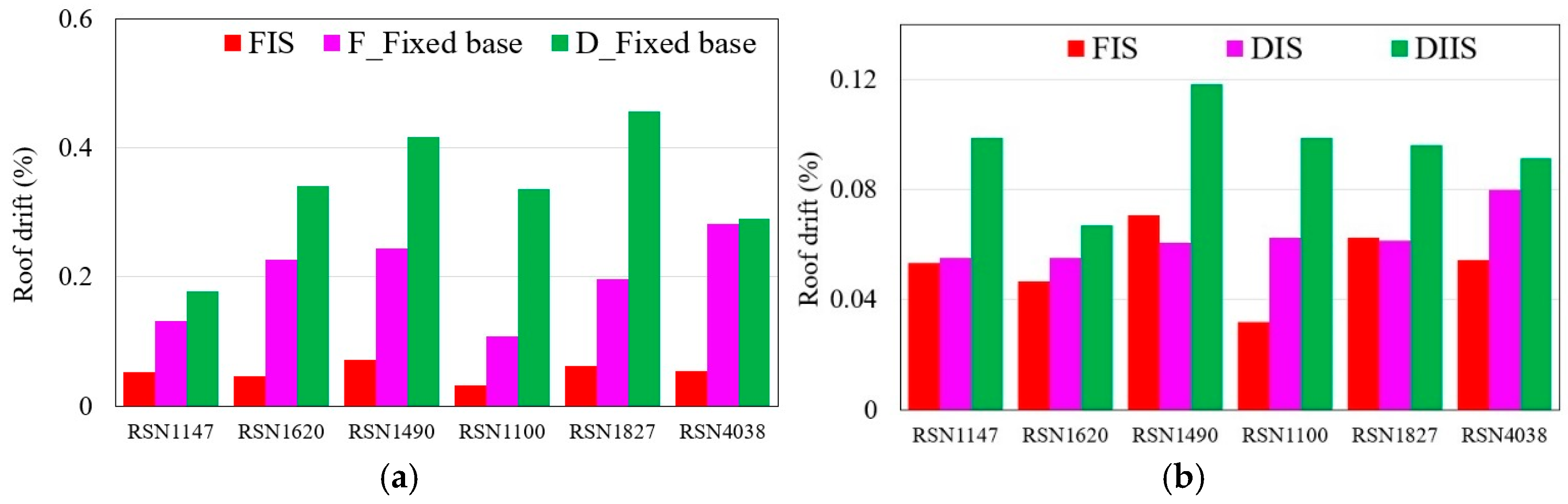
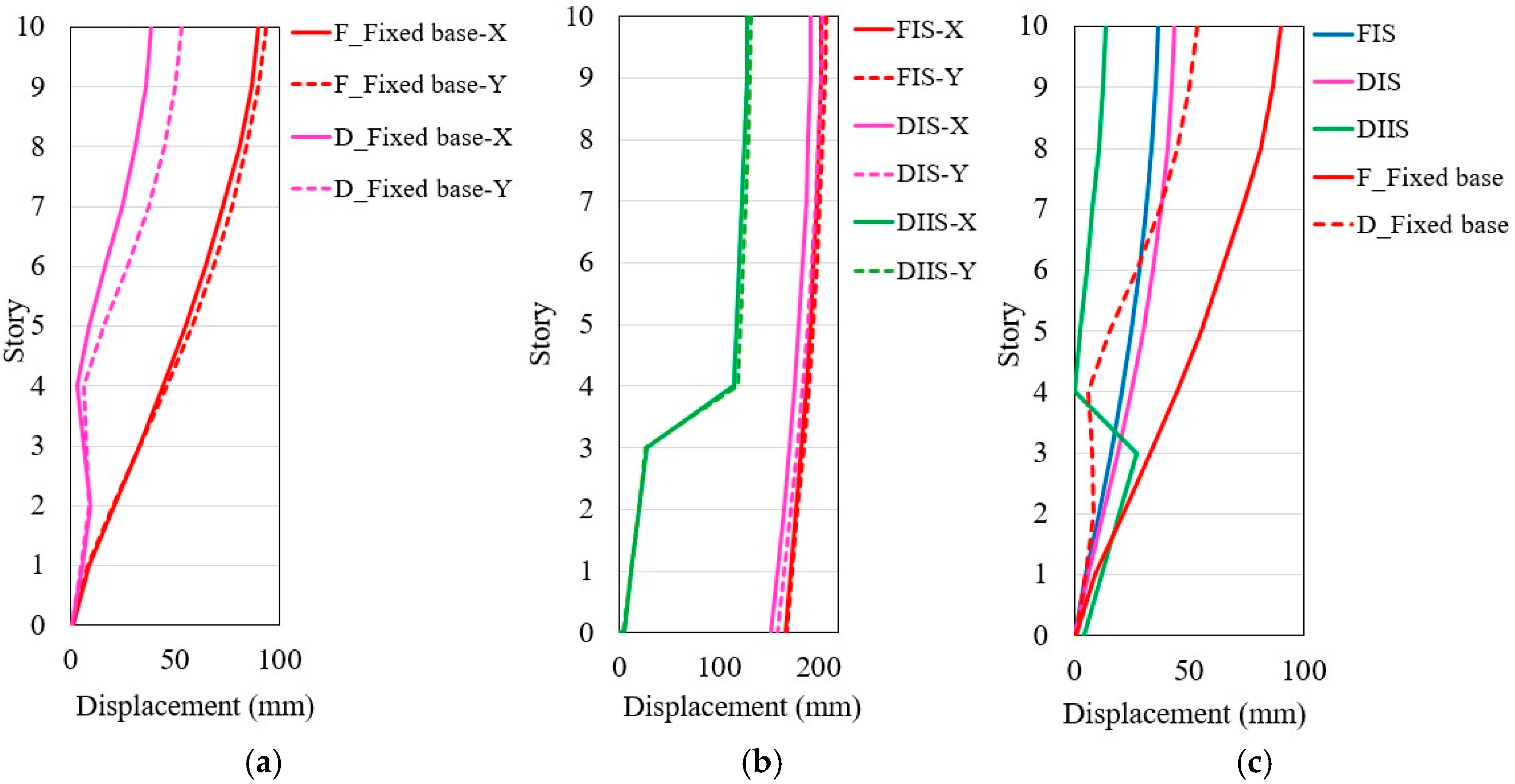
4.4. Maximum Story Displacement
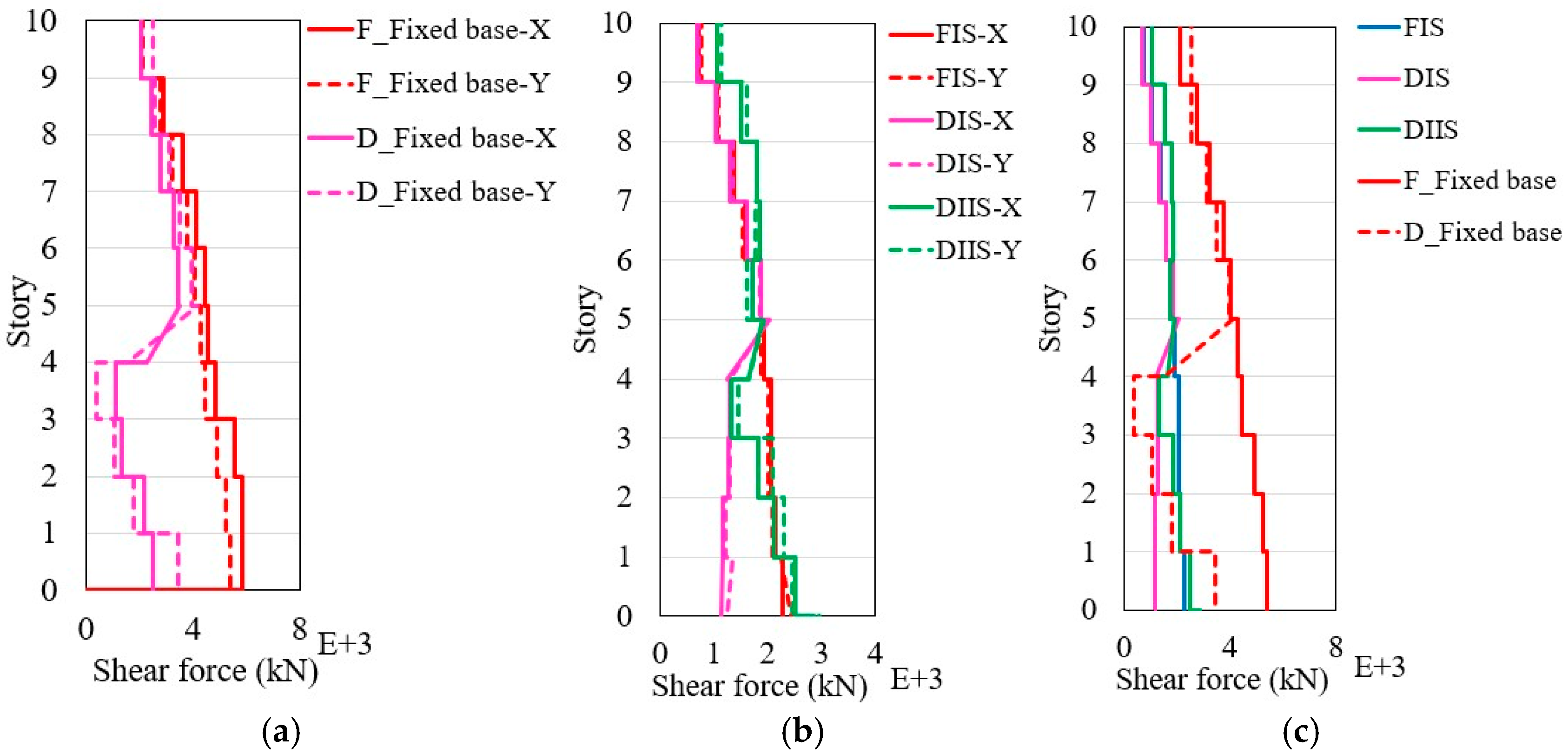
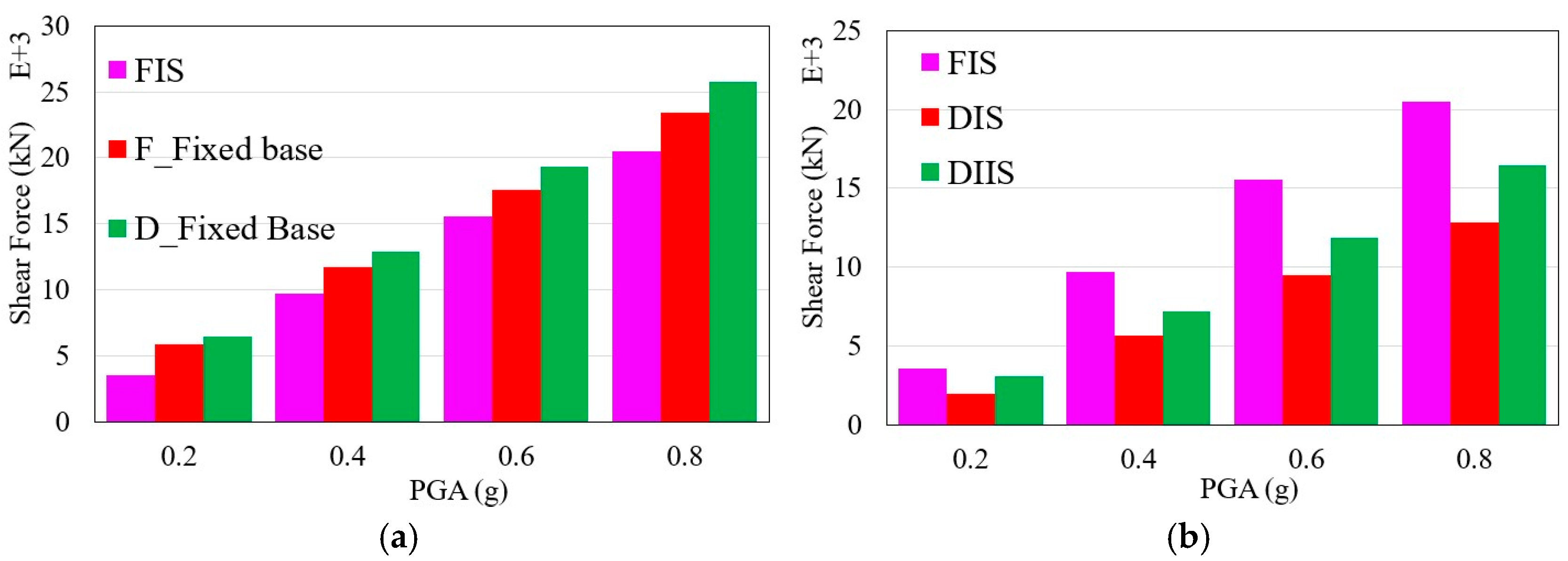
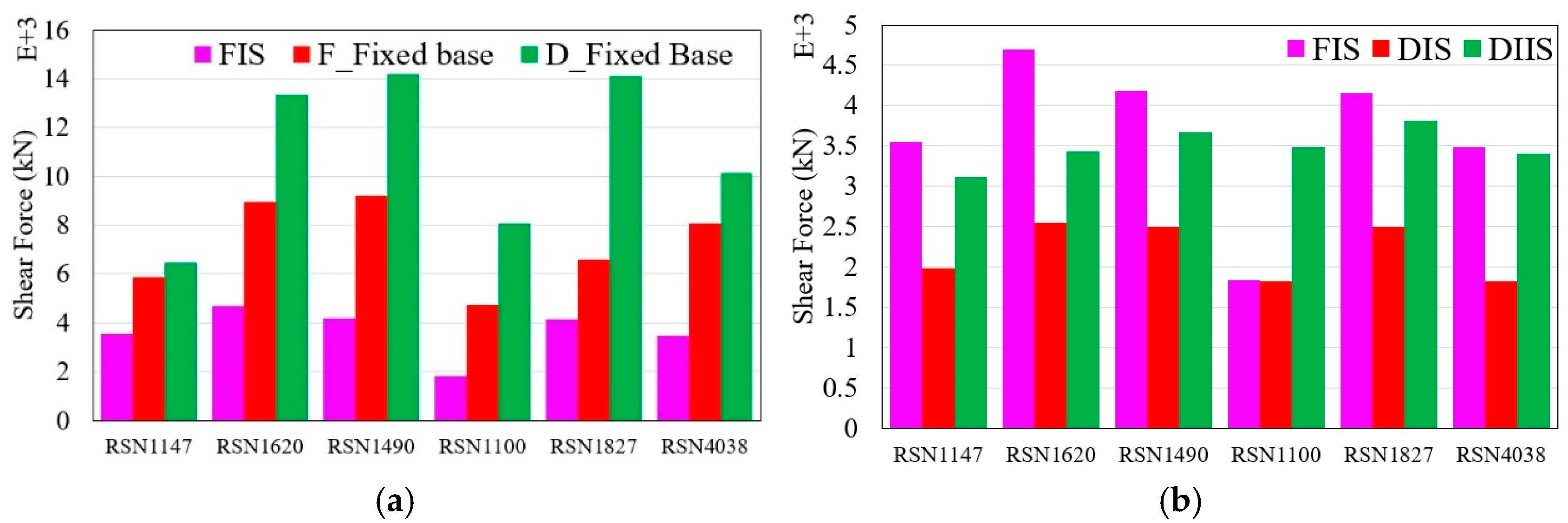
4.5. Story Shear Force
4.6. Overturning Moment
4.7. Base Shear Force
5. Conclusions
- The HDRBs exhibited consistent hysteresis behavior and proficient energy dissipation at different earthquake intensities. Buildings with HDRBs experienced significantly reduced story shear forces, ranging from 90% to 100% compared to non-isolated structures. This demonstrates the ability of HDRBs to absorb substantial seismic energy without permanent deformation, thereby enhancing the structural resilience of flat-plane and split-foundation structures.
- Base isolation techniques, especially in the FIS model, led to an almost 90% decrease in the peak roof acceleration compared to fixed-base structures. The DIS and DIIS models also exhibited a considerable reduction of approximately 80%. Additionally, the DIS and DIIS models exhibited noteworthy decreases in base shear forces of 70% and 55%, respectively, compared to non-isolated split-foundation structures.
- The isolated structures demonstrated an 80% reduction in the maximum inter-story drift compared to the non-isolated structures, underscoring the effectiveness of base and inter-story isolation in bolstering structural stability and mitigating seismic risk, particularly in hillside structures with split foundations.
- The analysis confirmed that the selected properties of an isolation period of 2.75 s and 20% damping ratio were highly effective for this hillside structure. The 2.75 s period successfully decoupled the building from the dominant energy content of the earthquake ground motions, which was the primary mechanism behind the substantial reductions in acceleration responses (up to 90%). Concurrently, the 20% damping ratio provided optimal energy dissipation, effectively controlling bearing displacements while still mitigating force-based demands, as evidenced by the up to 78% reduction in inter-story drift and 70% reduction in base shear. The discussion explicitly analyzed the interplay between period lengthening and damping, highlighting how these specific parameters are central to the enhanced seismic resilience demonstrated in the results.
- Base isolation effectively reduced the overturning moments in both the X- and Y-directions, showing values that were much lower than those of the non-isolated models. This indicates enhanced stability and a reduced risk of structural failure or tipping during seismic activity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bahuguna, A.; Firoj, M. Numerical simulation of seismic response of Slope–Foundation–Structure interaction for mid–rise RC buildings at various locations. Structures 2022, 44, 343–356. [Google Scholar] [CrossRef]
- Gómez, M.A.; Díaz-Segura, E.G.; Vielma, J.C. Nonlinear numerical assessment of the seismic response of hillside RC buildings. Earthq. Eng. Eng. Vib. 2021, 20, 423–440. [Google Scholar] [CrossRef]
- Rasa, A.Y.; Özyazıcıoğlu, M.H. Determination of the exact mode frequencies of multi-storey structures by state-space method and a comparison with mode superposition method. Chall. J. Struct. Mech. 2021, 7. [Google Scholar] [CrossRef]
- Athanassiadou, C.J. Seismic performance of R/C plane frames irregular in elevation. Eng. Struct. 2008, 30, 1250–1261. [Google Scholar] [CrossRef]
- Ning, P.; Gao, Y.; Wahab, A.G.; Zhong, T.; Bai, W.; Yang, W. Rammed earth construction for sustainable and seismic-resilient buildings: Structural advances and constraints methods. Mater. Struct. 2025, 58, 221. [Google Scholar] [CrossRef]
- Pinle, Z.; Wahab, A.G.; Xu, G.; Tao, Z.; Elias, S. Seismic performance of RC short-leg shear walls reinforced with HF-ECC: Experimental and numerical investigations. Structures 2025, 80, 110042. [Google Scholar] [CrossRef]
- Wahab, A.G.; Zhong, T.; Wei, F.; Hakimi, N.; Ahiwale, D.D. Seismic performance enhancement of RC framed structures through retrofitting and strengthening: An experimental and numerical study. Asian J. Civ. Eng. 2023, 25, 555–573. [Google Scholar] [CrossRef]
- Zhang, Z.; Tao, Z.; Zhang, Y.; Wu, L.; Liao, S.; Zhao, Z.; Ghafar, W.A. Molecular dynamics study on the interaction of phosphorus building gypsum /surfactant composites. J. Mol. Graph. Model. 2024, 126, 108650. [Google Scholar] [CrossRef] [PubMed]
- Von Winterfeldt, D.; Roselund, N.; Kitsuse, A. Framing Earthquake Retrofitting Decisions: The Case of Hillside Homes in Los Angeles; Pacific Earthquake Engineering Research Center, College of Engineering: Berkeley, CA, USA, 2000. [Google Scholar]
- Li, R.; Liu, L.; Li, Y.; Wang, G. Experimental Investigate on Seismic Performance of RC Hill-Side Stilted Buildings Affected by Vertical Stiffness Irregularity. J. Earthq. Eng. 2023, 28, 2273–2291. [Google Scholar] [CrossRef]
- Dai, B.; Tao, Z.; Wahab; Pei, Y.; Huang, R.; Yan, Z. Investigation and analysis of seismic damage to rural houses of Ninglang MS 5.5 earthquake. J. Nat. Disasters 2022, 31, 48–55. [Google Scholar] [CrossRef]
- Zheng, C.A.I.; Wen, P.A.N.; Qiang, Z.; Abdul, G.W.; Jing, Y. Seismic performance of an asymmetric twin-tower connected structure based on the hybrid energy dissipation technology. J. Vib. Shock 2024, 43, 288–300. [Google Scholar]
- Halkude, S.; Kalyanshetti, M.; Ingle, V. Seismic analysis of buildings resting on sloping ground with varying number of bays and hill slopes. Int. J. Eng. Res. Technol. 2013, 2, 3632–3640. [Google Scholar]
- Murthy, C. Open Ground Storey RC Frame Buildings with 230 mm Columns Unsafe During Earthquakes; National Seminar on Seismic Detailing of RCC Structures Proceedings: Kanpur, India, 2006; pp. 1–30. [Google Scholar]
- Ghosh, R.; Debbarma, R. Seismic Vulnerability Assessment of Soft Storeyed Structures with Plan Irregularity and Collapse Prevention. Int. J. Eng. Res. Technol. 2016, 5, 755–761. [Google Scholar]
- Roshan, P.; Pal, S. Structural challenges for seismic stability of buildings in hilly areas. Environ. Sci. Pollut. Res. Int. 2023, 30, 99100–99126. [Google Scholar] [CrossRef]
- Aggarwal, Y.; Saha, S.K. Seismic performance assessment of reinforced concrete hilly buildings with open story. Structures 2021, 34, 224–238. [Google Scholar] [CrossRef]
- Konakalla, R.; Chilakapati, R.D.; Raparla, H. Effect of vertical irregularity in multi-storied buildings under dynamic loads using linear static analysis. Int. J. Educ. Appl. Res. 2014, 5, 29–34. [Google Scholar]
- Surana, M.; Singh, Y.; Lang, D.H. Fragility analysis of hillside buildings designed for modern seismic design codes. Struct. Des. Tall Spec. Build. 2018, 27, e1500. [Google Scholar] [CrossRef]
- Birajdar, B.; Nalawade, S. Seismic analysis of buildings resting on sloping ground. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Raj, D.; Singh, Y.; Kaynia, A.M. Seismic fragility analysis of coupled building-slope systems. Earthq. Eng. Struct. Dyn. 2023, 53, 116–137. [Google Scholar] [CrossRef]
- Alhan, C.; Öncü-Davas, S. Performance limits of seismically isolated buildings under near-field earthquakes. Eng. Struct. 2016, 116, 83–94. [Google Scholar] [CrossRef]
- Ohsaki, M.; Miyamura, T.; Kohiyama, M.; Yamashita, T.; Yamamoto, M.; Nakamura, N. Finite-element analysis of laminated rubber bearing of building frame under seismic excitation. Earthq. Eng. Struct. Dyn. 2015, 44, 1881–1898. [Google Scholar] [CrossRef]
- Calvi, P.M.; Ruggiero, D.M. Numerical modelling of variable friction sliding base isolators. Bull. Earthq. Eng. 2015, 14, 549–568. [Google Scholar] [CrossRef]
- Pourmasoud, M.; Hajirasouliha, I.; Park, A.; Lim, J.B.P. A new approach to estimate the lead core characteristic strength of lead rubber bearings. Eng. Struct. 2022, 270, 114817. [Google Scholar] [CrossRef]
- Deringöl, A.H.; Güneyisi, E.M. Effect of Using High Damping Rubber Bearings for Seismic Isolation of the Buildings. Int. J. Steel Struct. 2021, 21, 1698–1722. [Google Scholar] [CrossRef]
- Riyadh, M.M.; Osman, S.S.; Alam, M.S. Experimental investigation of novel carbon-fiber reinforced elastomeric isolators with polyurethane cores under vertical and lateral loading. Eng. Struct. 2023, 275, 115186. [Google Scholar] [CrossRef]
- Rahgozar, A.; Estekanchi, H.E.; Mirfarhadi, S.A. On optimal lead rubber base-isolation design for steel moment frames using value-based seismic design approach. Soil Dyn. Earthq. Eng. 2023, 164, 107520. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Lin, G. Seismic performance of advanced three-dimensional base-isolated nuclear structures in complex-layered sites. Eng. Struct. 2023, 289, 116247. [Google Scholar] [CrossRef]
- Lal, K.M.; Whittaker, A.S.; Constantinou, M.C. Mid-height seismic isolation of equipment in nuclear power plants. Earthq. Eng. Struct. Dyn. 2023, 52, 998–1015. [Google Scholar] [CrossRef]
- Chen, P.; Wang, B.; Zhang, Z.; Li, T.; Dai, K. A generalized model of lead rubber bearing considering large strain stiffening and degradation. Eng. Struct. 2023, 275, 115264. [Google Scholar] [CrossRef]
- Sun, J.; Zhufu, G. Mechanical Behavior of Laminated Rubber Isolation Bearing with Buckling Steel Plate. Int. J. Steel Struct. 2022, 22, 1069–1085. [Google Scholar] [CrossRef]
- Mazza, F. Base-isolation of a hospital pavilion against in-plane-out-of-plane seismic collapse of masonry infills. Eng. Struct. 2021, 228, 111504. [Google Scholar] [CrossRef]
- Burtscher, S.L.; Dorfmann, A. Compression and shear tests of anisotropic high damping rubber bearings. Eng. Struct. 2004, 26, 1979–1991. [Google Scholar] [CrossRef]
- Gu, Z.; Lei, Y.; Qian, W.; Xiang, Z.; Hao, F.; Wang, Y. An Experimental Study on the Mechanical Properties of a High Damping Rubber Bearing with Low Shape Factor. Appl. Sci. 2021, 11, 59. [Google Scholar] [CrossRef]
- Losanno, D.; Hadad, H.A.; Serino, G. Design charts for eurocode-based design of elastomeric seismic isolation systems. Soil Dyn. Earthq. Eng. 2019, 119, 488–498. [Google Scholar] [CrossRef]
- Madera Sierra, I.E.; Losanno, D.; Strano, S.; Marulanda, J.; Thomson, P. Development and experimental behavior of HDR seismic isolators for low-rise residential buildings. Eng. Struct. 2019, 183, 894–906. [Google Scholar] [CrossRef]
- Mazza, F. In-plane–out-of-plane non-linear model of masonry infills in the seismic analysis of rc-framed buildings. Earthq. Eng. Struct. Dyn. 2019, 48, 432–453. [Google Scholar] [CrossRef]
- Kikuchi, M.; Aiken, I.D. An analytical hysteresis model for elastomeric seismic isolation bearings. Earthq. Eng. Struct. Dyn. 1997, 26, 215–231. [Google Scholar] [CrossRef]
- Yamamoto, M.; Minewaki, S.; Yoneda, H.; Higashino, M. Nonlinear behavior of high-damping rubber bearings under horizontal bidirectional loading: Full-scale tests and analytical modeling. Earthq. Eng. Struct. Dyn. 2012, 41, 1845–1860. [Google Scholar]
- Abe, M.; Yoshida, J.; Fujino, Y. Multiaxial behaviors of laminated rubber bearings and their modeling. I: Experimental study. J. Struct. Eng. 2004, 130, 1119–1132. [Google Scholar] [CrossRef]
- Grant, D.N.; Fenves, G.L.; Whittaker, A.S. Bidirectional modelling of high-damping rubber bearings. J. Earthq. Eng. 2004, 8, 161–185. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, Z. Seismic analysis of a reinforced concrete building isolated by high damping rubber bearings using deformation history integral type model. Struct. Des. Tall Spec. Build. 2020, 29, e1811. [Google Scholar] [CrossRef]
- Masaki, N.; Mori, T.; Murota, N.; Kasai, K. Validation of hysteresis model of deformation-history integral type for high damping rubber bearings. In Proceedings of the 16th World Conference on Earthquake Engineering (WCEE), Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Abe, M.; Yoshida, J.; Fujino, Y. Multiaxial behaviors of laminated rubber bearings and their modeling. II: Modeling. J. Struct. Eng. 2004, 130, 1133–1144. [Google Scholar] [CrossRef]
- CSI ETABS Software 2022, Computer and Structures, Inc.: Berkeley, CA, USA, 2024.
- GB50011; Code for Seismic Design of Buildings. National Standards of the People’s Republic of China: Beijing, China, 2010.
- Shang, J.; Tan, P.; Zhang, Y.; Han, J.; Mi, P. Seismic isolation design of structure using variable friction pendulum bearings. Soil Dyn. Earthq. Eng. 2021, 148, 106855. [Google Scholar] [CrossRef]
- Murota, N.; Suzuki, S.; Mori, T.; Wakishima, K.; Sadan, B.; Tuzun, C.; Sutcu, F.; Erdik, M. Performance of high-damping rubber bearings for seismic isolation of residential buildings in Turkey. Soil Dyn. Earthq. Eng. 2021, 143, 106620. [Google Scholar] [CrossRef]
- International Code Council. International Building Code 2000; Dearborn Trade Publishing: Chicago, IL, USA, 2000. [Google Scholar]
- Ghafar, W.A.; Tao, Z.; Hasan, M.M.; Liang, Y.M. Seismic Analysis of a Hillside Reinforced Concrete Building Isolated by High-Damping Rubber Bearings Using DHI Model Type. In Proceedings of the First International Conference on Engineering Structures, Singapore, 18–20 February 2025; pp. 959–971. [Google Scholar]
- GB/T 51408-2021; Standard for Seismic Isolation Design of Building. National Standards of the People’s Republic of China: Beijing, China, 2021.
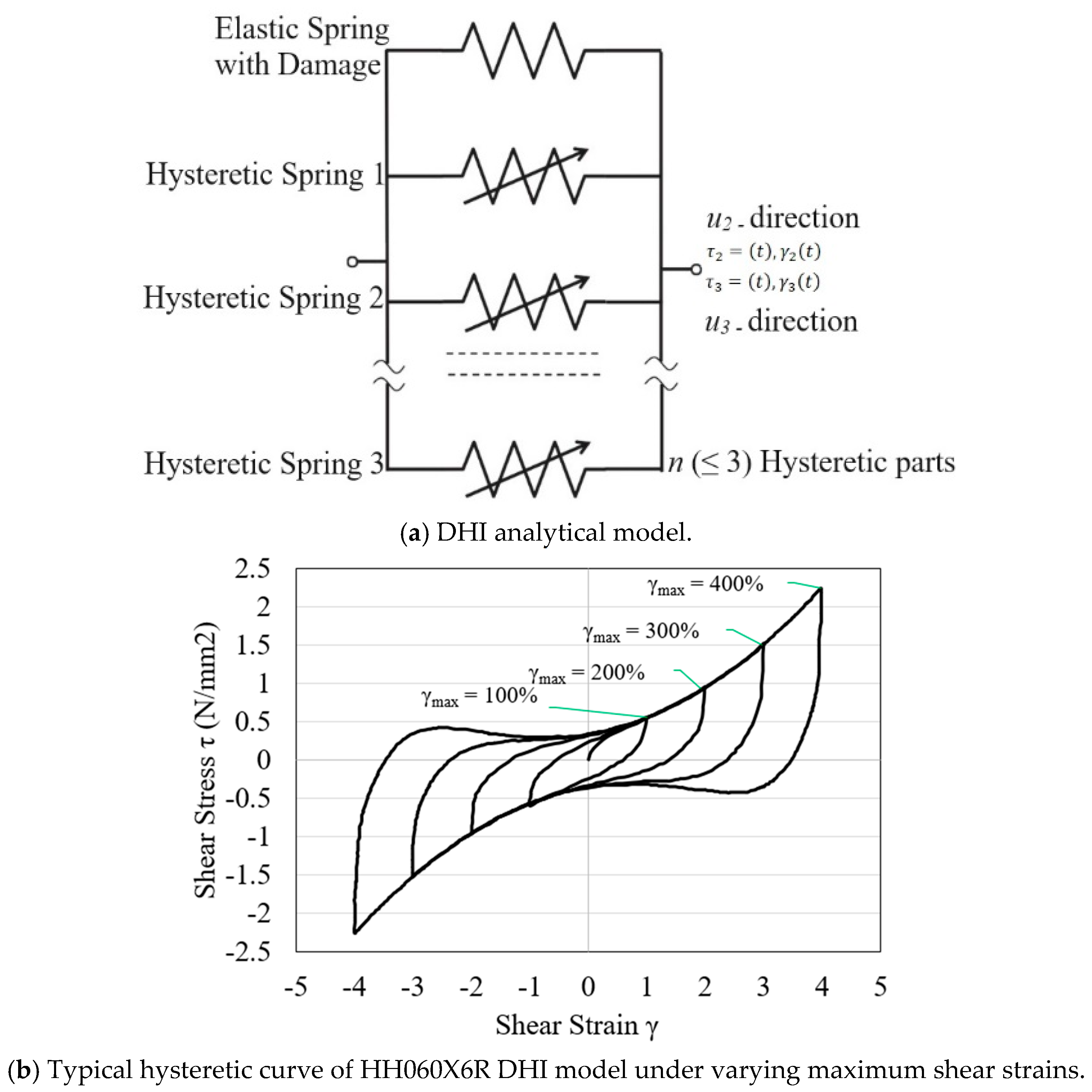




| HDRB Model | Total Rubber Thickness (mm) | Effective Plane Area (cm2) | (MPa) | (MPa) | (MPa) | ||||
|---|---|---|---|---|---|---|---|---|---|
| HH060X6R | 200 | 2826 | 0.53 | 0.46 | 0.42 | 0.036 | 2.47 | 0.50 | 0.35 |
| HH065X6R | 198 | 3317 | 0.53 | 0.46 | 0.42 | 0.036 | 2.47 | 0.50 | 0.35 |
| HH070X6R | 202 | 3847 | 0.53 | 0.46 | 0.42 | 0.036 | 2.47 | 0.50 | 0.35 |
| Model ID | Interior Columns (mm) | Edge Columns (mm) | Corner Columns (mm) | Cantilevered Columns (mm) | Beams (mm) | Slab Thickness (mm) |
|---|---|---|---|---|---|---|
| F_Fixed base | 700 × 700 | 600 × 600 | 500 × 500 | 800 × 800 | 300 × 500 | 150 |
| FIS | 700 × 700 | 600 × 600 | 500 × 500 | 800 × 800 | 300 × 500 | 150 |
| D_Fixed base | 700 × 700 | 600 × 600 | 500 × 500 | 800 × 800 | 300 × 500 | 150 |
| DIS | 700 × 700 | 600 × 600 | 500 × 500 | 800 × 800 | 300 × 500 | 150 |
| DIIS | 700 × 700 | 600 × 600 | 500 × 500 | 800 × 800 | 300 × 500 | 150 |
| HDRB Model | Effective Shear Stiffness (kN/m) | Compressive Stiffness (kN/m) | Characteristic Strength (kN) | Post-Yield Stiffness (kN/m) | Nominal Long-Term Column Load Bearing (kN) | Equivalent Damping Ratio |
|---|---|---|---|---|---|---|
| HH060X6R | 876 | 1.97 × 106 | 71.5 | 519 | 1860 | 0.20 |
| HH065X6R | 1040 | 2.34 × 106 | 83.9 | 615 | 2690 | 0.20 |
| HH070X6R | 1180 | 2.66 × 106 | 97.3 | 699 | 3500 | 0.20 |
| Model ID | Period (s) Mode 1 | CircFreq rad/s | Period (s) Mode 2 | CircFreq rad/s | Period (s) Mode 3 | CircFreq rad/s | Mass Participation Ratio |
|---|---|---|---|---|---|---|---|
| F_Fixed base | 1.463 | 4.2941 | 1.426 | 4.406 | 1.251 | 5.0216 | 0.998 |
| FIS | 3.453 | 1.8193 | 3.171 | 1.9813 | 2.946 | 2.1324 | 0.997 |
| D_Fixed base | 0.915 | 6.8665 | 0.859 | 7.315 | 0.752 | 8.353 | 0.998 |
| DIS | 3.164 | 1.986 | 3.042 | 2.0654 | 2.486 | 2.5264 | 0.997 |
| DIIS | 2.770 | 2.3014 | 2.713 | 2.3162 | 2.301 | 2.7227 | 0.997 |
| RSN | Year | Earthquake Name | Magnitude | Epicenter Distance (km) | Vs30 (m/s) | PGA (g) |
|---|---|---|---|---|---|---|
| 1147 | 1999 | Kocaeli_ Turkey | 7.51 | 68.09 | 175 | 0.189 |
| 1620 | 1999 | Duzce_ Turkey | 7.14 | 45.16 | 411.9 | 0.164 |
| 1490 | 1999 | Chi-Chi_ Taiwan | 7.64 | 29.49 | 542.41 | 0.162 |
| 1100 | 1995 | Kobe_ Japan | 6.9 | 24.85 | 256 | 0.183 |
| 1827 | 1999 | Hector Mine | 7.13 | 101.71 | 332.53 | 0.166 |
| 4038 | 2003 | Bom_ Iran | 6.6 | 137.92 | 376.7 | 0.199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wahab, A.G.; Tao, Z.; Li, H.; Rasa, A.Y.; Huma, T.; Liang, Y. Dynamic Simulation and Seismic Analysis of Hillside RC Buildings Isolated by High-Damping Rubber Bearings. Infrastructures 2025, 10, 239. https://doi.org/10.3390/infrastructures10090239
Wahab AG, Tao Z, Li H, Rasa AY, Huma T, Liang Y. Dynamic Simulation and Seismic Analysis of Hillside RC Buildings Isolated by High-Damping Rubber Bearings. Infrastructures. 2025; 10(9):239. https://doi.org/10.3390/infrastructures10090239
Chicago/Turabian StyleWahab, Abdul Ghafar, Zhong Tao, Hexiao Li, Ahmad Yamin Rasa, Tabasum Huma, and Yuming Liang. 2025. "Dynamic Simulation and Seismic Analysis of Hillside RC Buildings Isolated by High-Damping Rubber Bearings" Infrastructures 10, no. 9: 239. https://doi.org/10.3390/infrastructures10090239
APA StyleWahab, A. G., Tao, Z., Li, H., Rasa, A. Y., Huma, T., & Liang, Y. (2025). Dynamic Simulation and Seismic Analysis of Hillside RC Buildings Isolated by High-Damping Rubber Bearings. Infrastructures, 10(9), 239. https://doi.org/10.3390/infrastructures10090239







