Probability-Based Macrosimulation Method for Evaluating Airport Curbside Level of Service

Abstract

The air transportation industry is challenged to address airport curbside delay problems that affect landside service quality and can potentially impact check-in operations. Methodological advances guided by industry requirements are needed to support curbside improvement studies. Existing methods require verification of assumptions prior to application or need expensive surveys to acquire data for use in microsimulations. A probability-based macrosimulation method is advanced for the evaluation of the level of service and capacity of the curbside processor. A key component of the method is the simulation of the stochastic balance of demand and available curb space for unloading/loading tasks using the Monte Carlo simulation model. The method meets the planning and operation requirements with the ability to analyze conditions commonly experienced at the curb area. Example applications illustrate the flexibility of the method in evaluating existing as well as planned facilities of diverse designs and sizes. The developed method can contribute to curbside processor delay reduction and due to the macroscopic nature of the method, the data requirements can be met by an airport authority without costly surveys.

1. Introduction

Airports are accessed by regional multimodal transportation systems, comprising mainly of road modes, and at some airports, rail-based service is provided [1,2]. The landside curb area of the airport is of specific interest in this research. It is used by private vehicles, shuttle services, taxis, limousines, and shared mobility services provided by Transportation Network Companies (TNCs). The curb for the passenger terminal building is the most convenient location for drop-off and pick-up tasks. Airport roads are designed to serve curb areas, parking, and other facilities. To help prevent vehicles occupying curb spaces while waiting for passengers, cell phone holding areas are provided at some airports. Examples are O’hare in Chicago [3] and Toronto Pearson Airport [4].

Taxis and limousines use waiting areas when not serving passengers so that they do not occupy scarce curb spaces in front of the terminal building. A relatively new consideration is the need for TNCs (e.g., Uber) to serve the air travelling public. Their vehicles are allowed to wait in a designated location at the airport before moving to a curbside spot for serving arriving customers [5,6,7]. However, at some airports with severe shortages of curb spaces in front of the terminal building, the customers are expected to walk to the waiting TNC vehicles in the designated location [8].

Given the growth in air travel and the dominance of the automobile for airport access, methodological advances are needed to predict if user expectation of acceptable quality of service can be met during the unloading/loading operations at the curbside. For assessing the performance of existing curbside facilities as well as for planning improvements, airport planners, operations personnel, and managers can be assisted with new research in curbside level of service (LOS).

Over the years, research studies have contributed knowledge on the LOS and capacity of processors in the terminal building (e.g., check-in, baggage collection) [9,10,11,12,13,14,15]. One study reviewed these as well as other sources of information on approaches for evaluation of the LOS at airport passenger terminals [16]. But only a few research studies have been reported that focus on the LOS of the curb part of the airport. These are reviewed in a later section of this paper.

The LOS is an indicator of the quality of service experienced by travellers. According to the International Air Transport Association (IATA), the LOS as a basic airport planning tool can be used for many purposes, including processor assessment, capacity analysis, and planning and design of new facilities [17,18,19]. To be useful, a qualitative indicator of the LOS is supported with a quantitative measure such as space or delay time.

In the case of airport roads that connect with the terminal curb area, the Highway Capacity Manual (HCM), published by the Transportation Research Board (TRB), can be used for assessing the service quality provided to users [20]. A logical measure for the LOS offered by the curbside is the probability of accessing space and corresponding delay. For airport planning and operations, the relationship between LOS and capacity of the curbside processor should be known. The capacity of the curbside facility can be viewed as the maximum unloading/loading events per selected time duration (e.g., an hour), without causing a functional breakdown of operations. At the present state of knowledge, the quantitative criteria (i.e., delay) for curbside LOS grades, including capacity level operation, are not well developed.

This paper contributes a probability-based macrosimulation method for evaluating the LOS offered to curb space users. The developed method can support operations and planning tasks. The following sections of the paper cover the research approach, model formulation, macrosimulation method, LOS, delay index, robustness verification, applications, discussion, and conclusions and recommendations.

2. Research Approach

In this section, the need for a new method is explained for addressing curbside planning and operation problems. Existing methods are reviewed, and requirements are defined that are to be met by a new method.

2.1. Curbside Planning and Operation Problems

Key issues affecting airport ground access are defined in reference [21]. At the landside system level, curb area operation is challenging during high demand periods [22,23,24]. Depending upon the airport size, the configuration of curb space varies greatly. For a small airport or a terminal within an airport with multiple terminals, one curbside lane is usually sufficient for departing as well as arriving passengers, supplemented by another two lanes used for maneuvering and through movements. If allowed by the airport authority (e.g., in Beijing, China, Capital Airport Terminal 3), the lane next to the curb lane may be used for unloading/loading tasks during peak conditions (called “double parking”) [25].

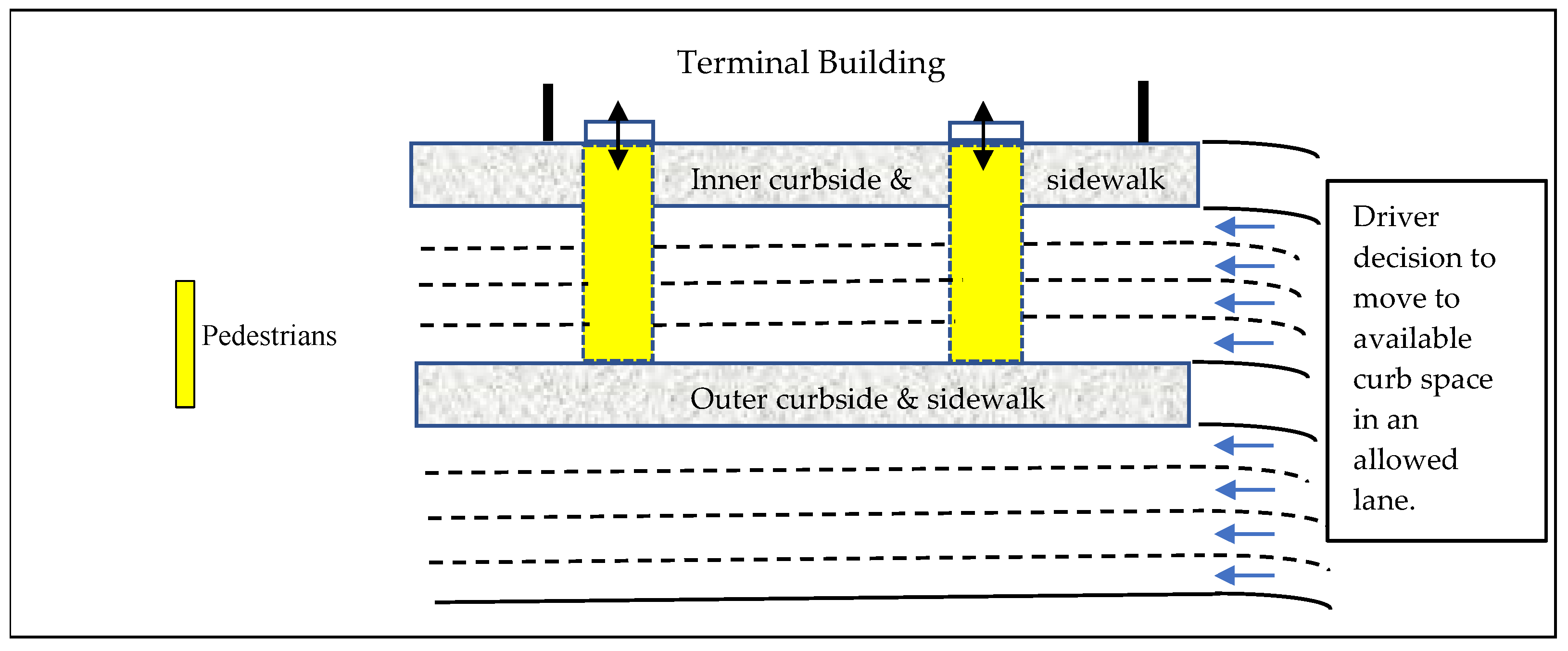
According to the National Academy of Sciences, Engineering and Medicine (NAS), a four-lane cross section is commonly used at airports that allow double parking during peak times [26]. The two outer lanes enable maneuvering and through movements. At large airports, two parallel curb fronts (i.e., inner and outer curb lanes) are provided, separated by a pedestrian island (Figure 1). Some passenger terminals have the lane configuration of the curbside processor shown in Figure 1, but with three lanes in each parallel curbfront. The arrival curbfront of Pearson Airport Terminal 1 in Toronto is an example [27].

For efficient operations, the curbfront traffic is usually separated into passenger cars and commercial vehicles (e.g., parking shuttles, rental car shuttles, hotel/motel shuttles, taxis, limousines, etc.). Depending upon the airport policy, the lanes closest to the terminal building can be used by larger vehicles such as shuttle buses and the outer curb lanes are used for private vehicles. Examples are the Toronto Pearson Airport [27] and Los Angeles International Airport [28]. Many passenger terminals are designed with two-level curbfronts. The upper level is typically used for departing passengers and the lower level is best suited for arriving passengers who collect their bags before leaving the airport (e.g., International Airport Authority Ottawa) [29]. Other design configurations are used for specialized applications such as dedicated curb spaces for various vehicle types and functions. An example is accessible vehicle unloading/loading [30,31].

As the driver of a vehicle arrives in the vicinity of the passenger terminal building, the driver follows instructions regarding inner curb or outer curb and decides to move to an available curb space. As noted above, at some airports, inner curb lanes are reserved for shuttles, etc., and private vehicles use outer curb lanes. In a future scenario, if connected and automated vehicles are used for delivering passengers and meeting arriving passengers, an automated curb operation system will guide vehicles to available curb spaces. In situations when demand for curb use exceeds the availability of curb spaces, vehicles form queues and wait for available curb spaces.

The design of curbside and travel lanes (as shown in Figure 1) prevents vehicle interaction. Vehicles wait in their selected lanes and when an unoccupied space is detected, they use a travel lane to approach the vacant space. The occupancy time obtained from a survey accounts for simultaneous movements of approaching and exiting vehicles. Also, the survey-based time accounts for time needed for pedestrians to cross lanes.

For the planning and operation tasks, it is necessary to study the dynamics of demand versus supply of curb spaces. Airport authorities and planners need a method that can be used to obtain LOS and associated delay answers without the need for expensive studies.

The number of curb spaces to serve demand for various types of vehicles depends upon vehicle characteristics, unloading/loading operation, and allowed curbfront length. If double parking is allowed during high demand periods, the supply of spaces increases. The time duration for the use of a curb space by a vehicle can be affected by the extent of double parking. A simulation study of Toronto Pearson Airport Terminal 1 arrivals area (with three lanes for private vehicle use) applied an average 133 s wait time per vehicle to go to the curb space and enter it for the base case and found 150 s for the double-parking scenario [32]. The increased wait time is due to double parking.

2.2. Past Research in Curbside Level of Service

Over the years, researchers have used analytical and simulation approaches to assess the performance of overall landside processors, including the curbside area [33]. However, published research with a focus on curbside LOS is scarce. In general, the analytical approaches lack theoretical foundation and validation information is rarely provided. Recent research has applied macroscopic, mesoscopic, and microscopic simulation techniques that provide higher fidelity results on curbside facility performance than analytical methods.

Macroscopic simulation models the demand and availability of curbside space in aggregate terms, rather than as individual units. Existing macroscopic simulation tools provide performance results, but the validation of the assumptions of queueing theory functions is data-intensive. The microscopic simulation tools provide a high level of detail for each user of the curb but require a lot of data. The mesoscopic simulation technique can provide a microscopic level detail of selected variables and macroscopic simulation of other variables for which detailed level of analysis is not warranted [32,34].

2.2.1. Curbside Performance

Several Airport Cooperative Research Program (ACRP) reports on terminal planning, design, and operations were published by the NAS in 2010, 2011, and 2019. The ACRP Report 55 [15] scans practices regarding quality of passenger services and spatial planning for airport terminals. The ACRP Synthesis Report 98 [33] provides an overview of simulation options for airport planning.

Volume 1 of ACRP Report 25 serves as a guidebook on terminal curb and roadway requirements [22]. Volume 2 of the ACRP Report 25 describes queueing theory-based spreadsheet models [23]. The ACRP Report 40 presents an overview of analytical and simulation methods [26]. The Quick Analysis Tool for Airport Roadways (QATAR) is described, which is intended to quantify curb space utilization under specified demand, lane configuration, and associated curb space supply.

The QATAR is structured as a queueing model. The logic of the method assumes infinite calling population, steady state system, Poisson probability distribution of vehicle arrivals, and exponential probability distribution of service times. The ACRP Report 40 [26] also includes an application of a microsimulation method noted in the next section of this paper.

Several types of macroscopic simulation software are described in the literature. Examples are the discrete simulation tools [35,36] and the Terminal, Roadway, and Curbside Simulation (TRACS) [37]. A numerical simulation technique to estimate length of the terminal curb at Beijing Capital Airport’s Terminal 3 is described in reference [25]. A mesoscopic simulation model of curbside operations at Pearson Airport in Toronto is reported in reference [32], which was used to study double parking, alternative parking space allocation, increased passenger demand, and enforced dwell times. Microscopic simulation software has been used for airport ground side facilities [26,34,38,39].

2.2.2. Level of Service Grades Based on Quantifiable Performance Measures

According to Airports Council International (ACI), the concept of LOS used for airport terminal design as well as the use of a wide range of service levels (A to F) were originally advanced by Transport Canada in 1970s [40]. IATA followed this practice for many years. However, the latest information on IATA’s best practice for the terminal building components classifies LOS as Optimum, Sub-optimum, Overdesign, or Underprovided [17,18]. Reference 19 describes rationale for IATA’s change from the LOS A to F scheme to the new four-grade scheme. For the curbside, there is no guide available from IATA.

One of the earliest attempts to include the LOS concept in curbside performance analysis and design is reported in reference [41]. With the use of a probability theory-based model, a three-range service level was defined. The first known attempt to define a wide range of service levels (A to F) for curbside application was reported by Transport Canada with the use of a multichannel queueing model [42,43,44]. The usual queueing model assumptions were used, namely the Poisson probability distribution for arrival and service channels was assumed to have exponential distribution for service time. The model was used to determine the probability that a vehicle entering the curb area in the design hour would find an open space at the curb frontage. The LOS (ranging from A to F) was quantified according to the probability of access to a curb space: higher than 0.95 for A, 0.90–0.94 for B, 0.80–0.89 for C, 0.65–0.79 for D, 0.5–0.64 for E, and below 0.5 for F.

Several researchers attempted to relate LOS to percent of double to triple parking in the curbside area. Examples are [45,46]. The ACRP Report 25 Volume 2 [23] describes an approach to define LOS and capacity based on the availability of a curb space or having to double park. For example, the user will experience LOS A if demand for a curb space is equal to or less than 50% of double-parking capacity. At LOS E, parking demand is between 85% and 100% of double-parking capacity. The LOS F represents operating conditions when parking demand exceeds 100% of double-parking capacity [23]. Methodological details are provided in the ACRP Report 07–04 [47].

The ACRP Report 40 [26] defines delay corresponding to the highest level of service (i.e., LOS A) and the saturation (capacity)-level delay (i.e., at LOS E). Using a linear interpolation, delays corresponding to LOS B to D are inferred. The magnitudes of delay for LOS A and E are based on the use of microsimulator VISSIM [39]. The curbside capacity is the double-parking capacity of the curb lanes.

The above literature review shows that researchers were interested in defining a framework that resembled the HCM’s LOS grades ranging from A (the most favourable service perceived by users) to F (highly unfavourable) [20]. It was recognized that the HCM approach was applicable to vehicle movements on airport roads. However, no widely accepted approach was defined for the curbside processor operation which requires the availability of a curb space. Most researchers have used traditional queueing models that are based on Poisson and negative exponential probability distribution function assumptions. The use of microsimulation software to estimate delay requires a lot of data. Due to their limitations, none of the currently available methods have achieved wide acceptance by airport planners, designers, operations personnel, and managers to the same extent that the HCM has achieved for roads and highways [20].

2.2.3. Requirements to Be Met in Infrastructure Planning

In the development of the method, the following requirements were defined:

• Demand, supply, delay, level of service, and capacity should be modelled together.
• For realism, the demand versus curb space availability should be treated as a stochastic phenomenon. Although at hub airports, flights are often grouped into arrival and departure clusters, demand may not be entirely random. But at the same time, it cannot be considered “deterministic”. That is, demand cannot be considered as pre-programed regarding arrival at the curb processor. Therefore, there will always be randomness even if for practical purposes it can be considered roughly “predictable”.
• The LOS ranges should be the same as those used by the HCM (i.e., A to F) and those suggested by the authors of the ACRP Report 40 [26] titled Airport Curbside and Terminal Area Roadway Operations.
• This method should enable prediction of probability of accessing an available curb space and corresponding delay under conditions commonly experienced at the curb area. These probability ranges and associated delays will form the basis of defining LOS grades A to F, including the capacity of the curbside processor (represented by LOS E).
• The method should be flexible so that it can be applied to various curb configurations and vehicle types for which the number of spaces and curb occupancy duration information is commonly available. This method should be applicable to facilities where double parking is not allowed as well as those where double parking is allowed. Permission to double park will increase curb spaces.
• To avoid the limitations of analytical methods in modeling the complexities of curb area operation and the highly demanding data needs for microsimulation, a new probability-based model should be formulated and developed as a macrosimulation method. This method should incorporate a continuous probability distribution function that represents the stochastic phenomenon noted above and for which data can be obtained by the airport authority without expensive surveys.
• The developed method should support planning and operation tasks.

3. Model Formulation

Treating both the demand for curb use and the availability of curb space as uncertain is in line with the real-world phenomenon. In formulating the method, elements of the well-known Monte Carlo simulation statistical method were adapted. The rationale for its use is the computational ability to randomly sample probability distributions and use the results in macroscopic simulation of the curbside processor operation. This probability-based macrosimulation approach was previously used by Khan [48] in shared mobility models that estimated vehicle and seat availability to a subscribing customer or group of customers. Also, the balancing of demand and supply of fast chargers for electric vehicles under uncertainty was studied by Khan with these models [48]. An introduction to simulation and Monte Carlo methods is provided by Rubinstein and Kroese [49].

3.1. Probability-Based Macrosimulation Method

For application to the dynamic interaction of demand and supply of curb space time slots, a probability-based macrosimulation method is developed with the application of the Monte Carlo simulation model in association with applicable probability distribution functions (Figure 2). Details of time slots are provided in later sections of the paper.

The method is implemented in five steps. In step one, the supply of unloading/loading curb time slots are defined using the probability distribution function. Next, a similar step is followed to characterize the demand for curb time slots. In the third step, the Monte Carlo simulation model is activated which uses random numbers to sample supply and demand cumulative probability distribution functions. For running simulations, different random number streams can be defined.

In the fourth step, each run of the model produces results on the expected numbers of time slots available, time slots demanded, and their balance. Following one hundred simulations, the results are compiled in the fifth step that includes the expected mean value of available time slots, standard deviation, and the probability of curb space availability. The expected mean value of available time slots and the probability outputs are used in further analyses. The mean value and the standard deviation are required by the software for probability calculation.

3.2. Choice of Probability Distribution Function

For use in airport curbside processor research, candidate continuous probability distribution functions include the uniform, triangular, and normal probability distributions. These are commonly used in Monte Carlo simulation applications. The required inputs for these functions are as follows:

• Uniform probability distribution function: A minimum value and a maximum value.
• Triangular probability distribution function: A minimum value, a maximum value, and the mode (i.e., the highest frequency value).
• Normal probability distribution function: The mean value and the standard deviation.

The mathematical formulas for the above probability distribution functions can be viewed in references [49,50].

In the condition of there being minimal data availability for planning under uncertainty, the uniform and the triangular distributions are commonly used. The uniform distribution represents an equal likelihood for all possible outcomes of a random variable to occur within the analyst-specified range. In scientific terms, this probability function is considered as the maximum entropy probability function for a stochastic variable [50]. Although this function simulates the values of variables, the random number-based sampling produces high probabilities for values in the central part of the range.

As noted above, the continuous triangular probability distribution function is defined by three values: the minimum value, the maximum value, and the peak (i.e., the mode) value. For risk analysis of estimates of planning variables, the normal distribution is commonly used in situations when the mean and standard deviation can be obtained and skewed distribution of probabilities is not applicable.

To go beyond the above noted features of the three candidate continuous probability functions, these were applied to the following curbside processor for comparison purposes: the curbside features the supply of 40 time slots (during a 2 h period) for passenger cars and during the off-peak period of this duration, the demand can reach up to 20 time slots. The inputs and simulation results for the three probability distribution functions are presented in

Table 1. Comparison of candidate continuous probability distribution functions.

Uniform distribution Inputs: Supply of time slots: 0–40. Demand for time slots: 0–20 Results:     •   Expected mean value of (available slots–needed slots) 10.5, standard deviation 12.2     •   Probability (available time slot > 0) = 0.81        ○   P(0–10 available slots) =     0.29        ○   P(11–20 available slots) =   0.30        ○   P(21–30 available slots) =   0.17        ○   P(31–40 available slots) =   0.05                  Sum    0.81

Triangular distribution Inputs: Supply of time slots: 0–40. Mode: 20. Demand for time slots: 0–20, mode: 10 Results:     •   Expected mean value of (available slots–needed slots) 10. Standard deviation 9.3     •   Probability (available time slot > 0) = 0.86        ○   P(0–10 available slots) =   0.36        ○   P(11–20 available slots) =    0.36        ○   P(21–30 available slots) =    0.12        ○   P(31–40 available slots) =    0.02                  Sum      0.86

Normal distribution Inputs: Supply of time slots: mean value 20 (midpoint of 0 to 40 slots), standard deviation 10 (assumed). Demand for time slots: mean value 10 (midpoint of 0 to 20 slots), St. deviation 5 (assumed). Results:     •   Expected mean value of (available slots–needed slots) 9.2. Standard deviation 12.3.     •   Probability (available time slot > 0) = 0.77        ○   P(0–10 available slots)     =  0.31        ○   P(11–20 available slots)   =  0.28        ○   P(21–30 available slots)   =  0.15        ○   P(31–40 available slots)   =  0.03                  Sum      0.77

.

The uniform and triangular distribution functions require inputs that airport planners can specify with confidence. The maximum supply value is based on the physical characteristics of the curbside facility. The maximum value for the demand variable and the mode value for the triangular distribution are obtainable from a low-cost routine survey. In such surveys, demand can be recorded on a short time interval basis (e.g., 3–5 min). The mean and standard deviation values required for the normal probability function require curbside surveys.

The uniform and triangular distribution produce logical results for the simulated condition that exhibits the maximum supply of time slots of 40 to serve the maximum needed time slots of 20. In the case of the normal distribution, similar results are obtained for the mean values applied and the assumed standard deviations. Due to different mathematical formulations of probability distributions, the results cannot be expected to be identical. But given uncertainties, the results are generally similar and acceptable.

For this research, the normal probability distribution is not favoured due to difficulty in obtaining input dataand cannot model skewed peaks. Although the uniform probability function requires only the minimum and maximum values for the supply and demand variables, it cannot model real-life peaking characteristics. On balance, the triangular probability distribution function is best suited for airport curbside research.

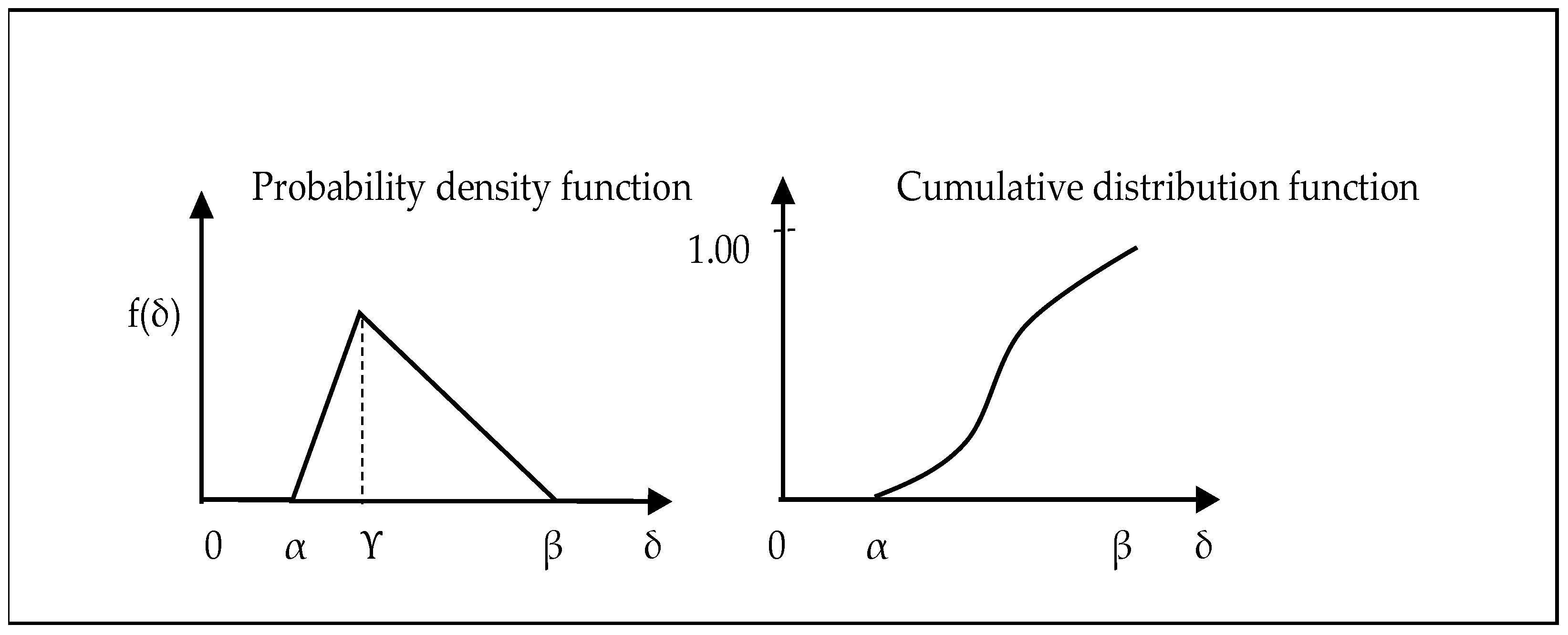
For enhanced characterization and to strengthen justification of the choice of the continuous triangular probability function, additional information is provided next. Figure 3 represents the probability of demand for a curb use time slot. This function also represents the probability of the availability of a curb space. The cumulative distribution function is used by the Monte Carlo simulation method to randomly sample the triangular probability distribution.

As previously noted, this function is defined by three values: the minimum value α, the maximum value β, and the peak value ϒ represents the mode. Due to the following characteristics, this probability distribution function has been widely applied [50]:

• For any application (in this research, a specific airport terminal), the analyst can estimate values for α, β, and ϒ based on available data or an inexpensive survey.
• The assignment of these values can be performed without knowing the mean and standard deviation.
• Definite upper and lower limits enable the analyst to avoid unnecessary extreme values.
• A good model for skewed distributions.

Well-known organizations apply the triangular probability distribution in Monte Carlo simulations. Examples are the World Bank Institute (WBI) [51] and the Federal Highway Administration (FHWA) [52].

The notable statistics for the triangular probability density function are shown below, in Equations (1)–(3):

P(δ) = 2(δ − α)/[(β − α)(ϒ − α)] for α ≤ δ ≤ ϒ

(1)

P(δ) = 2(β − δ)/[(β − α)(β − ϒ)] for ϒ ≤ δ ≤ β

(2)

P(δ) = 0 for δ < α and δ > β

(3)

δ is the x-axis descriptor (shown above and in Figure 3, Figure 4 and Figure 5).

• where ϒ ∊ |α,β| is the mode.
• The mean is 1/[3(α + β + ϒ)].

Representing demand with μ and supply with λ, the minimum, maximum, and mode values for demand and supply of curb use time slot can be written as follows:

• For demand: αμ, βμ, ϒμ;
• For supply: αλ, βλ, ϒλ.

In the application of the model, the differences in mode values can be shown as ϒλ- ϒμ when the highest frequency value of supply exceeds the highest frequency value of demand. For the opposite case, ϒμ − ϒλ can be used.

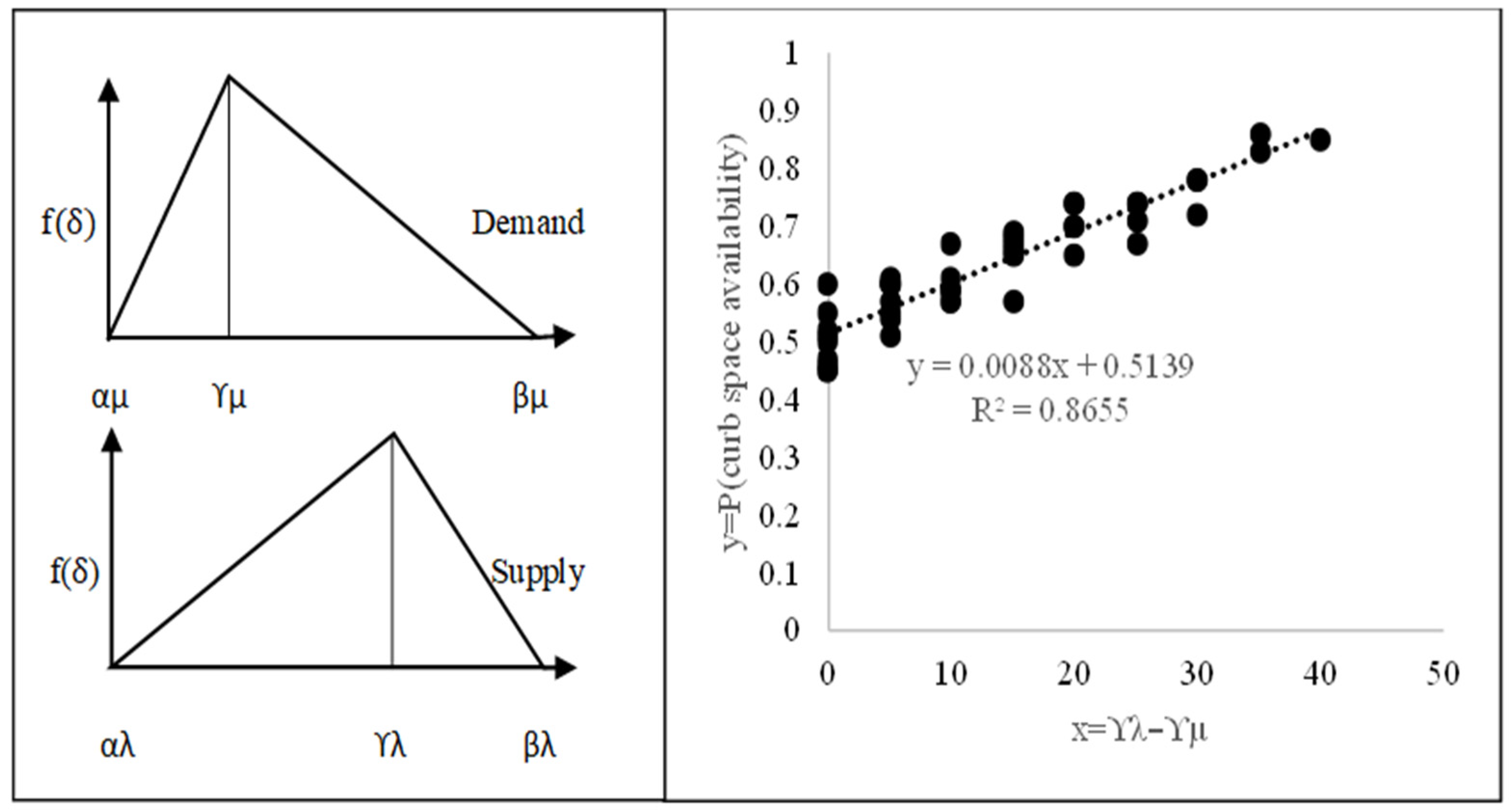
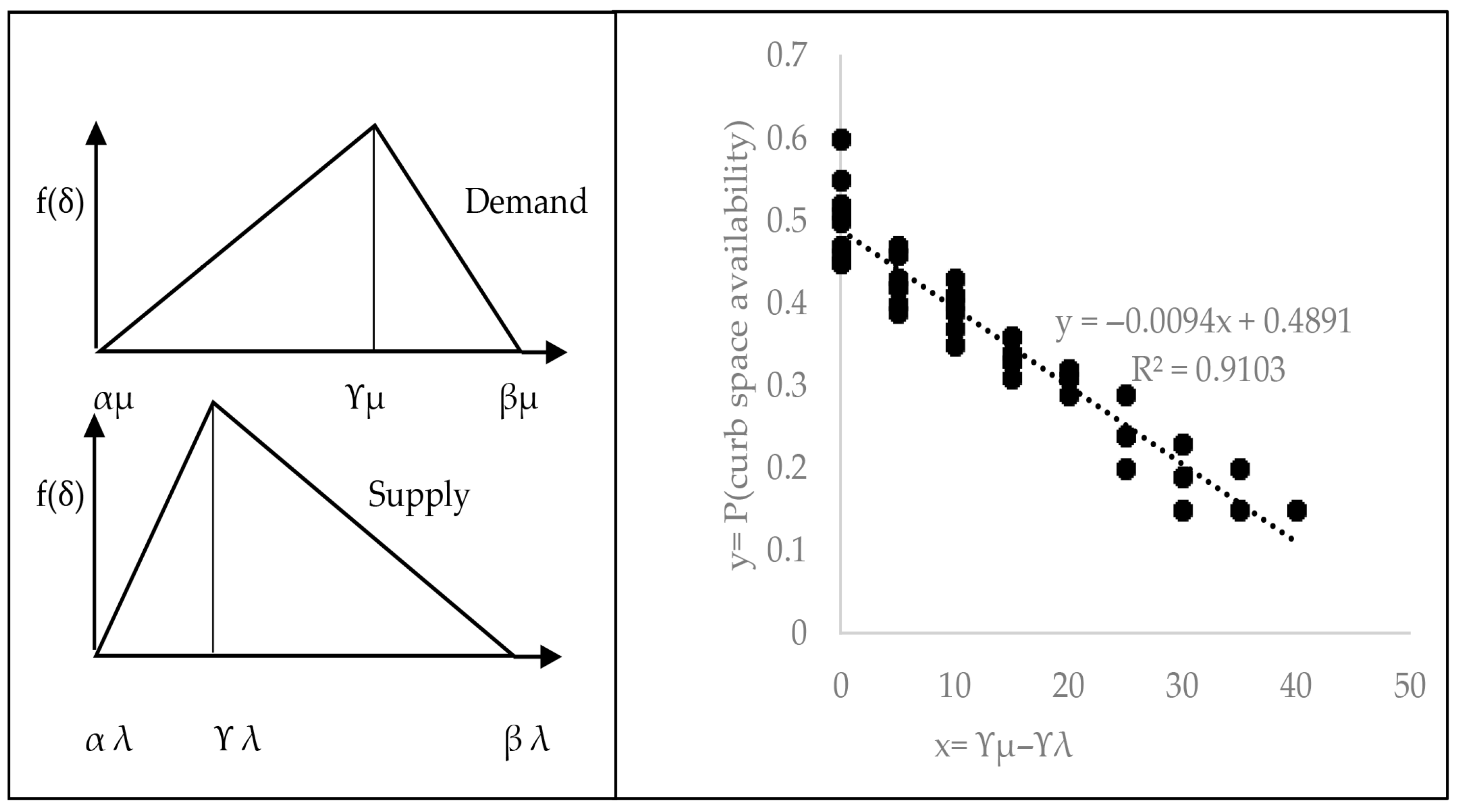
Using the simulation results, the relationship between P(curb space availability) and the mean value of expected number of time slots was studied. Figure 4 illustrates the results obtained for simulation cases when the supply of curb time slots exceeds demand. The probability of an available curb time slot varies from 0.5 to approximately 1. Figure 5 illustrates the simulation results for cases when demand exceeds the supply of available curb time slots. As expected, the probability values vary from 0.5 to approximately 0.0. The simulated scenarios result in queues and delays. The extent of delay depends upon the imbalance of supply and demand for curb time slots.

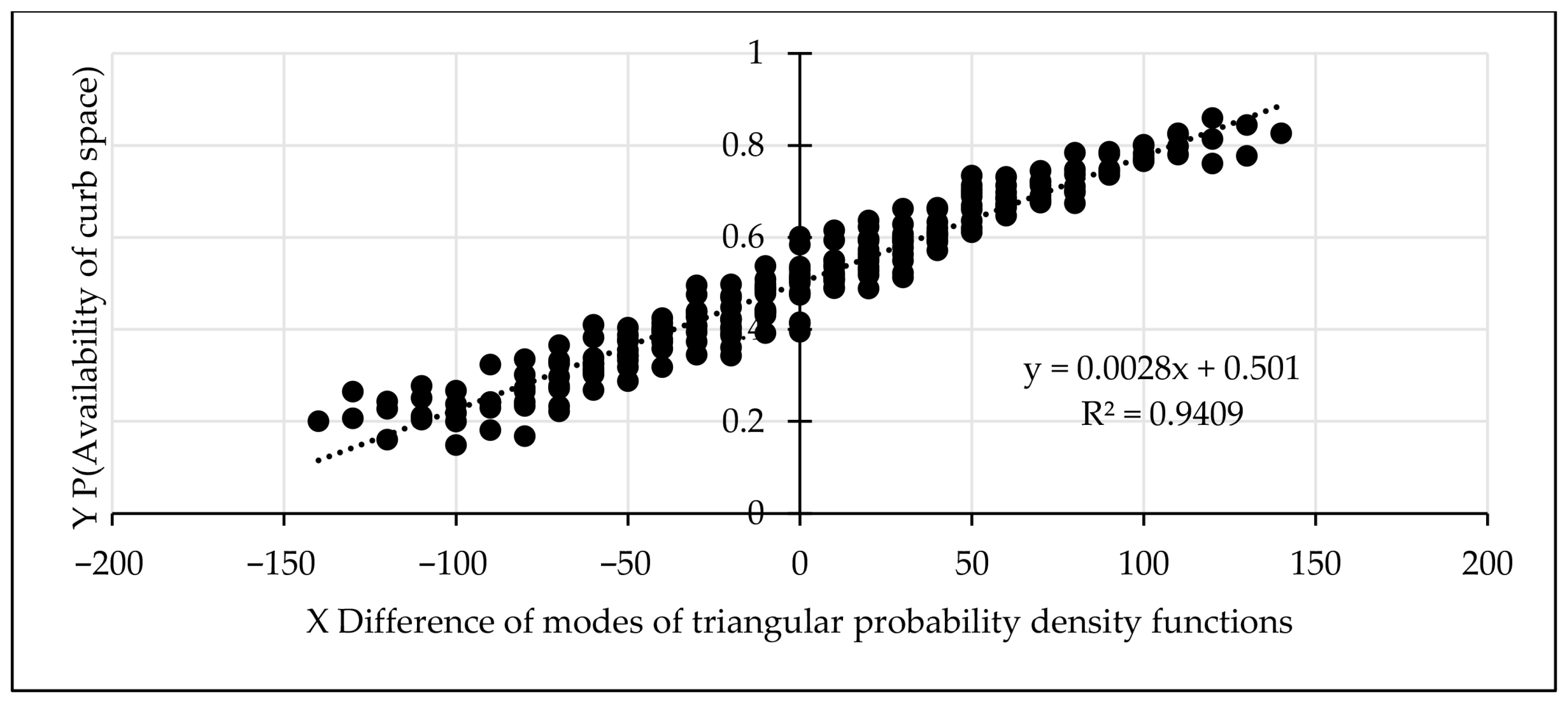
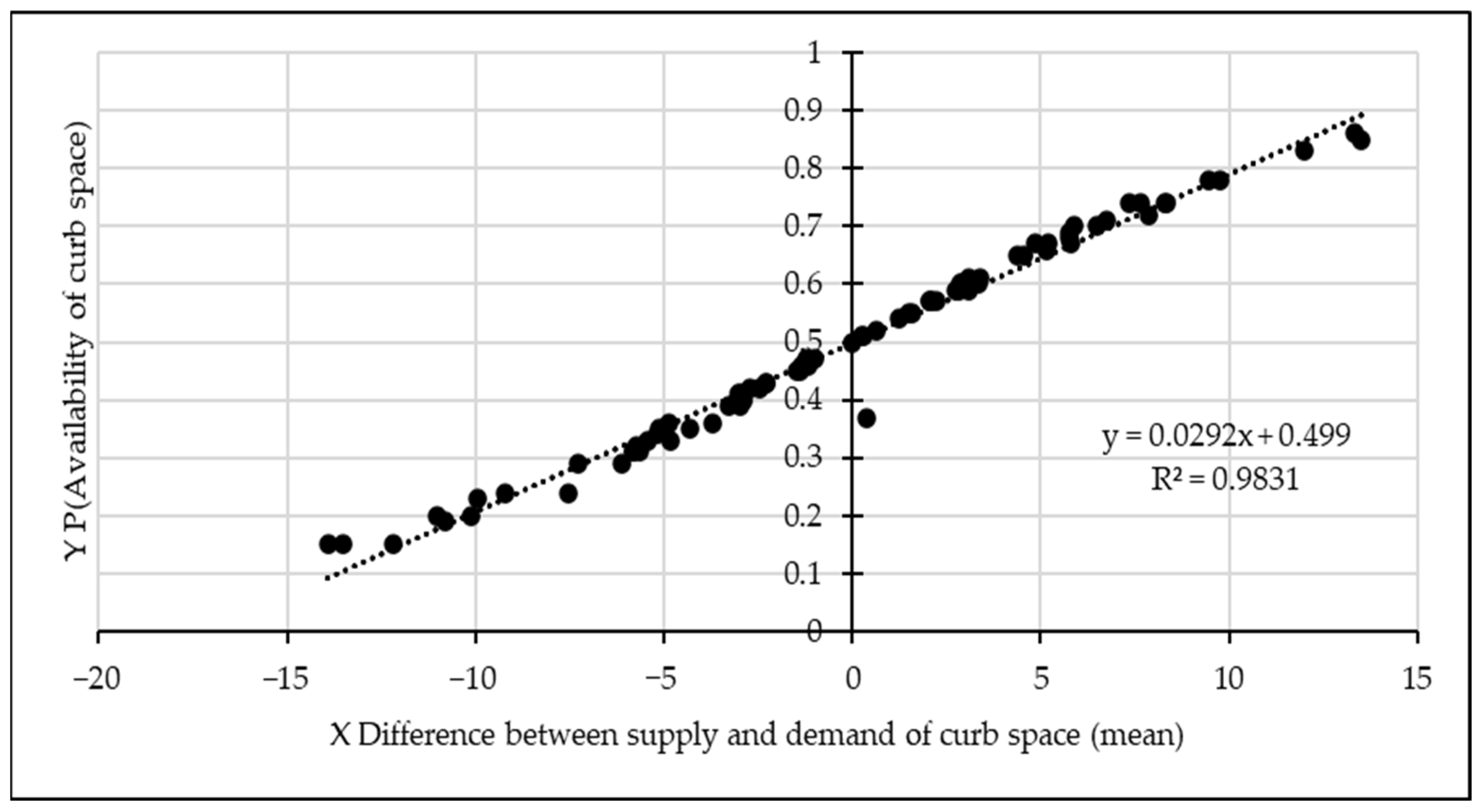
The regression model of the probability of available curb space as a function of the difference in modes (i.e., ϒλ − ϒμ) shows a very high correlation coefficient. The regression model is computed using the minimization of the square of deviations. The Excel software provides results for a number of mathematical forms, including the linear version. The linear model shown in Figure 4 and in other figures appears to be the best fit of the data.

Specifically, as can be seen in Figure 4 and Figure 5, the regression models have high R² (0.8655 in Figure 4, 0.9103 in Figure 5). Therefore, these models can be used with confidence for the study of LOS and the corresponding delay index described later in this paper. Also presented in later parts of this paper are other results that show very high values of R² (0.9921 in Figure 6 and 0.9831 in Figure 7).

4. Level of Service Ranges

The methodology described and illustrated above provides the basis for estimating the probability of curbside time slot availability. In turn, these probabilities form the basis of defining the LOS experienced by the users of the airport curbside. The user is a human driver, or, in the future, it will be an automated vehicle. As previously noted, although attempts have been made in the past to define LOS concepts for the curbside part of an airport, these are not widely accepted in practice due to their limited theoretical foundation or assumptions that may not be verifiable in real world applications (e.g., infinite pool of users, Poisson probability distribution for arrival, exponential probability distribution for service time). The proposed method reported here overcomes the deficiencies of other methods by treating the stochastic nature of demand and supply of curb space with a model that can be operationalized with data commonly available to airport authorities.

Table 2. Level of service concepts.

Level of Service (LOS)	Probability of Curb Space Availability When Demanded	Comments
A	0.9–1.0	Represents no delay condition; low demand periods.
B	0.8–0.89	Almost no delay; moderate demand periods.
C	0.7–0.79	Average demand periods; moderate delays can be expected.
D	0.6–0.69	Onset of peak demand condition and delays can be expected.
E	0.5–0.59	LOS E reflects capacity-level operations to accommodate peak demand condition. Due to demand surges, LOS E can deteriorate to LOS F.
F	Below 0.5	At LOS F, the operations at the curb part of the airport break down. Due to high delays, double and triple illegal parking may be attempted by some demand agents in the absence of traffic control.

shows LOS ranges for the use of curb space by passenger vehicles in drop-off and/or pick-up operations. The following comments characterize the LOS ranges:

• The LOS and capacity designations should be regarded as probabilistic in nature (i.e., these cannot be regarded as deterministic).
• The LOS designation in transportation is based on many factors that commonly require subjective decisions regarding some factors (e.g., user comfort, convenience).
• The LOS E is commonly used to describe capacity level operations and can easily deteriorate to LOS F. Therefore, the onset of LOS E is commonly used to initiate measures to improve LOS. These measures can include intelligent technologies supported by advanced methods, and if necessary, infrastructure additions are considered.

In cases when the P(available curb space) goes below 0.5, this condition reflects disruption and inefficiency in the operation of the airport landside system. For this reason, in the practice of transportation, the subject of capacity and LOS has assumed much importance. From the perspective of stakeholders (e.g., travellers, airport managers, airport concessions) interested in the smooth operations of the transportation facilities and systems, it is highly unlikely that the conditions that result in P(available curb space) < 0.5 will be acceptable and capacity improvements will be put in action on a priority basis. Of course, during a few very high demand hours (i.e., peak times of the year), such conditions are commonly tolerated to avoid overprovision [17,18].

5. Delay Index

A necessary extension of the concept of LOS is to go beyond the qualitative description of its ranges (i.e., LOS A to LOS F) by developing a delay index for each probability of accessing a curb use time slot. Further, for the delay index to be useful, it is necessary to define these so that these will be applicable to various curb use time slots that can differ from one processor to another. For example, a time slot for the curbside unloading/loading operation of a passenger car or a taxi or a low occupancy van can be of 3 min in duration. On the other hand, a shuttle vehicle that can serve about 8 to 15 passengers will require a time slot of about 6 min due to higher occupancy, and such shuttle vehicles are expected to accommodate a wheelchair.

The average occupancy time of 3 min for passenger cars is based on a survey at a regional airport in Ontario. This is the time needed to approach the vacant space, occupy it during unloading/loading operations, and pull out. It accounts for simultaneous movements of approaching and exiting vehicles and time needed for pedestrians to cross lanes. The 3 min curb use time slot does not include waiting time before a curb space becomes available.

The index is defined as a multiple of a time slot, and the value of the multiple depends upon the probability of curb space availability. That is, for LOS A, the value of the multiple is lower than for LOS B. For LOS C, the value is higher than for LOS B. This capability leads to the quantification of delay for various LOSs.

For example, a delay index of 0.2 multiplied by a time slot of 3 min in duration results in 0.6 min or 36 s of expected delay while the vehicle is in a queue. A delay index of 1 multiplied to the time slot implies 3 min of waiting in a queue before a space becomes available. If the delay index exceeds 1, the time spent in the queue will be more than one time slot. This can happen during high peak season and/or at some very large airports where capacity improvements generally lag behind the increasing air travel demand. Such a condition can also occur during highly adverse weather conditions.

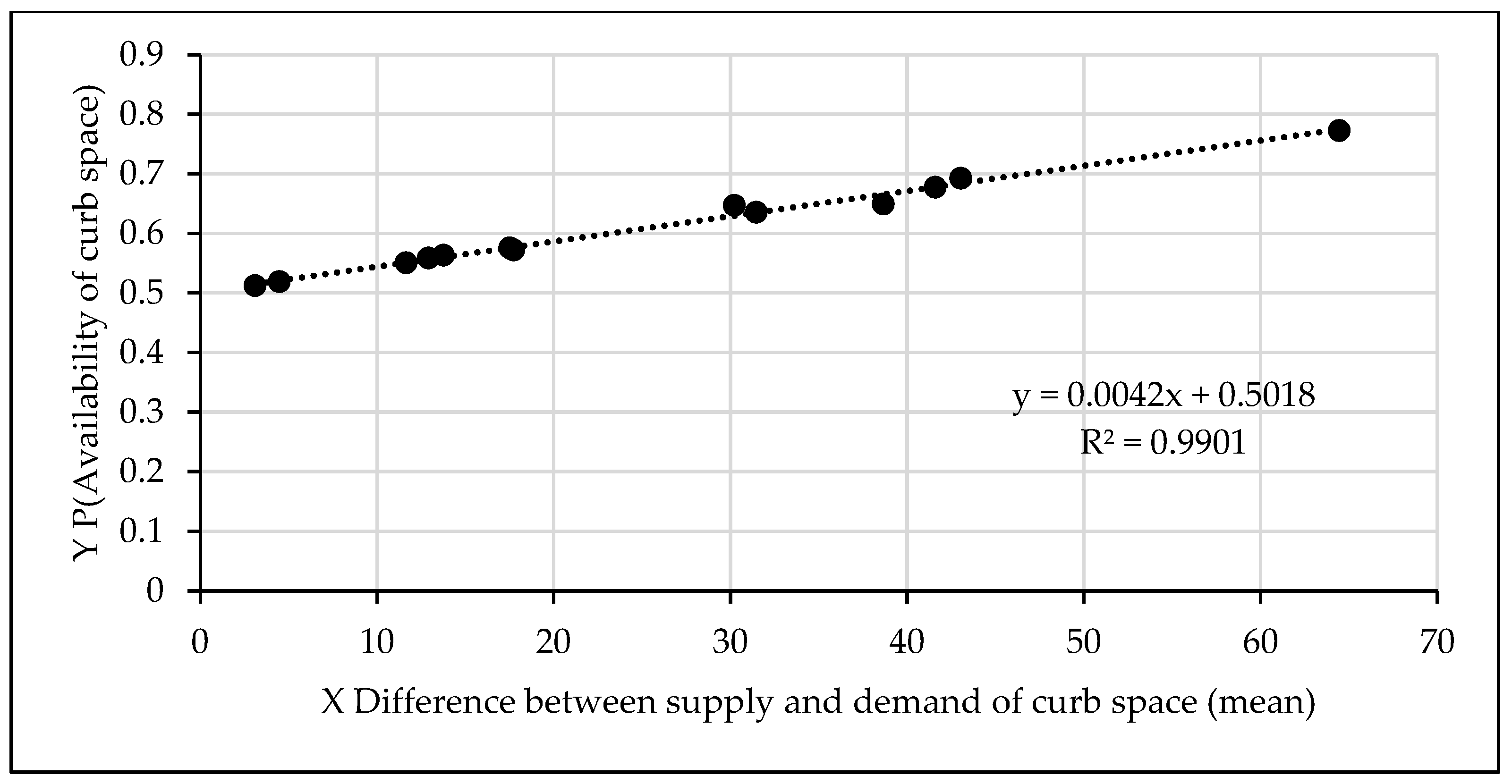
The expected mean value of available time slots that corresponds to the P(curb space availability) is the starting point for making the delay index operational. A regression model calibrated with simulation outputs is used for this purpose. For example, in the case of 140 demand and 140 supply time slots, the regression model is shown in Figure 6. For P(curb space availability) equal to 1.0, the expected available time slots (mean value) are 58.65. For P(curb space availability) equal to 0.9, the expected available time slots (mean value) are 46.88.

The philosophical basis for estimating delay is as follows: When 58.65 slots (mean value) are available, the probability is 1.0 that a vehicle will find an empty time slot and therefore the delay index is set at 0. When 46.88 slots are available, the probability is 0.9 that a vehicle will find an available slot. Since the probability is less than 1.0, a short delay can be expected. How can we gauge the delay for this case, i.e., what is the value of the delay index?

Since 58.65 slots are associated with zero delay, we can set this as the base for estimating the value of the delay index for other probabilities of slot availability. That is, at P = 1.0, the proportion of available slots out of 58.65 slots for zero delay = 58.65/58.65 =1.0 (all 58.65 slots are available). This becomes the base case for estimating the value of the delay index and in this case, the value of the delay index = 0 (i.e., zero delay).

At P = 0.9, the proportion of available time slots out of slots for zero delay = 46.88/58.65 = 0.8 (this can also be viewed as 80%). Since delay has a direct association with unavailability of slots, the unavailability proportion is 1–0.8 = 0.2 (20%).

If we associate the delay index value with the duration of the time slot of 3 min, the multiplication of 0.2 × 3 min results in 0.6 min or 36 s of delay. The application of this method to the case of 140 demand time slots as well as 140 supply time slots results in the answers shown in

Table 3. Delay index for 140 demand and supply time slots.

Level of Service (LOS)	Probability of the Availability of a Time Slot	Expected Mean Available Slots	Time Slot Unavailability Index	Delay Index (Multiple of the Time Slot Duration)
A	1.00 0.90	58.65 46.88	1 − (58.65/58.65) = 0 1 − (46.88/58.65) = 0.20	0 0.20
B	0.89 0.80	45.71 35.12	1 − (45.71/58.65) = 0.22 1 − (35.21/58.65) = 0.40	0.22 0.40
C	0.79 0.70	33.94 23.32	1 − (33.94/58.65) = 0.42 1 − (23.32/58.65) = 0.60	0.42 0.60
D	0.69 0.60	22.18 11.59	1 − (22.18/58.65) = 0.62 1 − (11.59/58.65) = 0.80	0.62 0.80
E	0.59 0.50	10.41 0	1 − (10.41/58.65) = 0.82 1 − (0/58.65) = 1.00	0.82 1.00

.

To check if the method gives reasonable results when applied to other cases of supply versus demand for curb use time slots, the following case is used: four curb spaces with a 6 min duration for a single time slot. Therefore, the supply of time slots is equal to 40/hour. Further, for illustration purposes, the demand for time slots is also set equal to 40. The simulation results presented in Figure 7 show a model with very high R² (i.e., 0.9831). This model is used to calculate expected mean available time slots that correspond to various probabilities of interest in the LOS study. Next, these expected mean values of available time slots are used as input to the delay index method.

Table 4. Delay index for 40 demand and supply time slots.

Level of Service (LOS)	Probability of the Availability of a Time Slot	Expected Mean Available Slots	Slot Unavailability Index	Delay index (Multiple of the Time Slot Duration)
A	1.00 0.90	17.16 13.73	1 − (17.16/17.16) = 0.00 1 − (13.73/17.16) = 0.20	0 0.20
B	0.89 0.80	13.39 13.31	1 − (13.39/17.16) = 0.22 1 − (13.31/17.16) = 0.40	0.22 0.40
C	0.79 0.70	9.97 6.88	1 − (9.97/17.16) = 0.42 1 − (6.88/17.16) = 0.60	0.42 0.60
D	0.69 0.60	6.54 3.46	1 − (6.54/17.16) = 0.62 1 − (3.46/17.16) = 0.80	0.62 0.80
E	0.59 0.50	3.12 0.03	1 − (3.12/17.16) = 0.82 1 − (0.03/17.16) = 1.00	0.82 1.00

presents inputs and outputs of the delay index method for 40 demand and supply time slots. An examination of the delay index results for this case suggests that these are identical to those shown in Table 3. This observation implies that delay index values can be applied to any curbside design (

Table 5. Checks made on delay index.

Level of Service (LOS)	Probability of the Availability of a Time Slot	Delay Index for 140 Time Slots Case (Multiple of a Time Slot)	Delay Index for 40 Time Slots Case (Multiple of a Time Slot)
A	1.00 0.90	0.0 0.20	0.0 0.20
B	0.89 0.80	0.22 0.40	0.22 0.40
C	0.79 0.70	0.42 0.60	0.42 0.60
D	0.69 0.60	0.62 0.80	0.62 0.80
E	0.59 0.50	0.82 1.0	0.82 1.00

NOTE: For LOS F, the delay index will exceed 1.0.

). Also, for the application of the LOS method, there is no need for the user of the method to develop regression models and the delay index values shown in Table 3, Table 4 and Table 5 can be applied to any curbside design and size.

6. Verification of the Methodology’s Robustness

To check the logic of the methodology, two cases are studied in terms of P(curb space availability) that exhibit different numbers of time slots, but similar demand versus supply conditions.

CASE 1: A curbside with seven spaces and a time slot of 3 min is studied for the most favourable and most unfavourable conditions in serving users. The airport management wishes to obtain answers regarding P(curb space availability) for a 3 min period. In this case, seven time slots are analyzed.

Table 6. Comparison of P(curb space availability) for different numbers of time slots.

Demand versus supply condition	CASE 1: Seven curb spaces, 3 min time slots, study duration is 3 min	CASE 2: Seven curb spaces, 3 min time slots, study duration is one hour
Most favourable condition Low demand, high supply Most unfavourable condition High demand, low supply	Demand: α = 0, β = 7, ϒ = 0 Supply: α = 0, β = 7, ϒ = 7 P(curb space availability) = 0.84 Demand: α = 0, β = 7, ϒ = 7 Supply: α = 0, β = 7, ϒ = 0 P(curb space availability) = 0.18	Demand: α = 0, β = 140, ϒ = 0 Supply: α = 0, β = 140, ϒ = 140 P(curb space availability) = 0.83 Demand: α = 0, β = 140, ϒ = 140 Supply: α = 0, β = 140, ϒ = 0 P(curb space availability) = 0.20

presents the demand and supply inputs to the macrosimulation method and the results. The P(curb space availability) is 0.84 for the scenario of low demand and high supply. On the other hand, when the demand is high and supply is low, the P(curb space availability) is 0.18.

CASE 2: For the above curbside, the airport management is interested in obtaining probabilities for a one-hour study duration. As compared to the seven time slots in CASE 1, the demand and supply interaction is studied in this case for 140 time slots. The results shown in Table 6 are almost identical to CASE 1.

The implication of the results is that the probabilities are comparable for similar demand versus supply conditions. In CASE 1, the stochastic demand versus supply study is based on 7 time slots and in CASE 2, the stochastic balance of demand and supply is based on 140 time slots. Due to the random number-driven nature of the methodology, the probabilities need not match perfectly.

7. Verification Based on External Sources of Delay Estimates

Further checks are made on the validity of the LOS method by comparing delay values reported by other researchers. The ACRP Report 40 published by the National Academies Press includes information that is used here for comparison purposes [26] (

Table 7. Comparison with delay estimates reported by other studies.

Level of Service (LOS)	Probability of Curb Use Time Slot Availability	Delay Index (Multiple of a Time Slot) +	Delay (Sec.) +	Delay Comparison (Seconds)
				Small Hub Airports *	Smaller Medium Airports *	Medium Hub Airports *	BIA International Airport **
A	1.00–0.90	0.0–0.20	0–36	6	12	30	14–20
B	0.89–0.80	0.22–0.40	40–72	20	39	98	31–95
C	0.79–0.70	0.42–0.60	76–108	33	66	165
D	0.69–0.60	0.62–0.80	112–144	47	93	233
E	0.59–0.50	0.82–1.0	148–180	60	120	300
F	<0.50	>1.0	>180	>60	>120	>300	316

⁺ Based on 3 min time slot (for a regional airport in Ontario, Canada). See Table 2, Table 3 and Table 4. * NAS (2010c) (based on microsimulation) [26]. ** Bandaranaike Int. Airport (Sri Lanka) (based on field data and analytical method) [54].

). Airport categories noted in the table are defined by the Federal Aviation Administration (FAA) [53]. The microsimulation-based methodology used by the authors of the ACRP Report 40 is described in an earlier section of this paper. Also shown in the table are delay values estimated by researchers for the Bandaranaike International Airport (Sri Lanka) using field data and an analytical method [54,55]. In viewing the delay values shown in Table 7, the reader is advised that the duration of curb use time slots (minutes) is not identical in the three studies. Therefore, the comparison is intended for general information only.

8. Applications of the Method

The curbside location and specific users are to be identified (e.g., the curbside area designated for the use of passenger cars). If the application is intended for an existing facility, depending upon the length of the curbside allocated for this use and vehicle dimensions, the number of spaces can be found. Based on data that is usually available or can be collected with field observations, the duration of a curb use time slot can be defined. As noted earlier, the curb use time does not include waiting time. For the unloading or loading task, it consists of the following time components: time to move to the vacant curb space location, maneuvering time, occupancy time, and exit time. The combination of curb space data and curb use time duration define time slots/hour [56].

For an existing curbside, a peak period field survey can provide demand as well as availability (supply) data on curb use time slots. Data analysis will lead to the quantification of the minimum, the maximum, and the highest frequency values for the triangular probability distribution function. For future planning, the planner can define these values. The next step in the application of the LOS method is to run simulations and obtain results.

Following the completion of the simulation step, the methodology provides the following outputs:

• Expected value of available curb time slots (mean): this result can be less than or equal to zero, or greater than zero.
• Standard deviation.
• P(curb space availability) (the range is 0 to 1).

8.1. Evaluation of an Existing Curbside Operation

To illustrate the application of the method, the curbside operation of a regional airport is studied [56]. In the base case, the supply of time slots is limited to 140 per hour, provided by seven curb spaces. During peak usage condition, when all 140 slots/hour are in use (i.e., occupied) and there is zero available supply, the minimum value of αλ = 0. In the low-traffic condition, when all 140 time slots are available, the maximum value of βλ = 140. The highest frequency value ϒλ can take positions from αλ to βλ (i.e., from no available spaces to all spaces available), depending upon the usage pattern of the curb space. The demand for curb space use exhibits a similar pattern. In this example application, many demand versus supply conditions were simulated and each case was run 100 times. For illustration, the value of ϒ was varied.

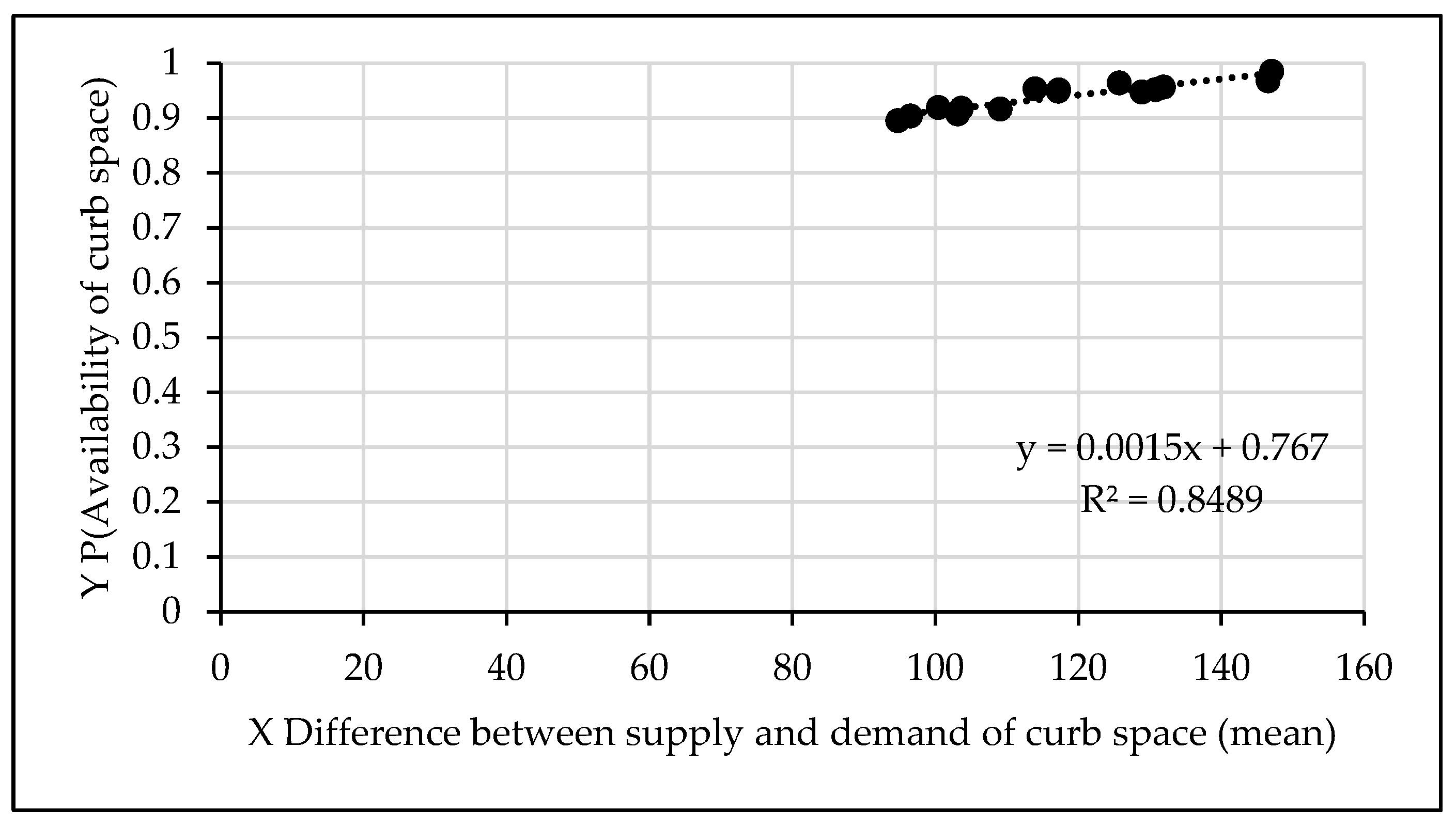
Figure 8 shows the results for all cases that cover the entire range of demand and supply conditions, based on 140 time slots. As expected, the probability values for the availability of curb space are at 0.5 or higher for favourable supply condition. On the other hand, for the unfavourable supply of curb space availability, the probability falls below 0.5. Results for several conditions shown in Figure 8 suggest that LOS F can be encountered due to a lack of availability of curb space. For a selected value of the difference in modes of the triangular probability distribution, the probability of curb space availability is found. Based on the probability value, the LOS is inferred.

Also, the delay estimate is found with the use of the corresponding delay index shown in Table 3, Table 4 and Table 5. If the user of the methodology is not interested in the full range of results shown in Figure 8, a single set of answers can be obtained for a selected value of ϒ for demand and a selected value of ϒ for supply. The best fit model as well as corresponding R² (i.e., 0.9409) values are shown for information. As noted earlier, for the application of the methodology, the analyst need not develop or use regression models.

8.2. Illustration of a Planning Task

In the regional airport example, the LOS improvements that are obtainable from curb extension are studied next. If the airport authority decides to extend the curb from 7 to 14 spaces, the extended curb with 14 spaces can offer 280 time slots of 3 min each. Although the demand will grow over time, at the outset, the highest demand is assumed to be the same as for the base case of 140 time slots. Conditions of demand versus supply are defined and simulated. The results are shown in Figure 9. Note that the LOS is A under all conditions.

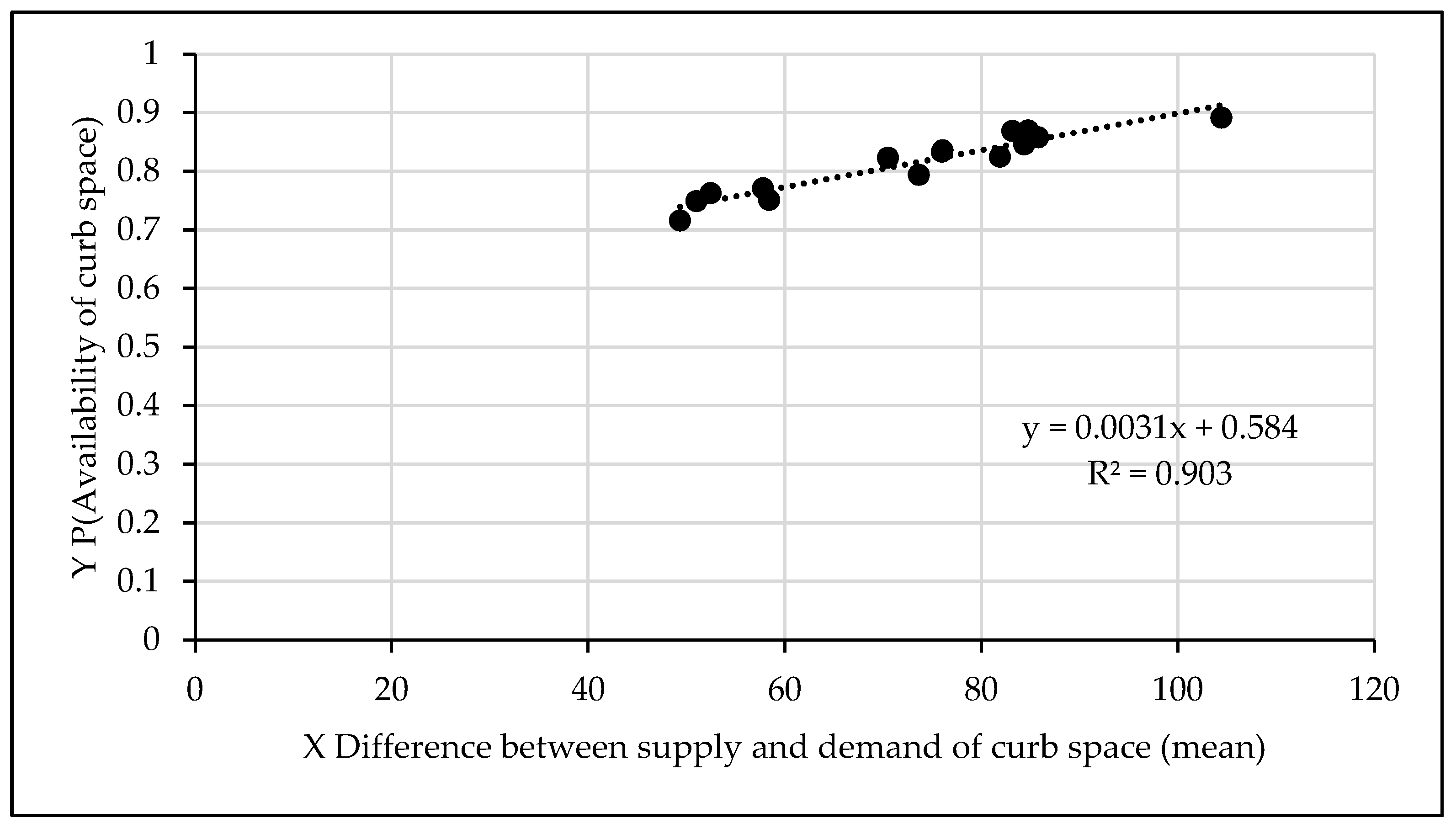
Given that over time the demand will rise, the effect of a 50% increase in demand was studied next. Simulations were run for 210 time slot demand and 280 time slot supply. Results are shown in Figure 10. As expected, LOS drops very slightly, but is high enough for a highly favourable travel experience.

It is useful to study the LOS that can be experienced if a 100% increase in demand occurs. Simulations were run for 280 time slot demand and 280 time slot supply. Results are shown in Figure 11. As expected, although an equal number of supply and demand time slots interact, due to stochastic conditions, the LOS E experience is like the base case condition when both demand and supply time slots were equal to 140. In Figure 11, the LOS F result is not shown.

9. Discussion

In model formulation, for realism, the dynamic interaction of demand and supply of curbside time slots is treated as a stochastic phenomenon. The probability distribution function choice study reported in Section 3.2 shows that the triangular probability distribution is best suited for this purpose. Many well-known organizations, including the World Bank and the U.S. Federal Highway Administration, are using it in their methodologies. For application, the probability-based model is transformed into a macrosimulation method.

The well-calibrated predictive (regression) models enable the estimation of the probability of accessing curb space under the specified demand and supply of curbside time slots condition. Following many simulation runs, the inputs and results are used to develop details of the methodology (i.e., delay index corresponding to LOS A to F, delay values that correspond to duration of curbside time slot). The robustness of the developed method is verified in Section 6 and Section 7.

The steps for the application of the methodology noted in Section 8 are summarized below for convenient access. These were followed in the example applications illustrated in Section 8.1 and Section 8.2.

(1)

Define minimum, maximum, and mode time slot values for supply and demand conditions. For an existing curbside processor, these values can be obtained with an inexpensive survey. For a future case, planners can provide these inputs.

(2)

Apply the simulation method to obtain the probability of curb space availability.

(3)

Based on the probability result and information provided in Table 2, Table 3, Table 4 and Table 5, define the LOS.

(4)

Based on information provided in Table 3, Table 4 and Table 5, find the magnitude of delay with the use of the delay index that corresponds to the LOS and the applicable time slot duration.

As previously noted, there is no need for the user of the method to develop or use regression equations. The equations and curves are intended to illustrate the developed method. With the application of steps 1 to 4 noted above, an airport operations person or a planner can obtain one answer for the probability of an available time slot. The equations are calibrated using such answers that represent many curbside supply versus demand simulated conditions.

For practical applications of the developed method, Table 2 serves as a guide. Here, further information is provided. LOS C is suggested for planning a new curbside facility or operation of an existing facility at small and medium hub airports. At a large hub airport, LOS D should be acceptable to users of an existing curbside processor. However, during peak periods of operation within a year, the LOS may decrease to LOS E or lower.

10. Conclusions and Recommendations

As a part of an airport landside system, the curbside is recognized as a critical facility. A method is proposed for use in studies aimed at airport curbside processor performance improvement and prevention of the adverse spillover effect of congestion on check-in operation in the terminal building. The developed probability-based macrosimulation method overcomes deficiencies of existing methods that require verification of their constituent queueing and service time models prior to application or need data for use in microsimulations obtainable from expensive surveys.

The demand versus curb space availability is modelled as a stochastic phenomenon. For this purpose, a widely used probability distribution function is built into the macrosimulation method that can be implemented by airport authorities without expensive data acquisition surveys. The developed probability-based macroscopic simulation method satisfies the industry requirements inferred from the U.S. Airport Cooperative Research Program studies. The range of LOS (i.e., A to F) is consistent with the transportation industry’s preference as revealed by the wide acceptance of the TRB’s HCM.

The developed method is flexible regarding application. It has the capability to assess LOS and corresponding delay under a wide range of operating conditions at the curb area. It enables analysis of various curb configurations, vehicle types, curb facility sizes, and operating rules regarding “double parking.” The results enable the assessment of operational performance (i.e., LOS) of an existing or planned curbside facility during selected time periods (e.g., peak periods, off-peak periods). The airport personnel can use the results in support of recommendations for operational improvements of existing curbside facilities and for planning facility expansion.

Although the choice of delay and the level of service grades are well-supported with references, future research could incorporate surveys or field interviews to further enhance the practical relevance of the LOS scale. Also, attempts can be made to align the curbside LOS evaluation enabled by the developed method with IATA-recommended practice for the planning, design, and operation of airport terminal components.