A Novel Master Curve Formulation with Explicitly Incorporated Temperature Dependence for Asphalt Mixtures: A Model Proposal with a Case Study
Abstract
1. Introduction
2. Background
| Formulations | Advantages | Disadvantages | References |
|---|---|---|---|
| GS model (Equation (1)) | These are the most straightforward expressions; their mathematical structure is simple and only requires 4 parameters. Thus, only 4 experimental measurements need to be made for their calibration. This calibration procedure can even be quickly conducted using trial-and-error techniques. | These expressions employ frequency as the only state variable, so they cannot reproduce the stiffness dependence on temperature (or other analogous variables) without incorporating shift factors. When the experimental measurements of the stiffness modulus are carried out in a narrow range of frequencies, it is possible for the calibration of the equations to not converge properly. | [21,22,23] |
| CS model (Equation (2)) | |||
| SLG model (Equation (3)) | |||
| Uniaxial model (Equation (4)) | |||
| Generalized logistic sigmoidal model: | Due to the incorporation of an additional fitting parameter (i.e., λ), this model allows adjustment to asymmetric curves. | This formulation holds the limitations of the traditional models (Equations (1)–(4)). Compared to traditional models, this formulation requires an additional experimental measurement for its calibration. Inadequate calibration of λ can lead to the construction of unrealistic non-symmetric master curves. | [28] |
| Christensen–Anderson–Marasteanu model: | This model allows the direct specification of the minimum and maximum stiffness moduli through the parameters and , respectively. It permits the high-accuracy reproduction of viscoelastic behaviour. | This formulation holds the limitations of the traditional models (Equations (1)–(4)). Also, the trend of the simulated curves depends on one location parameter () and two tuning parameters ( and ). Counterintuitively, using few fitting parameters increases the complexity of model calibration because if the experimental data are noisy, the associated error can be increasingly propagated. | [29] |
| Modified Christensen–Anderson–Marasteanu model: | Regarding the original Christensen–Anderson–Marasteanu model, this enhanced version allows the incorporation of the rheological index (), which can be used as a rotation factor to couple time–temperature–aging shift functions. | This formulation holds the limitations of the original Christensen–Anderson–Marasteanu model. | [4] |
|
Continuous relaxation spectrum model: | This formulation excels by the incorporation of the continuous relaxation spectrum (through the relaxation time—τ—and angular frequency—ω—parameters) into the calculation of the stiffness modulus. Thus, the model considers the linear viscoelastic properties of asphalt materials. Also, thanks to the use of incremental constitutive relations, the numerical stability of this model is extremely high. | As in the traditional formulations (Equations (1)–(4)), this model does not consider the effects of the temperature without incorporating shift factors. Due to the use of multiple integral equations, this model increases its mathematical complexity excessively, which makes its implementation difficult in more extensive simulations. Therefore, the calibration of this model involves the exploration of non-trivial solutions. | [15] |
| Modified Havriliak–Negami model: | This model is especially suitable for asphalt mixtures that develop complex liquid-like and solid-like phases throughout the frequency spectrum. | This formulation holds the limitations of the traditional models (Equations (1)–(4)). The model is complex both from a mathematical and physical standpoint. On the one hand, this formulation should not be calibrated with a simple iteration for error minimization. On the other hand, the physical interpretation of the fitting parameters is non-intuitive, as is the case with conventional models. | [30,31] |
3. Mathematical Modelling
4. Case Study
4.1. Materials
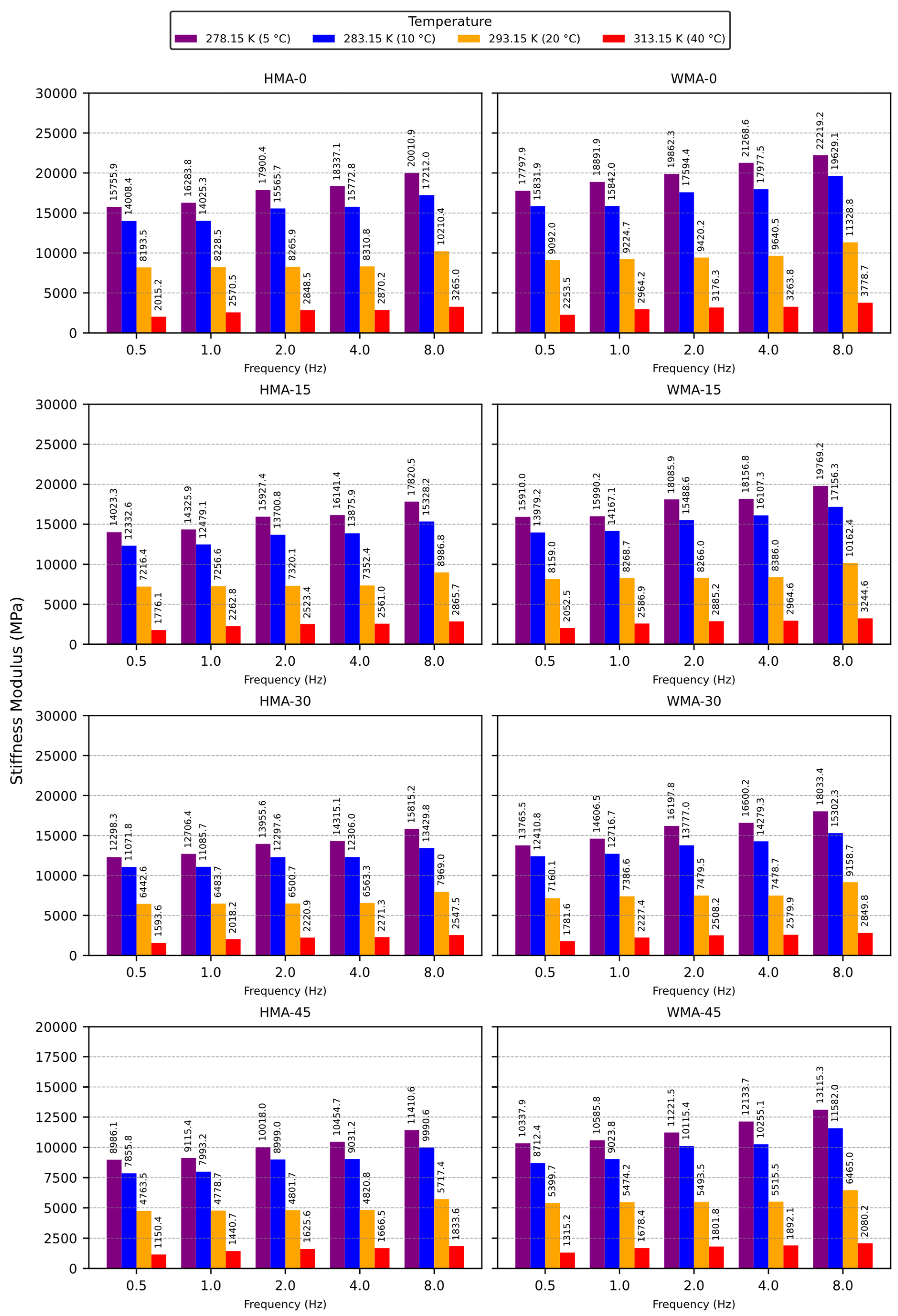
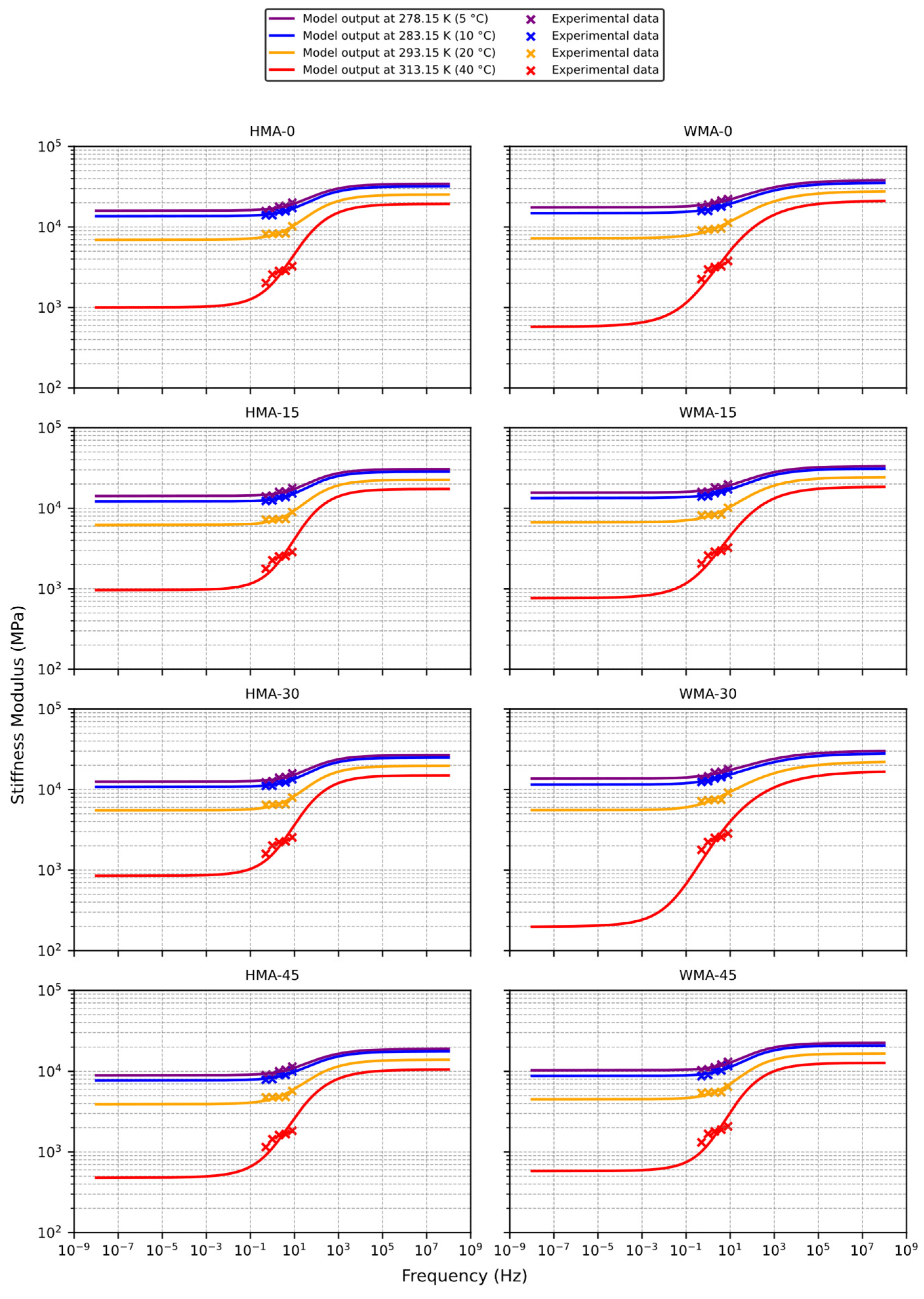
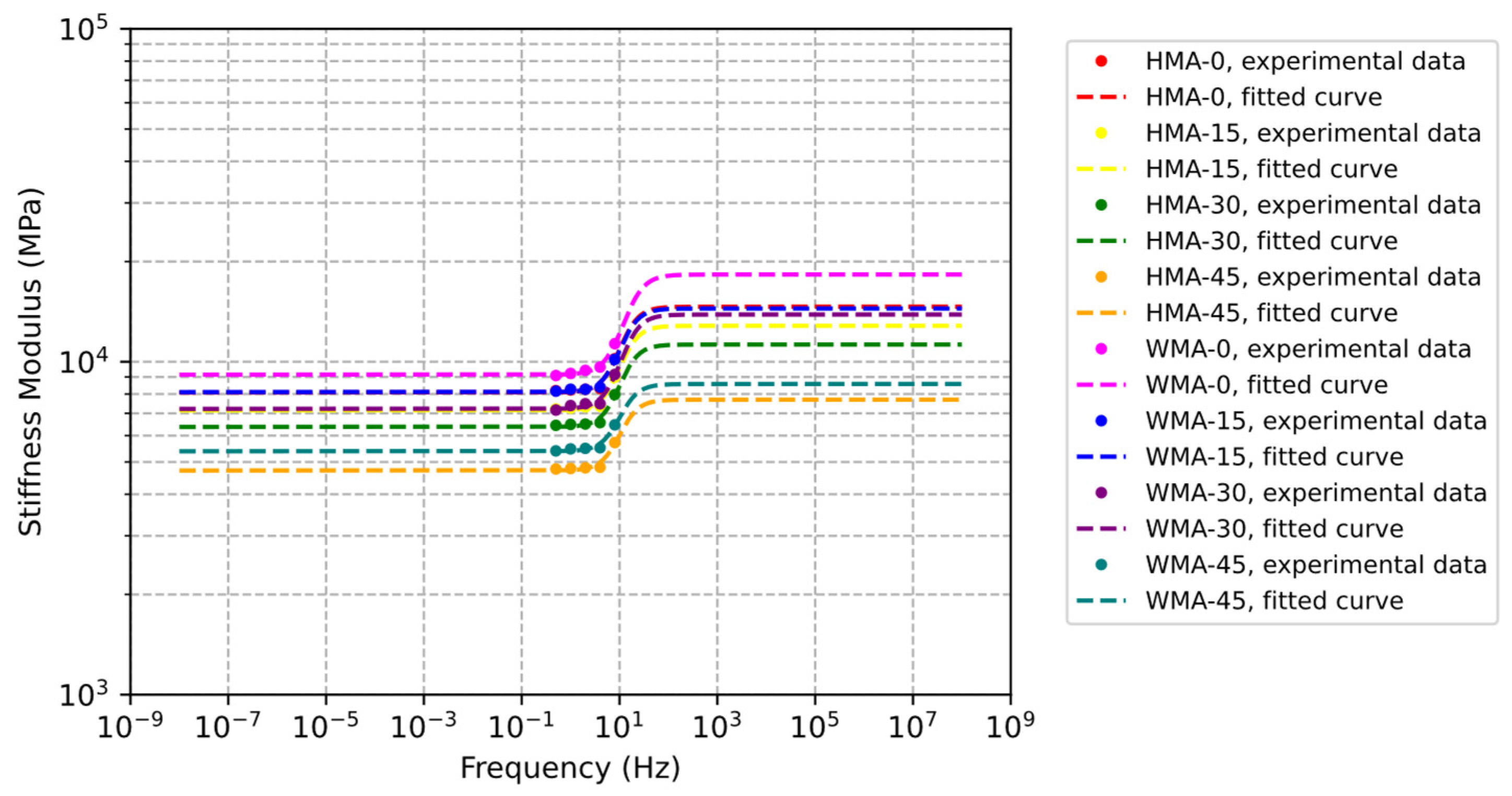
4.2. Results
| Fitting Parameters | Accuracy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (-) | MAPE (%) | |||||||||
| Asphalt Mixtures | HMA-0 | 2.457944 | −0.591082 | 1.103802 | 4.271044 | 0.523182 | −3.721008 | 0.000375 | 0.9920 | 7.34 |
| HMA-15 | 2.452728 | −0.731821 | 1.197044 | 4.222030 | 0.599018 | −3.725021 | 0.000410 | 0.9917 | 7.37 | |
| HMA-30 | 2.418613 | −0.715055 | 1.169234 | 4.159372 | 0.599273 | −3.705805 | 0.000383 | 0.9916 | 7.21 | |
| HMA-45 | 2.140254 | −0.399350 | 1.033227 | 4.008499 | 0.374255 | −3.704619 | 0.000330 | 0.9905 | 7.90 | |
| WMA-0 | 2.058495 | 0.127287 | 0.774247 | 4.317418 | −0.176631 | −3.721431 | 0.000266 | 0.9937 | 6.73 | |
| WMA-15 | 2.332162 | −0.247539 | 0.906308 | 4.253895 | 0.260827 | −3.720097 | 0.000292 | 0.9923 | 7.09 | |
| WMA-30 | 0.938964 | 0.769965 | 0.643573 | 4.225295 | −1.208403 | −3.716841 | 0.000244 | 0.9912 | 7.86 | |
| WMA-45 | 2.147436 | −0.449215 | 1.100028 | 4.089946 | 0.396154 | −3.705144 | 0.000392 | 0.9895 | 8.48 | |
| Statistical Description | Minimum | 0.938964 | −0.731821 | 0.643573 | 4.008499 | −1.208403 | −3.725021 | 0.000244 | ||
| Maximum | 2.457944 | 0.769965 | 1.197044 | 4.317418 | 0.599273 | −3.704619 | 0.000410 | |||
| Average | 2.118325 | −0.279601 | 0.990933 | 4.193437 | 0.170959 | −3.714996 | 0.000337 | |||
| Median | 0.854465 | 0.706769 | 2.602772 | 2.303886 | −2.456511 | −1.852188 | 0.000353 | |||
| Std | 0.468890 | 0.474661 | 0.185565 | 0.095495 | 0.571656 | 0.007880 | 0.000059 | |||
| Skewness | −2.309464 | 1.474897 | −0.865064 | −0.863506 | −2.040599 | 0.388598 | −0.386632 | |||
| Kurtosis | 5.801566 | 1.973254 | −0.486327 | 0.066587 | 4.247876 | −2.042569 | −1.667467 | |||
5. Discussion
5.1. Convergence Challenges
5.2. Benchmarking Against the Traditional Approach
5.3. Graphical Representation
5.4. Contributions to the Literature and Practical Applications
5.5. Research Limitations
5.6. Future Research Lines
6. Summary and Conclusions
- The development of the TSI model from thermodynamics-based principles (such as Eyring’s rate theory and activation free energy) and the TTSP proves that it is possible to accurately simulate the stiffness modulus of asphalt mixtures by explicitly accounting for both temperature and frequency as state variables. Specifically, the TSI model improves upon the traditional GS model by introducing three thermal-related fitting parameters (i.e., , , and ), which enable a more precise and physically grounded characterization of the temperature-dependent behaviour of asphalt mixtures.
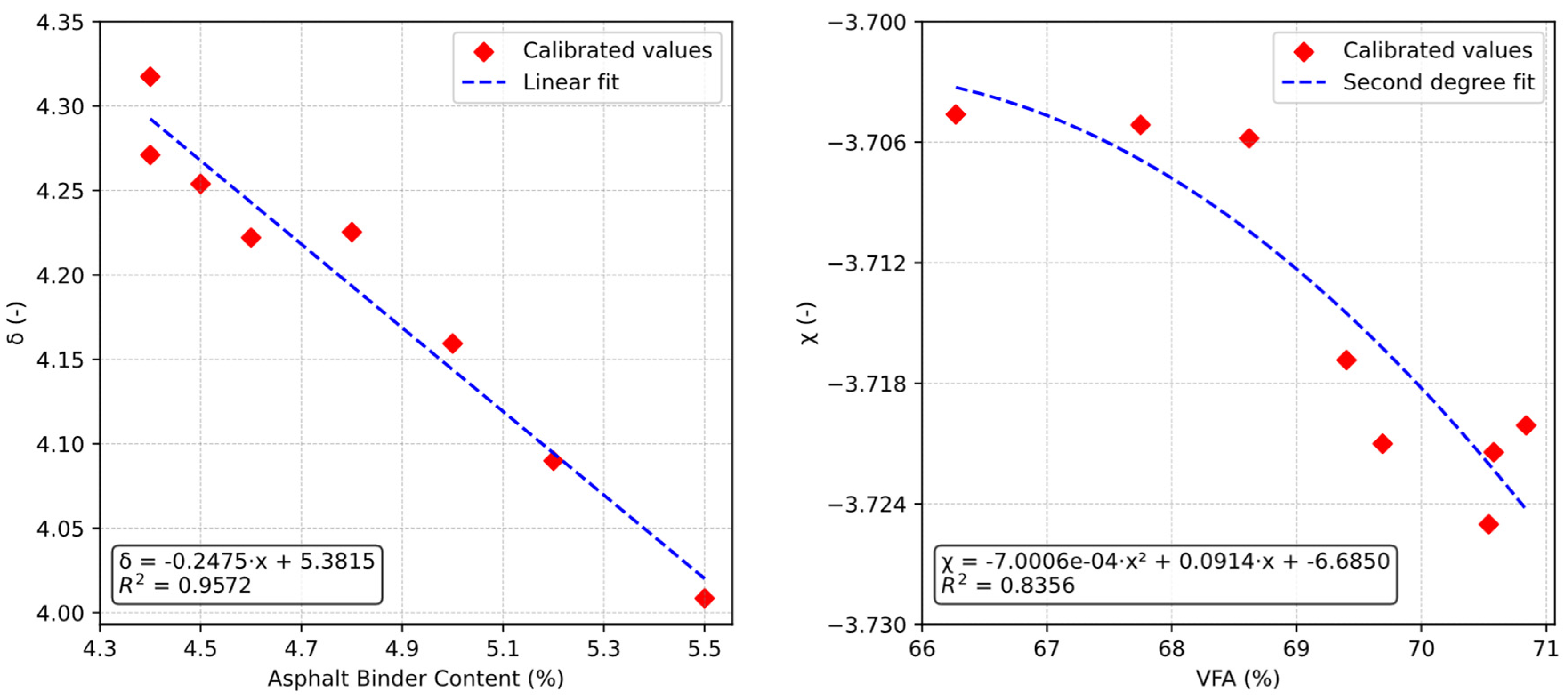
- The fitting parameters and capture the influences of the activation entropy and activation enthalpy, respectively. Meanwhile, introduces transition rate control and asymmetry into the model, enabling a more realistic representation of thermo-rheological behaviour in asphalt mixtures with complex mechanical responses; the preceding is particularly useful to account for effects caused by polymer modification, aging, and additive incorporation.
- For the addressed case study, the TSI model delivers highly accurate predictions of the asphalt mixture’s stiffness modulus, with R2 scores above 0.98 and MAPE values below 8.5%. In particular, the TSI model demonstrated exceptional computational stability, with a non-convergence rate of just 0.04% across 8000 runs, making it 4 to 45 times more stable than traditional master curve models such as GS, uniaxial, CS, and SLG. This level of stability is remarkably high, especially considering that the calibration was performed over a narrow frequency spectrum (i.e., from 0.5 to 8 Hz), a condition under which conventional models often struggle. This superior performance is attributed to its dual-sigmoidal structure and foundation on the (also stable) GS model, allowing for localized fitting and improved robustness during calibration.
- A benchmarking analysis confirmed that the proposed TSI model offers greater reliability than the traditional approach, which builds a master curve at a reference temperature and further relies on shift factors (e.g., Arrhenius or WLF formulations) to estimate stiffness at target temperatures. While the traditional method produced larger prediction errors (e.g., exceeding 200% at 40 °C), the TSI model maintained consistent accuracy across all loading conditions, with generally lower MAPE values and higher R2 scores, revealing its superior robustness and predictive capability.
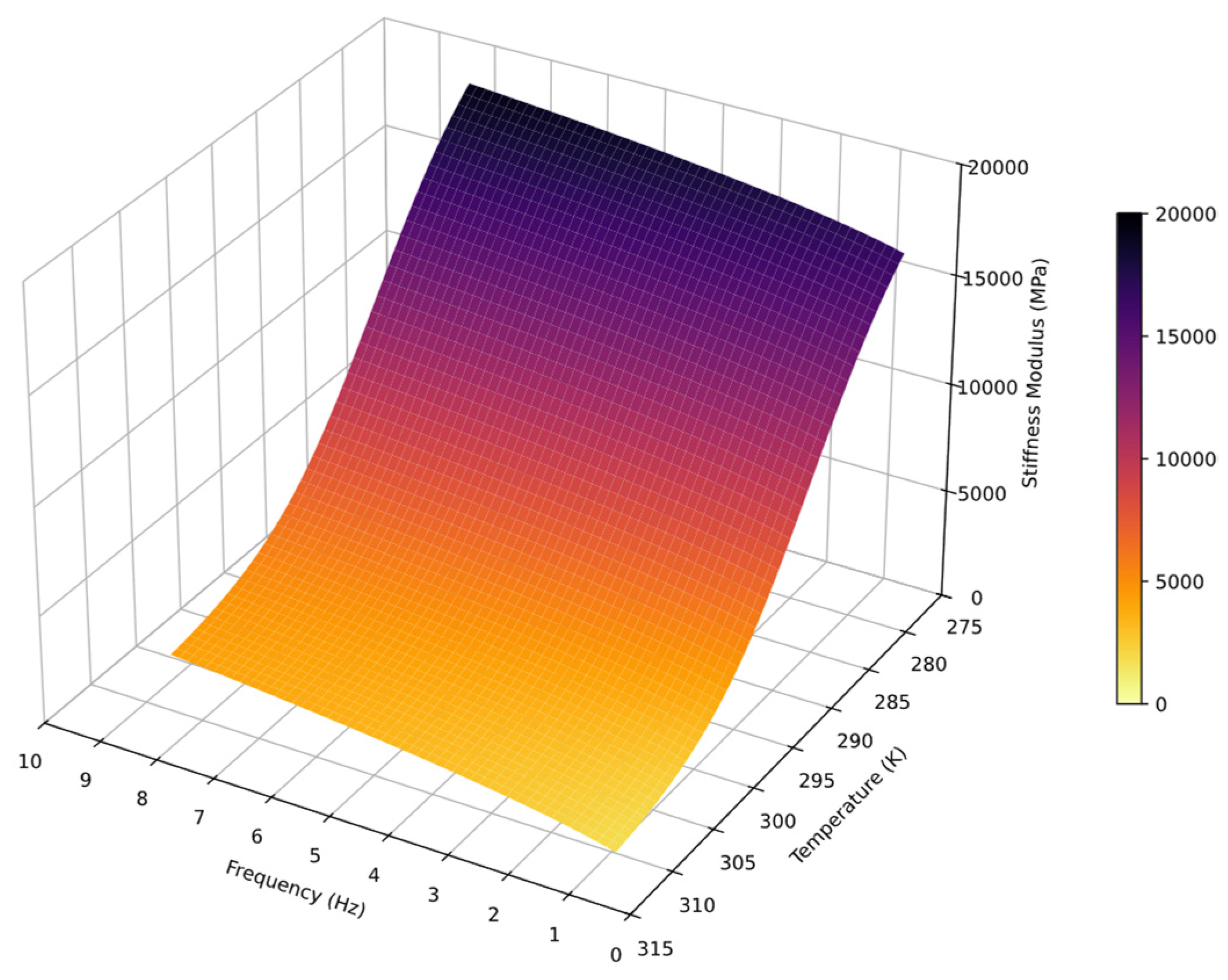
- The TSI model lays the foundation for advancing beyond the traditional master curve concept toward a new notion introduced in this study, i.e., the SPS. Basically, the SPS can be defined as a continuous hypersurface representing the full range of possible stiffness modulus values within the boundaries of the experimentally assessed loading conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Adham, K.; Baig, M.G.; Wahhab, H.A.A. Prediction of Dynamic Modulus for Elastomer-Modified Asphalt Concrete Mixes at Desert Environment. Arab. J. Sci. Eng. 2019, 44, 4141–4149. [Google Scholar] [CrossRef]
- Brondani, C.; Menezes Vestena, P.; Faccin, C.; Lisboa Schuster, S.; Pivoto Specht, L.; da Silva Pereira, D. Moisture Susceptibility of Asphalt Mixtures: 2S2P1D Rheological Model Approach and New Index Based on Dynamic Modulus Master Curve Changes. Constr. Build. Mater. 2022, 331, 127316. [Google Scholar] [CrossRef]
- Primusz, P.; Tóth, C. Use of the Modified Ramberg-Osgood Material Model to Predict Dynamic Modulus Master Curves of Asphalt Mixtures. Materials 2023, 16, 531. [Google Scholar] [CrossRef] [PubMed]
- Ling, M.; Luo, X.; Gu, F.; Lytton, R.L. Time-Temperature-Aging-Depth Shift Functions for Dynamic Modulus Master Curves of Asphalt Mixtures. Constr. Build. Mater. 2017, 157, 943–951. [Google Scholar] [CrossRef]
- Fan, X.; Lv, S.; Ge, D.; Liu, C.; Peng, X.; Ju, Z. Time-Temperature Equivalence and Unified Characterization of Asphalt Mixture Fatigue Properties. Constr. Build. Mater. 2022, 359, 129118. [Google Scholar] [CrossRef]
- Naderi, K.; Nejad, F.M.; Khodaii, A. Time-Temperature-Age Superposition Validation for Linear Viscoelastic Properties of Bituminous Materials. J. Mater. Civ. Eng. 2018, 30, 04017292. [Google Scholar] [CrossRef]
- Qin, X.; Ma, L.; Wang, H. Comparison Analysis of Dynamic Modulus of Asphalt Mixture: Indirect Tension and Uniaxial Compression Test. Transp. A Transp. Sci. 2019, 15, 165–178. [Google Scholar] [CrossRef]
- Lee, K.; Pape, S.; Castorena, C.; Kim, Y.R. Evaluation of Small Specimen Geometries for Asphalt Mixture Performance Testing and Pavement Performance Prediction. Transp. Res. Rec. 2017, 2631, 74–82. [Google Scholar] [CrossRef]
- Jing, R.; Varveri, A.; Liu, X.; Scarpas, A.; Erkens, S. Differences in the Ageing Behavior of Asphalt Pavements with Porous and Stone Mastic Asphalt Mixtures. Transp. Res. Rec. 2021, 2675, 1138–1149. [Google Scholar] [CrossRef]
- Zhao, Y.; Bai, L.; Liu, H. Implementation of a Triaxial Dynamic Modulus Master Curve in Finite-Element Modeling of Asphalt Pavements. J. Mater. Civ. Eng. 2014, 26, 491–498. [Google Scholar] [CrossRef]
- Zou, G.; Zhang, X.; Xu, J.; Chi, F. Morphology of Asphalt Mixture Rheological Master Curves. J. Mater. Civ. Eng. 2010, 22, 806–810. [Google Scholar] [CrossRef]
- Podolsky, J.H.; Williams, R.C.; Cochran, E. Effect of Corn and Soybean Oil Derived Additives on Polymer-Modified HMA and WMA Master Curve Construction and Dynamic Modulus Performance. Int. J. Pavement Res. Technol. 2018, 11, 541–552. [Google Scholar] [CrossRef]
- Gu, L.; Chen, L.; Zhang, W.; Ma, H.; Ma, T. Mesostructural Modeling of Dynamic Modulus and Phase Angle Master Curves of Rubber Modified Asphalt Mixture. Materials 2019, 12, 1667. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Lu, W.; Liu, K.; Lv, S.; Peng, X.; Yang, S.; Ding, S. Research on Failure Strength Master Curve and Fatigue Performance of Asphalt Mixture Containing High-Proportion Reclaimed Asphalt Pavement. Constr. Build. Mater. 2023, 370, 130537. [Google Scholar] [CrossRef]
- Xi, L.; Luo, R.; Ma, Q.; Tu, C.; Shah, Y.I. An Improved Method to Establish Continuous Relaxation Spectrum of Asphalt Materials. Constr. Build. Mater. 2022, 354, 129182. [Google Scholar] [CrossRef]
- Bi, Y.; Wei, R.; Li, R.; Zhang, J.; Pei, J. Evaluation of Rheological Master Curves of Asphalt Mastics and Asphalt-Filler Interaction Indices. Constr. Build. Mater. 2020, 265, 120046. [Google Scholar] [CrossRef]
- Chen, H.; Barbieri, D.M.; Zhang, X.; Hoff, I. Reliability of Calculation of Dynamic Modulus for Asphalt Mixtures Using Different Master Curve Models and Shift Factor Equations. Materials 2022, 15, 4325. [Google Scholar] [CrossRef]
- Wang, D.; Cannone Falchetto, A.; Riccardi, C.; Wistuba, M.P. Investigation on the Low Temperature Properties of Asphalt Binder: Glass Transition Temperature and Modulus Shift Factor. Constr. Build. Mater. 2020, 245, 118351. [Google Scholar] [CrossRef]
- Lorenz, B.; Pyckhout-Hintzen, W.; Persson, B.N.J. Master Curve of Viscoelastic Solid: Using Causality to Determine the Optimal Shifting Procedure, and to Test the Accuracy of Measured Data. Polymer 2014, 55, 565–571. [Google Scholar] [CrossRef]
- Chen, M.; Javilla, B.; Hong, W.; Pan, C.; Riara, M.; Mo, L.; Guo, M. Rheological and Interaction Analysis of Asphalt Binder, Mastic and Mortar. Materials 2019, 12, 128. [Google Scholar] [CrossRef]
- Su, N.; Xiao, F.; Wang, J.; Amirkhanian, S. Precision Analysis of Sigmoidal Master Curve Model for Dynamic Modulus of Asphalt Mixtures. J. Mater. Civ. Eng. 2018, 30, 04018290. [Google Scholar] [CrossRef]
- Calderon, E.; Leiva, P.; Loria, L.; Clark, D. LM-PI-UMP-017-R3: Herramienta de Calculo de La Curva Maestra de Modulo Dinamico-IModin 2.0. LanammeUCR. 2019, pp. 1–29. Available online: https://www.lanamme.ucr.ac.cr/repositorio/bitstream/handle/50625112500/194/LM-PI-UMP-017.pdf (accessed on 20 August 2025).
- Zhao, Y.; Tang, J.; Liu, H. Construction of Triaxial Dynamic Modulus Master Curve for Asphalt Mixtures. Constr. Build. Mater. 2012, 37, 21–26. [Google Scholar] [CrossRef]
- Pszczola, M.; Jaczewski, M.; Szydlowski, C. Assessment of Thermal Stresses in Asphalt Mixtures at Low Temperatures Using the Tensile Creep Test and the Bending Beam Creep Test. Appl. Sci. 2019, 9, 846. [Google Scholar] [CrossRef]
- Tabatabaee, H.; Velasquez, R.; Bahia, H. Modeling Thermal Stress in Asphalt Mixtures Undergoing Glass Transition and Physical Hardening. Transp. Res. Rec. 2012, 2296, 106–114. [Google Scholar] [CrossRef]
- Tan, G.; Wang, W.; Cheng, Y.; Wang, Y.; Zhu, Z. Master Curve Establishment and Complex Modulus Evaluation of SBS-Modified Asphalt Mixture Reinforced with Basalt Fiber Based on Generalized Sigmoidal Model. Polymers 2020, 12, 1586. [Google Scholar] [CrossRef]
- Liu, H.; Luo, R. Development of Master Curve Models Complying with Linear Viscoelastic Theory for Complex Moduli of Asphalt Mixtures with Improved Accuracy. Constr. Build. Mater. 2017, 152, 259–268. [Google Scholar] [CrossRef]
- Li, J.; Xiao, F.; Amirkhanian, S.N.; Xu, O. Dynamic and Rutting Characteristics of Recycled Asphalt Mixtures Containing Natural Sand and Anti-Stripping Agents. J. Clean. Prod. 2021, 280, 124365. [Google Scholar] [CrossRef]
- Bayane, B.M.; Yang, E.; Yanjun, Q. Dynamic Modulus Master Curve Construction Using Christensen-Anderson-Marasteanu (CAM) Model. Int. J. Eng. Res. Appl. 2017, 7, 53–63. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, P.; Cao, D. Extension of Modified Havriliak-Negami Model to Characterize Linear Viscoelastic Properties of Asphalt Binders. J. Mater. Civ. Eng. 2016, 28, 04015195. [Google Scholar] [CrossRef]
- Vestena, P.M.; Schuster, S.L.; de Almeida, P.O.B., Jr.; Faccin, C.; Specht, L.P.; da Silva Pereira, D. Dynamic Modulus Master Curve Construction of Asphalt Mixtures: Error Analysis in Different Models and Field Scenarios. Constr. Build. Mater. 2021, 301, 124343. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, J.; Wang, T.; Amirkhanian, S.N.; Xiao, F. Linear Visco-Elasticity of Asphalt in View of Proportion and Polarity of SARA Fractions. Fuel 2024, 363, 130955. [Google Scholar] [CrossRef]
- Graziani, A.; Cardone, F.; Virgili, A. Characterization of the Three-Dimensional Linear Viscoelastic Behavior of Asphalt Concrete Mixtures. Constr. Build. Mater. 2016, 105, 356–364. [Google Scholar] [CrossRef]
- He, W.; Zhao, Z.; Zhang, Z.; Xiao, F. Modification and Application of the Arrhenius Equation Based on Activated Energy Methods from Various Asphalt Binders. J. Mater. Civ. Eng. 2024, 36, 04024123. [Google Scholar] [CrossRef]
- Tian, W.; Hu, C. Arrhenius Model-Based Analysis of High-Temperature Properties and Temperature Sensitivity of SBS/CR Modified Asphalt. Constr. Build. Mater. 2025, 476, 141298. [Google Scholar] [CrossRef]
- Liang, B.; Chen, Y.; Lan, F.; Zheng, J. Evaluation of Rheological and Aging Behavior of Modified Asphalt Based on Activation Energy of Viscous Flow. Constr. Build. Mater. 2022, 321, 126347. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- McCrum, N.G.; Pogany, G.A. Time-Temperature Superposition in the α Region of an Epoxy Resin. J. Macromol. Sci. Part B 1970, 4, 109–125. [Google Scholar] [CrossRef]
- Alrashydah, E.I.; Abo-Qudais, S.A. Hot Mix Asphalt Time-Temperature Shifting and Fitting Techniques: A Comparative Study. Constr. Build. Mater. 2017, 146, 514–523. [Google Scholar] [CrossRef]
- Pellinen, T.K.; Witczak, M.W.; Bonaquist, R.F. Asphalt Mix Master Curve Construction Using Sigmoidal Fitting Function with Non-Linear Least Squares Optimization. In Advances in Materials Characterization and Modeling of Pavement Systems; American Society of Civil Engineers: Reston, VA, USA, 2003; pp. 83–101. [Google Scholar]
- Fesko, D.G.; Tschoegl, N.W. Time-Temperature Superposition in Styrene/Butadiene/Styrene Block Copolymers. Int. J. Polym. Mater. 1974, 3, 51–79. [Google Scholar] [CrossRef]
- Qadir, A. Investigation of Glass Transition Temperature of Asphalt Concrete. J. Test. Eval. 2017, 45, 1680–1690. [Google Scholar] [CrossRef]
- Kang, Y.; Zhou, D.; Wu, Q.; Liang, R.; Shangguan, S.; Liao, Z.; Wei, N. Molecular Dynamics Study on the Glass Forming Process of Asphalt. Constr. Build. Mater. 2019, 214, 430–440. [Google Scholar] [CrossRef]
- Yang, G.; Wang, X.; Zhou, X.; Wang, Y. Experimental Study on the Phase Transition Characteristics of Asphalt Mixture for Stress Absorbing Membrane Interlayer. Materials 2020, 13, 474. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Sun, Y.; Wang, W.; Chen, J. Using the Viscoelastic Parameters to Estimate the Glass Transition Temperature of Asphalt Binders. Constr. Build. Mater. 2017, 153, 908–917. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Guo, S. Asphalt Rheological Properties Transformation from Frequency Domain to Temperature Domain Based on WLF Equation. Int. J. Pavement Res. Technol. 2023, 16, 167–175. [Google Scholar] [CrossRef]
- Ashter, S.A. Mechanics of Materials. Thermoforming of Single and Multilayer Laminates; Elsevier: Amsterdam, The Netherlands, 2014; pp. 123–145. [Google Scholar]
- Duque, J.; Martinez-Arguelles, G.; Nuñez, Y.; Peñabaena-Niebles, R.; Polo-Mendoza, R. Designing Climate Change (CC)-Resilient Asphalt Pavement Structures: A Comprehensive Literature Review on Adaptation Measures and Advanced Soil Constitutive Models. Results Eng. 2024, 24, 103648. [Google Scholar] [CrossRef]
- Lali, F.A.; Singh, R.R.; Haider, S.W.; Kutay, M.E.; Chatti, K.; Schenkel, J.P. Characterizing the Damaged Dynamic Modulus Master Curves of Existing Hot Mix Asphalt (HMA) Layers for Rehabilitation Design. Constr. Build. Mater. 2025, 483, 141808. [Google Scholar] [CrossRef]
- Forough, S.A.; Nejad, F.M.; Khodaii, A. Comparing Various Fitting Models to Construct the Tensile Relaxation Modulus Master Curve of Asphalt Mixes. Int. J. Pavement Eng. 2016, 17, 314–330. [Google Scholar] [CrossRef]
- Hou, S.; Deng, Y.; Jin, R.; Shi, X.; Luo, X. Relationships between Physical, Mechanical and Acoustic Properties of Asphalt Mixtures Using Ultrasonic Testing. Buildings 2022, 12, 306. [Google Scholar] [CrossRef]
- Zhang, R.; Sias, J.E.; Dave, E.V. Using Mix Design Information for Modelling of Fundamental Viscoelasticity of Asphalt Mixtures. Constr. Build. Mater. 2022, 329, 127029. [Google Scholar] [CrossRef]
- Oshone, M.; Sias, J.E.; Dave, E.V.; Martin, A.E.; Kaseer, F.; Rahbar-Rastegar, R. Exploring Master Curve Parameters to Distinguish between Mixture Variables. Road Mater. Pavement Des. 2019, 20, S812–S826. [Google Scholar] [CrossRef]
- Nitta, K. On a Thermodynamic Foundation of Eyring Rate Theory for Plastic Deformation of Polymer Solids. Philos. Mag. Lett. 2023, 103, 2186190. [Google Scholar] [CrossRef]
- Hao, T. The Empty World–A View from the Free Volume Concept and Eyring’s Rate Process Theory. Phys. Chem. Chem. Phys. 2024, 26, 26156–26191. [Google Scholar] [CrossRef]
- American Chemical Society. Eyring Outlines Absolute Rate Theory for Chemical Reactions. Chem. Eng. News Arch. 1951, 29, 1100–1101. [Google Scholar] [CrossRef]
- Urry, D.W. Henry Eyring (1901–1981): A 20th Century Physical Chemist and His Models. Math. Model. 1982, 3, 503–522. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, F.; Liu, X.; Afzal, W.; He, M. Viscosity of Oxygenated Fuel: A Model Based on Eyring’s Absolute Rate Theory. Fuel 2019, 241, 218–226. [Google Scholar] [CrossRef]
- Hu, Y.F.; Lee, H. Prediction of Viscosity of Mixed Electrolyte Solutions Based on the Eyring’s Absolute Rate Theory and the Semi-Ideal Hydration Model. Electrochim. Acta 2003, 48, 1789–1796. [Google Scholar] [CrossRef]
- He, M.; Zhu, C.; Liu, X. Estimating the Viscosity of Ionic Liquid at High Pressure Using Eyring’s Absolute Rate Theory. Fluid Phase Equilib. 2018, 458, 170–176. [Google Scholar] [CrossRef]
- Hernández, A.; Khosharay, S. Investigation on the Surface Tension and Viscosity of (Dimethylsulfoxide + Alcohol) Mixtures by Using Gradient Theory and Eyring’s Rate Theory. Int. J. Thermophys. 2020, 41, 150. [Google Scholar] [CrossRef]
- Eyring, H.; Urry, D.W. The Theory of Absolute Reaction Rates in Solution. Berichte Der Bunsenges. Für Phys. Chem. 1963, 67, 731–740. [Google Scholar] [CrossRef]
- Li, S. Numerical Investigation on Viscoelastic Response of Asphalt Mixture under Tire Braking Slip. Case Stud. Constr. Mater. 2023, 18, e02009. [Google Scholar] [CrossRef]
- Zhang, J.; Faruk, A.N.M.; Karki, P.; Holleran, I.; Hu, X.; Walubita, L.F. Relating Asphalt Binder Elastic Recovery Properties to HMA Cracking and Fracture Properties. Constr. Build. Mater. 2016, 121, 236–245. [Google Scholar] [CrossRef]
- Bai, T.; Cheng, Z.; Hu, X.; Fuentes, L.; Walubita, L.F. Viscoelastic Modelling of an Asphalt Pavement Based on Actual Tire-Pavement Contact Pressure. Road Mater. Pavement Des. 2021, 22, 2458–2477. [Google Scholar] [CrossRef]
- Modi, S.H.; Orešković, M.; Dave, E.V.; Sias, J.E. Application of Time-Temperature Superposition Principle for Cracking Characterization of Asphalt Mixtures Using Semi-Circular Bend Test. Constr. Build. Mater. 2024, 443, 137647. [Google Scholar] [CrossRef]
- Phan, T.N.; Nguyen, N.H.; Do, T.T.; Nguyen, H.T.T.; Nguyen, M.L. Verification of Time-Temperature Superposition Principle for Viscoplastic Strains of Asphalt Mixtures Obtained from Creep-Recovery Tests in the Low-Strain Regime. Road Mater. Pavement Des. 2025, 26, 958–995. [Google Scholar] [CrossRef]
- Bradai, M.A.; Tapsoba, N.; Sauzéat, C.; Di Benedetto, H.; Neji, J. Validation of the Time-Temperature Superposition Principle (TTSP) in the Non-Linear Domain for Bituminous Mixtures with Reclaimed Asphalt Pavement (40% RAP). In RILEM International Symposium on Bituminous Materials; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1925–1931. [Google Scholar]
- Zhao, Y.; Richard Kim, Y. Time–Temperature Superposition for Asphalt Mixtures with Growing Damage and Permanent Deformation in Compression. Transp. Res. Rec. J. Transp. Res. Board 2003, 1832, 161–172. [Google Scholar] [CrossRef]
- Covilla-Varela, E.; Turbay, E.; Polo-Mendoza, R.; Martínez-Arguelles, G.; Cantero-Durango, J. Recycled Concrete Aggregates (RCA)-Based Asphalt Mixtures: A Performance-Related Evaluation with Sustainability-Criteria Verification. Constr. Build. Mater. 2023, 403, 133203. [Google Scholar] [CrossRef]
- Martinez-Arguelles, G.; Dugarte, M.; Fuentes, L.; Sanchez, E.; Rondon, H.; Pacheco, C.; Yepes, J.; Lagares, R. Characterization of Recycled Concrete Aggregate as Potential Replacement of Natural Aggregate in Asphalt Pavement. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 471, p. 102045. [Google Scholar] [CrossRef]
- Le, T.M.; Fatahi, B.; Khabbaz, H.; Sun, W. Numerical Optimization Applying Trust-Region Reflective Least Squares Algorithm with Constraints to Optimize the Non-Linear Creep Parameters of Soft Soil. Appl. Math. Model. 2017, 41, 236–256. [Google Scholar] [CrossRef]
- Rahman, A.A.; Wang, B.; Yan, J.; Wang, H.; Jin, T.; Gan, Z. Developed Empirical Correlation for Self-Pressurization in Multi-Configuration Non-Venting Liquid Hydrogen Tanks Using Trust-Region Reflective Algorithm. Int. J. Hydrogen Energy 2025, 142, 122–129. [Google Scholar] [CrossRef]
- Weiping, W.; Hongchun, W.; Haofeng, Z.; Xiong, X. A Pn-Wave Spectral Inversion Technique Based on Trust Region Reflective Algorithm. J. Appl. Geophy. 2024, 230, 105525. [Google Scholar] [CrossRef]
- Shireman, E.; Steinley, D.; Brusco, M.J. Examining the Effect of Initialization Strategies on the Performance of Gaussian Mixture Modeling. Behav. Res. Methods 2017, 49, 282–293. [Google Scholar] [CrossRef]
- Karlis, D.; Xekalaki, E. Choosing Initial Values for the EM Algorithm for Finite Mixtures. Comput. Stat. Data Anal. 2003, 41, 577–590. [Google Scholar] [CrossRef]
- Singh, R.R.; Lali, F.; Muslim, H.B.; Haider, S.W.; Dolan, K.D. Scaled Sensitivity of Pavement–Mechanistic-Empirical Transfer Function Coefficients for Flexible and Rigid Pavements. Transp. Res. Rec. J. Transp. Res. Board 2025, 2679, 630–640. [Google Scholar] [CrossRef]
- Scharmack, D.K. An Initial Value Method for Trajectory Optimization Problems. In Advances in Control Systems; Elsevier: Amsterdam, The Netherlands, 1967; pp. 51–132. [Google Scholar]
- Korošec, P.; Eftimov, T. Insights into Exploration and Exploitation Power of Optimization Algorithm Using DSCTool. Mathematics 2020, 8, 1474. [Google Scholar] [CrossRef]
- Biernacki, C.; Celeux, G.; Govaert, G. Choosing Starting Values for the EM Algorithm for Getting the Highest Likehood in Multivariate Gaussian Mixture Models. Comput. Stat. Data Anal. 2003, 41, 561–575. [Google Scholar] [CrossRef]
- Brugnano, L.; Trigiante, D. Convergence and Stability of Boundary Value Methods for Ordinary Differential Equations. J. Comput. Appl. Math. 1996, 66, 97–109. [Google Scholar] [CrossRef]
- Walubita, L.F.; Scullion, T.; Leidy, J.; Liu, W. Non-Destructive Testing Technologies: Application of the Ground Penetrating Radar (GPR) to Perpetual Pavements. Road Mater. Pavement Des. 2009, 10, 259–286. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, J.; Lin, W.; Timm, D.; Huber, G. Binzhou Perpetual Pavement Test Road: Dynamic Response of Pavement under Very Heavy Loads. Road Mater. Pavement Des. ICAM 2009, 10, 151–165. [Google Scholar] [CrossRef]
- Mazumder, M.; Kim, H.; Lee, S.J. Perpetual Pavement: Future Pavement Network. J. Adv. Constr. Mater. 2015, 19, 35–49. [Google Scholar]
- El-Hakim, M.Y.; Tighe, S.L. Sustainability of Perpetual Pavement Designs: Canadian Perspective. Transp. Res. Rec. 2012, 2304, 10–16. [Google Scholar] [CrossRef]
- Halle, M.; Rukavina, T.; Domitrovic, J. Influence of Temperature on Asphalt Stiffness Modulus. In Proceedings of the 5th Eurasphalt & Eurobitume Congress, Istanbul, Turkey, 13–15 June 2012; pp. 1–12. [Google Scholar]
- Moghaddam, T.B.; Soltani, M.; Karim, M.R. Stiffness Modulus of Polyethylene Terephthalate Modified Asphalt Mixture: A Statistical Analysis of the Laboratory Testing Results. Mater. Des. 2015, 68, 88–96. [Google Scholar] [CrossRef]
- Radwan, M.M.; Mousa, A.; Zahran, E.M.M. Enhancing Pavement Sustainability: Prediction of the Pavement Condition Index in Arid Urban Climates Using the International Roughness Index. Sustainability 2024, 16, 3158. [Google Scholar] [CrossRef]
- Al-Abdul Wahhab, H.I.; Balghunaim, F.A. Asphalt Pavement Temperature Related to Arid Saudi Environment. J. Mater. Civ. Eng. 1994, 6, 8–14. [Google Scholar] [CrossRef]
- Emmerich, M.; Yang, K.; Deutz, A.; Wang, H.; Fonseca, C.M. A Multicriteria Generalization of Bayesian Global Optimization. In Advances in Stochastic and Deterministic Global Optimization; Pardalos, P.M., Zhigljavsky, A., Žilinskas, J., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 229–242. [Google Scholar]
- Li, C.; Grossmann, I.E. A Review of Stochastic Programming Methods for Optimization of Process Systems Under Uncertainty. Front. Chem. Eng. 2021, 2, 622241. [Google Scholar] [CrossRef]
- Arora, J.S.; Elwakeil, O.A.; Chahande, A.I.; Hsieh, C.C. Global Optimization Methods for Engineering Applications: A Review. Struct. Optim. 1995, 9, 137–159. [Google Scholar] [CrossRef]
- Kuptametee, C.; Michalopoulou, Z.H.; Aunsri, N. A Review of Efficient Applications of Genetic Algorithms to Improve Particle Filtering Optimization Problems. Measurement 2024, 224, 113952. [Google Scholar] [CrossRef]
- Neumann, A.; Hajji, A.; Rekik, M.; Pellerin, R. A Didactic Review On Genetic Algorithms For Industrial Planning And Scheduling Problems. IFAC-Pap. 2022, 55, 2593–2598. [Google Scholar] [CrossRef]
- Bi, Y.; Wu, S.; Pei, J.; Wen, Y.; Li, R. Correlation Analysis between Aging Behavior and Rheological Indices of Asphalt Binder. Constr. Build. Mater. 2020, 264, 120176. [Google Scholar] [CrossRef]
- Leite, L.F.M.; Osmari, P.H.; Aragão, F.T.S. Rheological Indexes for Asphalt Binders Considering Different Aging Conditions: Evaluation and Correlations with Performance. Constr. Build. Mater. 2022, 338, 127549. [Google Scholar] [CrossRef]
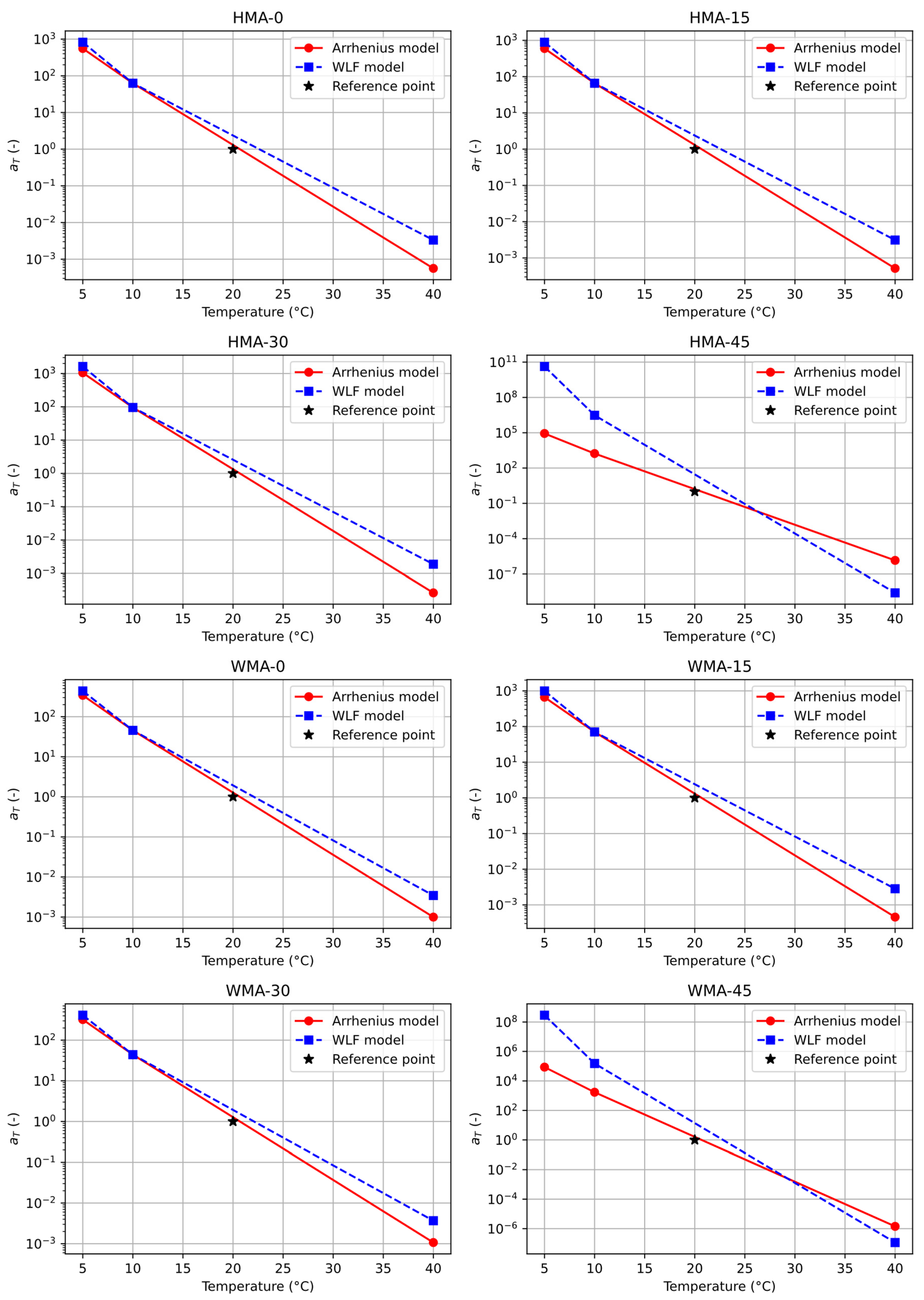
| Formulations | Best Temperature Range | Unreliable Temperature Range | Notes | References |
|---|---|---|---|---|
| Arrhenius (Equation (6)) | Low temperatures (glassy, below ) | At or above (rubbery) | Assumes constant activation energy; suitable for glassy regime. | [36,45] |
| WLF (Equation (7)) | Around and above | Deep in glassy region (low T) | Empirical constants; best near Tg. | [17,18] |
| Kaelble: | Below and around (sub-) | Far above (highly rubbery region) | More symmetric than WLF for sub-Tg; useful for describing both sides of Tg. | [38,41] |
| Log-linear: | Wide temperature range (empirical) | May lack physical basis at extremes | Simple, flexible; used for practical fitting. | [17] |
| Quadratic polynomial: | Wide temperature range (empirical) | May overfit or lack physical meaning | Useful for complex blends or modified asphalts. | [17,39] |
| Asphalt Mixtures a | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| HMA-0 | HMA-15 | HMA-30 | HMA-45 | WMA-0 | WMA-15 | WMA-30 | WMA-45 | ||
| Gravimetric composition | Fine NAs (%) | 47.80 | 47.70 | 47.50 | 47.25 | 47.80 | 47.75 | 47.60 | 47.40 |
| Coarse NAs (%) | 47.80 | 40.55 | 33.25 | 25.99 | 47.80 | 40.59 | 33.32 | 26.07 | |
| Fine RCA (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Coarse RCA (%) | 0 | 7.16 | 14.25 | 21.26 | 0 | 7.16 | 14.28 | 21.33 | |
| Asphalt binder (%) | 4.40 | 4.60 | 5.00 | 5.50 | 4.40 | 4.50 | 4.80 | 5.20 | |
| Laboratory characterization | Mixing temperature (°C) | 160.00 | 160.00 | 160.00 | 160.00 | 120.00 | 120.00 | 120.00 | 120.00 |
| Compaction temperature (°C) | 140.00 | 140.00 | 140.00 | 140.00 | 110.00 | 110.00 | 110.00 | 110.00 | |
| Bulk density (kg/m3) | 2361.04 | 2351.37 | 2331.33 | 2322.25 | 2363.12 | 2333.98 | 2337.34 | 2317.63 | |
| VFA (%) | 69.69 | 70.54 | 68.62 | 66.27 | 70.58 | 70.84 | 69.40 | 67.75 | |
| VMAs (%) | 14.32 | 15.41 | 15.71 | 16.10 | 14.65 | 15.50 | 15.85 | 16.28 | |
| VTMs (%) | 4.34 | 4.54 | 4.93 | 5.43 | 4.31 | 4.52 | 4.85 | 5.25 | |
| Marshall flow value (mm) | 3.17 | 3.65 | 6.32 | 6.86 | 2.62 | 2.96 | 6.29 | 6.39 | |
| Marshall stability (kN) | 15.13 | 14.57 | 13.74 | 12.88 | 15.93 | 15.22 | 14.60 | 13.89 | |
| Asphalt Mixtures | Number of Non-Convergent Runs | ||||
|---|---|---|---|---|---|
| GS Model | CS Model | SLG Model | Uniaxial Model | TSI Model | |
| HMA-0 | 2 | 22 | 10 | 4 | 0 |
| HMA-15 | 1 | 12 | 17 | 2 | 0 |
| HMA-30 | 2 | 19 | 24 | 3 | 0 |
| HMA-45 | 1 | 17 | 26 | 1 | 0 |
| WMA-0 | 2 | 13 | 21 | 3 | 1 |
| WMA-15 | 1 | 19 | 11 | 1 | 0 |
| WMA-30 | 2 | 22 | 16 | 2 | 0 |
| WMA-45 | 2 | 14 | 18 | 2 | 2 |
| Total | 13 | 138 | 143 | 18 | 3 |
| Non-convergence (%) | 0.16 | 1.73 | 1.79 | 0.23 | 0.04 |
| Traditional model/proposed model ratio (-) | 4 | 43 | 45 | 6 | |
| Asphalt Mixtures | Fitting Parameters | |||
|---|---|---|---|---|
| HMA-0 | 3.907667 | −5.1 | 5.1 | 4.165368 |
| HMA-15 | 3.853796 | −5.1 | 5.1 | 4.108047 |
| HMA-30 | 3.804261 | −5.1 | 5.1 | 4.051765 |
| HMA-45 | 3.673245 | −5.1 | 5.1 | 3.886199 |
| WMA-0 | 3.961070 | −5.1 | 4.740254 | 4.262092 |
| WMA-15 | 3.908768 | −5.1 | 5.1 | 4.160014 |
| WMA-30 | 3.858396 | −5.1 | 4.983891 | 4.141897 |
| WMA-45 | 3.731134 | −5.1 | 5.1 | 3.933298 |
| Asphalt Mixtures | Arrhenius Model | WLF Model | |
|---|---|---|---|
| (J/mol) | (-) | (K) | |
| HMA-0 | 285,678.66 | 11.97 | 76.61 |
| HMA-15 | 288,933.55 | 12.10 | 76.54 |
| HMA-30 | 314,577.16 | 13.13 | 76.35 |
| HMA-45 | 513,774.30 | 38.10 | 68.76 |
| WMA-0 | 263,700.42 | 14.30 | 96.19 |
| WMA-15 | 293,735.47 | 12.29 | 76.51 |
| WMA-30 | 261,119.83 | 14.09 | 95.77 |
| WMA-45 | 513,693.15 | 31.54 | 70.89 |
| Asphalt Mixtures | Arrhenius Model | WLF Model | ||||
|---|---|---|---|---|---|---|
| HMA-0 | 5.5553 × 102 | 6.2733 × 101 | 5.6158 × 10−4 | 8.2233 × 102 | 6.2733 × 101 | 3.3214 × 10−3 |
| HMA-15 | 5.9701 × 102 | 6.5762 × 101 | 5.1568 × 10−4 | 8.8825 × 102 | 6.5762 × 101 | 3.1187 × 10−3 |
| HMA-30 | 1.0528 × 103 | 9.5351 × 101 | 2.6339 × 10−4 | 1.6254 × 103 | 9.5351 × 101 | 1.8790 × 10−3 |
| HMA-45 | 8.6333 × 104 | 1.7087 × 103 | 1.4257 × 10−6 | 4.2690 × 1010 | 3.0466 × 106 | 2.6027 × 10−9 |
| WMA-0 | 3.4162 × 102 | 4.5625 × 101 | 9.9883 × 10−4 | 4.3861 × 102 | 4.5625 × 101 | 3.4546 × 10−3 |
| WMA-15 | 6.6392 × 102 | 7.0500 × 101 | 4.5472 × 10−4 | 9.9453 × 102 | 7.0500 × 101 | 2.8353 × 10−3 |
| WMA-30 | 3.2267 × 102 | 4.3951 × 101 | 1.0687 × 10−3 | 4.1402 × 102 | 4.3951 × 101 | 3.6779 × 10−3 |
| WMA-45 | 8.6178 × 104 | 1.7067 × 103 | 1.4288 × 10−6 | 2.9222 × 108 | 1.5148 × 105 | 1.1457 × 10−7 |
| Asphalt Mixtures | GS Model (20 °C) | Arrhenius Model | WLF Model | ||||
|---|---|---|---|---|---|---|---|
| 5 °C | 10 °C | 40 °C | 5 °C | 10 °C | 40 °C | ||
| HMA-0 | 1.66 | 16.52 | 6.35 | 205.77 | 16.52 | 6.35 | 205.71 |
| HMA-15 | 1.56 | 17.43 | 6.48 | 205.76 | 17.42 | 6.47 | 205.78 |
| HMA-30 | 1.47 | 17.82 | 6.86 | 206.62 | 17.82 | 6.86 | 206.62 |
| HMA-45 | 1.37 | 22.42 | 11.61 | 213.28 | 22.42 | 11.60 | 213.25 |
| WMA-0 | 0.79 | 9.08 | 4.40 | 204.81 | 9.10 | 4.40 | 204.77 |
| WMA-15 | 1.33 | 17.22 | 6.83 | 202.47 | 17.22 | 6.81 | 202.49 |
| WMA-30 | 1.78 | 11.93 | 3.69 | 209.99 | 11.95 | 3.69 | 209.93 |
| WMA-45 | 1.20 | 24.70 | 12.81 | 214.49 | 24.73 | 12.82 | 214.48 |
| Asphalt Mixtures | GS Model (20 °C) |
|---|---|
| HMA-0 | 0.9470 |
| HMA-15 | 0.9522 |
| HMA-30 | 0.9542 |
| HMA-45 | 0.9458 |
| WMA-0 | 0.9887 |
| WMA-15 | 0.9621 |
| WMA-30 | 0.9523 |
| WMA-45 | 0.9514 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez-Arguelles, G.; Casas, D.; Peñabaena-Niebles, R.; Guerrero-Bustamante, O.; Polo-Mendoza, R. A Novel Master Curve Formulation with Explicitly Incorporated Temperature Dependence for Asphalt Mixtures: A Model Proposal with a Case Study. Infrastructures 2025, 10, 227. https://doi.org/10.3390/infrastructures10090227
Martinez-Arguelles G, Casas D, Peñabaena-Niebles R, Guerrero-Bustamante O, Polo-Mendoza R. A Novel Master Curve Formulation with Explicitly Incorporated Temperature Dependence for Asphalt Mixtures: A Model Proposal with a Case Study. Infrastructures. 2025; 10(9):227. https://doi.org/10.3390/infrastructures10090227
Chicago/Turabian StyleMartinez-Arguelles, Gilberto, Diego Casas, Rita Peñabaena-Niebles, Oswaldo Guerrero-Bustamante, and Rodrigo Polo-Mendoza. 2025. "A Novel Master Curve Formulation with Explicitly Incorporated Temperature Dependence for Asphalt Mixtures: A Model Proposal with a Case Study" Infrastructures 10, no. 9: 227. https://doi.org/10.3390/infrastructures10090227
APA StyleMartinez-Arguelles, G., Casas, D., Peñabaena-Niebles, R., Guerrero-Bustamante, O., & Polo-Mendoza, R. (2025). A Novel Master Curve Formulation with Explicitly Incorporated Temperature Dependence for Asphalt Mixtures: A Model Proposal with a Case Study. Infrastructures, 10(9), 227. https://doi.org/10.3390/infrastructures10090227







