Concrete Bridge Crack Detection Using Unmanned Aerial Vehicles and Image Segmentation

Abstract

Concrete bridge cracks are critical indicators for maintenance planning. Traditional visual inspections are often subjective, labor-intensive, and time-consuming, requiring close-range access by inspectors. In contrast, UAV-based remote sensing, combined with advanced image processing, offers a more efficient and accurate solution. This study proposes an enhanced crack detection method combining Laplacian of Gaussian (LoG) filtering and Otsu thresholding to improve segmentation accuracy through background noise suppression. The proposed approach extracts key crack characteristics—including area, length, centroid, and main direction—enabling precise damage assessment. Experimental validation on a real bridge dataset demonstrates significant improvements in detection accuracy. The method provides a reliable tool for automated structural health monitoring, supporting data-driven maintenance decisions.

1. Introduction

Civil infrastructure safety has been an actively researched topic over the past decade [1,2,3]. Concrete bridges are particularly susceptible to fatigue cracks due to heavy traffic loads and environmental exposure [4,5,6,7]. Accumulated cracks progressively reduce load-bearing capacity and may ultimately cause complete bridge failure [8,9]. Consequently, stringent inspection regulations have been established globally. For instance, Chinese and U.S. standards implement graded maintenance strategies based on crack width specifications [10,11], mandating quarterly inspections for concrete bridges and immediate repairs for cracks exceeding 3 mm.

Conventional damage quantification requires advanced non-destructive evaluation techniques to assess structural deterioration. Accurate crack measurement is essential for determining bridge damage status and functional conditions [12]. Studies have proposed innovative methodologies: Shannon entropy integrated with statistical indices and fuzzy logic classifiers for cable-loss detection in cable-stayed bridges [13]; comparative analyses of damage detection algorithms (e.g., six fractal dimensions (FDs), homogeneity index (HI), and Shannon entropy index (SEI)), demonstrating HI and SEI’s superior capability in detecting, localizing, and severity-classifying damage scenarios [14]; and partial-model-based approaches employing stiffness separation techniques for parameter estimation in long-span steel truss bridges [15,16]. Additionally, empirical mode decomposition and Hilbert–Huang Transform enable damage identification by extracting stiffness-change-induced impulse peaks from measurement data [17].

Compared to traditional manual inspections, unmanned aerial vehicle (UAV) damage detection offers significant advantages in operational efficiency, labor reduction, and comprehensive data documentation [18,19,20]. UAVs equipped with cameras access hard-to-reach areas for surface imaging. However, manual review of large-scale image datasets (e.g., SDNET2018 containing 56,000 bridge images [21]) is error-prone. Image processing technologies thus enhance inspection accuracy and efficiency. For instance, the six-rotor UAV “Ptarmigan” was utilized for bridge inspections using image-based 3D modeling techniques [22].

Cracks—the most prevalent damage in concrete bridges—manifest as threshold variations in RGB images. Edge-detector-based algorithms (e.g., Roberts operator, Fourier transform, Sobel filter, Canny filter, Laplacian of Gaussian, and Gaussian filter [23,24,25,26]) identify cracks via threshold segmentation and gradient computation. Despite over two decades of application, these methods remain widely adopted for spatial/frequency-domain pixel gradient analysis. Unlike machine learning approaches [27,28,29,30,31,32], edge detection eliminates complex data labeling and model training, offering notable time-efficiency advantages. Studies comparing six-filter edge detection with deep convolutional neural networks [33] and similar cross-method evaluations across diverse image datasets [34,35,36] further validate this paradigm.

Recent advances in UAV-based crack identification include: real-bridge crack width quantification [37] and detection of 116 concrete cracks using 647 aerial images (GSD: 0.21 cm/pixel) [38]. Nevertheless, existing research predominantly focuses on detection outcomes, with limited analysis of crack geometric characteristics. Background interference-induced false identifications also persist, undermining detection model accuracy.

This paper proposes an enhanced crack detection method that integrates Laplacian of Gaussian (LoG) filtering with Otsu thresholding to suppress noise and improve segmentation accuracy. The approach enables extraction of critical crack characteristics (e.g., area, length) for damage assessment. Experimental results demonstrate markedly improved detection accuracy compared to conventional solutions, providing reliable technical support for automated structural health monitoring and data-driven maintenance decisions.

2. Methodology

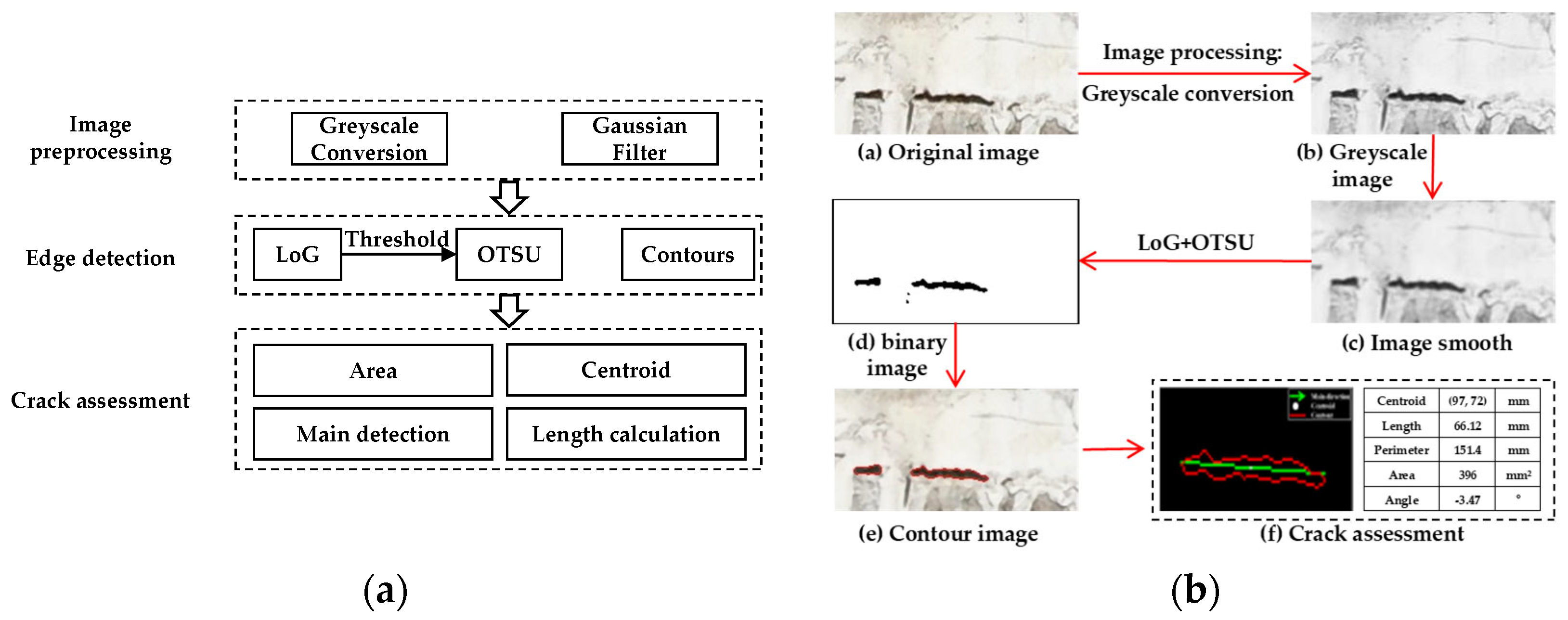
2.1. Workflow

Figure 1 illustrates the proposed bridge crack detection workflow. First, grayscale conversion preprocessing is performed on the original images in the dataset to obtain grayscale images, followed by median filtering. Then, according to the improved threshold gradient (Otsu + LoG) proposed in this paper, edges in the image are detected to obtain a binary image. After that, all straight lines in the background and edges are filtered to divide the image into two groups: cracked areas and non-cracked areas, which is the contour image in Figure 1b. Finally, all detected cracks are analyzed to obtain information such as their area, centroid, main direction, perimeter, and length.

2.2. Image Preprocessing

The purpose of this process is mainly to reduce the negative effects of noise to prevent false detection and enhance positive effects of following edge detection. The first step is to convert the RGB image to the grayscale image, for a better performance in following edge detection according to previous research [33,39,40,41]. Typical electronic imagery is recorded as digital values from minimum (0) to maximum (255) levels by three basic RGB colors. The conversion of the RGB image to grayscale image can be formulated as:

$$I\left(x,y\right)=0.2989R\left(x,y\right)+0.5870G\left(x,y\right)+0.1104B(x,y)$$

(1)

where I(x, y) is the pixel value in the grayscale image at the (x, y) coordinate and R(x, y), G(x, y), B(x, y) are the corresponding pixel values of red, green, blue channels in the RGB image, respectively.

Since concrete surfaces are inherently rough and noisy, even in undamaged areas, a nonlinear median filter is applied to the image to reduce “salt and pepper” noise and smooth the surface.

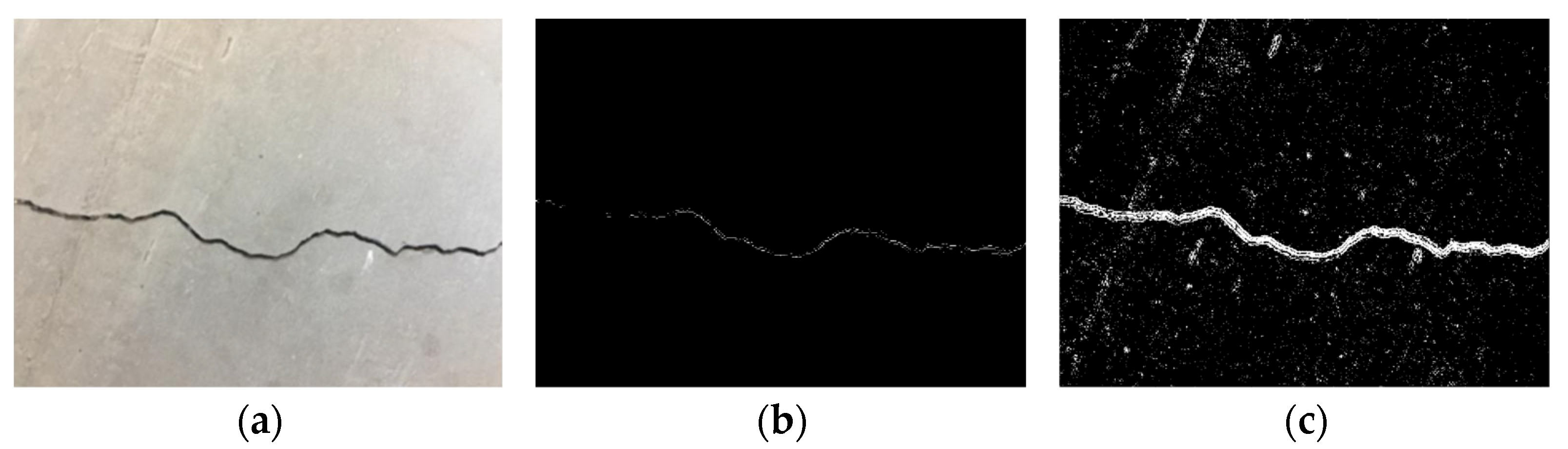
2.3. Laplacian of Gaussian (LoG)

There are many image-processing algorithms that detect damage in images using different edge filters, which are applied as a kernel (a small matrix of values) through a mathematical operation known as convolution [42]. We compared different edge detection filters using a dataset containing 100 concrete crack images. The results demonstrate that the LoG operator achieves the lowest noise ratio, the highest damage recall rate, and superior edge continuity compared to other methods. The procedure consists of two steps, combining Gaussian smoothing and Laplacian operator. Thus, it achieves both high precision and low noise, the process for which is detailed as follows. First, the noise is reduced by a two-dimensional Gaussian smoothing filter, which is described as follows:

$$\mathrm{G}\left(\mathrm{x},\mathrm{y}\right)={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{x^2+y^2}{2{\sigma }^2}})$$

(2)

where x and y are the spatial coordinates in image I(x, y), $\sigma$ is the distribution parameter kernel. Then, the Laplacian operator considers both edges and noise in the image, using the second order differential operator:

$${\nabla }^2={\displaystyle \frac{{\partial }^{2}I}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}I}{{\partial y}^2}}$$

(3)

At last, LoG filter was formulated as:

$$\mathrm{L}\mathrm{o}\mathrm{G}={\nabla }^2\left[(\right.\mathrm{G}\left(\mathrm{x},\mathrm{y}\right)\left.)\right]={\displaystyle \frac{{\partial }^{2}G(x,y)}{x^2}}+{\displaystyle \frac{{\partial }^{2}G\left(x,y\right)}{y^2}}={\displaystyle \frac{x^2+y^2-2{\sigma }^2}{4{\sigma }^4}}\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{x^2+y^2}{2{\sigma }^2}})$$

(4)

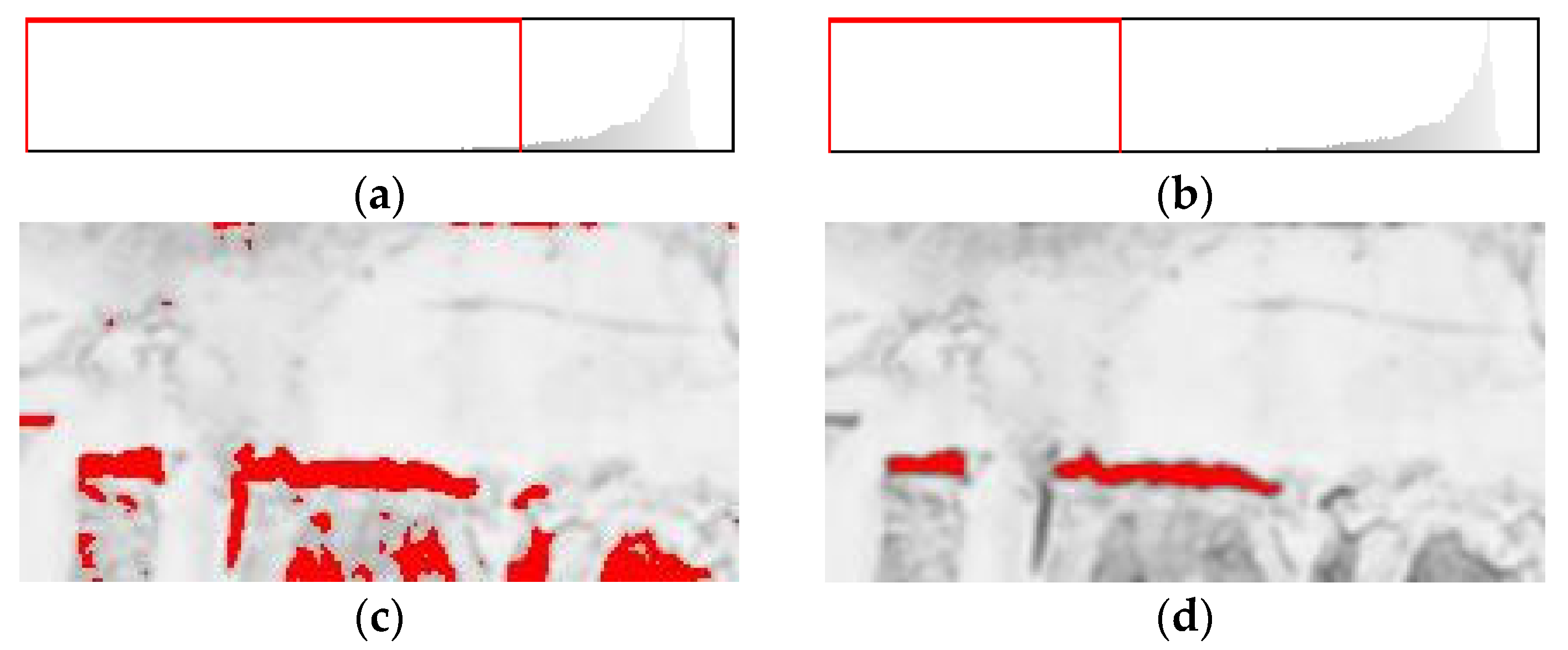
2.4. Crack Contour Detection

According to the threshold setting, all process image pixels were classified into two types in Equation (5):

• If a candidate pixel’s value (P_v) is less than the threshold value, the pixel was identified as undamaged area and the pixel value in I(x, y) was set to 0.
• On the contrary, if a candidate pixel’s value (P_v) is equal or greater than the threshold value, the pixel was identified as damaged area and the pixel value in I(x, y) was set to 1.

$$I\left(x,y\right)=\left\{\begin{array}{c}0, P_v\left(x,y\right)<T\\ 1, P_v\left(x,y\right)\ge T\end{array}\right.$$

(5)

After this step, the RGB format image was converted to binary image, as shown in Figure 2. This threshold is crucial to the damage detection result, because high thresholds indicate missing damages and low thresholds indicate noise undamaged areas.

The Otsu method is a common method: the basic principle is to calculate a threshold to divide all pixels in an image into two parts, image pixels and the background. The optimal threshold calculation is performed by maximizing the between-class variance in image pixels. The image contains many grey levels: average lower grey value than assumed threshold is m₁ and average greater grey value than assumed threshold is m₂.

$${\sigma }^2={p_1(m_1-M)}^2+{p_2(m_2-M)}^2$$

(6)

where M is average grey value of global pixel, $M=p_1{m}_1+p_2{m}_2$, $m_1={\displaystyle \frac{1}{p_1}}{\sum }_{i=0}^k{p}_{i}i$, $m_2={\displaystyle \frac{1}{p_2}}{\sum }_{i=k+1}^l{p}_{i}i$, where $p_1={\sum }_{i=0}^k{p}_i$, $p_2={\sum }_{i=k+1}^l{p}_i$, i is the grey value.

Thus, the threshold that maximizes ${\sigma }^2$ is calculated as the final segmentation threshold. In the case of concrete damage detection, there exists the obvious shortcoming that damage only occupies a small number of pixels, which leads to a relatively large threshold and a large amount of noise. It should be noted that if the segmentation threshold is further reduced below a certain critical value, the number of false positive pixels increases. Although there are noise filters in subsequent steps, false positives need to be avoided. In our improved method, the segmentation threshold was calculated after the LoG filter and their comparison was shown in Figure 3. The preprocessing step of LoG makes sense and decreases these errors in crack detection.

2.5. Crack Feature Calculation

2.5.1. Area Calculation

Following image processing, another assignment is to calculate the size of these cracks. The areas of all detected cracks are calculated by:

$$A_d={\mathrm{G}\mathrm{S}\mathrm{D}}^2\ast A_p$$

(7)

where A_d is area of this damage (mm²), A_p is amount of pixels, $A_p=\sum _{i=1}^{row}(C_{max}-C_{min})$, and GSD is ground sample distance (mm) depended on flight height H and focal length f:

$$GSD={\displaystyle \frac{H}{f}}\ast {\mathrm{C}}_{\mathrm{s}}$$

(8)

in which Cs represents camera sensor size, an inherent attribute of image camera.

Although filter algorithms are applied, the uneven distribution in concrete surfaces may cause small noise area and decrease detection accuracy. To remove these small contours on the binary image, the number of pixels in every area is calculated and the areas less than 50 pixels were eliminated.

2.5.2. Centroid Location

Crack position in the concrete structure is crucial for the following maintenance. The centroid of detected cracks is calculated by moments, an inherent attribute dependent on graphic shape. Spatial moments of graphs are basic concept in probability and statistics, and the calculation rule is

$$M_{ij}={\sum }_{xy}(P\left(x,y\right)·x^i{y}^j)$$

(9)

In which x and y are pixel position, P(x, y) is pixel value in the position of (x, y), i and j are coefficient of spatial moment. According to zero-order and first-order spatial moment of graphs, the coordinate (cx, cy) calculation formula of the graph centroid is

$$cx={\displaystyle \frac{M_{10}}{M_{00}}}, cy={\displaystyle \frac{M_{01}}{M_{00}}}$$

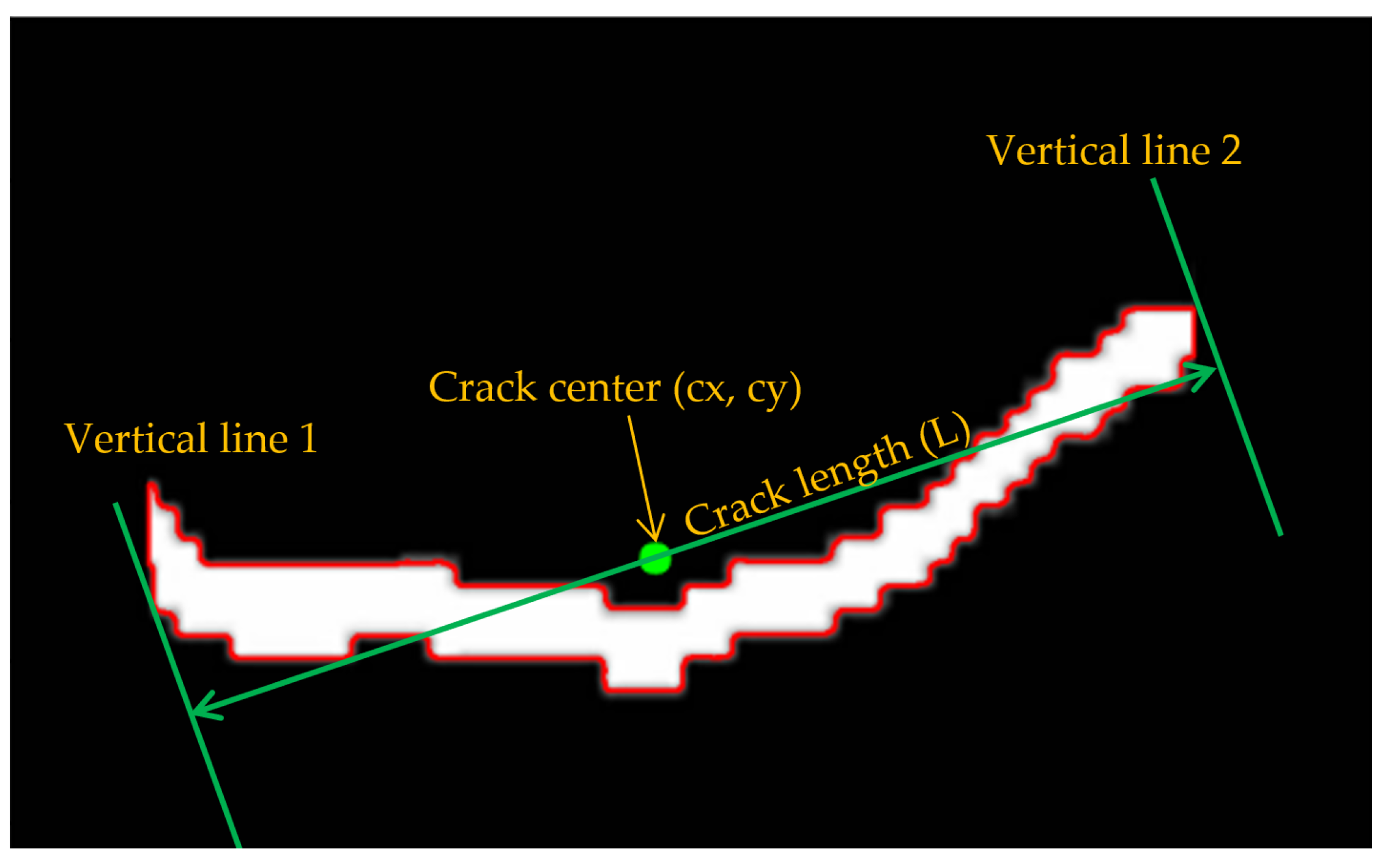
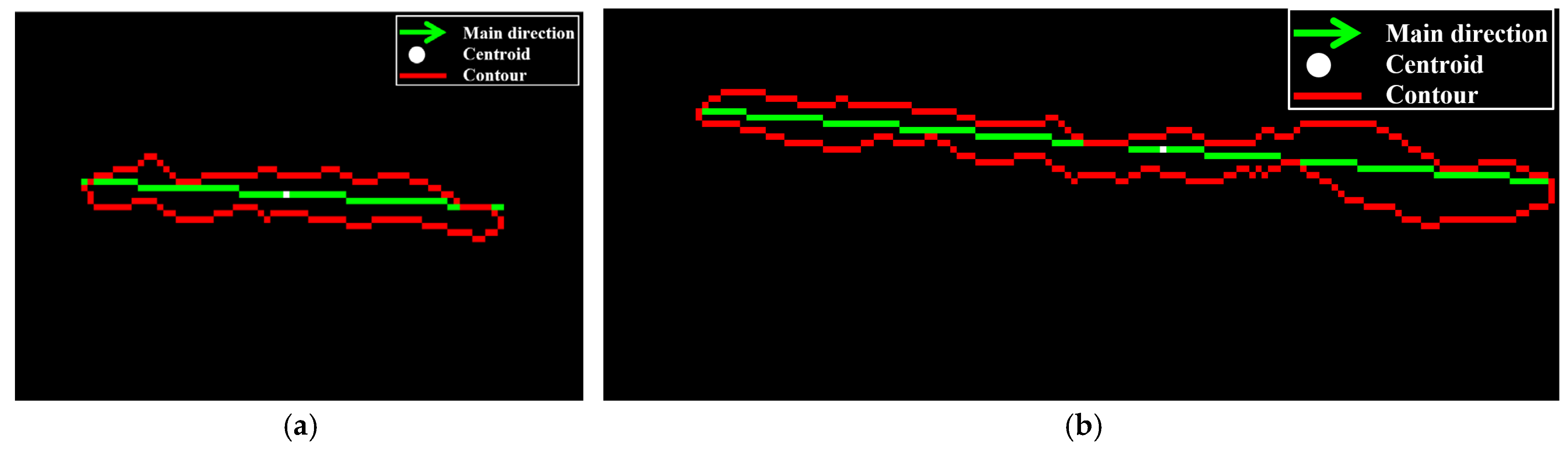
2.5.3. Main Direction

The main direction is the possible extension direction of the crack, and detailed calculation of the main direction angle can be formulated as

$$\theta =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{2b}{a-c}}\right)$$

(10)

In the formulation, $a={\displaystyle \frac{M_{20}}{M_{00}}}-{cx}^2$, $b={\displaystyle \frac{M_{10}}{M_{00}}}-cx·cy$, $c={\displaystyle \frac{M_{02}}{M_{00}}}-{cy}^2$.

2.5.4. Length Calculation

Regarding the damage length calculation, we use distance between two vertical lines in crack direction. According to the crack center (cx, cy) and the main direction calculated below, a line of constant slope and its vertical lines were displayed in the edge of the graph, as shown in Figure 4. The distance between two vertical lines is marked as crack length.

The line pass crack center can be formulated as

$$y-cy=tan\theta ·(x-cx)$$

(11)

The intersection point with two vertical lines are denoted as (cx₁, cy₁) and (cx₂, cy₂), the distance between two points is calculated as crack length.

3. Results

3.1. Experimental Environment

The experiment was conducted on Gushanhe Bridge, which is located in Yitong County, Siping City, China. This bridge is 54 m in length, 7 m in width, and stands 6 m above the river, as depicted in Figure 5. The concrete structure of this bridge’s side surface was taken as test target in this experimental validation for the following reasons:

• Logistics: A village is located nearby, and it was easy to transport and recharge equipment;
• Security considerations: Travel was conducted discreetly, and the number of operators was minimized. This research did not attract a crowd, which would have been unsafe. Also, drones often attract audiences who want to talk and ask questions, thereby distracting the operators;
• Legal issues: The bridge is in open country distant from airports and no-fly zones.

The DJI Air 3 UAV was utilized in this study, featuring a total weight of 720 g and capable of achieving a maximum vertical acceleration of 10 m/s². With a maximum horizontal flight speed of 21 m/s and an extended hover endurance of 46 min, the system demonstrated precise positioning capabilities including vertical accuracy < 0.1 m and horizontal accuracy < 0.3 m. Equipped with dual imaging sensors (wide-angle and medium telephoto cameras), this configuration provided comprehensive visual coverage for structural inspection tasks.

3.2. Damage Detection

The algorithm was validated using all cracks detected on the side surfaces of the study bridge. Damage detection results in whole workflow were clarified by three example photos in Figure 6. Five phases of damage detection results were shown: (1) origin images—original bridge side surface images shot by UAV, (2) grayscale images—grayscale conversion for a better performance in following steps, (3) smooth images—eliminate noises in concrete surface, (4) threshold images—threshold segmentation results by improved Otsu, (5) contour images—damage contour detection after small area filtering.

3.3. Damage Assessment

All detected damage was applied for analyzing crack characteristics and the obtained results are compared with validation measurements. A caliper was used to measure crack attributes. The geometric characteristics of Crack A and Crack B were analyzed, as shown in Figure 7 and

Table 1. Geometric characteristics of cracks.

Crack	Number of Cracks	Centroid (mm)	Length (mm)	Perimeter (mm)	Area (mm2)	Angle (°)
Crack A	1	(97, 72)	66.12	151.4	396	−3.47
Crack B	1	(89, 73)	133.45	305.14	910	−4.73

.

3.4. Comparative Analysis of Different Detectors for Crack Detection

To demonstrate the superiority of the proposed method, a comparative analysis was conducted comparing the Otsu + LoG algorithm with three edge detectors—Roberts [43], Laplacian of Gaussian [25], and Sobel [43]—using the same set of concrete bridge images. First, a dataset comprising 115 crack-containing images and 312 crack-free images was constructed. Then, the four detection methods were evaluated based on the following metrics:

• True Positive (TP): The edge detector correctly identifies cracks in images containing cracks.
• True Negative (TN): The edge detector correctly detects no cracks in crack-free images.
• False Negative (FN): The edge detector fails to detect cracks in images that actually contain cracks.
• False Positive (FP): The edge detector incorrectly detects cracks in crack-free images.

Subsequently, each crack detection method was evaluated based on the following metrics: True Positive Rate (TPR), True Negative Rate (TNR), Accuracy (ACC), Positive Predictive Value (PPV), and Negative Predictive Value (NPV), which are defined as follows:

$$TPR=\left({\displaystyle \frac{TP}{TP+FN}}\right)$$

(12)

$$TNR=\left({\displaystyle \frac{TN}{TN+FP}}\right)$$

(13)

$$ACC=\left({\displaystyle \frac{TP+TN}{TP+FN+TN+FP}}\right)$$

(14)

$$PPV=\left({\displaystyle \frac{TP}{TP+FP}}\right)$$

(15)

$$NPV=\left({\displaystyle \frac{TN}{TN+FN}}\right)$$

(16)

The four detection methods were tested on the constructed dataset, with the statistical results of different evaluation metrics for each method presented in

Table 2. Statistical results of crack detection by different methods.

Detector	TPR	TNR	ACC	PPV	NPV
Roberts	0.45	0.96	0.82	0.79	0.83
Sobel	0.69	0.97	0.89	0.89	0.89
LoG	0.78	0.97	0.92	0.91	0.92
Otsu + LoG	0.93	0.98	0.96	0.94	0.97

.

As shown in Table 2, the proposed Otsu + LoG method achieves the highest TPR of 93%, followed by the LoG method. Meanwhile, the Otsu + LoG approach also demonstrates the best PPV performance. The quantitative results in Table 2 confirm the superiority of the proposed method.

4. Discussion

Comprehensive and precise Ground Control Points (GCPs) are crucial for achieving reliable and accurate results. The implementation of quadratic and binary quadratic equations for pixel coordinate geometric calibration has yielded significant error reductions. Figure 8 shows the precise extraction of GCPs.

Comparative image analyses show that the improved Otsu-based images exhibit orthophotograph-like characteristics, a conclusion further corroborated by Euler angle matrix observations. The successful implementation of hover mode during image acquisition significantly enhanced system stability, effectively mitigating adverse effects caused by lens jitter. This confirms that our UAV and camera system maintained stable operation throughout the entire testing process.

5. Conclusions

In this study, we developed an enhanced image processing method for concrete bridge crack detection that overcomes the limitations of conventional visual inspection techniques. By integrating UAV remote sensing with advanced image processing algorithms, the proposed approach significantly improves crack detection accuracy. The method enhances traditional Otsu thresholding through incorporation of the Laplacian of Gaussian (LoG) operator, enabling more effective differentiation between actual cracks and background noise.

Experimental validation using real-world bridge images demonstrates the method’s capability to accurately identify and quantify cracks through four key geometric parameters: centroid coordinates, crack length, surface area, and principal orientation. These quantitative metrics enable comprehensive damage characterization, thereby facilitating precise severity assessment and optimized maintenance scheduling.

The developed technique exhibits three notable advantages: (1) substantial reduction in false positive detections, (2) improved computational efficiency for field applications, and (3) reliable automated assessment of crack morphology. These advancements establish the method as a practical solution for structural health monitoring of concrete bridges.

The findings demonstrate that this integrated UAV image processing approach can potentially transform current bridge inspection paradigms, offering a cost-effective, accurate, and scalable alternative to manual inspection methods. Future research will leverage the crack features detected and extracted in this study to assess crack severity and its impact on bridge integrity. Concurrently, we will develop weather-resilient UAV-based inspection methods for complex meteorological conditions and extend applications to broader infrastructure systems (e.g., steel trusses and pavements).