Adaptive Warning Thresholds for Dam Safety: A KDE-Based Approach †
Abstract
1. Introduction
2. Materials and Methods
2.1. Conventional Approach
2.2. Proposed Approach
- The monitoring data are split into a training set and a test set.
- A boosted regression tree (BRT) predictive model is fitted for each output variable considered.
- The relative importance of the BRT model inputs is computed, and the most influential input related to each of the main loads is selected (reservoir level and air temperature).
- The KDE of the training data set is computed on the plane defined by the inputs selected in Step 2, considering the relative importance of each of the main loads on each output variable.
- The adaptive WT is computed for each load combination and output based on the density value of the associated loads.
- The resulting warning thresholds are compared against the values of the response variables in the test set.
- Figure 1 includes a flowchart of the methodology.
2.3. Data
2.4. Model Development
2.5. Feature Importance Analysis
2.6. KDE Area Calculation
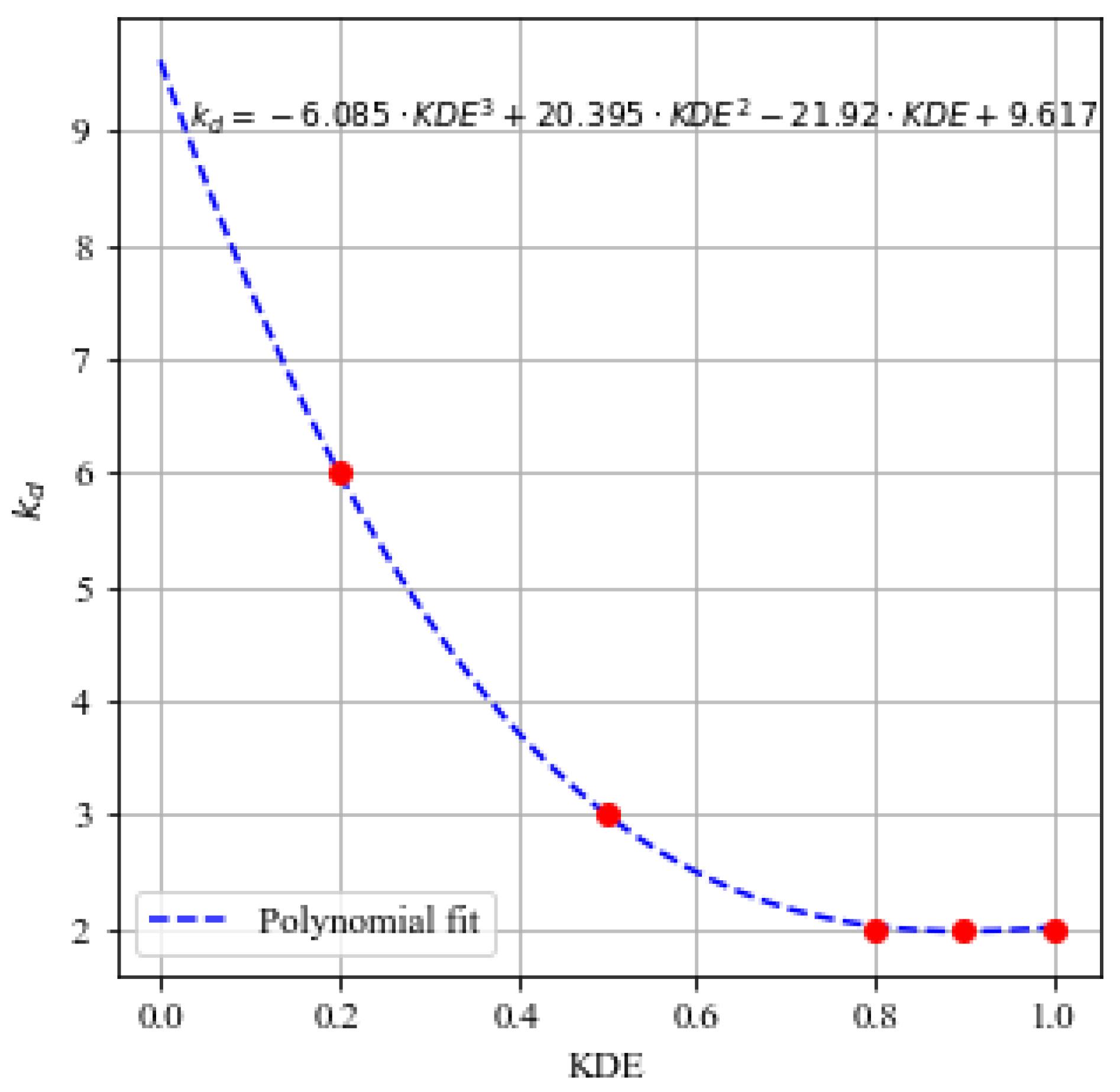
2.7. Density Factor and Adaptive Warning Threshold
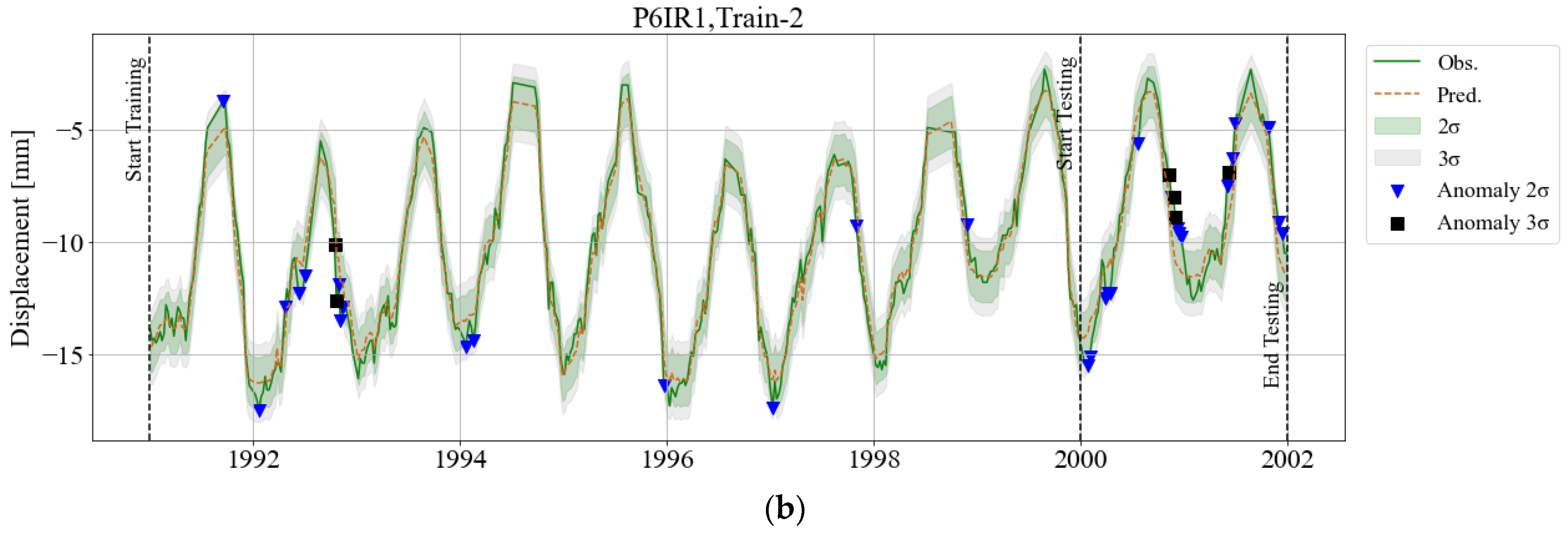
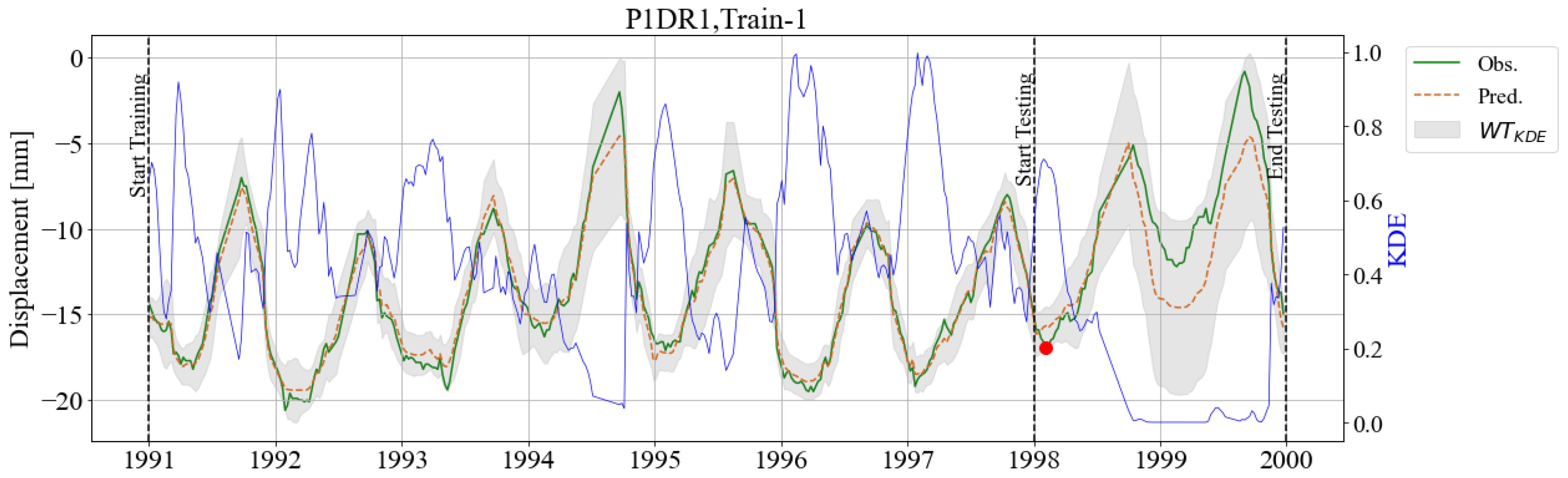
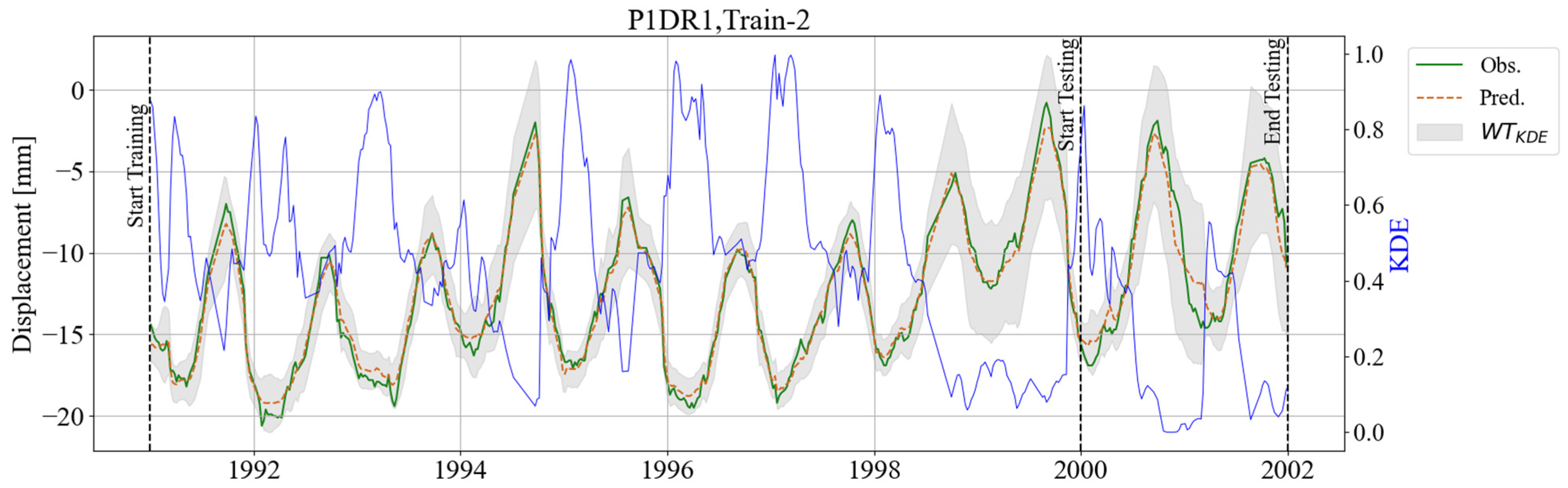
3. Results
3.1. BRT Model and Feature Importance
3.2. KDE Area
3.3. Adaptive Warning Threshold (WTKDE)
4. Discussion and Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
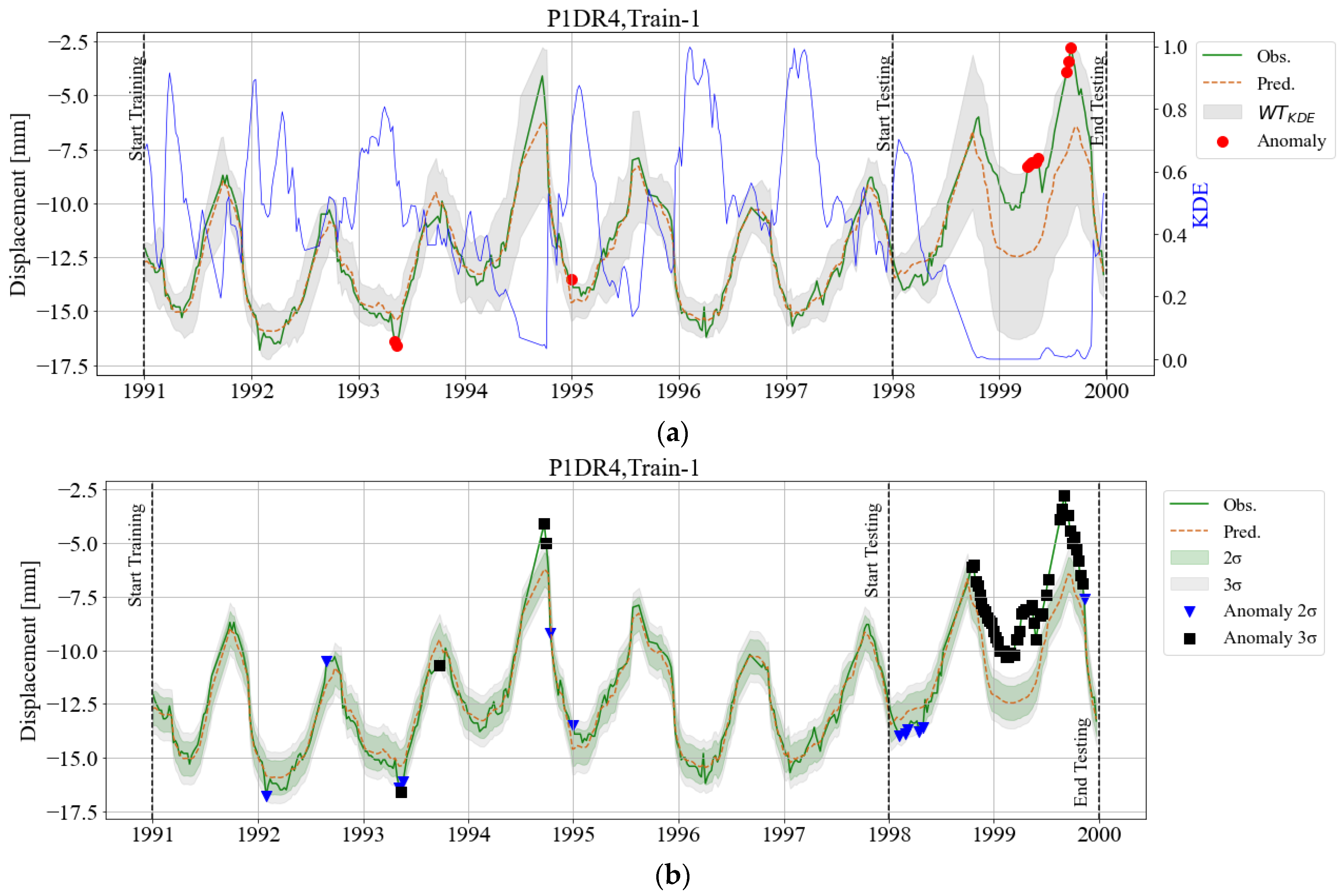
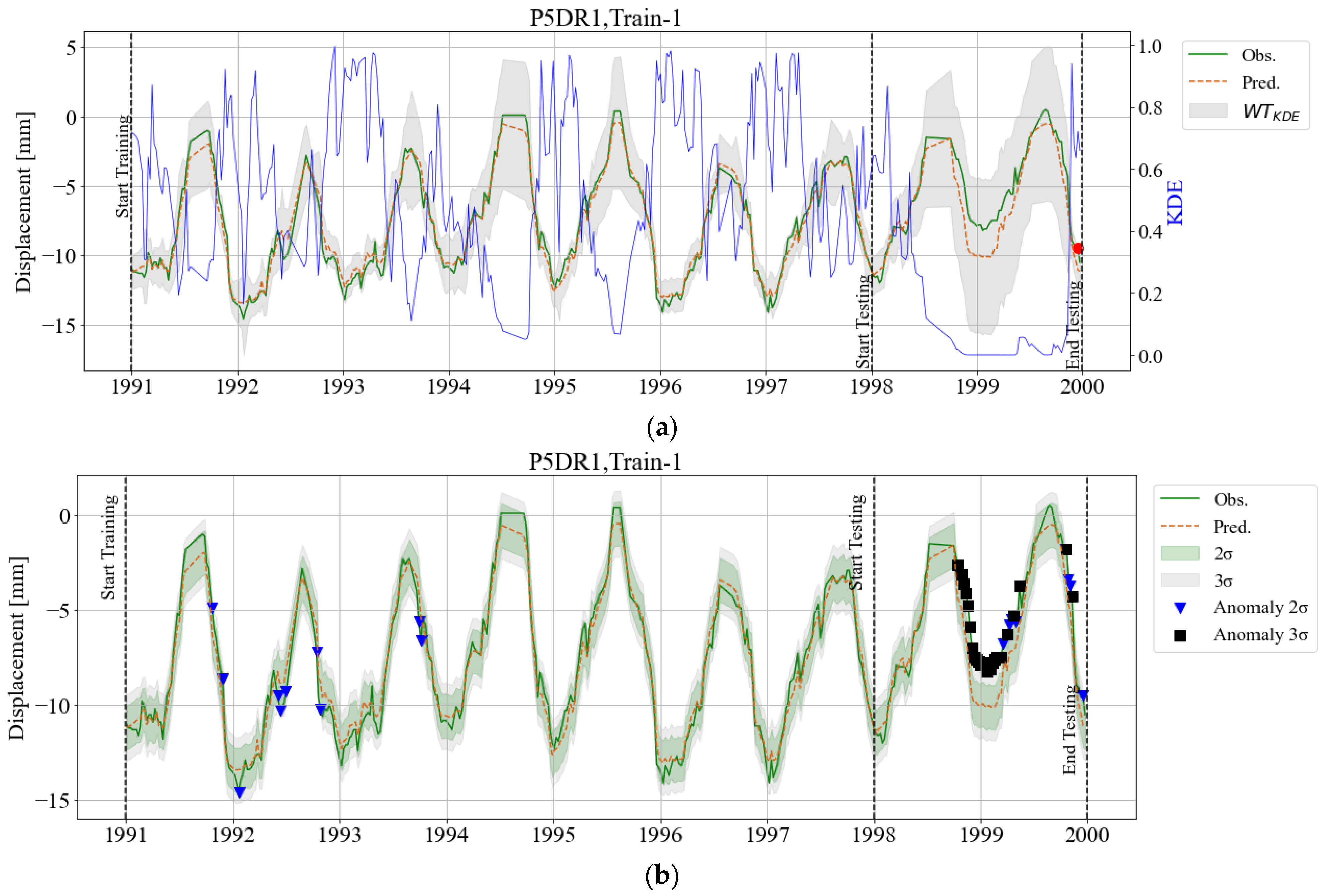

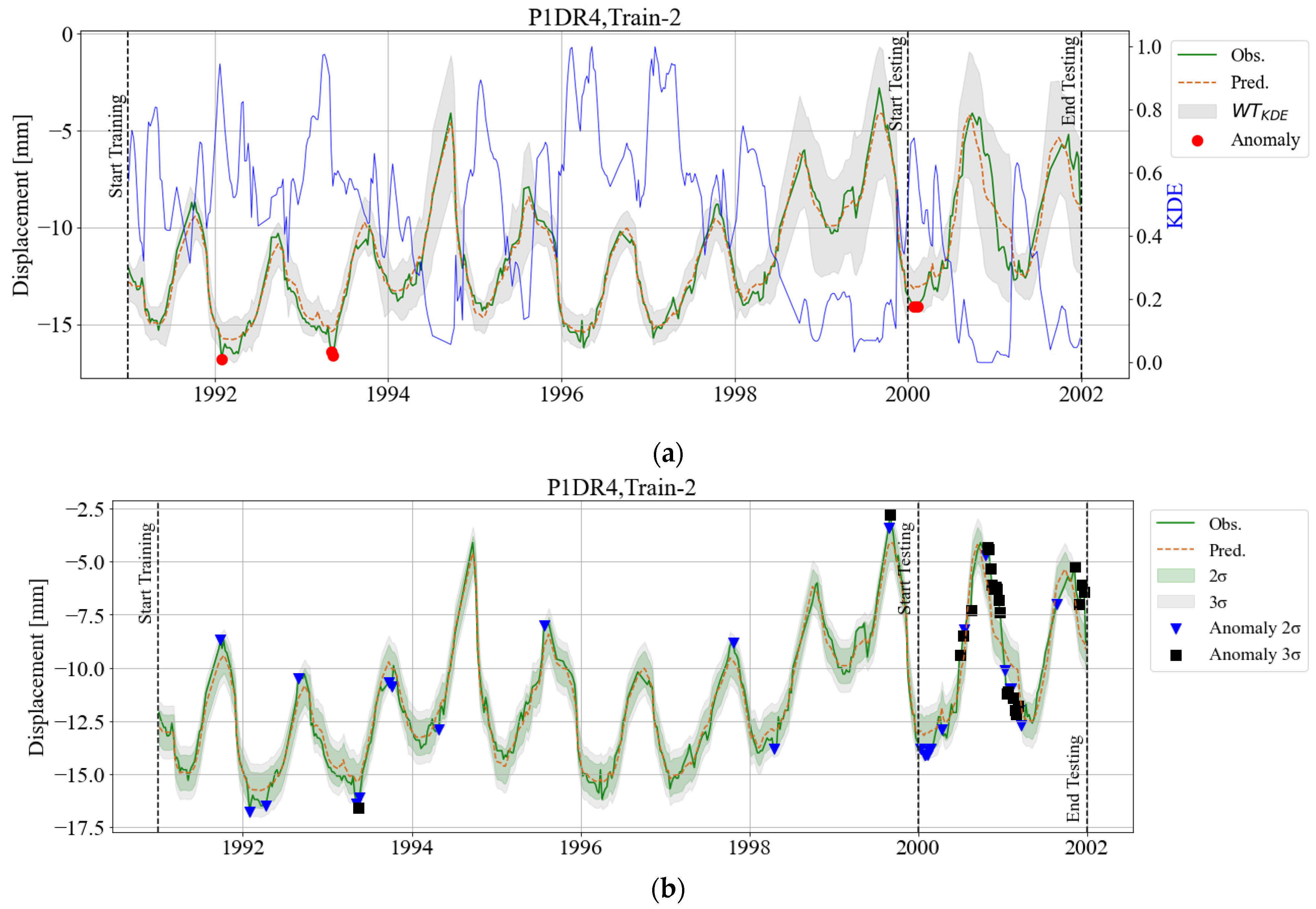

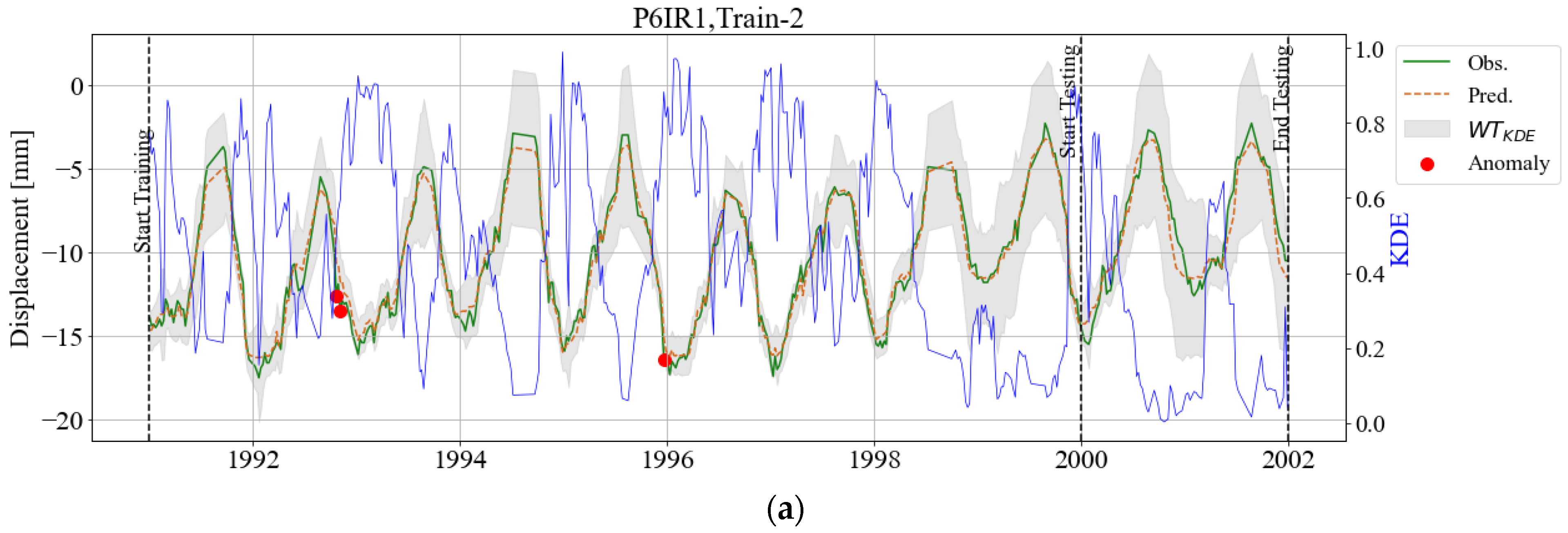
References
- Perera, D.; Smakhtin, V.; Williams, S.; North, T.; Curry, R. Ageing Water Storage Infrastructure: An Emerging Global Risk; UNU-INWEH Report Series; Issue 11; United Nations University Institute for Water, Environment and Health: Hamilton, ON, Canada, 2021. [Google Scholar] [CrossRef]
- ICOLD Incident Database Bulletin 99 Update: Statistical Analysis of Dam Failures; International Commission on Large Dams (ICOLD): Paris, France, 2019.
- Swiss Committee on Dams. Methods of analysis for the prediction and the verification of dam behaviour. In Proceedings of the 21st Congress of the International Comission on Large Dams, Montreal, QC, Canada, 16–20 June 2003. [Google Scholar]
- Cheng, L.; Zheng, D.L. Two online dam safety monitoring models based on the process of extracting environmental effect. Adv. Eng. Softw. 2013, 57, 48–56. [Google Scholar] [CrossRef]
- Li, B.; Yang, J.; Hu, D.J. Dam monitoring data analysis methods: A literature review. Struct. Control Health Monit. 2019, 27, e2501. [Google Scholar] [CrossRef]
- Pereira, S.; Magalhães, F.; Gomes, J.P.; Cunha, Á.; Lemos, J.V. Dynamic monitoring of a concrete arch dam during the first filling of the reservoir. Eng. Struct. 2018, 174, 548–560. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Gu, M. Optimal sensor placement for structural health monitoring based on multiple optimization strategies. Struct. Des. Tall Spéc. Build. 2011, 20, 881–900. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Zhang, X.-D. Sensor placement on Canton Tower for health monitoring using asynchronous-climb monkey algorithm. Smart Mater. Struct. 2012, 21, 125023. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch Comput. Methods 2017, 24, 1–21. [Google Scholar] [CrossRef]
- Salazar, F. A Machine Learning Based Methodology for Anomaly Detection in Dam Behaviour. Ph.D. Thesis, Universitat Politècnica de Catalunya, Les Corts, Barcelona, 2017. [Google Scholar]
- Willm, G.; Beaujoint, N. Les méthodes de surveillance des barrages au service de la production hydraulique d’Electricité de France-Problèmes ancients et solutions nouvelles. In Proceedings of the 9th ICOLD Congres, Istanbul, Türkiye, 4–8 September 1967; pp. 529–550. [Google Scholar]
- Salazar, F.; Conde, A.; Irazábal, J.; Vicente, D.J. Anomaly Detection in Dam Behaviour with Machine Learning Classification Models. Water 2021, 13, 2387. [Google Scholar] [CrossRef]
- Su, H.; Chen, Z.; Wen, Z. Performance improvement method of support vector machine-based model monitoring dam safety. Struct. Control Health Monit. 2015, 23, 252–266. [Google Scholar] [CrossRef]
- Mata, J.; Salazar, F.; Barateiro, J.; Antunes, A. Validation of Machine Learning Models for Structural Dam Behaviour Interpretation and Prediction. Water 2021, 13, 2717. [Google Scholar] [CrossRef]
- Hellgren, R.; Malm, R.; Ansell, A. Performance of data-based models for early detection of damage in concrete dams. Struct. Infrastruct. Eng. 2021, 17, 275–289. [Google Scholar] [CrossRef]
- Lin, C.; Chen, S.; Hariri-Ardebili, M.A.; Li, T.; Del Grosso, A. An Explainable Probabilistic Model for Health Monitoring of Concrete Dam via Optimized Sparse Bayesian Learning and Sensitivity Analysis. Struct. Control Health Monit. 2023, 2023, 2979822. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Lu, X.; Wang, Y.; Zhang, H.; Zhang, P. An online anomaly recognition and early warning model for dam safety monitoring data. Struct. Health Monit. 2020, 19, 796–809. [Google Scholar] [CrossRef]
- Su, H.; Yan, X.; Liu, H.; Wen, Z. Integrated Multi-Level Control Value and Variation Trend Early-Warning Approach for Deformation Safety of Arch Dam. Water Resour. Manag. 2017, 31, 2025–2045. [Google Scholar] [CrossRef]
- Mata, J.; Tavares de Castro, A.; Sá da Costa, J.M.; Barateiro, J.; Miranda, P. Threshold Definition for Internal Early Warning Systems for Structural Safety Control of Dams. Application to a Large Concrete Dam, October 2012. In Proceedings of the First International Dam World Conference 2012, Maceió, Brazil, 8–11 October 2012. [Google Scholar]
- Mata, J.; Miranda, F.; Antunes, A.; Romão, X.; Santos, J. Characterization of Relative Movements between Blocks Observed in a Concrete Dam and Definition of Thresholds for Novelty Identification Based on Machine Learning Models. Water 2023, 15, 297. [Google Scholar] [CrossRef]
- Klun, M.; Salazar, F.; Simon, A.; Malm, R.; Hellgren, R. Behaviour Prediction of a Concrete Arch Dam: Description and Synthesis of Theme A. In Proceedings of the 16th International Benchmark Workshop on Numerical Analysis of Dams, Ljubljana, Slovenia, 5–6 April 2022. [Google Scholar]
- Salazar, F.; Toledo, M.A.; Oñate, E.; Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef]
- Salazar, F.; Irazábal, J.; Conde, A. SOLDIER: SOLution for Dam behavior Interpretation and safety Evaluation with boosted Regression trees. SoftwareX 2024, 25, 101598. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A guide for data scientists. O’Reilly Media: Sebastopol, CA, USA, 2017. [Google Scholar]
- Parzen, E. On Estimation of a Probability Density Function and Mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Chen, Y.-C. A tutorial on kernel density estimation and recent advances. Biostat. Epidemiol. 2017, 1, 161–187. [Google Scholar] [CrossRef]
- Xiong, L.; Liang, J.; Qian, J. Multivariate Statistical Process Monitoring of an Industrial Polypropylene Catalyzer Reactor with Component Analysis and Kernel Density Estimation. Chin. J. Chem. Eng. 2007, 15, 524–532. [Google Scholar] [CrossRef]
- Silva-Cancino, N.; Salazar, F.; Irazábal, J.; Mata, J. Adaptive warning thresholds in dam safety using kernel density estimation. In Proceedings of the Fifth International Dam World Conference, Lisbon, Portugal, 13–17 April 2025. [Google Scholar]









| External Variable | Derived Variable | Abbrev. |
|---|---|---|
| Time | Daily record | - |
| Reservoir Level | Daily mean | Level_001D |
| Moving average of 7 days | Level_007D | |
| Moving average of 14 days | Level_014D | |
| Moving average of 30 days | Level_030D | |
| Moving average of 60 days | Level_060D | |
| Moving average of 90 days | Level_090D | |
| Ambient Temperature | Daily mean | Tair_001D |
| Moving average of 7 days | Tair_007D | |
| Moving average of 14 days | Tair_014D | |
| Moving average of 30 days | Tair_030D | |
| Moving average of 60 days | Tair_060D | |
| Moving average of 90 days | Tair_090D | |
| Moving average of 120 days | Tair_120D | |
| Moving average of 150 days | Tair_150D | |
| Moving average of 180 days | Tair_180D |
| Density Value | kd |
|---|---|
| 0.2 | 6 |
| 0.5 | 3 |
| 0.8 | 2 |
| 0.9 | 2 |
| 1.0 | 2 |
| Pendulum | σϵ (mm) | σϵ (mm) | ||
|---|---|---|---|---|
| Train1 | Test1 | |||
| P1DR1 | Level_001D/Tair_090D | 0.25/0.74 | 0.529 | 1.753 |
| P1DR4 | Level_001D/Tair_090D | 0.30/0.68 | 0.400 | 1.601 |
| P5DR1 | Level_001D/Tair_060D | 0.15/0.83 | 0.579 | 1.024 |
| P6IR1 | Level_001D/Tair_030D | 0.12/0.87 | 0.519 | 1.058 |
| Train2 | Test2 | |||
| P1DR1 | Level_001D/Tair_090D | 0.43/0.56 | 0.554 | 1.258 |
| P1DR4 | Level_001D/Tair_120D | 0.60/0.38 | 0.415 | 1.111 |
| P5DR1 | Level_001D/Tair_060D | 0.23/0.75 | 0.602 | 0.950 |
| P6IR1 | Level_001D/Tair_030D | 0.18/0.81 | 0.572 | 0.936 |
| (294 Samples) | (81 Samples) | |||||
|---|---|---|---|---|---|---|
| Pendulum | 2σϵ (%) | 3σϵ (%) | WTKDE (%) | 2σϵ (%) | 3σϵ (%) | WTKDE (%) |
| P1DR1 | 2.7 | 0.7 | 0.0 | 64.2 | 59.3 | 1.2 |
| P1DR4 | 3.7 | 1.4 | 0.7 | 66.7 | 59.3 | 11.1 |
| P5DR1 | 3.7 | 0.0 | 0.0 | 43.2 | 33.3 | 1.2 |
| P6IR1 | 4.1 | 0.0 | 0.7 | 42.0 | 30.9 | 1.2 |
| (375 Samples) | (82 Samples) | |||||
| P1DR1 | 4.8 | 0.0 | 0.5 | 39.0 | 18.3 | 0.0 |
| P1DR4 | 4.0 | 0.5 | 0.8 | 43.9 | 26.8 | 1.2 |
| P5DR1 | 4.3 | 0.3 | 0.3 | 25.6 | 11.0 | 0.0 |
| P6IR1 | 4.0 | 0.8 | 0.8 | 24.4 | 6.1 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva-Cancino, N.; Salazar, F.; Irazábal, J.; Mata, J. Adaptive Warning Thresholds for Dam Safety: A KDE-Based Approach. Infrastructures 2025, 10, 158. https://doi.org/10.3390/infrastructures10070158
Silva-Cancino N, Salazar F, Irazábal J, Mata J. Adaptive Warning Thresholds for Dam Safety: A KDE-Based Approach. Infrastructures. 2025; 10(7):158. https://doi.org/10.3390/infrastructures10070158
Chicago/Turabian StyleSilva-Cancino, Nathalia, Fernando Salazar, Joaquín Irazábal, and Juan Mata. 2025. "Adaptive Warning Thresholds for Dam Safety: A KDE-Based Approach" Infrastructures 10, no. 7: 158. https://doi.org/10.3390/infrastructures10070158
APA StyleSilva-Cancino, N., Salazar, F., Irazábal, J., & Mata, J. (2025). Adaptive Warning Thresholds for Dam Safety: A KDE-Based Approach. Infrastructures, 10(7), 158. https://doi.org/10.3390/infrastructures10070158









