A Probabilistic Design Framework for Semi-Submerged Curtain Wall Breakwaters
Abstract
1. Introduction
2. Materials and Methods
2.1. Expressions for Calculating Wave Transmission Under Curtain Breakwaters
2.2. Uncertainty of Design Parameters
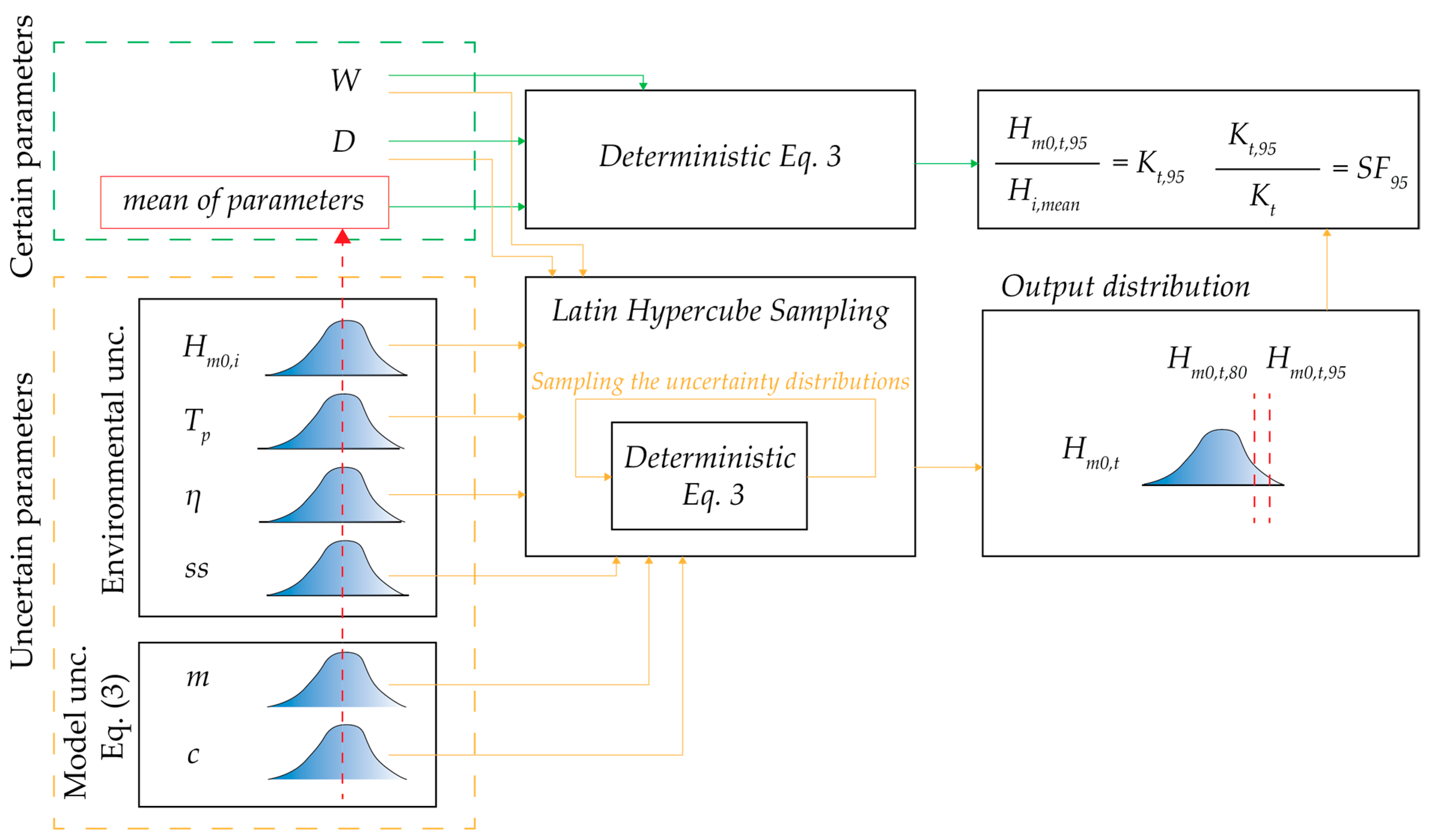
2.3. Uncertainty Quantification Method and Implementation
3. Results
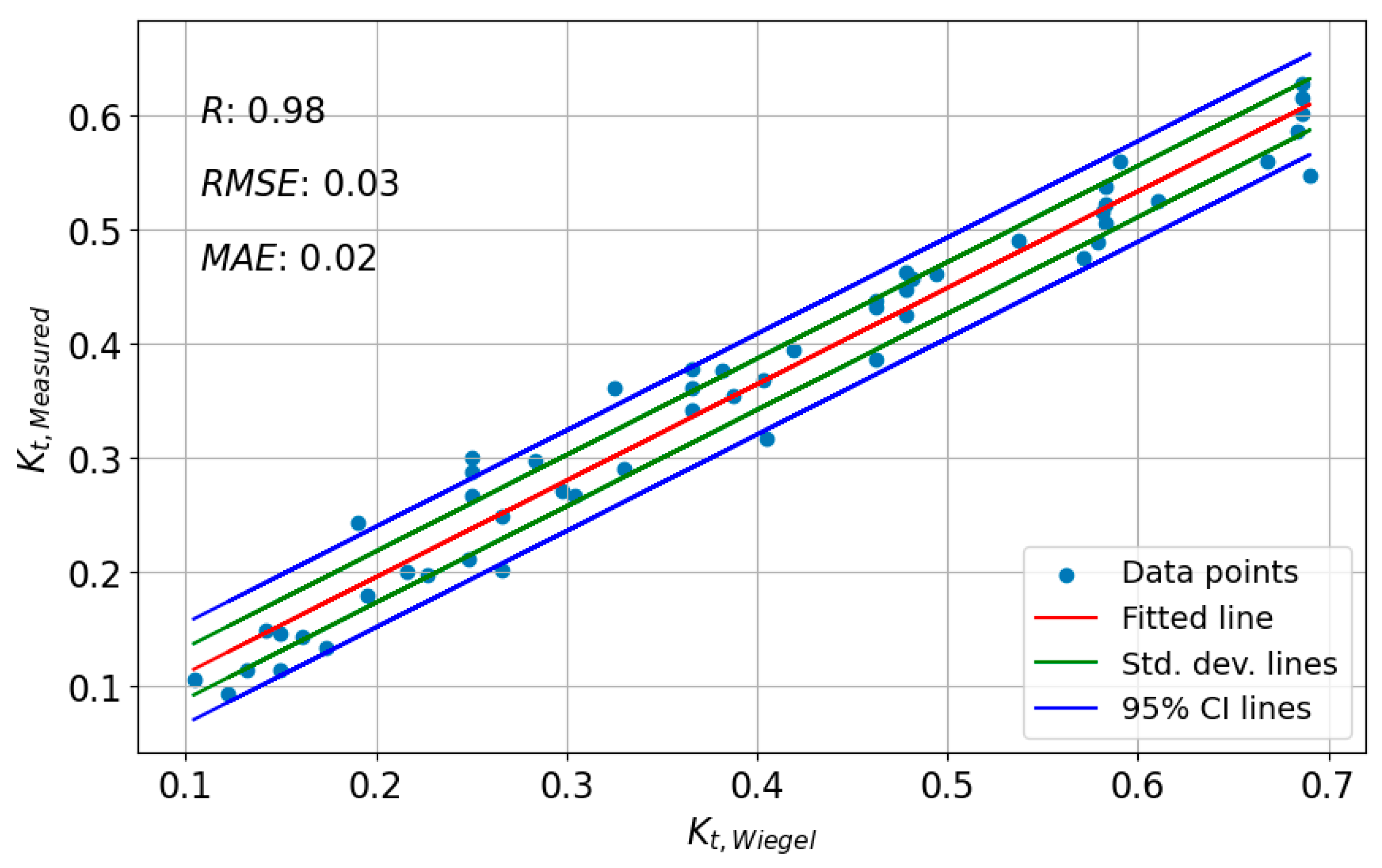
3.1. Applicability of Deterministic Equations for Irregular Waves
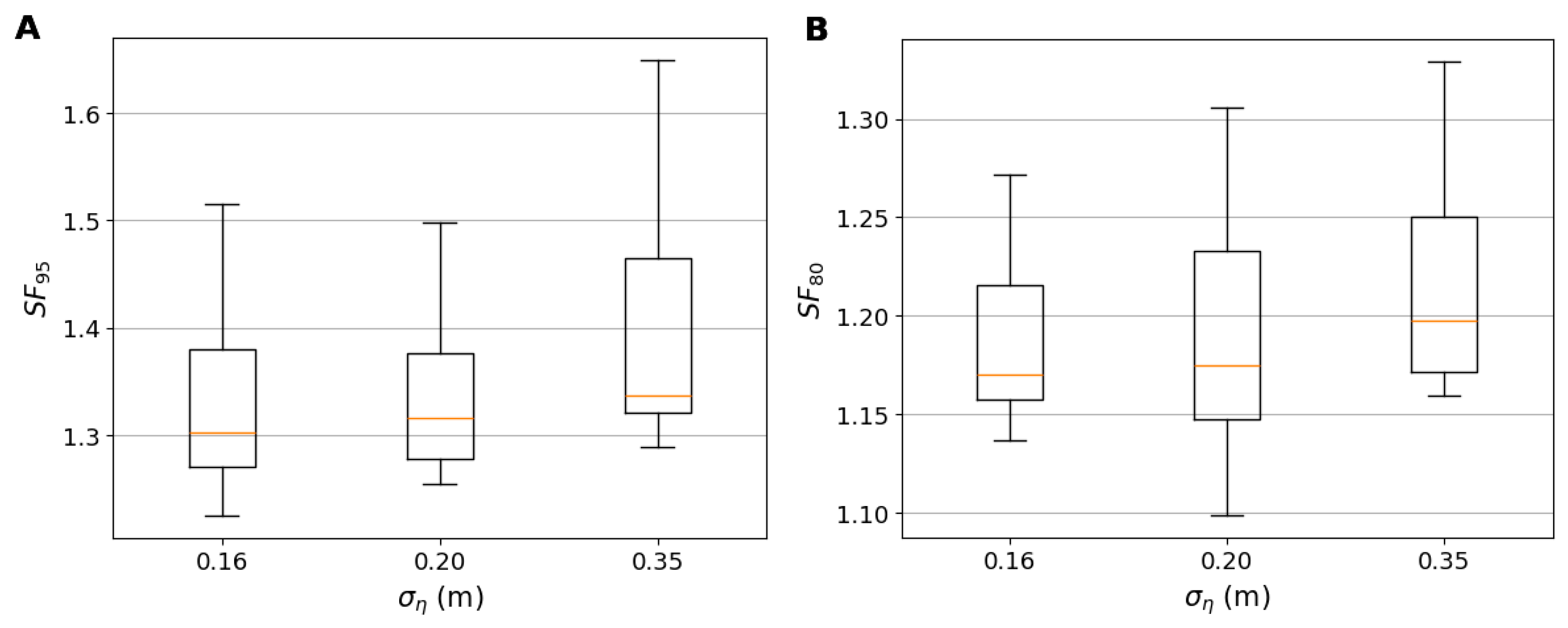
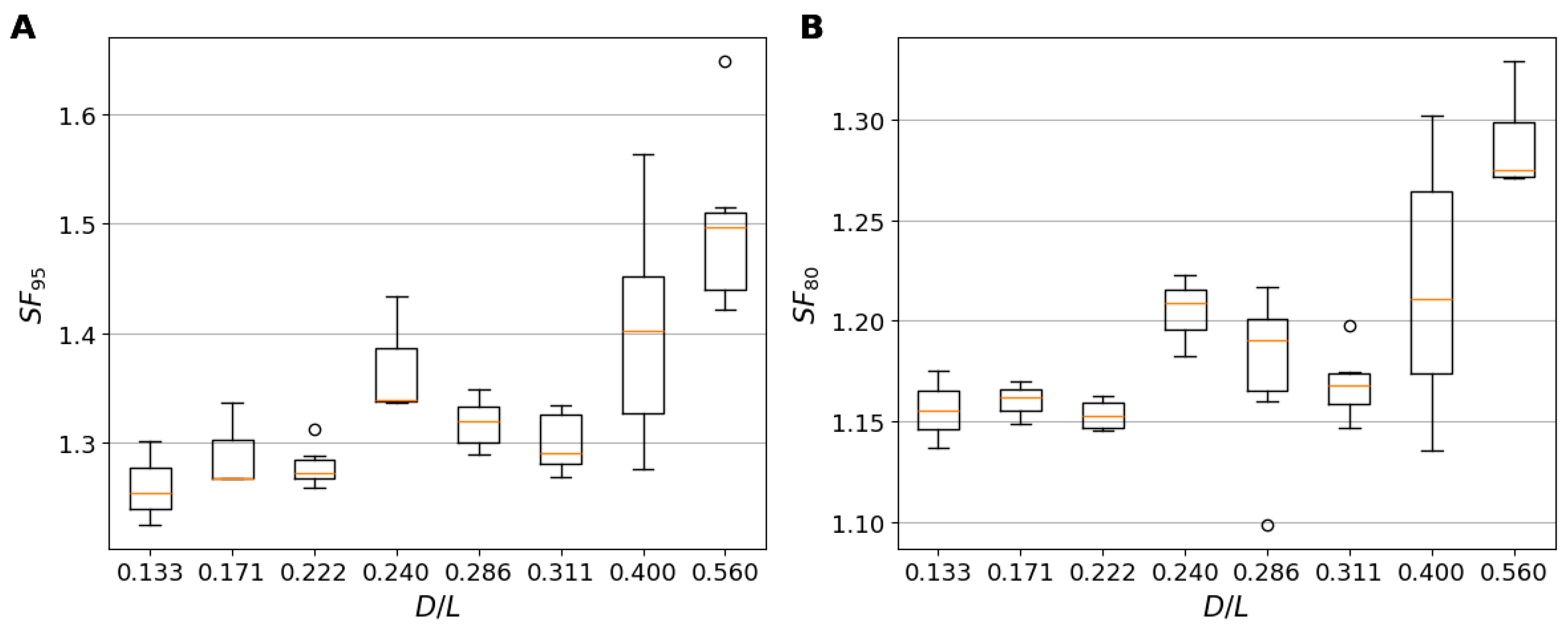
3.2. Uncertainty Analysis of Wave Energy Transmission
3.3. Safety Factor Equation for Submerged in Curtain Breakwaters
3.4. Parameter Uncertanty Relavence in the Uncertainty Quantification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoàng Thái Dương, V.; Zemann, M.; Oberle, P.; Seidel, F.; Nestmann, F. Investigating Wave Transmission through Curtain Wall Breakwaters under Variable Conditions. J. Coast. Hydraul. Struct. 2023, 2, 2022. [Google Scholar] [CrossRef]
- Subekti, S.; Shulhany, A. Transmission and reflection of waves on curtain wall breakwater. Tek. J. Sains Dan Teknol. 2021, 17, 100–105. [Google Scholar] [CrossRef]
- Carevic, D.; Bujak, D.; Potočki, K.; Drašković, J. Wave Transmission Below Breakwaters with Semi- Immersed Curtain. In Proceedings of the 16h International Symposium on Water Management and Hydraulic Engineering, Skopje, North Macedonia, 5–7 September 2019. [Google Scholar]
- Bartolić, I.; Lončar, G.; Bujak, D.; Carević, D. The Flow Generator Relations for Water Renewal through the Flushing Culverts in Marinas. Water 2018, 10, 936. [Google Scholar] [CrossRef]
- Lončar, G.; Bartolić, I.; Bujak, D. Contribution of Wind and Waves in Exchange of Seawater through Flushing Culverts in Marinas. Teh. Vjesn.-Tech. Gaz. 2018, 25, 1587–1594. [Google Scholar] [CrossRef]
- Karimi, M.S.; Mohammadi, R.; Raisee, M.; Hendrick, P.; Nourbakhsh, A. Robust optimization of a marine current turbine using a novel robustness criterion. Energy Convers. Manag. 2023, 295, 117608. [Google Scholar] [CrossRef]
- Ni, P.; Li, J.; Hao, H.; Xia, Y.; Du, X. Stochastic dynamic analysis of marine risers considering fluid-structure interaction and system uncertainties. Eng. Struct. 2019, 198, 109507. [Google Scholar] [CrossRef]
- Burcharth, H.F. Uncertainty Related to Environmental Data and Estimated Extreme Events: PIANC PTC II Working Group 12, Report of Subgroup B; Aalborg Universitetsforlag: Aalborg, Denmark, 1992. [Google Scholar]
- PIANC (Ed.) Breakwaters with Vertical and Inclined Concrete Walls: Report of Working Group 28 of the Maritime Navigation Commission; PIANC General Secretariat: Bruxelles, Belgium, 2003; ISBN 978-2-87223-139-3. [Google Scholar]
- Schüttrumpf, H.; Kortenhaus, A.; Peters, K.; Fröhle, P. Expert judgement of uncertainties in coastal structure design. In Proceedings of the Coastal Engineering 2006, San Diego, CA, USA, 3–8 September 2006; World Scientific Publishing Company: San Diego, CA, USA, 2007; pp. 5267–5278. [Google Scholar]
- Suh, K.-D.; Kim, S.-W.; Mori, N.; Mase, H. Effect of Climate Change on Performance-Based Design of Caisson Breakwaters. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 215–225. [Google Scholar] [CrossRef]
- Eurotop EurOtop II. European Overtopping Manual—Wave Overtopping of Sea Defences and Related Structures: Assessment Manual; Envrionment Agency: Rotherham, UK, 2018.
- Wiegel, R.L. Transmission of Waves Past a Rigid Vertical Thin Barrier. J. Waterw. Hourbours Div. 1960, 86, 1–12. [Google Scholar] [CrossRef]
- Kriebel, D.L.; Bollman, C.A.; Billy, L.E. Wave transmission past vertical wave barriers. In Proceedings of the 25th International Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996. [Google Scholar]
- Yu, Y.; Guo, Z.; Ma, Q. Transmission of Water Waves under Multiple Vertical Thin Plates. Water 2018, 10, 517. [Google Scholar] [CrossRef]
- Lee, C.-E.; Kwon, H.J. Reliability analysis and evaluation of partial safety factors for random wave overtopping. KSCE J. Civ. Eng. 2009, 13, 7–14. [Google Scholar] [CrossRef]
- Tsimopoulou, V. Probabilistic Design of Breakwaters in Shallow, Hurricane-Prone Areas. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2011. [Google Scholar]
- Oumeraci, H.; Allsop, W.; Groot, M.; Crouch, R.; Vrijling, J. Proverbs: Probabilistic Design Tools for Vertical Breakwaters; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Doan, N.S.; Huh, J.; Mac, V.H.; Kim, D.; Kwak, K. Probabilistic Risk Evaluation for Overall Stability of Composite Caisson Breakwaters in Korea. J. Mar. Sci. Eng. 2020, 8, 148. [Google Scholar] [CrossRef]
- Oumeraci, H. Proverbs: Probabilistic Design Tools for Vertical Breakwaters; CRC Press: Boca Raton, FL, USA, 1999; Volume 2. [Google Scholar]
- Kortenhaus, A. Probabilistische Methoden für Nordseedeiche; Technical University of Braunschweig: Braunschweig, Germany, 2003. [Google Scholar] [CrossRef]
- Katalinić, M.; Parunov, J. Uncertainties of Estimating Extreme Significant Wave Height for Engineering Applications Depending on the Approach and Fitting Technique—Adriatic Sea Case Study. J. Mar. Sci. Eng. 2020, 8, 259. [Google Scholar] [CrossRef]
- Kim, S.-W.; Suh, K.-D. Performance Analysis of Vertical Breakwaters Designed by Partial Safety Factor Method. J. Coast. Res. 2013, 65, 296–301. [Google Scholar] [CrossRef]
- Suh, K.-D.; Kwon, H.-D.; Lee, D.-Y. Some statistical characteristics of large deepwater waves around the Korean Peninsula. Coast. Eng. 2010, 57, 375–384. [Google Scholar] [CrossRef]
- Bujak, D.; Loncar, G.; Carevic, D.; Kulic, T. The Feasibility of the ERA5 Forced Numerical Wave Model in Fetch-Limited Basins. J. Mar. Sci. Eng. 2023, 11, 59. [Google Scholar] [CrossRef]
- Bujak, D.; Bogovac, T.; Carević, D.; Miličević, H. Filling Missing and Extending Significant Wave Height Measurements Using Neural Networks and an Integrated Surface Database. Wind 2023, 3, 151–169. [Google Scholar] [CrossRef]
- Takagi, H.; Goda, Y. A Reliability Design Method of Caisson Breakwaters with Optimal Wave Heights. Coast. Eng. J. 2000, 42, 357–387. [Google Scholar] [CrossRef]
- Kim, T.-M.; Takayama, T. Computational Improvement for Expected Sliding Distance of a Caisson-Type Breakwater by Introduction of a Doubly-Truncated Normal Distribution. Coast. Eng. J. 2003, 45, 387–419. [Google Scholar] [CrossRef]
- Karatzetzou, A. Uncertainty and Latin Hypercube Sampling in Geotechnical Earthquake Engineering. Geotechnics 2024, 4, 1007–1025. [Google Scholar] [CrossRef]
- Hajihassanpour, M.; Kesserwani, G.; Pettersson, P.; Bellos, V. Sampling-Based Methods for Uncertainty Propagation in Flood Modeling Under Multiple Uncertain Inputs: Finding Out the Most Efficient Choice. Water Resour. Res. 2023, 59, e2022WR034011. [Google Scholar] [CrossRef]
- PIANC. Seismic Design Guidelines for Port Structures; PIANC: Brussels, Belgium, 2001. [Google Scholar]
- U.S. Army Corps of Engineers. Coastal Engineering Manual; U.S. Army Corps of Engineers: Washington, DC, USA, 2002. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC) (Ed.) Summary for Policymakers. In Climate Change 2021—The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2023; pp. 1–2. ISBN 978-1-009-15788-9. [Google Scholar]



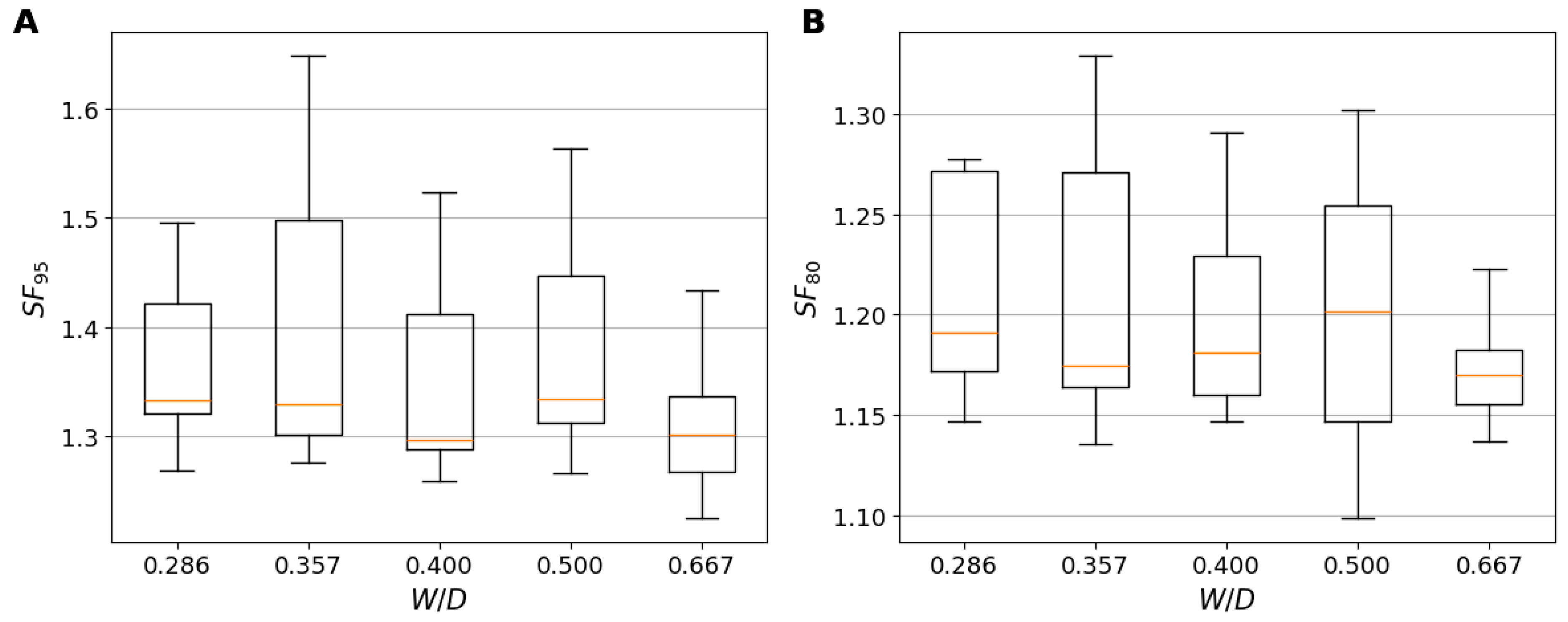
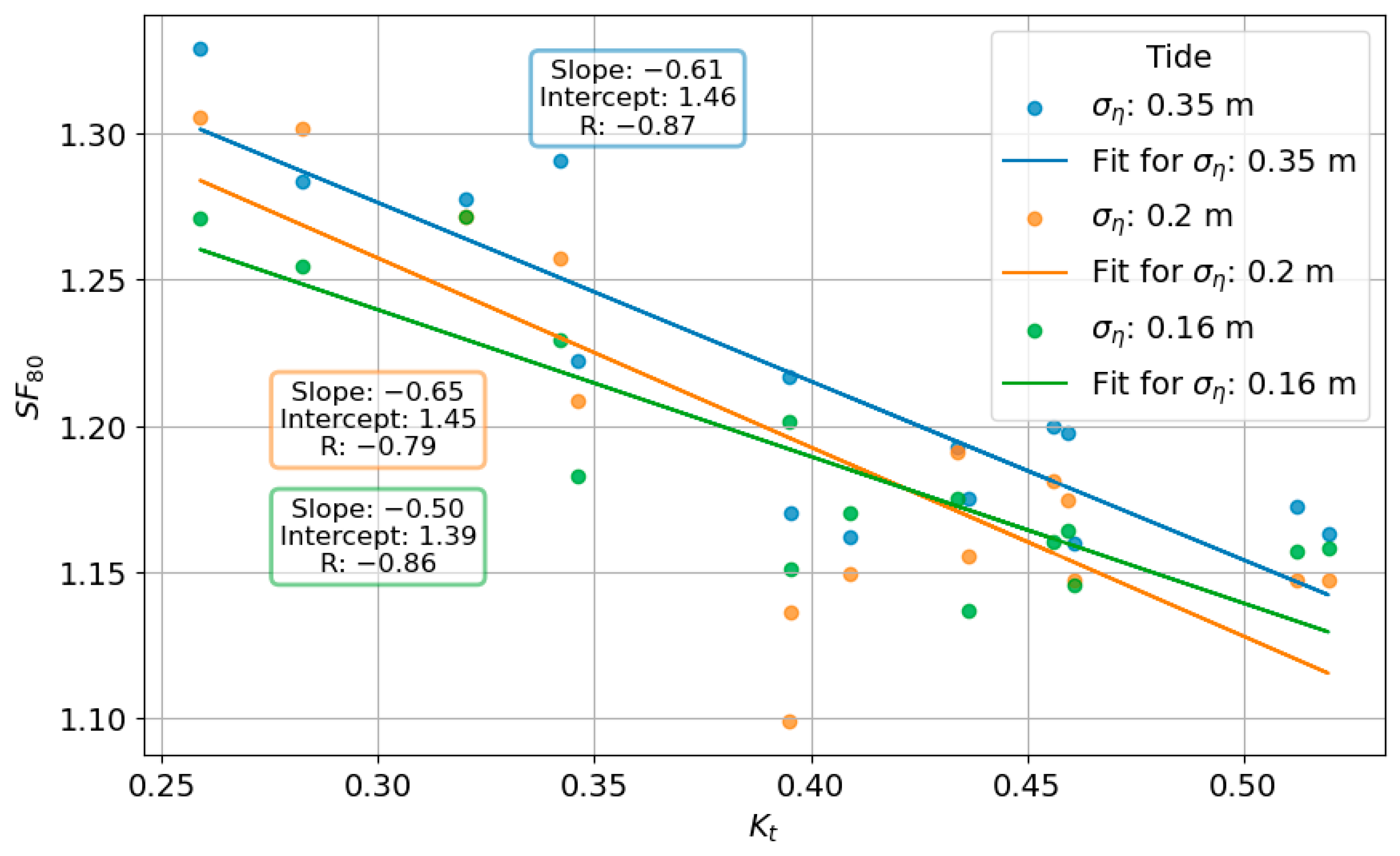
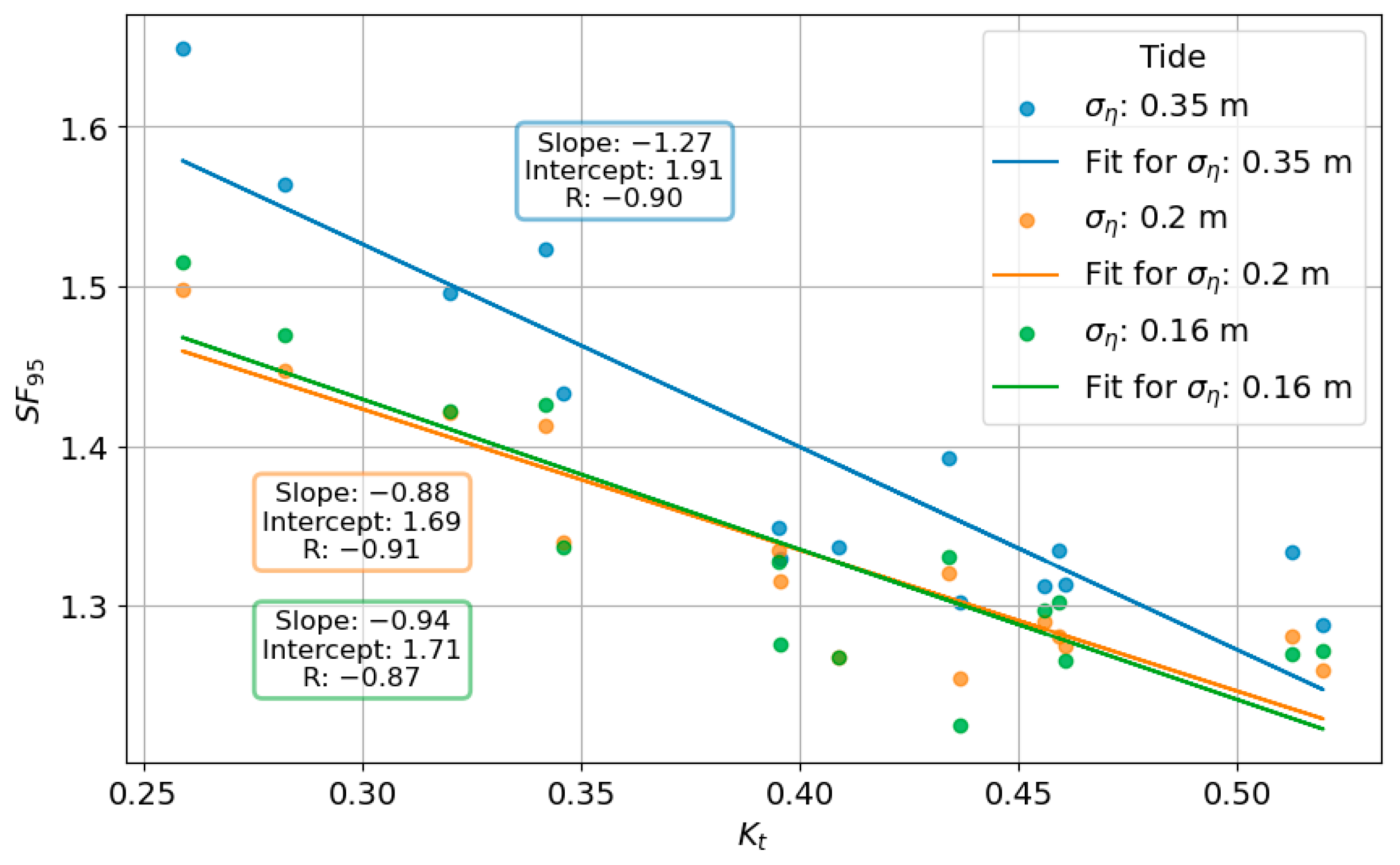

| Parameter | Symbol | Method of Determination | CoV (σ’) | Reference |
|---|---|---|---|---|
| Sig. wave height | Hm0 | Measurement | 0.05–0.10 | [8,9] |
| 0.022–0.036 | [10] | |||
| Hindcast (SMB method) | 0.10–0.20 | [8,9] | ||
| 0.040–0.049 | [10] | |||
| Numerical model | 0.10–0.20 | [8,9] | ||
| 0.040–0.044 | [10] | |||
| Manual calculation | 0.15–0.35 | [8,9] | ||
| Visual observations | 0.2 | [8,9] | ||
| 0.044–0.052 | [10] | |||
| - | 0.05 | [12] | ||
| 0.09–0.125 | [21] | |||
| 0.05 | [22] ** | |||
| 0.1 | [11] | |||
| 0.1–0.2 | [23] | |||
| Peak wave period | Tp | Measurement | 0.028–0.029 | [10] |
| Hindcast | 0.048–0.055 | [10] | ||
| Numerical model | 0.043 | [10] | ||
| Visual observation | 0.036–0.047 | [10] | ||
| - | 0.05 | [12] | ||
| 0.2 | [21] | |||
| 0.12 | [11,24] | |||
| Mean wave period | Tm | Measurement | 0.02 | [8,9] |
| Visual observations | 0.15 | [8,9] | ||
| - | 0.05 | [12] | ||
| 0.1–0.2 | [23] | |||
| Water level (Astronomical tide and surge) | η + ss | |||
| 0.15–0.3 | [21] | |||
| 0.03 | [12] | |||
| Astronomical tide | η | Sine function approximation of astronomical tide | 0.707A * (standard deviation, not CoV) | [11] |
| Measurements | Calculated from measurements | |||
| Storm surge | ss | Numerical models | 0.1–0.25 | [8,9] |
| Parameter | Symbol | CoV (σ’) | STD (σ) |
|---|---|---|---|
| Sig. wave height | Hm0 | 0.10 | - |
| Peak wave period | Tp | 0.08 | - |
| Astronomical tide | - | 0.707A | |
| Storm surge | 0.2 | - |
| N | Hm0,i,mean (m) | Tp,mean (s) | Tide—ση (m) | Surgemean (m) | Sea Depth—D (m) | Draft—W (m) |
|---|---|---|---|---|---|---|
| 1 | 0.7 | 3.35 | 0.35 | 0.07 | 3 | 2 |
| 2 | 0.7 | 3.35 | 0.35 | 0.07 | 5 | 2 |
| 3 | 0.7 | 3.35 | 0.35 | 0.07 | 7 | 2 |
| 4 | 0.7 | 3.35 | 0.35 | 0.07 | 3 | 2.5 |
| 5 | 0.7 | 3.35 | 0.35 | 0.07 | 5 | 2.5 |
| 6 | 0.7 | 3.35 | 0.35 | 0.07 | 7 | 2.5 |
| 7 | 0.7 | 3.35 | 0.20 | 0.07 | 3 | 2 |
| 8 | 0.7 | 3.35 | 0.20 | 0.07 | 5 | 2 |
| 9 | 0.7 | 3.35 | 0.20 | 0.07 | 7 | 2 |
| 10 | 0.7 | 3.35 | 0.20 | 0.07 | 3 | 2.5 |
| 11 | 0.7 | 3.35 | 0.20 | 0.07 | 5 | 2.5 |
| 12 | 0.7 | 3.35 | 0.20 | 0.07 | 7 | 2.5 |
| 13 | 0.7 | 3.35 | 0.16 | 0.07 | 3 | 2 |
| 14 | 0.7 | 3.35 | 0.16 | 0.07 | 5 | 2 |
| 15 | 0.7 | 3.35 | 0.16 | 0.07 | 7 | 2 |
| 16 | 0.7 | 3.35 | 0.16 | 0.07 | 3 | 2.5 |
| 17 | 0.7 | 3.35 | 0.16 | 0.07 | 5 | 2.5 |
| 18 | 0.7 | 3.35 | 0.16 | 0.07 | 7 | 2.5 |
| 19 | 0.5 | 2.83 | 0.35 | 0.05 | 3 | 2 |
| 20 | 0.5 | 2.83 | 0.35 | 0.05 | 5 | 2 |
| 21 | 0.5 | 2.83 | 0.35 | 0.05 | 7 | 2 |
| 22 | 0.5 | 2.83 | 0.35 | 0.05 | 3 | 2.5 |
| 23 | 0.5 | 2.83 | 0.35 | 0.05 | 5 | 2.5 |
| 24 | 0.5 | 2.83 | 0.35 | 0.05 | 7 | 2.5 |
| 25 | 0.5 | 2.83 | 0.20 | 0.05 | 3 | 2 |
| 26 | 0.5 | 2.83 | 0.20 | 0.05 | 5 | 2 |
| 27 | 0.5 | 2.83 | 0.20 | 0.05 | 7 | 2 |
| 28 | 0.5 | 2.83 | 0.20 | 0.05 | 3 | 2.5 |
| 29 | 0.5 | 2.83 | 0.20 | 0.05 | 5 | 2.5 |
| 30 | 0.5 | 2.83 | 0.20 | 0.05 | 7 | 2.5 |
| 31 | 0.5 | 2.83 | 0.16 | 0.05 | 3 | 2 |
| 32 | 0.5 | 2.83 | 0.16 | 0.05 | 5 | 2 |
| 33 | 0.5 | 2.83 | 0.16 | 0.05 | 7 | 2 |
| 34 | 0.5 | 2.83 | 0.16 | 0.05 | 3 | 2.5 |
| 35 | 0.5 | 2.83 | 0.16 | 0.05 | 5 | 2.5 |
| 36 | 0.5 | 2.83 | 0.16 | 0.05 | 7 | 2.5 |
| 37 | 0.9 | 3.80 | 0.35 | 0.09 | 3 | 2 |
| 38 | 0.9 | 3.80 | 0.35 | 0.09 | 5 | 2 |
| 39 | 0.9 | 3.80 | 0.35 | 0.09 | 7 | 2 |
| 40 | 0.9 | 3.80 | 0.35 | 0.09 | 3 | 2.5 |
| 41 | 0.9 | 3.80 | 0.35 | 0.09 | 5 | 2.5 |
| 42 | 0.9 | 3.80 | 0.35 | 0.09 | 7 | 2.5 |
| 43 | 0.9 | 3.80 | 0.20 | 0.09 | 3 | 2 |
| 44 | 0.9 | 3.80 | 0.20 | 0.09 | 5 | 2 |
| 45 | 0.9 | 3.80 | 0.20 | 0.09 | 7 | 2 |
| 46 | 0.9 | 3.80 | 0.20 | 0.09 | 3 | 2.5 |
| 47 | 0.9 | 3.80 | 0.20 | 0.09 | 5 | 2.5 |
| 48 | 0.9 | 3.80 | 0.20 | 0.09 | 7 | 2.5 |
| 49 | 0.9 | 3.80 | 0.16 | 0.09 | 3 | 2 |
| 50 | 0.9 | 3.80 | 0.16 | 0.09 | 5 | 2 |
| 51 | 0.9 | 3.80 | 0.16 | 0.09 | 7 | 2 |
| 52 | 0.9 | 3.80 | 0.16 | 0.09 | 3 | 2.5 |
| 53 | 0.9 | 3.80 | 0.16 | 0.09 | 5 | 2.5 |
| 54 | 0.9 | 3.80 | 0.16 | 0.09 | 7 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bujak, D.; Carević, D.; Lončar, G.; Miličević, H. A Probabilistic Design Framework for Semi-Submerged Curtain Wall Breakwaters. Infrastructures 2025, 10, 144. https://doi.org/10.3390/infrastructures10060144
Bujak D, Carević D, Lončar G, Miličević H. A Probabilistic Design Framework for Semi-Submerged Curtain Wall Breakwaters. Infrastructures. 2025; 10(6):144. https://doi.org/10.3390/infrastructures10060144
Chicago/Turabian StyleBujak, Damjan, Dalibor Carević, Goran Lončar, and Hanna Miličević. 2025. "A Probabilistic Design Framework for Semi-Submerged Curtain Wall Breakwaters" Infrastructures 10, no. 6: 144. https://doi.org/10.3390/infrastructures10060144
APA StyleBujak, D., Carević, D., Lončar, G., & Miličević, H. (2025). A Probabilistic Design Framework for Semi-Submerged Curtain Wall Breakwaters. Infrastructures, 10(6), 144. https://doi.org/10.3390/infrastructures10060144






