Seismic Reliability Analysis of Highway Pile–Plate Structures Considering Dual Stochasticity of Parameters and Excitation via Probability Density Evolution
Abstract
1. Introduction
2. Methodology
2.1. Probability Density Evolution Equation
2.2. Solution of the Evolution Equation of Probability Density
2.3. Structural Seismic Reliability Analysis Methods
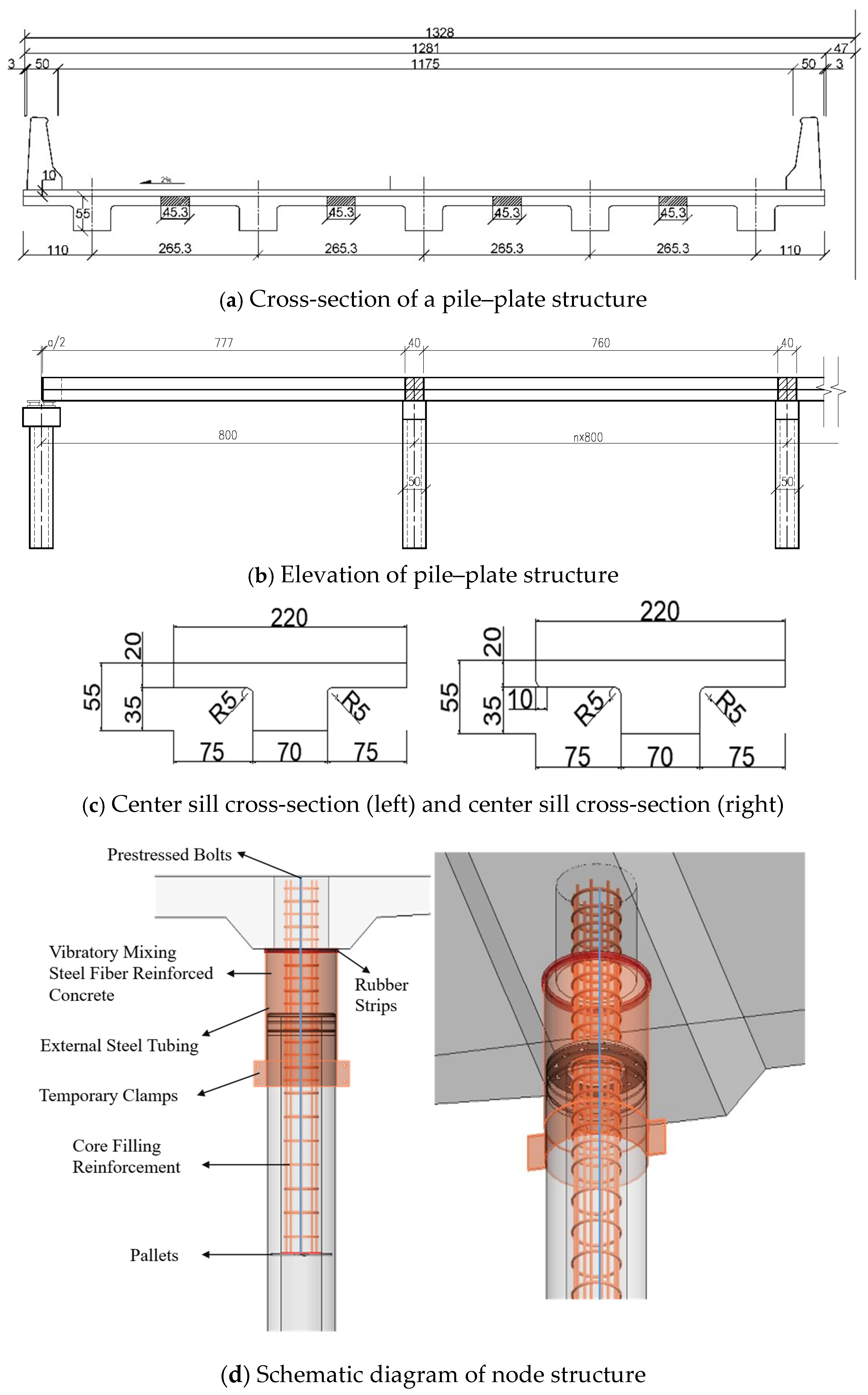
3. Seismic Reliability Analysis of Pile–Slab Structure Considering Randomness of Concrete
3.1. Random Structure Analysis Model of Pile–Plate Structure
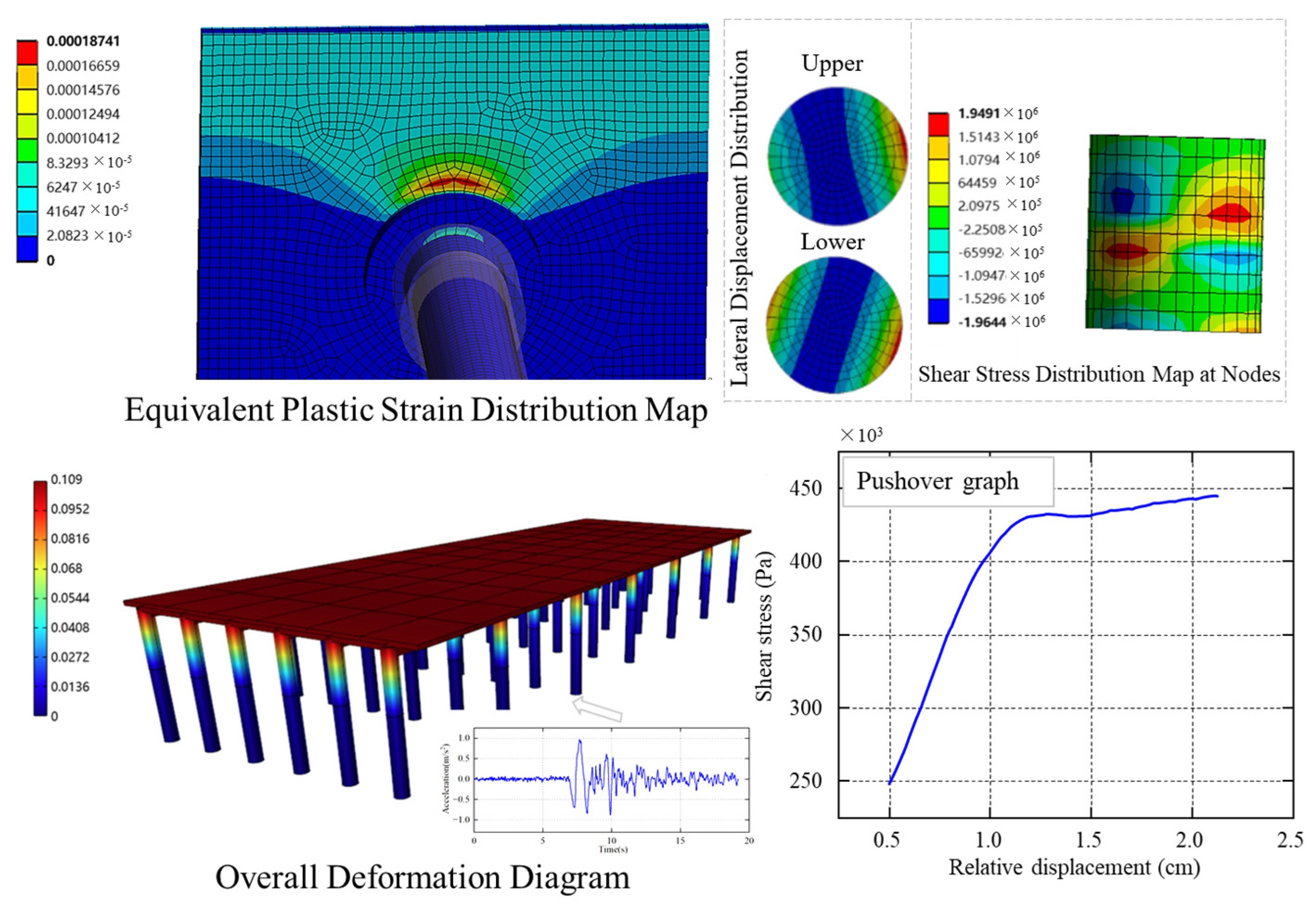
3.2. Calculation of Seismic Reliability of Random Structure of Pile–Plate Structure
4. Reliability Analysis of Structures Under Random Earthquake Excitations
4.1. Physical Stochastic Function Model of Engineering Ground Shaking
4.2. Stochastic Seismic Response Analysis and Seismic Reliability Assessment of Pile–Plate Structures
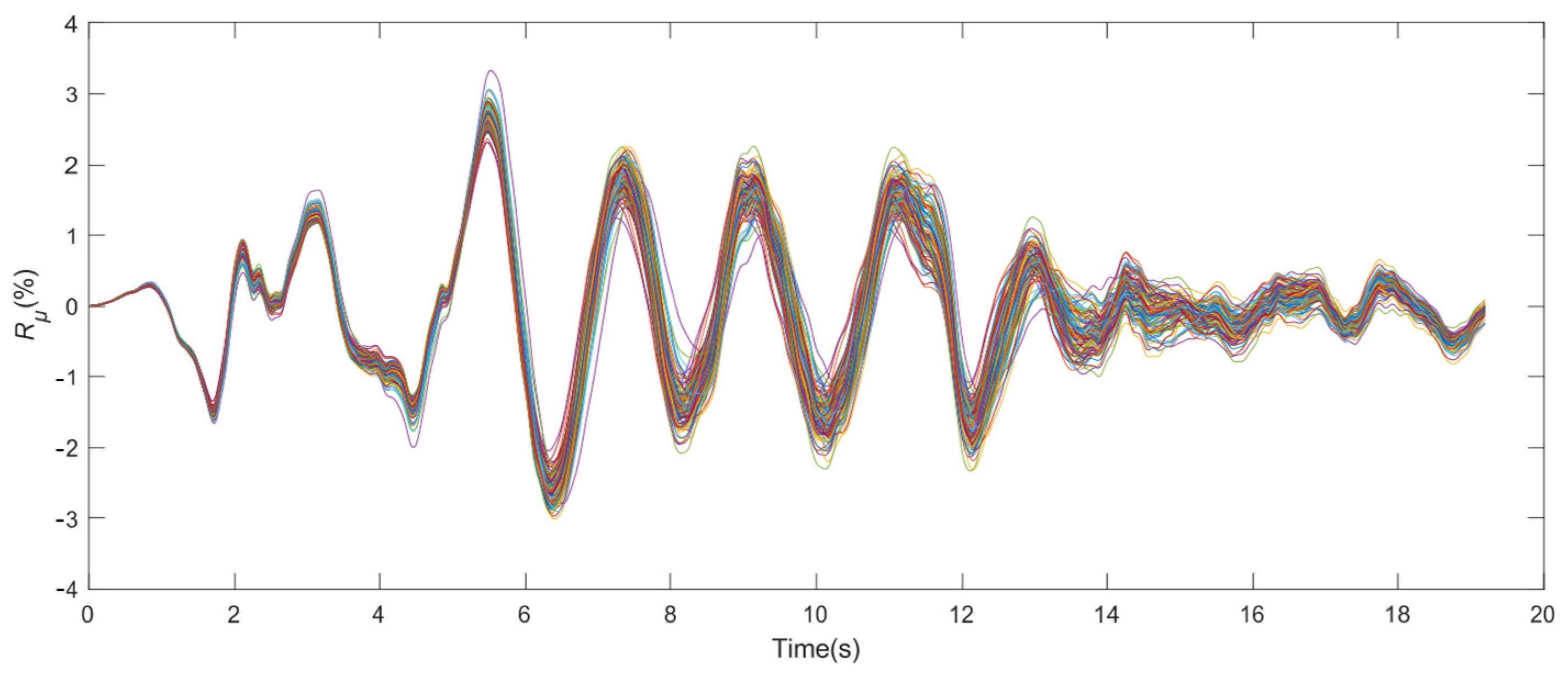
4.3. Seismic Reliability Analysis of Pile–Plate Structure Considering Parameter–Excitation Composite Randomness
4.3.1. Analysis and Evaluation Method for Composite Random Seismic Response of Pile–Plate Structure
4.3.2. Composite Random Seismic Reliability Analysis of Pile–Plate Structure
4.4. Comparative Study of Seismic Reliability of Pile–Plate Structure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stewart, E.A. The 1999 Jl-Jl Earthquake Tiwan—The Investigation into the Damage to Civil Engineering Structures; Japan Society of Civil Engineering: Tokyo, Japan, 1999; Volume 12. [Google Scholar]
- Wang, X.; Yang, Z.; Yates, J.; Jivkov, A.; Zhang, C. Monte carlo simulations of mesoscale fracture modelling of concrete with random aggregates and pores. Constr. Build. Mater. 2015, 75, 35–45. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S. Multiscale modeling of concrete from mesoscale to macroscale. Arch. Comput. Methods Eng. 2011, 18, 341–393. [Google Scholar] [CrossRef]
- Guan, J.; Yuan, P.; Hu, X.; Qing, L.; Yao, X. Statistical analysis of concrete fracture using normal distribution pertinent to maximum aggregate size. Theor. Appl. Fract. Mech. 2019, 101, 236–253. [Google Scholar] [CrossRef]
- Ren, Q.W.; Yin, Y.J.; Shen, L. Fractal study of random distribution of concrete aggregates and its effect on damage characteristics. J. Water Resour. 2020, 51, 1267–1277. [Google Scholar]
- Husek, M.; Kala, J. Material structure generation of concrete and its further usage in numerical simulations. Struct. Eng. Mech. 2018, 68, 335–344. [Google Scholar]
- Feng, D.C.; Li, J. Stochastic nonlinear behavior of reinforced concrete frames. Ii: Numerical simulation. J. Struct. Eng. 2016, 142, 4015163. [Google Scholar] [CrossRef]
- Zhang, J.C. Simulation of Concrete Damage Process Considering the Effect of Material Non-Homogeneity; Southeast University: Nanjing, China, 2015. [Google Scholar]
- Liu, Z.J.; Zheng, L.H.; Ruan, X.X. Reduced-dimensional simulation of ground vibration considering randomness and correlation of site soil parameters. Vib. Shock. 2021, 40, 165–172. [Google Scholar]
- Zeng, M.H.; Wu, Z.M.; Wang, Y.J. A stochastic model considering heterogeneity and crack propagation in concrete. Constr. Build. Mater. 2020, 254, 119289. [Google Scholar] [CrossRef]
- Feng, D.C.; Yang, C.D.; Ren, X.D. Multi-scale stochastic damage model for concrete and its application to rc shear wall structure. Eng. Comput. 2018, 35, 2287–2307. [Google Scholar] [CrossRef]
- Liang, R.J.; Wang, H.; Shen, H.J. Dynamic response analysis of continuous girder bridge with seismic isolation curve considering randomness of ground vibration. J. Vib. Eng. 2020, 33, 834–841. [Google Scholar]
- Xu, B.; Pang, R.; Zhou, Y. Verification of stochastic seismic analysis method and seismic performance evaluation based on multi-indices for high cfrds. Eng. Geol. 2020, 264, 105412. [Google Scholar] [CrossRef]
- Kavitha, P.E.; Beena, K.S.; Narayanan, K.P. A review on soil–structure interaction analysis of laterally loaded piles. Innov. Infrastruct. Solut. 2016, 1, 14. [Google Scholar] [CrossRef]
- Islam, R.; Das Turja, S.; Van Nguyen, D.; Forcellini, D.; Kim, D. Seismic soil-structure interaction in nuclear power plants: An extensive review. Results Eng. 2024, 23, 110783. [Google Scholar] [CrossRef]
- Liu, J.; Jin, Q.; Dong, Y.; Tian, L.; Wu, Z. Resilience-based seismic safety evaluation of pile-supported overhead transmission lines under depth-varying spatial ground motions. Reliab. Eng. Syst. Saf. 2025, 256, 110783. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Song, L. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations. Comput. Geotech. 2021, 136, 104241–104245. [Google Scholar] [CrossRef]
- Wu, Y.; Mo, H.H.; Yang, C. Study on dynamic performance of a three-dimensional high frame supported u-shaped aqueduct. Eng. Struct. 2006, 28, 372–380. [Google Scholar] [CrossRef]
- Liang, J.Y.; Wang, H.; Xu, X.Y. Analysis of seismic dynamic properties of ferry structure based on viscoelastic boundary. People’s Yellow River 2020, 42, 81–84, 102. [Google Scholar]
- Li, J.; Chen, J.B. Probability density evolution equation in stochastic dynamical systems and its research progress. Adv. Mech. 2010, 40, 170–188. [Google Scholar]
- Liu, Z.J.; Chen, J.B.; Li, J. Probabilistic density evolution method for nonlinear stochastic seismic response of structures. J. Solid Mech. 2009, 30, 489–495. [Google Scholar]
- Chen, J.B.; Li, J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters. Struct. Saf. 2007, 29, 77–93. [Google Scholar] [CrossRef]
- Goller, B.; Pradlwarter, H.J.; Schueller, G.I. Reliability assessment in structural dynamics. J. Sound Vib. 2013, 332, 2488–2499. [Google Scholar] [CrossRef]
- Su, C.; Xu, R. Time domain solution for dynamic reliability of structural systems under non-stationary random excitation. J. Mech. 2010, 42, 512–520. [Google Scholar]
- Liu, Z.J.; Li, J. Dynamic Reliability Assessment of Non-Linear Structures Under Earthquake Loads; Science Press: Beijing, China, 2007. [Google Scholar]
- Chen, J.B.; Li, J. Dynamic reliability analysis of composite random vibration systems. Eng. Mech. 2005, 22, 52–57. [Google Scholar]
- Li, J.; Chen, J.B. The dimension-reduction strategy via mapping for probability density evolution analysis of nonlinear stochastic systems. Probabilistic Eng. Mech. 2006, 21, 442–453. [Google Scholar] [CrossRef]
- Li, J. Stochastic Structural Systems—Analysis and Modeling; Science Press: Beijing, China, 1996. [Google Scholar]
- Li, J.; Chen, J.B. A probabilistic density evolution method for the analysis of dynamic response of stochastic structures. J. Mech. 2003, 35, 437–442. [Google Scholar]
- Li, J.; Chen, J.B. The probability density evolution method for dynamic response analysis of non-linear stochastic structures. Int. J. Numer. Methods Eng. 2006, 65, 882–903. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.B. Probabilistic density evolution method for dynamic reliability analysis of stochastic structures. J. Vib. Eng. 2004, 17, 121–125. [Google Scholar]
- Chen, J.B.; Li, J. Density evolution method for dynamic reliability of nonlinear stochastic structures. J. Mech. 2004, 36, 196–201. [Google Scholar]
- Chen, J.B.; Li, J. Probability density evolution method for composite random vibration analysis of random structures. Eng. Mech. 2004, 21, 90–95. [Google Scholar]
- Li, J.; Chen, J.B. The principle of preservation of probability and the generalized density evolution equation. Struct. Saf. 2008, 30, 65–77. [Google Scholar] [CrossRef]
- Li, J. Progress of research on overall reliability analysis of engineering structures. J. Civ. Eng. 2018, 51, 1–10. [Google Scholar]
- Li, J.; Chen, J.B.; Fan, W.L. The equivalent extreme-value event and evaluation of the structural system reliability. Struct. Saf. 2007, 29, 112–131. [Google Scholar] [CrossRef]
- Li, J.; Yan, Q.; Chen, J.B. Stochastic modeling of engineering dynamic excitations for stochastic dynamics of structures. Probabilistic Eng. Mech. 2012, 27, 19–28. [Google Scholar] [CrossRef]
- Chen, J.B.; Li, J. Development-process-of-nonlinearity-based reliability evaluation of structures. Probabilistic Eng. Mech. 2007, 22, 267–275. [Google Scholar] [CrossRef]
- Chen, J.B.; Jie, L. A note on the principle of preservation of probability and probability density evolution equation. Probabilistic Eng. Mech. 2009, 24, 51–59. [Google Scholar] [CrossRef]
- Chen, J.B.; Li, J. Dynamic response and reliability analysis of non-linear stochastic structures. Probabilistic Eng. Mech. 2005, 20, 33–44. [Google Scholar] [CrossRef]
- Huang, H.; Li, Y.; Li, W. Dynamic reliability analysis of stochastic structures under non-stationary random excitations based on an explicit time-domain method. Struct. Saf. 2023, 101, 102313. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Code for Seismic Design of Buildings (GB 50011-2010); China Construction Industry Press: Beijing, China, 2010. [Google Scholar]
- Chen, J.B.; Yang, J.Y.; Li, J. A GF-discrepancy for point selection in stochastic seismic response analysis of structures with uncertain parameters. Struct. Saf. 2016, 59, 20–31. [Google Scholar] [CrossRef]
- Villaverde, R. Methods to assess the seismic collapse capacity of building structures: State of the art. J. Struct. Eng. 2007, 133, 57–66. [Google Scholar] [CrossRef]
- Li, J.L.J.; Zhou, H.Z.H.; Ding, Y.D.Y. Stochastic seismic collapse and reliability assessment of high-rise reinforced concrete structures. Struct. Des. Tall Spéc. Build. 2017, 27, e1417. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, B.; Xu, J.G.; Huang, L. Reliability analysis of water transfer function of large ferry structure under earthquake. J. Civ. Environ. Eng. 2020, 42, 144–152. [Google Scholar]
- Chen, J.B.; Li, J. New Advances in Stochastic Vibration Theory and Applications; Tongji University Press: Shanghai, China, 2009. [Google Scholar]
- Li, J.; Ai, X.Q. Research on physics-based stochastic ground vibration model. Earthq. Eng. Eng. Vibration 2006, 26, 21–26. [Google Scholar]
- Ding, Y.Q.; Peng, Y.B.; Li, J. A stochastic semi-physical model of seismic ground motions in time domain. J. Earthq. Tsunami 2018, 12, 1012–1033. [Google Scholar] [CrossRef]
- Ding, Y.Q.; Peng, Y.B.; Li, J. Cluster analysis of earthquake ground-motion records and characteristic period of seismic response spectrum. J. Earthq. Eng. 2020, 24, 1012–1033. [Google Scholar] [CrossRef]
- Ding, Y.Q.; Li, J. Parameter identification and statistical modeling of physical models of engineering stochastic ground shaking. Chin. Sci. Tech. Sci. 2018, 48, 1422–1432. [Google Scholar]
- Li, J.; Wang, D. Parameter statistics and testing of physical models of engineering stochastic ground shaking. Earthq. Eng. Eng. Vib. 2013, 33, 81–88. [Google Scholar]
- Chen, J.B.; Li, J. Stochastic seismic response analysis of structures exhibiting high nonlinearity. Comput. Struct. 2010, 88, 395–412. [Google Scholar] [CrossRef]

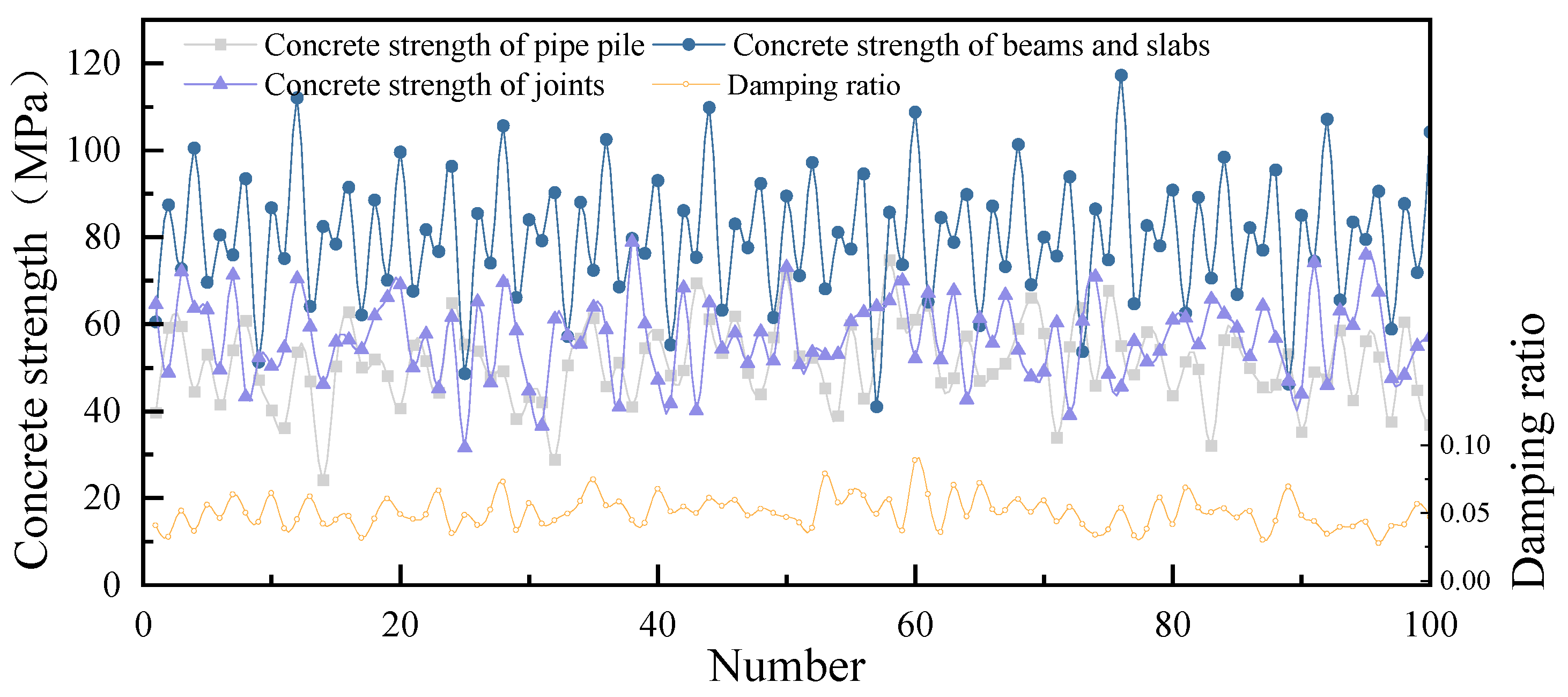



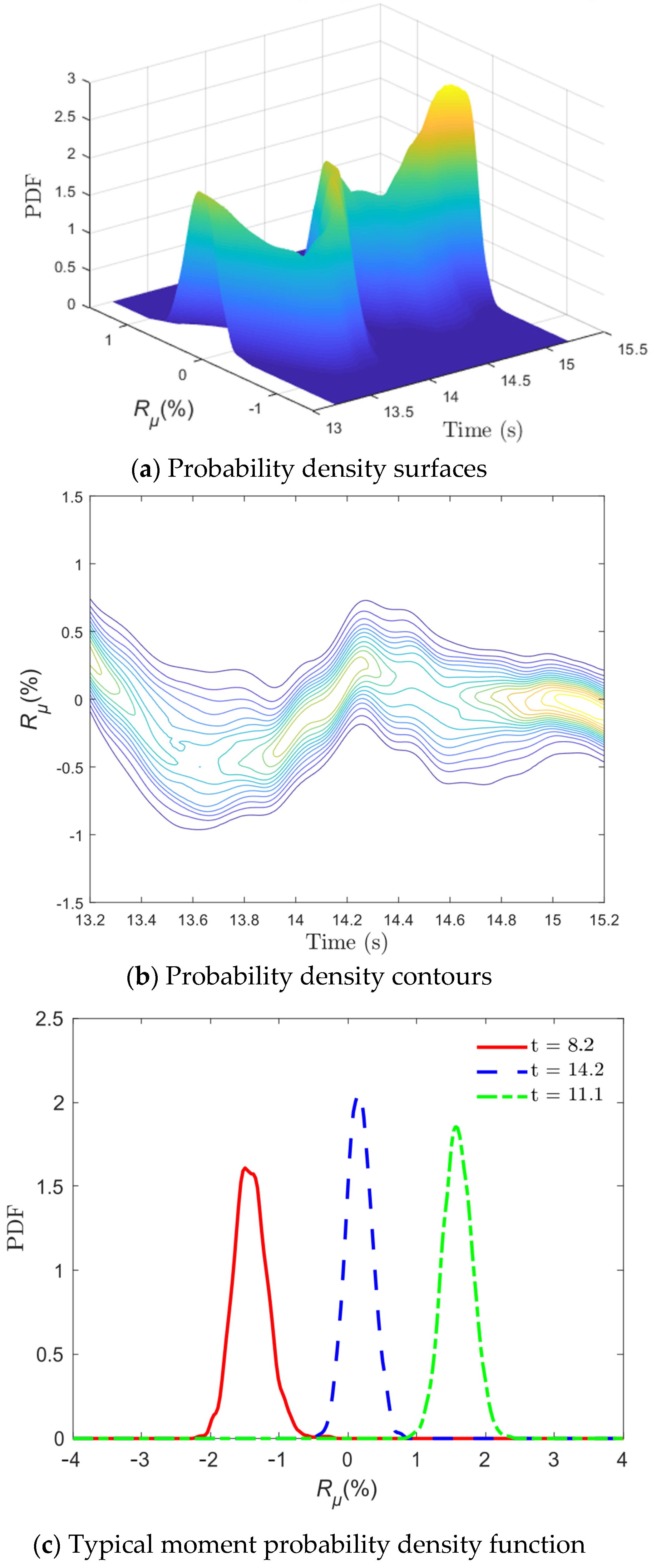


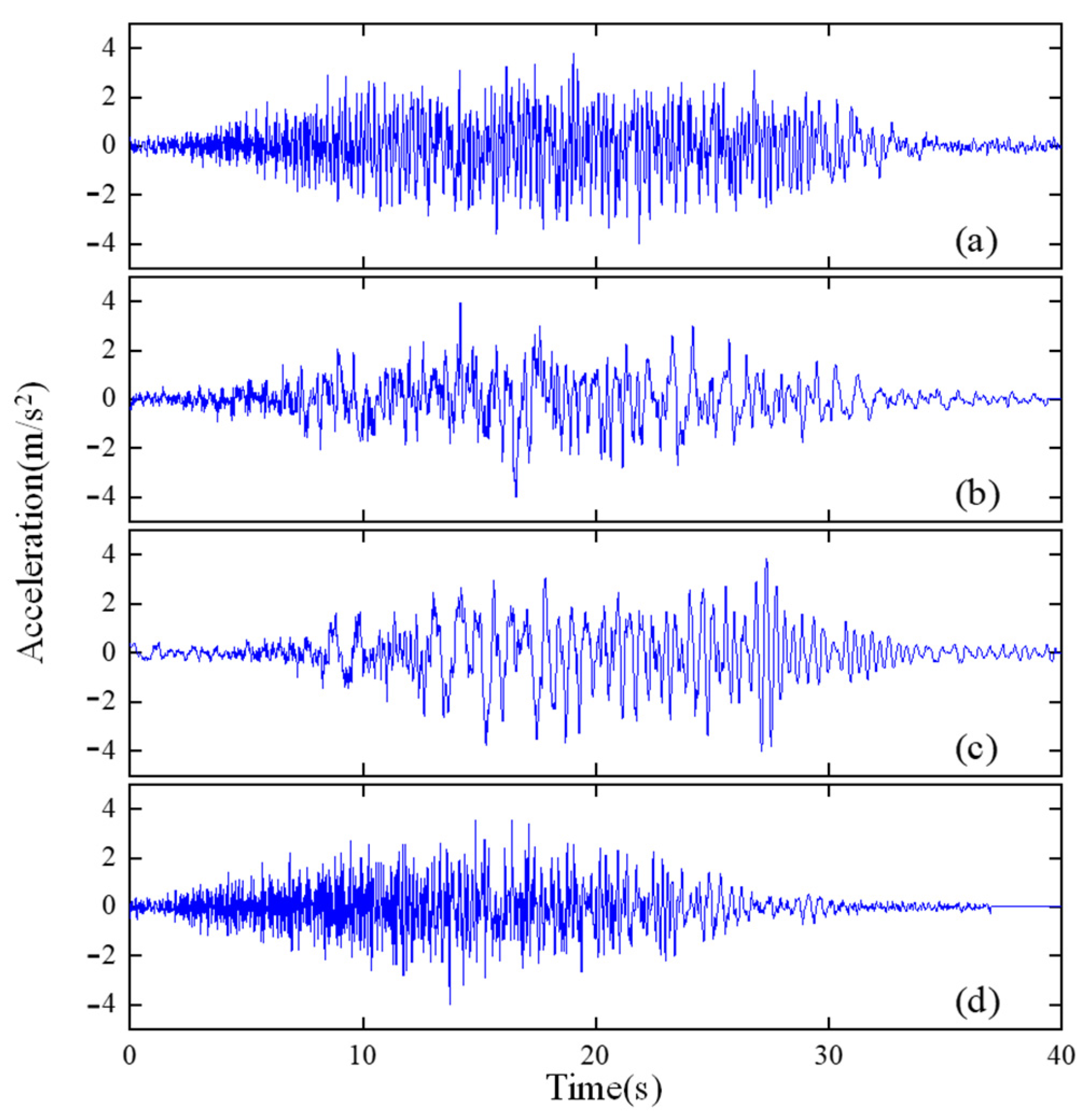
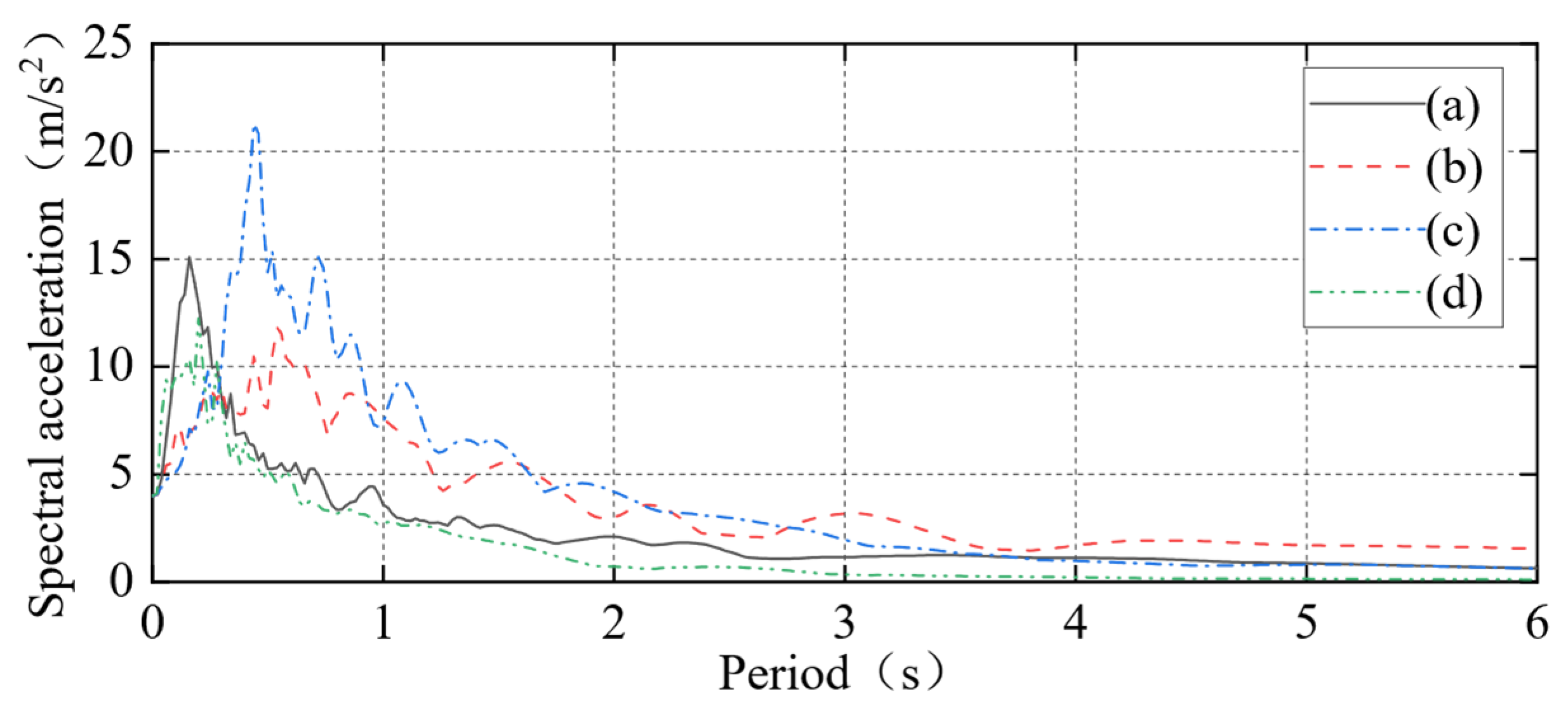

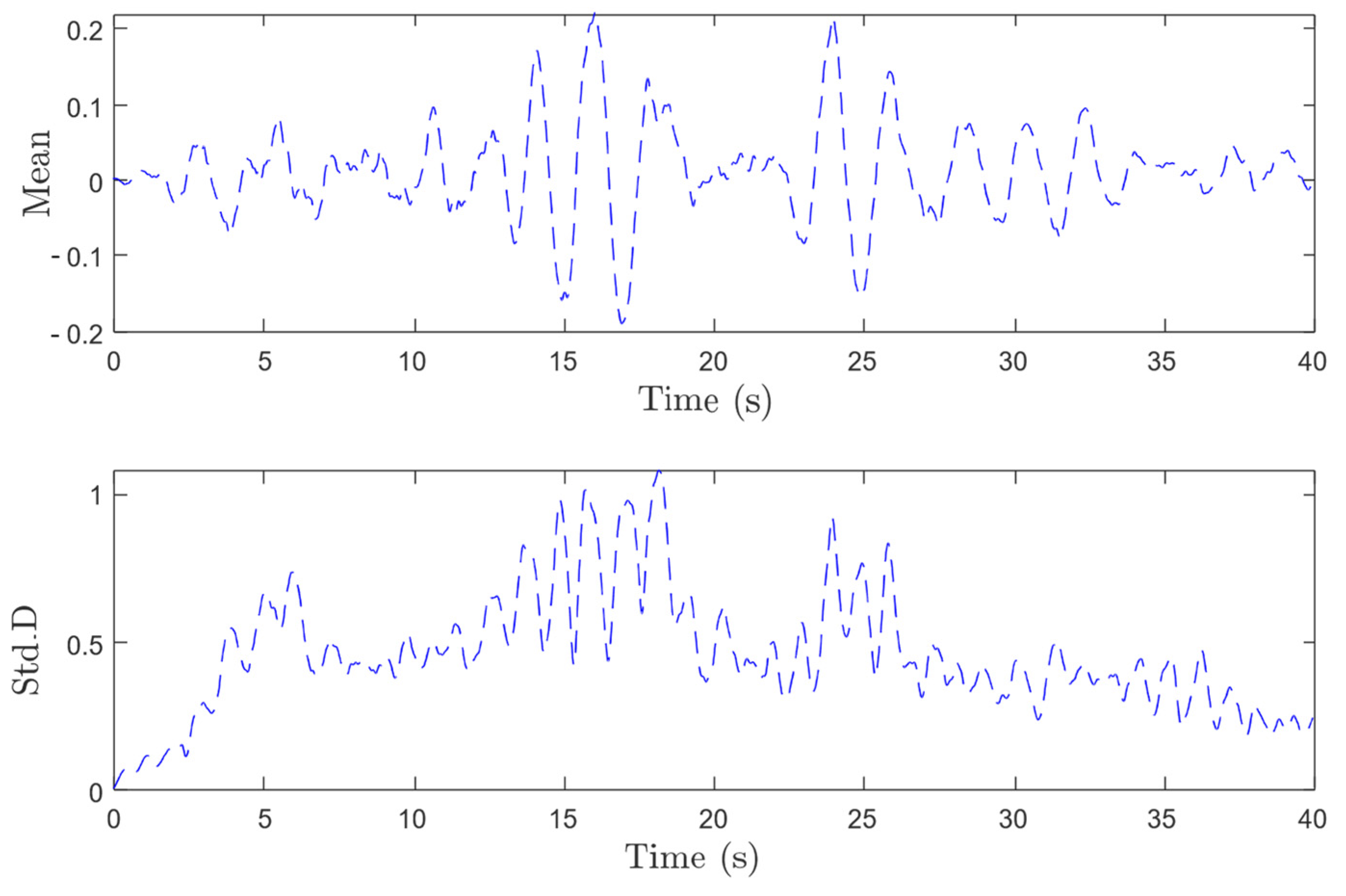
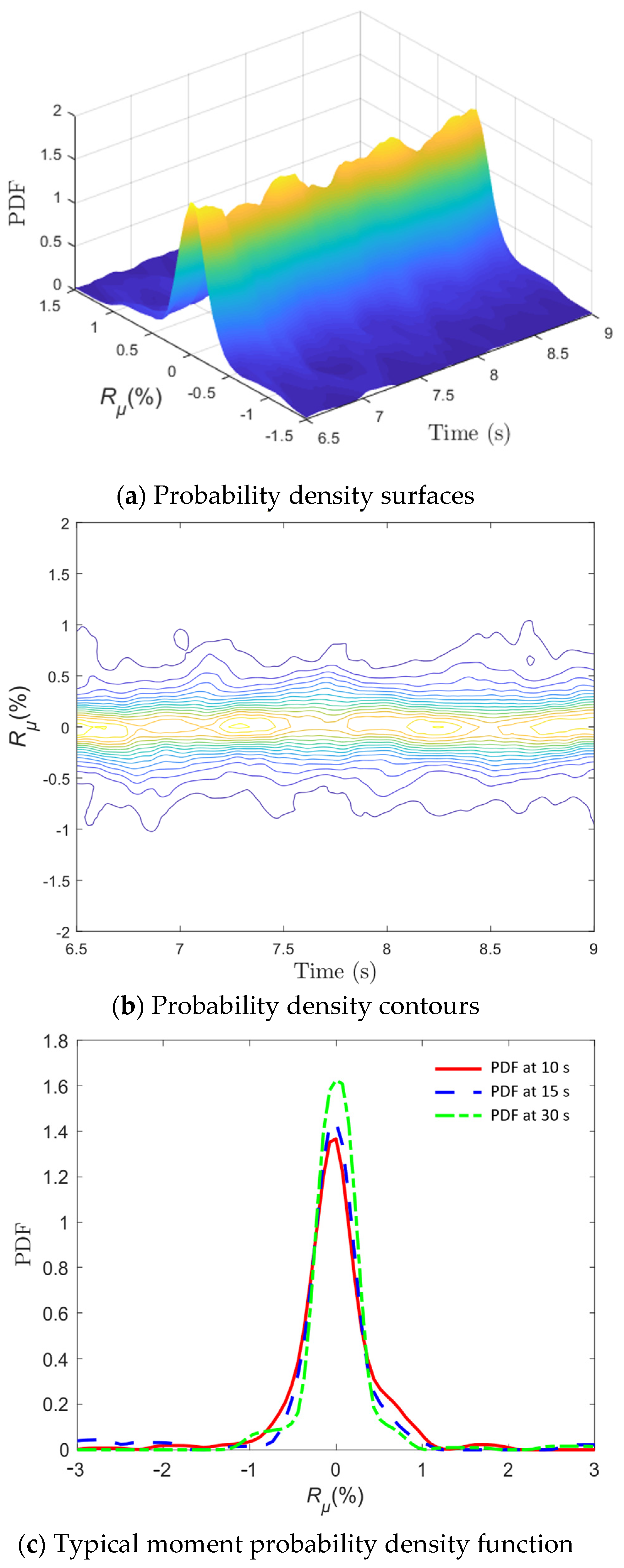

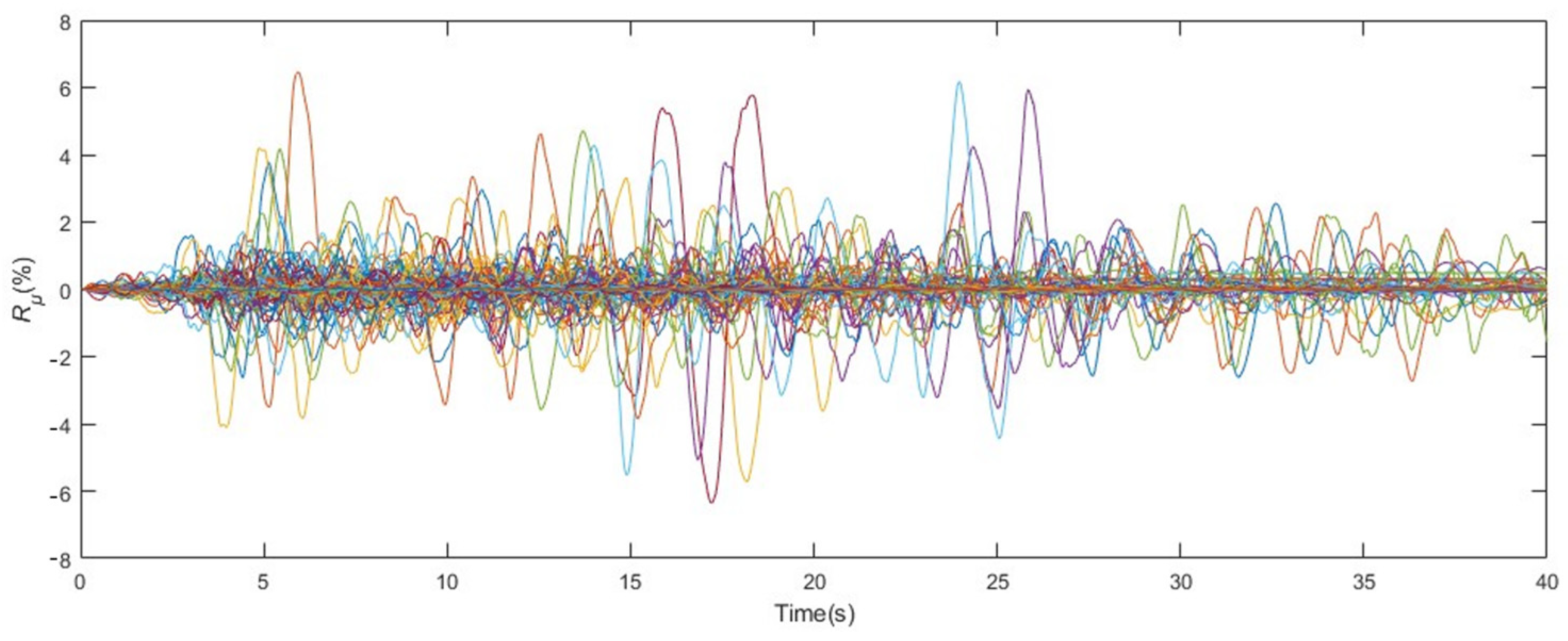

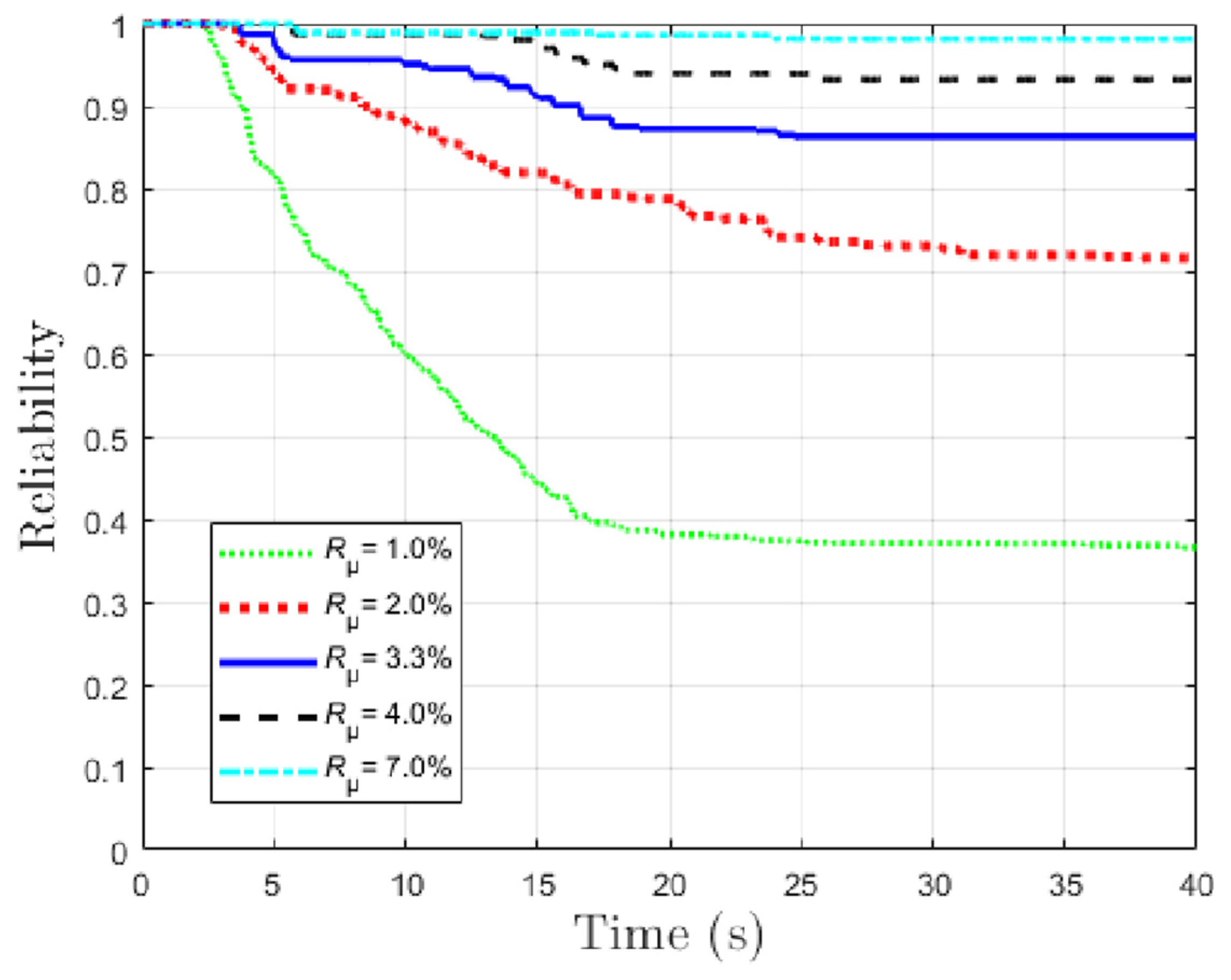
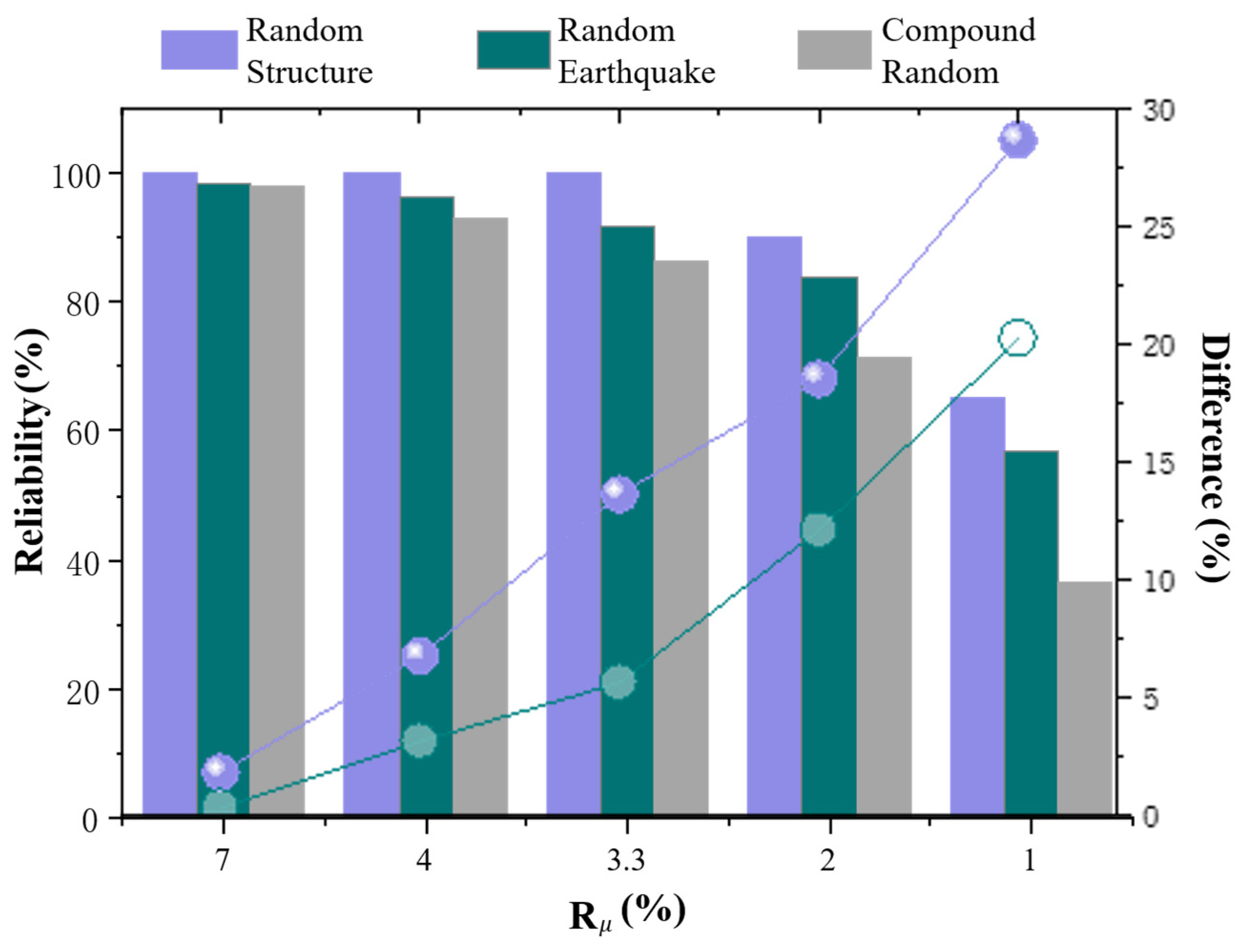
| Random Variables | Mean | Coefficient of Variation | Distribution Type | |
|---|---|---|---|---|
| Concrete strength of pipe pile | fr,v1 (C60) | 60 MPa | Normal distribution | |
| Concrete strength of beams and slabs | fr,v2 (C50) | 50 MPa | Normal distribution | |
| Concrete strength of joints | fr,v3 (CF40) | 56.5 MPa | Normal distribution | |
| Damping ratio | ζ | Lognormal distribution |
| Rμ/% | Reliability |
|---|---|
| 3.3 | 100.00% |
| 2.1 | 98.05% |
| 2.0 | 90.17% |
| 1.0 | 65.26% |
| Physical Random Parameters | Distribution Type | Probability Density Function Parameter Value | |||
|---|---|---|---|---|---|
| Lognormal | Venue type | ||||
| I | −1.4306 | 0.9763 | 0.05 | ||
| II | −1.2712 | 0.8267 | 0.05 | ||
| III | −1.1047 | 0.7388 | 0.15 | ||
| IV | −0.9280 | 0.6380 | 0.25 | ||
| Lognormal | Venue type | ||||
| I | −1.3447 | 1.4724 | 0.10 | ||
| II | −1.2403 | 1.3436 | 0.05 | ||
| III | −1.1574 | 1.1341 | 0.10 | ||
| IV | −0.9712 | 1.0553 | 0.20 | ||
| Gamma distribution | Venue type | ||||
| I | 3.9368 | 0.1061 | 0.05 | ||
| II | 5.1326 | 0.0800 | 0.05 | ||
| III | 6.1838 | 0.0689 | 0.05 | ||
| IV | 6.4089 | 0.0658 | 0.25 | ||
| Gamma distribution | Venue type | ||||
| I | 2.0994 | 9.9279 | 0.10 | ||
| II | 2.2415 | 7.4136 | 0.05 | ||
| III | 2.0866 | 5.6598 | 0.25 | ||
| IV | 1.9401 | 5.5265 | 0.20 | ||
| Rμ/% | Reliability |
|---|---|
| 7.0 | 98.49% |
| 4.0 | 96.38% |
| 3.3 | 92.01% |
| 2.0 | 83.74% |
| 1.0 | 56.82% |
| Rμ/% | Reliability |
|---|---|
| 7.0 | 98.18% |
| 4.0 | 93.24% |
| 3.3 | 86.38% |
| 2.0 | 71.65% |
| 1.0 | 36.62% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Li, G.; Du, C.; Guan, Y.; Xu, S.; Li, S. Seismic Reliability Analysis of Highway Pile–Plate Structures Considering Dual Stochasticity of Parameters and Excitation via Probability Density Evolution. Infrastructures 2025, 10, 131. https://doi.org/10.3390/infrastructures10060131
Huang L, Li G, Du C, Guan Y, Xu S, Li S. Seismic Reliability Analysis of Highway Pile–Plate Structures Considering Dual Stochasticity of Parameters and Excitation via Probability Density Evolution. Infrastructures. 2025; 10(6):131. https://doi.org/10.3390/infrastructures10060131
Chicago/Turabian StyleHuang, Liang, Ge Li, Chaowei Du, Yujian Guan, Shizhan Xu, and Shuaitao Li. 2025. "Seismic Reliability Analysis of Highway Pile–Plate Structures Considering Dual Stochasticity of Parameters and Excitation via Probability Density Evolution" Infrastructures 10, no. 6: 131. https://doi.org/10.3390/infrastructures10060131
APA StyleHuang, L., Li, G., Du, C., Guan, Y., Xu, S., & Li, S. (2025). Seismic Reliability Analysis of Highway Pile–Plate Structures Considering Dual Stochasticity of Parameters and Excitation via Probability Density Evolution. Infrastructures, 10(6), 131. https://doi.org/10.3390/infrastructures10060131





