Macro-Level Modeling of Traffic Crash Fatalities at the Scene: Insights for Road Safety
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Database
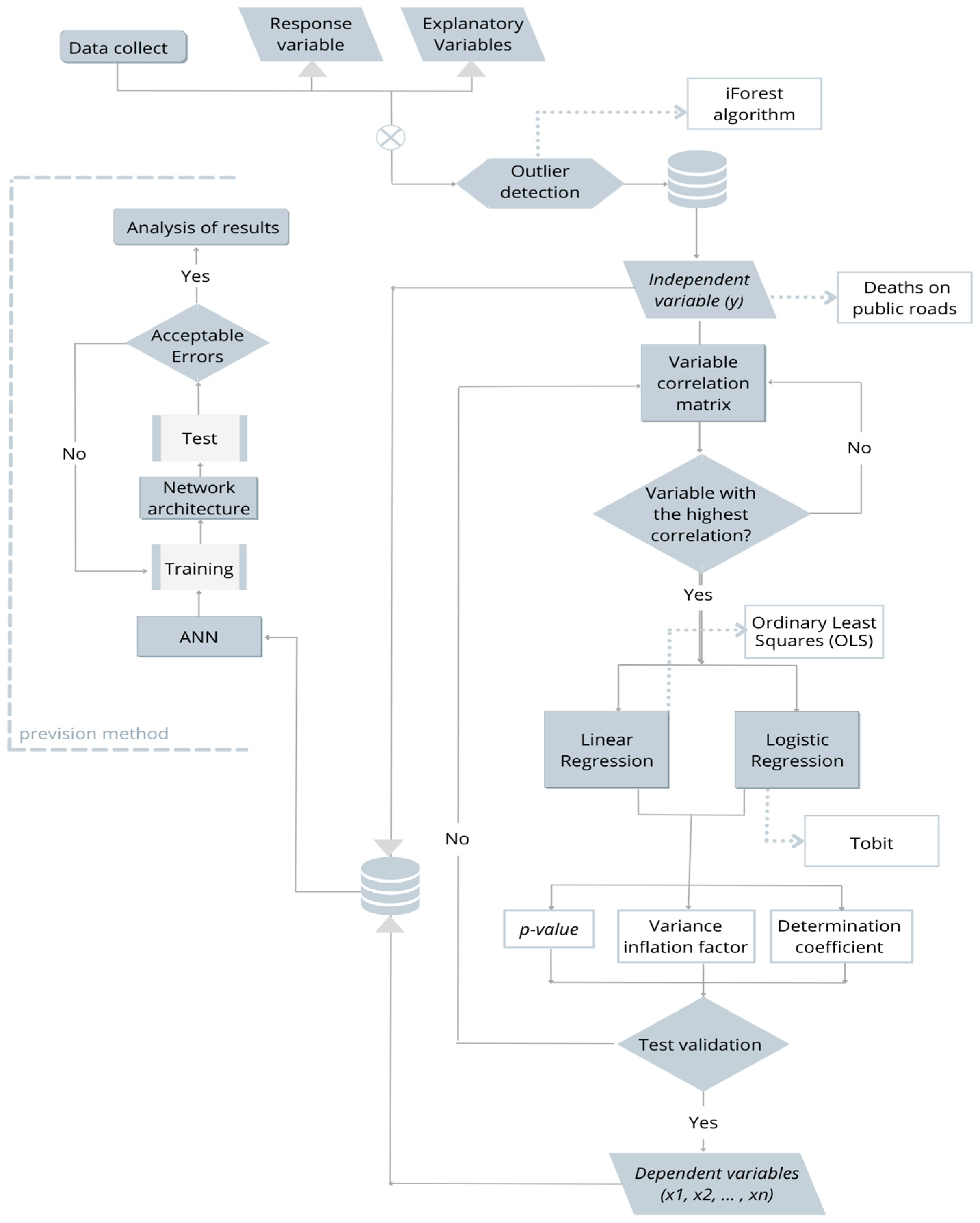
2.3. Methodological Steps
2.3.1. Database Treatment
2.3.2. Correlation Statistics and Linearity Verifications
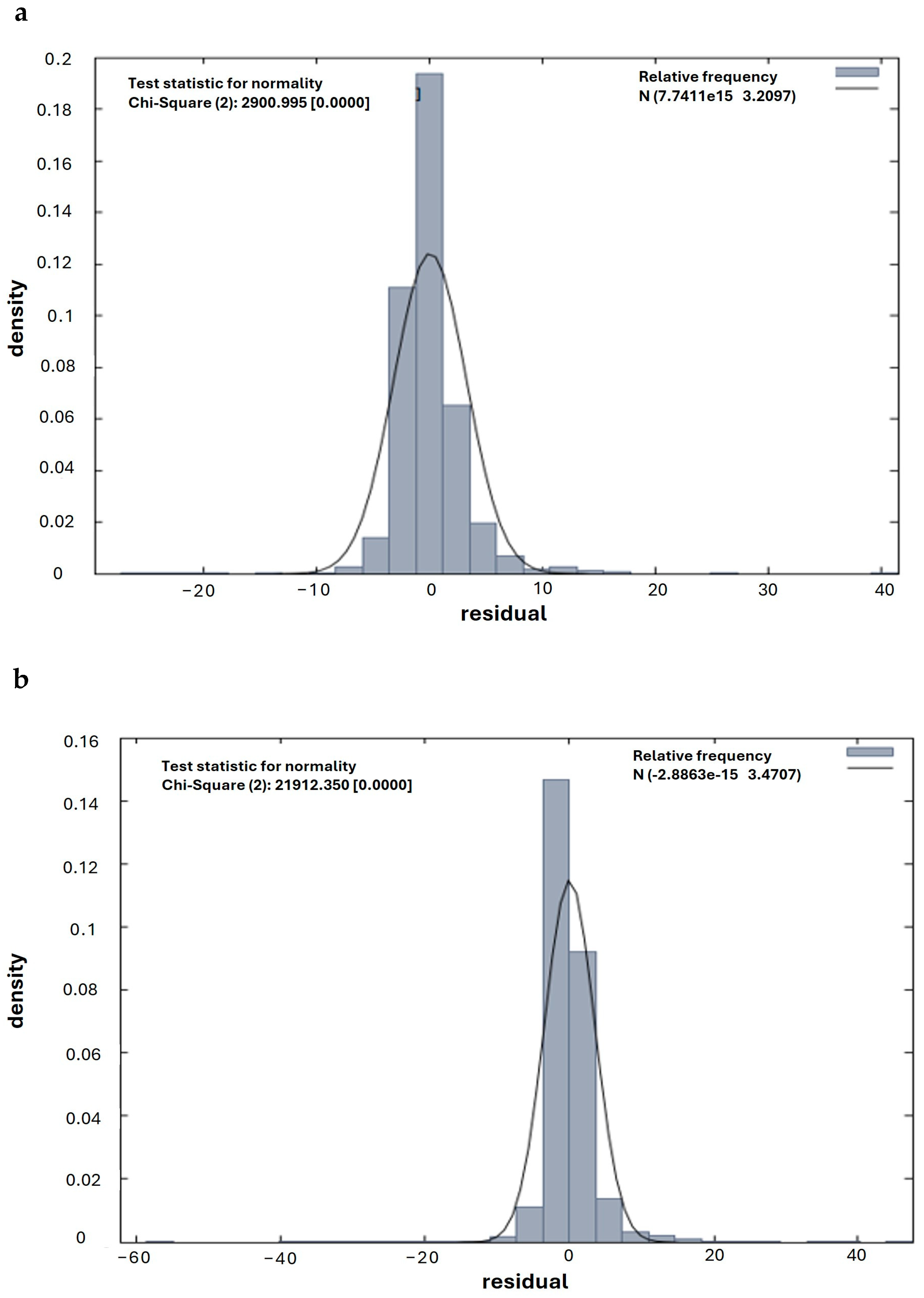
2.3.3. Regression Models and Statistical Validation
2.3.4. Predicting Occurrences with Artificial Neural Networks (ANNs)
3. Results
3.1. Mutual Information Statistics
3.2. Artificial Neural Network Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- WHO. Global Status Report on Road Safety 2023. Available online: https://www.who.int/publications/i/item/9789241565684 (accessed on 12 March 2025).
- UN. Improving Global Road Safety. Available online: https://undocs.org/en/A/RES/74/299 (accessed on 20 October 2024).
- UN. The Millennium Development Goals Report 2015. Available online: https://www.un.org/millenniumgoals/2015_MDG_Report/pdf/MDG%202015%20rev%20(July%201).pdf (accessed on 20 October 2024).
- WHO. Road Traffic Injuries. Available online: https://www.who.int/health-topics/road-safety#tab=tab_1 (accessed on 20 October 2024).
- ONSV. Estudos e Pesquisas. Available online: http://iris.onsv.org.br/iris-beta/#/stats/maps (accessed on 20 October 2024).
- Lu, P.; Zheng, Z.; Ren, Y.; Zhou, X.; Keramati, A.; Tolliver, D.; Huang, Y. A gradient boosting crash prediction approach for highway-rail grade crossing crash analysis. J. Adv. Transp. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Rahman, M.S.; Abdel-Aty, M.; Hasan, S.; Cai, Q. Applying machine learning approaches to analyze the vulnerable road-users’ crashes at statewide traffic analysis zones. J. Saf. Res. 2019, 70, 275–288. [Google Scholar] [CrossRef] [PubMed]
- Pervaz, S.; Bhowmik, T.; Eluru, N. Integrating macro and micro level crash frequency models considering spatial heterogeneity and random effects. Anal. Methods Accid. Res. 2022, 36, 100238. [Google Scholar] [CrossRef]
- HSM. Highway Safety Manual, 3rd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010; p. 19192. [Google Scholar]
- Ramírez, A.F.; Valencia, C. Spatiotemporal correlation study of traffic accidents with fatalities and injuries in Bogota, Colombia. Accid. Anal. Prev. 2021, 149, 105848. [Google Scholar] [CrossRef]
- Pljakić, M.; Jovanović, D.; Matović, B.; Mićić, S. Macro-level accident modeling in Novi Sad: A spatial regression approach. Accid. Anal. Prev. 2019, 132, 105259. [Google Scholar] [CrossRef]
- Tang, J.; Gao, F.; Liu, F.; Han, C.; Lee, J. Spatial heterogeneity analysis of macro-level crashes using geographically weighted Poisson quantile regression. Accid. Anal. Prev. 2020, 148, 105833. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Wang, Y.; Wang, Y. Geographically weighted poisson regression under linear model of coregionalization assistance: Application to a bicycle crash study. Accid. Anal. Prev. 2021, 159, 106230. [Google Scholar] [CrossRef]
- Oluwajana, S.D.; Park, P.Y.; Cavalho, T. Macro-level collision prediction using geographically weighted negative binomial regression. J. Transp. Saf. Secur. 2022, 14, 1085–1120. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Pei, Y. A systematic approach to macro-level safety assessment and contributing factors analysis considering traffic crashes and violations. Accid. Anal. Prev. 2024, 194, 107323. [Google Scholar] [CrossRef]
- Ambo, T.B.; Ma, J.; Fu, C.; Atumo, E.A. Investigating road conditions of crash blackspots in Addis Ababa, Ethiopia: A random parameters negative binomial model. Int. Jor. Crashworthiness 2024, 29, 521–532. [Google Scholar] [CrossRef]
- Yuan, J.; Abdel-Aty, M. Approach-level real-time crash risk analysis for signalized intersections. Accid. Anal. Prev. 2018, 119, 274–289. [Google Scholar] [CrossRef]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O. Prediction and modeling of traffic flow of human-driven vehicles at a signalized road intersection using artificial neural network model: A South African road transportation system scenario. Transp. Eng. 2021, 6, 100095. [Google Scholar] [CrossRef]
- Amorim, B.D.S.P.; Firmino, A.A.; Baptista, C.D.S.; Júnior, G.B.; Paiva, A.C.D.; Júnior, F.E.D.A. A Machine Learning Approach for Classifying Road Accident Hotspots. ISPRS Int. J. Geo-Inf. 2023, 12, 227. [Google Scholar] [CrossRef]
- Delen, D.; Sharda, R.; Bessonov, M. Identifying significant predictors of injury severity in traffic accidents using a series of artificial neural networks. Accid. Anal. Prev. 2006, 38, 434–444. [Google Scholar] [CrossRef]
- Silva, F.G.F.; Falcão, V.A.; de Farias Domingos, M.C.; Negri, N.A.R. Analysis of the generalized use of logit models in simulating changes in decision attributes at the airport check-in. Res. Transp. Econ. 2022, 92, 101182. [Google Scholar] [CrossRef]
- Leão e Silva, C.J.; de Andrade, M.O.; Falcão, V.A.; da Silva, C.F.A. The geographical characteristics of subsidized air routes serving as lifelines. J. Air Transp. Manag. 2022, 104, 102280. [Google Scholar] [CrossRef]
- Silva, C.F.A.; de Andrade, M.O.; dos Santos, A.M.; de Melo, S.N. Road network and deforestation of indigenous lands in the Brazilian Amazon. Transp. Res. Part D Transp. Environ. 2023, 119, 103735. [Google Scholar] [CrossRef]
- Silva, C.F.A.; de Andrade, M.O.; dos Santos, A.M.; Falcão, V.A.; Martins, S.F.S. The drivers of illegal mining on Indigenous Lands in the Brazilian Amazon. Extr. Ind. Soc. 2023, 16, 101354. [Google Scholar] [CrossRef]
- Wang, C.; Quddus, M.A.; Ison, S.G. Predicting accident frequency at their severity levels and its application in site ranking using a two-stage mixed multivariate model. Accid. Anal. Prev. 2011, 436, 1979–1990. [Google Scholar] [CrossRef]
- Hasan, A.S.; Kabir, M.A.B.; Jalayer, M.; Das, S. Severity modeling of work zone crashes in New Jersey using machine learning models. J. Transp. Saf. Secur. 2023, 15, 604–635. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C.; Halkias, B.M. Freeway operations, spatiotemporal-incident characteristics, and secondary-crash occurrence. Transp. Res. Rec. 2010, 21781, 1–9. [Google Scholar] [CrossRef]
- Jia, R.; Khadka, A.; Kim, I. Traffic crash analysis with point-of-interest spatial clustering. Accid. Anal. Prev. 2018, 121, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Cantillo, V.; Márquez, L.; Díaz, C.J. An exploratory analysis of factors associated with traffic crashes severity in Cartagena, Colombia. Accid. Anal. Prev. 2020, 146, 105749. [Google Scholar] [CrossRef]
- Santos, A.M.; Santos, B.R.I.; da Silva, C.F.A.; de Almeida Junior, P.M.; Falcão, V.A. Spatio-temporal analysis of accident hotspots on federal highways in the state of Goiás, Brazil. GeoJournal 2021, 87, 3839–3854. [Google Scholar] [CrossRef]
- Wachnicka, J.; Palikowska, K.; Kustra, W.; Kiec, M. Spatial differentiation of road safety in Europe based on NUTS-2 regions. Accid. Anal. Prev. 2021, 150, 105849. [Google Scholar] [CrossRef]
- Mathew, S.; Pulugurtha, S.S.; Duvvuri, S. Exploring the effect of road network, demographic, and land use characteristics on teen crash frequency using geographically weighted negative binomial regression. Accid. Anal. Prev. 2022, 168, 106615. [Google Scholar] [CrossRef] [PubMed]
- Campos, C.I.D.; Santos, M.C.D.; Pitombo, C.S. Characterization of municipalities with high road traffic fatality rates using macro-level data and the CART algorithm. J. Appl. Res. Technol. 2018, 16, 79–94. [Google Scholar] [CrossRef]
- IBGE. Estimativas da População em 2020. Available online: https://www.ibge.gov.br/estatisticas/sociais/populacao/9103-estimativas-de-populacao.html (accessed on 20 October 2024).
- Ministério da Infraestrutura. Available online: https://www.gov.br/infraestrutura/pt-br (accessed on 20 October 2024).
- SENATRAN. Frota Veicular. Available online: https://portalservicos.senatran.serpro.gov.br/#/home (accessed on 20 October 2024).
- IBGE. Divisão Territorial. Available online: https://educa.ibge.gov.br/criancas/brasil/nosso-territorio/19637-divisao-territorial.html (accessed on 20 October 2024).
- DATASUS. Taxa de Mortalidade por Acidentes de Transporte. Available online: http://tabnet.datasus.gov.br/cgi/idb2000/fqc12_1.htm (accessed on 20 October 2024).
- De Oliveira, L.K.; de Oliveira, I.K.; Caliari, P.H.C.; de Mello, C.A.; Maia, M.L.A. Influence of demographic and socioeconomic factors on motorcycle usage in Brazil. Case Stud. Transp. Policy 2021, 94, 1757–1769. [Google Scholar] [CrossRef]
- IBGE. Estimativas da População em 2019. Available online: https://www.ibge.gov.br/estatisticas/sociais/populacao/9103-estimativas-de-populacao.html (accessed on 20 October 2024).
- IBGE. Censo 2010. Available online: https://censo2010.ibge.gov.br/ (accessed on 20 October 2022).
- DNIT. 2020. Available online: https://www.gov.br/dnit/pt-br/acesso-a-informacao/servidores/processos-seletivos/Edital42.2020.pdf (accessed on 20 October 2022).
- Banco Central. 2019. Available online: https://dadosabertos.bcb.gov.br/ (accessed on 20 October 2024).
- Ferraz, A.C.P.; Raia, A.A., Jr.; Bezerra, B.; Bastos, T.; Rodrigues, K. Segurança Viária; Suprema Gráfica e Editora: São Carlos, SP, Brazil, 2012. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Hussain, F.; Li, Y.; Arun, A.; Haque, M.M. A hybrid modelling framework of machine learning and extreme value theory for crash risk estimation using traffic conflicts. Anal. Methods Accid. Res. 2022, 36, 100248. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences, 3rd ed.; Brooks/Cole Publishing: Pacific Grove, CA, USA, 1996. [Google Scholar]
- Greene, W.H. The Behavior of the Fixed Effects Estimator in Nonlinear Models. unpublished work.
- Amore, M.D.; Murtinu, S. Tobit models in strategy research: Critical issues and applications. Glob. Strateg. J. 2021, 11, 331–355. [Google Scholar] [CrossRef]
- Schutz, M.; Decroze, C.; Lalande, M.; Lenoir, B. Neural networks to increase range resolution of FMCW Radar. IEEE Sens. Lett. 2020, 48, 1–4. [Google Scholar] [CrossRef]
- Luger, G.F. Inteligência Artificial: Estruturas e Estratégias Para a Solução de Problemas Complexos, 3rd ed.; Bookman: Porto Alegre, Brazil, 2004. [Google Scholar]
- Chen, Z.; Wang, Y.; Zhou, L. Predicting weather-induced delays of high-speed rail and aviation in China. Transp. Policy 2021, 101, 1–13. [Google Scholar] [CrossRef]
- Yu, B.; Guo, Z.; Asian, S.; Wang, H.; Chen, G. Flight delay prediction for commercial air transport: A deep learning approach. Transp. Res. Part E 2019, 125, 203–221. [Google Scholar] [CrossRef]
- Sultan, Z.; Ngadiman, N.I.; Kadir, F.D.A.; Roslan, N.F.; Moeinaddini, M. Factor analysis of motorcycle crashes in Malaysia. Plan. Malays. 2016, 14. Special Issue 4. [Google Scholar] [CrossRef]
- Zare Sakhvidi, M.J.; Yang, J.; Mohammadi, D.; FallahZadeh, H.; Mehrparvar, A.; Stevenson, M.; Dadvand, P. Extreme environmental temperatures and motorcycle crashes: A time-series analysis. Environ. Sci. Pollut. Res. 2022, 29, 76251–76262. [Google Scholar] [CrossRef]
- French, M.T.; Gumus, G. Watch for motorcycles! The effects of texting and handheld bans on motorcyclist fatalities. Soc. Sci. Med. 2018, 216, 81–87. [Google Scholar] [CrossRef]
- Chang, Y.H.; Hou, W.H.; Wu, K.F.; Li, C.Y.; Hsu, I.L. Risk of motorcycle collisions among patients with type 2 diabetes: A population-based cohort study with age and sex stratifications in Taiwan. Acta Diabetol. 2022, 59, 1625–1634. [Google Scholar] [CrossRef]
- Kent, T.; Miller, J.; Shreve, C.; Allenback, G.; Wentz, B. Comparison of injuries among motorcycle, moped and bicycle traffic accident victims. Traffic Inj. Prev. 2022, 23, 34–39. [Google Scholar] [CrossRef]
- Tumwesigye, N.M.; Atuyambe, L.M.; Kobusingye, O.K. Factors Associated with Injuries among Commercial Motorcyclists: Evidence from a Matched Case Control Study in Kampala City, Uganda. PLoS ONE 2016, 11, e0148511. [Google Scholar] [CrossRef]
- Ha, N.T.; Ederer, D.; Vo, V.A.H.; Pham, A.V.; Mounts, A.; Nolen, L.D.; Sugerman, D. Changes in motorcycle-related injuries and deaths after mandatory motorcycle helmet law in a district of Vietnam. Traffic Inj. Prev. 2018, 19, 75–80. [Google Scholar] [CrossRef]
- Kitamura, Y.; Hayashi, M.; Yagi, E. Traffic problems in Southeast Asia featuring the case of Cambodia’s traffic accidents involving motorcycles. IATSS Res. 2018, 42, 163–170. [Google Scholar] [CrossRef]
- Wali, B.; Ahmad, N.; Khattak, A.J. Toward better measurement of traffic injuries–Comparison of anatomical injury measures in predicting the clinical outcomes in motorcycle crashes. J. Saf. Res. 2022, 80, 175–189. [Google Scholar] [CrossRef]
- Silva, I.M.R. Perfil dos acidentes motociclísticos: Uma revisão integrativa na Região Nordeste do Brasil. Arch. Health 2022, 32, 175–178. Available online: https://ojs.latinamericanpublicacoes.com.br/ojs/index.php/ah/article/view/924 (accessed on 8 December 2023).
- Cavalcanti, A.L.; Lucena, B.; Rodrigues, I.S.; Silva, A.L.; Lima, T.T.; Xavier, A.F.C. Motorcycle accidents: Morbidity and associated factors in a city of northeast of Brazil. Tanzan. J. Health Res. 2013, 15, 209–215. [Google Scholar] [CrossRef][Green Version]
- Siman-Tov, M.; Radomislensky, I.; Israel Trauma Group; Peleg, K. The casualties from electric bike and motorized scooter road accidents. Traffic Inj. Prev. 2017, 18, 318–323. [Google Scholar] [CrossRef]
- Salehi, M.A.S.; Mehmandar, M.; Mobaderi, T. Application of Growth Mixture Model to Analysis of Road Traffic Death Rate in the World, 2007–2013. Iran. J. Pub. Health. 2017, 46, 112–119. [Google Scholar]
- Gómez-García, L.; Hidalgo-Solórzano, E.; Pérez-Núñez, R.; Jacobo-Zepeda, V.F.; Ascencio-Tene, R.G.; Lunnen, J.C.; Mehmood, A. Factors associated with the severity of road traffic injuries from emergency department based surveillance system in two Mexican cities. BMC Emerg. Med. 2022, 22, 1–11. [Google Scholar] [CrossRef]
- Cabral, E.L.D.S.; Castro, W.R.S.; Florentino, D.R.D.M.; Viana, D.D.A.; Costa Junior, J.F.D.; Souza, R.P.D.; Medeiros, A.C. Response time in the emergency services. Systematic review. Acta Cir. Bras. 2018, 33, 1110–1121. [Google Scholar] [CrossRef]
- Truong, D. Using causal machine learning for predicting the risk of flight delays in air transportation. J. Air Transp. Manag. 2021, 91, 101993. [Google Scholar] [CrossRef]


| State | Resident Population | Car Fleet | Deaths on Public Roads | Number of Municipalities |
|---|---|---|---|---|
| Acre (AC) | 881,935 | 91,615 | 119 | 22 |
| Alagoas (AL) * | 3,337,357 | 374,169 | 610 | 102 |
| Amapá (AP) | 845,731 | 85,529 | 85 | 16 |
| Amazonas (AM) | 4,144,597 | 412,140 | 471 | 62 |
| Bahia (BA) * | 14,873,064 | 1,907,497 | 2470 | 417 |
| Ceará (CE) * | 9,132,078 | 1,192,715 | 1640 | 184 |
| Distrito Federal (DF) | 3,015,268 | 1,328,622 | 339 | 1 |
| Espírito Santo (ES) | 4,018,650 | 990,203 | 759 | 78 |
| Goiás (GO) | 7,018,354 | 1,910,006 | 1480 | 246 |
| Maranhão * (MA) | 7,075,181 | 457,104 | 1280 | 217 |
| Mato Grosso (MT) | 3,484,466 | 764,931 | 1038 | 141 |
| Mato Grosso do Sul (MS) | 2,778,986 | 763,091 | 638 | 79 |
| Minas Gerais (MG) | 21,168,791 | 6,467,501 | 3337 | 853 |
| Pará (PA) | 8,602,865 | 631,396 | 1428 | 144 |
| Paraíba (PB) * | 3,996,496 | 552,067 | 774 | 223 |
| Paraná (PR) | 11,433,957 | 4,573,703 | 2433 | 399 |
| Pernambuco (PE) * | 9,557,071 | 1,369,199 | 1511 | 185 |
| Piauí (PI) * | 3,273,227 | 380,035 | 923 | 224 |
| Rio de Janeiro (RJ) | 17,264,943 | 4,646,402 | 1526 | 92 |
| Rio Grande do Norte (RN) * | 3,506,853 | 579,196 | 473 | 167 |
| Rio Grande do Sul (RS) | 11,377,239 | 4,432,248 | 1663 | 497 |
| Rondônia (RO) | 1,777,225 | 298,059 | 382 | 52 |
| Roraima (RR) | 605,761 | 78,387 | 124 | 15 |
| Santa Catarina (SC) | 7,164,788 | 3,053,350 | 1440 | 295 |
| São Paulo (SP) | 44,996,070 | 18,753,362 | 5057 | 645 |
| Sergipe (SE) * | 2,298,696 | 341,946 | 401 | 75 |
| Tocantins (TO) | 1,572,866 | 223,715 | 478 | 139 |
| Variable Group | Variable Name | Description | Year | Unit | Variable Group |
|---|---|---|---|---|---|
| Response Variable | Deaths on public roads | Deaths on public roads due to traffic crashes | 2019 | Absolute number | [38] |
| Explanatory Variables | Road fatality rate | Deaths divided by population multiplied by 100,000 | 2019 | Deaths/100,000 inhabitants | [38,40] |
| Deaths by type | Deaths resulting from a specific incident | 2019 | Absolute number | [40] | |
| Deaths by Occurrence rate | Deaths by occurrence divided by the population of a given area, then multiplied by 100,000 inhabitants. | 2019 | Deaths/100,000 inhabitants | [38,40] | |
| Cars per capita | Motorized vehicles per inhabitant | Vehicles/inhabitant | [36,40,41] | ||
| Motorcycles and scooters per capita | Motorcycles and scooters per inhabitant | 2019 | Motorcycle/inhabitant | [36,40,41] | |
| Road extension by cars | Total road mileage divided by the number of cars | 2019 | km/car | [36,42] | |
| Road extension by motorcycles | Total road mileage divided by the number of motorcycles | 2019 | km/motorcycle | [36,42] | |
| Municipal human development index | A composite measure of indicators from three dimensions of human development: longevity, education, and income | 2019 | Index | [41] | |
| Road extension by municipality | Length of roads per municipality road mileage in km | 2019 | km | [40,42] | |
| Road density | Road Mileage in km per inhabitant | 2020 | km/inhabitant | [40,42] | |
| Investment in road infrastructure per capita | Monetary values (in Brazilian reals) invested in road infrastructure per inhabitant | 2020 | R$/inhabitant | [43] | |
| Investment in housing and urban development per capita | Monetary values (in real) invested in housing and urbanization per inhabitant | 2019 | R$/inhabitant | [43] | |
| GDP per capita | Gross domestic product per capita | 2019 | R$/inhabitant | [40,43] | |
| Demographic density | Number of people divided by the area of the municipality | 2019 | Inhabitants/km2 | [40] | |
| SUS emergency units | Number of health units with emergency care | 2019 | Absolute number | [38] |
| Variable | Mean | Median | Stan. Dev. | Min | Max |
|---|---|---|---|---|---|
| Deaths on public roads | 3.00 | 1.00 | 6.85 | 0.00 | 242.00 |
| Road fatality rate | 13.71 | 8.18 | 22.26 | 0.00 | 585.50 |
| Deaths by occurrence | 5.91 | 2.00 | 21.58 | 0.00 | 763.00 |
| Deaths by occurrence rate | 18.40 | 13.09 | 30.46 | 0.00 | 1099.00 |
| Cars per capita | 0.20 | 0.18 | 0.21 | 0.00 | 11.56 |
| Motorcycles and scooters per capita | 0.14 | 0.13 | 0.10 | 0.00 | 5.61 |
| Extension of highways by cars | 0.66 | 0.24 | 2.36 | 0.00 | 105.90 |
| Extension of highways by motorcycles | 0.45 | 0.29 | 0.88 | 0.01 | 41.24 |
| HDI-M | 0.66 | 0.67 | 0.08 | 0.00 | 0.86 |
| Road extension by municipality | 660.70 | 415.60 | 874.90 | 16.27 | 20,918.00 |
| Road density | 1.35 | 1.02 | 1.60 | 0.00 | 20.93 |
| Investment in transportation per capita | 124.60 | 33.10 | 241.60 | 0.00 | 4498.00 |
| Investment in housing and urban development per capita | 300.50 | 243.90 | 262.30 | 0.00 | 3645.00 |
| GDP per capita | 24.55 | 18.19 | 25.55 | 4.48 | 464.90 |
| Demographic density | 120.00 | 25.07 | 627.40 | 0.05 | 14,208.00 |
| SUS emergency units | 1.87 | 1.00 | 6.18 | 0.00 | 303.00 |
| (a) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 1 | |||||||||||||||
| 2 | 0.1 | 1 | ||||||||||||||
| 3 | 0.9 | 0 | 1 | |||||||||||||
| 4 | 0.2 | 0.9 | 0.1 | 1 | ||||||||||||
| 5 | 0.1 | 0 | 0.1 | 0 | 1 | |||||||||||
| 6 | 0.1 | 0 | 0 | 0 | 0.6 | 1 | ||||||||||
| 7 | −0.1 | 0 | 0 | 0 | −0.2 | −0.1 | 1 | |||||||||
| 8 | −0.1 | 0.1 | −0.1 | 0.1 | −0.1 | −0.2 | 0.6 | 1 | ||||||||
| 9 | 0.2 | 0 | 0.2 | 0.1 | 0.6 | 0.2 | −0.3 | −0.1 | 1 | |||||||
| 10 | 0.7 | 0 | 0.7 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0.2 | 1 | ||||||
| 11 | 0.3 | 0.1 | 0.4 | −0.1 | 0.2 | 0 | −0.1 | −0.1 | 0.3 | 0.2 | 1 | |||||
| 12 | −0.1 | 0.1 | −0.1 | 0 | 0.3 | 0.1 | 0 | 0.1 | 0.3 | −0.1 | 0 | 1 | ||||
| 13 | 0 | 0.1 | 0 | 0 | 0.2 | 0 | 0 | 0 | 0.3 | 0 | 0.1 | 0.1 | 1 | |||
| 14 | 0.1 | 0.1 | 0.1 | 0.1 | 0.3 | 0 | −0.1 | 0 | 0.4 | 0.2 | 0.2 | 0.2 | 0.4 | 1 | ||
| 15 | 0.3 | −0.1 | 0.4 | 0 | 0.1 | 0 | 0 | −0.1 | 0.2 | 0.2 | 0.8 | −0.1 | 0 | 0.1 | 1 | |
| 16 | 0.8 | 0 | 0.9 | 0 | 0.1 | 0 | 0 | −0.1 | 0.2 | 0.6 | 0.4 | −0.1 | 0 | 0.1 | 0.4 | 1 |
| (b) | ||||||||||||||||
| Variables | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 1 | |||||||||||||||
| 2 | 0.3 | 1 | ||||||||||||||
| 3 | 0.8 | 0 | 1 | |||||||||||||
| 4 | 0.3 | 0.9 | 0.2 | 1 | ||||||||||||
| 5 | 0.4 | 0 | 0.4 | 0.1 | 1 | |||||||||||
| 6 | 0.2 | 0.1 | 0.1 | 0.2 | 0.5 | 1 | ||||||||||
| 7 | −0.1 | 0 | −0.1 | 0 | −0.3 | −0.2 | 1 | |||||||||
| 8 | −0.2 | 0 | −0.1 | 0 | −0.2 | −0.4 | 0.7 | 1 | ||||||||
| 9 | 0.5 | 0 | 0.4 | 0.1 | 0.6 | 0.3 | −0.2 | −0.3 | 1 | |||||||
| 10 | 0.6 | 0 | 0.5 | 0.2 | 0.3 | 0.1 | 0.1 | 0.2 | −0.3 | 1 | ||||||
| 11 | 0.4 | −0.1 | 0.5 | −0.1 | 0.5 | 0 | −0.2 | −0.1 | 0.2 | 0.2 | 1 | |||||
| 12 | 0 | 0 | 0 | 0 | −0.1 | 0 | 0.1 | 0.1 | −0.1 | 0 | −0.1 | 1 | ||||
| 13 | 0 | 0 | 0 | 0 | 0.2 | 0 | 0 | 0.1 | 0.1 | 0 | 0.1 | 0.1 | 1 | |||
| 14 | 0.2 | 0 | 0.1 | 0.1 | 0.2 | 0.1 | 0 | 0.1 | 0.3 | 0.3 | 0.2 | 0.2 | 0.3 | 1 | ||
| 15 | 0.4 | −0.1 | 0.6 | 0 | 0.3 | 0 | −0.1 | −0.1 | 0.4 | 0.2 | 0.8 | 0 | 0 | 0.1 | 1 | |
| 16 | 0.7 | 0 | 0.8 | 0.1 | 0.4 | 0.1 | −0.1 | −0.1 | 0.4 | 0.5 | 0.5 | 0 | 0 | 0.2 | 0.7 | 1 |
| Variable | Code |
|---|---|
| Deaths on public roads | 1 |
| Road fatality rate | 2 |
| Deaths by occurrence | 3 |
| Deaths by occurrence rate | 4 |
| Cars per capita | 5 |
| Motorcycles and scooters per capita | 6 |
| Extension of highways by cars | 7 |
| Extension of highways by motorcycles | 8 |
| HDI-M | 9 |
| Road extension by municipality | 10 |
| Road density | 11 |
| Investment in transportation per capita | 12 |
| Investment in housing and urban development per capita | 13 |
| GDP per capita | 14 |
| Demographic density | 15 |
| SUS emergency units | 16 |
| Data Set | Brazil | Northeast Region | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Models | OLS | TOBIT | OLS | TOBIT | ||||||
| Variable | Coef | p-Value | Coef | p- Value | VIF | Coef | p-Value | Coef | p- Value | VIF |
| Constant | −2.907 | <0.001 | −6.14512 | <0.001 | - | −6.682 | <0.001 | −8.942 | <0.001 | - |
| Motorcycles and scooters per capita | 1.127 | 0.0144 | 2.242 | <0.001 | 1.049 | 7.344 | 0.0021 | 10.025 | 0.0011 | 1.495 |
| HDI-M | 4.332 | <0.001 | 7.378 | <0.001 | 1.241 | 3.323 | 0.0049 | 4.105 | 0.0062 | 1.711 |
| Road extension per municipality | 0.003 | <0.001 | 0.0036 | <0.001 | 1.702 | 0.002 | <0.001 | 13.452 | <0.001 | 1.373 |
| Investment in transportation per capita | −0.001 | <0.001 | −0.0039 | <0.001 | 1.115 | −0.0002 | <0.001 | −0.003 | <0.001 | 1.055 |
| Investment in housing and urban development per capita | −0.0004 | 0.0217 | −0.0012 | <0.001 | 1.077 | −0.002 | 0.090 | −0.004 | <0.001 | 1.088 |
| Demographic density | 0.0002 | 0.0767 | 0.0003 | 0.0162 | 1.275 | −6.75 × 10−6 | <0.001 | 0.002 | 0.0369 | 1.095 |
| SUS emergency health units | 0.607 | <0.001 | 0.583 | <0.001 | 1.940 | 0.054 | <0.001 | 0.542 | <0.001 | 2.321 |
| Architecture | 1st Layer Intermediate | 2nd Layer Intermediate | 3rd Layer Intermediate | Use in the Model | ||||
|---|---|---|---|---|---|---|---|---|
| No. of Neurons | Activation Function | No. of Neurons | Activation Function | No. of Neurons | Activation Function | Brazil | Northeast | |
| A | 10 | Linear | 1 | Linear | - | - | X | X |
| B | 10 | * | 1 | * | - | - | X | X |
| C | 10 | Linear | 1 | * | - | - | X | X |
| D | 10 | Linear | 10 | Linear | 1 | Linear | X | X |
| E | 15 | Linear | 15 | Linear | 1 | Linear | X | - |
| F | 10 | * | 10 | * | 1 | * | - | X |
| Metric Brazil | ANN Architectures | ||||
| A | B | C | D | E | |
| RTraining | 0.86217 | 0.5467 | 0.75952 | 0.86244 | 0.86197 |
| F1 Score | 0.41 | 0.37 | 0.59 | 0.88 | 0.87 |
| Metric Northeast Region | ANN Architectures | ||||
| A | B | C | D | F | |
| RTraining | 0.7822 | 0.87094 | 0.75381 | 0.78467 | 0.83798 |
| F1 Score | 0.89 | 0.95 | 0.76 | 0.89 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, C.F.A.d.; Andrade, M.O.d.; Campos, C.; Santos, A.M.d.; Queiroz Júnior, H.d.S.; Falcão, V.A. Macro-Level Modeling of Traffic Crash Fatalities at the Scene: Insights for Road Safety. Infrastructures 2025, 10, 117. https://doi.org/10.3390/infrastructures10050117
Silva CFAd, Andrade MOd, Campos C, Santos AMd, Queiroz Júnior HdS, Falcão VA. Macro-Level Modeling of Traffic Crash Fatalities at the Scene: Insights for Road Safety. Infrastructures. 2025; 10(5):117. https://doi.org/10.3390/infrastructures10050117
Chicago/Turabian StyleSilva, Carlos Fabricio Assunção da, Mauricio Oliveira de Andrade, Cintia Campos, Alex Mota dos Santos, Hélio da Silva Queiroz Júnior, and Viviane Adriano Falcão. 2025. "Macro-Level Modeling of Traffic Crash Fatalities at the Scene: Insights for Road Safety" Infrastructures 10, no. 5: 117. https://doi.org/10.3390/infrastructures10050117
APA StyleSilva, C. F. A. d., Andrade, M. O. d., Campos, C., Santos, A. M. d., Queiroz Júnior, H. d. S., & Falcão, V. A. (2025). Macro-Level Modeling of Traffic Crash Fatalities at the Scene: Insights for Road Safety. Infrastructures, 10(5), 117. https://doi.org/10.3390/infrastructures10050117







