Empirical Investigation of the Effects of the Measurement-Data Size on the Bayesian Structural Model Updating of a High-Speed Railway Bridge
Abstract
1. Introduction
2. Measurement and Model Updating Methods
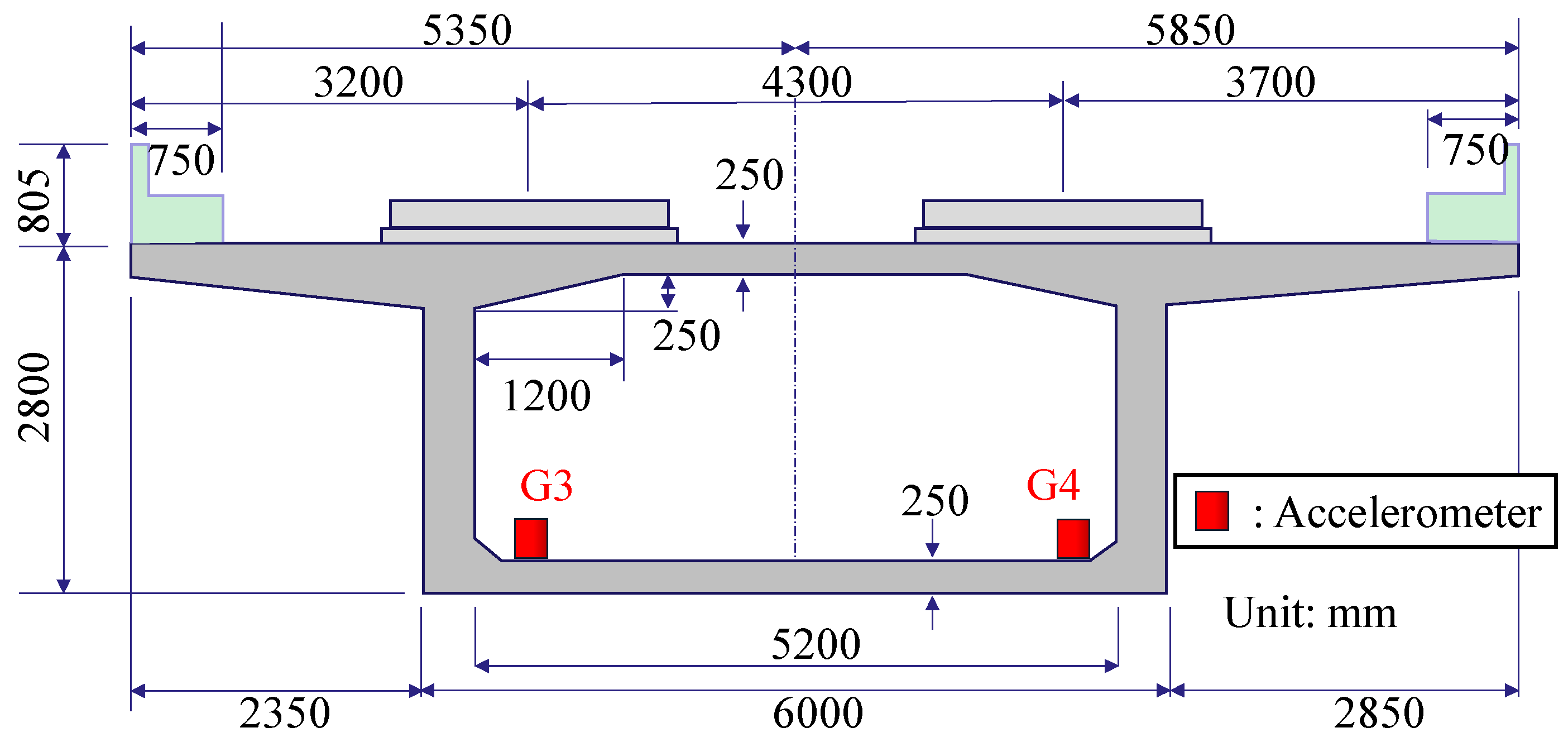
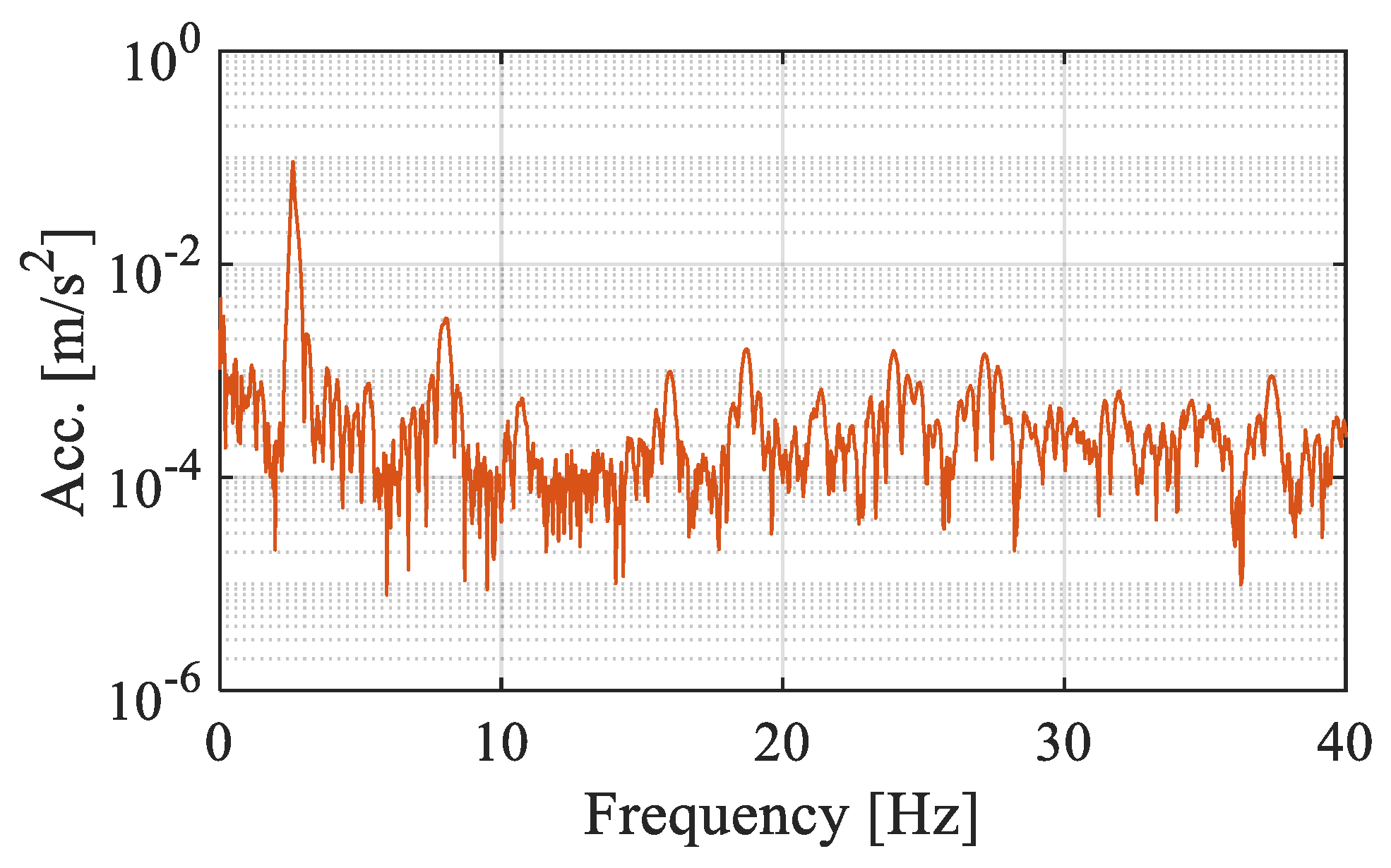
2.1. Test Bridge and Measurement Method
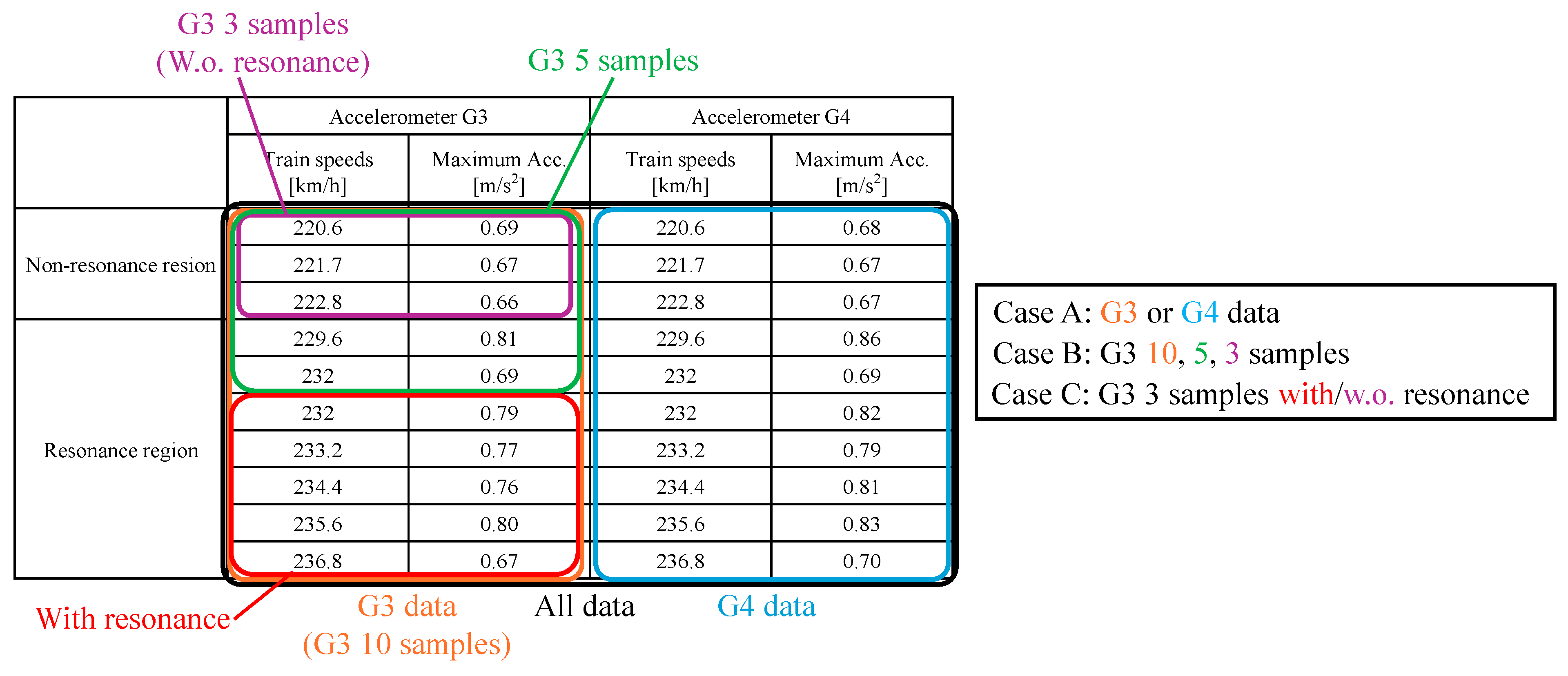
- All data (the all observation data from G3 and G4);
- Case A: G3 or G4 data;
- Case B: 10, 5, 3 samples from G3 data;
- Case C: with/without (w.o) resonance from G3 data.
2.2. Structural Modeling
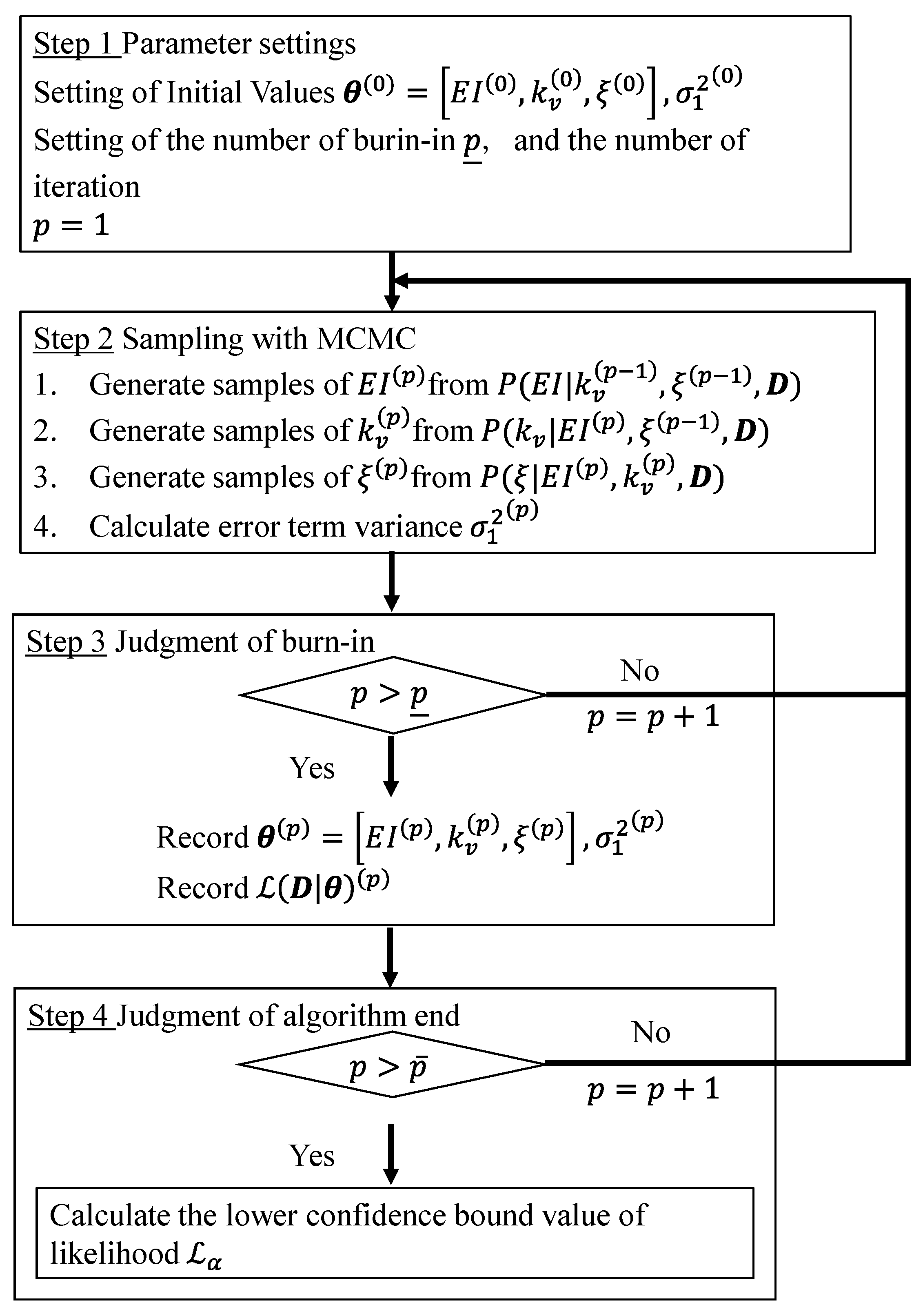
2.3. Structural Model Updating Method
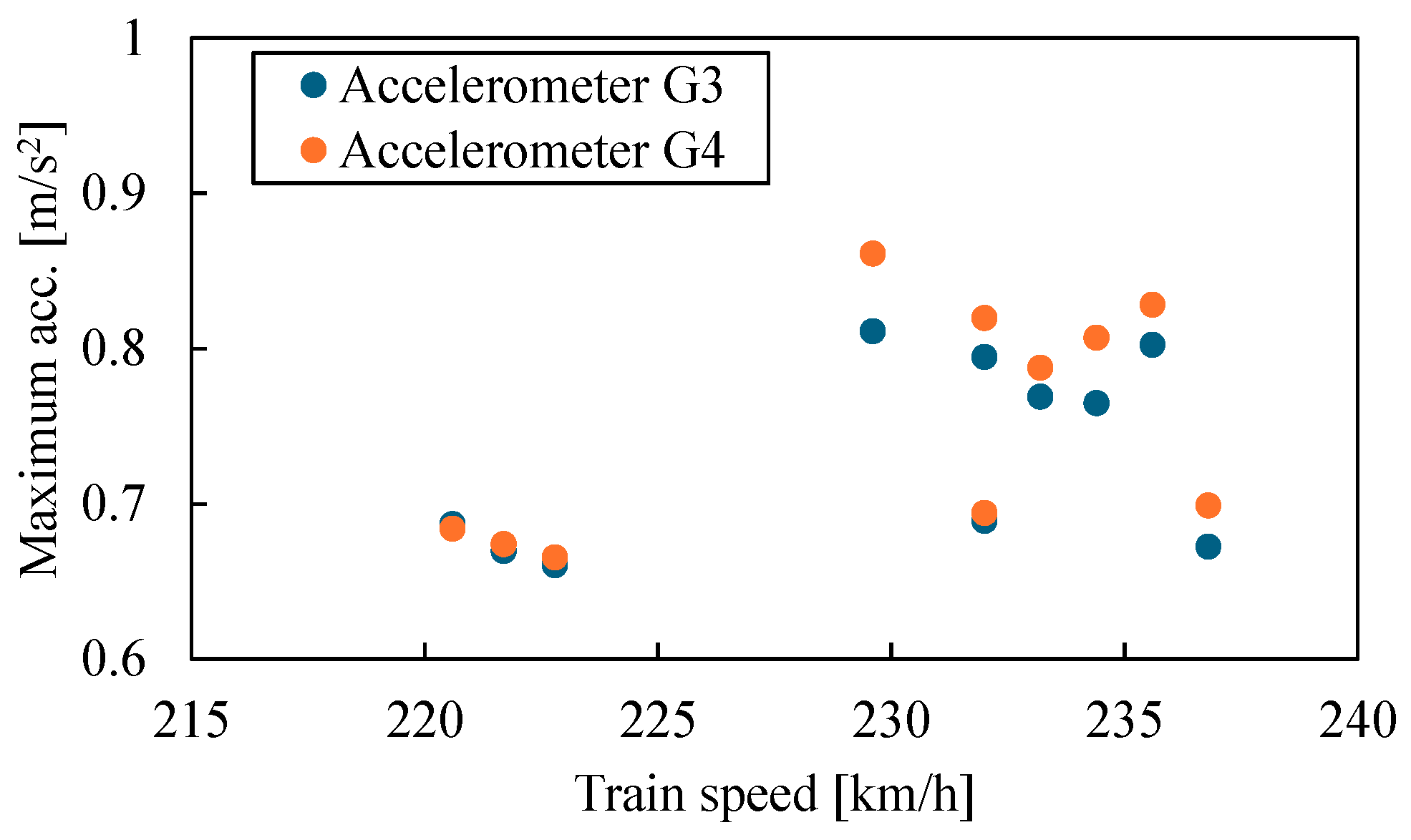
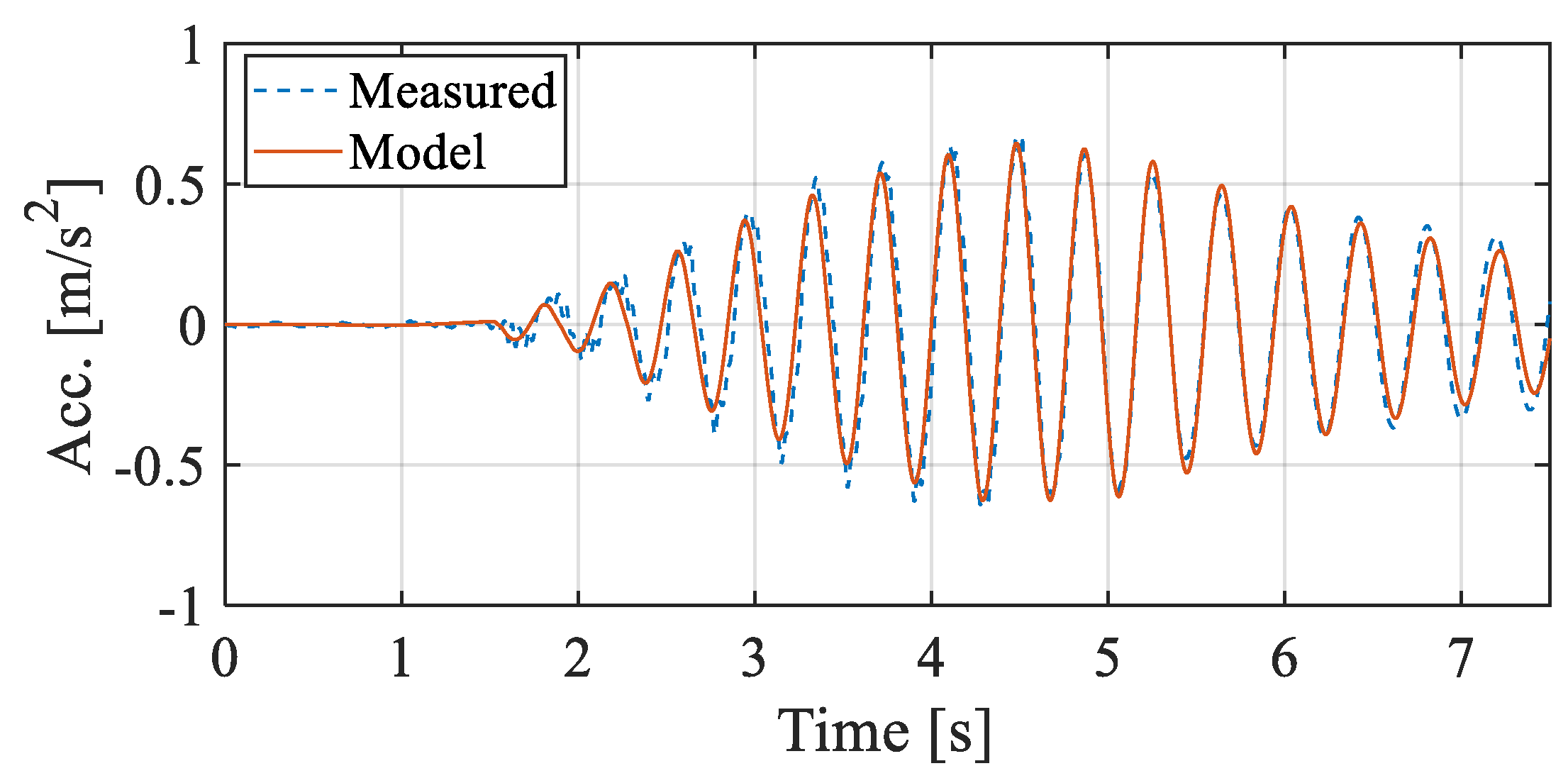
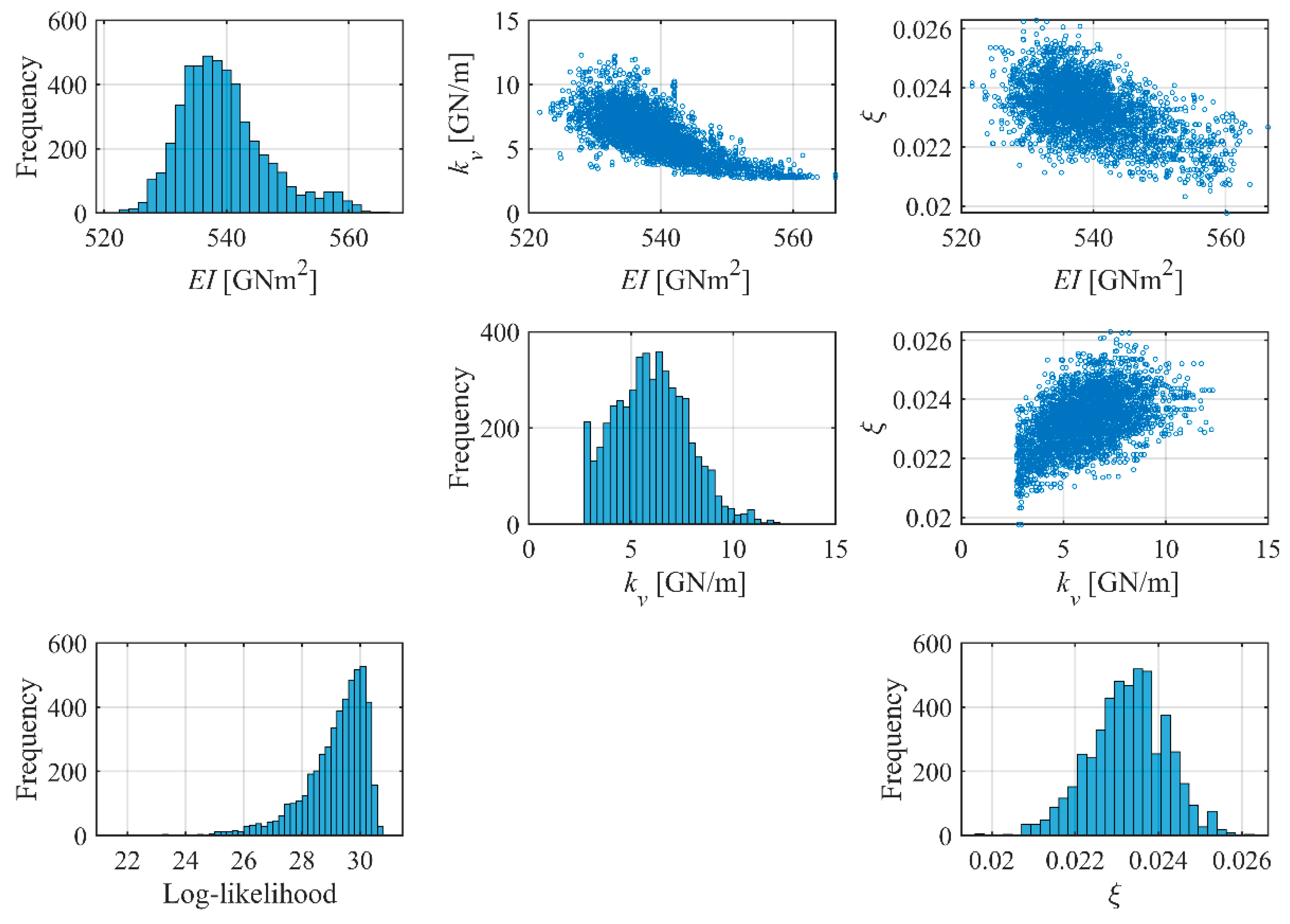
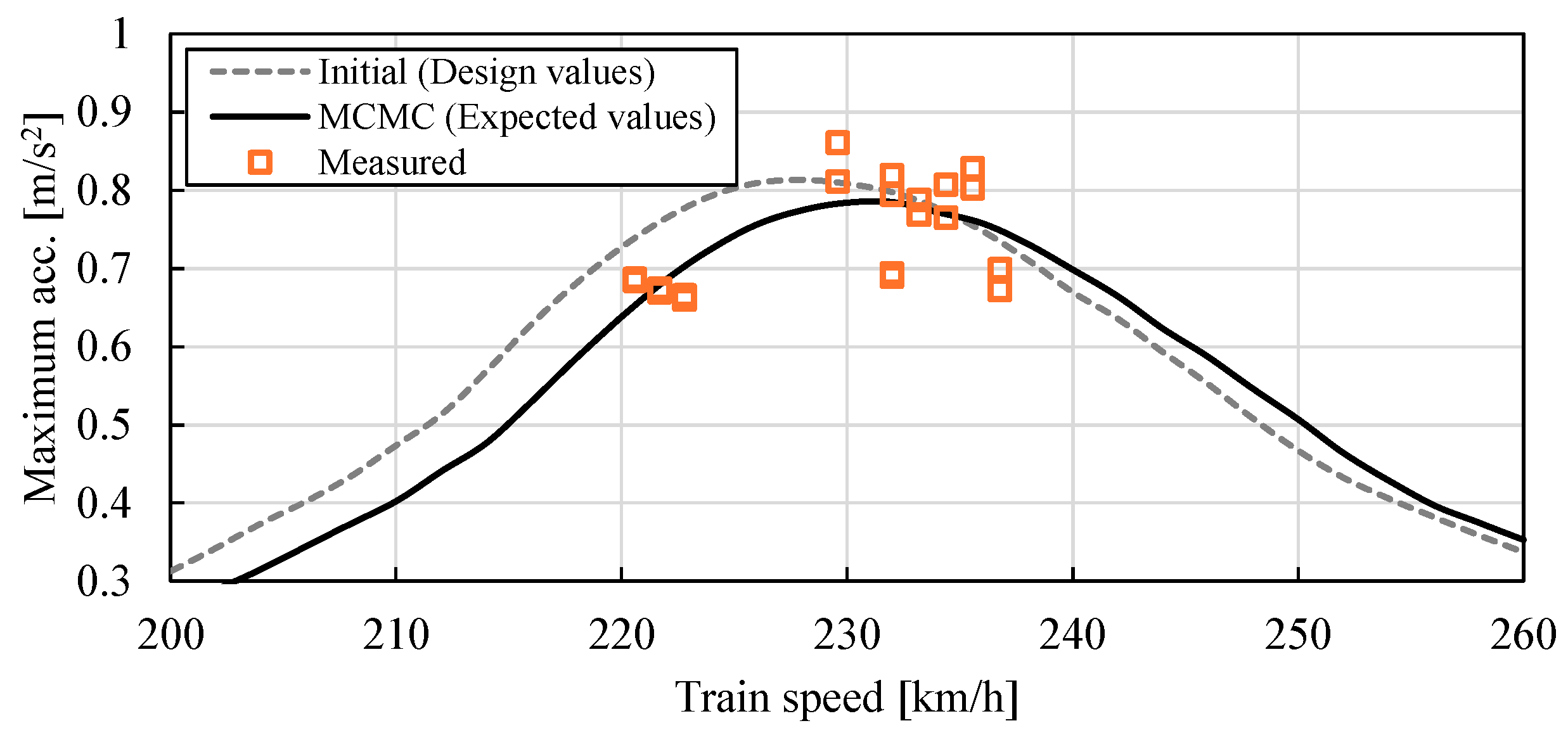
3. Estimation Results for All the Data
4. Discussion About Sample Size
4.1. Effect of the Number of Accelerometers
4.2. Effect of the Observation-Sample Number
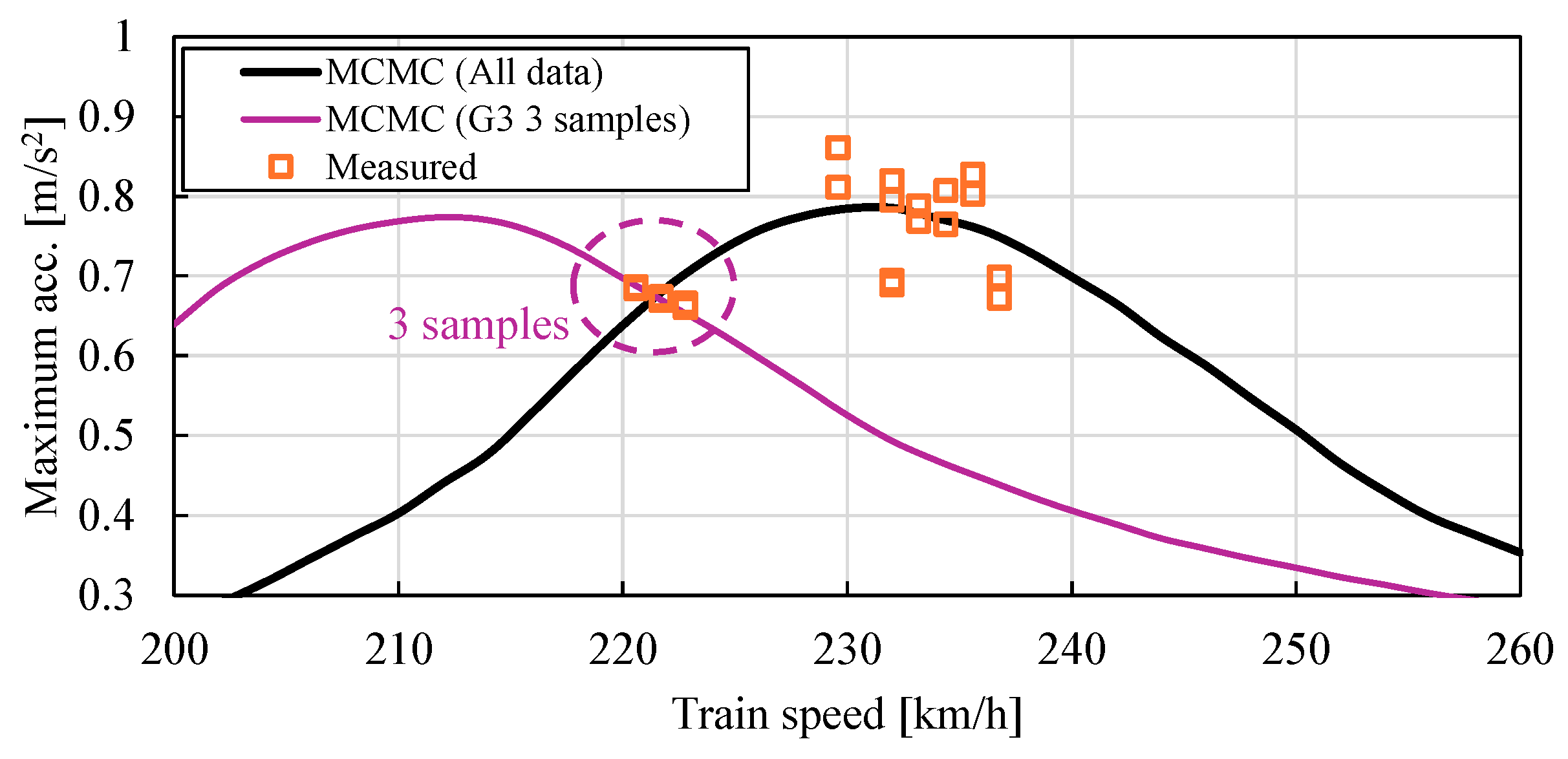
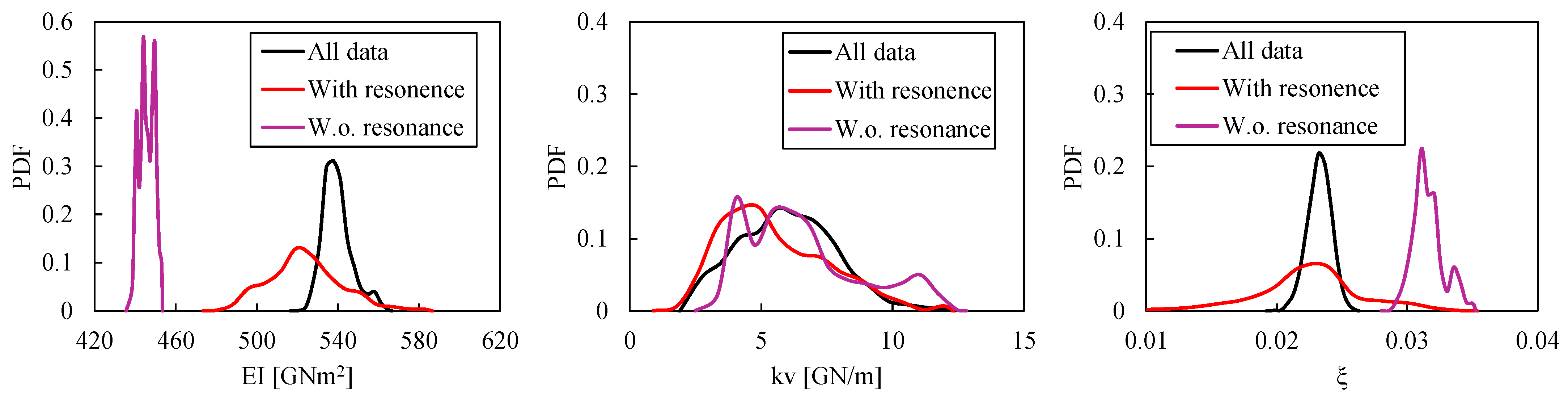
4.3. Effect of the Observation Samples of the Resonant Region
4.4. Perspectives on Practical Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HSR | High-speed railway |
| SMU | Structural model updating |
| SHM | Structural health monitoring |
| MCMC | Markov chain Monte Carlo simulation |
| LPF | Low-pass filter |
| Prior distribution | |
| Bending stiffness | |
| Posterior distribution | |
| Unit-length mass | |
| RW-MH | Random-walk Metropolis–Hastings |
| Modal damping ratio | |
| CI | Confidence interval |
| Support stiffness/bearing-spring constant | |
| Axle load | |
| Expectation | |
| Variance |
References
- Frýba, L. Vibration of Solids and Structures Under Moving Loads; Springer Nature: Dordrecht, The Netherlands, 2013; Volume 1. [Google Scholar] [CrossRef]
- Ju, S.H.; Lin, H.T. Resonance characteristics of high-speed trains passing simply supported bridges. J. Sound Vib. 2003, 267, 1127–1141. [Google Scholar] [CrossRef]
- Sogabe, M.; Matsumoto, N.; Kanamori, M.; Sato, T.; Wakui, H. Impact factors of concrete girders coping with train speed-up. Q. Rep. RTRI 2005, 46, 46–52. [Google Scholar] [CrossRef]
- He, X.; Wu, T.; Zou, Y.; Chen, Y.F.; Guo, H.; Yu, Z. Recent developments of high-speed railway bridges in China. Struct. Infrastruct. Eng. 2017, 13, 1584–1595. [Google Scholar] [CrossRef]
- Ferreira, G.; Montenegro, P.; Andersson, A.; Henriques, A.A.; Karoumi, R.; Calçada, R. Critical analysis of the current Eurocode deck acceleration limit for evaluating running safety in ballastless railway bridges. Eng. Struct. 2024, 312, 118127. [Google Scholar] [CrossRef]
- Sogabe, M.; Furukawa, A.; Shimomura, T.; Iida, T.; Matsumoto, N.; Wakui, H. Deflection limits of structures for train speed-up. Q. Rep. RTRI 2005, 46, 130–136. [Google Scholar] [CrossRef]
- Frýba, L. A rough assessment of railway bridges for high speed trains. Eng. Struct. 2001, 23, 548–556. [Google Scholar] [CrossRef]
- Matsuoka, K.; Tokunaga, M.; Kaito, K. Bayesian estimation of instantaneous frequency reduction on cracked concrete railway bridges under high-speed train passage. Mech. Syst. Signal Process. 2021, 161, 107944. [Google Scholar] [CrossRef]
- Matsuoka, K.; Collina, A.; Somaschini, C.; Sogabe, M. Influence of local deck vibrations on the evaluation of the maximum acceleration of a steel-concrete composite bridge for a high-speed railway. Eng. Struct. 2019, 200, 109736. [Google Scholar] [CrossRef]
- Ülker-Kaustell, M.; Karoumi, R. Influence of non-linear stiffness and damping on the train-bridge resonance of a simply supported railway bridge. Eng. Struct. 2012, 41, 350–355. [Google Scholar] [CrossRef]
- Li, J.; Su, M. The resonant vibration for a simply supported girder bridge under high-speed trains. J. Sound Vib. 1999, 224, 897–915. [Google Scholar] [CrossRef]
- Matsuoka, K.; Kaito, K.; Sogabe, M. Bayesian time–frequency analysis of the vehicle–bridge dynamic interaction effect on simple-supported resonant railway bridges. Mech. Syst. Signal Process. 2020, 135, 106373. [Google Scholar] [CrossRef]
- Ubertini, F.; Gentile, C.; Materazzi, A.L. Automated modal identification in operational conditions and its application to bridges. Eng. Struct. 2013, 46, 264–278. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite element model updating of a bowstring-arch railway bridge based on experimental modal parameters. Eng. Struct. 2012, 40, 413–435. [Google Scholar] [CrossRef]
- Matsuoka, K.; Shinozaki, S.; Kaito, K. Structural model update considering uncertainty and reliability assessment of strengthening effect: Application to additional supporting strengthening of a high-speed railway bridge. J. Jpn. Soc. Civ. Eng. Ser. A1 2020, 76, 560–579. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Friswell, M.I. Model updating in structural dynamics: A survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damage assessment: A review. Mech. Syst. Signal Process. 2015, 56, 123–149. [Google Scholar] [CrossRef]
- Ierimonti, L.; Cavalagli, N.; Venanzi, I.; García-Macías, E.; Ubertini, F. A transfer Bayesian learning methodology for structural health monitoring of monumental structures. Eng. Struct. 2021, 247, 113089. [Google Scholar] [CrossRef]
- Yu, X.; Li, X.; Bai, Y. Evaluating maximum inter-story drift ratios of building structures using time-varying models and Bayesian filters. Soil. Dyn. Earthq. Eng. 2022, 162, 107496. [Google Scholar] [CrossRef]
- Kammouh, O.; Gardoni, P.; Cimellaro, G.P. Probabilistic framework to evaluate the resilience of engineering systems using Bayesian and dynamic Bayesian networks. Reliab. Eng. Syst. Saf. 2020, 198, 106813. [Google Scholar] [CrossRef]
- Vanik, M.W.; Beck, J.L.; Au, S.K. Bayesian probabilistic approach to structural health monitoring. J. Eng. Mech. 2000, 126, 738–745. [Google Scholar] [CrossRef]
- Johansson, C.; Pacoste, C.; Karoumi, R. Closed-form solution for the mode superposition analysis of the vibration in multi-span beam bridges caused by concentrated moving loads. Comput. Struct. 2013, 119, 85–94. [Google Scholar] [CrossRef]
- Mao, L.; Lu, Y. Critical speed and resonance criteria of railway bridge response to moving trains. J. Bridge Eng. 2013, 18, 131–141. [Google Scholar] [CrossRef]
- Nakada, M.; Matsuoka, K. Closed form solution of multipoint support beam under moving load for simple calculation of dynamic response of railway continuous bridges. Trans. Jpn. Soc. Civ. Eng. 2023, 79, 22-15052. [Google Scholar] [CrossRef]
- Yotsui, H.; Matsuoka, K.; Kaito, K. Dual sampling method for evaluating uncertainty when updating a Bayesian estimation model of a high-speed railway bridge. Reliab. Eng. Syst. Saf. 2025, 259, 110901. [Google Scholar] [CrossRef]
- Matsuoka, K.; Tanaka, H.; Kawasaki, K.; Somaschini, C.; Collina, A. Drive-by methodology to identify resonant bridges using track irregularity measured by high-speed trains. Mech. Syst. Signal Process. 2021, 158, 107667. [Google Scholar] [CrossRef]
- Matsuoka, K.; Tanaka, H. Drive-by deflection estimation method for simple support bridges based on track irregularities measured on a traveling train. Mech. Syst. Signal Process. 2023, 182, 109549. [Google Scholar] [CrossRef]
- Ereiz, S.; Duvnjak, I.; Jiménez-Alonso, J.F. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]



| Devices | Specifications |
|---|---|
| Piezoelectric Accelerometers (PV-85; Rion Co., Ltd., Kokubunji, Japan) | Frequency range: 1–7000 Hz Sensitivity: 6.42 pC/(m/s2) |
| Preamplifier (NH-22; Rion Co., Ltd.) | Frequency range: 1–10,000 Hz |
| A/D Converter (Ni cDAQ-9172·Ni9233; National Instruments Japan Co., Ltd., Tokyo, Japan) | Sampling frequency: 2000–10,000 Hz |
| Control System (Labview) | Multipoint synchronization Sampling frequency: 2000 Hz |
| Laptop PC (CF-SV; Panasonic Co., Ltd., Kadoma, Japan) | CPU: i5 4.4 GHz Memory capacity: 16 GB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsuoka, K.; Yotsui, H.; Kaito, K. Empirical Investigation of the Effects of the Measurement-Data Size on the Bayesian Structural Model Updating of a High-Speed Railway Bridge. Infrastructures 2025, 10, 108. https://doi.org/10.3390/infrastructures10050108
Matsuoka K, Yotsui H, Kaito K. Empirical Investigation of the Effects of the Measurement-Data Size on the Bayesian Structural Model Updating of a High-Speed Railway Bridge. Infrastructures. 2025; 10(5):108. https://doi.org/10.3390/infrastructures10050108
Chicago/Turabian StyleMatsuoka, Kodai, Haruki Yotsui, and Kiyoyuki Kaito. 2025. "Empirical Investigation of the Effects of the Measurement-Data Size on the Bayesian Structural Model Updating of a High-Speed Railway Bridge" Infrastructures 10, no. 5: 108. https://doi.org/10.3390/infrastructures10050108
APA StyleMatsuoka, K., Yotsui, H., & Kaito, K. (2025). Empirical Investigation of the Effects of the Measurement-Data Size on the Bayesian Structural Model Updating of a High-Speed Railway Bridge. Infrastructures, 10(5), 108. https://doi.org/10.3390/infrastructures10050108





