From Negative Knowledge to Best Practices for Enhancing Reusability of Sketches in Procedural 3D CAD Models
Abstract
1. Introduction
2. Background
3. Error-Based Negative Knowledge in CAD Models
- Instead of using simple examples to test the effect of each possible error in isolation, the impact of different errors on somewhat more complex models is examined. The rationale is that, while simple examples allow us to isolate the effect of individual failures, they are highly unrealistic case studies, since designers rarely make mistakes in simple models. González-Luch and Plumed [30] identified several quality errors that frequently occur during model creation, particularly impacting models of average or high complexity. To uncouple the effects of potentially combined errors, redesigns were repeated in different orders to gain insight into the individual effects of each error.
- The attempt is to validate hypotheses developed from the authors’ experience as instructors of industrial designers. Insights come not only from training engineers for over 15 years but also from consulting the help system of a representative CAD software [31]. Unsurprisingly, like many others, this help system focuses on command usage rather than work strategies, offering little to no documented guidance on problem-solving or error prevention. Beyond validating the hypotheses, the work also explores the underlying negative knowledge and examines the associated negative consequences linked to common deficiencies in CAD model usability and reusability.
- The hierarchical arrangement of columns in Table 2 shows that a single error can generate multiple negative knowledge hypotheses. In the case study, it will become clearer that negative knowledge can extend to increasingly specific cases, giving rise to practical rules that can be arranged “in cascade,” with very specific rules for highly specific cases at the lower levels and generally recommendable rules at higher levels.
4. Negative Knowledge from Sketches
4.1. Case Study
4.2. Negative Knowledge Simulations
- Case 1. Failure in constraining sketches by overlooking dimensional (continuous) and/or geometric (discrete) constraints. This case demonstrates how the framework can be extended “in cascade” by studying different subcases of poorly constrained sketches selected based on authors’ experience: (1) leaving the entire sketch unconstrained, (2) removing only geometric constraints, (3) removing only dimensional constraints, and (4) removing just some constraints, which may be dimensional, geometric, or some critical.
- Case 2. Artificially simulating how excessive overconstraining limits sketch editability.
- Case 3. Replicating sketches with inconsistent geometry to analyze their reusability.
4.2.1. Case 1.1: Fully Unconstrained Sketch
- Unconstrained sketches (commonly found in imported models with reconstructed features) may be usable as-is, but they are rarely reusable when modifications are needed.
- Experienced users may manage to repair distortions that arise when editing an unconstrained sketch, but doing so requires a combination of time, skill, and luck.
- Hidden constraints, such as links connecting the endpoints of polylines, lead to even more unpredictable sketch behavior during editing than the total absence of constraints.
- Always constrain sketches, or at least constrain them before reusing them (even if the constraints added by an automatic algorithm are not optimal).
- Avoid editing individual components of polylines separately. Instead, treat the polyline as a single element and start by fixing its simpler, more independent components, which helps reduce their tendency towards chaotic behavior. CAD applications that support polylines often allow users to manage each line separately, but they rarely provide simple ways to “break” the polyline using easily editable constraints. Typically, separating the endpoints of consecutive lines requires specific editing operations.
4.2.2. Case 1.2: Dimensionally Unconstrained Sketch
- Moving the lower-strength segment resulted in a new deformed sketch affecting its size (Figure 3b,e). In both cases, a local shrinkage appeared, as if the sketch had been stretched.
- Moving a joint point on the lower segment resulted in a new deformed sketch affecting its size (Figure 3c,f). Local swelling appeared, while other parts seemed stretched.
- The sequence of restoration did not affect the final geometry.
- A common mistake is that many sketch editors automatically add most geometric constraints but do not usually add dimensional constraints by default; relying solely on geometric constraints results in unpredictable sketch behavior when edited.
- When a sketch lacks dimensional constraints, it may still be reusable, but rescaling (inflates/deflates) occurs unpredictably during editing. This makes the sketch unreliable for reuse, as it limits the ability to maintain desired proportions and causes size deformations
- Attempting to manually repair unequal inflations requires trial and error, with no guarantee of restoring the original dimensions, increasing effort during redesign.
- Individual dimensional constraints control local size, while their joint application governs overall rescaling.
- When sketch rescaling leads to irregular or unexpected inflation/deflation, the dimensional constraints and their interrelations must be reviewed.
- When a poorly constrained sketch inflates or deflates locally during editing, size constraints are often missing in the affected area.
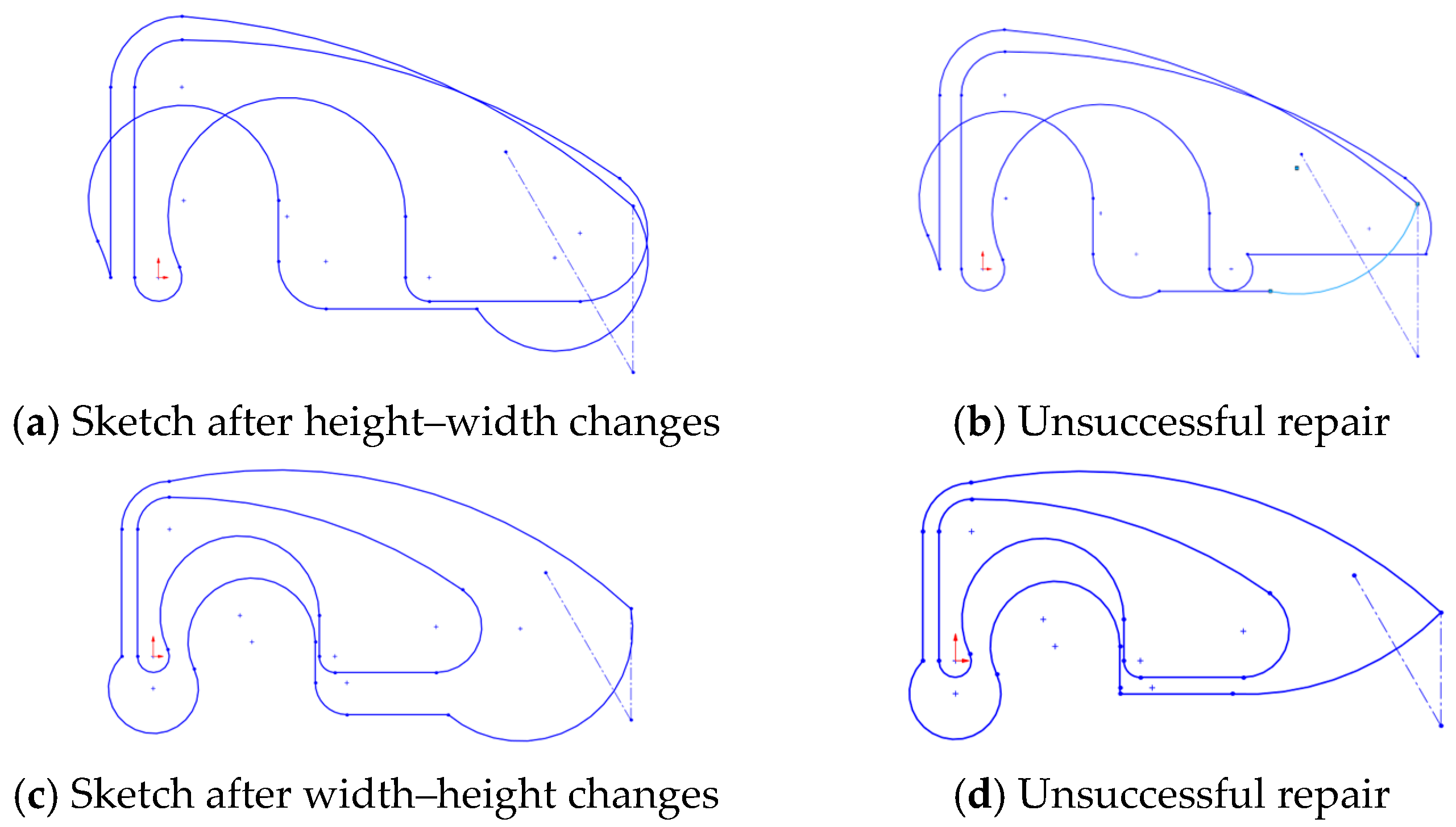
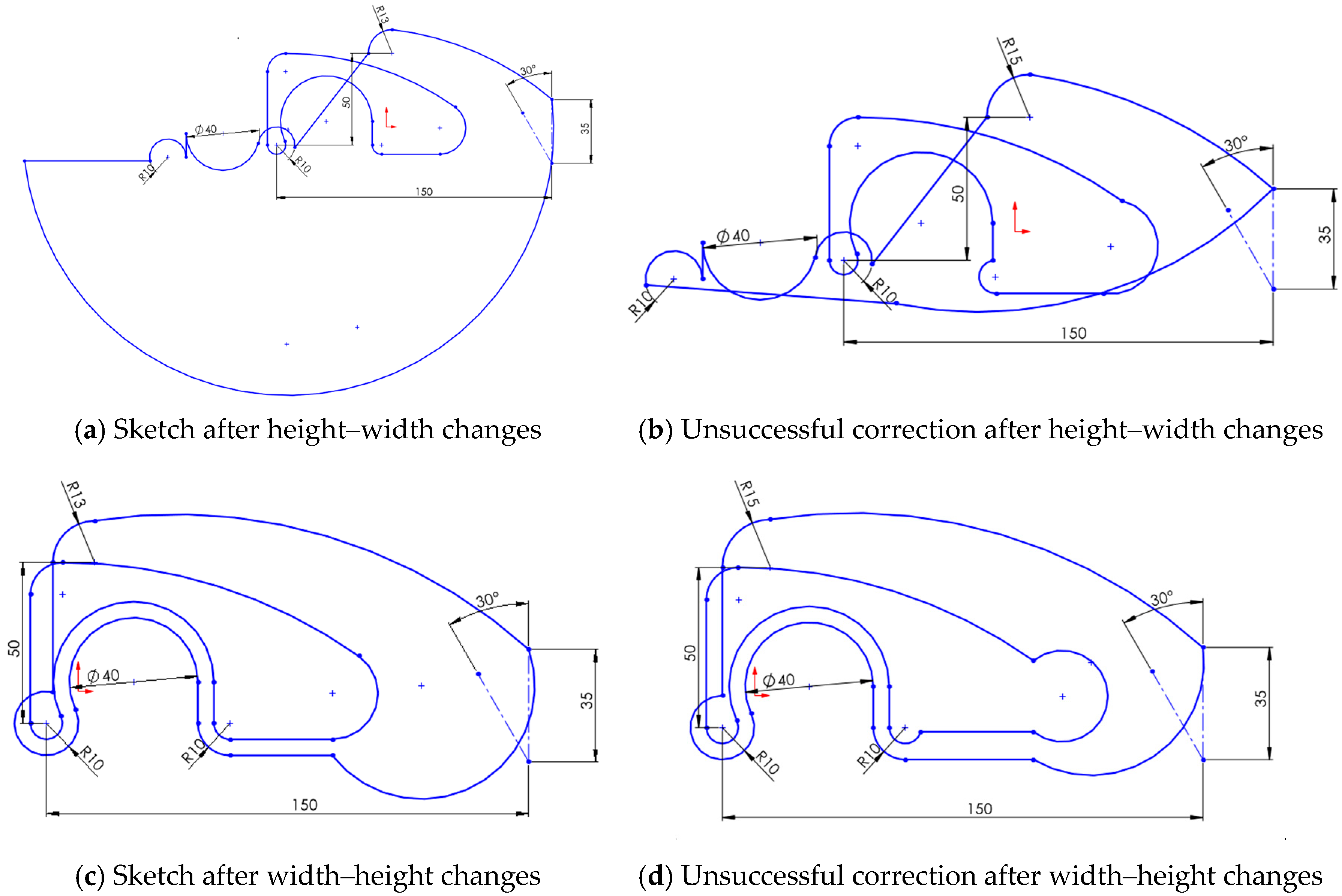
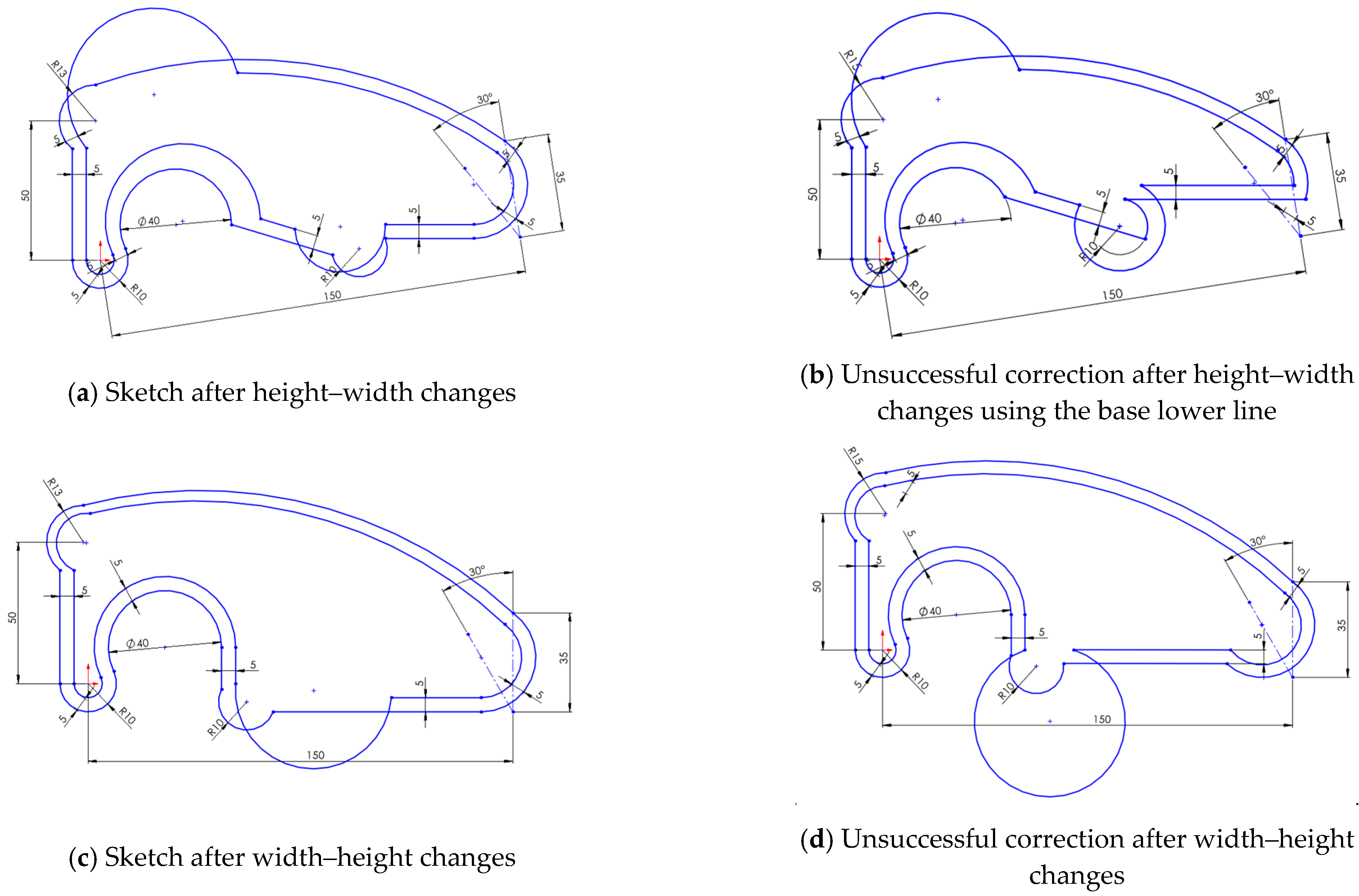
4.2.3. Case 1.3: Geometrically Unconstrained Sketch
- The inner profile remained unchanged when editing the outer profile, since most of the links between them had been removed. In other words, when the exterior profile is not geometrically constrained or connected to the interior, it is more susceptible to distortion during editing.
- Both sequences resulted in uncontrolled deformation (Figure 4b,d), producing twists in the sketch.
- The order of restoration affected the final geometry.
- The topology was mostly affected in the height–width sequence, while shape and size were primarily altered in the reverse (width–height) sequence.
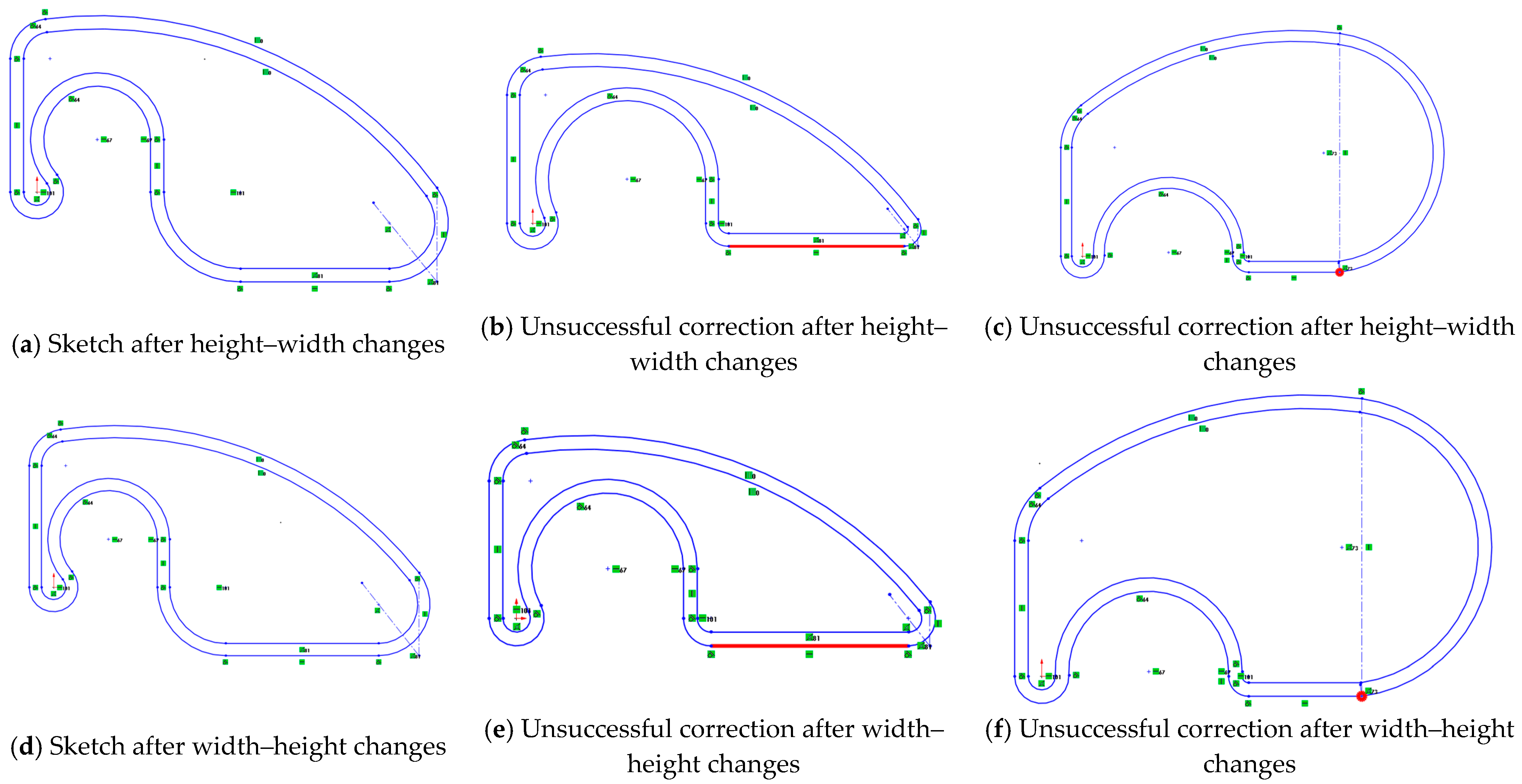
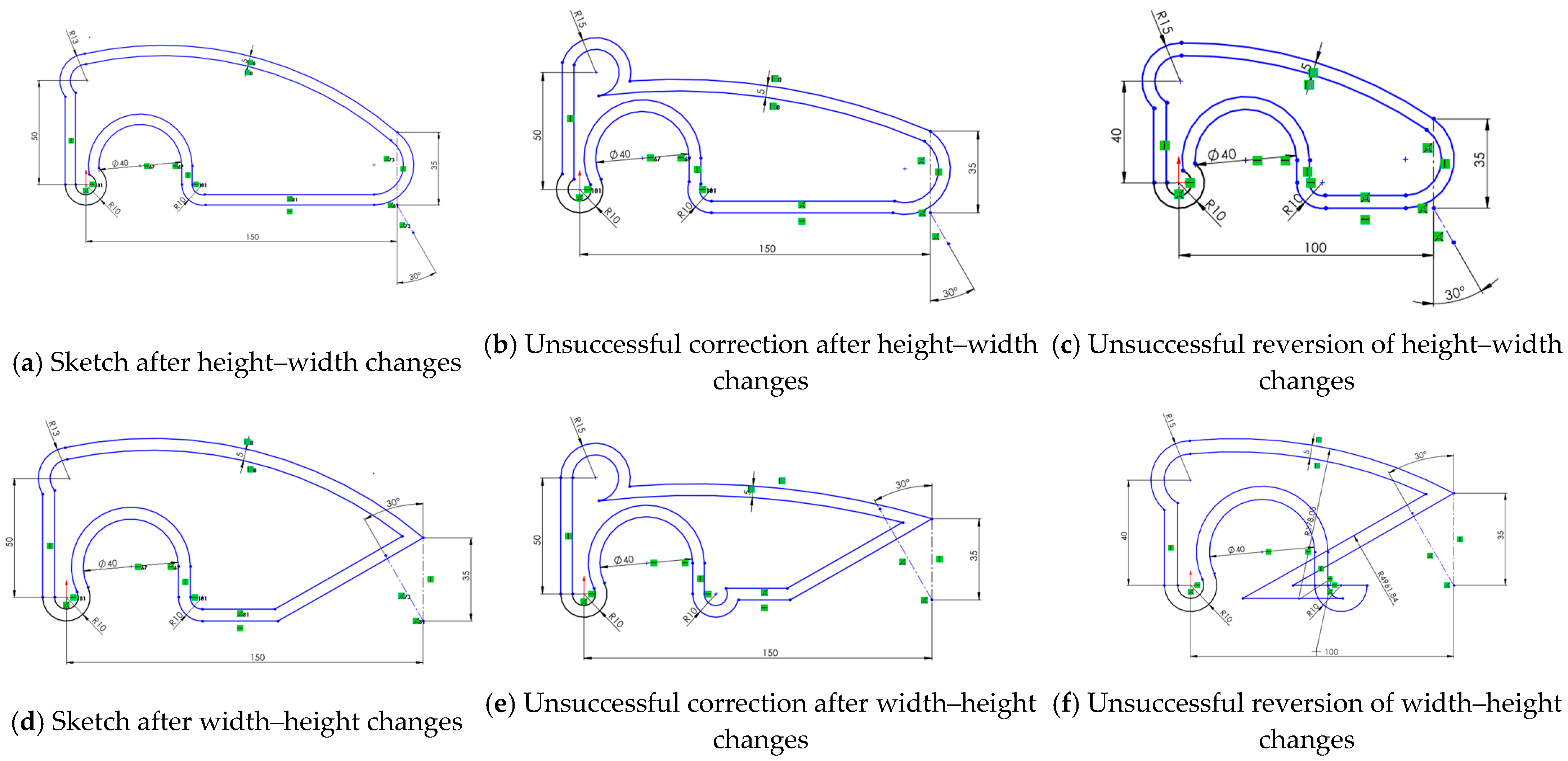
- Uncontrolled deformations in both sequences (Figure 5b,d).
- The order of restoration tasks affecting the final geometry.
- Topology being somewhat affected in the height–width sequence, while geometry (shape and size) was primarily affected in the reverse (width–height) sequence.
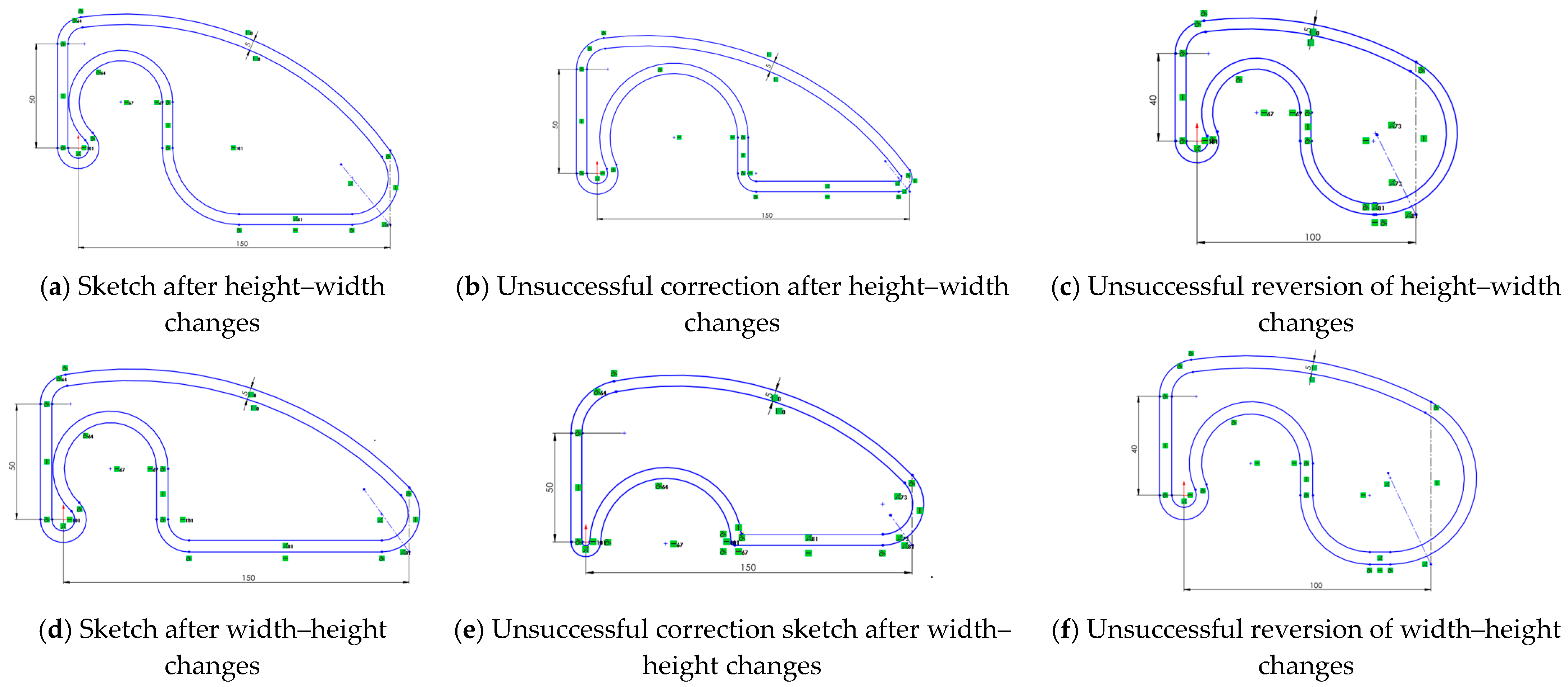
- Dimensional constraints alone are insufficient to prevent unexpected deformations during sketch editing.
- Removing complex geometric constraints, such as equidistance, critically affects certain types of geometric figures and often results in non-reusable sketches.
- Editing sketches with missing dimensions can easily produce local distortions.
- Manually editing sketches with missing dimensions rarely causes swelling or shrinking but often introduces local twists.
- Equidistance constraints strongly link otherwise unconnected profiles, enhancing robustness against undesired changes. However, they also make editing more difficult, so temporarily removing them while editing the original profile may be advantageous.
4.2.4. Case 1.4: Partly Incomplete Dimensional Constraints
- The absence of tangency constraints between arcs results in first-order discontinuities, preventing smooth curve transitions and compromising both form and model regeneration.
- Loss of tangency leads to abrupt shape changes during dimensional adjustments, even with minimal edits, due to unstable directional continuity at junctions.
- Dimensional constraints alone cannot adequately replace tangency constraints when smooth curves or parametric consistency are required.
- To ensure the reusability of sketches with curved geometry, tangency should be considered essential, not merely aesthetic refinement.
- To avoid visual or functional discontinuities, tangent constraints must be applied wherever there are curved transitions between arcs or between an arc and a straight line.
- Sketches missing tangencies may appear stable initially but become unpredictable under edits, particularly dimensional changes, making them unsuitable for reuse.
- Missing tangencies is more common than expected, as even users who are aware of the importance of tangencies often rely on automatic tangency detection during sketching.
4.2.5. Case 1.5: Sketch Only Missing Less-Relevant Dimensional Constraints
- Geometric constraints are crucial for ensuring reusable sketches, while dimensional constraints primarily prevent deformations.
- Sketches containing only main dimensions do not guarantee full reusability, as missing secondary constraints can still lead to uncontrolled deformations during parametric changes.
- Even seemingly redundant dimensional constraints may be required in conjunction with geometric constraints to avoid distortions when multiple dependent entities are modified.
- Assuming a sketch is reusable solely because it includes main dimensions is a mistake. Secondary constraints necessary to maintain proportions are equally important.
- Dimensional constraints should be reviewed not only for the most obvious or fundamental dimensions of the sketch (height, width, and thickness) but also for their role in preventing unexpected cumulative deformations.
4.2.6. General Negative Knowledge and Lessons Learned from Case 1
- Simpler case studies are not “rich” enough to allow the simulation of different failure modes in more realistic situations.
- If the failure modes are not isolated and decoupled, clear conclusions cannot be drawn, because the consequences of one failure can either enhance another failure or mask it.
- Case studies must be designed that, without being overly complex, are similar to intricate real-world design situations.
- When analyzing case studies, special attention should be paid to looking for possible hidden geometric interactions that falsify the conclusions.
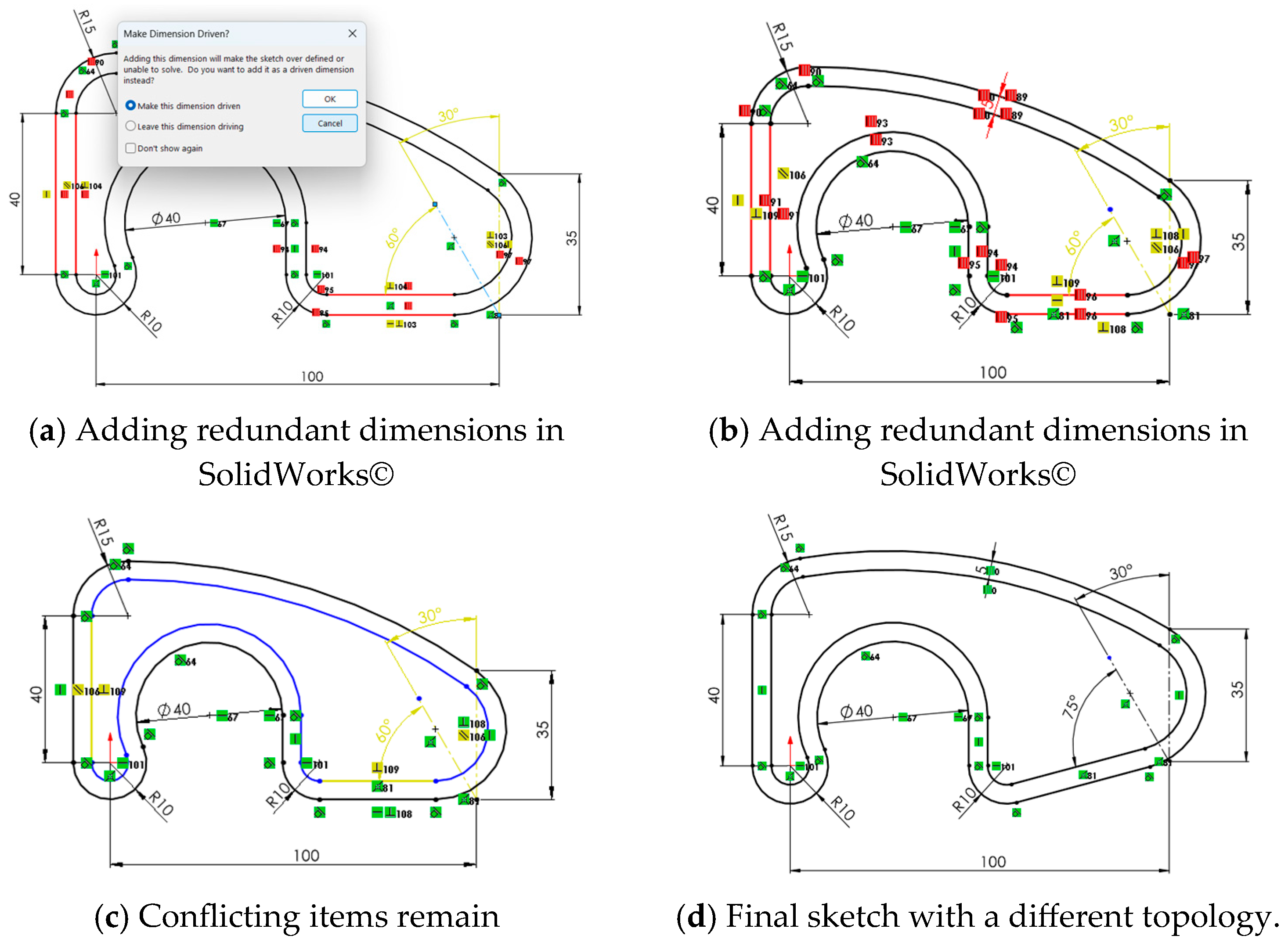
4.2.7. Case 2: Overconstrained Sketches
- Do not assume that simply removing the “last added” constraint will restore the sketch. Some effects are cumulative and difficult to reverse.
- Add constraints incrementally, validating sketch stability before continuing. Redundant constraints can significantly slow down the design process, as the software must solve a more complex system of equations.
- Test the behavior of constrained sketches with small parameter changes before saving them. The combined effects of constraints should be tested early, not after the model is complete.
- Constraints that manage the location of the “drawing” on the “sheet” (such as the fix constraint) are largely obsolete.
- Intrinsic constraints require some mental effort when applied but generally convey design intent more reliably than extrinsic constraints.
4.2.8. Case 3: Sketches with Inconsistent Geometry
- Fragmented or open profiles lead to severe topological errors. Extrusions may produce cracked solids or unpredictable 3D shapes. In some cases, the CAD system permits the operation but produces unusable results; in others, it blocks the operation but provides little diagnostic guidance.
- Duplicate lines, especially when underconstrained, introduce redundancy and ambiguity in the sketch. These duplications are difficult to detect visually and are often not flagged by the software. Fully constrained duplicates are slightly more manageable but still risky in collaborative or long-term design processes. Hidden degrees of freedom caused by duplicated lines make the user lose control of the sketch.
- Incorrect use of construction or geometry lines, although syntactically valid, can completely undermine the sketch’s intent and function. For instance, drawing entirely with construction lines results in a sketch that cannot be used for 3D operations. Conversely, mistakenly converting auxiliary lines into geometric elements may introduce unintended profiles, which can affect the model’s logic and reusability.
- Software support is inconsistent. Some deficiencies (like open profiles) are flagged without actionable suggestions. Others (such as duplicate lines or axis misclassifications) are not detected at all, which means that relying solely on system warnings is insufficient. Designers must critically interpret software behavior and perform manual checks when necessary.
- Reversibility is not guaranteed, even when the deformation appears minor. Once a sketch with inconsistent geometry is edited, recovering the original shape is often impossible without full reconstruction. In most cases, manual corrections add time, increase user frustration, and reduce confidence in the model’s robustness.
- Ensuring sketch continuity is non-negotiable. Gaps, breaks, or overlaps must be systematically prevented and resolved to ensure the sketch serves as a valid and reusable base.
- Visual cues can be misleading. A sketch may look correct but contain deep structural flaws—fragmented lines, redundant entities, or incorrect classifications—that degrade quality.
- Full constraint does not imply correctness. A fully constrained sketch may still contain duplicate or misclassified lines that compromise model intent.
- Profile continuity must be reviewed, analyzing both “automatic” connections (such as polyline unions described in Section 4.2.1) and user-added constraints.
- Build with intent and review with suspicion. Especially for imported geometry or collaborative work, each sketch should be verified beyond its appearance or constraint status.
- Design reusability requires clean geometry and proper constraints, but also awareness of modeling practices that go beyond the interface’s feedback. This includes understanding how sketch inconsistencies silently propagate into later stages, where correction is more complex and costly.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAD | Computer-Aided Design |
| PDQ | Product Data Quality |
| MQT | Model Quality Testing |
| S | Sketch |
| D | Datum |
| PMT | Procedural Model Tree |
References
- Camba, J.D.; Contero, M.; Company, P. Parametric CAD modeling: An analysis of strategies for design reusability. Comput. Aided Des. 2016, 74, 18–31. [Google Scholar] [CrossRef]
- Aranburu, A.; Justel, D.; Contero, M.; Camba, J.D. Geometric variability in parametric 3D models: Implications for engineering design. In Proceedings of the 32nd CIRP Design Conference, Gif-sur-Yvette, France, 28–30 March 2022. [Google Scholar] [CrossRef]
- LaCourse, D.E. Handbook of Solid Modeling; McGraw-Hill, Inc.: Columbus, OH, USA, 1995; ISBN 978-0070357884. [Google Scholar]
- Lombard, M. Mastering SolidWorks; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; ISBN 978-1119300571. [Google Scholar]
- ISO/PAS 26183:2006; SASIG—Product Data Quality for the Global Automotive Industry. International Organization for Standardization: Geneva, Switzerland, 2014.
- Bodein, Y.; Rose, B.; Caillaud, E. Explicit reference modeling methodology in parametric CAD system. Comput. Ind. 2014, 65, 136–147. [Google Scholar] [CrossRef]
- Gebhard, R. A Resilient Modeling Strategy. SolidEdge University, 2013. Available online: https://learnrms.com (accessed on 20 July 2019).
- Company, P.; Contero, M.; Camba, J.; Aramburu, A.; Justel, D. A Hierarchical Multilevel Modeling Framework for the Creation of High-Quality Solid Models in Parametric Feature-Based CAD Systems. Comput. Aided Des. Appl. 2025, 22, 229–244. [Google Scholar] [CrossRef]
- Jackson, C.; Buxton, M. The Design Reuse Benchmark Report: Seizing the Opportunity to Shorten Product Development; Aberdeen Group: Boston, MA, USA, 2007. [Google Scholar]
- Contero, M.; Company, P.; Vila, C.; Aleixos, N. Product data quality and collaborative engineering. IEEE Comput. Graph. Appl. 2002, 22, 32–42. [Google Scholar] [CrossRef]
- Company, P.; Contero, M.; Otey, J.; Plumed, R. Approach for developing coordinated rubrics to convey quality criteria in MCAD training. Comput. Aided Des. 2015, 63, 101–117. [Google Scholar] [CrossRef]
- González-Lluch, C.; Company, P.; Contero, M.; Camba, J.D.; Plumed, R. A survey on 3D CAD model quality assurance and testing tools. Comput. Aided Des. 2017, 83, 64–79. [Google Scholar] [CrossRef]
- Aranburu, A.; Justel, D.; Angulo, I. Reusability and flexibility in parametric surface based models: A review of modeling strategies. Comput. Aided Des. Appl. 2021, 18, 864–874. [Google Scholar] [CrossRef]
- Nerents, T.B.; Ebro, M.; Nielsen, M.; Eifler, T.; Nielsen, K.L. Exploring barriers for the use of FEA-based variation simulation in industrial development practice. Des. Sci. 2021, 7, e21. [Google Scholar] [CrossRef]
- Herron, J.B. Re-Use Your CAD: The Model-Based CAD Handbook; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2021; ISBN 979-8597987880. [Google Scholar]
- Branoff, T.J.; Wiebe, E.N.; Hartman, N.W. Integrating constraint-based CAD into an introductory engineering graphics course: Activities and grading strategies. In Proceedings of the 2003 American Society for Engineering Education Annual Conference & Exposition, Session 1338, Nashville, TN, USA, 22–25 June 2003; pp. 1–10. [Google Scholar] [CrossRef]
- Branoff, T.J. Constraint-based modeling in the engineering graphics curriculum: Laboratory activities and evaluation strategies. In Proceedings of the Midyear Conference on Engineering Design Graphics Division of the American Society for Engineering Education, Williamsburg, VA, USA, 21–23 November 2004; pp. 132–138. [Google Scholar]
- Devine, K.L.; Laingen, M.A. Assessing Design Intent in an Introductory-Level Engineering Graphics Course. In Proceedings of the 68th Mid-Year Conference, ASEE Engineering Design Graphics Division, Worcester, MA, USA, 20–22 October 2013; pp. 59–63. [Google Scholar]
- Barbero, B.R.; Pedrosa, C.M.; Samperio, R.Z. Learning CAD at university through summaries of the rules of design intent. Int. J. Technol. Des. Educ. 2016, 27, 481–498. [Google Scholar] [CrossRef]
- Landers, D.M.; Khurana, P. Horizontally-Structured CAD/CAM Modeling for Virtual Concurrent Product and Process Design. US Patent 6775581, 10 August 2004. [Google Scholar]
- Aranburu, A.; Camba, J.D.; Justel, D.; Contero, M. An Improved Explicit Reference Modeling Methodology for Parametric Design. Comput.-Aided Des. 2023, 161, 103541. [Google Scholar] [CrossRef]
- Chester, I. Teaching for CAD expertise. Int. J. Technol. Des. Educ. 2007, 17, 23–35. [Google Scholar] [CrossRef]
- Minsky, M. The Society of Mind; Simon and Schuster: New York, NY, USA, 1986; ISBN 978-0434467587. [Google Scholar]
- Minsky, M. Negative Expertise. Int. J. Expert Syst. 1994, 7, 13–19. [Google Scholar]
- Oser, F.; Spychiger, M. Lernen ist Schmerzhaft: Zur Theorie des Negativen Wissens und zur Praxis der Fehlerkultur; Beltz: Weinheim, Germany, 2005; ISBN 978-3407253736. [Google Scholar]
- Parviainen, J.; Eriksson, M. Negative Knowledge, Expertise and Organisations. Int. J. Manag. Concepts Philos 2006, 2, 140–153. [Google Scholar] [CrossRef]
- Mandorli, F.; Otto, H.E. Negative knowledge and a novel approach to support MCAD education. Comput. Aided Des. Appl. 2013, 10, 1007–1020. [Google Scholar] [CrossRef]
- ISO/DIS 24351:2025; Technical Product Documentation (TPD)-General Requirements of the Construction of Three-Dimensional Models for Mechanical Products. International Organization for Standardization: Geneve, Switzerland, 2025.
- ISO 5459:2024; Geometrical Product Specifications (GPS)-Geometrical Tolerancing-Datums and Datum Systems. International Organization for Standardization: Geneve, Switzerland, 2024.
- González-Lluch, C.; Plumed, R. Towards Enhanced Quality Assessment: Dimensional Analysis of Common Errors in CAD 3D Modeling Process. In Proceedings of the Mechanics, Design Engineering and Manufacturing V (JCM 2024), Valencia, Spain, 12–14 June 2024; pp. 1057–1073. [Google Scholar] [CrossRef]
- SolidWorks API Help. Available online: https://help.solidworks.com/2025/english/api/sldworksapiprogguide/Welcome.htm (accessed on 1 October 2025).
- Company, P.; González-Lluch, C. CAD 3D con SolidWorks ® Tomo I: Diseño Básico; Colección Sapientia, Núm. 86; Publicacions de la Universitat Jaume I: Castelló de la Plana, Spain, 2021; Volume 1, Available online: http://cad3dconsolidworks.uji.es (accessed on 20 November 2025).
- González-Lluch, C.; Company, P.; Contero, M.; Pérez, D.; Camba, J.D. On the effects of the fix geometric constraint in 2D profiles on the reusability of parametric 3D CAD models. Int. J. Technol. Des. Educ. 2019, 29, 821–841. [Google Scholar] [CrossRef]
- Company, P.; Naya, F.; Contero, M.; Camba, J.D. On the role of geometric constraints to support design intent communication and model reusability. Comput. Aided Des. Appl. 2020, 17, 61–76. [Google Scholar] [CrossRef]
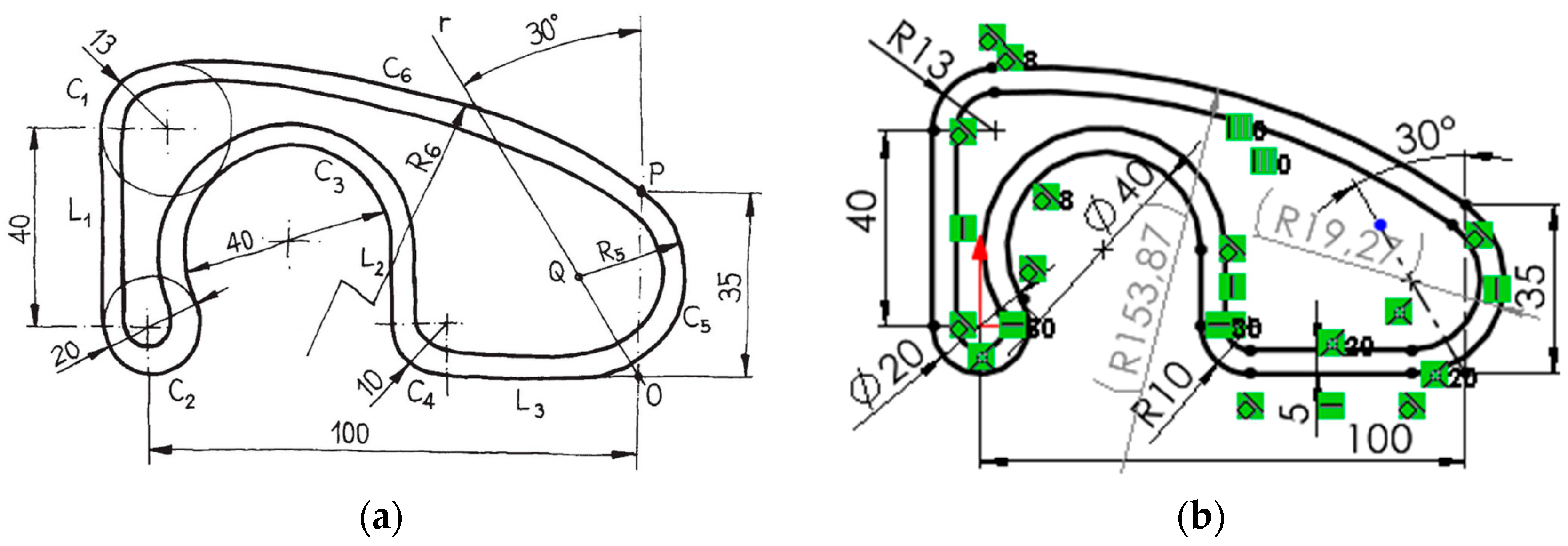

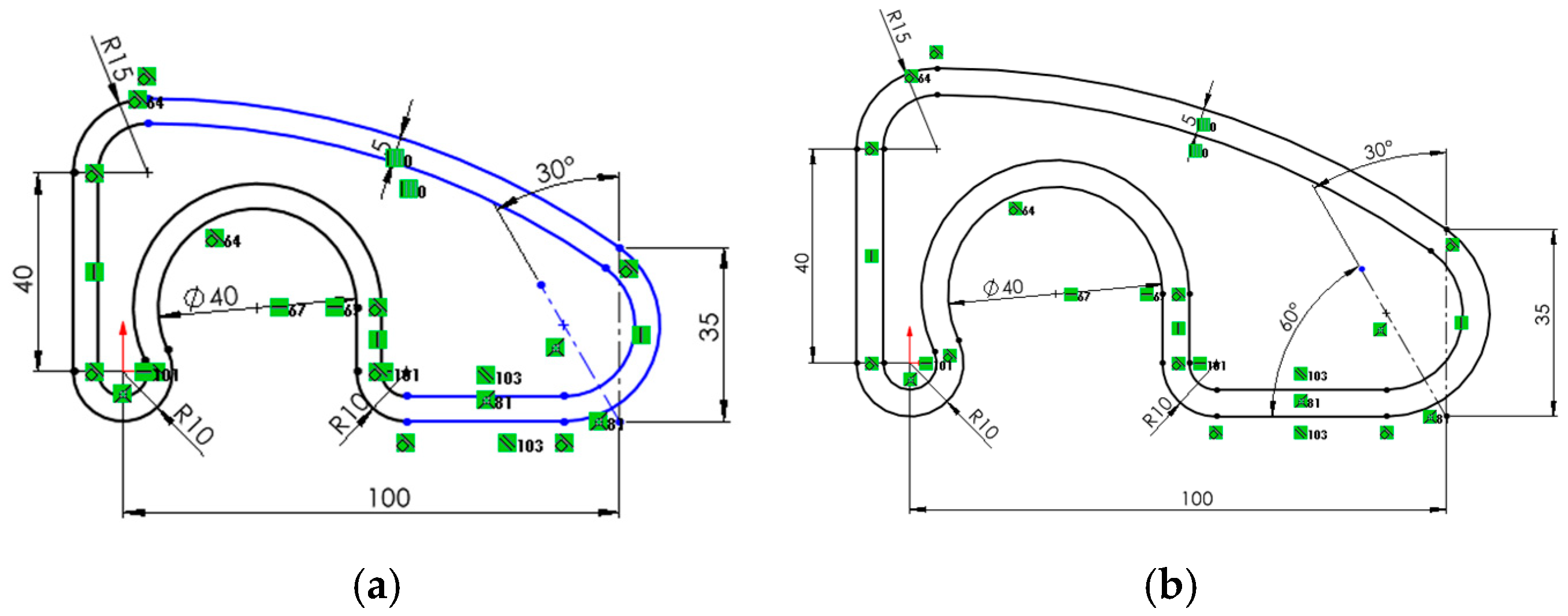

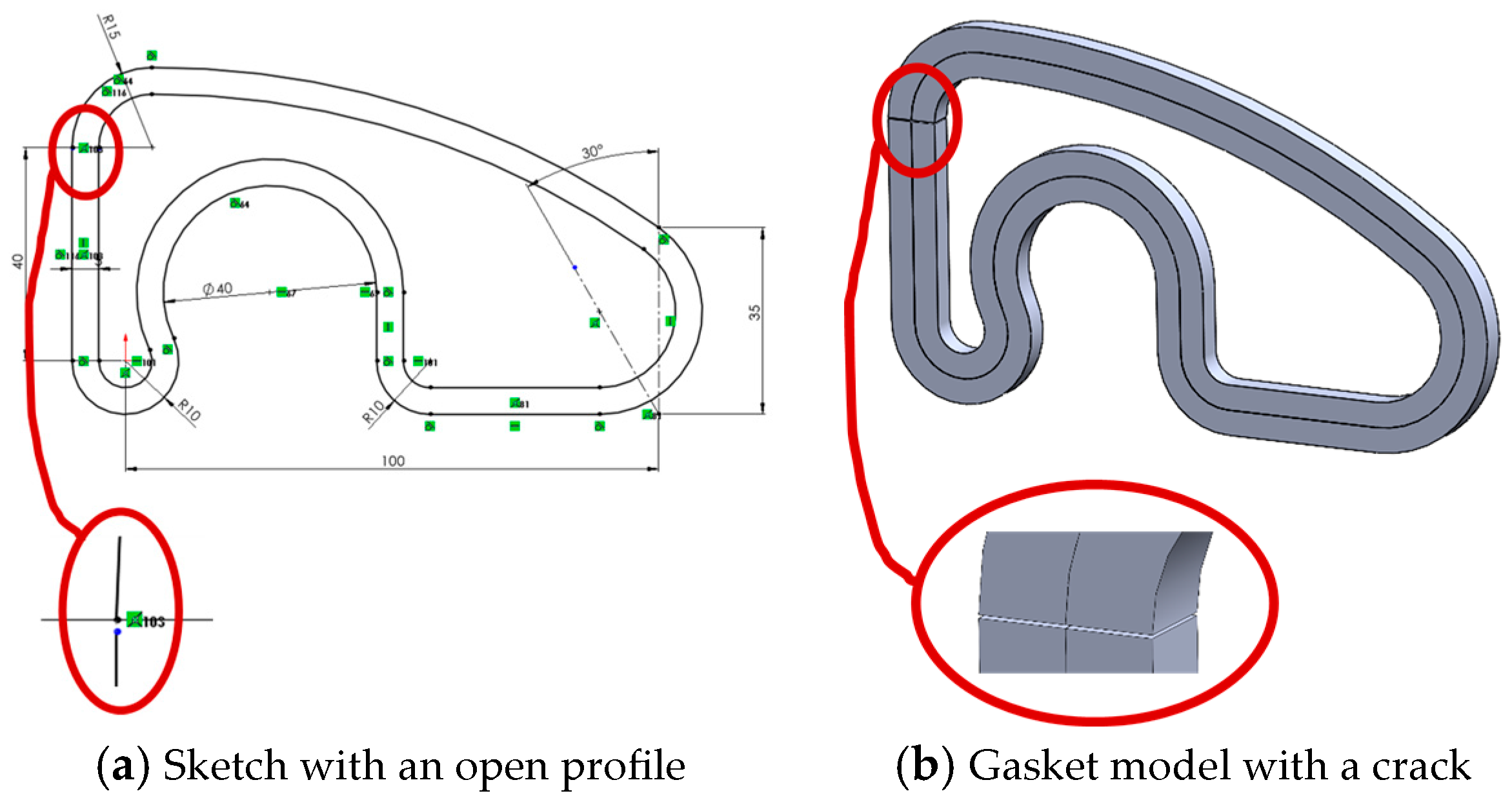

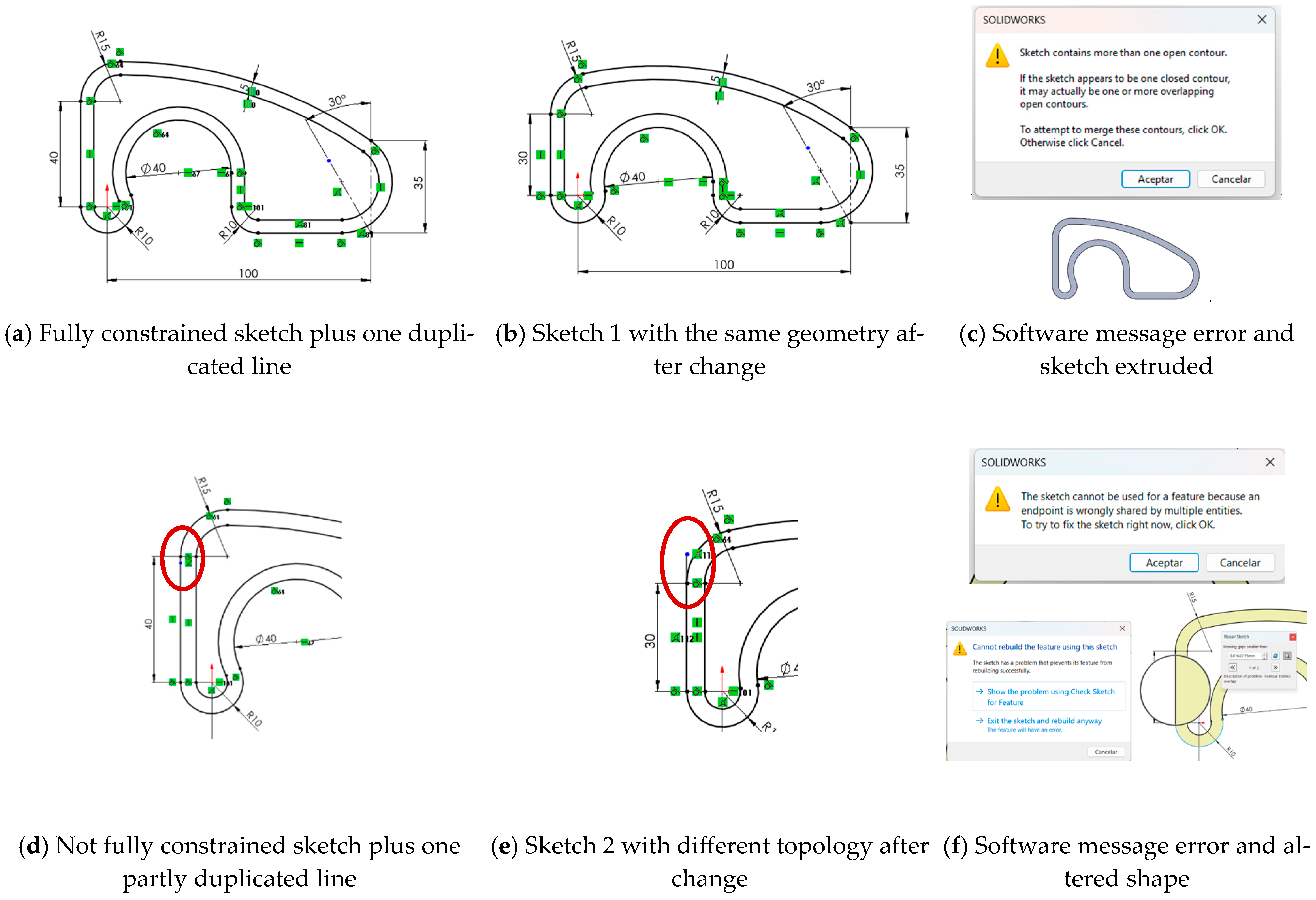
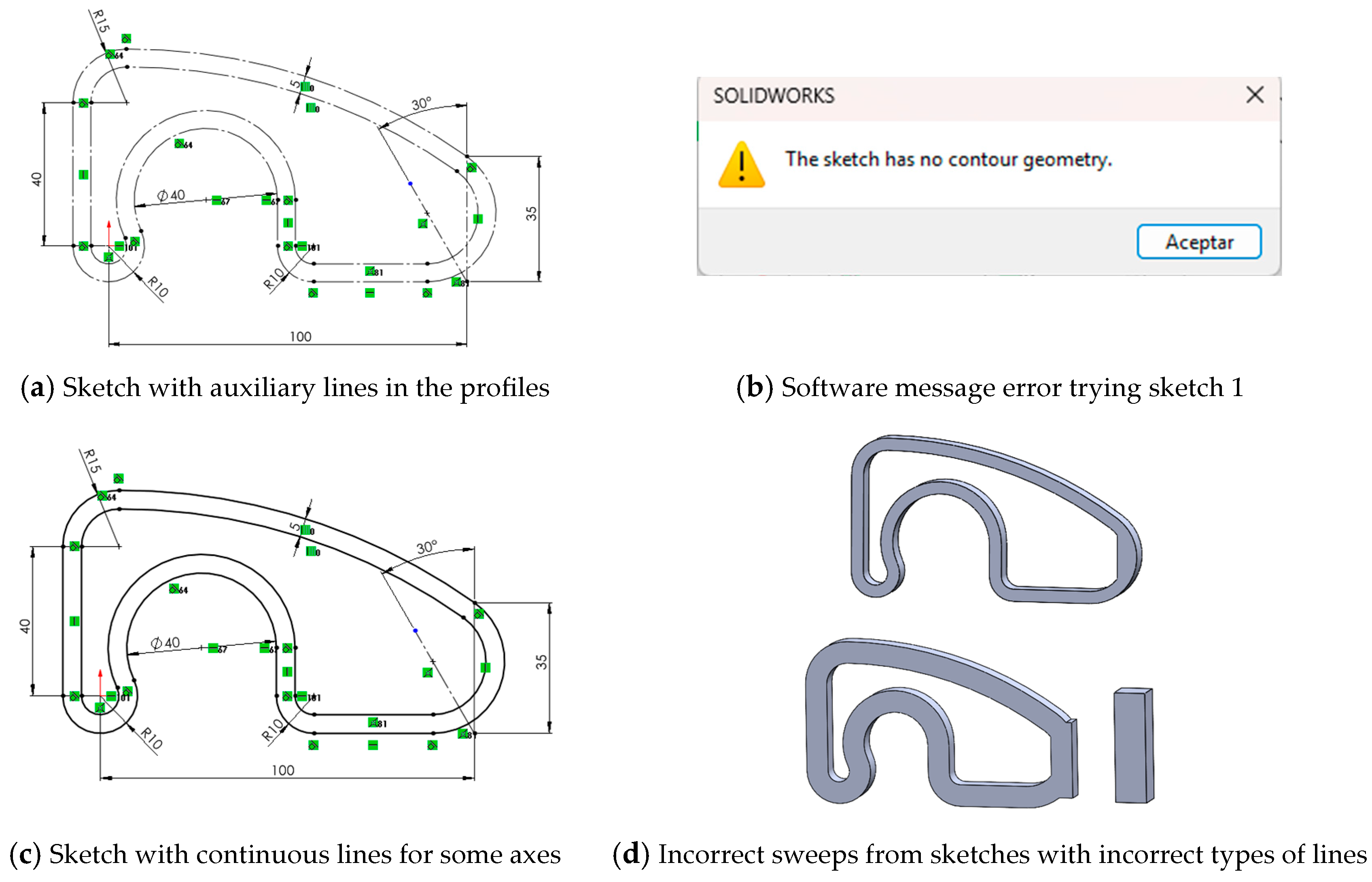
| Quality Item Error | Quality Sub-Item Error | Error Description | Influence |
|---|---|---|---|
| The model fails to be CONSISTENT Design changes typically cause unpredictable or potentially catastrophic results. | Poorly drawn or poorly constrained sketches lead to design changes that produce unpredictable results. | Sketches are partially unconstrained or miss critical constraints. | S |
| Sketches have many (or at least some critical) segmented lines, causing continuity issues. | S | ||
| Sketches have incorrect or duplicate lines (too many of them or at least some critical ones). | S | ||
| Model is incorrectly positioned relative to the references. | Model is not aligned or oriented to the global reference system. | D | |
| Model lacks suitable datums for building and editing. | D | ||
| Different functional elements are modeled together or unnecessarily interrelated. | Model tree has an excess of unnecessary dependencies. | D | |
| Functional elements are not defined by independent modeling operations. | PMT | ||
| The model fails to be CONCISE Model contains significant repetitive or fragmented constraints, datums and features; it never uses pattern operations, thus managing more geometry than strictly required to build and edit the model. | The model includes many repetitive or fragmented constraints, datums or features, or at least one potentially catastrophic. | Sketches have excessive or critical repetitive/fragmented constraints. | S |
| Model has significant or critical repetitive or fragmented datums. | D | ||
| Model has significant or critical repetitive or fragmented features. | PMT | ||
| Workable replication operations (translate-and-repeat, rotate-and-repeat and symmetry) are never used in parts with patterns. | Workable pattern operations (translate-and-repeat, rotate-and-repeat) are never used. | PMT | |
| Workable modeling operations of symmetry are never used to define the model. | PMT |
| Hypotheses | General Negative Knowledge | # | Detailed Negative Knowledge |
|---|---|---|---|
| Unconstraining sketches in general, and profiles in particular, negatively affect the quality of CAD models, while not all the missing or inappropriate constraints have the same negative impact on topology and geometry. | Sketches with no constraints are not reusable because they become unstable when edited. | H1 | Fully unconstrained sketches are non-reusable, as unpredictable alterations occur when edited. |
| H2 | Dimensional constraints mainly control size; thus, their absence easily leads to uncontrolled global inflation or deflation edition. | ||
| H3 | Geometric constraints mainly control shape; thus, their absence has a greater impact on reusability as edited models easily become globally tangled or distorted. | ||
| The loss of some constraints always reduces reusability, while intensity depends on the nature of the missing constraints. | H4 | Partial incompleteness of dimensional constraints easily leads to uncontrolled local inflation or deflation while editing. | |
| H5 | Partial incompleteness of geometric constraints easily derives in uncontrolled locally tangled or distorted shapes while editing. | ||
| H6 | Some constraints (mainly those restricting few and local degrees of freedom) have a minor influence on topology while retaining an important influence on geometry variations during editing. | ||
| Overconstrained sketches, with excessive or incompatible constraints, are difficult to edit and may become unusable. | Overconstraining affects reusability of sketches. | H7 | Overconstrained sketches are difficult to edit but still reusable if the surplus constraints are redundant. |
| H8 | Overconstrained sketches are non-reusable and even unusable if the surplus constraints are incompatible. | ||
| Some specific constraints always increase the risk of overconstraining. | H9 | Fix constraint (anchor) is prone to producing unintended restrictions when combined with dimensional constraints, thus limiting the ability to modify the design. | |
| H10 | Extrinsic constraints are more prone to overconstraining than their intrinsic counterparts. | ||
| Inconsistent geometry always affects sketches reusability. | Continuity issues result in hard editing sketches, which sometimes do not sweep to build features. | H11 | Broken continuity in sketches typically prevents their usability as result in cracked shapes or even sweep failures. |
| H12 | Sketches constrained to less than optimal continuity (fragmented continuity) sometimes prevent sweeping features, while others aggravate edition. | ||
| Redundancies affect reusability of sketches. | H13 | Overlapping lines result in sketches that sometimes do not sweep to build features, while typically becoming unperceived and mistakenly edited. | |
| H14 | Tail lines result in sketches that typically cannot sweep to build features. | ||
| Incorrect assignment of line types (line classification) makes geometry uninterpretable. | H15 | Import failures that result in overall incorrect line types make imported models neither reusable nor usable. | |
| H16 | Mistakenly changing some line types results in local inconsistencies that produce incorrect topologies when sweeping, or even failure to sweep. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Lluch, C.; Plumed, R.; Company, P. From Negative Knowledge to Best Practices for Enhancing Reusability of Sketches in Procedural 3D CAD Models. Designs 2025, 9, 132. https://doi.org/10.3390/designs9060132
González-Lluch C, Plumed R, Company P. From Negative Knowledge to Best Practices for Enhancing Reusability of Sketches in Procedural 3D CAD Models. Designs. 2025; 9(6):132. https://doi.org/10.3390/designs9060132
Chicago/Turabian StyleGonzález-Lluch, Carmen, Raquel Plumed, and Pedro Company. 2025. "From Negative Knowledge to Best Practices for Enhancing Reusability of Sketches in Procedural 3D CAD Models" Designs 9, no. 6: 132. https://doi.org/10.3390/designs9060132
APA StyleGonzález-Lluch, C., Plumed, R., & Company, P. (2025). From Negative Knowledge to Best Practices for Enhancing Reusability of Sketches in Procedural 3D CAD Models. Designs, 9(6), 132. https://doi.org/10.3390/designs9060132






