Abstract
Open-cellular Ti6Al4V lattice structures have found application in porous scaffolds that can match the properties of human bone, which consists of a dense cortical shell and a less-dense cancellous core with an apparent density ranging from 1.3 to 2.1 g/cm3 and 0.1 to 1.3 g/cm3, respectively. The implantation of porous scaffolds is essential for treating large bone defects and must mimic natural bone’s geometric and mechanical behaviour. Functionally graded lattice structures offer spatial variation in mechanical properties, making them suitable for biomedical applications. While the mechanical behaviour of lattice structures is typically evaluated under compression, their flexural properties remain largely underexplored. The aim of this research is to assess the flexural rigidity of a novel lattice material, namely Triply Arranged Octagonal Rings (TAORs), with both uniform and functionally graded architectures, to reproduce the flexural properties of long bones. Titanium alloy scaffolds have been designed with a TAOR cell, whose relative densities range from 10% to 40% with full and hollow sections. Morphological considerations were carried out during the design process to obtain a scaffold geometry which complies with the optimal characteristics required to promote osteointegration. A non-linear finite element (FE) model was developed. Three- and four-point bending tests were simulated, and the results were compared with those of a bone surrogate for long bones. Scaffolds with 10% and 20% relative densities showed flexural rigidity close to that of the bone surrogate and proved to be potential candidates for application in biomedical devices for long bones.
1. Introduction
The increasing demand for orthopaedic implants and the advances in biomaterials resulting in the creation of intricate bone-mimicking structures [1] drive the scientific idea of helping people suffering from bone fractures or damage caused by accidents or pathologies to go through their lives normally [2]. Despite bone’s ability for self-regeneration, in the presence of massive defects, a surgical process with the implantation of a biomedical device is required to support the healing process [3]. The main challenge in the design of a porous implant is the mimicking of the mechanical characteristics of a graded structure like human bone [4], which is composed of a dense cortical shell and a less-dense cancellous core with a wide range of mechanical properties [5,6,7] and an apparent density ranging from 1.3 to 2.1 g/cm3 and 0.1 to 1.3 g/cm3, respectively [8]. Matching the implant’s structural properties to those of bone is essential to avoid stress shielding, where excessive implant stiffness alters the distribution of strain and shields loads away from adjacent bone, leading to bone resorption, according to Wolff’s law and more recently, Frost’s Mechanostat theory [9]. To this purpose, functionally graded (FG) implants arouse interest thanks to their potential to vary their mechanical properties through their volume [10]. They can be effectively used in the design of a bone implant to reduce stress shielding and support the long-term survival of the implant by inducing physiological bone stress and reducing the chances of aseptic loosening due to implant-induced adaptive bone remodelling [11]. Mechanical tests of bone provide valuable information about material and structural properties useful for the comprehension and the treatment of bone pathologies [12]; the flexural rigidity of long bones is commonly used to evaluate the effects of treatment during the healing process of a bone fracture [13]. Several studies evaluated, experimentally and numerically, the flexural rigidity of titanium alloy Ti6Al4V lattice structures for orthopaedic applications [14,15]. Collins et al. [16] introduced a bone surrogate (BS) to mimic the flexural rigidity of long bones, featuring an elastic modulus of 2850 MPa for the cortical shell and 596 MPa for the cancellous core [16]. The surrogate was modelled after the geometry of a porcine femur diaphysis, featuring a rectangular cross-section and a cylindrical core [16].
Recent advances in implant design have increasingly leveraged additive manufacturing techniques, particularly 3D printing and selective laser melting techniques, which enable the fabrication of patient-specific FG scaffolds that closely replicate the mechanical properties of adjacent bone tissue [17,18,19]. An important geometric characteristic of lattice structures to be considered during the design process of porous scaffolds is the pore size, which affects cell penetration and bone ingrowth [20]. In a review, He et al. [21] determined the optimal pore size to promote osteointegration in the range of 500–800 μm; the authors also evaluated the optimal relative densities in the range of 10–40%. In another study, Distefano et al. [22] determined the optimal pore size to be equal to 522 μm.
Distefano et al. [23] proposed a novel biomimetic lattice structure, namely Triply Arranged Octagonal Rings (TAORs). The authors morphologically and mechanically characterised the novel TAOR lattice, with constant and FG relative densities [24], for applications in the biomedical field.
A further step in the characterisation of the TAOR lattice involved the evaluation of its flexural rigidity for orthopaedic application in devices for long bones. TAOR lattice specimens with square and hollow-square cross-sections were designed with constant and FG relative densities in the range of 10–40%. This study aimed to assess how different cross-sectional geometries (square and hollow square) and relative density distributions (constant and FG) influence the flexural rigidity of TAOR lattice structures. While much of the existing work has focused on compressive properties, this study addresses the gap in the literature by evaluating the flexural rigidity of FG TAOR lattices with both filled- and hollow-square cross-sections. To the best of the authors’ knowledge, this study is among the first to evaluate the flexural rigidity of FG lattice structures with structural properties relevant to orthopaedic implants, providing valuable insights for load-bearing scaffold design in long bone repair. The specimens were numerically tested by means of a non-linear finite element (FE) model simulating the conditions of three- and four-point bending tests. Moreover, the model of a BS for long bones developed by Collins et al. [16] was reproduced in the present work, and the results obtained for the TAOR lattices were compared to those of the BS.
2. Materials and Methods
2.1. Design of TAOR Strucures
The TAOR lattice specimens, for three- and four-point bending tests, were designed with filled-square and hollow-square cross-sections, with the geometric characteristics reported in Table 1 referring to Figure 1.

Table 1.
TAOR lattice specimens’ dimensions.
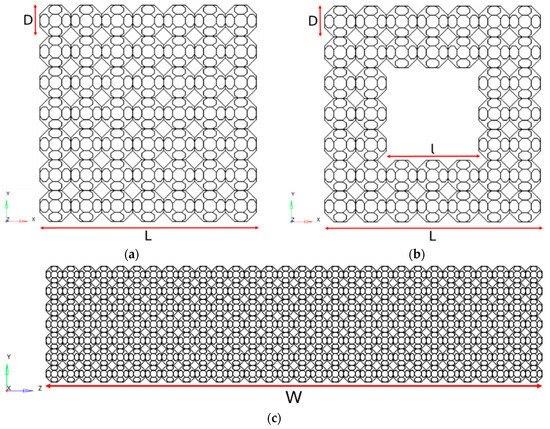
Figure 1.
TAOR lattice specimens’ cross-sections: (a) filled square; (b) hollow square. (c) TAOR lattice specimen lateral view.
The dimensions were chosen in accordance with those of a BS for long bones designed by Collins et al. [16]. The proposed model of the BS was reproduced and numerically tested in the present work, to obtain a reference result with which to compare the flexural rigidity of the TAOR lattices.
In Figure 1, D represents the unit cell size and, together with the other geometric parameters displayed in Figure 2, characterises the TAOR unit cell.
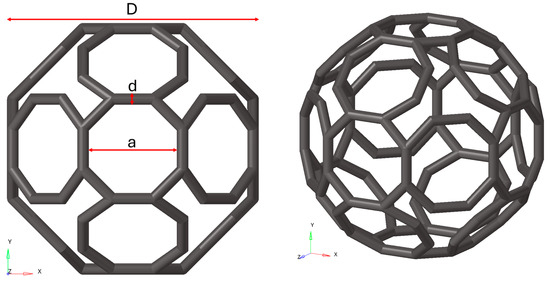
Figure 2.
Geometric characteristics of the TAOR unit cell.
Here, d is the strut size and a defines the pore size useful to promote osteointegration [20]. The unit cell’s dimensions were defined through Equation (1), which relates the relative density ρ*/ρs to the ratio d/D.
Equation (1) was obtained from the CAD model of the TAOR by changing the strut diameter d and the cell size D of the unit cell, therefore varying its relative density ρ*/ρs. Then, the ratio d/D was plotted against the relative density ρ*/ρs, and the fitting curve determined the equation. Four levels of relative densities were selected: 10%, 20%, 30% and 40%; therefore, the respective values of d and a were determined. The selected relative densities are in the reported optimal range to promote osteointegration [21]. Eight specimens were obtained: four with filled-square cross-sections and four with hollow-square cross-sections with the TAOR unit cells’ dimensions reported in Table 2.

Table 2.
TAOR unit cells’ dimensions.
The next step involved the design of the FG specimens. The relative density varies in the radial direction through the cross-section, as displayed in the scheme in Figure 3.
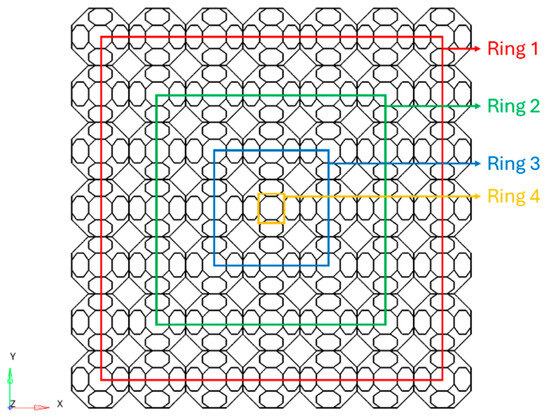
Figure 3.
Architecture of the TAOR lattice FG specimens.
Each ring shown in Figure 3 presents a constant relative density. The relative density decreases from ring 1, the outermost, to ring 4, the innermost. FG specimens present the same mean relative densities as the specimens with uniform relative density and a density gradient of 5%, defined as the difference between the relative density of ring 1 and the relative density of ring 4. The FG specimens with a hollow-square cross-section only contain rings 1 and 2; therefore, the density gradient is calculated between these two rings. The relative density and the density gradient of the FG lattices are reported in Table 3.

Table 3.
Relative density and density gradient of the TAOR lattice FG specimens.
The relative density of each ring was determined with the aim of maintaining a fixed density gradient between two subsequent rings of the FG specimen, thus obtaining a gradual variation of the geometric characteristics of the unit cells. The dimensions of the unit cells were calculated by means of Equation (1) and are summarised in Table 4 for each ring of the TAOR FG lattices.

Table 4.
TAOR unit cells’ dimensions for each ring of the FG specimens.
The pore size of the designed specimens against their relative density is shown in Figure 4. The green band represents the optimal range of pore sizes of 500–800 μm, which promotes bone ingrowth [21]; moreover, the analysed structures fall within the optimal range of relative densities of 10–40% [21].
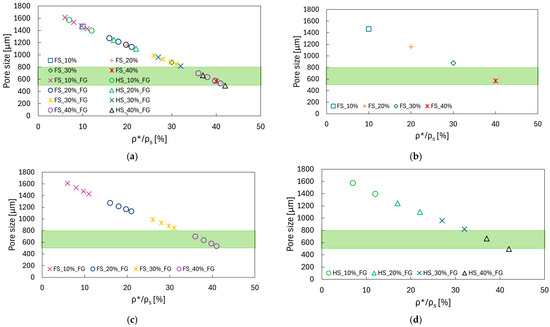
Figure 4.
Pore size vs. relative density to determine the TAOR specimens, with the optimal pore size to promote osteointegration shown in the green band: (a) all the configurations; (b) FS; (c) FS_FG; (d) HS_FG.
For the specimens with a constant relative density, just the data for the filled-square cross-sections are reported, since there are no differences between specimens with filled-square and hollow-square cross-sections. The pore sizes of the specimens with 40% relative density fall in the optimal range; for the other relative densities, the pore sizes present higher values than the recommended ones. Taking into account the wide range of relative densities considered, it is not possible to find a unique D value which allows optimal pore size values for all the considered cases. With the aim of mechanically characterising the TAOR lattices, it was preferred to maintain a constant D value for a better understanding of the results. By varying the parameters of Equation (1), it is possible to obtain the desired values of pore sizes, to fulfil the morphological requirements for biomedical applications.
2.2. Euler–Bernoulli Beam Theory
The TAOR lattice flexural rigidity EIEB in N* mm2 was estimated by means of the Euler–Bernoulli beam theory by applying Equation (2) for the three-point bending tests and Equation (3) for the four-point bending tests [25].
where L is the distance in mm between the bottom cylinders, a is the distance in mm between the top and the bottom cylinders and Ks is the bending stiffness in N/mm calculated by means of Equation (4) [25].
where F is the force in N and δ is the deflection measured in mm. The latter was evaluated by means of an FE model useful to estimate the TAOR’s flexural rigidity. Euler–Bernoulli theory assumes a slender beam, with a homogeneous, isotropic, linear–elastic material, uniform cross-section, and high support-length-to-diameter ratio or aspect ratio of at least 16:1 [26,27]. Given the low aspect ratio of the TAOR lattice (3:1), it is important to note that Timoshenko beam theory, which considers both bending and shear deformation, may provide more accurate results in modelling the flexural behaviour of these structures [26,27]. However, since the results are compared to the BS model by Collins et al., Euler–Bernoulli beam theory was used for consistency with previous work.
2.3. Finite Element Model
A non-linear FE model was developed, by means of the Altair HyperWorks® 2022.3 (Altair Engineering, Troy, MI, USA) software package with Optistruct 2022.3 as the implicit solver, for the evaluation of the flexural rigidity of the TAOR lattices made with Ti6Al4V alloy. Next to the TAOR lattice FE model, a model of the bulk Ti6Al4V was developed for the evaluation of the relative mechanical properties of the TAOR lattices. For comparison, the model of the BS proposed by Collins et al. [13] was also reproduced.
The TAOR lattices with filled-square cross-sections present 7 × 7 × 30 unit cells, and they were meshed with 1D beam elements CBEAM with six degrees of freedom per node. The beam elements present a circular cross-section, and their geometric properties were defined by modifying the strut diameter d of the unit cell according to the relative densities considered. Following a mesh sensitivity study, six elements were imposed on each strut of the unit cell. Two, four, six and eight elements on each strut were considered for the mesh sensitivity test, and the results were compared in two zones, in terms of axial stress and deflection under three-point bending, as shown in Figure 5.

Figure 5.
Zones of the specimens analysed for the mesh sensitivity study.
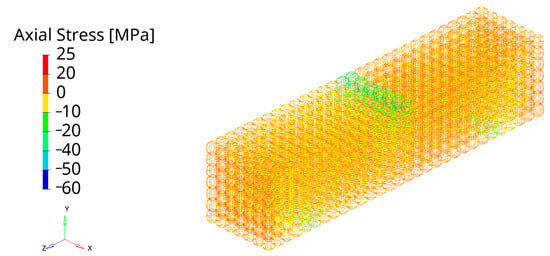
Figure 6.
Mesh sensitivity test results. Axial stress under three-point bending on the TAOR scaffolds meshed with six elements on each strut of the unit cell.

Table 5.
Comparison of the axial stress (z-axis) under three-point bending for the mesh sensitivity test.
Since the contour plots of the different mesh sizes were very similar in terms of stress distribution, only the results of the specimen with six elements, which is the one selected for the FE analyses, are reported in Figure 6. Indeed, no great influence of the element size on the results was detected during the mesh sensitivity test. Good agreement in the axial stress results under three-point bending was obtained with a coarser mesh with a small percentage difference, below 1%, from the finer mesh. In zone 1, from the comparison between the meshes of two and four elements, percentage differences of 0.58% and 0.55% in tension and compression were obtained. The comparison between the mesh with four and six elements on each strut resulted in a percentage error of 0.57% and 0.56% in tension and compression, respectively. The percentage error decreased to 0.36% and 0.27% in tension and compression from the comparison between the results with six and eight elements on the strut. The good agreement in the axial stress results is confirmed by the comparison of the results in zone 2 with a minimum difference of 0.03% and 0.05% in tension and compression between mesh with six and eight elements on the strut. Therefore, considering the negligible differences in the results, the mesh with six elements on each strut was selected for the FE model. The choice of 1D elements is consistent with the recent literature, where strut-based lattice structures with geometric properties comparable to the TAOR lattice were modelled with 1D elements and the results of the numerical analysis were experimentally validated [28].
On the top and bottom faces of the lattice structure, plates with a 1 mm thickness were placed to apply the boundary conditions of the bending tests. The plates were modelled with titanium alloy Ti6Al4V and were meshed with first-order 2D quad elements (CQUAD) of 0.14 mm. The nodes were merged to maintain the node continuity between the lattice structure and plates.
The boundary conditions were applied through cylinders with a 10 mm diameter, simulating the support of a testing machine and placed in contact with the top and bottom plates. The cylinders were modelled in steel and were meshed with first-order 2D quad elements (CQUAD) of 0.6 mm dimensions. The steel was chosen to model the cylinders in order to reproduce the behaviour of the cylinders of a testing machine during experimental tests. The cylinders were positioned for the three- and four-point bending tests, and the boundary conditions were applied on the cylinders through RBE2 rigid elements as displayed in Figure 7a,b. On the top cylinder, a vertical load of 1000 N along the y-axis was applied, while the bottom cylinders were fully constrained. For the four-point bending test, the 1000 N load was divided between the two top cylinders.
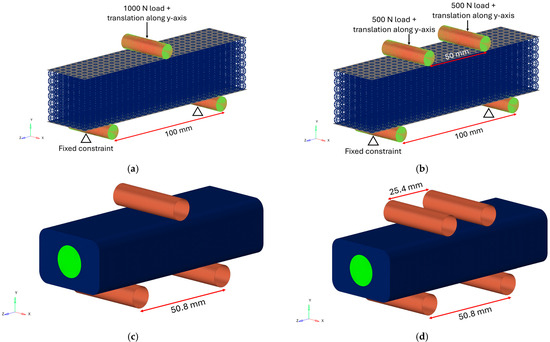
Figure 7.
The position of the cylinders and boundary conditions applied in the TAOR lattice FE model for the (a) three-point bending test and the (b) four-point bending test. The position of the cylinders to apply the boundary conditions in the BS FE model for the (c) three-point bending test and the (d) four-point bending test.
Between the cylinders and the specimen’s plates, a contact with a static Coulomb friction coefficient of 0.4 [29] was modelled, as reported in Figure 8. The cylinders were modelled as the main element while the plates were modelled as the secondary elements. The simulation of the contact requires a non-linear static solver.
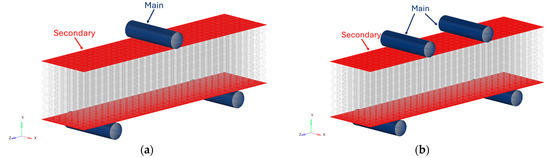
Figure 8.
Definition of the contact in the FE model for the (a) three-point bending test and the (b) four-point bending test.
The TAOR lattice structure and plates were modelled with titanium alloy Ti6Al4V [22,30], while the cylinders were simulated in steel [31]. The assumed material models were homogeneous, isotropic and linear–elastic. Despite 3D-printed Ti6Al4V alloy exhibiting anisotropic properties due to the nature of layered manufacturing, isotropic property approximation is commonly assumed to simulate the material behaviour in the FE models [32,33]. The mechanical properties are reported in Table 6.

Table 6.
Ti6Al4V and steel mechanical properties in the FE model of the TAOR lattice structure.
The bulk specimens were modelled with first-order hexahedral elements (CHEXA) of 1 mm. The bulk specimens present the same external dimensions as the lattice specimens, as visible in Figure 9
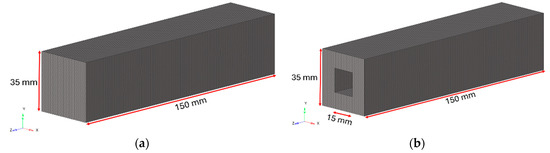
Figure 9.
Geometric characteristics of bulk Ti6Al4V specimens with (a) filled-square cross-section; (b) hollow-square cross-section.
The model of the BS was meshed with first-order hexahedral elements (CHEXA) of 0.6 mm. For both the bulk Ti6Al4V model and the BS model, the boundary conditions were applied in the same manner as the lattice structure model through cylinders, as shown in Figure 7. For the bulk titanium model, the cylinders were positioned at the same distances as the lattice model, displayed in Figure 5, while for the BS model, the cylinders were positioned for the three- and four-point bending test as shown in Figure 7c,d.
For both the bulk Ti6Al4V and the BS FE models, a contact between specimens and cylinders was simulated with a static Coulomb friction coefficient of 0.4 for the bulk titanium model [29] and 0.6 for the BS model [13]. In both cases, the cylinders were simulated as the main elements and the specimens as secondary elements. The material properties of the bulk Ti6Al4V FE model are the same as those of the TAOR lattice FE model reported in Table 5, while the material properties of the BS FE model were simulated according to [13] as reported in Table 7. The BS interface between the shell and core was modelled with merged nodes.

Table 7.
BS FE model mechanical properties [13].
3. Results and Discussion
The deflection δ used in the evaluation of the flexural rigidity EIEB was evaluated in the lower central part of the specimens as shown in Figure 10 with a black ring for the FS_20% specimen subjected to the three-point bending test. The same zone of the specimens was used for the evaluation of the deflection for the lattices subjected to four-point bending tests. The evaluated deflection δ values are summarised in Table 8.
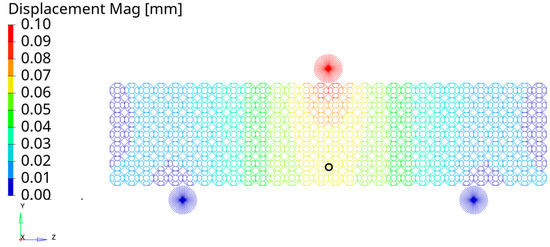
Figure 10.
Vertical displacement along the y-axis evaluated in the black ring for the FS_20% specimen for the three-point bending test.

Table 8.
Deflection δ evaluated with the FE analyses of TAOR specimens and BS.
As expected, the three-point bending test results in higher deflections compared to those obtained with the four-point tests. To assess the accuracy of the FE analyses, a comparison between the deflection δ numerically obtained for the bulk specimens and analytically calculated by applying Euler–Bernoulli and Timoshenko beam theories [34] was performed. Timoshenko theory was applied by means of Equations (5) and (6) for the three- and four-point bending tests, respectively, while Euler–Bernoulli theory was applied through Equations (7) and (8) for the three- and four-point bending tests, respectively. The comparison is shown in Table 9.

Table 9.
Comparison between the deflection δ evaluated with the FE analyses and analytically calculated through Euler–Bernoulli and Timoshenko beam theories.
The relative flexural rigidity EI* was estimated as the ratio between the flexural rigidity of the TAOR lattice specimen EIEBL and the flexural rigidity of the bulk specimen EIEBB, as reported by Equation (9) [25].
The performance index α [35] with the grade of porosity was calculated by Equation (10) as the ratio between the relative flexural rigidity EI* and the relative density ρ*/ρs.
The flexural rigidity EIEB estimated with Euler–Bernoulli beam theory for the three- and four-point bending tests is reported in Figure 11.
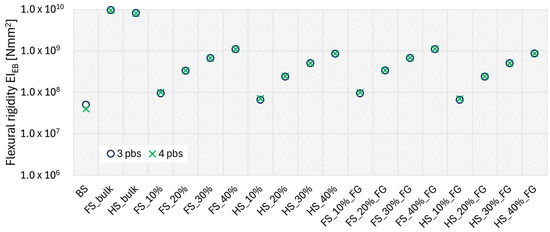
Figure 11.
The scatter plot presents the flexural rigidity EIEB calculated for the three- (blue) and four-point (green) bending tests.
For both the three- and four-point bending tests, the comparison with the results of the BS, the bulk Ti6Al4V and the TAOR lattices found that the lattice structure lowered the Ti6Al4V’s flexural rigidity from that of the bulk beams to closer to that of the bone. In both cases, the bulk specimen’s flexural rigidity was two orders of magnitude greater than that of the BS. For the three-point bending test, the TAOR lattices with relative densities in the range of 20% to 40% had higher flexural rigidity compared to the BS. The specimens with a relative density of 10% had flexural rigidity comparable to that of the BS; however, the FS_10% specimen had a higher flexural rigidity compared to the BS with a percentage difference of 88.7%, while the specimen HS_10% with a hollow-square cross-section had a flexural rigidity greater than that of the BS with a percentage difference of 32.5%. Similar considerations can be made for the four-point bending tests. Also, in this case, the TAOR lattices with relative densities in the range of 20–40% present higher flexural rigidity than that of the BS, while the lattices with 10% relative density have flexural rigidity values comparable to those of the bone. For both three- and four-point bending tests, the FG specimens did not show significant differences compared to the uniform-density specimens.
For a better understanding of the results, the relative flexural rigidity EI* is plotted in a graph against the relative density ρ*/ρs as shown in Figure 12a,b for the three- and four-point bending tests, respectively.
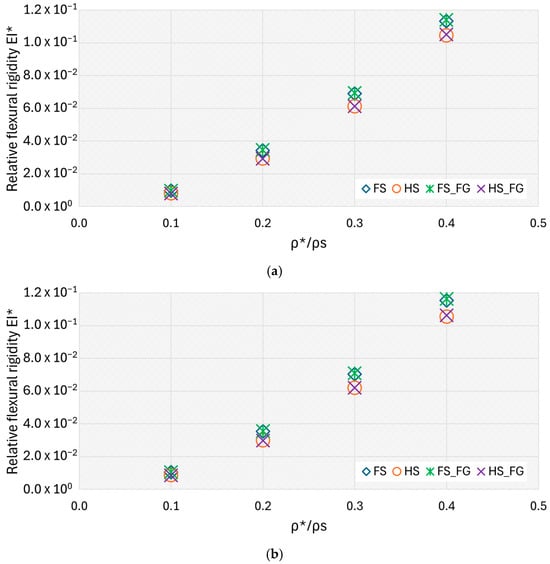
Figure 12.
The scatter plot presents the results of the FE model in terms of relative flexural rigidity against relative density of the different configurations of TAOR specimens: (a) three-point bending test; (b) four-point bending test.
The relative flexural rigidity and the relative density are related to each other by a power law function in the form of Equation (11).
where C and n are the constant coefficients of the equation. Their values were evaluated, and the results are summarised in Table 10.

Table 10.
Evaluation of the coefficients C and n of the power law function between relative flexural rigidity and relative density.
The curve fit of the C coefficient did not show differences between the different specimens’ configurations. The hollow-square specimens have n values higher than the values of the filled-square specimens. Thus, the curves of the hollow-square specimens grow faster than those of the square specimens. This suggests that hollow designs can achieve enhanced rigidity efficiency at higher densities. While these findings are promising, the fabrication feasibility of hollow lattice structures must be considered [19,36]. Powder bed fusion techniques have made it possible to reliably fabricate complex hollow geometries with controlled wall thickness and internal channels [37]. Nonetheless, challenges remain in terms of post-processing, such as ensuring complete powder removal from enclosed cavities and maintaining dimensional accuracy [36,37,38]. These factors must be addressed to reliably implement hollow lattice scaffolds in pre-clinical and clinical applications [36,37,38]. The data in Figure 12 shows that the relative flexural rigidity increased while the relative density increased. Specimens with a filled-square cross-section had higher flexural rigidity than those of the hollow-square specimens; in particular, the hollow-square cross-section helps decrease the TAOR lattices’ flexural rigidity up to 1.44 times, as summarised in Table 11. Moreover, the hollow cross-section helps to lower the TAOR lattice flexural rigidity to that of the BS.

Table 11.
Comparison between the flexural rigidity ratios of TAOR specimens with filled-square and hollow-square cross-sections.
The comparison of flexural rigidity ratios between TAOR lattices with constant and FG relative densities did not show differences in their values. This outcome is in accordance with the recent literature on the TAOR lattice [24], in which the apparent elastic moduli of TAOR specimens with constant and FG densities were found to have similar values.
Figure 13 shows a comparison of the performance index α of the numerically tested TAOR specimens.
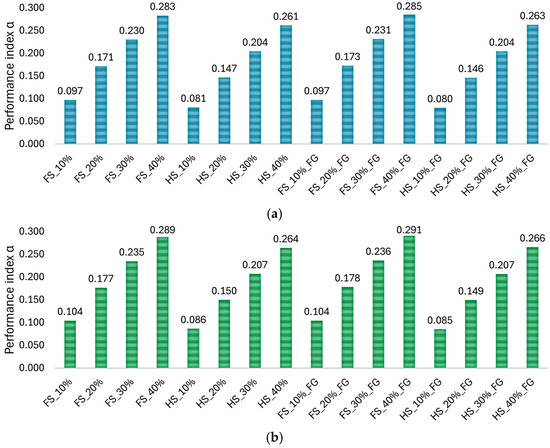
Figure 13.
The bar plots present a comparison between the performance index of the different configurations of TAOR lattices for the (a) three-point bending test and the (b) four-point bending test.
TAOR specimens with a filled-square cross-section had a higher performance index than those with a hollow-square cross-section, while no substantial differences were found from the comparison between specimens with constant and FG relative densities.
4. Conclusions
The results of the FE analyses of three- and four-point bending tests showed that the TAOR lattice lowered the flexural rigidity of a Ti6Al4V scaffold from the bulk beam to that of long bone. The TAOR lattice scaffolds aim to reproduce the mechanical characteristics of long bones. The comparison between the results of the BS and the TAOR lattice specimens showed that the scaffolds with lower relative densities had a flexural rigidity comparable to that of the BS. The TAOR lattice specimens with a hollow cross-section showed promising results compared to those with a filled-square cross-section by achieving a flexural rigidity closer to that of the BS.
The current study has some limitations. First, the findings are based solely on FE simulations, and experimental validation should be performed to verify the numerical results. Second, although Euler–Bernoulli beam theory was used to remain consistent with previous work and facilitate comparison with the bone surrogate model, incorporating Timoshenko beam theory in future analyses can improve accuracy for such geometries.
Despite these limitations, no substantive difference was encountered from the comparison between the flexural rigidity of the specimens with constant densities and FG densities, showing that the apparent flexural rigidity only depends on the mean relative density and not on the FG density.
The results of this research offer valuable insights into the design of porous bone implants, determining the optimal relative density and geometric features of TAOR lattices to mimic the characteristics of long bones.
Author Contributions
Conceptualisation, F.D. and G.E.; methodology, F.D.; investigation, F.D., G.E., M.Z. and H.-L.P.; data curation, F.D., G.E., M.Z. and H.-L.P.; writing—original draft preparation, F.D.; writing—review and editing, F.D., G.E., M.Z. and H.-L.P.; visualisation, F.D. and G.E.; supervision, G.E. and H.-L.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Intravaia, J.T.; Graham, T.; Kim, H.S.; Nanda, H.S.; Kumbar, S.G.; Nukavarapu, S.P. Smart Orthopedic Biomaterials and Implants. Curr. Opin. Biomed. Eng. 2023, 25, 100439. [Google Scholar] [CrossRef] [PubMed]
- Abd-Elaziem, W.; Darwish, M.A.; Hamada, A.; Daoush, W.M. Titanium-Based Alloys and Composites for Orthopedic Implants Applications: A Comprehensive Review. Mater. Des. 2024, 241, 112850. [Google Scholar] [CrossRef]
- Oryan, A.; Alidadi, S.; Moshiri, A.; Maffulli, N. Bone Regenerative Medicine: Classic Options, Novel Strategies, and Future Directions. J. Orthop. Surg. Res. 2014, 9, 18. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.; Humayun, A.; Cohen, D.J.; Boyan, B.D.; Schwartz, Z. Additively Manufactured 3D Porous Ti-6Al-4V Constructs Mimic Trabecular Bone Structure and Regulate Osteoblast Proliferation, Differentiation and Local Factor Production in a Porosity and Surface Roughness Dependent Manner. Biofabrication 2014, 6, 045007. [Google Scholar] [CrossRef] [PubMed]
- Öhman-Mägi, C.; Holub, O.; Wu, D.; Hall, R.M.; Persson, C. Density and Mechanical Properties of Vertebral Trabecular Bone—A Review. JOR Spine 2021, 4, e1176. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, D.; Elbestawi, M.A. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review. J. Manuf. Mater. Process. 2017, 1, 13. [Google Scholar] [CrossRef]
- Mirzaali, M.J.; Schwiedrzik, J.J.; Thaiwichai, S.; Best, J.P.; Michler, J.; Zysset, P.K.; Wolfram, U. Mechanical Properties of Cortical Bone and Their Relationships with Age, Gender, Composition and Microindentation Properties in the Elderly. Bone 2016, 93, 196–211. [Google Scholar] [CrossRef]
- Oftadeh, R.; Perez-Viloria, M.; Villa-Camacho, J.C.; Vaziri, A.; Nazarian, A. Biomechanics and Mechanobiology of Trabecular Bone: A Review. J. Biomech. Eng. 2015, 137, 010802. [Google Scholar] [CrossRef]
- Frost, H.M. A 2003 Update of Bone Physiology and Wolff’s Law for Clinicians. Angle Orthod. 2004, 74, 3–15. [Google Scholar]
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical Properties and Energy Absorption Capabilities of Functionally Graded Lattice Structures: Experiments and Simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- Jain, T.; Sharma, G.K.; Ghosh, R. Design of Functionally Graded Porous Lattice Structure Tibial Implant for TAR. Int. J. Mech. Sci. 2024, 281, 109671. [Google Scholar] [CrossRef]
- Martin, D.E.; Severns, A.E.; Kabo, J.M. Determination of Mechanical Stiffness of Bone by PQCT Measurements: Correlation with Non-Destructive Mechanical Four-Point Bending Test Data. J. Biomech. 2004, 37, 1289–1293. [Google Scholar] [CrossRef]
- Collins, C.J.; Yang, B.; Crenshaw, T.D.; Ploeg, H.L. Evaluation of Experimental, Analytical, and Computational Methods to Determine Long-Bone Bending Stiffness. J. Mech. Behav. Biomed. Mater. 2021, 115, 104253. [Google Scholar] [CrossRef] [PubMed]
- Kharin, N.; Bolshakov, P.; Kuchumov, A.G. Numerical and Experimental Study of a Lattice Structure for Orthopedic Applications. Materials 2023, 16, 744. [Google Scholar] [CrossRef]
- Horn, T.J.; Harrysson, O.L.A.; Marcellin-Little, D.J.; West, H.A.; Lascelles, B.D.X.; Aman, R. Flexural Properties of Ti6Al4V Rhombic Dodecahedron Open Cellular Structures Fabricated with Electron Beam Melting. Addit. Manuf. 2014, 1, 2–11. [Google Scholar] [CrossRef]
- Collins, C.J.; Boyer, M.; Crenshaw, T.D.; Ploeg, H.L. Design of a Surrogate for Evaluation of Methods to Predict Bone Bending Stiffness. J. Mech. Behav. Biomed. Mater. 2018, 88, 346–351. [Google Scholar] [CrossRef] [PubMed]
- Aufa, A.N.; Hassan, M.Z.; Ismail, Z. Recent Advances in Ti-6Al-4V Additively Manufactured by Selective Laser Melting for Biomedical Implants: Prospect Development. J. Alloys Compd. 2022, 896, 163072. [Google Scholar] [CrossRef]
- Dhiman, S.; Sidhu, S.S.; Bains, P.S.; Bahraminasab, M. Mechanobiological Assessment of Ti-6Al-4V Fabricated via Selective Laser Melting Technique: A Review. Rapid Prototyp. J. 2019, 25, 1266–1284. [Google Scholar] [CrossRef]
- Aufa, A.N.; Hassan, M.Z.; Ismail, Z.; Ramlie, F.; Jamaludin, K.R.; Md Daud, M.Y.; Ren, J. Current Trends in Additive Manufacturing of Selective Laser Melting for Biomedical Implant Applications. J. Mater. Res. Technol. 2024, 31, 213–243. [Google Scholar] [CrossRef]
- Chang, B.; Song, W.; Han, T.; Yan, J.; Li, F.; Zhao, L.; Kou, H.; Zhang, Y. Influence of Pore Size of Porous Titanium Fabricated by Vacuum Diffusion Bonding of Titanium Meshes on Cell Penetration and Bone Ingrowth. Acta Biomater. 2016, 33, 311–321. [Google Scholar] [CrossRef]
- He, S.; Zhu, J.; Jing, Y.; Long, S.; Tang, L.; Cheng, L.; Shi, Z. Effect of 3D-Printed Porous Titanium Alloy Pore Structure on Bone Regeneration: A Review. Coatings 2024, 14, 253. [Google Scholar] [CrossRef]
- Distefano, F.; Pasta, S.; Epasto, G. Titanium Lattice Structures Produced via Additive Manufacturing for a Bone Scaffold: A Review. J. Funct. Biomater. 2023, 14, 125. [Google Scholar] [CrossRef] [PubMed]
- Distefano, F.; Mineo, R.; Epasto, G. Mechanical Behaviour of a Novel Biomimetic Lattice Structure for Bone Scaffold. J. Mech. Behav. Biomed. Mater. 2023, 138, 105656. [Google Scholar] [CrossRef] [PubMed]
- Distefano, F.; Epasto, G. Effect of Density Grading on the Mechanical Behaviour of Advanced Functionally Graded Lattice Structures. J. Mech. Behav. Biomed. Mater. 2024, 153, 106477. [Google Scholar] [CrossRef] [PubMed]
- Zojaji, M. Quantifying the Accuracy of Euler-Bernoulli and Timoshenko Beam Theories for Long Bones in Three- and Four-Point Bend Tests with Finite Element Analysis. Master’s Thesis, Queen’s University, Kingston, ON, Canada, 2021. [Google Scholar]
- D790-17; ASTM Standard D790-17, Standard Test Methods for Flexural 400 Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM International: West Conshohocken, PA, USA, 2017. [CrossRef]
- Young, W.C.; Budynas, R.G.; Sadegh, A.M. Roark’s Formulas for Stress and Strain; McGraw-Hill: New York, NY, USA, 2002; ISBN 007072542X. [Google Scholar]
- Della Ripa, M.; Paolino, D.S.; Amorese, A.; Tridello, A. Numerical Modelling of the Mechanical Response of Lattice Structures Produced through AM. Procedia Struct. Integr. 2021, 33, 714–723. [Google Scholar] [CrossRef]
- Straffelini, G.; Molinari, A. Dry Sliding Wear of Ti-6Al-4V Alloy as Influenced by the Counterface and Sliding Conditions. Wear 1999, 236, 328–338. [Google Scholar] [CrossRef]
- Chen, L.Y.; Huang, J.C.; Lin, C.H.; Pan, C.T.; Chen, S.Y.; Yang, T.L.; Lin, D.Y.; Lin, H.K.; Jang, J.S.C. Anisotropic Response of Ti-6Al-4V Alloy Fabricated by 3D Printing Selective Laser Melting. Mater. Sci. Eng. A 2017, 682, 389–395. [Google Scholar] [CrossRef]
- Shi, Y.; Han, Z. Effect of Weld Thermal Cycle on Microstructure and Fracture Toughness of Simulated Heat-Affected Zone for a 800 MPa Grade High Strength Low Alloy Steel. J. Mater. Process. Technol. 2008, 207, 30–39. [Google Scholar] [CrossRef]
- Yan, X.; Li, Q.; Yin, S.; Chen, Z.; Jenkins, R.; Chen, C.; Wang, J.; Ma, W.; Bolot, R.; Lupoi, R.; et al. Mechanical and in Vitro Study of an Isotropic Ti6Al4V Lattice Structure Fabricated Using Selective Laser Melting. J. Alloys Compd. 2019, 782, 209–223. [Google Scholar] [CrossRef]
- Cansizoglu, O.; Harrysson, O.; Cormier, D.; West, H.; Mahale, T. Properties of Ti-6Al-4V Non-Stochastic Lattice Structures Fabricated via Electron Beam Melting. Mater. Sci. Eng. A 2008, 492, 468–474. [Google Scholar] [CrossRef]
- Timoshenko, S. Strength of Materials, Part 1—Elementary Theory and Problems; D Van Nostrand Company Inc.: New York, NY, USA, 1940. [Google Scholar]
- Li, B.; Shen, C. Solid Stress-Distribution-Oriented Design and Topology Optimization of 3D-Printed Heterogeneous Lattice Structures with Light Weight and High Specific Rigidity. Polymers 2022, 14, 2807. [Google Scholar] [CrossRef] [PubMed]
- Bozkurt, Y.; Karayel, E. 3D Printing Technology; Methods, Biomedical Applications, Future Opportunities and Trends. J. Mater. Res. Technol. 2021, 14, 1430–1450. [Google Scholar] [CrossRef]
- Joshua, R.J.N.; Raj, S.A.; Hameed Sultan, M.T.; Łukaszewicz, A.; Józwik, J.; Oksiuta, Z.; Dziedzic, K.; Tofil, A.; Shahar, F.S. Powder Bed Fusion 3D Printing in Precision Manufacturing for Biomedical Applications: A Comprehensive Review. Materials 2024, 17, 769. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Sing, S.L.; de Looze, G.; Wilson, R.; Yeong, W.Y. Laser Powder Bed Fusion of Titanium-Tantalum Alloys: Compositions and Designs for Biomedical Applications. J. Mech. Behav. Biomed. Mater. 2020, 108, 103775. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).