Abstract
This study focuses on the participation of energy storage in primary frequency regulation of offshore wind farms. A frequency regulation performance evaluation indicator is designed, and the black-start capability of the wind farm after shutdown is also considered. By equivalently processing the black-start time, a black-start capability evaluation indicator is designed. An energy storage strategy is adopted to balance power charging and discharging during the primary frequency regulation cycle. Considering the service life of energy storage batteries and the maximum number of charge/discharge cycles, a multi-objective comprehensive optimization model is proposed, which integrates frequency regulation performance, annual average investment cost of energy storage, black-start capability, and wind energy utilization rate. The designed model is solved using a genetic algorithm. Finally, a case study of an offshore wind farm is given to compare and analyze the primary frequency regulation with energy storage participation and the joint frequency regulation of wind and energy storage, which verifies the effectiveness of the proposed designed model and algorithm.
1. Introduction
With the global energy structure transitioning towards low carbonization, offshore wind power, as an important part of clean energy, continues to rapidly increase in its installed capacity. However, the large-scale grid integration of offshore wind power poses new challenges to the power system. On one hand, the fluctuation and intermittency of wind power generation threaten the grid frequency stability severely, making it urgent for wind farms to provide primary frequency regulation support and mitigate frequency fluctuations [1,2]. On the other hand, in the event of extreme weather or fault scenarios, the power system may face the risk of large-scale blackouts. Offshore wind farms, as potential emergency power sources, need to possess black-start capabilities to quickly restore regional power supply [3,4]. As a result, how to further optimize energy storage configuration while simultaneously balancing the dual functions of frequency regulation and black-start capability is an issue that requires in-depth research.
Many scholars have conducted research on the optimal configuration of energy storage capacity in wind farms. In terms of primary frequency regulation, Ref. [5] proposes a real-time cooperation scheme to exploit their complementary characteristics and an optimal bidding strategy for them in joint energy and regulation markets, considering battery cycle life. Ref. [6] study the dynamic configuration strategy for large-scale wind power frequency regulation reserve capacity, which has significant impacts on grid frequency regulation capability, wind power generation economy, and grid peak load regulation. Ref. [7] propose a capacity optimization model for joint shared energy storage of multiple wind farms in primary frequency modulation based on opportunity constrained planning. It converts the planning into deterministic planning via an improved P-effective point method, achieving rapid solution through Cplex and verifying wind–storage frequency modulation feasibility. On the basis of virtual synchronous control of inertia support and primary frequency regulation, Ref. [8] establishes an energy storage output model to respond to grid frequency fluctuations and proposes an energy storage configuration method. Ref. [9] investigate an optimization strategy for sizing a battery energy storage system to support primary frequency regulation in photovoltaic power plants. By integrating an optimization model and a performance assessment algorithm, it incorporates a state-of-charge penalty function to prevent inappropriate SOC trajectories that could affect PFR performance and evaluates the effectiveness of the BESS design. Ref. [10] indicate that optimizing the allocation of battery energy storage systems can significantly enhance grid voltage and frequency stability. The adaptive gray wolf optimization algorithm effectively determines the optimal capacity and placement of BESS, with simulations verifying its benefits for grid stability and reliability, providing valuable insights for power system planning. Ref. [11] propose an optimal management strategy for a photovoltaic–battery system that both generates power and provides primary frequency regulation. The key contribution is the development of a two-level control framework, optimizing energy trading and real-time adjustments to ensure reliable operation. The study demonstrates that the proposed strategy effectively manages uncertainties in photovoltaic generation and frequency dynamics, ensuring efficient and stable system performance. Ref. [12] establish a bi-layer model combining planning and operation layers for wind farms with dual tasks of smoothing wind power fluctuations and participating in primary frequency regulation, embedding an improved particle swarm optimization algorithm to achieve optimal energy storage capacity configuration. Ref. [13] construct an optimal allocation model for energy storage system capacity for primary frequency regulation on the basis of the ant lion algorithm, considering the frequency regulation dead zone and capacity margin issues to enhance system frequency regulation capability.
In terms of black-start capability, Ref. [14] studies the black-start technology of wind–energy storage integrated systems, formulates black-start schemes, and verifies their effectiveness. Ref. [15] propose a capacity configuration method for energy storage considering energy storage operation strategies to solve the problem of wind power fluctuation during the black-start process of wind farms. Ref. [16] specifically address the requirements of WECSs and propose a decentralized control system for the black-start of WECSs operating in parallel. Ref. [17] propose an optimal configuration method for energy storage in wind farms for black-start capability based on an asymmetric Copula function, enabling wind farms to have black-start power capabilities. Ref. [18] design a black-start scheme for photovoltaic–energy storage systems using a hierarchical optimization strategy, from data analysis to coordinated optimization and dispatch control, effectively enhancing the recovery capability of regional power grids. Ref. [19] propose a capacity configuration planning method based on positive-sum game theory for solar–wind–battery hybrid systems participating in black-start, achieving good results in balancing black-start capacity needs and economic benefits. Ref. [20] propose a capacity configuration method for wind farms by determining the energy storage demand for starting a single wind turbine and establishing a hierarchical planning model, realizing black-start of wind farms with a smaller capacity of energy storage. The research results show that configuring small-capacity energy storage on the wind turbine side can realize the black-start of wind–energy storage systems, providing a feasible solution for wind farms as the black-start power sources.
Although the existing studies have made some progress in primary frequency regulation and black-start capability of wind–storage systems (as shown in Table 1), most of the literature focuses solely on optimizing a single function, lacking an in-depth exploration of the coordination mechanism between primary frequency regulation and black-start capability. Refs. [5,6,7,8,9,10] enhance frequency stability through real-time coordinated control and dynamic reserve allocation strategies but fail to establish an evaluation framework for black-start capability. Refs. [14,15,16,17] explore the feasibility of energy storage participation in black-start but overlook the quantitative analysis of frequency regulation performance. This fragmented research approach results in energy storage configuration schemes that fail to meet multi-scenario demands, leading to an imbalance between functionality and cost. Moreover, these existing black-start optimization models often simplify energy storage as a continuous power supply unit, lacking a systematic evaluation of key indicators such as startup time and reliability, and failing to consider coordinated startup strategies with wind turbines.

Table 1.
Comparison of research on energy storage optimization configuration in the literature.
To address the aforementioned disadvantages, this study follows a research framework of functional coordination–model construction–case validation. Section 2 analyzes the technical requirements of primary frequency regulation and black-start and proposes evaluation metrics for frequency regulation effectiveness and black-start capability. Section 3, considering the multi-objective coupling characteristics, establishes a quadrilateral comprehensive evaluation model and employs an adaptive genetic algorithm to optimize energy storage capacity allocation through charge/discharge strategies. Section 4 verifies the feasibility of the proposed optimization strategy through a comparative analysis of three case studies. Finally, Section 5 summarizes the research conclusions and provides engineering insights.
2. Analysis of Primary Frequency Regulation and Black-Start Requirements and Design of Evaluation Indicators
The primary frequency regulation of a generating unit acts during the initial stage of a frequency event in the power system (such as sudden load changes or generator tripping). It is crucial for suppressing system frequency deviation and ensuring the stability and quality of the power system frequency. Therefore, this paper mainly focuses on the energy storage capacity configuration that enables wind farms to possess primary frequency regulation capabilities.
An imbalance in the active power of the power system will cause changes in system frequency. When the frequency deviation exceeds the deadband of frequency regulation , the governor of the generating unit is activated to adjust the active power output of conventional generating units, thereby reducing the system frequency deviation. This process is called primary frequency regulation, PFR [20], as shown in Figure 1. The primary frequency regulation characteristic of a generating unit is reflected in the droop coefficient:
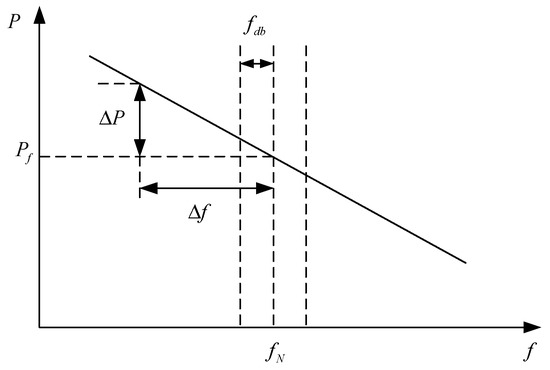
Figure 1.
Power–frequency characteristic curve of traditional generators.
In the formula, represents the rated frequency of the power system; represents the power generation of the generator set; represents the frequency deviation; represents the change in active power. The droop coefficient R generally ranges from 0.04 to 0.06.
Affected by wind speed, the power generation of wind turbines has a large range of variation. Moreover, when wind power generation is at its peak, its impact on the power system frequency is more pronounced. Therefore, determining the primary frequency regulation reserve capacity of a wind farm based on its instantaneous power is more in line with engineering practice.
According to Equation (1), in order for the wind farm to possess primary frequency regulation capabilities similar to those of traditional generator sets, the primary frequency regulation power and capacity it needs to provide are as follows:
In the formula, and represent the power and capacity required for the wind farm to participate in primary frequency regulation at time , respectively. is the sampling time interval. is the power generation of the wind farm at time .
The energy storage system (ESS) is characterized by its fast response time, flexible and diverse capacity configuration, and strong environmental adaptability. The role of configuring an ESS is twofold: on one hand, it helps to smooth the power fluctuations of a normally operating wind farm; on the other hand, it enables the wind farm to have self-starting capabilities.
Before evaluating the black-start support capability of energy storage for a wind farm, it is necessary to determine the black-start power demand of the wind turbines. Taking a 1.5 MW wind turbine as an example, the external power required for its startup is approximately 18 kVA, which is about 1.2% of the wind turbine’s rated power. Therefore, ignoring the losses in the collector system, the startup power required by the wind farm is approximately 1.2% of the total installed capacity of the wind farm.
Regarding the startup sequence of wind turbines, the required startup power is the highest when all wind turbines in the wind farm are started simultaneously. In this case, the self-starting time of the wind farm is the shortest, but a large energy storage capacity is needed. To address this, it is possible to consider using energy storage to prioritize the startup of some wind turbines first. The already started turbines, together with energy storage, can then form the black-start power source for the next round of wind turbine startups.
2.1. Design of Frequency Regulation Effectiveness Indicators
Regarding the primary frequency regulation performance of the wind–storage system, it is necessary to define corresponding indicators for measurement. Assuming that the wind farm does not have the capability for primary frequency regulation, the indicator reflecting the system frequency fluctuation is as follows:
After the wind farm reserves frequency regulation standby capacity or adds energy storage units to participate in frequency regulation, the indicator reflecting the system frequency fluctuation is as follows:
Indicators are proposed to reflect the effectiveness of primary frequency regulation:
In the formula, the smaller the value of J, the better the frequency adjustment effect.
2.2. Design of Black-Start Capability Indicators
Black-start refers to the ability of an electric power system to restore power after a complete blackout without relying on external grid support, using internal self-starting power sources. Since wind turbines do not have self-starting capabilities, energy storage is required. Firstly, the energy storage system supplies power for the initial round of wind turbine startups. Once the first round of turbines is successfully started, the combined output of the wind farm and energy storage system is used to determine which turbines can be started next, and these are started in parallel. This parallel startup process is repeated until all turbines are operational. In theory, parallel startup can reduce the total startup time. Taking a wind farm with S turbines as an example, the evaluation indicators for black-start capability are as follows:
- (1)
- Relying solely on energy storage to start units (first round of startup): for the first round of turbine startup, the energy storage system provides the startup power of 1.2% ∗ for the first turbine and sustains it for a duration of .
- (2)
- Stage 2 starts with the platform (the remaining energy storage and the wind turbines from the first round jointly serve as the black-start power source).
- (3)
- Final round start with platform (the round number for the final round could be 2, 3, 4, 5, …): The actual start time for the final round is still , but if , this indicates that the number of turbines that can be started in the final round has exceeded the required number. The equivalent start time for the final round, , is as follows:
The black-tart time is equivalently calculated as follows:
Taking the duration of a five-round start as the benchmark (since five rounds can already ensure the startup of all wind turbines in the wind farm), the longest black-start time is as follows:
The evaluation indicator for black-start capability is defined as follows:
In the formula, is between 0 and 1. The smaller the value, the shorter the equivalent black-start time, which means the stronger the black-start capability.
3. Multi-Objective Optimization Model for Energy Storage Capacity
The capacity of energy storage and the proportion of wind power reserve are one of the key issues for the economic feasibility of primary frequency regulation and black-start capability in a wind farm. This paper proposes an optimization method for energy storage capacity based on a polygon-based comprehensive evaluation. During the optimization process, to ensure the economic viability of energy storage configuration and reduce the construction cost of energy storage, an operation mode considering the coordinated support of wind turbines and energy storage for primary frequency regulation is designed. Finally, the optimal configuration capacity of energy storage and the proportion of wind power reserve are determined through a trade-off among multiple optimization indicators.
3.1. Multiple Energy Storage Power Distribution Control Layer
3.1.1. Optimization Configuration Model
The annual equivalent investment value of the energy storage device mainly includes the initial fixed capital for configuring the energy storage system and the daily maintenance costs. The total investment is converted into an annual investment cost for optimization. The mathematical model is as follows:
In the formula, and are the unit power cost and unit energy cost of the energy storage device, respectively. and are the power and capacity configured for the energy storage device. CRF is the capital recovery factor of the energy storage device. is the system operating period (in years). is the maintenance cost for the normal operation of the energy storage device.
3.1.2. Wind Energy Utilization Rate
The wind energy utilization rate is one of the important indicators for evaluating the rationality of the wind power reserve proportion. The wind energy utilization rate is defined as follows:
In the formula, and are the actual output power and theoretical output power of the wind farm at time , respectively. is the number of wind speed sampling data points.
3.1.3. Objective Function
The specific implementation process of establishing the quadrilateral comprehensive evaluation model is as follows:
- (1)
- Extend four axes from the origin of the coordinate system in different directions, such that these four axes divide a circle centered at the origin into four equal parts, with each axis separated by an angle of 90°.
- (2)
- Normalize the evaluation indicators for frequency regulation effectiveness, annual average investment cost of energy storage, black-start capability, and wind energy utilization rate.
- (3)
- Mark the normalized values of the four evaluation indicators on the respective axes and connect the points in sequence to form a quadrilateral. The area of this quadrilateral is then calculated.
Taking the maximization of the area of the quadrilateral comprehensive evaluation model as the objective, and subject to the operational constraints, the objective function is established as follows:
Among them, is the area of the quadrilateral comprehensive evaluation model; is the normalized frequency modulation effect indicator of the system; is the normalized annual evaluation investment cost of energy storage; is the normalized black-start capability indicator of the system; is the normalized wind energy utilization rate of the system.
3.1.4. Constraints
Based on the actual operating characteristics of energy storage batteries and wind farms, the following constraints need to be satisfied:
In the formula, and are the lower and upper limits of the state of charge (SOC) of the energy storage device. and are the charging and discharging efficiencies of the energy storage device.
In addition, during the long-term operation of energy storage batteries, their replacement frequency should take into account both the service life of the batteries and the maximum number of charge/discharge cycles. Within a certain operating period, if either of these conditions are met, the energy storage is considered to be scrapped.
3.2. Energy Storage Charging and Discharging Strategy
Energy storage batteries regulate system frequency by absorbing or releasing active power. However, when the remaining capacity or energy of the energy storage is insufficient, there are two options for its charging and discharging power modes:
- (1)
- Maximum Power Charging/Discharging ModeTaking discharging as an example, under this mode, the maximum discharging power of the energy storage configuration is used as a constraint. The battery discharges at the maximum power until all available energy is depleted.
- (2)
- Balanced Power Charging/Discharging ModeTaking discharging as an example, under this mode, the discharging power of the energy storage is lower than the configured power. Within a complete frequency regulation cycle, the available energy of the energy storage battery is evenly depleted. The discharging power is the ratio of the available energy to the frequency regulation cycle.
Given the same initial conditions, the frequency regulation outcomes after energy storage participates in frequency regulation using the two different charging and discharging modes are shown in Figure 2.
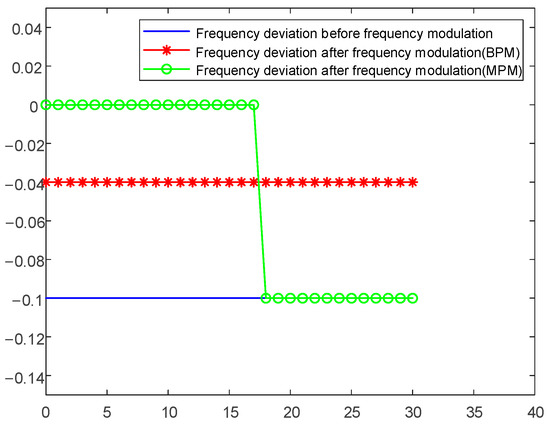
Figure 2.
Comparison of frequency deviation in different energy storage charge and discharge modes.
Considering the dispersion of frequency deviation values after frequency regulation using the variance formula, the average frequency deviation values are both −0.04 Hz when energy storage participates in frequency regulation in the maximum power charge/discharge mode and the balanced power charge/discharge mode. However, the frequency deviation values show better aggregation in the balanced power charge/discharge mode. Therefore, this paper selects the balanced power charge/discharge mode of energy storage to design the charge/discharge strategy. The charge/discharge strategies for energy storage participating in primary frequency regulation and the black-start of the wind farm are as follows:
Charge and Discharge Strategy for Energy Storage Participating in Primary Frequency Regulation of a Wind Farm
- ➀
- When the system frequency deviation exceeds the upper limit of the frequency regulation dead band : if , the energy storage battery charges; if , the energy storage remains inactive.
- ➁
- When the system frequency deviation exceeds the lower limit of the frequency regulation dead band : if , the energy storage battery charges; if , the energy storage remains inactive.
- ➂
- When the system frequency deviation is within the frequency regulation dead band , that is, , the energy storage does not need to take any action.
- (1)
- Charge and Discharge Strategy for Energy Storage Participating in the Black-start of a Wind Farm
- ➀
- Determine the maximum number of wind turbines that the energy storage can start in the first round. If , the energy storage discharges to start a wind turbine. If , the energy storage takes no action, and the first-round startup fails.
- ➁
- If the first round cannot complete the startup of all wind turbines, a subsequent startup process is required. If and , the energy storage discharges to start c wind turbines. If , the already-started turbines continue to start additional turbines and charge the energy storage simultaneously.
3.3. The Process of Energy Storage Capacity Configuration
This paper employs the Adaptive Genetic Algorithm (AGA) as the solution tool for the optimization configuration problem. Compared with other fundamental algorithms, the genetic algorithm exhibits global optimization capability, effectively circumventing entrapment in local optima while maintaining robust convergence properties.
The energy storage capacity configuration process is shown in Figure 3. First, an initial population is generated and encoded. Secondly, based on the energy storage participation in wind farm primary frequency regulation and black-start charging and discharging strategies designed in the previous text, the corresponding , , and values for each individual in the population are calculated. After standardizing the optimization objectives, the polygon area value is calculated, which represents the fitness value of the population individual. If is greater than the average value, the range is set to increase the crossover/mutation probability to improve the convergence rate of the optimization process; conversely, the crossover/mutation probability is decreased to protect excellent individuals from entering the next generation. Finally, the termination condition of the adaptive genetic algorithm is determined, and the output result is used as the optimal configuration plan.
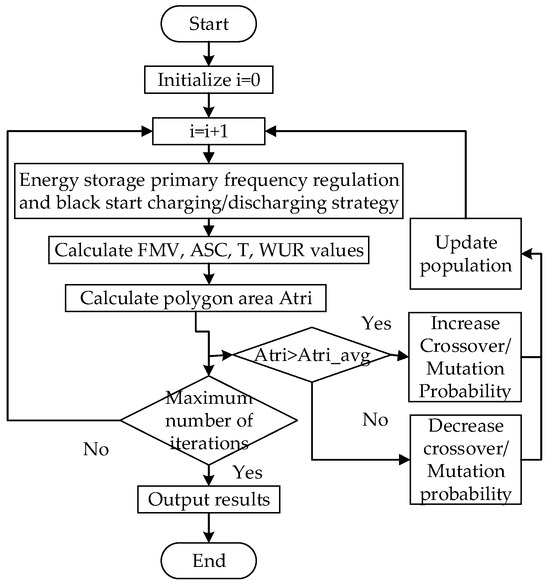
Figure 3.
Multi-objective optimization process for energy storage capacity configuration.
4. Case Study Analysis
4.1. Parameter Setting
This paper takes a certain offshore wind farm as an example, with an operation cycle of 20 years, during which the total installed capacity of the wind farm is 504 MW, the wind speed at which the wind turbine cuts in is 3 m/s, the rated wind speed is 15 m/s, and the cut-out wind speed is 25 m/s. The system frequency sampling time interval is 30 s. Other parameters are shown in Table 2.

Table 2.
Wind–storage system optimization parameters.
4.2. Optimization Configuration for Different Case Studies
This paper compares and analyzes three case studies under different conditions:
Case Study 1: Optimization configuration considering both primary frequency regulation and black-start (wind–storage joint frequency regulation).
Case Study 2: Optimization configuration considering only primary frequency regulation (wind–storage joint frequency regulation).
Case Study 3: Optimization configuration considering both primary frequency regulation and black-start (storage-only frequency regulation).
The configuration results of energy storage, wind power reserve conditions, and evaluation metrics under different case studies are shown in Table 3. The system frequency fluctuations before and after frequency regulation are illustrated in Figure 4.

Table 3.
Results of energy storage participation in wind farm frequency regulation.
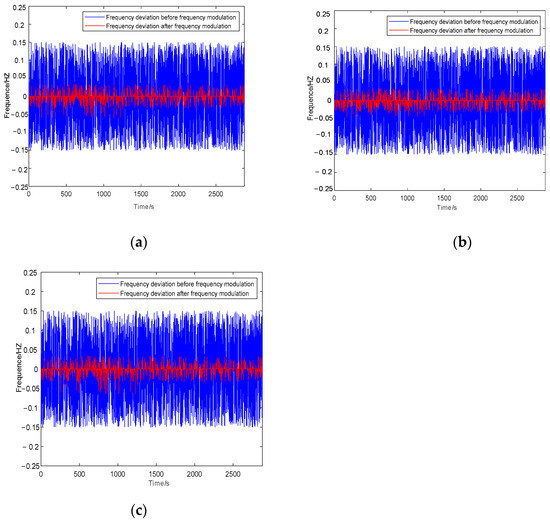
Figure 4.
Comparison of system frequency fluctuations before and after frequency regulation with energy storage participation. (a) Comparison of system frequency fluctuations before and after frequency regulation in Case Study 1. (b) Comparison of system frequency fluctuations before and after frequency regulation in Case Study 2. (c) Comparison of system frequency fluctuations before and after frequency regulation in Case Study 3.
From Table 3, it can be seen that under the optimized configuration conditions for primary frequency regulation and black-start (wind–storage joint frequency regulation) in Case 3, the optimal configurations for energy storage capacity and power are 3.19 MWh and 4.32 MW, respectively. Compared with the optimized configuration case that only considers primary frequency regulation (wind–storage joint frequency regulation), due to the consideration of the role of energy storage in black-starting the wind farm, the energy storage configuration capacity and power have increased by 0.22 MWh and 0.16 MW, respectively. However, the wind power reserve ratio has decreased from 5.04% to 3.52%, resulting in a relatively higher wind energy utilization rate. In the optimized configuration case that considers both primary frequency and black-start (energy storage alone for frequency regulation), due to the lack of wind power frequency regulation reserve, primary frequency regulation is entirely borne by energy storage; hence, the configuration capacity and power of energy storage are relatively large, at 17.66 MWh and 21.84 MW, respectively. There is a significant improvement in the capability to support black-start, but the annual cost of energy storage is excessively high. Overall, Case 1 has achieved a certain balance among various optimization indicators.
Under three case conditions, the optimization configuration results correspond to the polygon evaluation indicator diagram, as shown in Figure 5. The area Atri values corresponding to the polygons in the diagram are shown in Table 4.
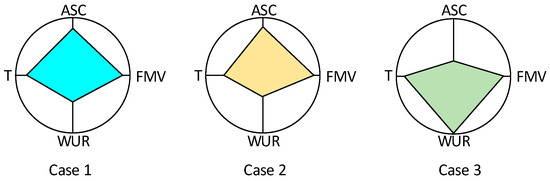
Figure 5.
Polygon evaluation indicator diagram for three different case studies.

Table 4.
Polygon areas for three different case studies.
From Table 4, it can be seen that the wind–storage joint optimization configuration, which takes into account both primary frequency regulation and black-start support capabilities, has the highest fitness value, reflecting the superiority of this case.
4.3. Sensitivity Analysis
In the optimization model for wind farm energy storage configuration, the performance degradation rate of storage batteries, frequency fluctuations, and wind speed variations are key factors affecting the system’s economic efficiency and reliability.
- (1)
- Impact of Storage Degradation
The capacity and charge/discharge efficiency of energy storage batteries degrade over time, typically modeled using an exponential decay formula:
In the equation, and represent the initial configuration capacity and the charge/discharge efficiency of the energy storage system, respectively. is the time constant, which indicates the time required for the energy storage to degrade to its initial value by a factor of , and is the decay constant.
When the time constant is set to 50 and the decay constant is 0.025, the degradation of the energy storage battery’s capacity and charge/discharge efficiency with respect to the years of usage is shown in Figure 6. Using Example 1 as a case, the impact of different degradation rates on the optimal storage configuration results is shown in Table 5.
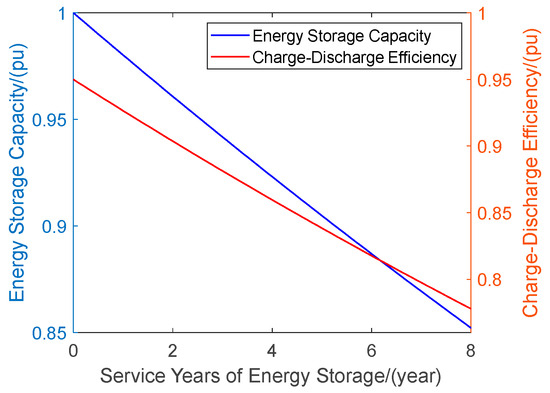
Figure 6.
Degradation of energy storage over years of use.

Table 5.
Configuration results considering different degradation rates of energy storage batteries.
From Table 5, it can be observed that when considering the degradation of the energy storage battery performance with usage time, the optimal storage configuration capacity and power increase accordingly to maintain the same primary frequency regulation effect as the original configuration. Additionally, the higher the degradation rate of the energy storage battery, the higher the required optimal storage configuration capacity and power.
- (2)
- Impact of Larger Frequency Fluctuations
To investigate the applicability of the proposed storage optimization method under severe frequency fluctuations in the grid, optimization simulations were performed using frequency fluctuation data with a larger variation based on Case 1. The system frequency reached a maximum of 50.213 Hz and a minimum of 49.798 Hz within the sampling period. The storage optimization results were as follows: storage capacity of 7.06 MWh, storage power of 5.84 MW, and a wind power reserve ratio of 3.77%. The fluctuation in the frequency before and after regulation is shown in Figure 7.
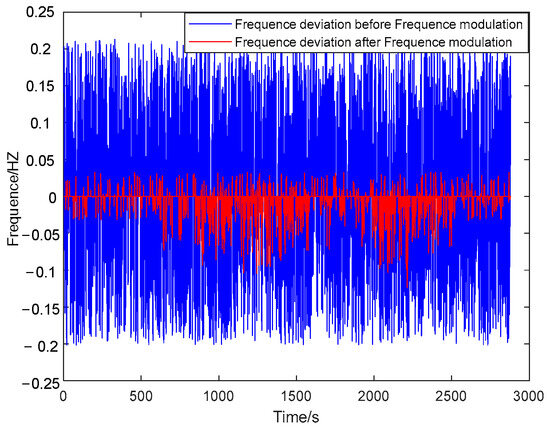
Figure 7.
Comparison of frequency fluctuations before and after frequency regulation under large frequency deviations.
5. Conclusions
This paper addresses the optimal configuration of energy storage capacity in offshore wind farms by proposing a multi-objective optimization strategy that comprehensively considers primary frequency regulation capability and black-start support capability. By constructing a comprehensive evaluation model that integrates frequency regulation performance, economic efficiency, black-start capability, and the wind energy utilization rate, and solving it using a genetic algorithm, the following conclusions are drawn:
- (1)
- The global advantage of wind–energy storage collaborative frequency regulation is significant. By coordinating the energy storage system with the wind power reserve capacity, the combined wind–energy storage frequency regulation can ensure frequency stability while significantly reducing the cost of energy storage configuration and improving wind energy utilization.
- (2)
- Frequency regulation performance and black-start indicators can enhance system reliability. The black-start indicator ensures rapid system recovery in the event of a fault, while the frequency regulation performance indicator strengthens the system’s ability to regulate frequency fluctuations. The combination of these two indicators provides an effective basis for energy storage configuration.
- (3)
- The multi-objective optimization model has practical significance. Although the introduction of the black-start evaluation indicator slightly increases the energy storage capacity, it enhances the system’s recovery capability. The multi-objective optimization model based on a quadrilateral comprehensive evaluation effectively balances the various objectives and provides a reliable scientific basis for energy storage configuration.
Based on the research in this paper, future work can explore the interaction mechanisms between centralized and distributed energy storage in frequency regulation and black-start, quantifying the impact of different configuration modes on frequency regulation and black-start capabilities, in order to select the appropriate configuration mode for different scenarios.
Author Contributions
Conceptualization, Y.W. and F.Z.; methodology, Y.W.; software, Z.H.; validation, Y.W. and J.Z. (Junxing Zhang); formal analysis, Y.W.; investigation, F.Z.; resources, Y.W.; data curation, Z.H.; writing—original draft preparation, W.X.; writing—review and editing, F.Z.; visualization, J.Z. (Junxing Zhang); supervision, H.N.; project administration, H.N.; funding acquisition, J.Z. (Jianyong Zhao). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Xiangshan Off-shore WindPower Co., Ltd., of Guodian Power Co., Ltd., Technology Project “Research and Application of Energy Storage Layout Optimization and Collaborative Control Technology in Offshore Wind farms”, grant number GDDL-23-32.
Data Availability Statement
The original study’s contributions are included in this article, and any further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors Yu Wang, Fuqiang Zhang, Junxing Zhang and Wangcheng Xu were employed by Xiangshan Off-shore WindPower Co., Ltd., of Guodian Power Co., Ltd. The remaining authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Kang, H.; Sun, Y.; Liu, J.; Chen, Z.; Shi, X.; Zhang, X.; Shi, Y.; Yang, P. Research on the Primary Frequency-Regulation Strategy of Wind-Storage Collaborative Participation Systems Considering the State of Charge of Energy Storage. Energies 2024, 17, 6333. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, C.; Zou, X. Frequency Regulation for High Wind Penetration Power System Based on Ocean Predator Algorithm Considering Storage Battery State. Energies 2025, 18, 671. [Google Scholar] [CrossRef]
- Li, C.; Zhang, S.; Li, J.; Zhang, H.; You, H.; Qi, J.; Li, J. Coordinated control strategy of multiple energy storage power stations supporting black-start based on dynamic allocation. J. Energy Storage 2020, 31, 101683. [Google Scholar] [CrossRef]
- Wang, R.; Xue, X.; Zhang, Y.; Liu, J.; Zhao, R.; Ai, X.; Fang, J.; Wen, J. Optimal Configuration of Mobile-stationary Hybrid Energy Storage Considering the Uncertainty of New Energy in Black-start. Power Syst. Technol. 2024, 48, 4031–4040. [Google Scholar]
- He, G.; Chen, Q.; Kang, C.; Xia, Q.; Poolla, K. Cooperation of wind power and battery storage to provide frequency regulation in power markets. IEEE Trans. Power Syst. 2016, 32, 3559–3568. [Google Scholar] [CrossRef]
- Li, S.; Tu, J.; Shu, Z. Dynamic configuration strategy for frequency regulation reserve capacity of large-scale wind power for promoting peak load regulation. Autom. Electr. Power Syst. 2020, 44, 53–59. [Google Scholar]
- Shi, J.; Jia, Y.; Han, X.; Liu, J.; Guo, Q.; Sun, L. Capacity Optimization of Joint Participation of Multiple Wind Farms with Shared Energy Storage in Primary Frequency Regulation Based on Improved p-Efficient Point Method. Acta Energiae Solaris Sin. 2024, 45, 503–512. [Google Scholar]
- Zhang, B.; Zhang, X.; Jia, J.; Zeng, Y.; Yan, X. Configuration method for energy storage unit of virtual synchronous generator based on requirements of inertia support and primary frequency regulation. Autom. Electr. Power Syst. 2019, 43, 202–216. [Google Scholar]
- Mejía-Giraldo, D.; Velásquez-Gomez, G.; Muñoz-Galeano, N.; Bernardo Cano-Quintero, J.; Lemos-Cano, S. A BESS sizing strategy for primary frequency regulation support of solar photovoltaic plants. Energies 2019, 12, 317. [Google Scholar] [CrossRef]
- Zhang, D.; Shafiullah, G.M.; Das, C.K.; Wong, K.W. Optimal allocation of battery energy storage systems to improve system reliability and voltage and frequency stability in weak grids. Appl. Energy 2025, 377, 124541. [Google Scholar] [CrossRef]
- Conte, F.; Massucco, S.; Schiapparelli, G.P.; Silvestro, F. Day-ahead and intra-day planning of integrated BESS-PV systems providing frequency regulation. IEEE Trans. Sustain. Energy 2019, 11, 1797–1806. [Google Scholar] [CrossRef]
- Duanmu, C.; Shi, L.; Jian, D.; Ding, R.; Li, Y.; Wu, F. Optimized Battery Capacity Allocation Method for Wind Farms with Dual Operating Conditions. Sustainability 2024, 16, 3615. [Google Scholar] [CrossRef]
- Yang, H.; Huang, R.; Shi, M.; Yan, Z.; Yan, L. Optimal Allocation of Primary Frequency Modulation Capacity of Battery Energy Storage Based on Antlion Algorithm. Energies 2023, 16, 6778. [Google Scholar] [CrossRef]
- Fan, J.; Niu, L.; Li, C.; Zhang, G.; Li, H.; Wang, Y.; Li, J.; Song, Q.; Sun, J.; Pan, J.; et al. Review of Black Start on New Power System Based on Energy Storage Technology. Energy Eng. 2023, 120, 2857–2878. [Google Scholar] [CrossRef]
- Yan, L.Q.; Cao, L.Y.; Xue, T.L. Optimal configuration of wind farm black start energy storage capacity: A method considering energy storage operation strategy. Power Syst. Prot. Control 2022, 50, 131–139. [Google Scholar]
- Asensio, A.P.; Gómez, S.A.; Rodriguez-Amenedo, J.L.; Cardiel-Álvarez, M.Á. Decentralized frequency control for black start of full-converter wind turbines. IEEE Trans. Energy Convers. 2020, 36, 480–487. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y. Optimal configuration of energy storage for wind farm black-start based on asymmetric Copula function. Autom. Electr. Power Syst. 2020, 44, 47–59. [Google Scholar]
- Li, J.; You, H.; Qi, J.; Kong, M.; Zhang, S.; Zhang, H. Stratified optimization strategy used for restoration with photovoltaic-battery energy storage systems as black-start resources. IEEE Access 2019, 7, 127339–127352. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Z.; Ma, Y. Positive-Sum Game-Based Capacity Configuration Planning Method of Solar-Wind-Battery System Designed for Black-Start. Int. Trans. Electr. Energy Syst. 2023, 2023, 6176839. [Google Scholar] [CrossRef]
- Li, C.; Zhang, S.; Zhang, J.; Qi, J.; Li, J.; Guo, Q.; You, H. Method for the energy storage configuration of wind power plants with energy storage systems used for black-start. Energies 2018, 11, 3394. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).