State Control Design of Ostensible Metzler Linear Systems with Unsigned Input Parameters

Abstract

This paper deals with the design of a complete state control for input unsigned, rank deficient matrix parameters of a linear system with system dynamics defined by ostensible structures of Metzler matrices. The proposed solution is based on the principle of diagonal stabilization of positive systems and uses a stabilizing additional component over the decomposition of the Metzler matrix in solving the incomplete internal positivity of such linear system structures. The novelty of the proposed approach is the unified representation of the parametric constraints of the Metzler matrix and the structurally constrained system inputs using linear matrix inequalities, which guarantees that the closed-loop system will be asymptotically stable. Despite the complexity of the constraint conditions on this class of linear continuous systems, the design conditions are formulated using sharp linear matrix inequalities only. A detailed design process is presented using a system-linearized mathematical model to verify the superiority and practicality of the proposed method.

1. Introduction

The common characteristic of positive systems is that their states are non-negative whenever the initial conditions are non-negative. These features motivate researchers to extend the idea of positiveness by constructing partly positive systems. The main barriers are the Metzler system matrix parametric constraints and the diagonal stabilization principle. Less ramparts are for the class of system with mathematical models exploiting ostensible Metzler system matrices where, e.g., turbofan engine mathematical models [1], linearized aircraft mathematical models [2], longitudinal dynamics mathematical models of unmanned aerial vehicle [3] and rocket fairing structural-acoustic mathematical models [4,5], represent the range of related applications. Their use in system diagnostics is supported by the fact that the methodologies used are based on state observers and functional observers, where the measurement output matrix is generally non-negative [6,7]. A generalization of the state observer synthesis for linear ostensible Metzler systems is focused in [8,9].

In existing results on linear positive Metzler systems, the positive control gain performances are commonly considered for dealing with the state control law. Due to the internal positivity, the closed-loop system should also be positive but, owing to the constraints on systems matrices, the poles of the closed-loop system cannot be placed arbitrarily [10]. Since ostensible Metzler systems are not internally positive, the task of synthesizing state control with a positive control law matrix requires an extended modification of the synthesis tasks [11,12]. These facts are strongly manifested in solutions of the network control of aircraft engines [13,14], as well as in the consensus control of positive networked systems [15,16], where used mathematical models are typically ostensible Metzler. Since these approaches are characterized by a non-negative static gain matrix, the result is only to ensure the stability of the system in a closed loop.

In the present paper, a generalization of the authors’ preliminary works for ostensible Metzler linear multi-input and multi-output (MIMO) systems is proposed to follow the above-mentioned trends. On the basis of new synthesis conditions in the form of linear matrix inequalities (LMIs) for state control of this class of systems, if in addition the task is limited by column rank deficient system input matrix, a less conservative approach is conceived in detail when reflecting the needs of system diagonal stabilization. A fundamental novelty is the set of constraints related to unsigned input matrix parameters with newly formulated LMI structures and the forced partial factorization of system dynamics matrices. Interacting with a pair of matrices produced by the decomposition of the ostensible Metzler matrix structure, the resulting LMI terms have fewer negative matrix elements in defining the positivity constraints. No further restrictions on the synthesis conditions are required except for the standard ones associated with the diagonal stability of Metzler systems.

The remaining part of the paper is organized as follows: Section 2 deals with strictly Metzler constraints and related design limits when applying the principle of diagonal stabilization in the control design task for this class of linear MIMO systems. Section 3 focuses on ostensible Metzler matrix structures and their structural decomposition, where the challenging aim is to unify the approach based on the set of linear matrix inequalities (LMIs). Section 4 generalizes the concepts of diagonal stability within the framework implying from the rank deficient input matrix. To show the applicability of the theoretical results and the system constraints roles, an example is given in Section 5 to deal in detail with the investigated design limits, and concluding remarks are presented in Section 6.

For sake of convenience, throughout this paper used notations reflect usual conventionality so that ${\mathit{x}}^{\mathrm{T}}$, ${\mathit{X}}^{\mathrm{T}}$ denotes the transpose of the vector x, and the matrix X, respectively, diag $[·]$ marks a (block) diagonal matrix, for a square symmetric matrix $\mathit{X}\prec 0$ means its negative definiteness, ${\mathit{I}}_n$ labels the n-th order unit matrix, ${\mathit{X}}^{-1},\rho \left(\mathit{X}\right)$ signifies the inverse and the eigenvalue spectrum of a square matrix X, the maximum real part of the eigenvalues of X is denoted by ${\lambda }_0:={max}_{\lambda \in \rho \left(X\right)}\Re \left(\lambda \right)$, $\mathbb{R}$ (${\mathbb{R}}_{+}$) marks the set of (nonnegative) real numbers, ${\mathbb{R}}^{n\times m}$ (${\mathbb{R}}_{+}^{n\times m}$) refers to the set of (nonnegative) real matrices and ${\mathbb{M}}_{-+}^{n\times n}$ (${\mathbb{M}}_{-\odot }^{n\times n}$) indicates the set of strictly (ostensible) Metzler matrices.

2. Positive System Constraints Formulation

This section considers a class of continuous-time linear positive systems given as:

$$\begin{array}{cc}\mathrm{\Xi }:\hfill & \begin{array}{c}\dot{\mathit{q}}\left(t\right)=\mathit{A}\mathit{q}\left(t\right)+\mathit{B}\mathit{u}\left(t\right),\hfill \\ \mathit{y}\left(t\right)=\mathit{C}\mathit{q}\left(t\right),\hfill \end{array}\hfill \end{array}$$

(1)

where $\mathit{q}\left(t\right)\in {\mathbb{R}}_{+}^n$, $\mathit{y}\left(t\right)\in {\mathbb{R}}_{+}^s$ are nonnegative vectors of state and output variables, $\mathit{u}\left(t\right)\in {\mathbb{R}}_{+}^r$ is vector of input variables, $\mathit{B}\in {\mathbb{R}}_{+}^{n\times r}$, $\mathit{C}\in {\mathbb{R}}_{+}^{s\times n}$ are nonnegative input and output matrices and the differential transition matrix $\mathit{A}\in {\mathbb{M}}_{-+}^{n\times n}$ is strictly (purely) Metzler.

Definition 1 ([17]).

A system is a positive system if its states are non-negative for any non-negative initial condition and any non-negative input.

Definition 2 ([18]).

System (1) is said to be positive if $\mathit{A}\in {\mathbb{M}}_{-+}^{n\times n}$ is a strictly (purely) Metzler matrix and $\mathit{B}\ge 0$ element-wise.

Definition 3 ([19]).

A matrix $\mathit{A}\in {\mathbb{M}}_{-+}^{n\times n}$ is called a strictly Metzler matrix if is represented by negative diagonal elements and by strictly positive off diagonal elements. A matrix $\mathit{A}\in {\mathbb{M}}_{-+}^{n\times n}$ is called purely Metzler matrix if is represented by negative diagonal elements and by nonnegative off diagonal elements.

Most articles related to Metzler systems define the conditions of synthesis of controllers and estimators based on the principle of linear programming. In the following, several Lemmas are presented, allowing to express the conditions of the synthesis of Metzler systems by means of linear matrix inequalities.

To remove any notational ambiguity, $a_{ij}$ is used for the (i,j)th entry of A so that a strictly Metzler $\mathit{A}={\left\{a_{ij}\right\}}_{i,j=1}^n\in {\mathbb{M}}_{-+}^{n\times n}$ states the parametric constraints

$$a_{ii}<0,i=j,a_{ij}>0,i\ne j,\forall i,j\in \langle 1,n\rangle$$

(2)

and a purely Metzler $\mathit{A}={\left\{a_{ij}\right\}}_{i,j=1}^n\in {\mathbb{M}}_{-+}^{n\times n}$ is limited by the parametric constraints

$$a_{ii}<0,i=j,a_{ij}\ge 0,i\ne j,\forall i,j\in \langle 1,n\rangle .$$

(3)

If the conditions of analysis of positive systems are based on linear matrix inequalities, the non sharp constraints of pure Metzler matrix parameters in (3) can be circumvented by using structured matrix variables.

Since the topic of the article is tied to the synthesis of the control of linear Metzler systems, the next overview is devoted only to this area of problems. The reader can find details regarding the use of the duality principle in the synthesis of state observers in [20]. Note, other limitations in the analysis and synthesis of linear positive systems result from the constraint that this class of systems is only diagonally stable [21].

Definition 4 ([22]).

System (1) is diagonally stable if there exists a Lyapunov function in the form of a quadratic form with a diagonal matrix that satisfies the requirements of the Lyapunov theorem on asymptotic stability.

Lemma 1 ([23]).

For the diagonal stability of the positive system (1), it is necessary and sufficient that the strictly (purely) Metzler matrix $\mathit{A}\in {\mathbb{M}}_{-+}^{n\times n}$ is Hurwitz that is there exists a diagonal positive definite matrix $\mathit{P}\in {\mathbb{R}}_{+}^{n\times n}$ such that it is satisfied the matrix inequality

$$\mathit{A}\mathit{P}+\mathit{P}{\mathit{A}}^{\mathrm{T}}\prec 0$$

(4)

In order to include the condition resulting from Lemma 1 in the state control synthesis, it is necessary to parameterize the structure of the Metzler matrix. The parametrization principle of a strictly Metzler matrix in the control tasks implies the following:

Lemma 2 ([24]).

If a strictly Metzler matrix $\mathit{A}={\left\{a_{ij}\right\}}_{i,j=1}^n\in {\mathbb{M}}_{-+}^{n\times n}$ is represented in the control rhombic form

$$A_{\mathrm{\Theta }}=\left[\begin{array}{cccccc}\hfill -a_{11}& a_{12}& a_{13}\hfill & \cdots & a_{1n}& \\ \hfill & -a_{22}& a_{23}\hfill & \cdots & a_{2n}& a_{21}& \\ \hfill & & -a_{33}\hfill & \cdots & a_{3n}& a_{31}& a_{32}\\ \hfill & & & \ddots & ⋮& ⋮& ⋮& \ddots \\ \hfill & & & & -a_{nn}& a_{n1}& a_{n2}& \cdots & a_{n,n-1}\end{array}\right],$$

(5)

whilst diagonals of (5) imply for $h=0,1,\cdots ,n-1$ the diagonal matrix structures

$${\mathit{A}}_{\mathrm{\Theta }}(\nu ,\nu +h)=\mathit{diag}\left[\begin{array}{cccccc}{a}_{1,1+h}& \cdots & a_{n-h,n}& a_{n-h+1,1}& \cdots & a_{n,h}\end{array}\right]$$

(6)

and by (2), it is further derived that

$$\left\{\begin{array}{cc}{\mathit{A}}_{\mathrm{\Theta }}(\nu ,\nu +h)\prec 0,\hfill & h=0,\hfill \\ {\mathit{A}}_{\mathrm{\Theta }}(\nu ,\nu +h)\succ 0,\hfill & h=1,\dots ,n-1,\hfill \end{array}\right.$$

(7)

Then the control parametrization form yields

$$\mathit{A}=\sum _{h=0}^{n-1}{\mathit{A}}_{\mathrm{\Theta }}(\nu ,\nu +h){\mathit{L}}^{h\mathrm{T}},$$

(8)

whilst the matrix $\mathit{L}\in {\mathbb{R}}_{+}^{n\times n}$ of the following structure:

$$\mathit{L}=\left[\begin{array}{cc}{0}^{\mathrm{T}}& 1\\ {\mathit{I}}_{n-1}& 0\end{array}\right]$$

(9)

is a circulant form of the permutation matrix, [25].

Corollary 1.

Equivalently to (7), it can be set as:

$$\left\{\begin{array}{cc}{\mathit{L}}^h\mathit{A}(\nu ,\nu +h){\mathit{L}}^{h\mathrm{T}}\prec 0,\hfill & h=0,\hfill \\ {\mathit{L}}^h\mathit{A}(\nu ,\nu +h){\mathit{L}}^{h\mathrm{T}}\succ 0,\hfill & h=1,\cdots ,n-1,\hfill \end{array}\right.$$

(10)

since on a diagonal matrix $\mathit{Z}=\mathrm{diag}\left[\begin{array}{cccc}{z}_1& z_2& \cdots & z_n\end{array}\right]$, $\mathit{Z}\in {\mathbb{R}}_{+}^{n\times n}$ the following matrix operation

$$\mathit{L}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\begin{array}{cccc}{z}_1& z_2& \cdots & z_n\end{array}\right]{\mathit{L}}^T=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\begin{array}{cccc}{z}_n& z_1& \cdots & z_{n-1}\end{array}\right]={\mathit{Z}}_{c1}$$

(11)

gives no change ${\mathit{Z}}_{c1}$ in definiteness with relation to Z.

As far as the state control problem is concerned, it is natural to point out the relations of diagonal stability consequence in state control design, presenting the following definition:

Definition 5

([24]). Give a nonnegative gain matrix $\mathit{K}\in {\mathbb{R}}_{+}^{r\times n}$ to shape up the full system state feedback control law

$$\mathit{u}\left(t\right)=-\mathit{K}\mathit{q}\left(t\right)$$

(12)

in the construction of the closed-loop system

$$\dot{\mathit{q}}\left(t\right)=(\mathit{A}-\mathit{B}\mathit{K})\mathit{q}\left(t\right)={\mathit{A}}_c\mathit{q}\left(t\right),$$

(13)

where for $\mathit{A}\in {\mathbb{M}}_{-+}^{n\times n}$, $\mathit{B}\in {\mathbb{R}}_{+}^{n\times r}$ the matrix ${\mathit{A}}_c=\mathit{A}-\mathit{B}\mathit{K}\in {\mathbb{M}}_{-+}^{n\times n}$ is strictly Metzler and Hurwitz.

Using ${\mathit{A}}_{\mathrm{\Theta }}(\nu ,\nu +h)\in {\mathbb{R}}^{n\times n}$ from (6) and diagonal matrices ${\mathit{B}}_l\in {\mathbb{R}}_{+}^{n\times n}$, ${\mathit{K}}_l,{\mathit{K}}_{lh}\in {\mathbb{R}}_{+}^{n\times n}$ such that

$$\mathit{B}=\left[\begin{array}{ccc}{\mathit{b}}_1& \cdots & {\mathit{b}}_r\end{array}\right],{\mathit{B}}_l=\mathit{diag}\left[\begin{array}{c}{\mathit{b}}_l\end{array}\right]=\mathit{diag}\left[\begin{array}{ccc}{b}_{l1}& \cdots & b_{ln}\end{array}\right],$$

(14)

$$\mathit{K}=\left[\begin{array}{c}{\mathit{k}}_1^{\mathrm{T}}\\ ⋮\\ {\mathit{k}}_r^{\mathrm{T}}\end{array}\right],{\mathit{K}}_l=\mathit{diag}\left[\begin{array}{c}{\mathit{k}}_l^{\mathrm{T}}\end{array}\right]=\mathit{diag}\left[\begin{array}{ccc}{k}_{l1}& \cdots & k_{ln}\end{array}\right],{\mathit{K}}_{lh}={\mathit{L}}^{h\mathrm{T}}{\mathit{K}}_l{\mathit{L}}^h,$$

(15)

then the parameterized form of ${\mathit{A}}_c=\mathit{A}-\mathit{B}\mathit{K}\in {\mathbb{M}}_{-+}^{n\times n}$ becomes

$${\mathit{A}}_c=\sum _{h=0}^{n-1}\left({\mathit{A}}_{\mathrm{\Theta }}(\nu ,\nu +h)-\sum _{l=0}^r{\mathit{B}}_l{\mathit{K}}_{lh}\right){\mathit{L}}^{h\mathrm{T}}.$$

(16)

These relations can be formulated in terms of auxiliary systems of linear matrix inequalities under the existence of the Lyapunov function in the quadratic form constructed on a positive definite diagonal matrix.

3. Results on a Class of Ostensible Metzler Systems

Until now, the design of the state control of linear ostensible Metzler linear systems has been an open question, and auxiliary constraints in the general framework need to be established. Let, for clarity, a system is described by (1), where $\mathit{B}\in {\mathbb{R}}_{+}^{n\times r}$ is a nonnegative matrix but $\mathit{A}\in {\mathbb{M}}_{-\odot }^{n\times n}$ is an ostensible Metzler system.

Definition 6.

The matrix $\mathit{A}\in {\mathbb{M}}_{-\ominus }^{n\times n}$ is an ostensible Metzler system if, in the structure of A, except a predominant number of positive off-diagonal elements, it is at least one negative off-diagonal element, whilst all diagonal elements of A are negative.

The structure of $\mathit{A}\in {\mathbb{M}}_{-\odot }^{n\times n}$ gives a base in separation of ostensible Metzler matrices.

Lemma 3 ([26]).

If for $\mathit{X},\mathit{Y}\in {\mathbb{R}}^{n\times n}$ it can be set $\mathit{Y}=c\mathit{X}+d{\mathit{I}}_n$ with scalars $c,d\in \mathbb{R}$, $c\ne 0$ and ${\mathit{I}}_n\in {\mathbb{R}}^{n\times n}$, then eigenvalues ${\eta }_k,k=1,\cdots ,n$ of $\mathit{Y}$ are

$${\eta }_k=c{\lambda }_k+d$$

(17)

where ${\lambda }_k$ runs over the eigenvalues of X and the eigenvectors of X and Y are identical.

Because the control problem for linear ostensible Metzler systems cannot be completely solved in the standard way, a separation of an ostensible Metzler $\mathit{A}\in {\mathbb{M}}_{-\ominus }^{n\times n}$ is proposed such that

$$\mathit{A}={\mathit{A}}_p+{\mathit{A}}_m,\mathit{A}={\left\{a_{ij}\right\}}_{i,j=1}^n,$$

(18)

where ${\mathit{A}}_p\in {\mathbb{M}}_{-+}^{n\times n}$ is strictly Metzler and ${\mathit{A}}_m\in {\mathbb{R}}_{-}^{n\times n}$ is element-wise negative and Hurwitz. Such separation converts design ideas for ostensible Metzler matrices into those for strictly Metzler matrices, parameterizing analogously, as above, the matrix ${\mathit{A}}_p\in {\mathbb{M}}_{-+}^{n\times n}$ by its rhombic form.

Note that sufficient information about the structure of the matrix ${\mathit{A}}_m\in {\mathbb{R}}_{-}^{n\times n}$ may not be satisfied in the general case. To solve such a problem, the following additional conditions were included in the design to transform the constraint problem described in Lemma 2 into an optimization problem:

Lemma 4 ([27]).

If for an ostensible Metzler $\mathit{A}\in {\mathbb{M}}_{-\ominus }^{n\times n}$ exist a strictly Metzler ${\mathit{A}}_p\in {\mathbb{M}}_{-+}^{n\times n}$ and an element-wise negative and Hurwitz ${\mathit{A}}_m\in {\mathbb{R}}_{-}^{n\times n}$ such that the prescribed performances to (18) are guaranteed then, in dependence on positive scalars $\eta ,\epsilon \in {\mathbb{R}}_{+}$, the following have to hold:

$${\mathit{A}}_m={\mathit{A}}_m^{\circ }-p{\mathit{I}}_n,{\mathit{A}}_p={\mathit{A}}_p^{\circ }+p{\mathit{I}}_n,$$

(19)

$${\mathit{A}}_p^{\circ }={\mathit{A}}_d+{\mathit{A}}^{+}+\eta \mathsf{\Sigma }+p{\mathit{I}}_n,{\mathit{A}}_m^{\circ }={\mathit{A}}^{-}-\eta \mathsf{\Sigma },{\mathit{A}}_d+p{\mathit{I}}_n\prec 0,$$

(20)

$${\mathit{A}}^{-}=\left[\begin{array}{ccccc}0& a_{12}^{-}& \cdots & a_{1,n-1}^{-}& a_{1n}^{-}\\ a_{21}^{-}& 0& \cdots & a_{2,n-1}^{-}& a_{2n}^{-}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_{n-1,1}^{-}& a_{n-1,2}^{-}& \cdots & 0& a_{n-1,n}^{-}\\ a_{n1}^{-}& a_{n2}^{-}& \cdots & a_{n-1,n-1}^{-}& 0\end{array}\right],{\mathit{A}}^{+}=\left[\begin{array}{ccccc}0& a_{12}^{+}& \cdots & a_{1,n-1}^{+}& a_{1n}^{+}\\ a_{21}^{+}& 0& \cdots & a_{2,n-1}^{+}& a_{2n}^{+}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_{n-1,1}^{+}& a_{n-1,2}^{+}& \cdots & 0& a_{n-1,n}^{+}\\ a_{n1}^{+}& a_{n2}^{+}& \cdots & a_{n-1,n-1}^{+}& 0\end{array}\right],$$

(21)

$$a_{ij}^{-}=\left\{\begin{array}{cc}{a}_{ij}\hfill & \mathrm{i}\mathrm{f}{a}_{ij}<0,\hfill \\ 0\hfill & \mathrm{i}\mathrm{f}{a}_{ij}>0,\hfill \end{array}\right.i,j\in \langle 1,n\rangle ,i\ne j,a_{ij}^{+}=\left\{\begin{array}{cc}{a}_{ij}\hfill & \mathrm{i}\mathrm{f}{a}_{\mathrm{i}\mathrm{f}}>0,\hfill \\ 0\hfill & \mathrm{i}\mathrm{f}{a}_{ij}<0,\hfill \end{array}\right.i,j\in \langle 1,n\rangle ,i\ne j,$$

(22)

$${\lambda }_o=\underset{k}{max}\left({\lambda }_k^{+}|{\lambda }_k^{+}=\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\left({\lambda }_k\right)>0,{\lambda }_k\in \rho \left({\mathit{A}}_m^{\circ }\right)\right),$$

(23)

$${\mathit{A}}_d=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\begin{array}{ccc}-a_{11}& -a_{22}& \cdots -a_{nn}\end{array}\right],p={\lambda }_o+\epsilon ,\mathsf{\Sigma }=\left[\begin{array}{ccccc}0& 1& \cdots & 1& 1\\ 1& 0& \cdots & 1& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 1& 1& \cdots & 1& 0\end{array}\right],$$

(24)

whilst $\rho \left({\mathit{A}}_m^{\circ }\right)$ is the spectrum of eigenvalues of the matrix ${\mathit{A}}_m^{\circ }$.

This separation makes the LMI formulation of design conditions for ostensible Metzler linear system straightforward and easy. In addition, in the separation procedure, values of the scalar parameters $\eta ,\delta \in {\mathbb{R}}_{+}$ can be set interactively when prescribing D-stability region [28] of ${\mathit{A}}_m$.

Note that since the matrix A is not strictly Metzler, such an autonomous part of the system $\mathrm{\Xi }$ is not internally positive, which means that only some state variables are non-negative.

The major interpretation can be summarized as follows: (i) A unified framework is proposed for ostensible Metzler systems representation in the continuous-time domain. (ii) The entire approach presents a standard result from the view of employing the quadratic Lyapunov function with a positive definite diagonal matrix variable.

These results impose a rather strong condition for the linear state control problem solution with positive (non-negative) control gain matrix $\mathit{K}\in {\mathbb{R}}_{+}^{r\times n}$ for ostensible linear Metzler systems.

4. Rank Deficient System Input Matrix of Ostensible Metzler Linear Systems

The results of the previous section can now be specialized to the case when the input of the ostensible Metzler linear system mathematical model (1) is limited by a rank deficient matrix $\mathit{B}\in {\mathbb{R}}^{n\times r}$ that is, there is a strip of zero rows in B and the real elements of its non-zero rows are bounded, but signum indefinite.

Since the d-th row from the strip of zero row vectors in B causes the d-th row of the ostensible Metzler matrix of the closed-loop ${\mathit{A}}_c$ remain identical to the d-th row of the ostensible Metzler matrix of the open-loop A under the state control, an extension to Lemma 4 is proposed, especially for irreducible cases. One way to solve this problem is the modification of elements assignment in (21) by changing the parametric constraint rules (22) as follows:

$$\begin{array}{c}{a}_{ij}^{-}=\left\{\begin{array}{ccc}{a}_{ij}\hfill & \mathrm{i}\mathrm{f}{a}_{ij}<0,\hfill & i,j\in \langle 1,n\rangle ,i\ne j,d,\hfill \\ 0\hfill & \mathrm{i}\mathrm{f}{a}_{ij}>0,\hfill & i,j\in \langle 1,n\rangle ,i\ne j,d,\hfill \\ 0\hfill & \hfill & i,j\in \langle 1,n\rangle ,i=d,\hfill \end{array}\right.\hfill \\ a_{ij}^{+}=\left\{\begin{array}{ccc}{a}_{ij}\hfill & \mathrm{i}\mathrm{f}{a}_{ij}>0,\hfill & i,j\in \langle 1,n\rangle ,i\ne j,\hfill \\ 0\hfill & \mathrm{i}\mathrm{f}{a}_{ij}<0,\hfill & i,j\in \langle 1,n\rangle ,i\ne j,\hfill \\ a_{dj}\hfill & \hfill & i,j\in \langle 1,n\rangle ,i=d,j\ne d,\hfill \end{array}\right.\hfill \end{array}$$

(25)

to transform the separation procedure to a relaxed form. The remaining separation conditions defined by Lemma 4 remain valid.

If the condition ${\mathit{A}}_{\Delta }+p{\mathit{I}}_n\prec 0$ from (20) is not fulfilled for a given value of the parameter $p>0$, even under these conditions does not exist parametrization of the matrix $\mathit{A}\in {\mathbb{M}}_{-\ominus }^{n\times n}$ according to (18), which guarantees a positive gain $\mathit{K}\in {\mathrm{M}}_{+}^{r\times n}$ to the control law (12).

The design task can now be formulated only as the construction of a Hurwitz stable ${\mathit{A}}_c=\mathit{A}-\mathit{B}\mathit{K}\in {\mathbb{M}}_{-\odot }^{n\times n}$ (16) on a hidden ostensible Metzler and Hurwitz matrix ${\mathit{A}}_{pc}\in {\mathbb{M}}_{-\odot }^{n\times n}$ when implementing the feedback (12) to continuous-time system (1) with ostensible Metzler $\mathit{A}\in {\mathbb{M}}_{-\ominus }^{n\times n}$ and rank deficient $\mathit{B}\in {\mathbb{R}}^{n\times r}$, where

$$\dot{\mathit{q}}\left(t\right)={\mathit{A}}_c\mathit{q}\left(t\right)=({\mathit{A}}_{pc}+{\mathit{A}}_m)\mathit{q}\left(t\right),{\mathit{A}}_{pc}={\mathit{A}}_p-\mathit{B}\mathit{K},{\mathit{A}}_c=\mathit{A}-\mathit{B}\mathit{K},$$

(26)

whilst $\mathit{K}\in {\mathbb{R}}^{r\times n}$, $\mathit{B}\in {\mathbb{R}}^{n\times r}$ are diagonalized as in (14). Moreover, positive element constraints cannot be ensured by negative feedback of each diagonal matrix from the rhombic representation of ${\mathit{A}}_{pc}$ if that includes a negative non-diagonal element from d-th row of the ostensible Metzler matrix A and this problem must be solved at the level of the conditions of positivity.

To design positive $\mathit{K}\in {\mathbb{R}}^{r\times n}$ the following theorem is given, having the ability to make the closed-loop system stable and to solve the design task in LMIs framework.

Theorem 1.

The matrices ${\mathit{A}}_c,{\mathit{A}}_{pc}\in {\mathbb{M}}_{-\odot }^{n\times n}$ are ostensible Metzler and Hurwitz if there exist positive definite diagonal matrices $\mathit{P}\in {\mathbb{R}}_{+}^{n\times n}$, ${\mathit{R}}_l\in {\mathbb{R}}_{+}^{n\times n}$ and matrices ${\mathit{V}}_{ch}\in {\mathbb{R}}_{+}^{n\times n}$, such that for $h=1,\dots ,n-1$, $l=1,\dots ,r$,

$$\mathit{P}\succ 0,{\mathit{R}}_l\succ 0,\left\{\begin{array}{cc}{\mathit{V}}_{ch}=0,\hfill & {\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)\succ 0,\hfill \\ {\mathit{V}}_{ch}\succ 0,\hfill & {\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)\mathit{is}\mathit{signum}\mathit{indefinite},\hfill \end{array}\right.$$

(27)

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu )\mathit{P}-\sum _{l=1}^r{\mathit{B}}_l{\mathit{R}}_l\prec 0,$$

(28)

$${\mathit{L}}^h{\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h){\mathit{L}}^{h\mathrm{T}}\mathit{P}-\sum _{l=1}^r{\mathit{L}}^h{\mathit{B}}_l{\mathit{L}}^{h\mathrm{T}}{\mathit{R}}_l\succ -{\mathit{V}}_{ch},$$

(29)

$$\mathit{A}\mathit{P}+\mathit{P}{\mathit{A}}^{\mathrm{T}}-\sum _{l=1}^r({\mathit{B}}_j\mathit{l}{\mathit{l}}^{\mathrm{T}}{\mathit{R}}_l+{\mathit{R}}_l\mathit{l}{\mathit{l}}^{\mathrm{T}}{\mathit{B}}_l)\prec 0,$$

(30)

where condition (6) implies

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)=\mathrm{diag}\left[\begin{array}{cccccc}{a}_{p,1,1+h}& \cdots & a_{p,n-h,n}& a_{p,n-h+1,1}& \cdots & a_{p,n,h}\end{array}\right],$$

(31)

${\mathit{B}}_l\in {\mathbb{R}}^{n\times n}$, $l=1,\cdots ,r$ result from diagonalization of the rank deficient matrix $\mathit{B}\in {\mathbb{R}}^{n\times r}$ by (15) and

$${\mathit{l}}^{\mathrm{T}}=\left[\begin{array}{ccc}1& \cdots & 1\end{array}\right],{\mathit{l}}^{\mathrm{T}}\in {\mathbb{R}}_{+}^n.$$

(32)

Within a feasible solution, the controller gain $\mathit{K}\in {\mathbb{R}}^{r\times n}$ is constructed sequentially with relation to (14) by its rows

$${\mathit{K}}_l={\mathit{R}}_l{\mathit{P}}^{-1},{\mathit{k}}_l^{\mathrm{T}}={\mathit{l}}^{\mathrm{T}}{\mathit{K}}_l,\mathit{K}=\left[\begin{array}{c}{\mathit{k}}_1^{\mathrm{T}}\\ ⋮\\ {\mathit{k}}_r^{\mathrm{T}}\end{array}\right].$$

(33)

Proof. 

Using the positive definite diagonal matrix $\mathit{Q}\in {\mathbb{R}}_{+}^{n\times n}$ to respect principle of diagonal stabilization, the following candidate for the Lyapunov function $v\left(\mathit{q}\right(t\left)\right)$ can be defined:

$$v\left(\mathit{q}\left(t\right)\right)={\mathit{q}}^{\mathrm{T}}\left(t\right)\mathit{Q}\mathit{q}\left(t\right)>0$$

(34)

and taking the derivative of $v\left(\mathit{q}\right(t\left)\right)$ along all trajectories of system (26) with ostensible Metzler $\mathit{A}\in {\mathbb{M}}_{-\ominus }^{n\times n}$ and rank deficient $\mathit{B}\in {\mathbb{R}}^{n\times r}$ it can be prescribed:

$$\dot{v}\left(\mathit{q}\left(t\right)\right)={\dot{\mathit{q}}}^{\mathrm{T}}\left(t\right)\mathit{Q}\mathit{q}\left(t\right)+{\mathit{q}}^{\mathrm{T}}\left(t\right)\mathit{Q}\dot{\mathit{q}}\left(t\right)<0.$$

(35)

When inserting (26) in (35), it is

$$\dot{v}\left(\mathit{q}\left(i\right)\right)={\mathit{q}}^{\mathrm{T}}\left(t\right){\mathit{A}}_c^{\mathrm{T}}\mathit{Q}\mathit{q}\left(t\right)+{\mathit{q}}^{\mathrm{T}}\left(t\right)\mathit{Q}{\mathit{A}}_c\mathit{q}\left(t\right)<0,$$

(36)

$${\mathit{A}}_c\mathit{Q}+\mathit{Q}{\mathit{A}}_c\prec 0,$$

(37)

respectively.

Thus, defining $\mathit{P}={\mathit{Q}}^{-1}\in {\mathbb{R}}_{+}^{n\times n}$ then, pre-multiplying the left side and post-multiplying the right side by P, inequality (37) it can be concluded that

$${\mathit{A}}_c\mathit{P}+\mathit{P}{\mathit{A}}_c^{\mathrm{T}}\prec 0,$$

(38)

where a diagonal positive definite P is the solution of (38).

With relation to (26) it bears

$${\mathit{A}}_c\mathit{P}=(\mathit{A}-\mathit{B}\mathit{K})\mathit{P}=\mathit{A}\mathit{P}-\sum _{l=1}^r{\mathit{b}}_l{\mathit{k}}_l^{\mathrm{T}}\mathit{P}=\mathit{A}\mathit{P}-\sum _{l=1}^r{\mathit{B}}_l\mathit{l}{\mathit{l}}^{\mathrm{T}}{\mathit{K}}_l\mathit{P},$$

(39)

where the row vector ${\mathit{l}}^{\mathrm{T}}$ defined in (32) projects given parameters to diagonal matrix representations and with the notation

$${\mathit{K}}_l\mathit{P}={\mathit{R}}_l,$$

(40)

then (37), (39) imply (30).

Since (16) with matrix parametric constraints (31) is generalizable as

$${\mathit{A}}_{pc}=\sum _{h=0}^{n-1}({\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)-\sum _{l=0}^r{\mathit{B}}_l{\mathit{K}}_{lh}){\mathit{L}}^{h\mathrm{T}},$$

(41)

interpreting (41) analogously to (10) then, for $h=0$,

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)-\sum _{l=1}^r{\mathit{B}}_l{\mathit{K}}_l\prec 0.$$

(42)

Multiplying the right side of (42) by P, it can be straight derived

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)P-\sum _{l=1}^r{\mathit{B}}_l{\mathit{K}}_{L}P\prec 0$$

(43)

and, using notation (40), then (43) implies (28).

The same interpretation of (10), (15), (41) for any $h\in \langle 1,n-1\rangle$ results in

$$\begin{array}{cc}\hfill & {\mathit{L}}^h{\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h){\mathit{L}}^{h\mathrm{T}}-{\displaystyle \sum _{l=1}^r}{\mathit{L}}^h{\mathit{B}}_l\left({\mathit{L}}^{h\mathrm{T}}{\mathit{K}}_l{\mathit{L}}^h\right){\mathit{L}}^{h\mathrm{T}}\hfill \\ =\hfill & {\mathit{L}}^h{\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h){\mathit{L}}^{h\mathrm{T}}-{\displaystyle \sum _{l=1}^r}{\mathit{L}}^h{\mathit{B}}_l{\mathit{L}}^{h\mathrm{T}}{\mathit{K}}_l\hfill \\ \succ \hfill & 0\hfill \end{array}$$

(44)

and substituting (40) after multiplying the right side by P, then (44) implies (29) with zero matrix on the right side if the associate rhombic diagonal matrix satisfies the condition ${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)\succ 0$.

In the opposite case, it is necessary to add to the right side the diagonal matrix variable $-{\mathit{V}}_h\prec 0$, ${\mathit{V}}_h\in {\mathbb{R}}_{+}^{n\times n}$ to construct extended form of (29). This concludes the proof. □

Remark 1.

If the rhombic diagonal matrix ${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +h)$ is signum indefinite, a component of the positive definite diagonal matrix variable P can converge to 0 and the solution of the control law gain problem becomes very large. This problem is solved by the proposed modification and is conditioned by the LMI constraint positiveness representation (29). If the requirements of Theorem 1 cannot be met prescribing negativeness by $-{\mathit{V}}_h\prec 0$, this means that the task is infeasible, and for the rank-deficit input matrix of the system specified in this way, there is no diagonal stabilization of the system. But this is not a problem conditioned by the method of separation of the ostensible Metzler matrix.

Remark 2.

Theorem 1 expresses conditions guaranteeing solutions with positive gain of the control law (12). Furthermore, it formulates the optimization problem which reveals the conditions for given parametric constraints. The presented synthesis method is relevant for that class of real applications based on ostensible Metzler mathematical models, which is presented in [1,2,3,4,5].

5. Illustrative Example

To illustrate the suitability of the proposed method, the design procedure for a linear ostensible Metzler system (1) is specified, with the system parameters coming from the linearized mathematical model of the B747-100/200 aircraft [29], where the state variables, necessary for the design of longitudinal control, are the pitch rate (radian per second), actual airspeed (meter per second), angle of attack (radian) and pitch angle (radian) and system inputs are elevator deflection, total thrust and horizontal stabilizer. Used mathematical model parameters are [29]:

$$\mathit{A}=\left[\begin{array}{cccc}\hfill -2.98& \hfill 0.930& \hspace{1em} 0\hfill & -0.0340\\ \hfill -0.99& -0.210& 0.035\hfill & -0.0011\\ \hfill \hspace{1em} 0& \hspace{1em}\hspace{1em}0& -2\hfill & \hspace{1em}\hspace{1em}1\\ \hfill 0.39& -5.555& \hspace{1em} 0\hfill & -1.8900\end{array}\right],\mathit{B}=\left[\begin{array}{ccc}\hfill -0.032& \hspace{1em}0.5& \hspace{1em}1.55\hfill \\ \hfill 0& \hspace{1em} 0& \hspace{1em}\hspace{1em}0\hfill \\ \hfill 0& \hspace{1em} 0& \hspace{1em}\hspace{1em}0\hfill \\ \hfill -1.600& 1.8& -2.00\hfill \end{array}\right],\mathit{C}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right],$$

whilst the ostensible Metzler matrix A is stable, since

$$\rho \left(\mathit{A}\right)=\left\{\begin{array}{cccc}\hfill -0.9181& -1.2009& -2.3219\hfill & -2.6390\end{array}\right\}$$

and the input matrix rank deficiency implies the row numbers $d=2,3$.

It is assumed that the parameters of the mathematical model are known and it is possible to implement the separation of the matrix A according to the methodology mentioned above. Thus, since only the first and the forth rows elements of A can be considered in the matrix A separation, it leads to

$${\mathit{A}}^{-}=\left[\begin{array}{cccc}\hfill 0& \hspace{1em}\hspace{1em}0& 0\hfill & -0.034\\ \hfill 0& \hspace{1em}\hspace{1em}0& 0\hfill & \hspace{1em}\hspace{1em}0\\ \hfill 0& \hspace{1em}\hspace{1em}0& 0\hfill & \hspace{1em}\hspace{1em}0\\ \hfill 0& -5.555& 0\hfill & \hspace{1em}\hspace{1em}0\end{array}\right],{\mathit{A}}^{+}=\left[\begin{array}{cccc}\hfill 0& 0.930& \hspace{1em} 0\hfill & \hspace{1em}\hspace{1em} 0\\ \hfill -0.990& \hspace{1em} 0& 0.035\hfill & -0.0011\\ \hfill \hspace{1em} 0& \hspace{1em} 0& \hspace{1em} 0\hfill & 1.0000\\ \hfill 0.390& \hspace{1em} 0& \hspace{1em} 0\hfill & \hspace{1em}\hspace{1em} 0\end{array}\right],\mathsf{\Sigma }=\left[\begin{array}{cccc}0& 1& 1& 1\\ 1& 0& 1& 1\\ 1& 1& 0& 1\\ 1& 1& 1& 0\end{array}\right],$$

$${\mathit{A}}_m^{\circ }=\left[\begin{array}{cccc}\hfill 0& -0.005& -0.005\hfill & -0.039\\ \hfill -0.005& \hspace{1em}\hspace{1em}0& -0.005\hfill & -0.005\\ \hfill -0.005& -0.005& \hspace{1em}\hspace{1em}0\hfill & -0.005\\ \hfill -0.005& -5.560& -0.005\hfill & \hspace{1em}\hspace{1em}0\end{array}\right],$$

where, for the predefined $\mu =0.005$,

$$\rho \left({\mathit{A}}_m^{\circ }\right)=\left\{\begin{array}{cccc}\hfill -0.1866& 0.1401& 0.0415\hfill & 0.0050\end{array}\right\},\delta =0.1401$$

Setting the D-stability region by $p=0.003$, the element-wise negative and Hurwitz ${\mathit{A}}_m$ (19) results, where

$${\mathit{A}}_m=\left[\begin{array}{cccc}\hfill -0.1431& -0.0050& -0.0050\hfill & -0.0390\\ \hfill -0.0050& -0.1431& -0.0050\hfill & -0.0050\\ \hfill -0.0050& -0.0050& -0.1431\hfill & -0.0050\\ \hfill -0.0050& -5.5600& -0.0050\hfill & -0.1431\end{array}\right],\rho \left({\mathit{A}}_m\right)=\left\{\begin{array}{c}\hfill -0.3297\\ \hfill -0.0030\\ \hfill -0.1016\\ \hfill -0.1381\end{array}\right\},$$

whilst, the main diagonal elements of A construct a negative definite diagonal matrix

$${\mathit{A}}_d=\mathrm{diag}\left[\begin{array}{cccc}\hfill -2.98& -0.21& -2.00\hfill & -1.89\end{array}\right],$$

the reference strictly Metzler matrix ${\mathit{A}}_p$, given by the rule ${\mathit{A}}_p={\mathit{A}}_d+{\mathit{A}}^{+}+\eta \mathsf{\Sigma }+p{\mathit{I}}_n$, is constructed as:

$${\mathit{A}}_p=\left[\begin{array}{cccc}\hfill -2.8369& \hfill 0.9350& \hfill 0.0050& \hfill 0.0050\\ \hfill -0.9850& \hfill -0.0669& \hfill 0.0400& \hfill 0.0039\\ \hfill 0.0050& \hfill 0.0050& \hfill -1.8569& \hfill 1.0050\\ \hfill 0.3950& \hfill 0.0050& \hfill 0.0050& \hfill -1.7469\end{array}\right],\rho \left({\mathit{A}}_p\right)=\left\{\begin{array}{c}-0.4488\\ -2.4644\\ -1.7972\pm 0.07\mathrm{i}\end{array}\right\},$$

where the set of eigenvalues $\rho \left({\mathit{A}}_p\right)$ is stable.

In the next step, matrix bounds must be constructed that express the Metzler dynamics ${\mathit{A}}_p$ with respect to the principle of diagonal stabilization. Thus, the rhombic related diagonal matrices to ${\mathit{A}}_p$, conditioned by rank of B, are derived as

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu )=\mathrm{diag}\left[\begin{array}{cccc}\hfill -2.8369& -0.0669& -1.8569\hfill & -1.7469\end{array}\right]$$

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +1)=\mathrm{diag}\left[\begin{array}{cccc}\hfill 0.935& 0.040& 1.005\hfill & 0.395\end{array}\right],{\mathit{B}}_1=\mathrm{diag}\left[\begin{array}{cccc}\hfill -0.032& 0& 0\hfill & -1.6\end{array}\right],$$

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +2)=\mathrm{diag}\left[\begin{array}{cccc}\hfill 0.005& 0.0039& 0.005\hfill & 0.005\end{array}\right],{\mathit{B}}_2=\mathrm{diag}\left[\begin{array}{cccc}\hfill 0.05& 0& 0\hfill & 1.8\end{array}\right],$$

$${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +3)=\mathrm{diag}\left[\begin{array}{cccc}\hfill 0.005& -0.985& 0.005\hfill & 0.005\end{array}\right],{\mathit{B}}_3=\mathrm{diag}\left[\begin{array}{cccc}\hfill 1.55& 0& 0\hfill & -2.0\end{array}\right].$$

It is obvious that ${\mathit{A}}_{\mathrm{\Theta }p}(\nu ,\nu +3)$ is not positive definite diagonal matrix and therefore the condition on the parametric constraints for $h=3$ must be modified as

$${\mathit{L}}^3{\mathit{A}}_{\mathrm{\Theta }}(\nu ,\nu +3){\mathit{L}}^{3\mathrm{T}}-\sum _{l=0}^r{\mathit{L}}^3{\mathit{B}}_l{\mathit{R}}_l{\mathit{L}}^{3\mathrm{T}}>-{\mathit{V}}_{c3},$$

whilst the rest positive constraints stay unchanged.

Fitting the design to this set of parameters by solving the conditions (27)–(30) using the SeDuMi [30] package in the MATLAB environment has a feasible solution in the form of positive definite diagonal matrices variables:

$$\mathit{P}=\mathrm{diag}\left[\begin{array}{cccc}0.3426& 2.0185& 0.8675& 0.8321\end{array}\right]\succ 0,{\mathit{V}}_{c3}=\mathrm{diag}\left[\begin{array}{cccc}1.0182& 0.8268& 0.6296& 1.4747\end{array}\right]\succ 0,$$

$${\mathit{R}}_1=\mathrm{diag}\left[\begin{array}{cccc}0.7282& 0.6050& 0.7222& 0.6071\end{array}\right]\succ 0,{\mathit{R}}_2=\mathrm{diag}\left[\begin{array}{cccc}0.5095& 1.0016& 0.0148& 0.8126\end{array}\right]\succ 0,$$

$${\mathit{R}}_3=\mathrm{diag}\left[\begin{array}{cccc}0.2619& 0.5474& 0.0086& 0.3607\end{array}\right]\succ 0,$$

and under the rule (33), this set of LMI variables predefined a positive element-wise state control law gain matrix as the final synthesis parameter

$$\mathit{K}=\left[\begin{array}{cccc}\hfill 2.1255& 0.2997& 0.8325\hfill & 0.7296\\ \hfill 1.4872& 0.4962& 0.0170\hfill & 0.9765\\ \hfill 0.7644& 0.2712& 0.0099\hfill & 0.4335\end{array}\right],$$

which forces the stable reference as well as the closed-loop dynamics

$${\mathit{A}}_{pc}=\left[\begin{array}{cccc}\hfill -4.6973& \hfill 0.2761& \hfill 0.0078& \hfill -1.1319\\ \hfill -0.9850& \hfill -0.0669& \hfill 0.0400& \hfill 0.0039\\ \hfill 0.0050& \hfill 0.0050& \hfill -1.8569& \hfill 1.0050\\ \hfill 2.6478& \hfill 0.1338& \hfill 1.3261& \hfill -1.4702\end{array}\right],\rho \left({\mathit{A}}_{pc}\right)=\left\{\begin{array}{c}-0.0653\\ -0.9457\\ -3.5402\pm 1.0383\mathrm{i}\end{array}\right\},$$

$${\mathit{A}}_c=\left[\begin{array}{cccc}\hfill -4.8404& 0.2711& 0.0028\hfill & -1.1709\\ \hfill -0.9900& -0.2100& 0.0350\hfill & -0.0011\\ \hfill 0& \hspace{1em}\hspace{1em}0& \hspace{1em}-2\hfill & \hspace{1em}\hspace{1em}1\\ \hfill 2.6428& -5.4262& 1.3211\hfill & -1.6133\end{array}\right],\rho \left({\mathit{A}}_c\right)=\left\{\begin{array}{c}-3.4470\\ \hfill -3.8531\hfill \\ -0.6818\pm 0.9090\mathrm{i}\end{array}\right\}.$$

From the set of eigenvalues and the simulation results, it can be found that the proposed method has an acceptable closed-loop system response and desired steady-state properties.

The simulations were realized in the standard way for the closed-loop system structure with the reference gain matrix, constant values of the desired outputs and the computed control law matrix parameter K, where

$$\mathit{u}\left(t\right)=-\mathit{K}\mathit{q}\left(t\right)+\mathit{W}\mathit{w},$$

$$\mathit{W}=\mathrm{diag}\left[\begin{array}{ccc}\hfill 1.0& 0.5& 0.2\hfill \end{array}\right],{\mathit{w}}^{\mathrm{T}}=\mathrm{diag}\left[\begin{array}{ccc}\hfill 0.9& 0.9& 6.5\hfill \end{array}\right],$$

$$\mathit{y}\left(t\right)=\mathit{C}\mathit{q}\left(t\right),\mathit{C}=\left[\begin{array}{cccc}\hfill 1& 0& 0\hfill & 0\\ \hfill 0& 0& 0\hfill & 1\\ \hfill 0& 1& 0\hfill & 1\end{array}\right].$$

Since the closed-loop dynamics do not represent a strictly positive system, the initial system state was set as ${\mathit{q}}^{\mathrm{T}}\left(0\right)=\left[1.600.012.000.00\right]$.

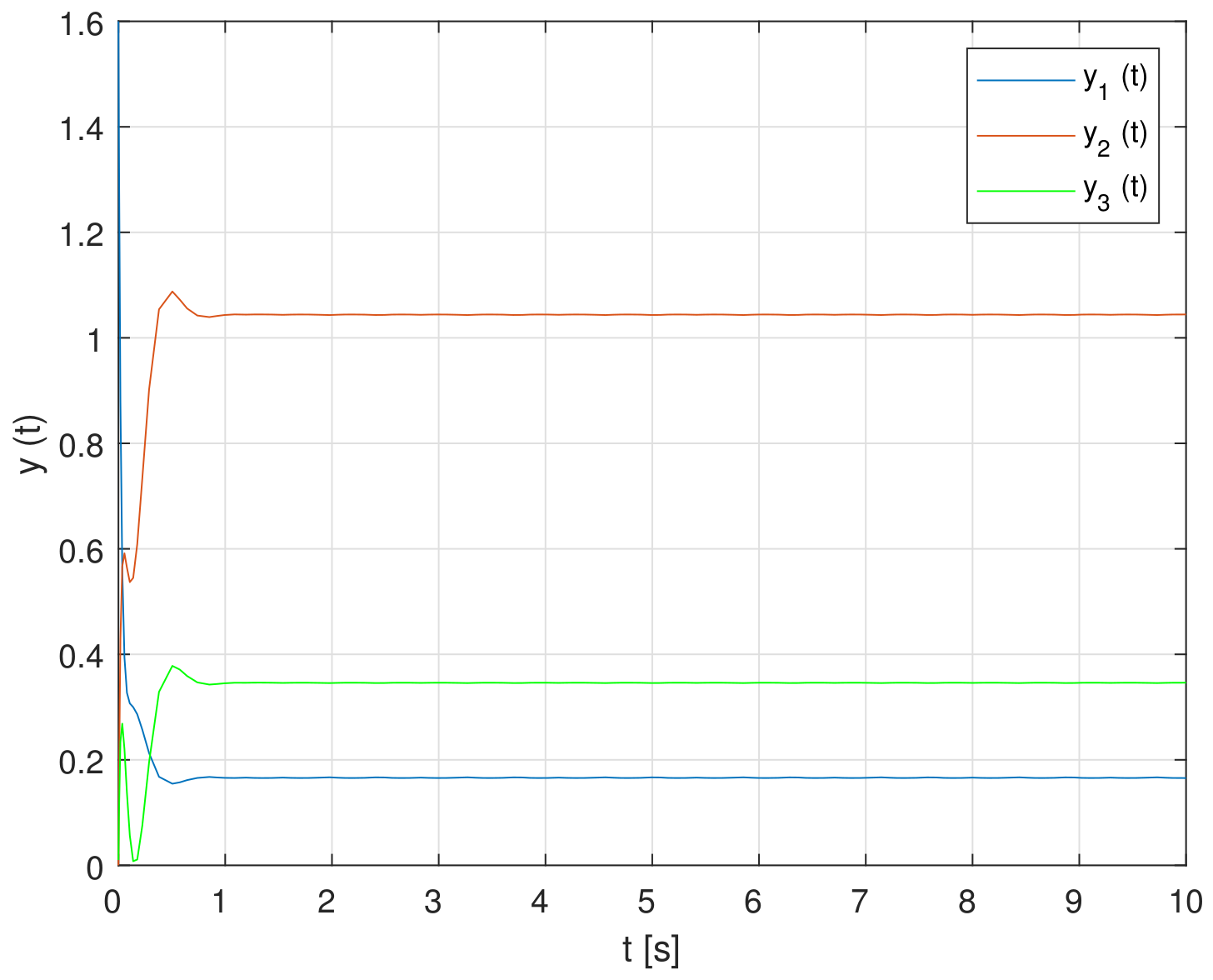
The simulation results are exhibited in Figure 1 to illustrate the problems of synthesis and to demonstrate the design boundedness of the control parameters. From Figure 1, it can be observed that the system output variables have to be positive in such an initialization setting, since ${\mathit{A}}_c$ is an ostensible Metzler system and Hurwitz and W, C and ${\mathit{w}}^{\mathrm{T}}$ are positive. Due to the resulting positivity of the closed-loop structure, the simulation results in Figure 1 completely illustrate the presented methodology.

In the existing works on this type of mathematical model (see, e.g., [31,32,33]), the constraints resulting from the structure of the matrix B are not included in the synthesis conditions, and therefore these works use reduction with respect to the state-space system model. Due to the nature of the methodology presented in this work, when using the system model of the original dimensionality, different properties of the system result, and therefore it would be incorrect to compare the results under unequal definitional conditions.

6. Concluding Remarks

In this paper, the diagonal stabilization is adapted for ostensible Metzler linear continuous-time systems with rank deficient input matrices and their signum-independent elements. By using a system matrix separation approach, the system parametrization task is resolved for a hidden system matrix part and it is shown that closed-loop system dynamics are accomplished under the given rank limitation of the system input matrix. The stability conditions are formulated using Lyapunov’s theory and outspreading LMI-based parametric constraints, the control design task being feasible one such that approximates closed-loop system positiveness as well as possible.

The contribution of this paper mainly consists of designing the state control with a higher degree of freedom to improve the ostensible Metzler system dynamics and to satisfy the desired guaranteed performances. To obtain relaxed criteria for stable closed-loop system dynamics, the entire development of this work is formulated in terms of quadratic Lyapunov function on positive diagonal matrix variable. A numerical example is used to verify the suitability of the used algorithms and to confirm the theoretical assumptions. The proposed approach discussed is encouraging and may help to motivate intensive future efforts toward the application of these ideas. Unlike other papers of similar focus, this paper investigates for the first time the problem of the specificity of state control design by considering the properties and bounds of this class of continuous-time ostensible Metzler linear systems. To the best of the authors’ knowledge and view, no comparable theoretical or practical results are available.

This type of control system seems to have particular meaning potentially with time-varying topologies within hierarchical network control structures [34], multi-agent systems with switching directed topologies [35] and unmanned aerial vehicle path following [36]. Studying the consensus control problems with suchlike system parametric limitations defined for high-order heterogeneous multi-agent systems containing one leader, we expect to find new and effective methods to deal with analogous design problems. Another prospective area of application of the presented methodology is fault-tolerant control for network systems with communication limits [37,38,39] in search of future research directions.