Abstract
In steel tied arch bridges where the hangers are made of rigid bars, the replacement of damaged hangers is rather complex. In fact, while generally the cable hangers are already prepared with anchors at the ends and their replacement traces the initial stages of construction with their prestressing, on the contrary, the rigid bars are welded to the arch and the deck, so their replacement must include the design of a new suspension system that allows the insertion of a pretension where this had never been considered. To check the reliability of this new system, a prototype of tensioner was studied for the case of a steel arch bridge in which the high level of corrosion made it necessary to replace all the original hangers with new ones. This entailed the need to test the tensioner performance with the aim of ensuring the axial force transmission between the two hanger segments without slippage in the threads, as well as to test the correct tension setting before construction and putting into service the hangers to be replaced. For this reason, a predictive experimental campaign was carried out on a prototype by means of tests for the mechanical characterization of the materials used, tensile tests of the system, and tensioning tests under load, measuring the displacements and strains of the system elements. The results of the tests, with slippage in the threads limited to the 2% of total elongation, and the turnaround-stressing curves were useful for the definition of the pieces to be assembled during on-site work and for addressing the operating procedures of the tensioning phases on-site during hanger replacement. Validation with the on-site monitoring of stressing operation was conducted at the end; the monitoring of tension through dynamic tests confirmed the agreement of on-site results with the predictive loading tests of the experimental campaign on the tensioner prototype.
1. Introduction
In bowstring arch bridges, the deck is suspended from the arch by means of hangers that can be made of steel bars, rigid profiles, or cables [1,2]. In the first case, the steel bars that connect the arch and the girder can present different types of connection to the two main elements, but generally, the function is that of bringing a predominantly axial force into a state of tension. Some bridges have, from their initial conception, the possibility of adjusting the tension in the hangers through an intermediate element that impresses distortion, that is, a tensioner; in other cases, instead, the bars are rigidly connected to the two ends and welded to the arch and to the deck girder. When this second case occurs, during construction, the load is transferred to the hangers directly by means of temporary intermediate supports. Hence, self-weight puts in tension the elements of the suspension system directly through the elastic deformation of arch and deck elements, activating the overall behaviour, when temporary supports are removed. In bridges built with this technique and this configuration of the suspension system, it is not possible to vary the stress state of the hangers in any way after construction, and no prestress or adjusting tensile forces can be applied to the elements over time. If the replacement of these hangers becomes necessary, it is therefore difficult to completely unload the hanger and to replace it with a new element that must take back the load already lost during the replacement phase. The problem therefore arises of designing a new suspension system, capable of restoring the stress state lost by cutting the damaged existing hangers. The sequence of the replacement and re-stressing of new hangers is then extremely important for the success of the intervention on an existing bridge, especially when maintenance implies the need to replace several hanger bars or the entire original suspension system. The introduction of a stress that recovers the previously released load is an operation that must be carried out by imposing a distortion in the new suspension bar that corresponds to an imposed shortening, in a tensioning stage. In the most common cases, the hanger consists of a cable and the cutting and replacing operation depends on the connections to the main supporting elements, as is the case of suspension bridges for hangers that connect the main cable to the deck. In the literature, these typologies have usually been studied, operating on strands and anchorages. Lan Wang et al. [3,4] specify the operations of replacement for concrete arch bridges in which steel hangers are made of cables, by choosing a methodology based on the displacement method. Sun et al. [5,6] studied the replacement of vertical cable hangers in suspension bridges, with similar issues to those of arch bridges. Wu [7] described the design approach of a new cable hanger in tied arches to enhance the robustness. Hayashi et al. [8,9] studied the problem of hanger replacement in the rehabilitation of Lohse arches, where hangers are inclined and the pretension depends on the maximum compressive forces induced by loads; although this case is similar to that of steel tied arches, it deals with strands and does not consider rigid elements. Martin [10] used the same method of cable hangers for suspension bridges in arch bridges, through common prestressing techniques. Other studies [11,12,13] give results of optimization forces in hanger prestressing and the performance of these suspension systems, while a review paper by Fan et al. [14] describes the robustness of the suspension systems through several cases of damaged bridges or failures. Other studies address the fatigue of cable hangers due to the oscillations of loads on the anchors [15] and the steel–composite connections [16]. A much less common problem is that of replacing the rigid bars, originally conceived welded at the end and without intermediate tensioner, that is, of hangers with rigid arch-to-deck connections, and this problem has not been considered in the literature to the authors’ knowledge. In the latter case, the release of tension during the replacement operation due to hanger cutting must be restored with a stressing operation on new rigid elements that must be specially designed and configured. In other words, there is a need to modify the initial engineering concept (similar to reticular steel structures) to insert a pretension on elements that originally did not foresee imposed distortions (similar to the cable bridges conception), by conceiving a new suspension system made of rigid bars with new end connections and with a tensioner.
This is the case of a steel arch bridge located in southern Italy, which, due to its proximity to the mouth of a river and an original protection against corrosion not being effective, presented the need for maintenance less than 20 years after construction, with the total replacement of the suspension system and a new corrosion protection of all steel structures [17]. The maintenance intervention provided for the replacement of 46 hangers consisting of rigid bars of lengths ranging from approximately 5 to 15 m, with a circular section of 70 mm diameter. The corrosion state of the hangers reduced the cross-sections and damaged the welded connections to arch and deck and especially the joint sleeves (couplers) of the bars longer than 12 m [18]. In this case, in fact, the connections to the arch and the girders were made directly through welds to the steel plates at the hanger ends, and the overall arch loading occurred by transferring self-weight through the removal of a single intermediate support during construction stages. To do this, the connection at the ends of the hanger must be modified, because the original concept was to make a rigid connection to the arch and the deck, while a modern hanger to be pretensioned must be conceived with hinges at the ends.
Figure 1a shows the bridge in its initial configuration, and Figure 1b shows the original hanger with welded connections of the rigid bar at arch and deck girder; Figure 1c reports a view of the new suspension system, while Figure 1d shows the new hanger with new connections and intermediate tensioner. After maintenance intervention, the new suspension system consists of bars of the same type as the original ones but connected by monoaxial hinge joints at the two ends. The bar is divided into two segments connected by a tensioner capable of inducing an inner relative displacement of the two upper and lower bar sections by a rotation set to the tensioner. The ends of the hanger are threaded so that the tensioner can give an imposed shortening deformation to the bar and then bring the ends connected to the arch and deck close to one another. A tensile stress inside the hanger corresponds to this imposed shortening, proportional to the rotation imposed to the tensioner, and this tension arises from the force imposed on the two extremes (Volterra distortion) together with the elastic deformation of the bar. Because the suspension system of the arch bridge presents hangers of different heights, the value of pretension depends on the position of the hanger in the suspension system of the entire bridge, on the axial stiffness of the bar, and on the mutual effect due to the hyperstatic nature of the system and to the axial–flexural stiffness of arch and deck girders. In the following sections, after an overview of the fundamental aspects of prestressing stages during hanger replacements, the engineering aspects of the tensioner prototype and load tests are described.

Figure 1.
The case study bridge. (a) Original configuration; (b) original hanger with welded connections at the end; (c) new suspension system; (d) new hanger with end connections and intermediate tensioner.
2. Stages of Hanger Replacement
The replacement of a single hanger within the entire suspension system is divided into three phases (Figure 2):
- -
- the ith hanger is removed: in this phase, the axial force N0,i, sustained by the existing hanger, is released and redistributed to the other hangers according to the principle of mutual effect (the two adjacent hangers are always the most influenced ones).
- -
- The new hanger is put in place, anchored to the upper arch and to the lower deck girder, in the transitory deformed configuration.
- -
- The new hanger is stressed through the tensioner by imposing a distortion in the steel bar (imposed shortening) until the axial force is totally restored to the initial value and/or the local deformation of arch and deck are nullified, once again achieving the original configuration or the design one.
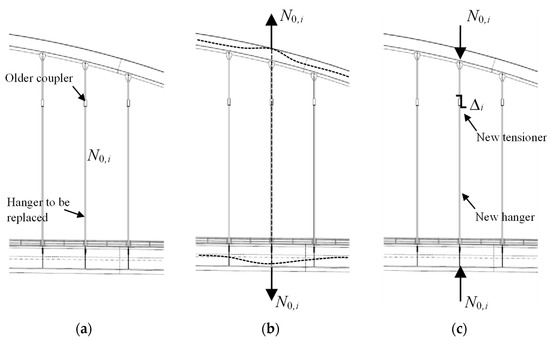
Figure 2.
Replacement sequence. (a) Original configuration; (b) hanger cutting and stress release (N0,i); (c) new hanger and imposed distortion Δi through tensioner.
In this procedure, it is necessary to know the stress value in the original configuration and/or the displacements of the anchor points at each stage of replacement, as well as the value of the prestress to supply to the new hanger. The original axial stress and the displacement of the anchor points can be determined a priori through an FE model of the bridge, but its actual value has to be controlled on-site through the strain monitoring of the bar when it is cut. This is because the construction stages can vary the actual distribution of axial forces in the elements of the suspension system with respect to the theoretical values of design; consequently, the target value of prestressing can be the theoretical one or that of the original configuration after construction, which are not identical. To know the actual value of axial force, only an in situ monitoring of strains on the original hanger can be operated, in order to verify the amount of tensile force in the existing hanger; this can be different from the theoretical one for a state of degradation or for errors during construction. This means that the value of final axial force in the new hanger can be evaluated as the target value by the engineer in the design of the replacement intervention, but the value of prestressing for the new hanger is not known a priori due to the hyperstatic system of arch–deck–hangers, as it occurs for cable-stayed bridges where the determination of the initial cable forces is a fundamental step of the stressing sequence [19,20,21]. The value of prestressing is conditioned by the necessity to recover the displacements of the two anchor points, and these depend on the stiffness of arch and deck. For this reason, the final value of the axial force in the new hanger is related to the following:
- (a)
- The value of distortion imposed by the tensioner.
- (b)
- The elastic deformation of the bar.
- (c)
- The stiffness of the arch-deck system.
If δi is the total relative displacement between deck and arch anchor points of the ith hanger, the initial displacement δ0,i can be determined numerically through an FE model and practically by measuring on-site the actual relative displacement of the two bar ends. In this way, it is possible to compare two data:
- -
- The theoretical and actual strains in the bar, which are directly related to the axial force of the hanger, together with the total displacement at the release stage.
- -
- The theoretical and actual displacements at the ends of the bar, which are instead related to the original distortion.
Hence, the engineer can choose the value of prestressing to be inserted in the new hanger: the original one, effectively measured on-site; or another value due to the design conditions if adjustments are needed with respect to the actual configuration of the existing bridge.
Therefore, the prestressing force Fi of the new ith hanger depends on the value of the relative displacement di that arises in the hanger anchor points because of the imposed unitary imposed distortion Δ1,i = −1 applied to the hanger of length Li:
where di depends on the stiffness of the whole structural system (arch, deck, and suspension system). The value of the distortion to be imposed and the corresponding value of the prestressing force Fi are found by imposing the condition δi = δ0,i, where δ0,i is the on-site measured value or the design one. The value of the distortion is then the following:
and correspondingly, the value of the prestressing force is the following:
δ1,i = di Δ1,i
Δi = δ0,i/di
Fi = EiAi/Li · δ0,i/di
With this prestressing value, the final axial force after replacement is the target value N0,i. It is worth noting that Fi and N0,i are not the same force, because they have different physical meanings: Fi is directly related to the distortion, while N0,i is the value of the effective axial force in the hanger. This value of the axial force depends on the hyperstatic system (N0,i < Fi), and the apparent prestressing loss (Fi − N0,i) is the force necessary to deform the arch and the girder, that is, the force necessary to make the distortion effective, by approaching the two extremes that had drifted apart during the tensional release. Therefore, the main issue of this procedure is the evaluation of the stiffness factors di and displacements δ0,i through the FE model for each hanger, together with the measurement of the experimental values of distortion on-site. Hence, the ability of the tensioner to apply the correct value of distortion Δi becomes fundamental to make this procedure effective during on-site work. It is worth noting that the overall procedure is non-linear because of the mutual effects between hangers, and it must be implemented in the complete model of the bridge and through an appropriate sequence of operations hanger-to-hanger. This sequence has to be optimized in such a way that the variation in the state of deformation and stress due to the mutual effect is the minimum possible, maintaining the effectiveness of the distortion imposed to each element [18,22,23]. This is, in fact, the most delicate aspect of the operation, which provides a different result if it is carried out only on one or a few elements or on the entire the suspension system.
It is therefore necessary to restore the deformation state prior to the replacement of the bar, through the tensioner, recovering not only the tension inside the element but also the redistribution that occurred in the adjacent elements due to the deformability of the arch and the beam of the deck, which establishes the mutual effect between hangers.
To accomplish this, the procedure chosen in the present case is as follows:
- (1)
- Analysis of the bridge using a detailed finite element model which, by means of a staged construction procedure, traces the original construction, allowing the theoretical determination of the tensile axial force in each hanger.
- (2)
- Determination of the real state of stress and deformation of the hanger by the on-site monitoring of strains during the cutting operation and removal of the bar.
- (3)
- Comparison between the data obtained on-site and the FE model for any modification and calibration of the model.
- (4)
- Assembly of the new bar and introduction of distortion through the tensioner, under strain monitoring, verification in the FE model and control of stresses in the adjacent hangers.
- (5)
- Adjustment of the applied distortion to the bar by means of the imposed tensioner couple.
- (6)
- Final verification of the new system by dynamic analysis of tensioned bars.
Moreover, through several numerical simulations, it is also possible to determine the sequence that minimizes the loss of tension by mutual effect for the entire intervention of bar replacement [18]. These simulations are repeated by changing the main parameters involved and the results are evaluated; particularly, analyses were made by changing the sequence of cutting and stressing of new hangers, the values of pre-tensions, and the number of hangers to be replaced at a time, to also evaluate the advantage or disadvantage of changing more hangers at a time. The result was that the more advantageous technique is to replace one hanger at a time, symmetrically from the ends of the bridge towards the midspan, regarding the deformability of the entire system.
Figure 3 shows the FE model of the bridge and a generic stage of the replacement sequence.
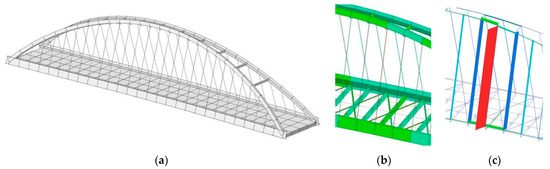
Figure 3.
FE model of the bridge. (a) Entire model; (b) stress variation in the hangers for a generic stage of replacement; (c) axial force diagram in the new hanger and in the adjacent ones after the application of distortion Δi through the tensioner.
The finite element model was carried out on MIDAS software. It was a three-dimensional model, with beam type elements for the steel members and shell type for the deck slab: the full model was composed of 636 joints, 761 beam elements, and 112 shell elements.
The sequence which appears to be the most convenient from the numerical simulations is the one which is performed with a single replacement at a time, going from the ends of the bridge towards the midspan both longitudinally and transversely. This stressing sequence was chosen for several reasons:
- (1)
- Only one hanger is replaced at a time, reducing the redistribution of stress in the adjacent hangers, which are already damaged by corrosion.
- (2)
- It proceeds from the more rigid hangers to the less rigid ones in order to reduce the deformation of the deck during the stressing operations.
- (3)
- The symmetrical hangers are replaced in sequence (both longitudinally and transversely) so that the bridge finds a perfect symmetry every four replaced hangers, recovering, at the same time, the global stress state.
This study will show the validation procedure of the tensioning system of the new hangers through the test campaign carried out on the prototype of the tensioner, tested under the most severe operating conditions.
To accomplish this, this paper presents in Section 3 the design of the steel elements for the suspension system and particularly of the tensioner; afterwards, the experimental campaign is divided in three parts: the material testing, the evaluation of threading slippage, and the evaluation of distortion effectiveness with tensioner turnaround. In Section 4, a summary of results is reported for a discussion of the technique’s reliability, and finally, Section 5 presents the application and validation on-site of the new suspension system, with actual results from hanger replacements and field tests.
3. Materials and Methods for Tensioner Prototype
3.1. Design of Tensioner Prototype
The configuration of the tensioner prototype is shown in Figure 4. Its geometry consists of the two lower and upper hanger segments with opposite threads and the central main element (the actual tensioner) that allows the connection of the bars, the transfer of tension between the two sections, and the introduction of the distortion. The prototype was equipped with two final rods (steel yield strength fy = 1000 MPa) of smaller diameter that allow coupling inside the jaws of the test machine, which does not have housings, making it possible to grab a bar of 70 mm diameter.
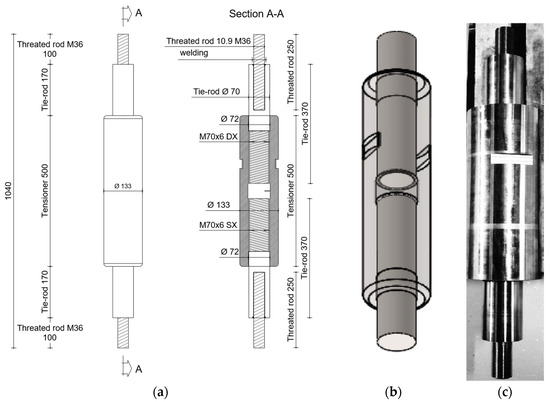
Figure 4.
Geometry of the tensioner prototype. (a) Lateral view and longitudinal cross-section (Measures in mm). (b) 3D view. (c) Real picture of the tensioner prototype.
After testing the constituent materials of the suspension system elements (mechanical tests on the steel used, type S355J2, with a nominal yield strength of 355 MPa), a test setup was designed in order to assess the tensioning rod and any slippage inside the threads as well as the tightness of the imposed tension. The test was carried out up to a load greater than 10% of that foreseen in the design phase for the characteristic combination at the Service Limit State, which is the irreversible condition of the most stressed hanger under the entire dead load and maximum traffic load provided by Eurocode 1 [24] and the Italian Code [25]. Subsequently, once the tightness of the system was verified together with the acceptability of the slippage in the threads of the assembled elements of the prototype, it was placed under a controlled load, and several tensioning tests were carried out to measure the turnaround of the tensioner and the introduction of the distortion in the hanger bars.
The tensioner is a steel tube with an external diameter of 135 mm and an internal diameter of 72 mm turned and machined with mechanical precision with two simple threads that have opposite directions of rotation (rightward at one end and leftward at the other end) and 6 mm pitch, so as to allow the two ends of the bars to move close to one another during the tensioning phase (imposed shortening is equivalent to the approaching measure of the two bars joined by the tensioner).
Figure 5 shows the conjunction of the hanger on-site with the two upper and lower hinge connections and the central tensioner.

Figure 5.
View of the whole hanger with the top (at the left side) and bottom (at the right side) connections with the central tensioner.
The following sections will provide data on the materials used and describe the tests carried out and the results obtained, as well as subsequent on-site applications, during the phases of hanger replacement.
3.2. Materials
The mechanical characteristics and the Brinell hardness of the steel, for the two main elements, were determined in advance. In particular, the following was measured:
- -
- The steel of the hanger bars was A105 grade, with a nominal yield strength of 355 MPa and a tensile strength of 510 MPa;
- -
- The tensioner steel was of S355J2H grade, with a nominal yield strength of 355 MPa and a tensile strength of 510 MPa.
Tensile tests on the bars obtained from the structural elements supplied the following values: average yield strength fy = 489 MPa, average tensile strength ft = 534 MPa, and the yield strength being rather high, with elongation at failure of about 20%. Figure 6 shows the stress–strain diagram of three tensile tests that overlapped very well but showed a conventional yield strength not clearly indicated by the curves and determined based on the deformation at the elastic limit according to ISO 6892 [26].

Figure 6.
Tensile tests on hanger bars. Stress–strain diagrams. (Colours are adopted for the three different samples).
The Brinell hardness tests provided an average hardness value of HB = 202 for the hanger bars and HB = 178 for the tensioner piece, in agreement with what was expected, the correlation coefficient between hardness and failure strength being around 3.
3.3. Load Test
The tensioner was placed in the Galdabini Quasar 600 tensile testing machine with 600 kN capacity and subjected to a maximum tension of 570 kN. The instrumentation used is described below.
- (1)
- The load was determined through the machine load cell.
- (2)
- The absolute and relative displacements were determined through six potentiometric transducers Gefran model PY-2-C-010 with precision 0.001 mm; in particular, the following was measured:
- -
- Transducer T1: fixed in the upper hanger bar in contrast with the upper head of the tensioner.
- -
- Transducer T2: fixed in the upper hanger bar in contrast with the load head of the test machine.
- -
- Transducer T3: fixed at the top of the tensioner in contrast with the load head of the test machine.
- -
- Transducer T4: fixed in the lower hanger in contrast with the upper head of the tensioner.
- -
- Transducer T5: fixed in the lower hanger in contrast with the load head of the test machine.
- -
- Transducer T6: fixed at the bottom of the tensioner in contrast with the load head of the test machine.
In this way, it was possible to clean the displacements read of the movements of the mouths of the machine and to obtain the relative displacements of all the parts.
- (3)
- The strains were determined through strain gauges (length 10 mm) placed with the same alignment at the centre of the lower and upper hanger bars (SG1 and SG3, respectively) and at the centre of the tensioner (SG2).
The test setup is shown in Figure 7.

Figure 7.
Test-setup. (a) Schematic layout (Ti transducers, SGi strain gauges); (b) picture of the piece on the machine.
The test piece was positioned vertically in the test machine by tightening the two bar extensions within the grab plates. Once all instruments were positioned, a clamping load (preload) at 20 kN was applied to settle the test system. The test was conducted, for successive steps of 100 kN, up to the maximum load of 300 kN for the first load cycle and up to 570 kN for the second cycle. The load speed was set at 1 kN/s, while the tightening to the target value of the load was reduced to 0.5 kN/s. Once the target value was reached, the constant load was maintained for 90 s, in order to obtain the stabilization of the measurements. The unloading phase was performed at a speed of 2 kN/s. Throughout the test, displacements and deformations were detected on the measuring instruments. At the end of the first cycle, the displacement/strain sensors were reset to zero. The entire sequence of pre-load and final load was repeated three times.
The results of the tests performed are summarized in Figure 8, where the load–displacement graphs are reported for the six transducers (Figure 8a), and the load–strain diagram is reported for the three strain gauges (Figure 8b).
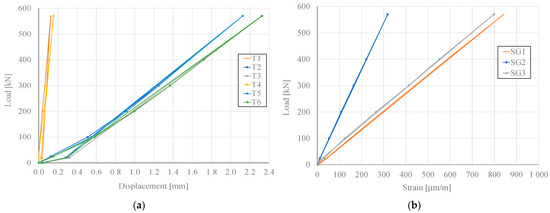
Figure 8.
Tensile test results. (a) Load–displacement graphs of transducers; (b) load–strain graphs of strain gauges.
It is worth noting that the transducers placed in the upper and lower parts of the sample behaved in the same way with curves almost completely overlapping; the same occurred for the strain trends, with increasing loads that were fully compatible with the measurements of the relative displacements. The difference between elastic deformation and relative displacements of the hanger and tensioner faces was assumed as the system slip to the upper and lower threads. The maximum slip values recorded at the threads was 0.07 mm in the upper one and 0.048 mm in the lower one, as can be seen in Figure 9.

Figure 9.
Tensile test results. Load–slip diagrams at the top and bottom threads.
By considering the displacements at the maximum load, the total slip is about the 2% of the total displacement between the prototype ends, which can be considered fully acceptable. The evaluation of slip and the keeping of this value within acceptable limits is of fundamental importance, since the sudden loss of tension at the time of prestressing depends on this value; the greater the intertwining slip between the threaded bar and the tensioner, the greater the loss of stress is together with a less effective distortion. In the stressing operation, the tension of the bar takes place through the turn of the tensioner and then the measure of slip associated with maximum tension must be correlated with the distortion imposed, as will be seen in the following.
3.4. Prestressing Test
The second part of prototype testing consisted of tensioning tests of the hanger maintaining the two ends anchored to the machine crossbeams, to measure the load induced in the hangers by turning the tensioner by means of a mechanical key (clamping wrench). This evaluation is necessary because on-site, it must operate through manual tensioning, so it is necessary to know the torque to give to the tensioner and the effect in terms of induced distortion.
Figure 10 shows the test setup. The load was recorded by the load cell of the machine and the three strain gauges were maintained operative during the entire sequence of tensioning. The test was carried out with five steps of the tensioner rotation, corresponding to five load values and strain measures read on the equipment.

Figure 10.
Tensioning tests. (a) Graduated area on the tensioner; (b) first test with rotation obtained by a universal wrench; (c) tensioning test carried out through a rigid specially manufactured wrench.
Figure 11 shows the load–strain graph of the four tests carried out, each performed at a different pre-load level: 0, 5, 10, and 20 kN. The test was performed up to a maximum possible load level of about 65 kN, depending on the length of the clamping wrench and the operator’s capacity for manual tensioning with this wrench. The arm of the wrench for the on-site operation was calculated from these evaluations for the maximum expected torque.
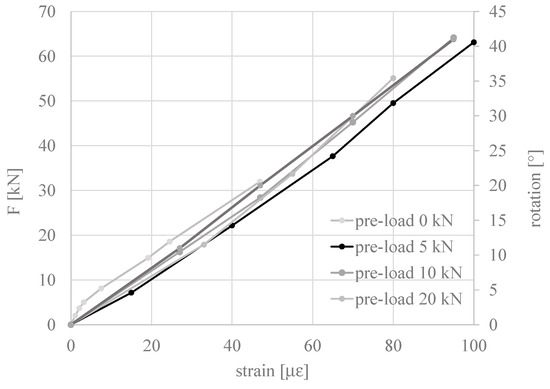
Figure 11.
Tensioning test results. Load–strain graphs of the four tests. The corresponding rotation of the tensioner is reported in the additional right vertical axis.
From the figure, it is evident that all the curves are almost overlapping, demonstrating that with the same turn of the tensioner, the load and the consequent strain in the three elements are comparable regardless of the applied preload. Small variations are due to the impossibility of keeping the extremes perfectly fixed due to the natural movements of the mechanical elements of the equipment. The trend is linear, and the stress reached in the hanger is about one-third of the average value needed during the stressing phases on the construction site. When tension is released, a perfect elastic behaviour is registered.
4. Interpretation and Discussion of Results
The tensile tests of the tensioner and hanger assembly were carried out up to a load greater than the one predicted for the most stressed hanger in the Service Limit State, considered as the irreversible condition. It corresponds to the stress value induced by all dead loads and the maximum traffic load value provided by Eurocode 1 for this type of bridge, which is the same used for the final load testing of the structure. This made it possible, first of all, to check whether the threads were damaged after the test and whether there was a slip and a consequent stress loss. The test was repeated three times and showed fully acceptable results for practical application on-site, with a maximum slip of 0.07 mm at maximum load (570 kN), which corresponds to less than 2% of the hanger’s elastic deformation under that load.
The tensioning tests, on the other hand, made it possible to establish the feasibility of the manual stressing operation and correlated the tensioner turn to the stress induced by the tensioner and to the resulting elastic deformation. The tests, carried out at different preload values, showed that the distortion Δi, which was to be introduced into the real hanger through the shortening imposed on the bar by the tensioner rotation, provided the required tension Fi in the hanger. The evaluation of the operator’s hand ability and the load reached also made it possible to create a new wrench of greater length to be used on-site by two or four operators, in order to achieve the maximum load required for hanger prestressing.
The tests also showed that, although it was possible to obtain the desired result of hanger prestressing, the initial state of the tensioner would not be known a priori in the phases of construction works, and this makes the evaluation of the total tensioner rotation difficult, because there is a rotation needed to give the pretension value and, afterwards, the rotation related to the actual distortion. The first rate of tensioner rotation depends on the installation conditions of the new hanger. For this reason, it is not possible to determine the stress induced in the hanger on-site by the mechanical action of the clamping wrench only, without the direct measurement of the tensile force induced on the hanger bar. To this aim, therefore, the test confirmed the judgment that continuous strain monitoring during the stressing phases was necessary on-site, because the measurements of the imposed shortening and of the tensioner turn would not have been sufficient by themselves to assess the goodness of the result due to the uncertainties related to the initial state of the hanger assembly. Consequently, as will be seen in the following section, the operations were afterwards conducted by direct measurement of strains in the stressing phase, leaving the measurement of the turnaround of the tensioner as a confirmation of the final result, starting from a minimum prestress level that ensured an initial state in which the hanger was well-aligned between arch and deck, with a minimum preload of about 10 kN.
5. On-Site Validation and Stressing Operations
During the stressing operations, a wrench of sufficient length was used to provide the correct lever arm and allow operators to provide the turnaround of the tensioner required in the project to introduce the distortion in the hanger. Strain gauges were applied to the hanger bar and the measures were carried out through a portable control unit connected to strain gauges. In addition to the hanger to be prestressed, the two adjacent hangers were monitored too. The sequence of operations was as follows:
- -
- Assembling of the hanger between the two hinged ends, connecting it to the arch and deck and inline placement of hanger bar in its own plane. Installation of strain gauges.
- -
- Achievement of preload and setting to zero the measurement of strain gauges. First pre-tensioning phase up to a value of strain equal to half of that foreseen in the project, turn of the tensioner, and measurement of the hanger strain. Waiting for measurement stabilization.
- -
- Afterward, the hanger was unloaded up to the zero value of deformation by a reverse turn of the tensioner.
- -
- Recovery of the preload value and new stressing phase until the design value was reached; turn of the tensioner and measurement of the hanger strain. Measurement stabilization, stress calculation, and comparison with the tensioner rotation value. Measurement of strains in the adjacent hangers.
- -
- End of monitoring and preparation for replacement operations of the next hanger.
Figure 12 shows some phases of hanger replacement: cutting and on-site stressing.

Figure 12.
Replacement of hangers. (a) Cutting of old hangers; (b) and (c) tensioning phases on-site of new hangers.
Figure 13a shows the result of stressing phase monitoring through the strain gauges of a hanger, where the curves show the tensile strain of the new hanger and the unloading of the hangers next to it. In this way, it was possible to register the entire tensioning phase and the mutual effects of the tensioning stages on the old hangers still present and on the new ones already installed.

Figure 13.
Monitoring of stressing stages. (a) Strain; (b) axial force.
The positive strain values are related to the tensile stress induced by the stressing operation, while the negative ones are related to the shortening of the adjacent hangers. The jumps that can be seen in the diagram are the stressing phases, which are the loading steps with the partial rotations induced by the operators at each movement of the wrench. The value clearly stabilizes at the end, and the stressing stage occurs in about 10 min from the achievement of the preload and the initial zeroing of the deformation value to the attainment of the design value. Figure 13b shows the same graph in terms of axial force N induced in the new prestressed hanger and the relaxation forces in the adjacent ones (obtained by knowing the elastic modulus of steel and the cross-section area of the bar).
This operation, repeated 46 times on the hangers removed and replaced, was possible thanks to the preliminary tests seen in the previous sections. These results provided both the proof of the final stressing value imposed by the threads and the proof of the goodness of the stressing operations to be carried out on-site through the clamping wrench together with the evaluation of the tensioner turnaround.
Table 1 gives the value of distortion Δi and the related axial forces induced in the new hangers at the end of the sequence.

Table 1.
Values of distortion and axial forces for the hangers.
The final validation of the tensile force in the hanger was operated through dynamic tests. The hangers were investigated by means of three accelerometers located at 1/6, 2/6 and 3/6 of the length in the perpendicular direction to the arch plane (transverse y direction) for identifying the modal shape and frequencies. The impulse was given through a hammer. Figure 14 shows pictures of the test.

Figure 14.
Dynamic tests for validation of stressing operations.
The dynamic behaviour of the hanger made of rigid bars shows the equal importance of the bending force (typical of beams) and the axial force (typical of tie rods) because it is a rigid bar with a diameter of 70 mm. The usual equations of the beam or vibrating string cannot be applied, since the frequencies depend on the flexural inertia and the axial force at the same time.
The fourth-order differential equation governing the problem of the dynamics of elements having both bending and axial stiffness and subjected to a significant axial force [27,28] is the following:
where ρ is the radius of inertia, μ is the mass per unit of volume, A is the cross-section area, μA is the mass per unit length, E is the elastic modulus, and N the value of the axial force.
Since the numerical solution of Equation (4) and the identification of the eigenvalues are rather complex [29], approximate solutions have been developed in the literature, for which the jth modal frequency is given by the following relationship [30]:
where L is the length of the element.
Equation (5) can be used in two ways: when the frequency is unknown for a fixed value of axial force N, it gives the value of frequency expected from the design value of forces; when, instead, N is obtained from a known value of frequency, it is possible to check the axial force which actually stresses the hanger from the on-site measurement of the hanger frequency. Regarding the identification of eigenvalues, useful references are reported in [31,32].
The results (Table 2) showed good agreement between the measured values of the frequencies and the expected axial force at the end of the stressing operations, with scatter within 10% and an average deviation of 5.6%, considering the target values of design in the replacement intervention. These values do not coincide with those found on-site in the existing bridge and with those of the original design, but it was decided to give higher prestress to the central hangers, in order to provide a little rise to the bridge at the midspan, compared to the side areas near the abutments, additional to the geometric camber of construction. This improves the bridge behaviour by increasing the stiffness in the central area, which is subject to the maximum deflections for traffic loads. Moreover, during the replacement operations, it has been observed that hangers n. 9 (at the quarters of the deck girders) had an excessive and unexpected relaxation of the hanger, which was probably not loaded properly during the construction stage when the temporary pier was removed.

Table 2.
Values of measured forces through dynamic tests.
6. Conclusions
Tests conducted on a prototype of a tensioner for bridge hangers consisting of round rigid bars were presented for the evaluation of the effectiveness of stress transfer through the hanger to the arch and deck of the bridge during the operation of replacing damaged hangers for maintenance. The need to carry out such tests derives from the fact that the replacement of the damaged hangers of a bridge with rigid bars, rigidly connected to the extremes via simple welding to the arch and the deck girder, involves the design and implementation of a new suspension system that restores the original condition of the bridge after cutting the old bars and replacing them with new bars. The introduction of prestressing depends therefore on the presence of a new steel component inside the bar that induces the imposed distortion, which is of a tensioner.
Tensile tests were carried out up to loads corresponding to the most severe working conditions for the evaluation of the hanger and tensioner system strength and the determination of any sliding in the threads during the stressing operations. In addition, prestressing tests were carried out by rotating the tensioner using a manual wrench, and the load values and deformations proportional to the tensioner turnaround were measured. The results show very limited values of slippage in the thread at the maximum tension load, which is about the 2% of the total elongation; the results also show the reliability of the new pieces designed for establishing the design value of prestressing and final axial forces in the hangers of the new suspension system. Load and pretension tests made it possible to verify the good efficiency of the tensioner in providing the required tension and to apply the necessary distortion to the hanger, according to the design expectations. It was also possible to evaluate how to proceed for the monitoring of the stressing sequence during on-site work and to test the operating modes of the tensioning phase in the hanger replacement operations.
Afterwards, on-site measurements during the stressing sequence and comparison with the experimental results allow engineers to apply the expected distortions to each replaced hanger. The verification of the assumptions made and of the effectiveness of tensioning phases was provided through the on-site monitoring of strains for cutting and stressing operations during each replacement; furthermore, dynamic tests were conducted at the ends for checking that the expected axial forces in the design have effectively been applied to the new suspension system through the turnaround of the tensioner. The results were in good accordance with the design values, showing an average deviation of 5.6% respect to the target axial force.
Author Contributions
Conceptualization, M.F.G. and B.F.; methodology, M.F.G., B.F. and M.R.; validation, M.F.G., B.F., M.R. and G.C.; formal analysis, M.F.G. and G.C.; investigation, M.F.G. and M.R.; data curation, M.R. and G.C.; writing—original draft preparation, M.F.G. and M.R.; writing—review and editing, M.F.G., B.F. and G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The on-site construction works were funded by the Libero Consorzio Comunale of Trapani, Sicily, Italy.
Data Availability Statement
Data are available from the author on reasonable request.
Acknowledgments
Acknowledgement is due to the Owner of the case-study bridge, Libero Consorzio Comunale di Trapani (Sicily, Italy), to the staff of ICARO PROGETTI Engineering and Architecture, Geotec snc Laboratory in Palermo and to the firm Metalwood srl.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fernández Troyano, L. Bridge Engineering: A global Perspective; Thomas Telford: London, UK, 2003. [Google Scholar]
- Granata, M.F.; Arici, M.; Longo, G.; Recupero, A. Steel and composite tied-arch bridges: A conceptual approach to structural design. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2021; Volume 174, pp. 281–298, ISSN 1478-4637. [Google Scholar] [CrossRef]
- Lan, R.; Jiang, G.; Wang, H.; Hao, T.; Wang, L.; Liang, Q. Research on the Suspender Replacement Process of Arch Bridge Based on the Measured Displacement Correction. IEEE Access 2020, 8, 226952. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Zhuo, X.; Huang, K.; Wang, X.; Wang, W. Study on the Precise Displacement Controlling Method for a Suspended Deck in the Hanger Replacement Process of an Arch Bridge. Appl. Sci. 2021, 11, 9607. [Google Scholar] [CrossRef]
- Sun, Z.; Ning, S.; Shen, Y. Failure investigation and replacement implementation of short suspenders in a suspension bridge. J. Bridge Eng. 2017, 22, 05017007. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Z.; Yao, Y. Hanger replacement and corrosion assessment in a suspension bridge. Structures 2023, 58, 105501. [Google Scholar] [CrossRef]
- Wu, W.; Wang, H.; Zhu, Y.; Yu, J.; Zhao, H.; Zhang, H. New Hanger Design Approach of Tied-Arch Bridge to Enhance Its Robustness. KSCE J. Civ. Eng. 2018, 22, 4547–4554. [Google Scholar] [CrossRef]
- Hayashi, T.; Ishiyama, K.; Watanabe, F.; Kumagai, Y.; Asai, H. Renewal of concrete Lohse arch bridge. Bridge Found. Eng. 2010, 44, 49–55. [Google Scholar]
- Hayashi, T.; Fujiwara, Y.; Kumagai, Y.; Asai, H.; Ishiyama, K. Rehabilitation of an old Concrete Lohse Arch Bridge: Replacement of all hangers. In Proceedings of the Third International Conference on Sustainable Construction Materials and Technologies, Kyoto, Japan, 18–21 August 2013; Kyoto Research Park: Kyoto, Japan, 2013. [Google Scholar]
- Martin, B.; Blabac, B.A. Replacing the suspender ropes of a tied arch bridge using suspension bridge methods. In Proceedings of the 25th US-Japan Bridge Engineering Workshop, Tsukuba, Japan, 19–21 October 2009; Public Works Research Institute (PWRI): Tsukuba, Japan, 2009. [Google Scholar]
- Modano, M.; Majumder, A.; Santos, F.; Luciano, R.; Fraternali, F. Fast and Optimized Calculation of the Cable Pretension Forces in Arch Bridges With Suspended Deck. Front. Built Environ. 2020, 6, 114. [Google Scholar] [CrossRef]
- Tan, Y.; Yao, Y. Optimization of hanger arrangement in pedestrian tied arch bridge with sparse hanger system. Adv. Struct. Eng. 2019, 22, 2594–2604. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, T.; Chen, L.; Lu, Z.; Hu, X.; Huang, X. Experimental Testing and Residual Performance Evaluation of Existing Hangers with Steel Pipe Protection Taken from an In-Service Tied-Arch Bridge. Appl. Sci. 2023, 13, 11070. [Google Scholar] [CrossRef]
- Fan, B.-H.; Su, J.-Z.; Chen, B.-C. Condition evaluation for through and half-through arch bridges considering robustness of suspended deck systems. Adv. Struct. Eng. 2021, 24, 962–976. [Google Scholar] [CrossRef]
- Berthellemy, J. Evaluation regarding fatigue for various type of hangers used for tied arch bridges. Procedia Eng. 2018, 213, 426–436. [Google Scholar] [CrossRef]
- Liang, H.; Tan, K.; Deng, K.; Zhang, Y.; Zhao, C.; Yang, T. Crack resistance of steel-concrete hybrid joint between concrete girder and steel-concrete composite girder in long-span cable-stayed bridge under hogging moment. J. Bridge Eng. 2023, 28, 05022013. [Google Scholar] [CrossRef]
- Granata, M.F. Effects of corrosion on a steel bowstring bridge in marine environment: A case-study of assessment and retrofit. Bridge Struct. 2020, 16, 121–137. [Google Scholar] [CrossRef]
- Granata, M.F. Stressing Sequence for Hanger Replacement of Tied-Arch Bridges with Rigid Bars. J. Bridge Eng. ASCE 2022, 27, 04021099. [Google Scholar] [CrossRef]
- Chen, D.W.; Au, F.T.K.; Tham, L.G.; Lee, P.K.K. Determination of initial cable forces in prestressed concrete cable-stayed bridges for given design deck profiles using the force equilibrium method. Comput. Struct. 2000, 74, 1–9. [Google Scholar] [CrossRef]
- Martins, A.M.B.; Simões, L.M.C.; Negrão, J.H.J.O. Optimization of cable forces on concrete cable-stayed bridges including geometrical nonlinearities. Comput. Struct. 2015, 155, 18–27. [Google Scholar] [CrossRef]
- Granata, M.F.; Longo, G.; Recupero, A.; Arici, M. Construction sequence analysis of long-span cable-stayed bridges. Eng. Struct. 2018, 174, 267–281. [Google Scholar] [CrossRef]
- Recupero, A.; Granata, M.F. A mixed approach for determination of initial cable forces in cable-stayed bridges and the parameters variability. Balt. J. Road Bridge Eng. 2015, 10, 141–150, ISSN 1822-427X. [Google Scholar] [CrossRef]
- Granata, M.F.; Margiotta, P.; Arici, M.; Recupero, A. Construction stages of cable-stayed bridges with composite deck. Bridge Struct. 2012, 8, 93–106, ISSN 1573-2487. [Google Scholar] [CrossRef]
- EN 1991-2; Traffic Loads on Bridges, Part 2. Eurocode 1. European Committee for Standardization CEN: Brussels, Belgium, 2005.
- DM 17/01/2018; Norme Tecniche per le Costruzioni. Italian Ministry of Infrastructures: Rome, Italy, 2018. (In Italian)
- ISO 6892-1:2019; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. International Standard Organization (ISO): Geneva, Switzerland, 2019; 78p.
- Clough, R.W.; Penzien, J. Dynamics of Structures, 2nd ed.; McGraw Hill: New York, NY, USA, 1993; ISBN 0-07-011394-7. [Google Scholar]
- Gatti, P.L.; Ferrari, V. Applied Structural and Mechanical Vibrations: Theory, Methods and Measuring Instrumentation; Taylor and Francis: Abingdon, UK, 1999; ISBN 0-419-22710-5. [Google Scholar]
- Lagomarsino, S.; Calderini, C. The dynamical identification of the tensile force in ancient tie-rods. Eng. Struct. 2005, 27, 846–856. [Google Scholar] [CrossRef]
- Graff, K. Wave Motion in Elastic Solids; Cover Publications Inc.: Tampa, FL, USA, 1991; ISBN 0-486-66745-6. [Google Scholar]
- Karimov, A.I.; Kopets, E.; Nepomuceno, E.G.; Butusov, D.C. Integrate-and-Differentiate Approach to Nonlinear System Identification. Mathematics 2021, 9, 2999. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Pearson College Div.: London, UK, 2011; 944p, ISBN 9780132858038. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).