Abstract
In order to address the Multi-Objective Optimization Problem (MOOP) in building a two-stage helical gearbox, this work presents a novel application of the Multi-Criterion Decision-Making (MCDM) method. The aim of the study is to determine the optimal primary design factors that will increase gearbox efficiency while decreasing gearbox volume. Three main design parameters were chosen for assessment in this work: the first stage’s gear ratio, and the first and second stages’ Coefficients of Wheel Face Width (CWFW). In addition, the MOOP is divided into two phases: phase 1 solves the single-objective optimization problem to reduce the gap between variable levels, and phase 2 solves the MOOP to determine the optimal primary design factors. Furthermore, the Entropy approach was picked to compute the weight criteria, and the MARCOS method was chosen as an MCDM method to handle the multi-objective optimization issue. The following are important characteristics of the study: Firstly, the MCDM method (MARCOS technique) was successfully applied to solve a MOOP for the first time. Secondly, this work has looked into power losses during idle motion to calculate the efficiency of a two-stage helical gearbox. The results of the study were used in the design of a two-stage helical gearbox in order to identify the optimal values for three important design parameters.
1. Introduction
Industrial applications frequently utilize helical gearboxes because of their low cost, minimal complexity, and ease of design and manufacture. Therefore, many scientists have been interested in finding the best design for helical gearboxes.
Numerous studies on single- and multi-objective optimization for helical gearboxes have been conducted up to this point. The optimization problem for helical gearboxes has been approached for several single-objective functions, including minimum gear mass [1,2], minimum gear volume [2,3,4], minimum gearbox mass [1,5], minimum gearbox length [6,7], minimum gearbox across section area [8,9], minimum gearbox cost [10,11,12], and so on. The single-objective helical gearbox optimization problem has been solved by many different methods such as particle swarm optimization [4], Matlab optimization tool box [2], the direct search method [5,13,14] etc. Also, for helical gearboxes with several stages, such as one [4,14], two [6,9], three [12,15], and four stages [1,16], single-objective optimal design has also been addressed.
With various single objectives, the MOOP has been resolved. The lowest gearbox power loss overall and the lowest gearbox volume were examined in [17]. In order to lower both the gearing mass and the flank adhesive wear speed, the authors in [18] conducted optimization research. In [19], two single targets were selected: the maximum gear stress and the minimum gear mass. The multi-objective optimization solutions in [20] have enhanced the transmission error signal’s root mean square values as well as its maximal contact pressures. Implemented in [21] is the multi-objective optimization issue of choosing the best gear material for a helical gearbox to maximize surface fatigue and increase wear resistance. The optimal major design factor for maximizing gearbox efficiency and decreasing gearbox mass was identified in [13]. Besides this, MOOPs have also been solved using a variety of techniques, including the response surface methods [22], the PSO (particle swarm optimization) method [18], the NSGA-II method [17,18], the NSGA-II and the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) methods [23], Grey Relation Analysis (GRA) and the Taguchi technique [13], etc. Recently, a genetic algorithm was used in [24] to solve a macro-geometry gear design optimization problem with two objective functions—gear mesh stiffness and dynamic behavior—in order to determine the optimal strategy for achieving a minimal amount of dynamic excitation. A computationally efficient and effective gear design optimization approach is provided based on the obtained results. A new framework for precise reliability analysis has been set out in [25]; it is predicated on employing metaheuristic algorithms to enhance the directional simulation. With the new improved version, the unit vector of direction is determined through the use of metaheuristic methods and expressed as a constrained optimization problem using the Harris Hawks Optimization technique. The suggested technique was compared to the performance of the first-order reliability method and six simulation-based reliability analysis methods. The outcomes demonstrate the enhanced directed simulation’s high performance capabilities in resolving extremely nonlinear engineering issues.
While helical gearbox multi-objective optimization has been extensively studied, the MCDM technique has not been used to find the optimal primary design parameters for these gearboxes. Moreover, the research indicated above did not account for the power loss that occurs when a gear is in an idle motion or when a gear is immersed in lubricant during bath lubrication. This paper presents the findings of a multi-objective optimization study conducted for a two-stage helical gearbox, with two specific objectives in mind: reducing gearbox volume and maximizing gearbox efficiency. The study looked at the first stage’s gear ratio and both stages’ CWFW as the three optimal primary design characteristics for the two-stage helical gearbox. Furthermore, the Entropy approach was utilized to determine the weights of the criteria, and the MARCOS method was chosen to handle the MOOP. One of the main conclusions of the research is the suggestion to apply an MCDM technique to tackle MOOPs in combination with two-step problem solving, tackling single- and multi-objective problems. In addition, the problem’s solutions are more effective than those of earlier studies. Moreover, the power losses incurred in idle motion have been added when calculating the efficiency of a two-stage helical gearbox.
2. Optimization Problem
In this part, the gearbox volume and efficiency are first calculated in order to build the optimization problem. Next, the specified objective functions and constraints are given. To facilitate calculations, the nomenclatures used in the optimization problem are presented in Table 1.

Table 1.
The nomenclatures for the optimization problem.
2.1. Calculation of Gearbox Volume
The volume of the gearbox can be calculated by (Figure 1):
where L, B1, and H are determined by [26]:
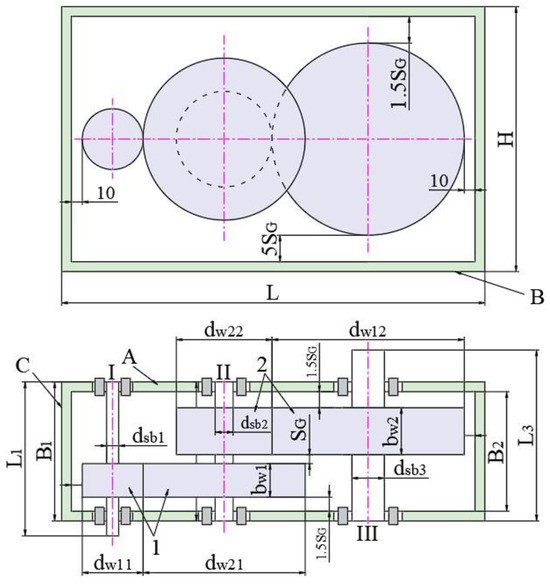
Figure 1.
Calculated schema.
In the above equations,
In Equations (6) to (9), is determined by [27]
In which
2.2. Calculation of Gearbox Efficiency
The efficiency of a two-stage helical gearbox (%) is determined by
In which Pl can be found by [28]
where Plg, Plb, Pls, and Pzo are determined in the following way.
Determination of Plg:
in which
can be calculated by [29]
while and can be found by [29]
In (16), f is calculated in the following way [13]:
- -
- If v ≤ 0.424 (m/s),
- -
- If v > 0.424 (m/s),
Determination of Plb [28]:
where i = 1 ÷ 6 and as the radical ball bearings with angular contact were used [28].
Determination of Ps [28]:
In which i is the ordinal number of the seal (i = 1 ÷ 2) and is calculated by
Determination of Pzo [28]:
In which k is the total number of gear pairs in the gearbox (k = 2); n is the number of revolutions of the driven gear; can be found by [28]
In (25), for stage 1 under the circumstance wherein the involved oil must pass the mesh, and for stage 2, is computed using the following equation (Figure 2):
where lhi is determined by [28]
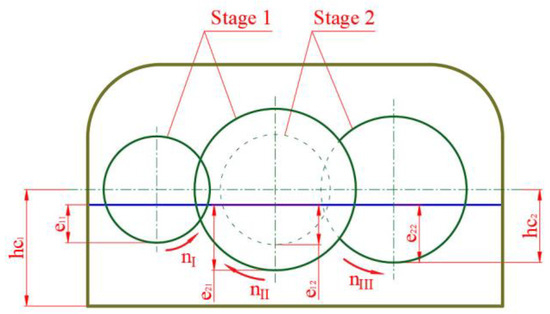
Figure 2.
Calculated schema of lubrication factors.
In (25), C1 and C2 are calculated by [28]
In which e0 = b0 = 10 (mm).
2.3. Multi-Objective Optimization Problem
In this work, the MOOP can be express as follows:
Here, two single objectives compose the MOOP:
- -
- Minimizing the gearbox volume—
- -
- Maximizing the gearbox efficiency—
The constraints that follow must be met by the multi-objective function
3. Methodology
3.1. Method to Solve the Multi-Objective Optimization
The multi-objective optimization issue with two objectives—minimum gearbox volume and highest gearbox efficiency—was described in Section 2. In addition, three primary design factors have been chosen to be variables in the optimization issue. Table 2 lists these variables along with their minimum and maximum values. In fact, applying an MCDM approach to the MOO (multi-objective optimization) problem is challenging. The reason for this is that there are numerous options or possible solutions available for MOO problems. Each of the parameters in this study have limits, as indicated in Table 2, and the step between variables is 0.02 to ensure parameter accuracy and prevent missing the optimization problem’s solution. In this instance, there are (runs) options (or experimental runs) that need to be identified and compared. Because of the wide range of options, it is not feasible to directly handle the OMO problem using the MCDM approach. In this paper, the MCDM problem was solved using the MARCOS method, and the criterion weights were determined using the Entropy approach. A simulation experiment was constructed in order to provide the input data for the MOOP for a two-stage helical gearbox in the MCDM problem. Since this is a simulation experiment, there is no restriction on the number of experiments that can be conducted by utilizing the full factorial design. Because there are three experimental variables (as previously specified) and five levels for each variable, the total number of experiments will be 53 = 125. However, u1, which runs from 1 to 9 in Table 2, has the broadest distribution of the three variables mentioned. As a result, even with five levels, there was still a significant disparity between the levels of this variable (in this case, ((9−1)/4 = 2). To reduce this disparity, save time, and improve the accuracy of the outcomes, a technique for solving multi-objective problems was proposed (Figure 3). This procedure is broken down into two phases: phase 1 factors reduce the gap between levels by solving the single-objective optimization problem, and phase 2 factors find the optimal primary design by solving the MOOP. Additionally, in the process of addressing the multi-objective problem, the MARCOS issue will be rerun using the smaller distance between two levels of variables if the levels of a variable are not sufficiently close to one another (≤0.02) (or the best answer is not appropriate for the requirement) (see Figure 3).

Table 2.
Input parameters.
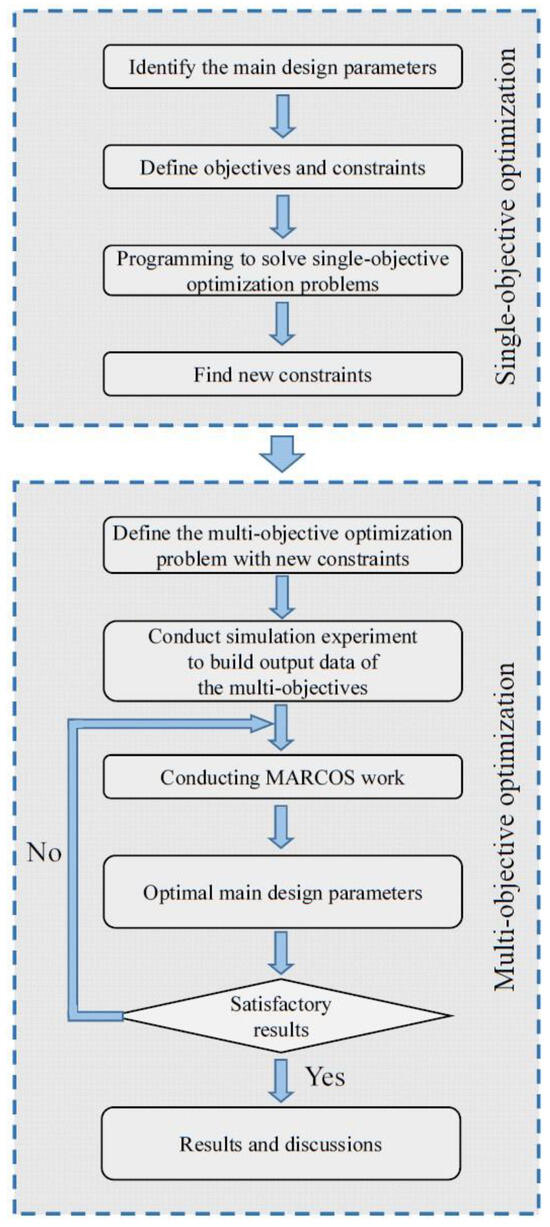
Figure 3.
The process for solving the multi-objective problem.
3.2. Method to Solve MCDM Problem
In this work, the MARCOS method was selected for solving the MCDM problem. To apply the MARCOS approach, the following steps must be taken [30]:
- -
- Making initial decision-making matrix
- -
- An extended initial matrix is produced by appending an ideal (AI) and anti-ideal solution (AAI) to the original decision-making matrix
Here, and if the requirement set with criterion j is as large as possible; and when criterion j is as small as possible; i = 1, 2, …, m; j = 1, 2,…, n;
- -
- One then normalizes the extended starting matrix (X). To calculate the normalized matrix , we use the following formula:
- -
- Determine the weighted normalized matrix by
- -
- Find the utility of alternatives Ki− and Ki+ by
In (42) and (43), Si (i = 1, 2, …, m) is the sum of the elements of the weighted matrix C, and Si is calculated by
- -
- Find the utility function f(Ki) of alternatives by
- -
- To determine which alternative has the highest utility function value, rank the options according to the final utility function values.
3.3. Method to Find the Weight of Criteria
In this paper, the entropy technique was used to establish the weights of the criteria. The actions listed below can be used to put this strategy into practice [31].
- -
- Finding indicator-normalized values,
- -
- Calculating the Entropy for each indicator,
- -
- Determining the weight of each indicator,
4. Single-Objective Optimization
In this study, the direct search strategy is used to solve the single-objective optimization problem. Moreover, a Matlab computer program has been created to address two single-objective issues: maximizing gearbox efficiency and minimizing gearbox volume. The following figures feature several of the program’s findings: In Figure 3, the connection between u1 and Vgb is shown. When u1 is at its optimal value, Vgb reaches its lowest value (Figure 4). Figure 5 shows the relationship between ηgb and u1. Furthermore, the optimal value of u1 at which ηgb achieves its maximum is depicted in Figure 5. Figure 6 and Figure 7 show the association of Xba1 and Xba2 with Vgb and ηgb, respectively. It can be seen that with an increase in Xba1, Vgb will decrease (Figure 6a). In contrast, Vgb will fall as Xba2 rises (Figure 7a). Additionally, as Xba1 and Xba2 rise, ηgb falls (Figure 6b and Figure 7b).
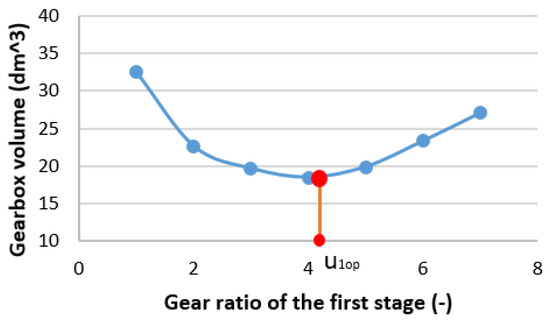
Figure 4.
Gearbox volume versus first stage gear ratio.
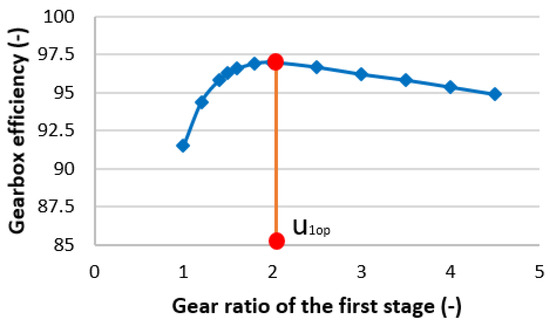
Figure 5.
Gearbox efficiency versus first stage gear ratio.
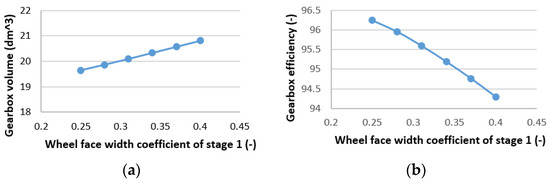
Figure 6.
Relation between Xba1 and gearbox volume (a) and gearbox efficiency (b).
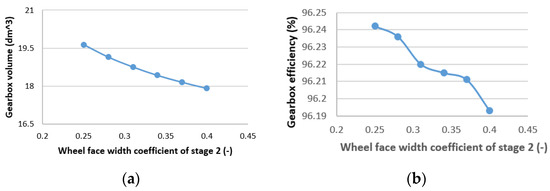
Figure 7.
Relation between Xba2 and gearbox volume (a) and gearbox efficiency (b).
The values of optimal major design factors of two single-objective functions, Vgb and ηgb, are shown in Table 3. From the table, it is clear that for the minimum Vgb, the minimum values of Xba1 and maximum values of Xba2 (Xba1 = 0.25 and Xba2 = 0.4) are the ideal values for Xba1 and Xba2. The reason for this is that the cross-section dimension (determined by H*L) must be small in order for Vgb to be tiny. Approximately equal values for dw21 and dw22 are required for this [32]. Given that the second stage gets a significantly greater torque than the first, aw2 will be significantly greater than aw1. Consequently, to make dw21 approximate, dw22 requires an increase in Xba2 to decrease aw2 and a decrease in Xba1 to increase aw1 (Formula (9)).

Table 3.
Optimum main design factors for minimum Vgb and maximum ηgb.
Figure 8 illustrates the relationship between the optimum gear ratio for the first stage (u1) and the overall gearbox ratio (ut). Additionally, Table 4 displays newly calculated constraints for the variable u1.
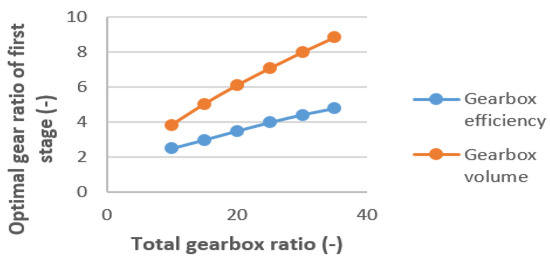
Figure 8.
Optimum gear ratio of the first stage versus total gearbox ratio.

Table 4.
New constraints of u1.
5. Multi-Objective Optimization
A computer program has been created to perform simulations. The gearbox ratios 10, 15, 20, 25, 30, and 35 were all considered for the analysis. For this problem, with ut = 15, the solutions is displayed below. This overall gearbox ratio was used for 125 initial testing runs (as specified in Section 3). The experiment’s output values, the gearbox volume and efficiency, will be sent into MARCOS as input parameters in order to solve the MOOP. This procedure will be repeated until there is less than 0.02 separating two levels of u1. The primary design parameters and output responses for ut = 15 in the fifth and final run of the MARCOS experiment are shown in Table 5 The criteria’s weights have been established using the Entropy technique (see Section 3.3), as follows: First, use Equation (48) to derive the normalized values of pij. Equation (49) is used to determine each indicator mej’s entropy value. Finally, use Equation (50) to find the weight of the criteria wj. The weights of Vgb and ηgb for the most recent MARCOS work run were determined to be 0.5565 and 0.4435, respectively. The MARCOS method’s multi-objective decision-making phases are outlined in Section 3.2. Specifically, they are as follows: Determine the ideal solution (AI) and the anti-ideal solution (AAI) using formula (36). The results show that, with AI, Vgb and ηgb were 17.21 (dm3) and 95.8 (%), and, with AAI, they were 20.1 (dm3) and 93.34 (%). The next step is to use Formulae (37) for Vgb and (39) for ηgb to derive the normalized values uij. The normalized values were then calculated using Formula (40), taking the weight cij into consideration. Moreover, the coefficients Ki- and Ki+ were obtained from Equations (42) and (43). The values of f(Ki−) and f(Ki+) were determined using Equations (46) and (47). It was found that f(Ki−) = 0.501 and f(Ki+) = 0.499. Lastly, the values of f(Ki) were computed using Formula (44). Table 6 displays the options’ ranking and the results of several parameters (for the last run of MARCOS work). Out of all the possibilities given, option 105 is the most ideal one, according to the table. Consequently, Table 5 shows the optimal values for the primary design features: u1 = 3.69, Xba1 = 0.25, and Xba2 = 0.4.

Table 5.
Main design parameters and output results for ut = 15 in the 5th run of MARCOS.

Table 6.
Several calculated results and rankings of alternatives by MARCOS for ut = 1.5.
Table 7 shows the optimal values for the main design parameters that correspond to the remaining ut values of 10, 20, 25, 30, and 35, building on the previous discussion. The information in Table 6 permits the following deductions to be drawn.

Table 7.
Optimum main design parameters.
Table 7 reveals that Xba1 selects the lowest value (Xba1 = 0.25), while Xba2 selects the highest value (Xba2 = 0.4). This is due to the fact that a small box’s cross-sectional area (LxH) is required to produce the smallest gearbox volume. In order to accomplish that, dw21 and dw22 must be about equal [32]. Additionally, because the second stage has a higher torque, a larger Xba2 is required in order to decrease the diameter of dw22. Conversely, a smaller Xba1 must be chosen in order to raise dw21 because the first stage has a lower torque.
The obtained values of the gearbox efficiency in this work were compared with the findings in [23] in order to evaluate the effectiveness in employing the formula for the power loss in the idle motion when calculating power loss in gears. Table 5 [23] shows that the gearbox efficiency, based on an input power of 10 kW, a maximum output power of 9.971 kW, and a minimum output power of 9.933 kW, will be between 99.33 and 99.71 percent when the overall gearbox ratio is 7.5. Furthermore, Table 4 indicates that the gearbox efficiency in this work will range from 93.258% to 95.963% when ut is increased from 10 to 35. Actually, a helical gear train’s efficiency is 0.93–0.98 (93–98%), whereas a pair of bearings’ efficiency is 0.99–0.995 (99–99.5%) [27]. The following formula will be used to calculate the efficiency of a two-stage helical gearbox based on these data:
From the above analysis, it is clear that the gearbox efficiency of this work (93.258–95.963%) is reasonably near to reality (83–95%), when comparing with that in [23]. Furthermore, the gearbox efficiency shown in [23] (99.33–99.71%) is dramatically high and incompatible with reality. This demonstrates that the power loss in idle motion formula used in this work is a useful new tool that needs to be used.
Figure 9 shows that there is a definite first-order link between the ideal values of u1 and ut. Additionally, it was found that the following regression equation (with R2 = 0.9804) may be used to calculate the optimal values of u1:
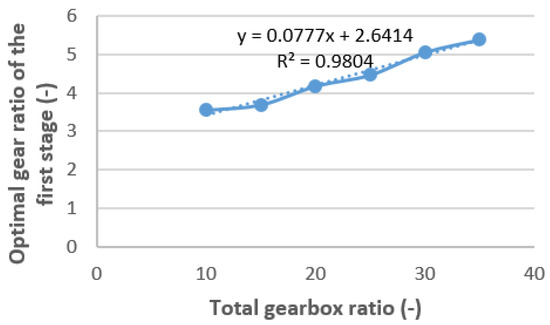
Figure 9.
Optimum gear ratio of the first stage versus total gearbox ratio.
Once u1 has been determined, the optimal value of u2 can be found using the following formula:
6. Conclusions
The MARCOS approach was utilized in this work to solve the MOOP related to the design of a two-stage helical gearbox. The study’s goal is to identify the best critical design factors that maximize gearbox efficiency while reducing gearbox volume. To do this, three essential design components were chosen: the CWFW for the first and second stages, and the first stage gear ratio. In addition, there are two steps in the MOOP solution process. Phase 1 is dedicated to solving the single-objective optimization problem of reducing the difference between variable values, whereas phase 2 is concerned with determining the optimal primary design factors. The following findings were drawn from this work:
- -
- The single-objective optimization problem speeds up and simplifies the resolution of the MOOP by bridging the gap between variable levels;
- -
- The three main design parameters for a two-stage helical gear gearbox, Equation (51) and Table 6, were recommended to have optimal values based on the study’s findings;
- -
- In regard to the important design characteristics, two single objectives—the minimal gearbox volume and the greatest gear-box efficiency—were assessed;
- -
- By using the MARCOS technique repeatedly until the desired results are reached, the MOOP can be solved more precisely (u1 has an accuracy of less than 0.02);
- -
- The experimental data’s extraordinary degree of concordance with the proposed model of u1 verifies their reliability;
- -
- Further research is required to determine how to apply the proposed approach for solving the MOOP for various domains and MCDM methods.
Author Contributions
The original idea was proposed by N.-P.V., and it was discussed by all the authors. With the help of T.-T.N., N.-P.V. handled the optimization problem and wrote the manuscript. Every author additionally contributed to the design of the simulation, the analysis of the experimental figures, and the interpretation of the experimental outcomes. N.-P.V. edited the manuscript with the help of T.-T.N. All authors have read and agreed to the published version of the manuscript.
Funding
This study obtained no outside funds.
Data Availability Statement
The data presented in this study are available in this article.
Acknowledgments
The authors would like to thank Thai Nguyen University of Technology for their support in this work.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Pi, V.N. Optimal determination of partial transmission ratios for four-step helical gearboxes with first and third step double gear-sets for minimal mass of gears. In Proceedings of the WSEAS International Conference on Applied Computing Conference, Istanbul, Turkey, 27–30 May 2008. [Google Scholar]
- Golabi, S.I.; Fesharaki, J.J.; Yazdipoor, M. Gear train optimization based on minimum volume/weight design. Mech. Mach. Theory 2014, 73, 197–217. [Google Scholar] [CrossRef]
- Rai, P.; Agrawal, A.; Saini, M.L.; Jodder, C.; Barman, A.G. Volume optimization of helical gear with profile shift using real coded genetic algorithm. Procedia Comput. Sci. 2018, 133, 718–724. [Google Scholar] [CrossRef]
- Tamboli, K.; Patel, S.; George, P.; Sanghvi, R. Optimal design of a heavy duty helical gear pair using particle swarm optimization technique. Procedia Technol. 2014, 14, 513–519. [Google Scholar] [CrossRef]
- Khai, D.Q.; Linh, N.H.; Danh, T.H.; Tan, T.M.; Cuong, N.M.; Hien, B.T.; Pi, V.N.; Dung, N.T.Q. Calculating Optimum Main Design Factors of a Two-Stage Helical Gearboxes for Minimum Gearbox Mass. In International Conference on Engineering Research and Applications; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Hung, L.X.; Hong, T.T.; Van Cuong, N.; Ky, L.H.; Thanh Tu, N.; Hong Cam, N.T.; Tuan, N.K.; Pi Vu, N. Calculation of optimum gear ratios of mechanical driven systems using two-stage helical gearbox with first stage double gear sets and chain drive. In Advances in Engineering Research and Application, Proceedings of the International Conference on Engineering Research and Applications, ICERA 2019, Thai Nguyen, Vietnam, 1–2 December 2019; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Van Cuong, N.; Le Hong, K.; Tran, T. Splitting total gear ratio of two-stage helical reducer with first-stage double gearsets for minimal reducer length. Int. J. Mech. Prod. Eng. Res. Dev. IJMPERD 2019, 9, 595–608. [Google Scholar]
- Pi, V.N.; Hong Came, N.T.; Hong, T.T.; Hung, L.X.; Tung, L.A.; Tuan, N.K.; Tham, H.T. Determination of optimum gear ratios of a two-stage helical gearbox with second stage double gear sets. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- Pi, V.N.; Hong, T.T.; Thao, T.T.P.; Tuan, N.K.; Hung, L.X.; Tung, L.A. Calculating optimum gear ratios of a two-stage helical reducer with first stage double gear sets. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- Danh, T.H.; Huy, T.Q.; Danh, B.T.; Tan, T.M.; Van Trang, N.; Tung, L.A. Determining Partial Gear Ratios of a Two-Stage Helical Gearbox with First Stage Double Gear Sets for Minimizing Total Gearbox Cost. In International Conference on Engineering Research and Applications; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Tuan, N.A.; Danh, B.T.; Lam, P.D.; Linh, N.H.; Quang, N.H.; Anh, L.H.; Ngoc, N.D.; Trang, N.V. Determining the Optimum Gear Ratios to Minimize the Cost of Two-Stage Helical Gearbox with Second-stage Double Gear Sets. J. Mech. Eng. Res. Dev. 2021, 44, 10–20. [Google Scholar]
- Vu, N.-P.; Nguyen, D.-N.; Luu, A.-T.; Tran, N.-G.; Tran, T.-H.; Nguyen, V.-C.; Bui, T.-D.; Nguyen, H.-L. The influence of main design parameters on the overall cost of a gearbox. Appl. Sci. 2020, 10, 2365. [Google Scholar] [CrossRef]
- Le, X.-H.; Vu, N.-P. Multi-objective optimization of a two-stage helical gearbox using taguchi method and grey relational analysis. Appl. Sci. 2023, 13, 7601. [Google Scholar] [CrossRef]
- Abuid, B.A.; Ameen, Y.M. Procedure for optimum design of a two-stage spur gear system. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2003, 46, 1582–1590. [Google Scholar] [CrossRef]
- Pi, V.N.; Tuan, N.K. Optimum determination of partial transmission ratios of three-step helical gearboxes for getting minimum cross section dimension. J. Environ. Sci. Eng. A 2016, 5, 570–573. [Google Scholar]
- Pi, V.N. Optimal calculation of partial transmission ratios for four-step helical gearboxes with first and third step double gear-sets for minimal gearbox length. In Proceedings of the American Conference on Applied Mathematics, Cambridge, MA, USA, 24–26 March 2008. [Google Scholar]
- Miler, D.; Zezelj, D.; Loncar, A.; Vuckovic, K. Multi-objective spur gear pair optimization focused on volume and efficiency. Mech. Mach. Theory 2018, 125, 185–195. [Google Scholar] [CrossRef]
- Tudose, L.; Buiga, O.; Jucan, D. Multi-objective optimization in helical gears design. In Proceedings of the Fifth International Symposium about Design in Mechanical Engineering-KOD, Novi Sad, Serbia, 15–16 April 2008. [Google Scholar]
- Wang, H.; Chen, D.; Pan, F.; Yu, D. Multi-objective Optimization Design of Helical Gear in Centrifugal Compressor Based on Response Surface Method. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Lagresle, C.; Guingand, M.; de Vaujany, J.-P.; Fulleringer, B. Optimization of tooth modifications for spur and helical gears using an adaptive multi-objective swarm algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 7292–7308. [Google Scholar] [CrossRef]
- Terán, C.V.; Martínez-Gómez, J.; Milla, J.C.L. Material selection through of multi-criteria decisions methods applied to a helical gearbox. Int. J. Math. Oper. Res. 2020, 17, 90–109. [Google Scholar] [CrossRef]
- Korta, J.A.; Mundo, D. Multi-objective micro-geometry optimization of gear tooth supported by response surface methodology. Mech. Mach. Theory 2017, 109, 278–295. [Google Scholar] [CrossRef]
- Maputi, E.S.; Arora, R. Multi-objective optimization of a 2-stage spur gearbox using NSGA-II and decision-making methods. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 477. [Google Scholar] [CrossRef]
- Marafona, J.D.; Carneiro, G.N.; Marques, P.M.; Martins, R.C.; António, C.C.; Seabra, J.H. Gear design optimization: Stiffness versus dynamics. Mech. Mach. Theory 2024, 191, 105503. [Google Scholar] [CrossRef]
- Meng, D.; Yang, H.; Yang, S.; Zhang, Y.; De Jesus, A.M.; Correia, J.; Fazeres-Ferradosa, T.; Macek, W.; Branco, R.; Zhu, S.-P. Kriging-assisted hybrid reliability design and optimization of offshore wind turbine support structure based on a portfolio allocation strategy. Ocean Eng. 2024, 295, 116842. [Google Scholar] [CrossRef]
- Römhild, I.; Linke, H. Gezielte Auslegung Von Zahnradgetrieben mit minimaler Masse auf der Basis neuer Berechnungsverfahren. Konstruktion 1992, 44, 229–236. [Google Scholar]
- Chat, T.; Van Uyen, L. Design and Calculation of Mechanical Transmissions Systems; Educational Republishing House: Hanoi, Vietnam, 2007; Volume 1. [Google Scholar]
- Jelaska, D.T. Gears and Gear Drives; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Buckingham, E. Analytical Mechanics of Gears; Courier Corporation: North Chelmsford, MA, USA, 1988. [Google Scholar]
- Stević, Ž.; Pamucar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Hieu, T.T.; Thao, N.X.; Thuy, L. Application of MOORA and COPRAS models to select materials for mushroom cultivation. Vietnam J. Agric. Sci. 2019, 17, 32–2331. [Google Scholar]
- Kudreavtev, V.N.; Gierzaves, I.A.; Glukharev, E.G. Design and Calculus of Gearboxes; Mashinostroenie Publishing: Sankt Petersburg, Russia, 1971. (In Russian) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).