Finite Element Analysis of Patient-Specific Cranial Implants under Different Design Parameters for Material Selection
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Identification
2.2. Design of the Patient-Specific Implant (PSI)
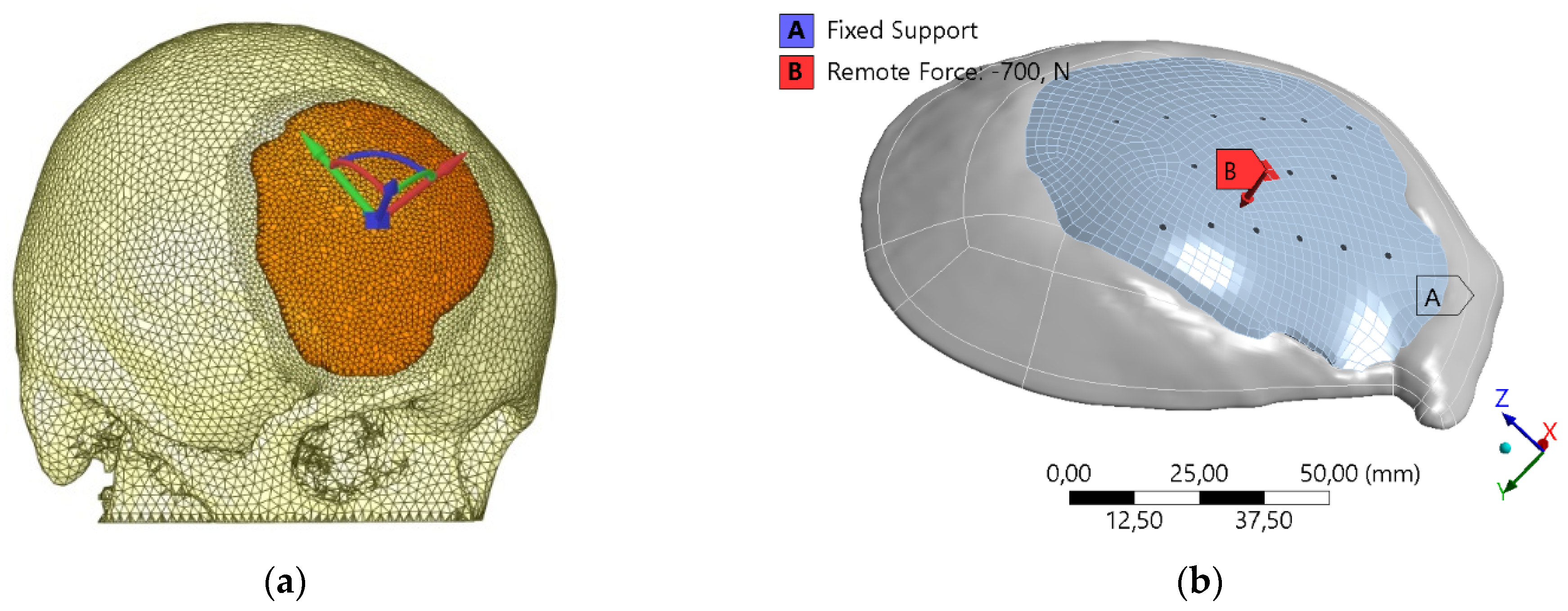
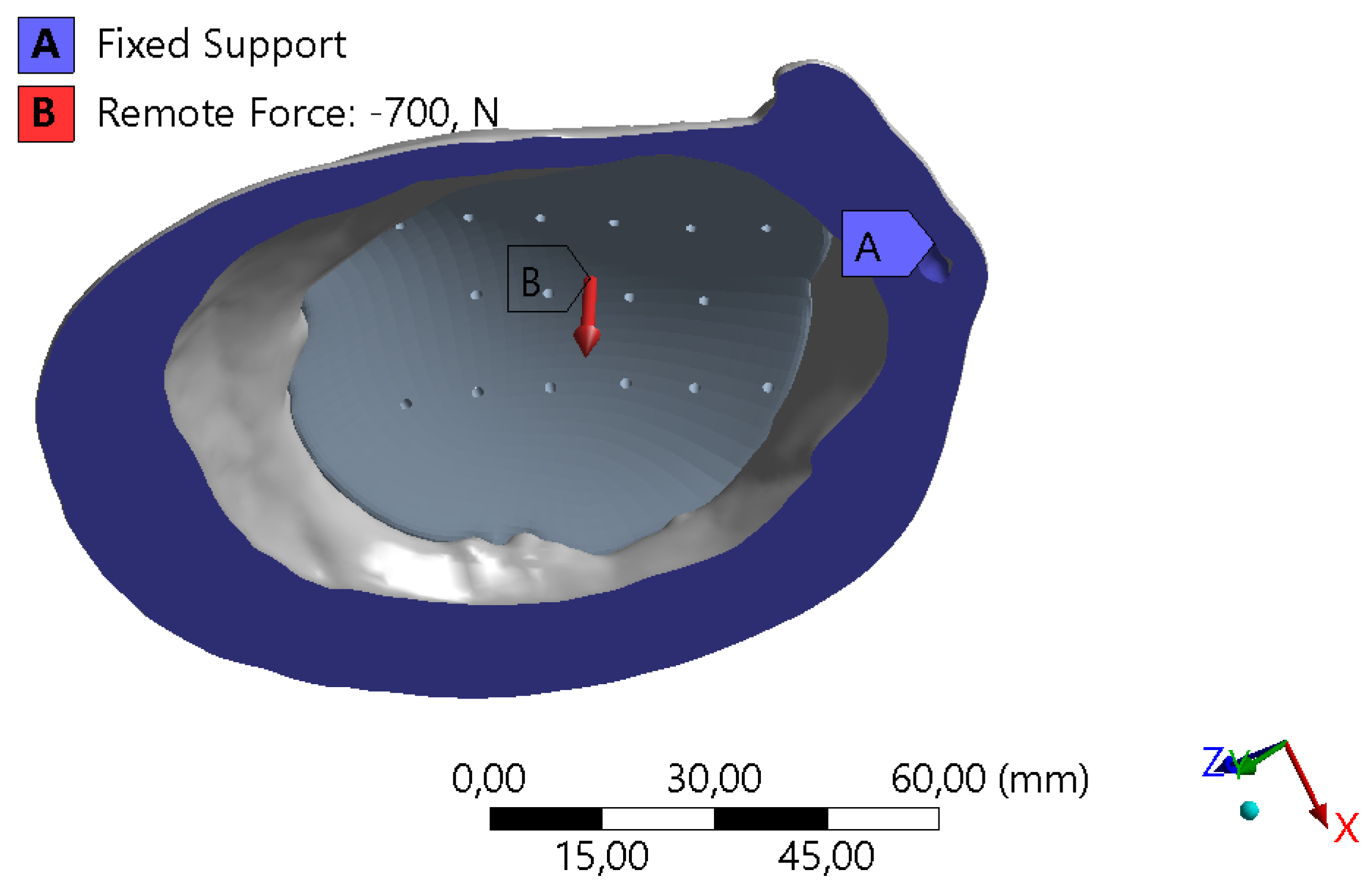
2.3. Finite Element Model
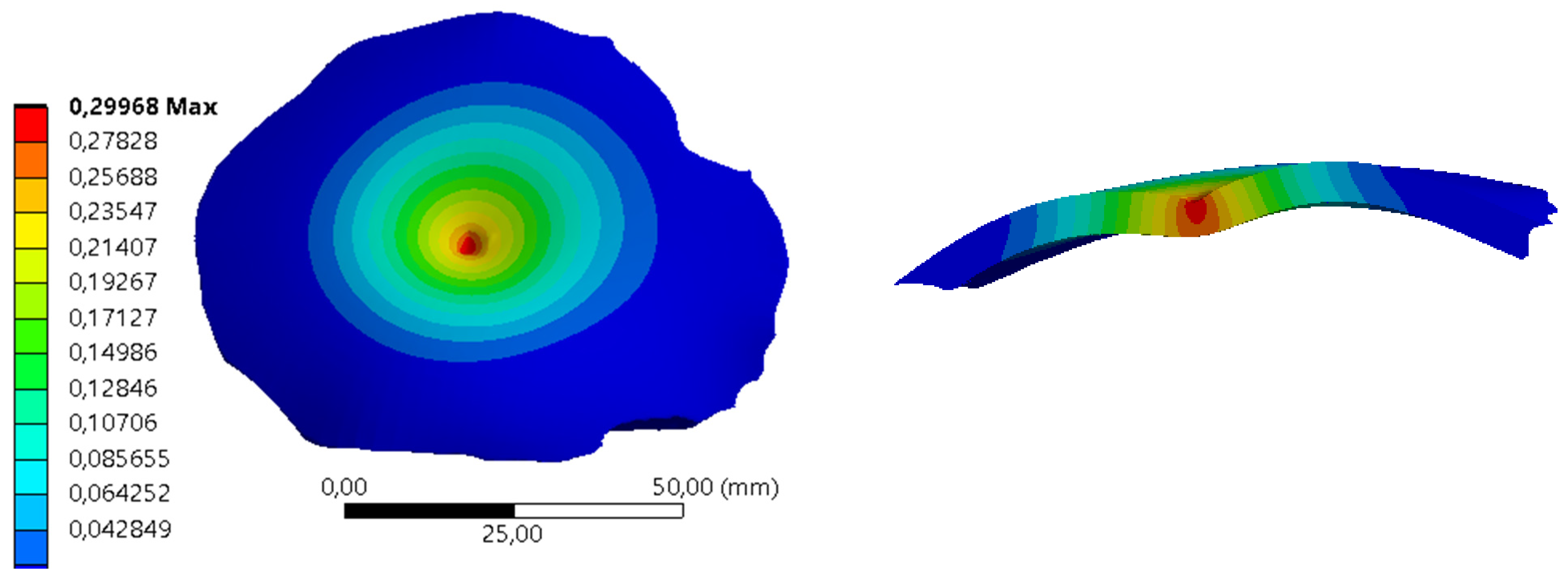
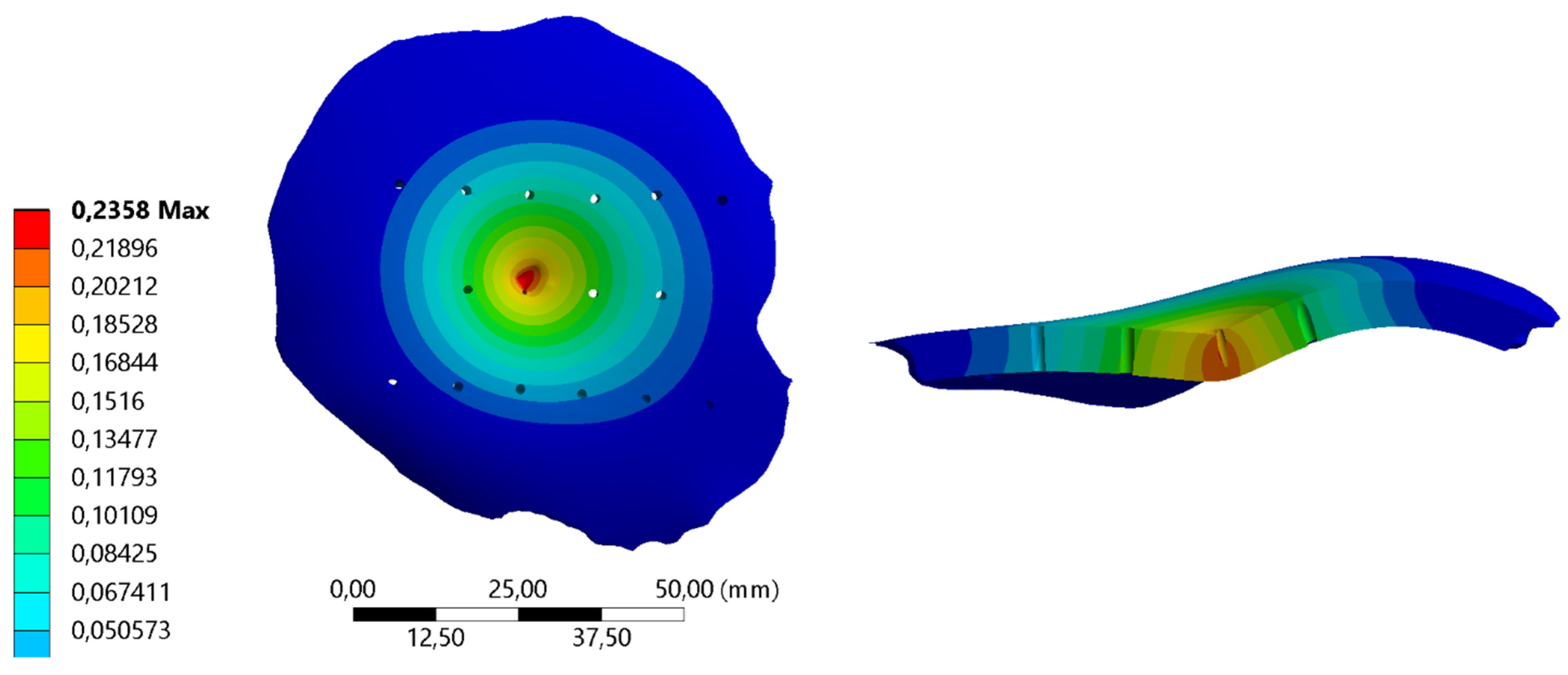
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Alted López, E.; Bermejo Aznárez, S.; Chico Fernández, M. Actualizaciones en el manejo del traumatismo craneoencefálico grave. Med. Intensiv. 2009, 33, 16–30. [Google Scholar] [CrossRef]
- Majdan, M.; Mauritz, W. Unintentional fall-related mortality in the elderly: Comparing patterns in two countries with different demographic structure. BMJ Open 2015, 5, e008672. [Google Scholar] [CrossRef]
- Faul, M.; Xu, L.; Wald, M.M.; Coronado, V.; Dellinger, A.M. Traumatic brain injury in the United States: National estimates of prevalence and incidence, 2002–2006. Inj. Prev. 2010, 16, A268. [Google Scholar] [CrossRef]
- Peñaherrera Oviedo, C.; Soria Viteri, J. Pregunta de investigación y estrategia PICOT. Medicina (B Aires) 2015, 19, 66. [Google Scholar] [CrossRef]
- Guzmán, F.; Moreno, M.C.; Montoya, A. Evolución de los pacientes con trauma craneoencefálico en el Hospital Universitario del Valle: Seguimiento a 12 meses. Colomb. Med. 2008, 39, 25–28. [Google Scholar] [CrossRef]
- Umaña Laiton, L.E. Características Sociodemográficas Relacionadas con la Mortalidad por Trauma Craneoencefálico en Adultos en Colombia. 2010–2017; Universidad del Rosario: Bogotá, Colombia, 2021. [Google Scholar]
- Kim, T.; See, C.W.; Li, X.; Zhu, D. Orthopedic implants and devices for bone fractures and defects: Past, present and perspective. Eng. Regen. 2020, 1, 6–18. [Google Scholar] [CrossRef]
- González-Estrada, O.A.; Pertuz Comas, A.D.; Ospina, R. Characterization of hydroxyapatite coatings produced by pulsed-laser deposition on additive manufacturing Ti6Al4V ELI. Thin Solid Films 2022, 763, 139592. [Google Scholar] [CrossRef]
- Altmann, M.; Cognet, J.-M.; Eschbach, L.; Gasser, B.; Richards, G.; Simon, P. Materiales utilizados en la osteosíntesis. EMC-Técnicas Quirúrgicas-Ortop. y Traumatol. 2009, 1, 1–8. [Google Scholar] [CrossRef]
- Bonda, D.J.; Manjila, S.; Selman, W.R.; Dean, D. The Recent Revolution in the Design and Manufacture of Cranial Implants. Neurosurgery 2015, 77, 814–824. [Google Scholar] [CrossRef] [PubMed]
- Corredor, E.; González-Estrada, O.A.; Ospina-Ospina, R. Deposición de láser pulsado de hidroxiapatita en Ti-6Al-4V producido por manufactura aditiva. Rev. UIS Ing. 2022, 21, 107–122. [Google Scholar] [CrossRef]
- Aydin, S.; Kucukyuruk, B.; Abuzayed, B.; Aydin, S.; Sanus, G.Z. Cranioplasty: Review of materials and techniques. J. Neurosci. Rural Pract. 2011, 2, 162–167. [Google Scholar] [CrossRef] [PubMed]
- Chmal-Fudali, E.; Basińska, D.; Kucharska-Jastrząbek, A.; Struszczyk, M.H.; Muzalewska, M.; Wyleżoł, M.; Wątrobiński, M.; Andrzejewski, J.; Tarzyńska, N.; Gzyra-Jagieła, K. Effect of the Advanced Cranial and Craniofacial Implant Fabrication on Their Degradation Affinity. Materials 2023, 16, 6070. [Google Scholar] [CrossRef] [PubMed]
- Caro-Osorio, E.; De la Garza-Ramos, R.; Martínez-Sánchez, S.; Olazarán-Salinas, F. Cranioplasty with polymethylmethacrylate prostheses fabricated by hand using original bone flaps: Technical note and surgical outcomes. Surg. Neurol. Int. 2013, 4, 136. [Google Scholar] [CrossRef] [PubMed]
- Webb, J.C.J.; Spencer, R.F. The role of polymethylmethacrylate bone cement in modern orthopaedic surgery. J. Bone Jt. Surg.-Ser. B 2007, 89, 851–857. [Google Scholar] [CrossRef] [PubMed]
- Liang, E.S.; Tipper, G.; Hunt, L.; Gan, P.Y.C. Cranioplasty outcomes and associated complications: A single-centre observational study. Br. J. Neurosurg. 2016, 30, 122–127. [Google Scholar] [CrossRef] [PubMed]
- Paredes, I.; Castaño-León, A.M.; Munarriz, P.M.; Martínez-Perez, R.; Cepeda, S.; Sanz, R.; Alén, J.F.; Lagares, A. Cranioplasty after decompressive craniectomy. A prospective series analyzing complications and clinical improvement. Neurocirugia 2015, 26, 115–125. [Google Scholar] [CrossRef]
- Huang, G.J.; Zhong, S.; Susarla, S.M.; Swanson, E.W.; Huang, J.; Gordon, C.R. Craniofacial reconstruction with poly(methyl methacrylate) customized cranial implants. J. Craniofac. Surg. 2015, 26, 64–70. [Google Scholar] [CrossRef]
- Cuppone, M.; Seedhom, B.B.; Berry, E.; Ostell, A.E. The Longitudinal Young’s Modulus of Cortical Bone in the Midshaft of Human Femur and its Correlation with CT Scanning Data. Calcif. Tissue Int. 2004, 74, 302–309. [Google Scholar]
- Fan, J.P.; Tsui, C.P.; Tang, C.Y.; Chow, C.L. Influence of interphase layer on the overall elasto-plastic behaviors of HA/PEEK biocomposite. Biomaterials 2004, 25, 5363–5373. [Google Scholar] [CrossRef]
- Iaccarino, C.; Viaroli, E.; Fricia, M.; Serchi, E.; Poli, T.; Servadei, F. Preliminary Results of a Prospective Study on Methods of Cranial Reconstruction. J. Oral Maxillofac. Surg. 2015, 73, 2375–2378. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, W.; Chen, J.; Yu, J.; Zhang, J.; Chen, J. The application of polyetheretherketone (PEEK) implants in cranioplasty. Brain Res. Bull. 2019, 153, 143–149. [Google Scholar] [CrossRef]
- Alonso-Rodriguez, E.; Cebrián, J.L.; Nieto, M.J.; Del Castillo, J.L.; Hernández-Godoy, J.; Burgueño, M. Polyetheretherketone custom-made implants for craniofacial defects: Report of 14 cases and review of the literature. J. Cranio-Maxillofac. Surg. 2015, 43, 1232–1238. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, G.; Ng, I.; Moscovici, S.; Lee, K.K.; Lay, T.; Martin, C.; Manley, G.T. Polyetheretherketone implants for the repair of large cranial defects: A 3-center experience. Neurosurgery 2014, 75, 523–528. [Google Scholar] [CrossRef] [PubMed]
- Ulmeanu, M.-E.; Mateș, I.M.; Doicin, C.-V.; Mitrică, M.; Chirteș, V.A.; Ciobotaru, G.; Semenescu, A. Bespoke Implants for Cranial Reconstructions: Preoperative to Postoperative Surgery Management System. Bioengineering 2023, 10, 544. [Google Scholar] [CrossRef] [PubMed]
- Geng, J.P.; Ma, Q.S.; Xu, W.; Tan, K.B.C.C.; Liu, G.R.R. Finite element analysis of four thread-form configurations in a stepped screw implant. J. Oral Rehabil. 2004, 31, 233–239. [Google Scholar] [CrossRef]
- Morrison, T.M.; Dreher, M.L.; Nagaraja, S.; Angelone, L.M.; Kainz, W. The Role of Computational Modeling and Simulation in the Total Product Life Cycle of Peripheral Vascular Devices. J. Med. Device 2017, 11, 024503. [Google Scholar] [CrossRef]
- Moiduddin, K.; Mian, S.H.; Alkhalefah, H.; Ramalingam, S.; Sayeed, A. Customized Cost-Effective Cranioplasty for Large Asymmetrical Defects. Processes 2023, 11, 1760. [Google Scholar] [CrossRef]
- Lethaus, B.; Safi, Y.; Ter Laak-Poort, M.; Kloss-Brandstätter, A.; Banki, F.; Robbenmenke, C.; Steinseifer, U.; Kessler, P. Cranioplasty with customized titanium and PEEK implants in a mechanical stress model. J. Neurotrauma 2012, 29, 1077–1083. [Google Scholar] [CrossRef]
- Chamrad, J.; Marcián, P.; Narra, N.; Borák, L. Evaluating Different Shapes of Cranial Fixation Mini-plates Using Finite Element Method. In EMBEC & NBC 2017: Joint Conference of the European Medical and Biological Engineering Conference (EMBEC) and the Nordic-Baltic Conference on Biomedical Engineering and Medical Physics (NBC), Tampere, Finland, June 2017; Springer: Singapore, 2018; pp. 747–750. [Google Scholar]
- Santos, P.O.; Carmo, G.P.; Sousa, R.J.A.d.; Fernandes, F.A.O.; Ptak, M. Mechanical Strength Study of a Cranial Implant Using Computational Tools. Appl. Sci. 2022, 12, 878. [Google Scholar] [CrossRef]
- Bogu, V.P.; Ravi Kumar, Y.; Khanara, A.K. Modelling and structural analysis of skull/cranial implant: Beyond mid-line deformities. Acta Bioeng. Biomech. 2017, 19, 125–131. [Google Scholar] [CrossRef]
- Phanindra Bogu, V.; Ravi Kumar, Y.; Kumar Khanra, A. Homogenous scaffold-based cranial/skull implant modelling and structural analysis—Unit cell algorithm-meshless approach. Med. Biol. Eng. Comput. 2017, 55, 2053–2065. [Google Scholar] [CrossRef]
- Mian, S.H.; Moiduddin, K.; Elseufy, S.M.; Alkhalefah, H. Adaptive Mechanism for Designing a Personalized Cranial Implant and Its 3D Printing Using PEEK. Polymers 2022, 14, 1266. [Google Scholar] [CrossRef]
- Moncayo-Matute, F.P.; Torres-Jara, P.B.; Vázquez-Silva, E.; Peña-Tapia, P.G.; Moya-Loaiza, D.P.; Abad-Farfán, G. Finite element analysis of a customized implant in PMMA coupled with the cranial bone. J. Mech. Behav. Biomed. Mater. 2023, 146, 106046. [Google Scholar] [CrossRef]
- Winder, J.; McKnight, W.; Golz, T.; Giese, A.; Busch, L. Comparison of Custom Cranial Implant Source Data: Manual, Mirrored and CAD generated skull surfaces. In Medical Image Computing & Computer Assisted Intervention; Medical Image Computing and Computer Assisted Intervention Society: Copenhagen, Denmark, 2006. [Google Scholar]
- Maldonado, J.A.; Puentes, D.A.; Quintero, I.D.; González-Estrada, O.A.; Villegas, D.F. Image-Based Numerical Analysis for Isolated Type II SLAP Lesions in Shoulder Abduction and External Rotation. Diagnostics 2023, 13, 1819. [Google Scholar] [CrossRef]
- Díaz, J.M.; González-Estrada, O.A.; López, C.I. Biomechanical analysis of a cranial patient specific implant on the interface with the bone using the finite element method. In Proceedings of the VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, Santander, Colombia, 26–28 October 2016; Springer: Berlin/Heidelberg, Germany, 2017; Volume 60, pp. 405–408. [Google Scholar]
- Tanaka, E.; Rodrigo, D.P.; Tanaka, M.; Kawaguchi, A.; Shibazaki, T.; Tanne, K. Stress analysis in the TMJ during jaw opening by use of a three-dimensional finite element model based on magnetic resonance images. Int. J. Oral Maxillofac. Surg. 2001, 30, 421–430. [Google Scholar] [CrossRef]
- Koolstra, J.H.; Van Eijden, T.M.G.J. Combined finite-element and rigid-body analysis of human jaw joint dynamics. J. Biomech. 2005, 38, 2431–2439. [Google Scholar] [CrossRef] [PubMed]
- Van Eijden, T.M.G.J.; Van Der Helm, P.N.; Van Ruijven, L.J.; Mulder, L. Structural and mechanical properties of mandibular condylar bone. J. Dent. Res. 2006, 85, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Reilly, D.T.; Burstein, A.H. The elastic and ultimate properties of compact bone tissue. J. Biomech. 1975, 8, 393–405. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Gatea, S.; Ou, H.; Lu, B.; Long, H. Fracture characteristics of PEEK at various stress triaxialities. J. Mech. Behav. Biomed. Mater. 2016, 64, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Preusser, T.; Rumpf, M.; Sauter, S.; Schwen, L.O. 3D composite finite elements for elliptic boundary value problems with discontinuous coefficients. SIAM J. Sci. Comput. 2011, 33, 2115–2143. [Google Scholar] [CrossRef]
- Safi, Y.; Hohenberger, S.; Robbenmenke, C.; Banki, F.; Kessler, P.; Schmitz-rode, T.; Steinseifer, U. Investigation of the failure behavior of a cranial implant-skull model under different load conditions using FEM. SIMULIA Cust. Conf. 2010, 1, 16. [Google Scholar]
- Czosnyka, M.; Pickard, J.D. Monitoring and interpretation of intracranial pressure. J. Neurol. Neurosurg. Psychiatry 2004, 75, 813–821. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, C.S.; Antonyshyn, O.; Midha, R.; Fialkov, J.A. Measuring Pulsatile Forces on the Human Cranium. J. Craniofac. Surg. 2005, 16, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Saboori, P.; Sadegh, A. Histology and Morphology of the Brain Subarachnoid Trabeculae. Anat. Res. Int. 2015, 2015, 279814. [Google Scholar] [CrossRef]
- Marcián, P.; Narra, N.; Borák, L.; Chamrad, J.; Wolff, J. Biomechanical performance of cranial implants with different thicknesses and material properties: A finite element study. Comput. Biol. Med. 2019, 109, 43–52. [Google Scholar] [CrossRef]
- Ridwan-Pramana, A.; Marcián, P.; Borák, L.; Narra, N.; Forouzanfar, T.; Wolff, J. Structural and mechanical implications of PMMA implant shape and interface geometry in cranioplasty—A finite element study. J. Cranio-Maxillofac. Surg. 2016, 44, 34–44. [Google Scholar] [CrossRef]
- Martínez, F.; Mañana, G.; Panuncio, A.; Laza, S. Revisión anatomo-clínica de las meninges y espacios intracraneanos con especial referencia al hematoma subdural crónico. Rev. Mex. Neurocienc. 2008, 9, 47–60. [Google Scholar]




| Factors | Coded Level | |
|---|---|---|
| −1 | +1 | |
| Implant thickness (A) | 3 mm | 5 mm |
| Biomaterial (B) | PEEK | PMMA |
| Perforations (C) | No | Yes |
| Material | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| PEEK | 4000 | 0.38 |
| PMMA | 3000 | 0.38 |
| Cranial bone | 15,000 | 0.3 |
| Number of Elements | Max. Total Displacement (mm) |
|---|---|
| 224,302 | 0.28775632 |
| 399,475 | 0.29616231 |
| 761,202 | 0.29734957 |
| 1,521,702 | 0.29806294 |
| Parameter | Implant | Bone |
|---|---|---|
| Edge length (mm) | 1 | 1 |
| Minimum edge length (mm) | 0.5 | 1 |
| Smooth transition | Yes | Yes |
| Bend angle | 7.5° | |
| Number of elements | 576,596 | 749,866 |
| Tetrahedra | Yes | Yes |
| Experiment | A | B | C | Outlet (mm) |
|---|---|---|---|---|
| ξ | ||||
| 1 | − | − | − | 0.787 |
| 2 | − | − | + | 0.811 |
| 3 | − | + | − | 1.089 |
| 4 | − | + | + | 1.125 |
| 5 | + | − | − | 0.225 |
| 6 | + | − | + | 0.237 |
| 7 | + | + | − | 0.300 |
| 8 | + | + | + | 0.316 |
| Main Effects | Effect | Standard Error |
|---|---|---|
| Thickness | −0.684 | ±0.01 |
| Biomaterial | 0.193 | ±0.01 |
| Perforations | 0.022 | ±0.01 |
| Two-factor interactions | ||
| Thickness × Biomaterial | −0.116 | ±0.01 |
| Thickness × Perforations | −0.008 | ±0.01 |
| Biomaterial × Perforations | 0.004 | ±0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mejía Rodríguez, M.; González-Estrada, O.A.; Villegas-Bermúdez, D.F. Finite Element Analysis of Patient-Specific Cranial Implants under Different Design Parameters for Material Selection. Designs 2024, 8, 31. https://doi.org/10.3390/designs8020031
Mejía Rodríguez M, González-Estrada OA, Villegas-Bermúdez DF. Finite Element Analysis of Patient-Specific Cranial Implants under Different Design Parameters for Material Selection. Designs. 2024; 8(2):31. https://doi.org/10.3390/designs8020031
Chicago/Turabian StyleMejía Rodríguez, Manuel, Octavio Andrés González-Estrada, and Diego Fernando Villegas-Bermúdez. 2024. "Finite Element Analysis of Patient-Specific Cranial Implants under Different Design Parameters for Material Selection" Designs 8, no. 2: 31. https://doi.org/10.3390/designs8020031
APA StyleMejía Rodríguez, M., González-Estrada, O. A., & Villegas-Bermúdez, D. F. (2024). Finite Element Analysis of Patient-Specific Cranial Implants under Different Design Parameters for Material Selection. Designs, 8(2), 31. https://doi.org/10.3390/designs8020031







