Optimal Domain-Partitioning Algorithm for Real-Life Transportation Networks and Finite Element Meshes
Abstract
1. Introduction
2. A Review of the Basic Seven-Step Heuristic Algorithm for Domain Partitioning
- Step 1.
- Initialise the problem: In this step, we simply provide the input data which describe the network’s connectivity information.
- Step 2.
- Determine nodal ranks: In this step, the rank for each node can be computed (or defined) as the number of surrounding nodes connected to the node.
- Step 3.
- Determine first-source (starting) node for each subdomain: The first starting node for the = 1th subdomain will be node N01 because node N01 has the lowest rank.
- Step 4.
- Determine other-source (starting) nodes for each remaining subdomain: The starting node for each remaining subdomain will also have the lowest rank. Furthermore, its starting node should be far away from the starting node of other subdomains. Based on these criteria (and the “tie-breaking” rules), the starting nodes for the second and third subdomains are nodes N11 and N06, respectively.
- Step 5.
- Populate more (two-node) LINE elements or (three-node) TRIANGULAR elements simultaneously to each subdomain: In this step, additional nodes are populated into each subdomain based on the following criteria: (i) the newly added node to its subdomain must be connected to at least one of the existing nodes and (ii) the newly added node to its subdomain must be very close to its subdomain’s starting node.
- Step 6.
- Identify system boundary nodes (SBN): The SBN can be found by creating a loop that will process every (LINE) element of the entire original network. For each (line) element, we can identify its two end-nodes. These two end-nodes are considered as “SBN” if these two end-nodes belong to different subdomains. Otherwise, these two end-nodes will be declared as “interior nodes”.
- Step 7.
- Renumber the nodes: In this (last) step, the entire original node numbering system will be re-numbered in such a way that all “SBN” will be numbered last. For example, the original SBNs N05, N08 and N012 will be renumbered as SBNs N013, N014 and N015, respectively.
3. Extension of the Basic Seven-Step Domain Partitioning Algorithm for General Finite Element Mesh Partitioning
- i.
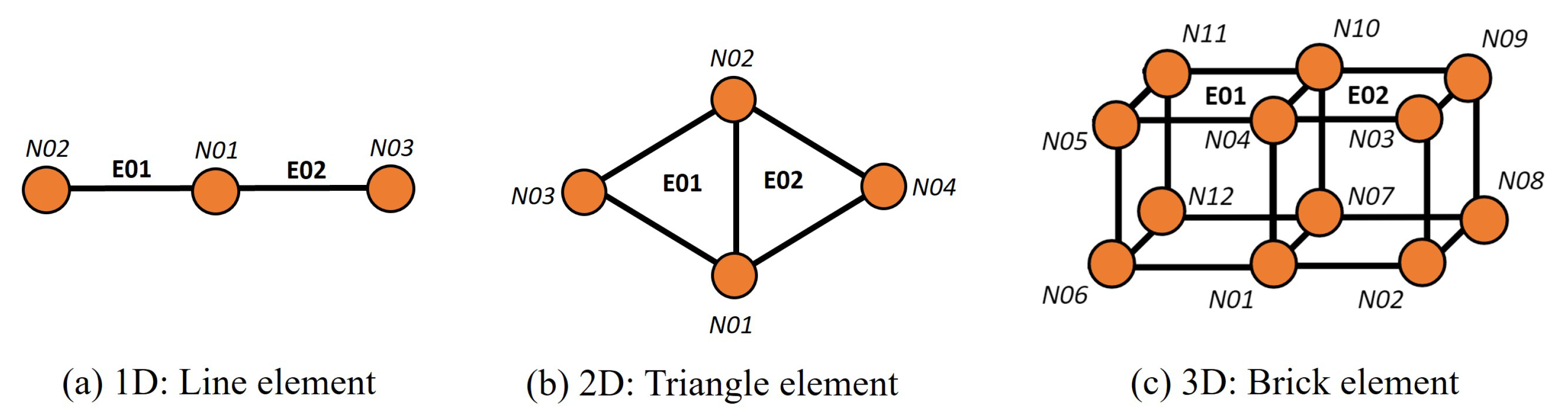
- The proposed seven-step DP algorithm can be generalised to include a wider range of different elements in the “elements library,” including two-node LINE elements that can serve as links or arcs in transportation networks or as two-node truss/beam elements in finite element (FE) meshes, as well as three-node triangular elements, four-node quadrilateral elements, eight-node brick elements, and four-node tetrahedral elements used in 2D and 3D FE analysis.
- ii.
- An emphasis was placed on enhancing the effectiveness of 2D and 3D FE analysis.
- The intersection of any (different) pair of (two-node) LINE elements will be a NODE (see Figure 2a).
- For 2D applications, the intersection of any (different) pair of (three-node) TRIANGULAR elements will be a LINE (see Figure 2b).
- For 3D applications, the intersection of any (different) pair of (eight-node) BRICK elements will be a four-node SURFACE (see Figure 2c).
3.1. Example 1: Two-Node LINE Elements for Truss (or Beam) FEA
- i.
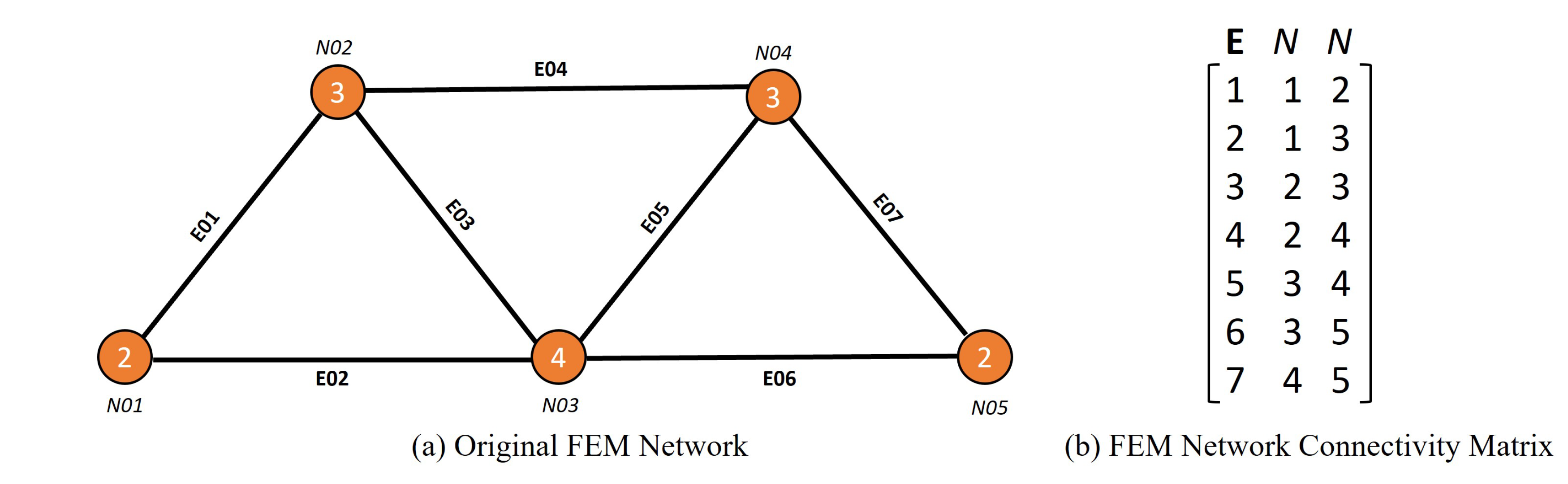
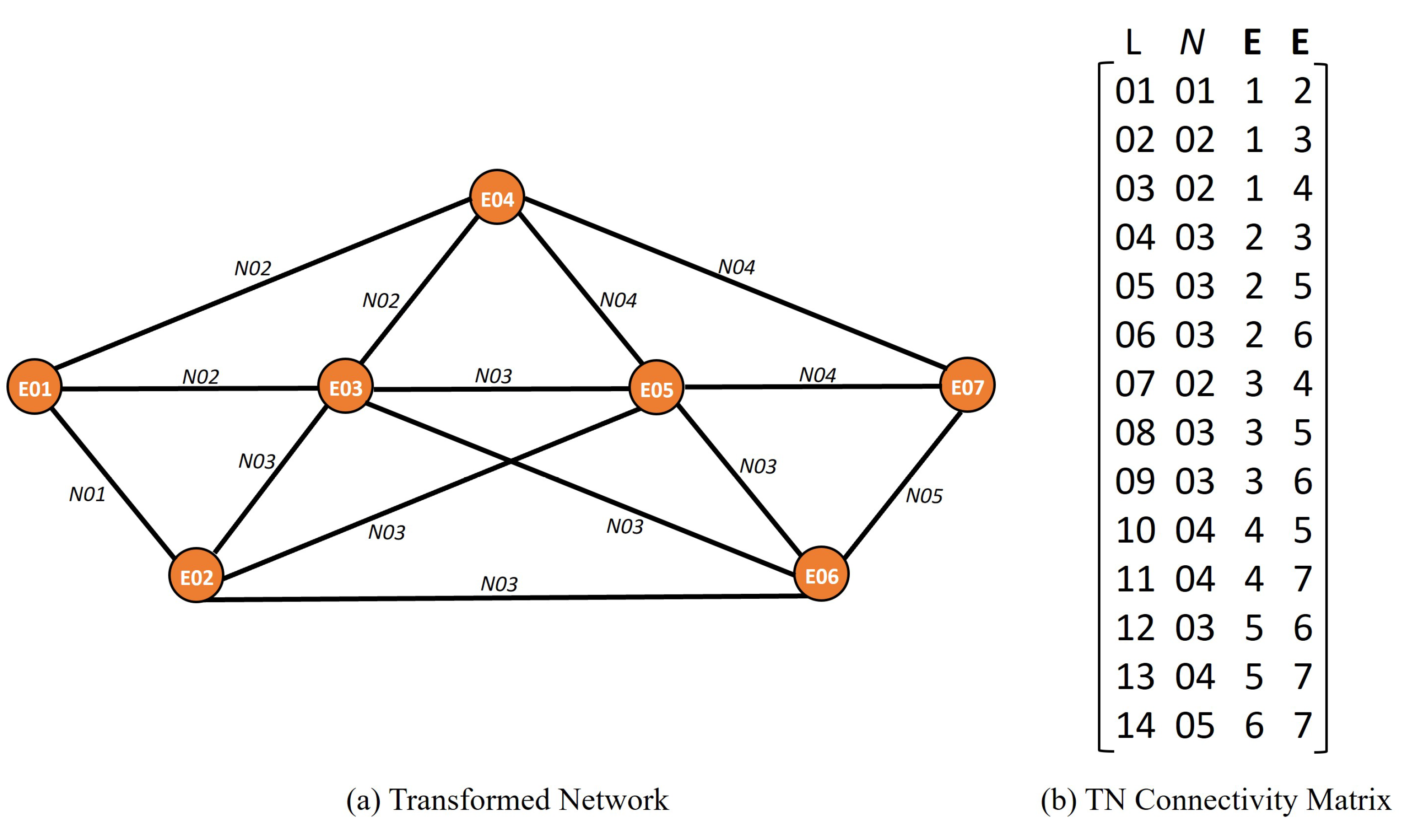
- The “transformed network” is constructed by assigning a “pseudo-node" to each actual LINE element in the original network, resulting in a total of seven pseudo-nodes in this example, which are labelled from E01 to E07 (see Figure 5a).
- ii.
- The number of “pseudo-links” in the “transformed network” corresponds to the total number of INTERSECTIONS between different pairs of LINE elements in the original network. As shown in Figure 5a, node N01 is the INTERSECTION of two LINE elements E01 and E02; thus, only one INTERSECTION (between E01 and E02) will be allocated a pseudo-link.
3.2. Example 2: Three-Node TRIANGULAR Elements for Finite Element Analysis (FEA)
- i.
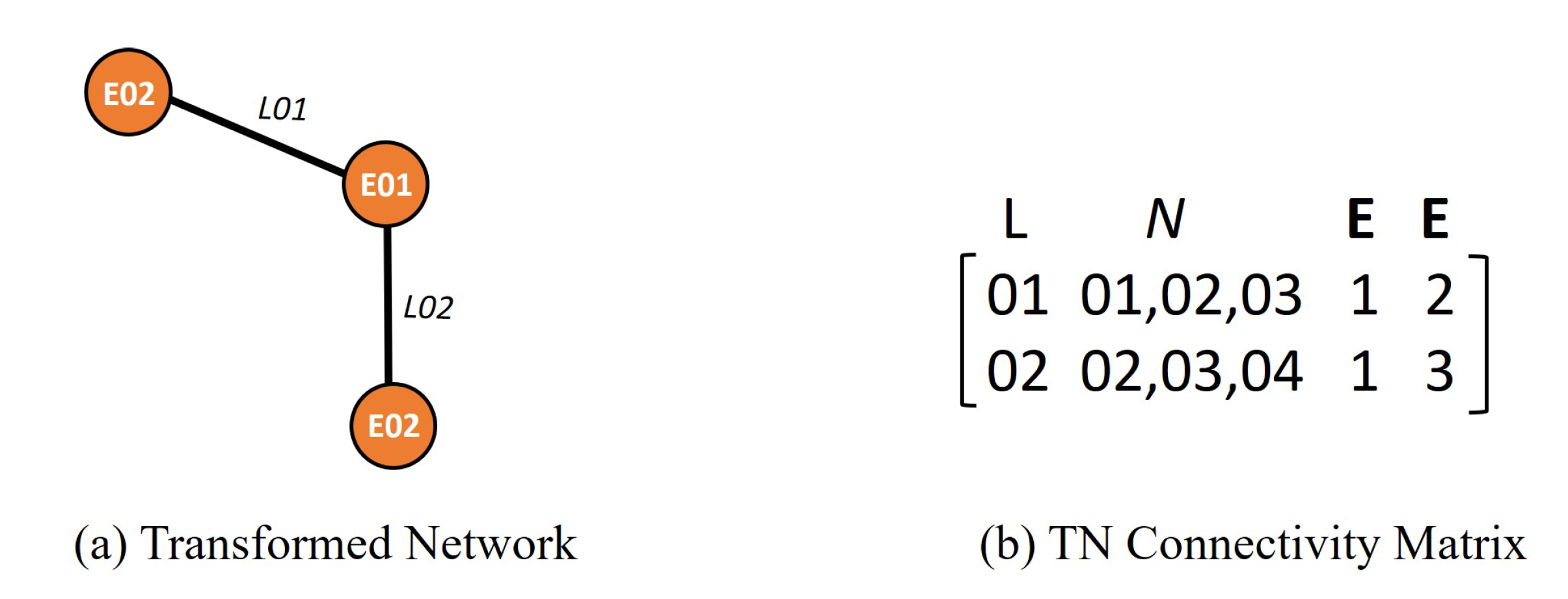
- The number of “pseudo-nodes” in the “transformed network” will be equal to the number of actual TRIANGULAR elements in the “original network”. Thus, in this example, the number of “pseudo-nodes” is equal to six, and these pseudo-nodes are labelled as node numbers E01, E02, …E06 (see Figure 6).
- ii.
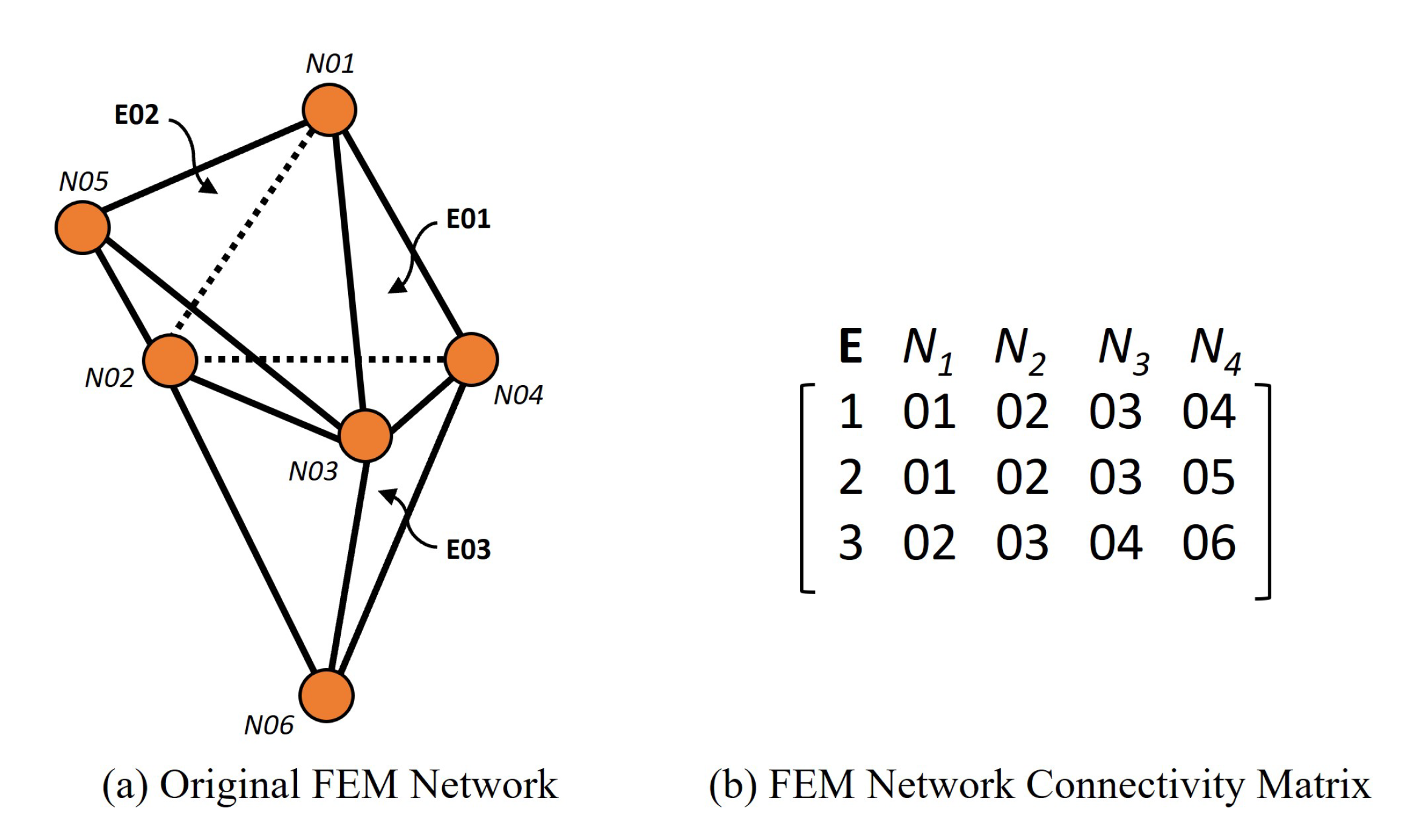
- The number of “pseudo-links” in the “transformed network” will be equal to “the total number of INTERSECTIONS of all (different) pairs of TRIANGULAR elements” in the “original network”. In Figure 6, triangular element E01 will INTERSECT with its adjacent (triangular element) neighbours E02, E05, and E06 at three “boundary LINES” connected by nodes N01 and N02, nodes N01 and N03, and nodes N03 and N02, respectively.
- iii.
- Similarly, triangular element E02 will INTERSECT with its adjacent (triangular element) neighbours E01, E03, and E04 at two additional (new) “boundary LINES” connected by nodes N02 and N04 and by nodes N01 and N06, respectively.
- In Figure 6, “Boundary LINE” connected by nodes N01 and N02 has already been accounted for in rule (ii); hence, this boundary line will not be counted twice.
- In Figure 6, triangular E03 is adjacent to triangular E02 and shares the “boundary LINE” connected by nodes N02 and N04, which has already been accounted for in rule (iii); hence, this boundary line will not be counted twice.
3.3. Example 3: Eight-Node BRICK Elements for Finite Element Analysis (FEA)
- i.
- The number of “pseudo-nodes” in the “transformed network” will be equal to the number of actual BRICK elements in the “original network”. Thus, in this example, the number of “pseudo-nodes” is equal to three, and these pseudo-nodes are labelled as node numbers E01, E02, and E03 (see Figure 9a).
- ii.
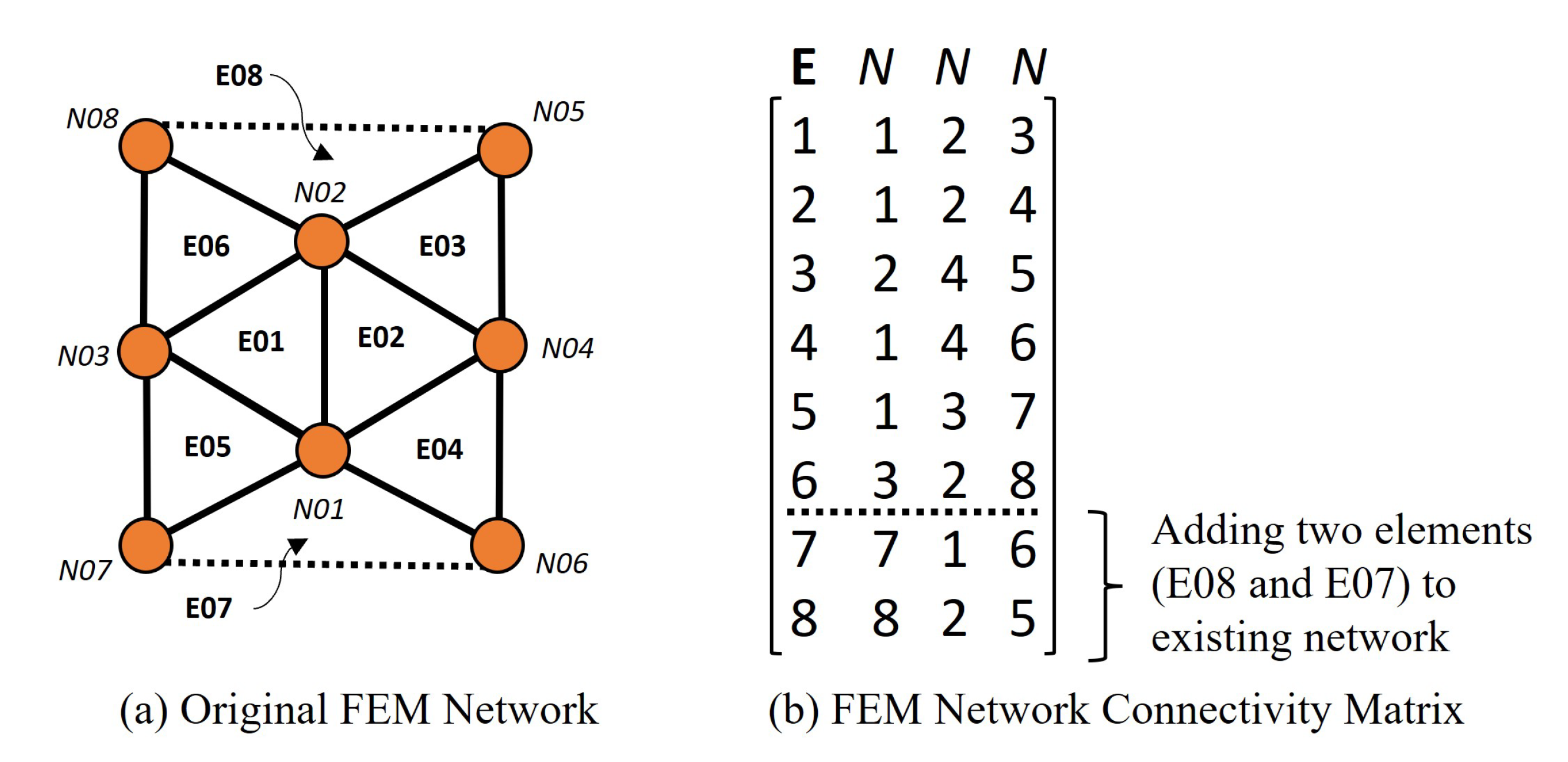
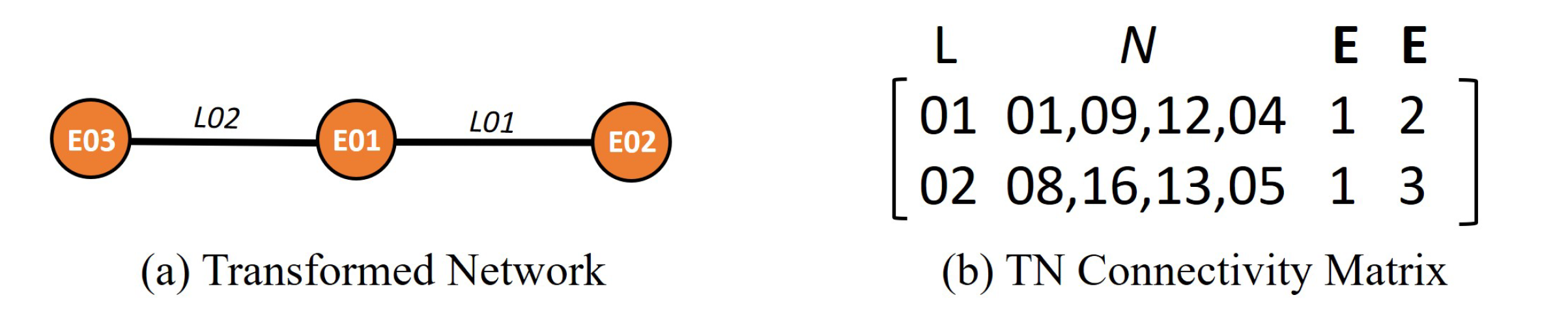
- The number of “pseudo-links” in the “transformed network” will be equal to “the total number of INTERSECTIONS of all (different) pairs of BRICK elements” in the “original network”. In Figure 8a, BRICK element E01 will INTERSECT with its adjacent (BRICK element) neighbours E02 and E03 at two “boundary (four-node) SURFACES” connected by nodes N01, N04, N12 and N09 and nodes N08, N05, N13 and N16, respectively.
3.4. Example 4: Four-Node TETRAHEDRAL Elements for Finite Element Analysis (FEA)
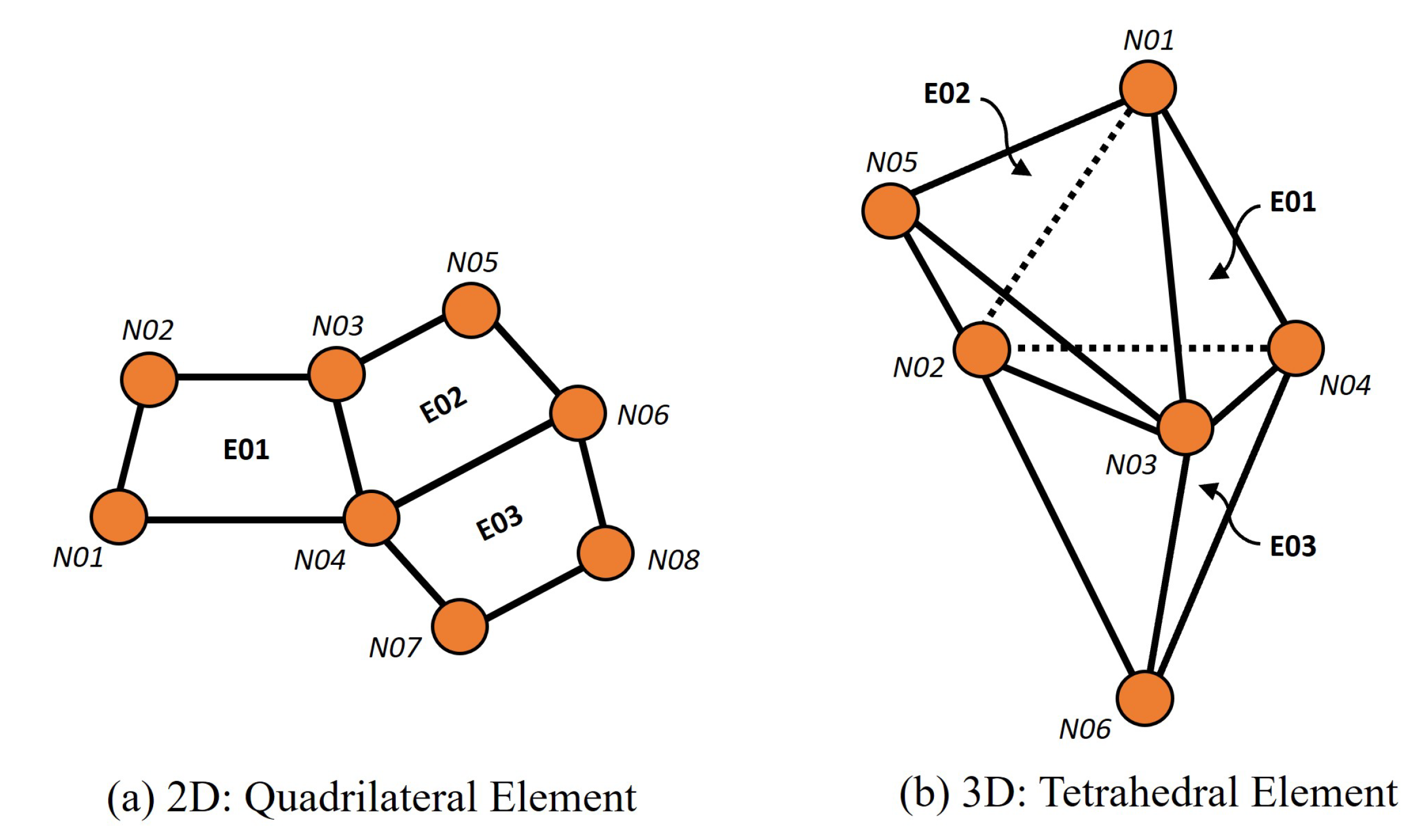
- i.
- The number of “pseudo-nodes” in the “transformed network” will be equal to the number of actual TETRAHEDRAL elements in the “original FEM network”. Thus, in this example, the number of “pseudo-nodes” is equal to three, and these pseudo-nodes are labelled as node numbers E01, E02, and E03 (see Figure 11).
- ii.
- The number of “pseudo-links” in the “transformed network” will be equal to “the total number of INTERSECTIONS of all (different) pairs of TETRAHEDRA elements” in the “original FEM network”. In Figure 10, TETRAHEDRAL element E01 will INTERSECT with its adjacent (TETRAHEDRAL element) neighbours E02, and E03 at two “boundary (three-node) SURFACES” connected by nodes N01, N02 and N03 and /by nodes N02, N03 and N04, respectively.
4. Domain-Partitioning Examples for Real-Life Transportation Network
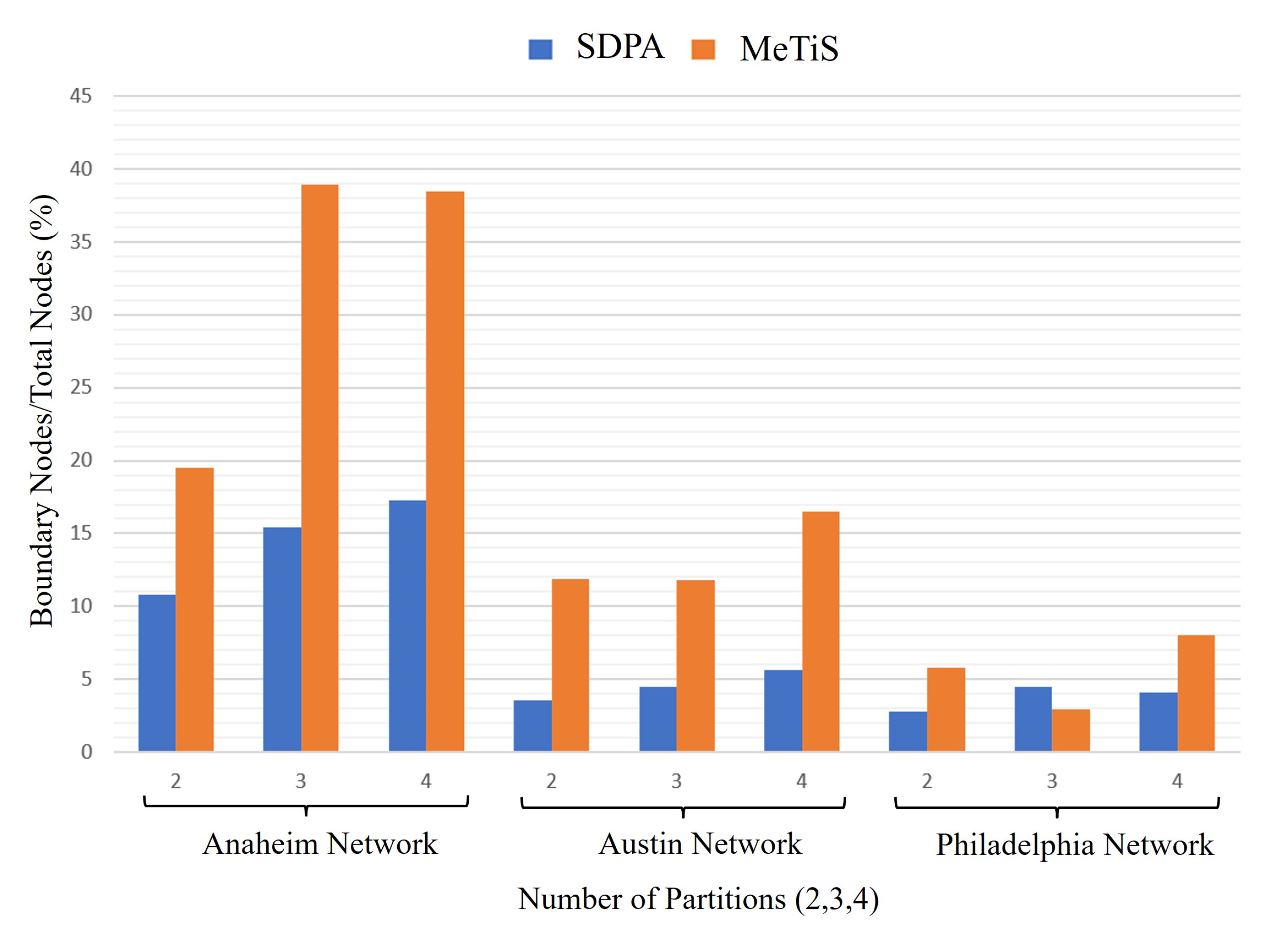
4.1. Example 1: Anaheim (Real-Life) Transportation Network
4.2. Example 2: Austin (Real-Life) Transportation Network
4.3. Example 3: Philadelphia (Real-Life) Transportation Network
5. Domain-Partitioning Examples for Finite Element Meshes
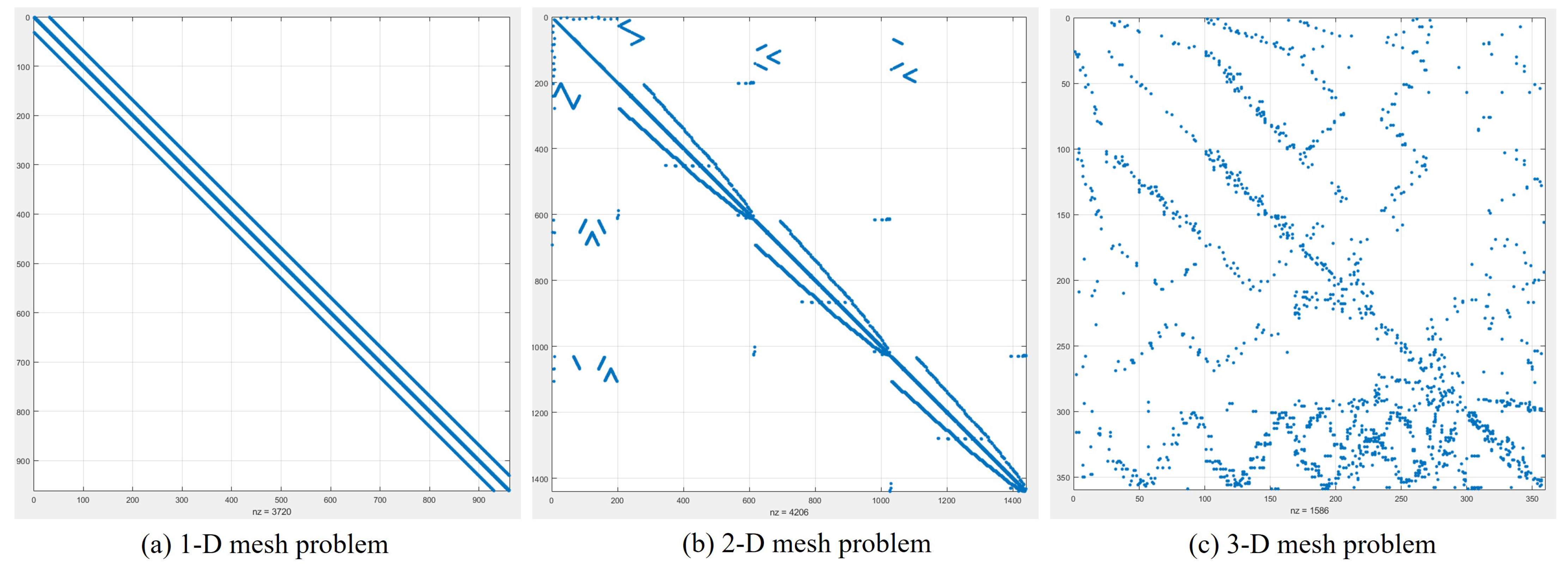
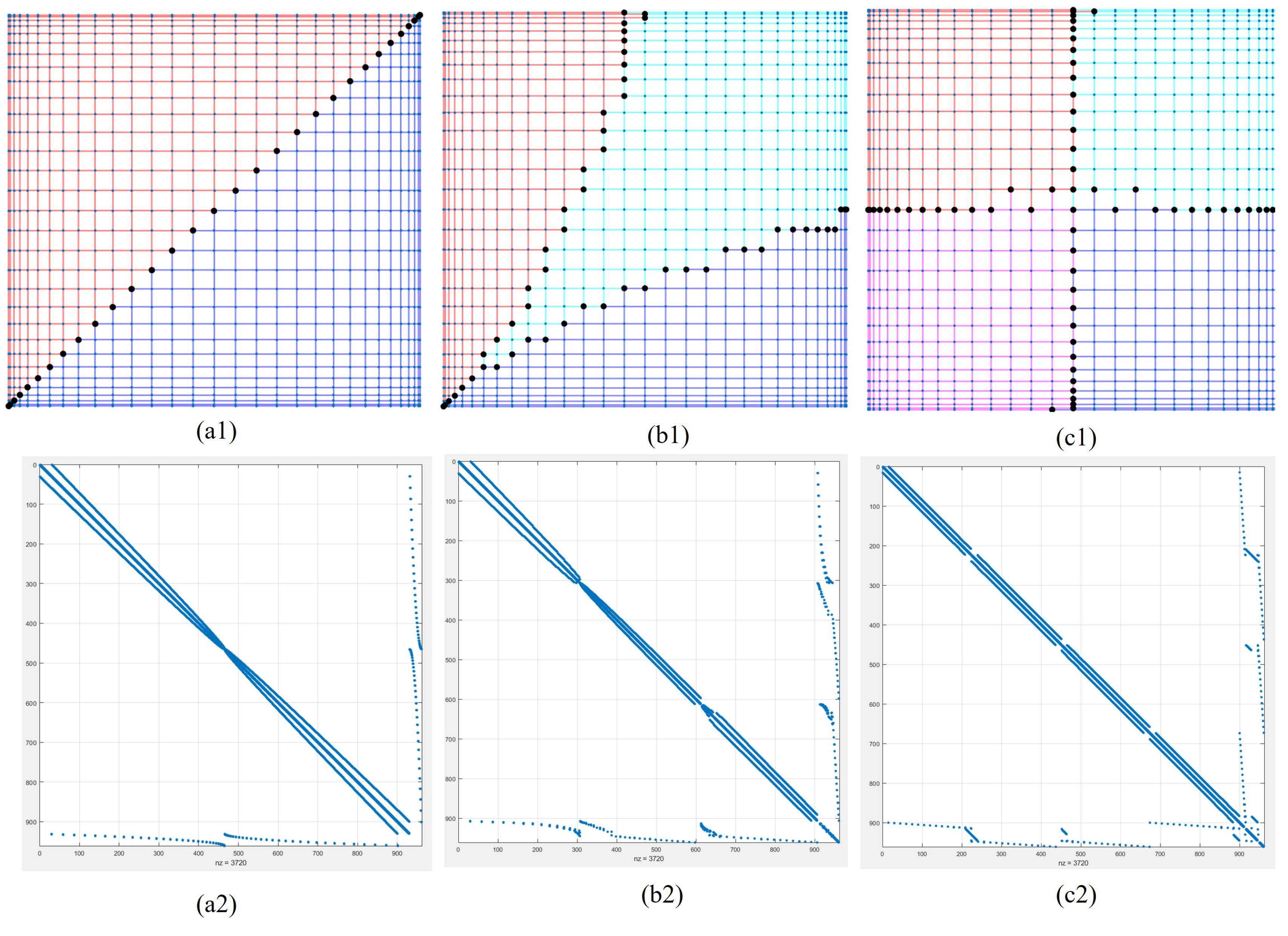
5.1. Example 1: One-Dimensional Grid Problem with 2–4 Subdomains
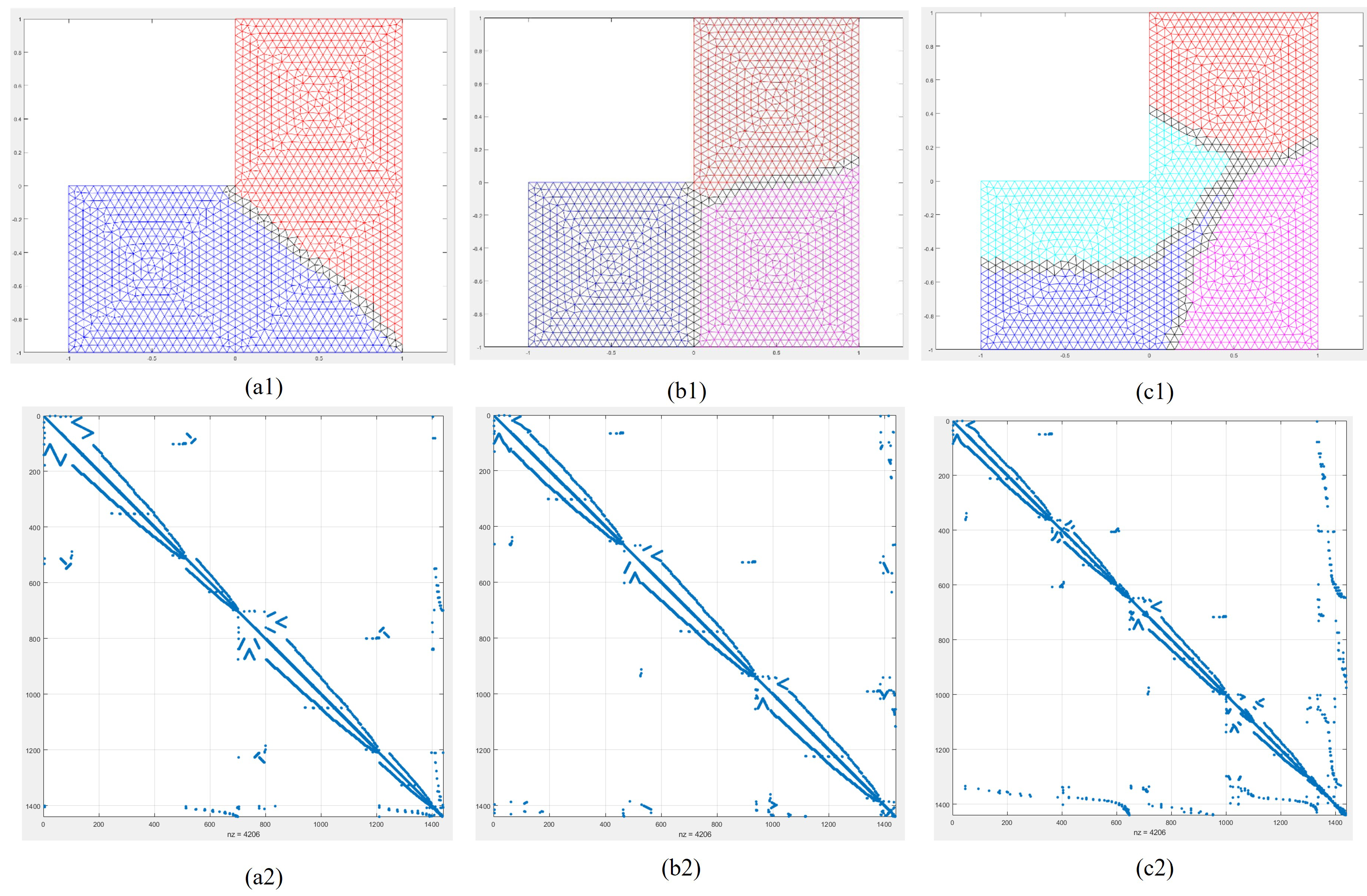
5.2. Example 2: Two-Dimensional Grid Problem with 2–4 Subdomains
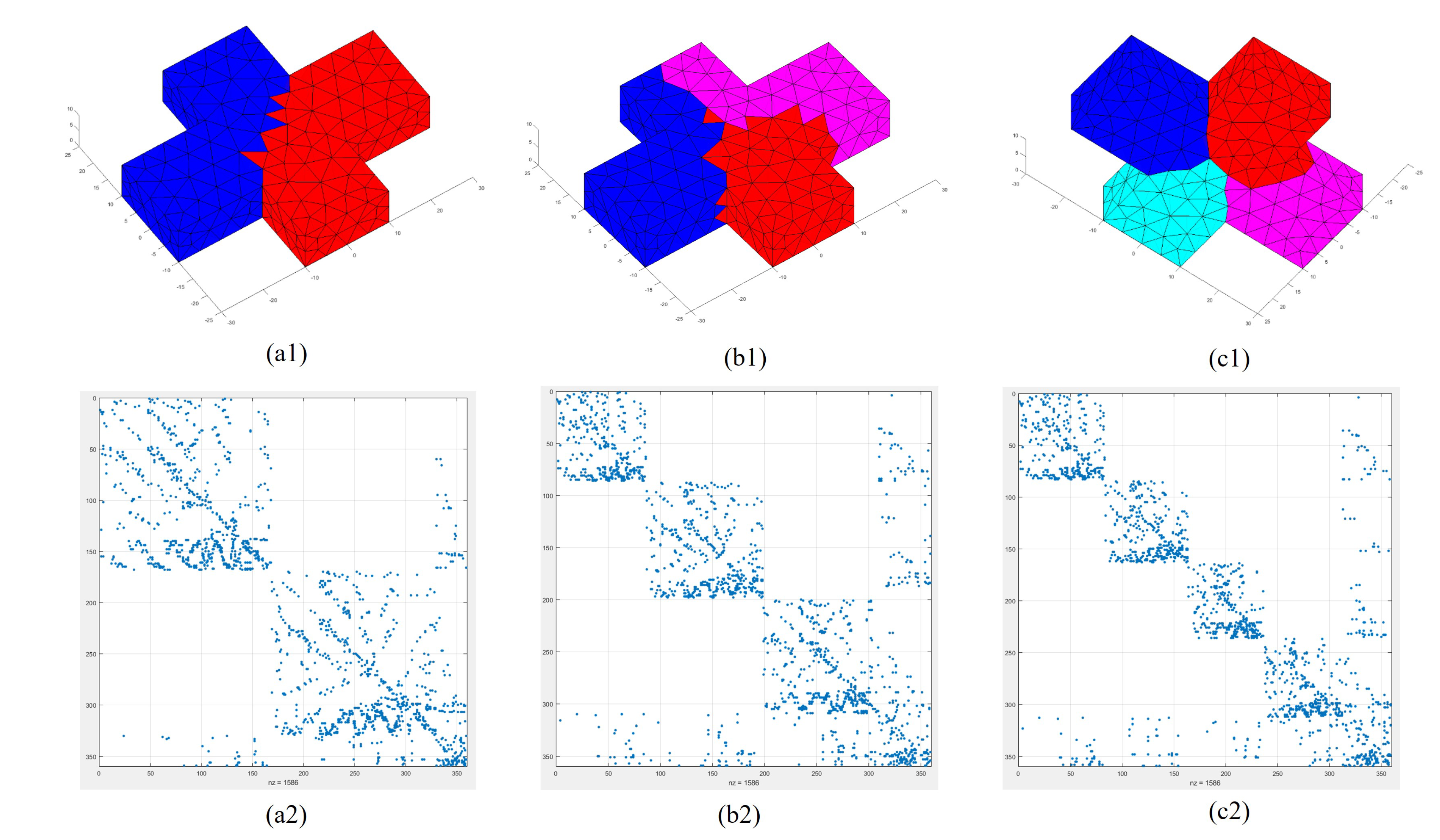
5.3. Example 3: Three-Dimensional Grid Problem with 2–4 Subdomains
6. Conclusions and Suggested Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johnson, P.; Nguyen, D.; Ng, M. Large-scale network partitioning for decentralised traffic management and other transportation applications. J. Intell. Transp. Syst. 2016, 20, 461–473. [Google Scholar] [CrossRef]
- Bank, R.E.; Holst, M. A New Paradigm for Parallel Adaptive Meshing Algorithms. SIAM J. Sci. Comput. 2000, 22, 1411–1443. [Google Scholar] [CrossRef]
- Achdou, Y.; Kuznetsov, Y.; Pironneau, O. Substructuring preconditioners for the mortar element method. Numer. Math. 1995, 71, 419–449. [Google Scholar] [CrossRef]
- deCougny, H.; Devine, K.; Flaherty, J.; Loy, R.; Özturan, C.; Shephard, M. Load balancing for the parallel adaptive solution of partial differential equations. Appl. Numer. Math. 1994, 16, 157–182. [Google Scholar] [CrossRef]
- Flaherty, J.; Loy, R.; Özturan, C.; Shephard, M.; Szymanski, B.; Teresco, J.; Ziantz, L. Parallel structures and dynamic load balancing for adaptive finite element computation. Appl. Numer. Math. 1998, 26, 241–263. [Google Scholar] [CrossRef]
- Fox, G.C.; Williams, R.D.; Messina, P.C. Parallel Computing Works! Parallel Processing Scientific Computing, Morgan Kaufmann: San Francisco, CA, USA, 1994. [Google Scholar]
- Kohn, S.; Weare, J.; Ong, M.E.; Baden, S. Software Abstractions and Computational Issues in Parallel Structured Adaptive Mesh Methods for Electronic Structure Calculations. Struct. Adapt. Mesh Refinement SAMR Grid Methods 2000, 117, 75–95. [Google Scholar]
- Selwood, P.M.; Berzins, M.; Dew, P.M. 3D Parallel Mesh Adaptivity: Data-Structures and Algorithms. In Proceedings of the SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, MN, USA, 14–17 March 1997. [Google Scholar]
- Walshaw, C.; Berzins, M. Dynamic load-balancing for PDE solvers on adaptive unstructured meshes. Concurr. Pract. Exp. 1995, 7, 17–28. [Google Scholar] [CrossRef]
- Williams, R.D. Performance of dynamic load balancing algorithms for unstructured mesh calculations. Concurr. Pract. Exp. 1991, 3, 457–481. [Google Scholar] [CrossRef]
- Nguyen, D.T. Finite Element Methods: Parallel-Sparse Statics and Eigen-Solutions; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Tallec, P.; Roeck, Y.; Vidrascu, M. Domain decomposition methods for large linearly elliptic three-dimensional problems. J. Comput. Appl. Math. 1991, 34, 93–117. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method, 3rd ed.; McGraw-Hill Series in Mechanical Engineering; McGraw-Hill: Boston, MA, USA, 2005. [Google Scholar]
- Dinh-Cong, D.; Nguyen-Thoi, T.; Nguyen, D.T. A FE model updating technique based on SAP2000-OAPI and enhanced SOS algorithm for damage assessment of full-scale structures. Appl. Soft Comput. 2020, 89, 106100. [Google Scholar] [CrossRef]
- CEE-718/815; Engineering Optimization, Spring 2022. Old Dominion University (ODU): Norfolk, VA, USA, 2022.
- Thompson, E.; Kontinis, M. Engineering-Based Heuristic Partitioning Algorithm For Finite Element Analysis of Field Problems; A Master Project Report; Mechanical & Aerospace Engineering (MAE) Department, Old Dominion University (ODU): Norfolk, VA, USA, 2022. [Google Scholar]
- Bramble, J.H.; Pasciak, J.E.; Schatz, A.H. The construction of preconditioners for elliptic problems by substructuring. I. Math. Comput. 1986, 47, 103–134. [Google Scholar] [CrossRef]
- Papadrakakis, M.; Stavroulakis, G.; Karatarakis, A. A new era in scientific computing: Domain decomposition methods in hybrid CPU–GPU architectures. Comput. Methods Appl. Mech. Eng. 2011, 200, 1490–1508. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. METIS: A Software Package for Partitioning Unstructured Graphs, Partitioning Meshes, and Computing Fill-Reducing Orderings of Sparse Matrices. Technical Report 97-061; University of Minnesota, Department of Computer Science and Engineering: Minneapolis, MN, USA, 1997. [Google Scholar]
- Berger, M.J.; Bokhari, S.H. A Partitioning Strategy for Nonuniform Problems on Multiprocessors. IEEE Trans. Comput. 1987, C-36, 570–580. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. Multilevel Algorithms for Multi-Constraint Graph Partitioning. In Proceedings of the IEEE/ACM SC98 Conference; IEEE: Orlando, FL, USA, 7–13 November 1998; p. 28. [Google Scholar]
- Spielman, D.A.; Teng, S.H. Spectral partitioning works: Planar graphs and finite element meshes. Linear Algebra Its Appl. 2007, 421, 284–305. [Google Scholar] [CrossRef]
- Tran-Ngoc, H.; Khatir, S.; Le-Xuan, T.; De Roeck, G.; Bui-Tien, T.; Abdel Wahab, M. Finite element model updating of a multispan bridge with a hybrid metaheuristic search algorithm using experimental data from wireless triaxial sensors. Eng. Comput. 2022, 38, 1865–1883. [Google Scholar] [CrossRef]
- Annicchiarico, W.; Cerrolaza, M. Structural shape optimization 3D finite-element models based on genetic algorithms and geometric modeling. Finite Elem. Anal. Des. 2001, 37, 403–415. [Google Scholar] [CrossRef]
- Tran-Ngoc, H.; Khatir, S.; Le-Xuan, T.; Tran-Viet, H.; De Roeck, G.; Bui-Tien, T.; Wahab, M.A. Damage assessment in structures using artificial neural network working and a hybrid stochastic optimization. Sci. Rep. 2022, 12, 4958. [Google Scholar] [CrossRef] [PubMed]
- Xu, J. Iterative Methods by Space Decomposition and Subspace Correction. SIAM Rev. 1992, 34, 581–613. [Google Scholar] [CrossRef]
- GIT-Hub Repository. Available online: https://github.com/bstabler/TransportationNetworks/find/master (accessed on 15 May 2022).



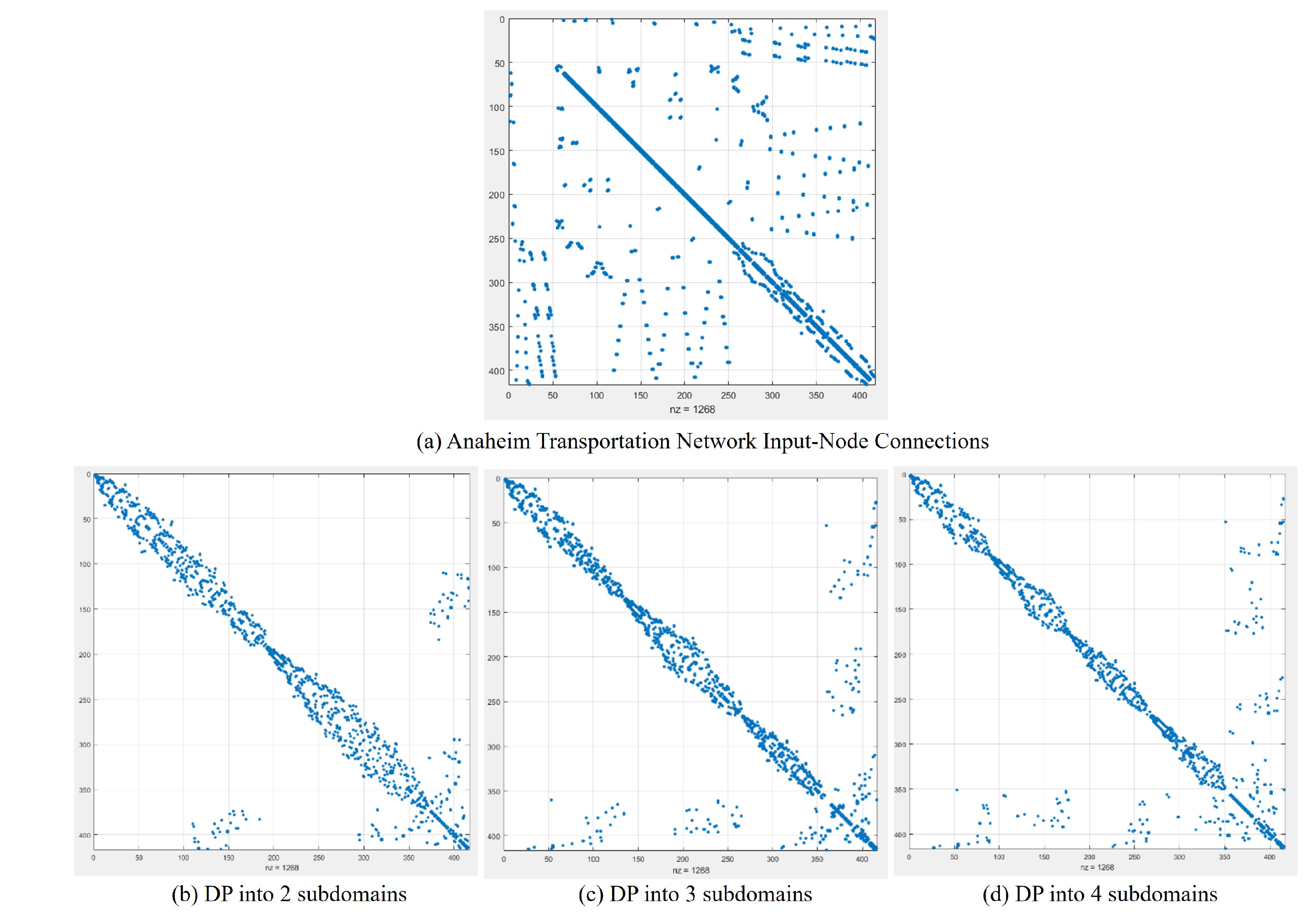
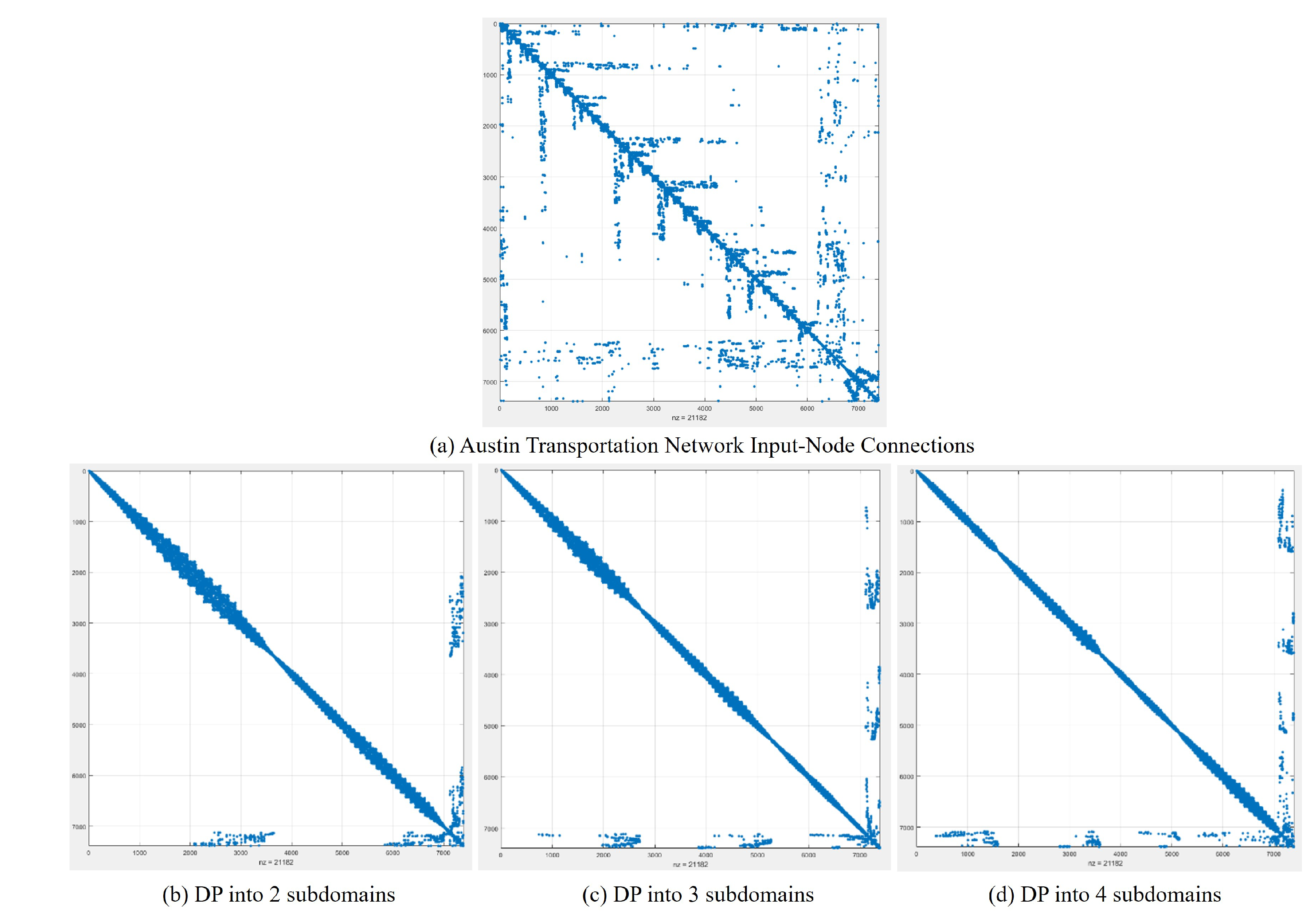
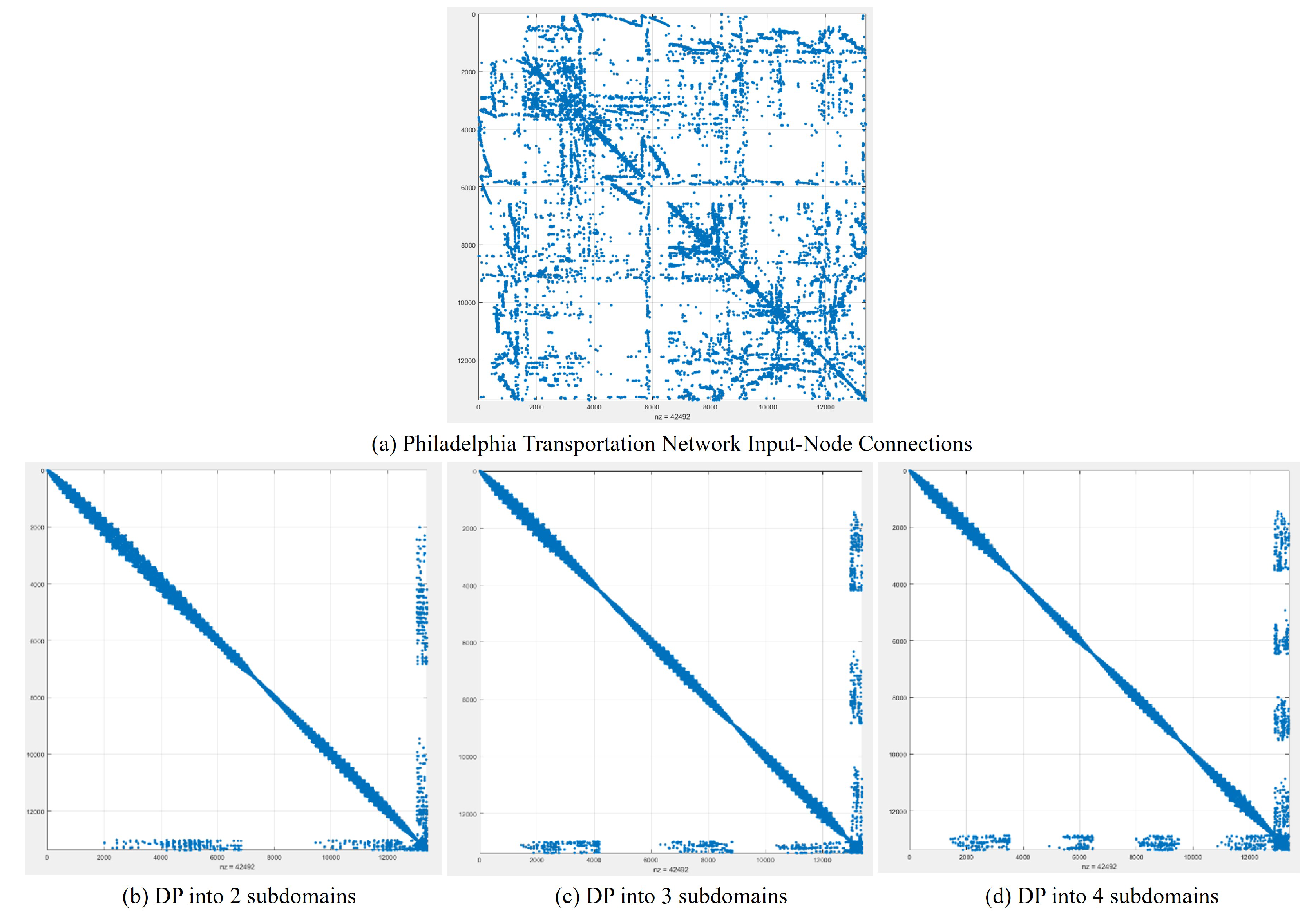
| NP = 2 | NP = 3 | NP = 4 | ||||
|---|---|---|---|---|---|---|
| Nodes | Boundary Elements | Nodes | Boundary Elements | Nodes | Boundary Elements | |
| Subdomain 1 | 212 | 153 | 102 | |||
| Subdomain 2 | 204 | 144 | 108 | |||
| Subdomain 3 | – | 45 | 119 | 64 | 104 | 72 |
| Subdomain 4 | – | – | 102 | |||
| Total Nodes | 416 | 416 | 416 | |||
| Metis Boundary Nodes | 416 | 81 | 416 | 162 | 416 | 160 |
| Step 1 Time | 0.0291 | 0.0281 | 0.035 | |||
| Step 2 Time | 0.0024 | 0.0024 | 0.0022 | |||
| Step 3 Time | 0.0018 | 0.014 | 0.0016 | |||
| Step 4 Time | 0.1127 | 0.1776 | 0.2489 | |||
| Step 5 Time | 0.0238 | 0.0258 | 0.0297 | |||
| Step 6 Time | 0.0245 | 0.0297 | 0.0246 | |||
| Step 7 Time | 0.0136 | 0.0166 | 0.0138 | |||
| Total Solution Time ⌃⌃ | 0.2080 | 0.2816 | 0.3564 | |||
| MeTiS Solution Time ** | 0.003 | 0.003 | 0.004 | |||
| NP = 2 | NP = 3 | NP = 4 | ||||
|---|---|---|---|---|---|---|
| Nodes | Boundary Elements | Nodes | Boundary Elements | Nodes | Boundary Elements | |
| Subdomain 1 | 3788 | 2691 | 1976 | |||
| Subdomain 2 | 3600 | 2159 | 1716 | |||
| Subdomain 3 | – | 265 | 2538 | 329 | 2009 | 414 |
| Subdomain 4 | – | – | 1687 | |||
| Total Nodes | 7388 | 7388 | 7388 | |||
| METIS Boundary Nodes | 7388 | 878 | 7388 | 872 | 7388 | 1221 |
| Step 1 Time (s) | 0.1326 | 0.1385 | 0.1470 | |||
| Step 2 Time (s) | 0.4265 | 0.3657 | 0.3881 | |||
| Step 3 Time (s) | 0.0035 | 0.0023 | 0.0026 | |||
| Step 4 Time (s) | 16.370 | 26.079 | 40.629 | |||
| Step 5 Time (s) | 0.5382 | 0.5028 | 0.5074 | |||
| Step 6 Time (s) | 1.2516 | 1.5658 | 1.3411 | |||
| Step 7 Time (s) | 0.0882 | 0.0874 | 0.1122 | |||
| Total Time (s) ⌃⌃ | 18.809 | 28.742 | 43.128 | |||
| MeTiS Time (s) ** | 0.006 | 0.009 | 0.01 | |||
| NP = 2 | NP = 3 | NP = 4 | ||||
|---|---|---|---|---|---|---|
| Nodes | Boundary Elements | Nodes | Boundary Elements | Nodes | Boundary Elements | |
| Subdomain 1 | 7502 | 5368 | 3525 | |||
| Subdomain 2 | 5887 | 1797 | 731 | |||
| Subdomain 3 | – | 370 | 6224 | 603 | 4994 | 548 |
| Subdomain 4 | – | – | 4139 | |||
| Total Nodes | 13389 | 13389 | 13389 | |||
| METIS Boundary Nodes | 13389 | 773 | 13389 | 393 | 13389 | 1080 |
| Step 1 Time (s) | 0.3282 | 0.3045 | 0.2839 | |||
| Step 2 Time (s) | 1.228 | 1.3234 | 1.2617 | |||
| Step 3 Time (s) | 0.0033 | 0.0031 | 0.0031 | |||
| Step 4 Time (s) | 53.285 | 89.893 | 121.97 | |||
| Step 5 Time (s) | 2.3435 | 2.6017 | 2.7539 | |||
| Step 6 Time (s) | 5.2156 | 6.0476 | 6.3865 | |||
| Step 7 Time (s) | 0.1172 | 0.1478 | 0.1363 | |||
| Total Time (s) ⌃⌃ | 62.521 | 100.321 | 132.796 | |||
| MeTiS Time (s) ** | 0.08 | 0.026 | 0.013 | |||
| NP = 2 | NP = 3 | NP = 4 | ||||
|---|---|---|---|---|---|---|
| Elements | Boundary Elements | Elements | Boundary Elements | Elements | Boundary Elements | |
| Subdomain 1 (red) | 930 | 620 | 465 | |||
| Subdomain 2 (blue) | 930 | 620 | 465 | |||
| Subdomain 3 (cyan) | – | 120 | 620 | 187 | 465 | 190 |
| Subdomain 4 (magenta) | – | – | 465 | |||
| Total FEM Elements | 1860 | 1860 | 1860 | |||
| FEM Nodes | 961 | 31 | 961 | 55 | 961 | 62 |
| Pre-processing Time | 100.60 | 93.99 | 90.81 | |||
| Step 1 Time | 0.025 | 0.015 | 0.0129 | |||
| Step 2 Time | 0.0051 | 0.0034 | 0.0029 | |||
| Step 3 Time | 0.0032 | 0.0021 | 0.0022 | |||
| Step 4 Time | 0.047 | 0.037 | 0.03 | |||
| Step 5 Time | 0.057 | 0.039 | 0.06 | |||
| Step 6 Time | 0.031 | 0.018 | 0.03 | |||
| Step 7 Time | 0.020 | 0.014 | 0.02 | |||
| Post-processing Time | 0.605 | 0.92 | 0.98 | |||
| Total Time ⌃⌃ | 101.39 | 95.042 | 91.93 | |||
| NP = 2 | NP = 3 | NP = 4 | ||||
|---|---|---|---|---|---|---|
| Elements | Boundary Elements | Elements | Boundary Elements | Elements | Boundary Elements | |
| Subdomain 1 (red) | 1359 | 907 | 707 | |||
| Subdomain 2 (blue) | 1359 | 907 | 614 | |||
| Subdomain 3 (magenta) | – | 65 | 904 | 91 | 707 | 183 |
| Subdomain 4 (cyan) | – | – | 690 | |||
| Total FEM Elements | 2718 | 2718 | 2718 | |||
| FEM Nodes | 1440 | 40 | 1440 | 56 | 1440 | 108 |
| Pre-processing Time | 205.8 | 197.49 | 205.67 | |||
| Step 1 Time | 0.012 | 0.01 | 0.01 | |||
| Step 2 Time | 0.0031 | 0.0028 | 0.0029 | |||
| Step 3 Time | 0.0022 | 0.0024 | 0.0022 | |||
| Step 4 Time | 0.035 | 0.048 | 0.04 | |||
| Step 5 Time | 0.083 | 0.102 | 0.094 | |||
| Step 6 Time | 0.014 | 0.018 | 0.015 | |||
| Step 7 Time | 0.018 | 0.003 | 0.0029 | |||
| Post-processing Time | 0.199 | 0.31 | 1.01 | |||
| Total Time ⌃⌃ | 206.15 | 197.988 | 206.84 | |||
| NP = 2 | NP = 3 | NP = 4 | ||||
|---|---|---|---|---|---|---|
| Elements | Boundary Elements | Elements | Boundary Elements | Elements | Boundary Elements | |
| Subdomain 1 (red) | 579 | 327 | 298 | |||
| Subdomain 2 (blue) | 559 | 403 | 277 | |||
| Subdomain 3 (magenta) | – | 53 | 408 | 109 | 279 | 99 |
| Subdomain 4 (cyan) | – | – | 284 | |||
| Total FEM Elements | 1138 | 1138 | 1138 | |||
| FEM Nodes | 359 | 30 | 359 | 50 | 359 | 47 |
| Pre-processing Time | 34.69 | 36.65 | 34.32 | |||
| Step 1 Time | 0.01 | 0.011 | 0.01 | |||
| Step 2 Time | 0.0032 | 0.0025 | 0.0025 | |||
| Step 3 Time | 0.0021 | 0.0021 | 0.0023 | |||
| Step 4 Time | 0.026 | 0.032 | 0.026 | |||
| Step 5 Time | 0.03 | 0.039 | 0.028 | |||
| Step 6 Time | 0.016 | 0.0137 | 0.013 | |||
| Step 7 Time | 0.002 | 0.003 | 0.0023 | |||
| Post-processing Time | 0.11 | 0.3897 | 0.29 | |||
| Total Time ⌃⌃ | 34.89 | 37.1461 | 34.70 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhagatji, J.; Asundi, S.; Thompson, E.; Nguyen, D.T. Optimal Domain-Partitioning Algorithm for Real-Life Transportation Networks and Finite Element Meshes. Designs 2023, 7, 82. https://doi.org/10.3390/designs7040082
Bhagatji J, Asundi S, Thompson E, Nguyen DT. Optimal Domain-Partitioning Algorithm for Real-Life Transportation Networks and Finite Element Meshes. Designs. 2023; 7(4):82. https://doi.org/10.3390/designs7040082
Chicago/Turabian StyleBhagatji, Jimesh, Sharanabasaweshwara Asundi, Eric Thompson, and Duc T. Nguyen. 2023. "Optimal Domain-Partitioning Algorithm for Real-Life Transportation Networks and Finite Element Meshes" Designs 7, no. 4: 82. https://doi.org/10.3390/designs7040082
APA StyleBhagatji, J., Asundi, S., Thompson, E., & Nguyen, D. T. (2023). Optimal Domain-Partitioning Algorithm for Real-Life Transportation Networks and Finite Element Meshes. Designs, 7(4), 82. https://doi.org/10.3390/designs7040082







