Binary Integer Formulations for Task Allocation and Optimal Labor Cost in Small and Medium Apparel Manufacturing

Abstract

In small apparel manufacturing, unit price determination is often based on production duration given by customers and design complexity rather than information relating to internal labor resources. However, labor expertise and skills are critical factors that outweigh the machinery and technology in small and medium apparel companies. The quality of the product greatly depends on the experience and delicacy of the tailors. Using data on labor skill and wage levels in the planning process will benefit human resource utilization, increasing productivity, and profits effectively. This paper proposes a general mathematical model for task allocation and cost optimization for small and medium apparel companies. The model handles task allocation and cost minimization problems that must ensure processing time requirements and balance workloads for operators. The developed model tests two case studies in a published paper. The results prove that although the proposed model is simple, it has high applicability and efficiency in solving allocation optimization problems. The authors then integrate the formulations into a Standalone desktop app in the MATLAB “App designer” module. With a standalone desktop app, end users can enjoy the application. This app has a user-friendly design. Users unfamiliar with computers or planners with no background in programming can use the app to tackle similar optimization problems. The proposed mathematical model can further expand to include more complex issues in apparel companies and can also be a good reference for other fields.

1. Introduction

The Vietnamese apparel industry varies in size and scale. According to a report by FPT Securities in 2017, 98% of those manufacturers have fewer than 5000 workers and employees [1]. Most of these manufacturers pursue the Cut-Make-Trim (CMT) model. In this business model, customers will provide materials, designs, and requirements, while the manufacturers are responsible for cutting, sewing, and packaging. Hence, the majority of profit comes mainly from labor costs, and companies gain a profit of 1–3% of the unit price [1].

For most sample shops and apparel manufacturers, the completion and quality of an order would receive more attention than production planning and job allocation. Regularly, the unit price is estimated based on the production duration given by customers and design complexity rather than information relating to internal resources. This estimation causes unforeseen risks with labor costs. Because the labor resource has not been considered from the beginning, the production progress is relaxing at the start but rapid and rushing at the end. Some employees have to work overtime to catch up with the due date. These overtime hours additionally impact labor costs and profits.

Reasons preventing shop managers from planning are mathematical skills and computer skills. Missing data collection and storage hinder the computation. Furthermore, the design diversity and small volume are distinct features of apparel manufacturing, leading to changes in the production process and resources. Planners require significant time to update the processing data for every order. Another factor is the mathematical and computer skills of planners. Planners are unfamiliar with using mathematical models and computer programming to store data or write code. Current practice in sample shops is to use Excel spreadsheets to record worker productivity for monthly salary payments.

The above difficulties can be solved if there is a model for job allocation with the objective of optimizing labor costs. The shop managers can rely on the provided cost to discuss with customers and obtain the optimal profit. Not only does the model help managers estimate the labor cost in advance, but it also provides managers with performance data on employees for further training.

Integer Linear Programming has been adopted in a wide range of fields in the manufacturing industry [2,3]. J. Blazewicz presented a general paradigm for scheduling problems, considering various constraints [4]. Peter Bucker then synthesized problems in scheduling algorithms and defined basic parameters for a scheduling problem, including task data, task characteristics, machine environment, and optimality criteria [5]. Theresa Metty et al., studied the procurement process at Motorola, Inc., before developing and applying Mixed-Integer programming to a web-based negotiation platform in 2005 [6]. The approach of Motorola, Inc., helped reduce the time and effort for travel, preparation, and negotiation with global suppliers and optimized contract awards across sectors. The approach saved more than $600 million for the company. This project is a notable example of the association between algorithms, software solutions, and business processes.

Carlos Gomes da Silva et al., proposed a mixed-integer linear programming model to solve an aggregate production planning problem [7]. The model considered constraints on plant operators, production capacity, and inventory level to define an optimal solution for profit, late orders, and workforce changes. The model assumes that the operator’s skill is equivalent for all operators. This assumption contradicts the situation in practice. The interactive feature of the proposed decision support system (DSS), which was not discussed, is another limitation of this research. Hadi Gökcen adopted integer linear programming that considered the subprocesses, available stations, and process cycle time to achieve balanced assembly lines [8]. Sirikarn Chansombat presented a model for maintenance scheduling that considers maintenance, production, and order dimensions [9]. The human resource dimension was not mentioned in this scheduling model. Joost T. de Kruijff studied the issue of a low-volume industry characterized by a moderate production quantity and the complexity of the supply chain [10]. This paper proposes a model with two algorithms to solve complex problems with over 7000 constraints and 13,000 variables.

Recently, several new approaches have been proposed to tackle complex scheduling problems. Wang et al., presented a multi-objective optimization challenge to consider both energy consumption and makespan. This problem is tackled using an enhanced algorithm called multi-objective invasive weed optimization (MOIWO). The paper outcomes demonstrate the MOIWO algorithm’s effectiveness over other methods for the scheduling problem under consideration [11]. The meta-heuristic algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), memetic algorithm (MA), and simulated annealing (SA), have been widely employed to effectively solve mixed integer linear programming (MILP) models in the context of production scheduling. These methods have been applied successfully in various industrial fields and demonstrate their advantages in tackling complex and large-scale problems [12,13,14,15]. However, the computational time is a big concern. To accelerate computing time, researchers have conducted extensive investigations into the integration of constraint programming concepts and problem decomposition methodologies [16,17].

Wong et al., also recognized the important role of operator skill. They applied operator skill and inventory capability in an optimization algorithm to achieve line balancing to minimize the overall operative idle time [18]. Mok et al., introduced a genetic algorithm to assign job orders to sewing lines [19]. This approach replaced the operator data with the sewing line data (number of lines, number of shifts, capacity constraints of production lines). Although the computational techniques in the above projects are quite advanced, their scope is limited to operational improvement [20]. One of their objectives is the production cost, which is determined by the unit cost in a plant and the manufactured quantity. However, the unit production cost is a difficult question when the apparel style changes dynamically and the labor resources constantly vary. A combination of operator skills and the corresponding labor wage in planning could help achieve both optimal allocation and financial benefit.

This paper aims to develop a general mathematical model for task allocation for small and medium apparel companies. The primary objective is to minimize the overall labor cost, considering constraints such as operator skills, labor wages, workload balance, and processing time. The structure of this paper is organized as follows: Section 2 provides a problem description and introduces the proposed mathematical model. In Section 3, the focus is on evaluating the effectiveness of the proposed mathematical model through case studies. Finally, Section 4 summarizes the findings and draws overall conclusions.

2. Problem Description and Proposed Mathematical Model

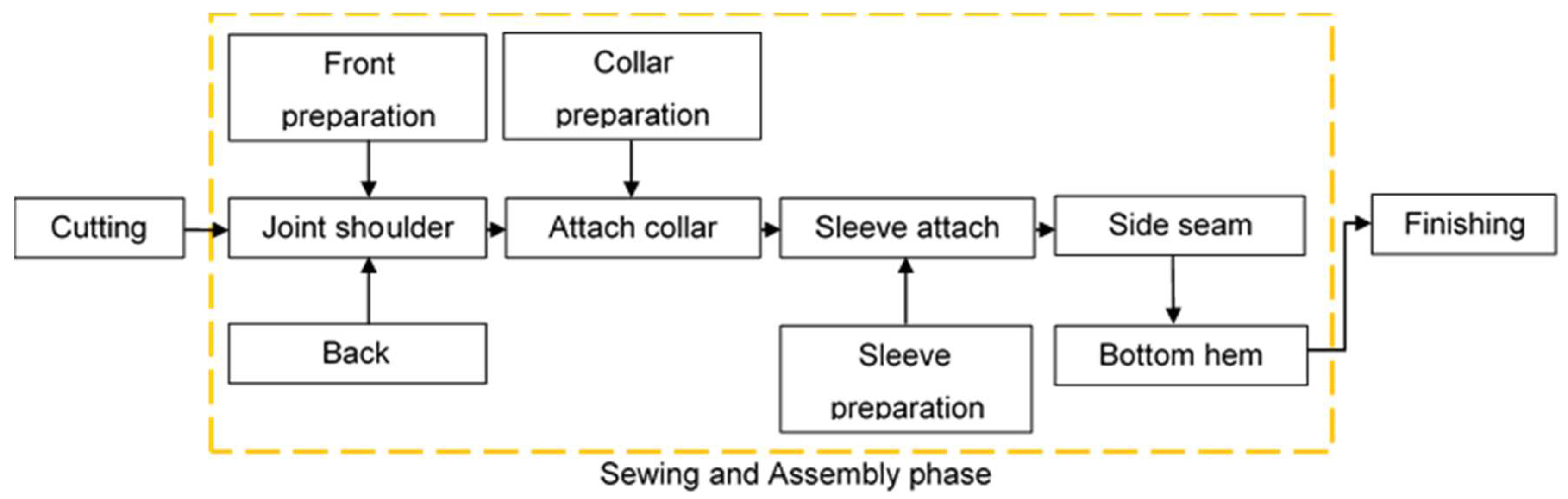
Cut-make-trim (CMT) is a model in the apparel production system in which manufacturers are responsible for cutting, sewing, and assembling the product [1] (Figure 1). In Vietnam, a vast majority of apparel manufacturers follow the CMT model, which will be the main objective of this paper.

An individual with multiple skills can execute all phases to complete the entire garment. However, this approach requires highly skilled labor, leading to costly pay. The approach is popular in sample rooms that produce in small quantities with a high focus on quality. Another approach is the group system, which is preferable in bulk production because it can save labor costs, employ more workers, and increase the potential for automation. In this system, an operator specializes in one major component and executes it from beginning to end [21]. Particularly, a group of operators specializing in collars will prepare the hood and then assemble the hood, collar, and body. They are also required to perform all operations, such as marking and trimming, to complete their components.

The specialization of operators in specific components is considered a worker’s skill. An operator with a high skill level can handle complex parts well. Each level has a corresponding wage.

In addition to operator skills, there are other important attributes in costing and production planning:

• Pool of operators;
• Type and quantity of processing equipment;
• The fund for working time;
• Daily working time;
• Time to produce a single product and time to produce each component piece;
• Number of products to be produced.

For apparel manufacturing, workmanship is a critical factor, outweighing machinery and technology. The quality of a product depends mainly on the dexterity, experience, and delicacy of the operators. Although the support of machinery, fixtures, and tools makes the production process approachable for more professional levels, it appears impossible to achieve equivalence in expertise for all operators. Few operators might be able to complete the entire product by themselves, while some can perform certain types of components in a product. Hence, skill level is an indicator of the ability and wages of workers. Two assumptions could be drawn from this practice. First, an operator at a specific skill level can perform components with correspondingly lower difficulty. Second, the parameter corresponding to the difficulty level of the process may be deduced based on the cycle time because the complex process requires greater carefulness and delicacy from operators.

The mathematical model in this paper considers a manufacturer who employs $n$ operators for a production process consisting of $m$ smaller processes. An operator $i$ whose skill level ${SL}_i$ is considered capable of the process $j$ if the difficulty level is denoted as ${DL}_j$ ≤ ${SL}_i.$ There are five levels for apparel operator skills, corresponding to 5 levels of difficulty ranging from 1 to 5. A binary variable SM_ij will equal 1 if the operator $i$ is capable of component $j$ and 0 otherwise.

The hourly wage $W_i$ of operators, the cycle time ${CT}_j$, and the order demand O are considered to determine the labor cost. The model considers the duration D that a customer requested from the manufacturers, but it does not equal the production time. The total available production time equals the subtraction of the given duration and the order processing time, which is the time for order receiving and processing, varying from organization to organization. By multiplying the total available production time with the hourly working time Wt, the total production time in hours can be obtained. The working time Wt at the manufacturer per day is constant.

The workload should be balanced among operators. Thus, the model considers the target capacity level Cap for all operators who are intended for this production. This level will act as a lower limit on the involvement of each operator in the production. If this parameter equals 0, it means operators might or might not be involved in the production. The model will provide a solution with an optimal operator quantity and cost in that case.

The amount of available equipment for producing a component is considered in this model. In addition, there are some additional assumptions:

• A process can be handled by one or more operators;
• There is initially no work in the progress buffer;
• There is no parallel process.

The objective of this model is to use the linear integer program principle to find an optimal labor cost and to obtain a job allocation plan. This plan can present the quantity of each component to be produced by a particular operator.

Objective: The objective function will consider the following components:

• Labor cost;
• Processing time;
• Workload.

A practical and satisfactory allocation must ensure the time requirement and balance the workload for operators. Ultimately, the primary goal is to have the minimum labor cost so that decision-makers can estimate the optimal outsourcing price.

Variables:

• SM_ij is a binary variable indicating the capability of operator $i$ to perform component j.
• $X_{ij}$ is an integer variable indicating the quantity of component j that shall be produced by operator $i$
• $Y_{ij}$ is a binary variable indicating whether operator i is assigned to component $j$

Parameters:

• $i$: index of operators $i\in$ {1, 2, 3, …,$n$}
• $j$: index of components $j\in$ {1, 2, 3, …,$m$}
• ${SL}_i$: skill level of operator $i$ ${SL}_i\in$ {1,2,3,4,5}
• ${DL}_j$: difficulty level of component $j$ ${DL}_j\in$ {1,2,3,4,5}
• $W_i$: hourly wage of each operator $i$($)
• ${CT}_j$: cycle time of a component $j$ (seconds)
• Oj: number of semiproducts in each process (pcs)
• D: duration given by customer (days)
• OPT: order processing time (days)
• APT: total available production time (days)
• Wt: working time per day (hours)
• Cap: target capacity level for all operators (%)
• $E_j$: quantity of available equipment for component $j$

The objective is to allocate tasks to operators for optimal labor cost, and the objective function can be presented as:

$$MIN\sum _{i=1}^n\sum _{j=1}^m{X}_{ij}\frac{{CT}_j·W_i}{3600}$$

(1)

The main goal of this model is to minimize the total labor cost, which is calculated using Equation (1). In the equation, $X_{ij}$ represents an integer variable indicating the quantity of component j that should be produced by an operator i. The cost that is paid for an operator i to make $X_{ij}$ component j is determined by the product of the component quantity $X_{ij}$, the cycle time of component j (in seconds), and the hourly wage of operator i (expressed in dollars) divided by 3600 (to convert it to seconds). In general, the problem has m different components and n operators. Therefore, the total cost is the sum of the payments for all n operators to produce all m different components.

Regarding constraints, the produced quantity at each component must equal the order amount from the customer, and only capable operators are allocated to the component.

$$\sum _{i=1}^n{X}_{ij}·{SM}_{ij}=O_j,\forall j\in J$$

(2)

In addition, the total working time of each operator must be within their working time fund:

$$\sum _{j=1}^m{X}_{ij}.\frac{{SM}_{ij}·{CT}_j}{3600}\le APT·Wt,\hspace{1em}\hspace{1em}\forall i\in I$$

(3)

where APT = D − OPT

To meet time requirements and balance workload, operators should be involved in the production process at a certain level. Thus, their capacity must be greater than the defined capacity.

$$Cap\le \sum _{j=1}^m{X}_{ij}.\frac{{SM}_{ij}·{CT}_j}{3600·APT·Wt},\hspace{1em}\hspace{1em}\forall i\in I$$

(4)

The number of operators involved in a component should be equal to or less than the amount of equipment available for that component. A binary decision variable $Y_{ij}$ is needed so that if an operator i is assigned to a component j, $Y_{ij}$ equals 1 and 0 otherwise. Therefore, the constraint is:

$$\sum _{i=1}^n{Y}_{ij}\le E_j,\forall j\in J$$

(5)

Constraints (5) and (6) show the relationship between variables X and Y:

$$X_{ij}\le {M.Y}_{ij},\forall j\in J and \forall i\in I$$

(6)

$$X_{ij}\ge Y_{ij},\forall j\in J and \forall i\in I$$

(7)

where M is a large positive number. In case an operator i is allocated for a component process j ($X_{ij}>0)$, then his allocation must be considered ($Y_{ij}=1)$. In contrast, if ($X_{ij}=0)$, then ($Y_{ij}=0)$. The number of operators that can be allocated to a process is limited by (Constraint (4)).

Other boundary constraints are:

$$X_{ij}\ge 0 and integer$$

(8)

$$Y_{ij}\in \left\{\mathrm{0,1}\right\}$$

(9)

The problem is solved in three steps:

• Defining the capability of the operator;
• Formulation of variables, objective functions, and constraints for the problem;
• Solving the linear integer problem.

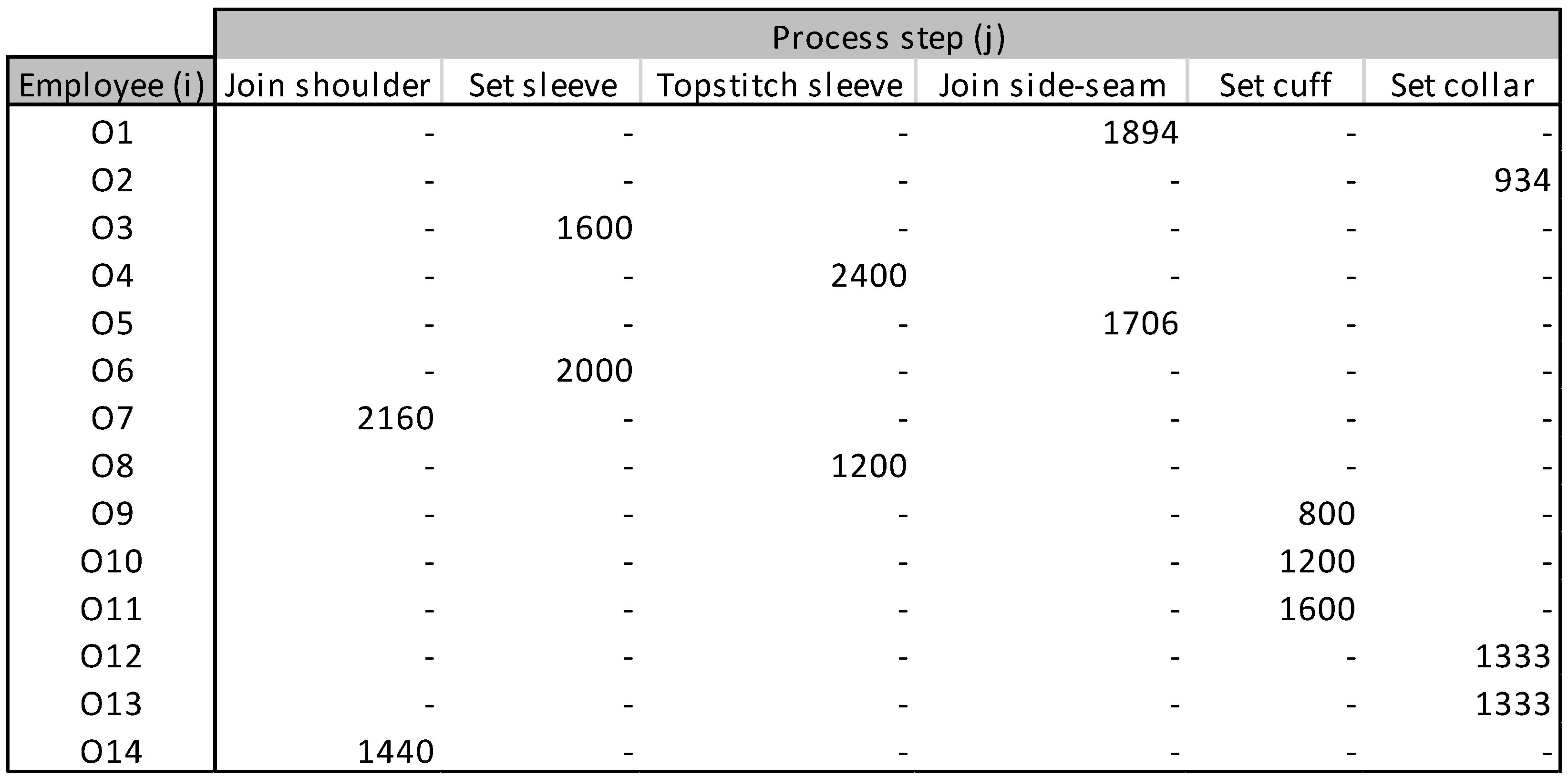
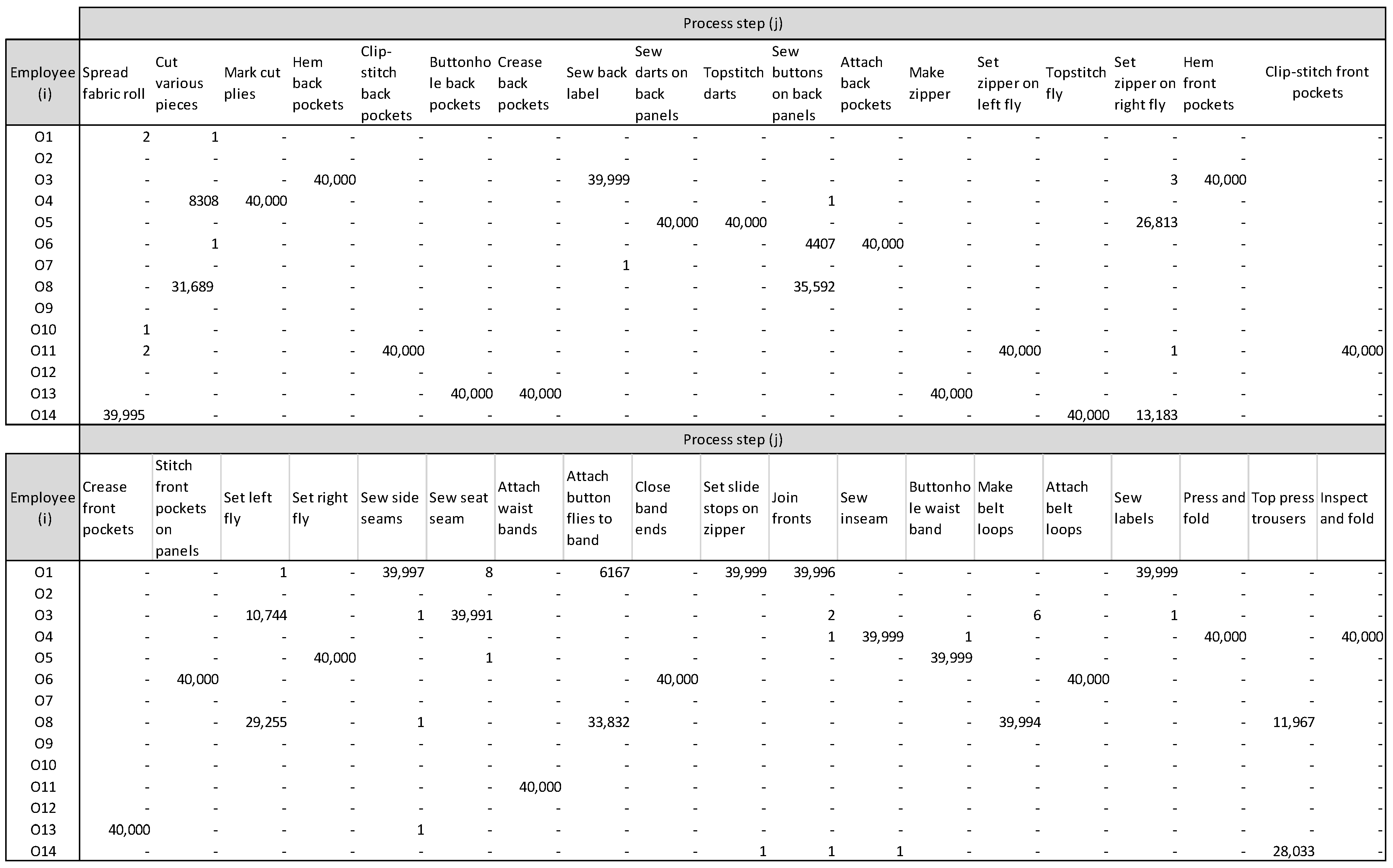
The operator’s skill and difficulty level are given in

Table 1. The skill matrix (SM_ij) indicates the capability of operators for components.

	$\mathbf{Process} \mathbf{Step} \left(\mathit{j}\right)$
Employee ($i$)	1	…	m
1	SM11	…	SM1m
2	SM21	…	SM2m
…	…	…	…
n	SMn1	…	SMnm

to define the operator’s capability. These steps can clearly define the pool of candidates for a particular process using a 0–1 indicator.

Subsequently, elements of the problem, such as decision variables and objective functions, are separately formulated. This approach is also known as the problem-based approach, which is more convenient and comprehensive for complex models [22]. As the model is programmed in MATLAB R2018b, all parameters must be declared as vectors and matrices. The quantity of x and y variables equals the number of operators and the number of processes. 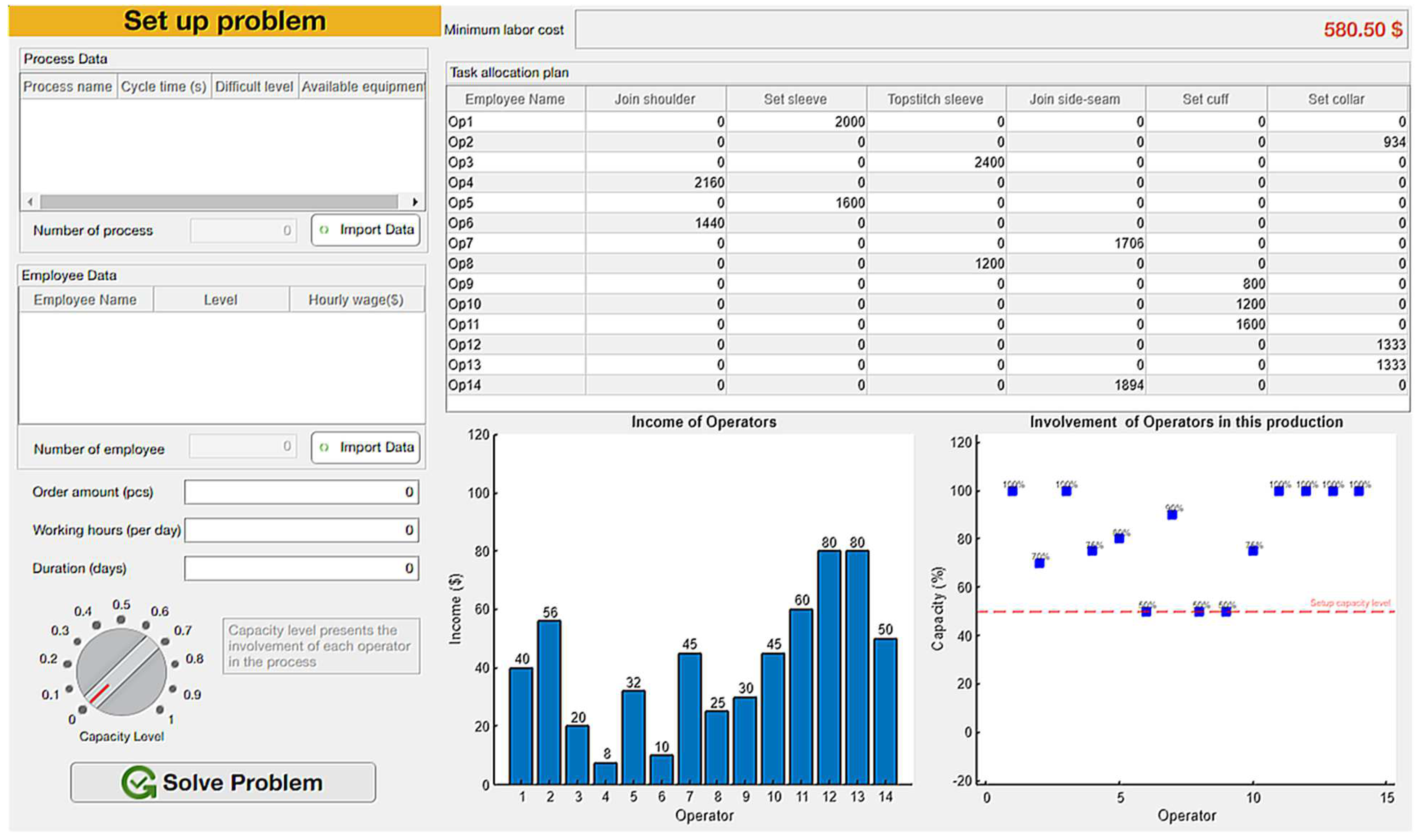The lower bounds of x and y are also vectors, similar to their upper bounds. The value of these bounds is mentioned in the previous section. Then, the objective function and model constraints are formulated following the mathematical model in the previous section before being structured into an optimization problem. Subsequently, this problem will be solved by the “intlinprog” function.

“intlinprog” is a function provided by the MATLAB optimization toolbox^TM for Integer linear programming problems. This section is comprehensive with reference to MATLAB’s Optimization Toolbox User’s Guide [15]. The mathematical model of IP in MATLAB is:

$$\mathit{min}{f}^{T}x subject to\left\{\begin{array}{c}x\left(intcon\right) are integers\\ A·x\le b\\ A_{eq}·x=b_{eq}\\ lb\le x\le ub\end{array}\right.$$

‘intlinprog’ is designed as a minimizer in the objective function. $’intcon’$ is the vector of integer decision variables. $A$ and $A_{eq}$ are coefficients of the decision variable $x$, while b and $b_{eq}$ are right-hand side coefficients in inequalities and equalities. $lb$ and $ub$ represent the lower bound and upper bound of the decision variables.

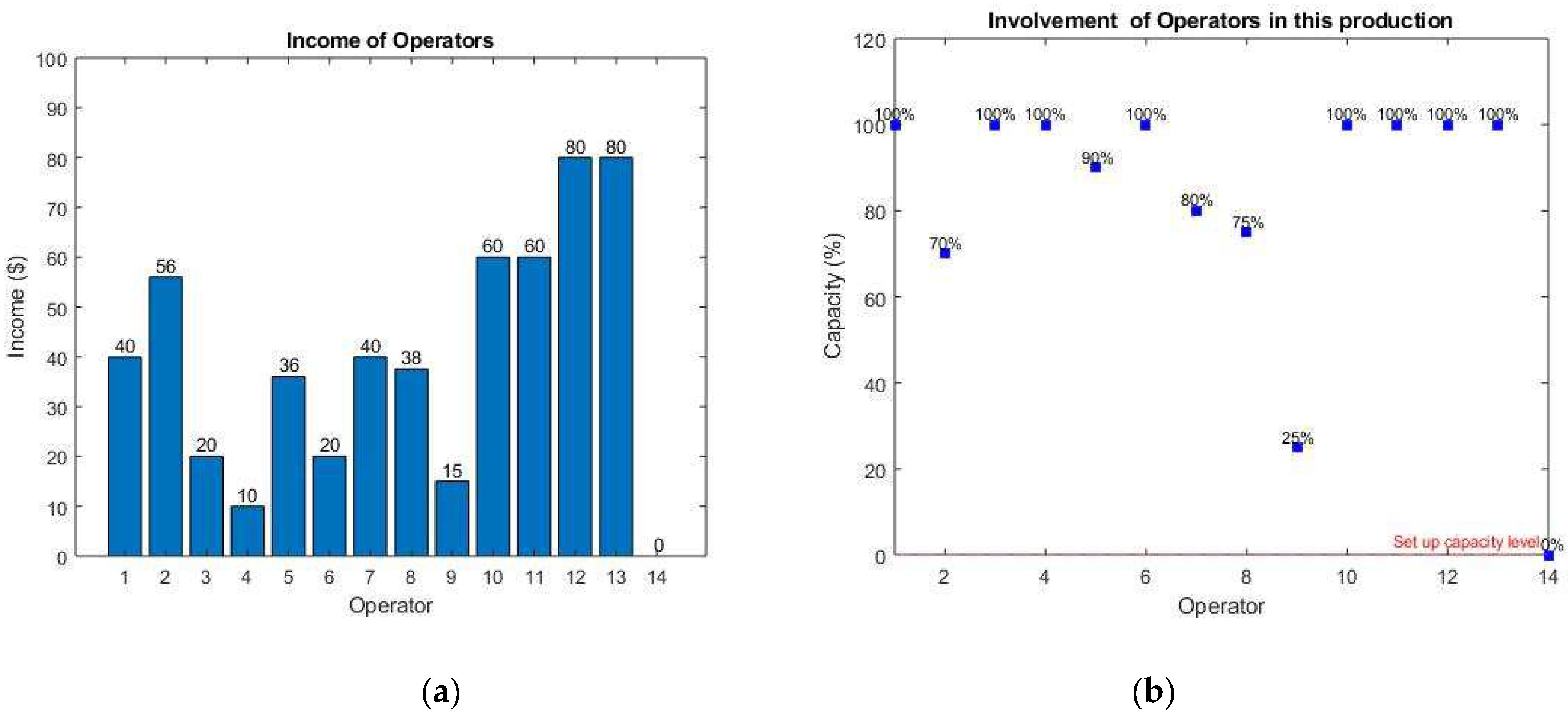
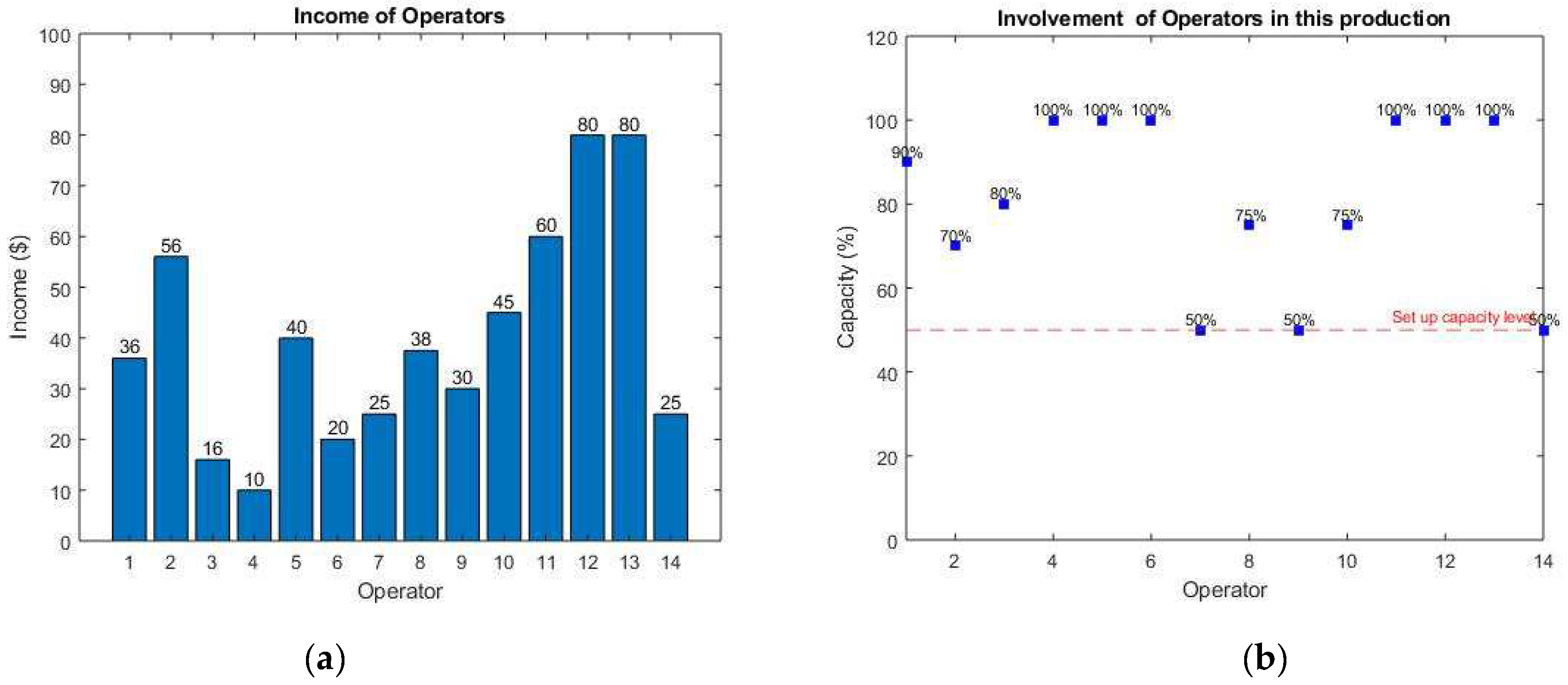
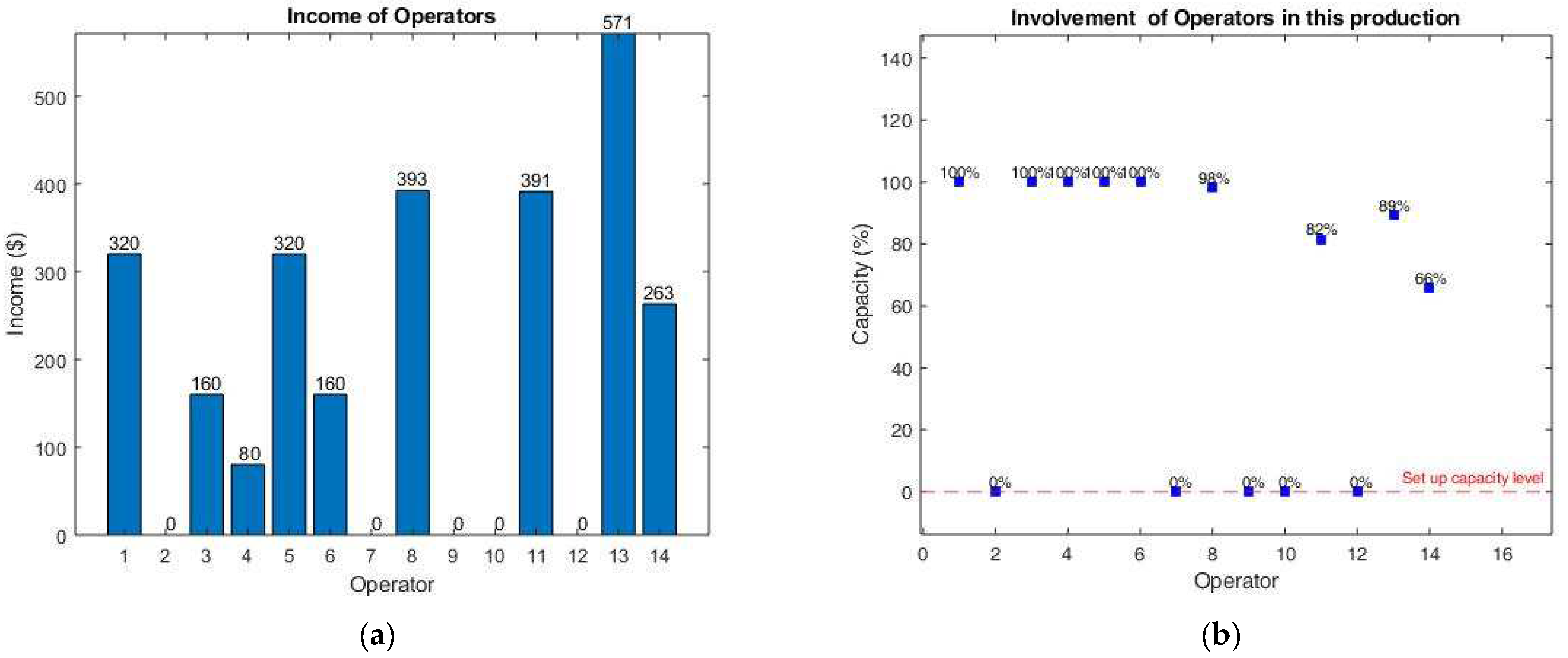
A linear integer problem can have multiple optimal solutions [23]. In this case, there can be multiple allocation plans (or vectors of x) with the same labor cost (or objective value). The difference among these solutions lies in the workload balance of operators. Here, the strategy of the algorithm is to use a constraint relating to the workload so that the integer problem must be solved once. Particularly, the capacity level Cap introduced to Constraint (3) ensures that all operators will be involved in the process with Cap% to 100% of their capacity. Therefore, the workload of operators will be balanced within a target range. With a smaller Cap, this range will be larger, and the workload balance will not be the priority. In that case, the priority will be the optimal labor cost and fewer participants, which are still satisfied by the algorithm.

In the next section, numerical datasets [18,24] are used to demonstrate the application of the model.

3. Evaluating the Proposed Mathematical Model through Case Studies

3.1. Case Study 1

Data on a line-balance problem from W.K. Wong et al. [18] is a reference. A manufacturing process includes 14 operators involved in a production with six assembly components. It is required to produce 3600 product pieces, and the total available processing time target is 72,000 s, or approximately 2.5 days (20 h). The production line works consecutively for 8 h per day. To demonstrate the significance of the target capacity level (Cap), two scenarios with Cap at 0% and 0.5% will be presented. The above data are listed in

Table 2. Operational data used in case study 1.

Parameters	Inputs
Number of operators (n)	14 operators
Number of components (m)	6 assembly components
Demand (O)	3600 pieces
Total available processing time (APT) days	2.5 days
Working time per day (Wt) hours	8 h
Target capacity level (Cap)	Scenario 1: 0
	Scenario 2: 0.5

.

The skill level of the work will be modified to be suitable for the objective of this model. The difficulty level of each component, the labor wage, and the amount of available equipment are also added. These data are presented in

Table 3. Detailed process used in case study 1.

Process Step (j)	Cycle Time (CT)	Difficulty Level (DL)	Available Equipment (E)
Join shoulder	25 s	1	2
Set sleeve	36 s	2	2
Topstitch sleeve	30 s	1	2
Join side-seam	38 s	3	2
Set cuff	45 s	4	3
Set collar	54 s	5	3

and

Table 4. Data of operators in the model.

Employee (i)	Level (SL)	Hourly Wage ($) (W)
O1	3	2
O2	5	4
O3	2	1
O4	1	0.5
O5	3	2
O6	2	1
O7	3	2.5
O8	3	2.5
O9	4	3
O10	4	3
O11	4	3
O12	5	4
O13	5	4
O14	3	2.5

.

The task allocation solutions for the two scenarios are presented in Figure 2 and Figure 3. With no target capacity level, the algorithm suggests involving 13 operators in the production. Operator number 14 will be excluded, which makes the labor cost approximately USD 555 (Figure 2). Consider the scenario when all operators are required to spend at least 50% of their capacity on the production, the optimal labor cost is USD 561 (Figure 3), and the income average and capacity average are USD 40 and 81%, respectively. Both scenarios can complete the production within the given time, indicating that depending on the priority and intention of the user, the model can provide solutions to meet practical demands in real-world situations, such as optimal cost, fewer resources, and a balanced workload. Highly skilled operators are assigned to complex components, increasing their income. Fresh operators are well employed in simple components, taking advantage of labor costs. Figure 4 and Figure 5 present the income and capacity of operators in this production for both scenarios.

To evaluate the proposed model objectively, a comparison between this model and the one from W.K. Wong et al. [18] that is the closest to the proposed model in terms of industrial field and objective. Both models also share the same perspective on the human aspect of the optimization model.

W.K. Wong et al. considered human aspects in optimizing the allocation of an assembly line. They discovered that incompatible operator skills would hinder the production rate of workstations. In their paper, they assumed that each operator could accomplish a set of components in which an operator could only achieve 100% efficiency at one assembly process. For the proposed model, the operators with higher skills can efficiently handle others with lower skills, which follows the apparel workmanship standard set by the Vietnam Ministry of Trade [21].

The model of W.K. Wong et al. [18] aimed for idle time when optimizing the allocation. They considered resource efficiency, while the proposed model considered three dimensions regarding cost, time, and resource efficiency.

The most important difference between the two models is the mathematical approach. W.K. Wong et al. applied the genetic algorithm in their algorithm, which is a computational algorithm based on genetic evolution theory. A potential solution to the problem will be represented as a set of variables. These variables (“genes”) are joined together to form a string of values (“chromosome”). A fitness function is then defined to measure the relative merit of each string in solving the particular optimization problem. A genetic algorithm is often considered a solution for integer problems with regard to nonlinear constraints. With a good initial population, this approach can provide the solution quickly without the branch-and-bound technique [25].

Table 5. Results of task allocation by proposed model and reference work.

	Assigned to Processes by
Operator	Proposed Model	Reference	Operator	Proposed Model	Reference
O1	J 4	J 3	O8	J 3	J 4
O2	J 6	J 6	O9	J 5	J 5
O3	J 2	J 2	O10	J 5	J 5
O4	J 3	J 1	O11	J 5	J 5
O5	J 4	J 3	O12	J 6	J 6
O6	J 2	J 2	O13	J 6	J 6
O7	J 1	J 4	O14	J 1	J 4

is the comparison of the allocations by two methods: the proposed model and W.K. Wong et al.’s work [26].

Despite differences in the problem assumption and objective, there is no significant difference between the two results. A slight difference appears mostly in the allocations for operators with low-level skills because the proposed model utilizes a low-cost operator for as long as it can. The W.K. Wong et al. model aims to reduce production time, so the model strives to assign operators with the highest speed to the target component. Consequently, the model could optimize the production time from 68,606 s to 65,086 s (an approximate 58-minute difference). In practice, the speed of the operator can fluctuate greatly; thus, saving 58 min is difficult to ensure.

Regarding the optimization approach, the reference model employed a genetic algorithm (GA), and the proposed model used a pure linear integer program (IP). The proposed model defines constraints based on the parameters of a practical manufacturing environment. These constraints are well satisfied by the proposed model, while the GA model is unable to satisfy them. In particular, there are in fact two machines for process 4 (J4), but the referenced model assigned three operators to this component. This is a common practice for GA, as it often violates the constraints to search for fitter values. Although the GA strategy seems advantageous in some situations, there are some constraints that must be followed in practice, such as facility and resource constraints. In terms of model performance, the computing time of the IP model is shorter than the computing time of GA (0.52 s compared to 50,400 s) (

Table 6. Differences between the proposed model and the referenced model.

	Proposed Model	Reference
Objective	Minimize labor cost	Minimize idle time
Approach	Binary integer program	Genetics algorithm
Objective component	3	1
Computing time (s)	0.52	50,400

). When there is only one factor of efficiency for consideration, there is plenty of choice for allocation. This might be one of the contributions to the long computing time for the W.K. Wong et al. work. For the proposed model, the branch and bound technique proved to be more efficient in this problem when the number of constraints is clearly defined in moderate quantity (7 constraints). These constraints are helpful in creating a solution bound, making the search time considerably shorter.

Additionally, while the W.K. Wong et al. model provides only the general allocation, the proposed model can specify the number of components that an operator will produce. These data can be utilized in the production planning phase.

3.2. Case Study 2

Consider the data from a discrete-event simulation in trouser manufacturing from Pamela S. Rosser et al. [24]. The dataset was selected from a large traditional trouser manufacturing plant with 37 assembly components. The plant often produced 40,000 product pieces per week, and the production line worked one 8-hour shift per day. Because the labor resource data were not provided, the operator data from Table 4 will be utilized, and the target capacity level will be 0. The operational data for this example are summarized in

Table 7. Operational data used in case study 2.

Parameters	Inputs
Number of operators (n)	14 operators
Number of components (m)	37 assembly components
Demand (O)	40,000 pieces
Total available processing time (APT)—days	20 days
Working time per day (Wt)—hours	8 h
Target capacity level (Cap)	0

and

Table 8. Detailed process used in case study 2.

Process Step (j)	Cycle Time (CT)	Difficulty Level (DL)	Available Equipment (E)
Spread fabric roll	2.80 s	1	4
Cut various pieces	3.40 s	1	11
Mark cut plies	3.48 s	1	14
Hem back pockets	3.34 s	2	3
Clip-stitch back pockets	2.61 s	4	2
Buttonhole back pockets	3.07 s	5	3
Crease back pockets	3.6 s	5	5
Sew back label	3.34 s	2	3
Sew darts on back panels	3.03 s	3	4
Topstitch darts	2.95 s	3	4
Sew buttons on back panels	2.94 s	1	3
Attach back pockets	3.47 s	2	13
Make zipper	2.58 s	5	1
Set zipper on left fly	2.95 s	4	4
Topstitch fly	3.28 s	3	5
Set zipper on right fly	3.24 s	2	5
Hem front pockets	3.34 s	2	3
Clip-stitch front pockets	2.61 s	4	2
Crease front pockets	3.6 s	5	4
Stitch front pockets on panels	3.47 s	2	13
Set left fly	3.46 s	1	7
Set right fly	3.22 s	1	7
Sew side seams	3.46 s	1	11
Sew seat seam	3.44 s	1	5
Attach waist bands	3.56 s	4	11
Attach button flies to band	3.54 s	1	3
Close band ends	3.6 s	2	13
Set slide stops on zipper	3.36 s	3	7
Join fronts	3.49 s	1	6
Sew inseam	3.37 s	1	12
Buttonhole waist band	3.01 s	1	4
Make belt loops	2.31 s	2	2
Attach belt loops	3.52 s	2	22
Sew labels	3.54 s	2	5
Press and fold	3.37 s	1	11
Top press trousers	3.28 s	1	5
Inspect and fold	3.46 s	1	19

.

The allocation details are presented in Figure 6. Figure 7 illustrates the income of operators and their involvement in the production scenario of case study 2.

When no target capacity level is needed, the production of 40,000 pairs of jeans in 20 days can cost USD 2659 for labor resources. The algorithm suggests involving 10 operators out of the 14 available operators in the production. Among the nine allocated operators, each will spend an average of 90% of their capacity on this production, earning an average of USD 273 for this production batch.

The dataset of case study 2 reflected a practical apparel assembly problem. In fact, a complete process usually comprises over 30 subprocesses or components with the support of different types of sewing machines. Via this example, the algorithm proved its application:

• The algorithm can provide the shop manager with how many labor resources he or she should use in this production;
• The algorithm can visualize the workload and income of operators in the production;
• The algorithm can confirm to the manager whether the production can be finished within the given time;
• Importantly, the algorithm can provide the manager with a data-based labor cost that he can use to define an appropriate outsource price.

Although the proposed model can provide apparel shop managers with optimal solutions, it requires programming skills to script and obtain the solution. For this reason, the model should be integrated into a user-friendly application so that users who are unfamiliar with the computer are able to use and take advantage of this application. The developed application as an interface between the human, the computer, and the mathematical model will make the interaction seamless. This part presents the approach to building the application. Because apparel manufacturing is a type of process industry, its scheduling application must meet some requirements [27]:

• Feasibility of schedules: the application is required to consider all critical dependencies and restrictions in the plant to ensure the feasibility of a schedule;
• Graphical interface: The application should have a user-friendly interface with visual charts so that the user can easily modify the schedule and evaluate different scenarios;
• Frequent updates: the application should be able to deal with flexibility and changes in processes. The data used in the application should be updated frequently.

In addition to the mentioned requirements, the application should be compatible with small and medium apparel manufacturing. The app should be designed for users unfamiliar with the computer or who can be confused by a large number of setup parameters. The application should ideally free users from the MATLAB license requirement. The MATLAB “App designer”, which is a module introduced in 2016, allows users to develop a standalone desktop app. With this app, end-users can enjoy the developed application without MATLAB installation or internet access. Figure 8 presents the interface of a standalone desktop app that integrates the proposed formulations for task allocation and cost optimization problems. This app can be used by small and medium apparel companies or in other fields.

4. Summary

Amid the global pandemic that greatly affected manufacturing industries, Vietnam reached the top two countries of apparel exporters in early 2021, being valued at over $29 billion [28], signaling the great potential growth of the Vietnamese apparel industry if there is support and investment in this industry.

One of the competitive advantages of Vietnamese apparel is the labor resource, also known as the cheap labor advantage. However, from the perspective of management, there are challenges hindering the proper determination of the outsourcing price. Currently, data collection and analysis have not been applied in this process due to the lack of affordable and user-friendly information systems in apparel production. The fundamental mathematical and computer skills of apparel small and medium shop managers make them unable to develop a labor cost application. Currently, there are a variety of mathematical models and information systems providing resource planning, but operator resource planning with regard to cost and workload is not seen. By researching the background of Vietnamese apparel production, this paper has proposed a mathematical model regarding operator data, equipment data, process data, and operational data. Among operator data, operator skill played an important role in allocation so that the solution could ensure the labor cost and the feasibility of the plan.

The model was integrated into an application programmed in MATLAB that was designed for users unfamiliar with the computer so that time and effort could be saved for computation. The application’s graphical visualization also helps users grab the solution quickly and easily.

The desktop standalone application can be further developed to become a decision support system and interact with other information systems in the enterprise. This direction has been greatly applied in recent years, as it can bring complex mathematical techniques and models closer to people. For mathematical techniques, the paper used integer linear programming, which can be considered a classic technique in the optimization field. However, the model can meet all requirements of the problem, and it can also provide a solution within a short amount of time. The research can be an example of the efficiency of integer linear programming over other optimization techniques. The mathematical model can be further implemented and improved with different case studies in the Vietnamese apparel industry and other fields.

In conclusion, this paper proposes a comprehensive mathematical model that effectively solves task allocation and cost optimization, specifically tailored for small and medium-sized apparel companies. By addressing critical challenges such as task allocation, cost minimization, processing time requirements, and workload balancing, this model offers a robust solution to these complex problems. To validate the effectiveness of the proposed model, two compelling case studies were meticulously examined and compared. The results unequivocally demonstrate that, despite its simplicity, the proposed model exhibits remarkable applicability and efficiency in optimizing task allocation strategies.

Furthermore, the authors have seamlessly integrated the model’s formulations into a Standalone desktop application using the MATLAB “App Designer” module. This user-friendly app allows end-users, including those without computer expertise or programming background, to effortlessly engage with the tool and effectively tackle similar optimization challenges. The application underwent testing with a select group of users who worked in the planning area and possessed limited computer familiarity. The results conclusively demonstrate that the developed app is remarkably uncomplicated to use, garnering positive feedback for its intuitive interface accompanied by visual charts. Consequently, users can effortlessly modify resource allocations and easily assess various scenarios.

It is worth noting that the proposed mathematical model can easily expand to tackle even more intricate issues within the apparel industry and can serve as a valuable reference for optimization problems in various other domains.