Control over Grid Reactive Power by Using a Powerful Regenerative Controlled-Speed Synchronous Motor Drive
Abstract
1. Introduction
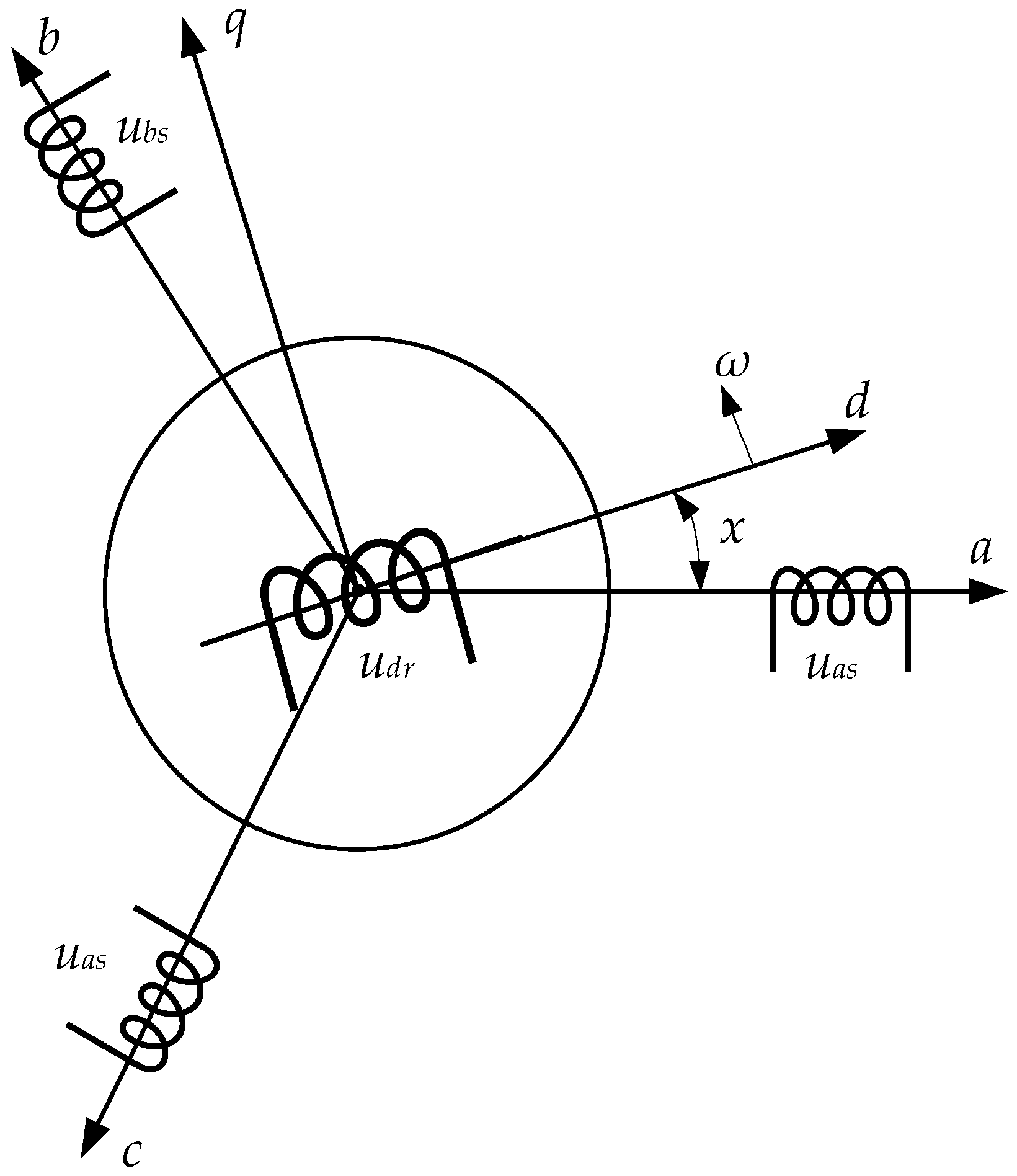
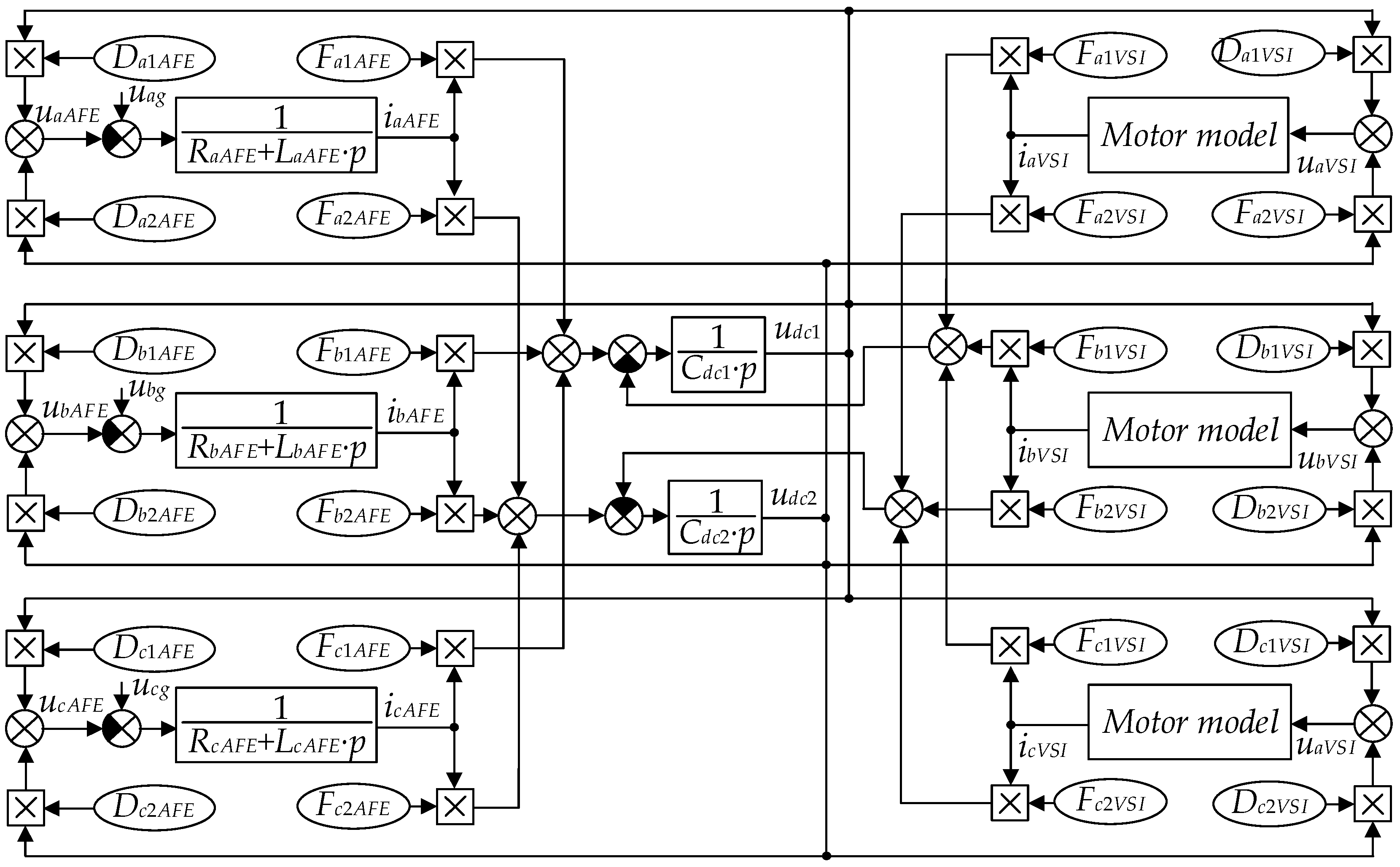
2. Developing a Mathematical Model of the SMD System
- Providing the SM operation with a rated stator flux linkage within the entire load change and speed control range (except for the field weakening mode with two-zone control):
- Providing the SM operation with a power factor equal to (or close to) unity:
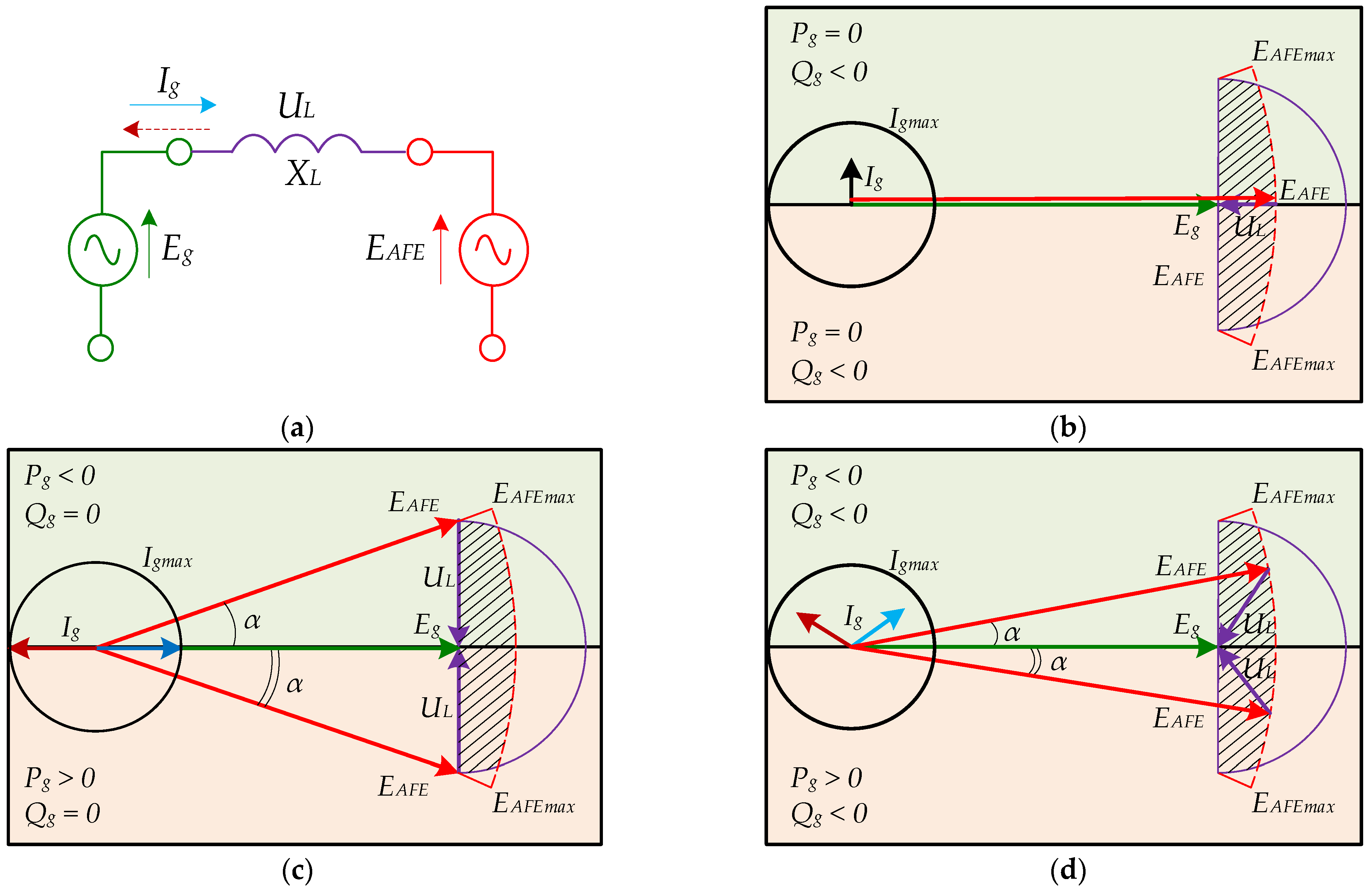
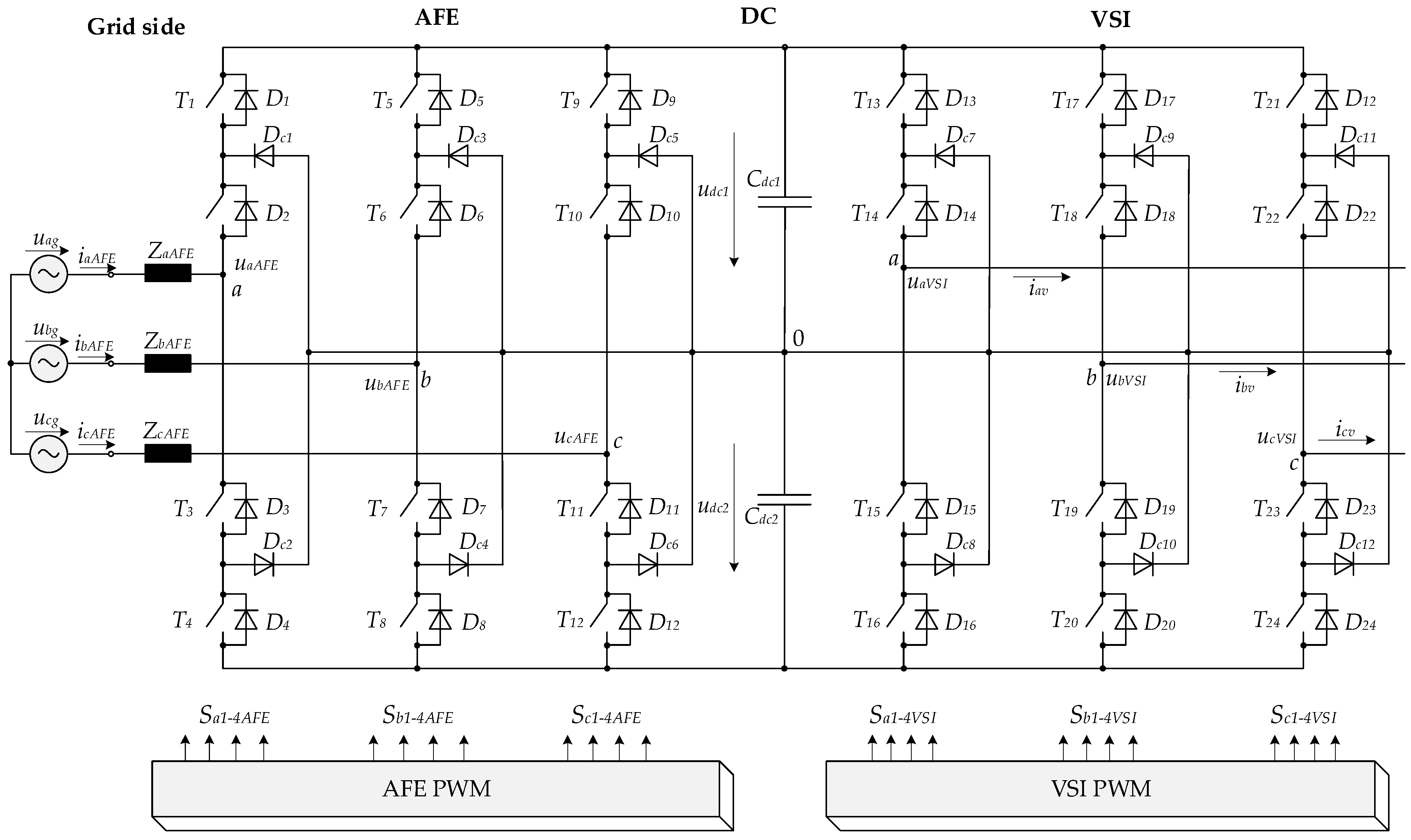
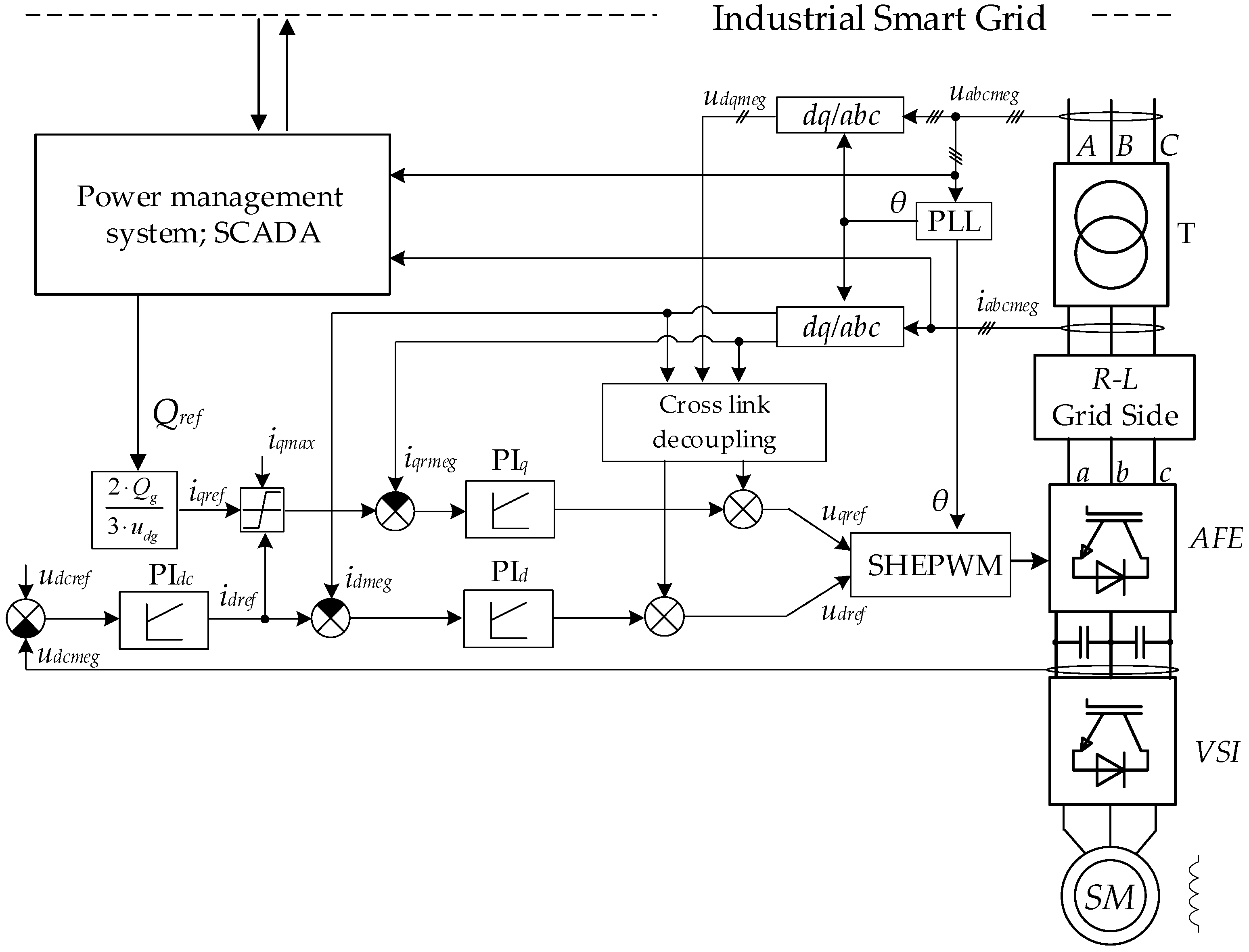
3. AFE Power Description
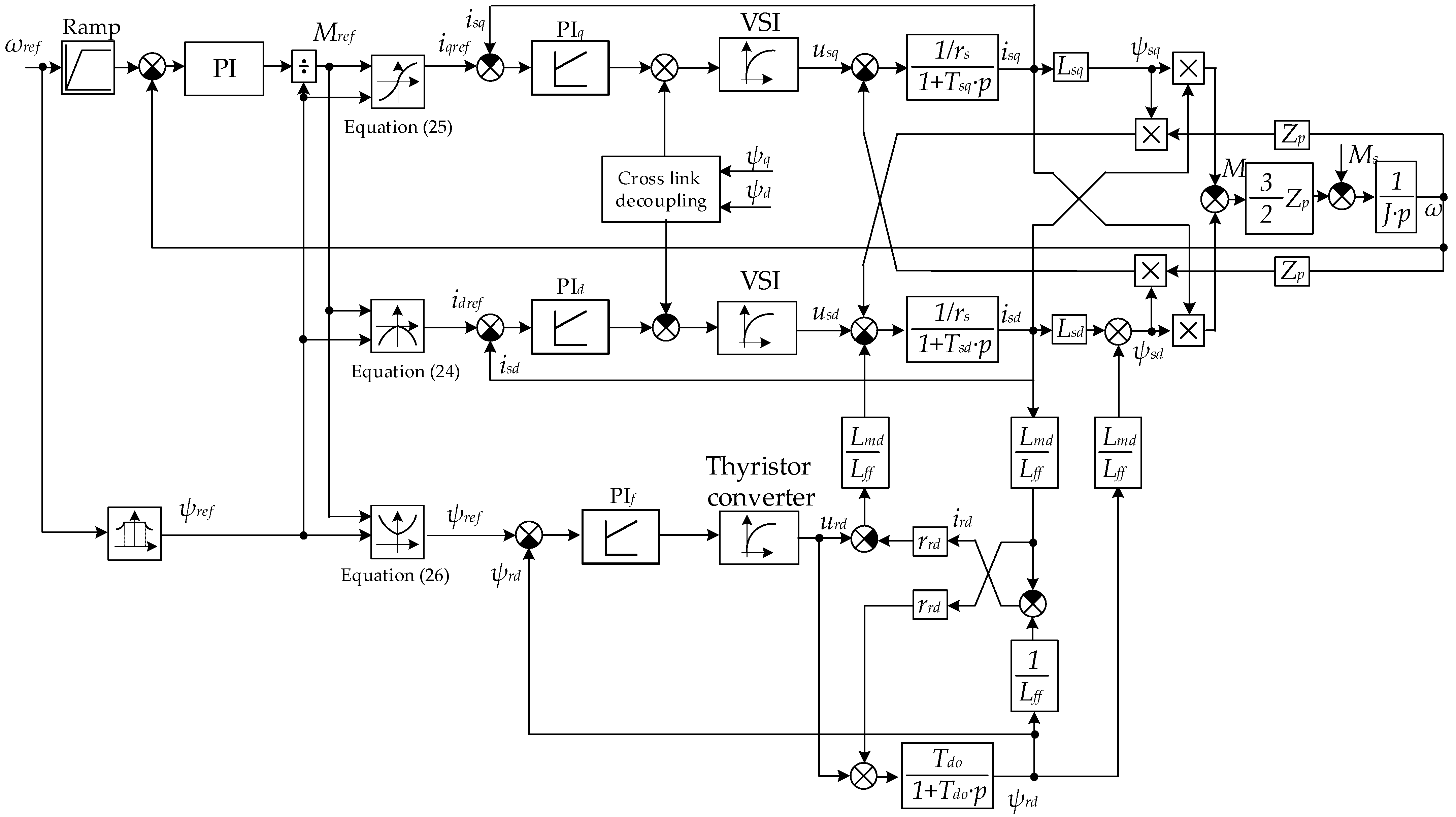
4. Synthesis of a 3L-NPC-AFE-VSI Control System
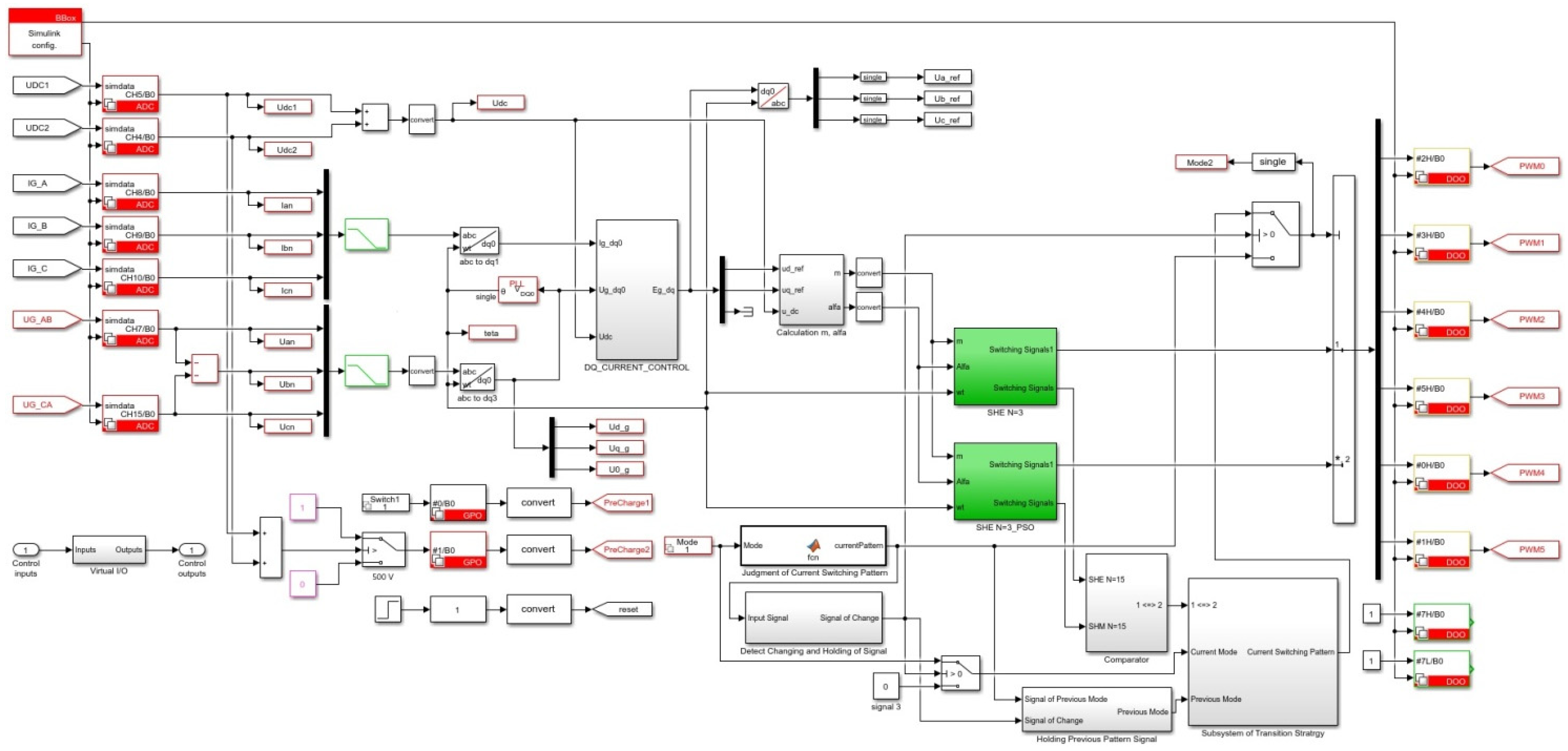
5. Experimental Studies
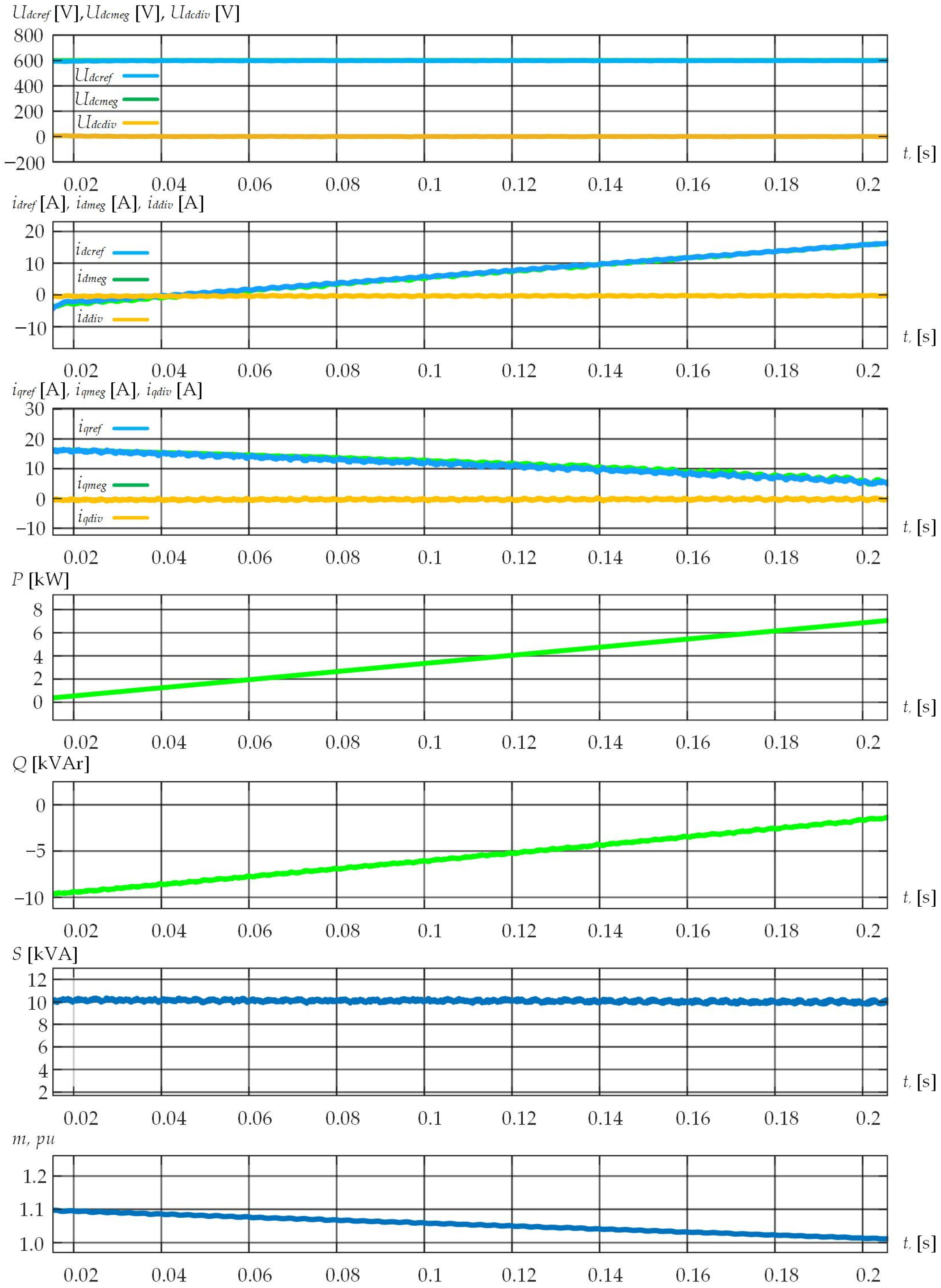
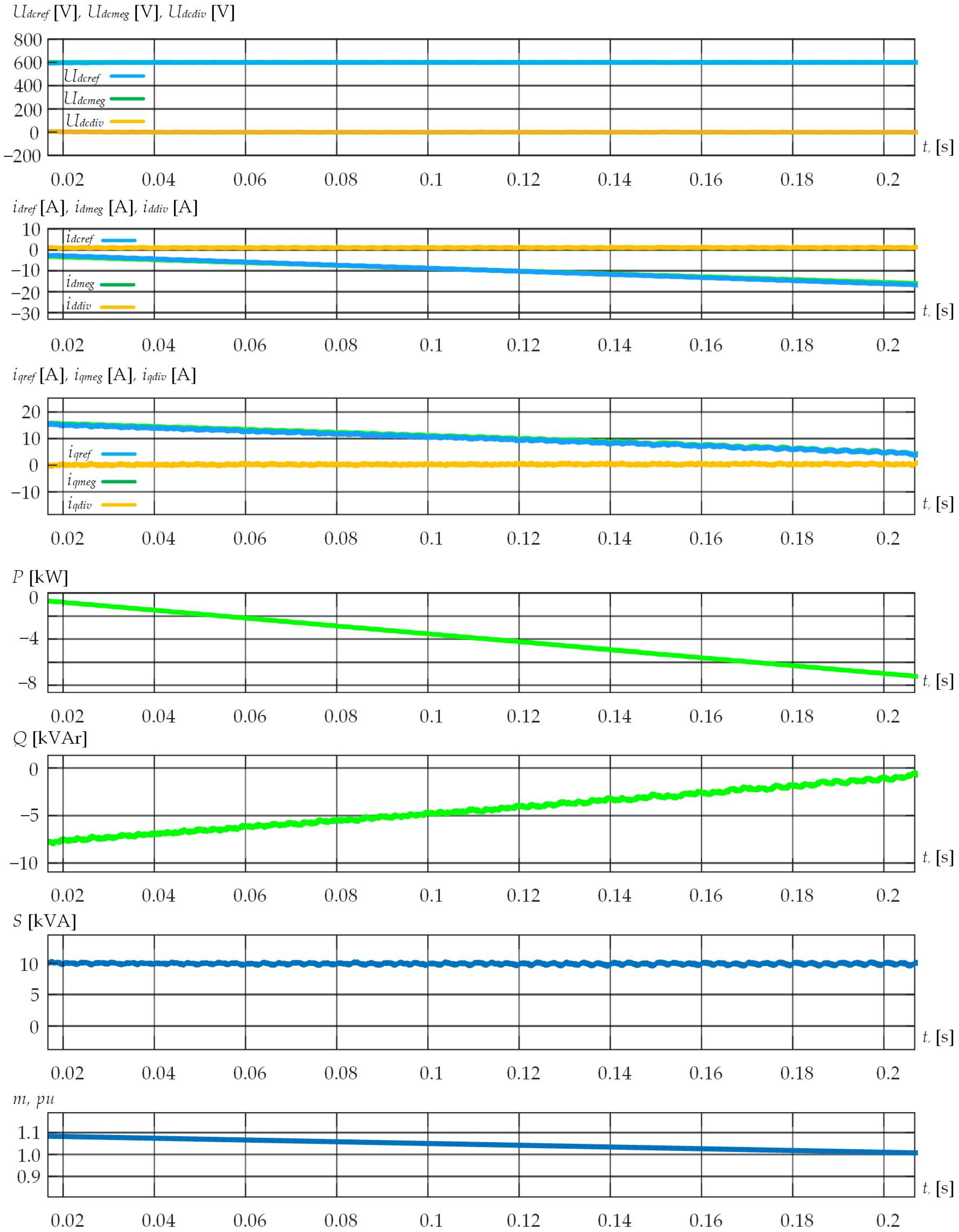
5.1. Laboratory Studies
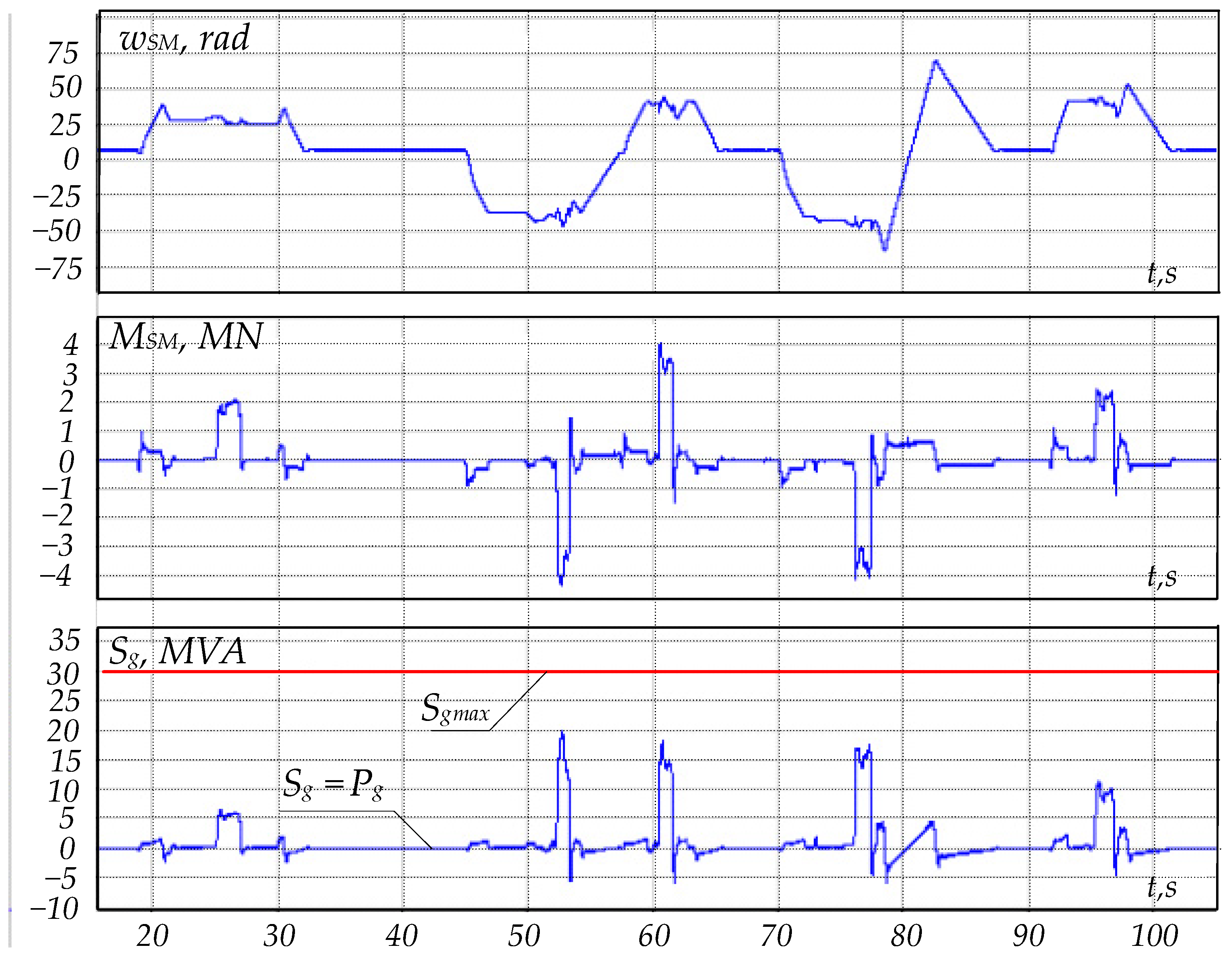
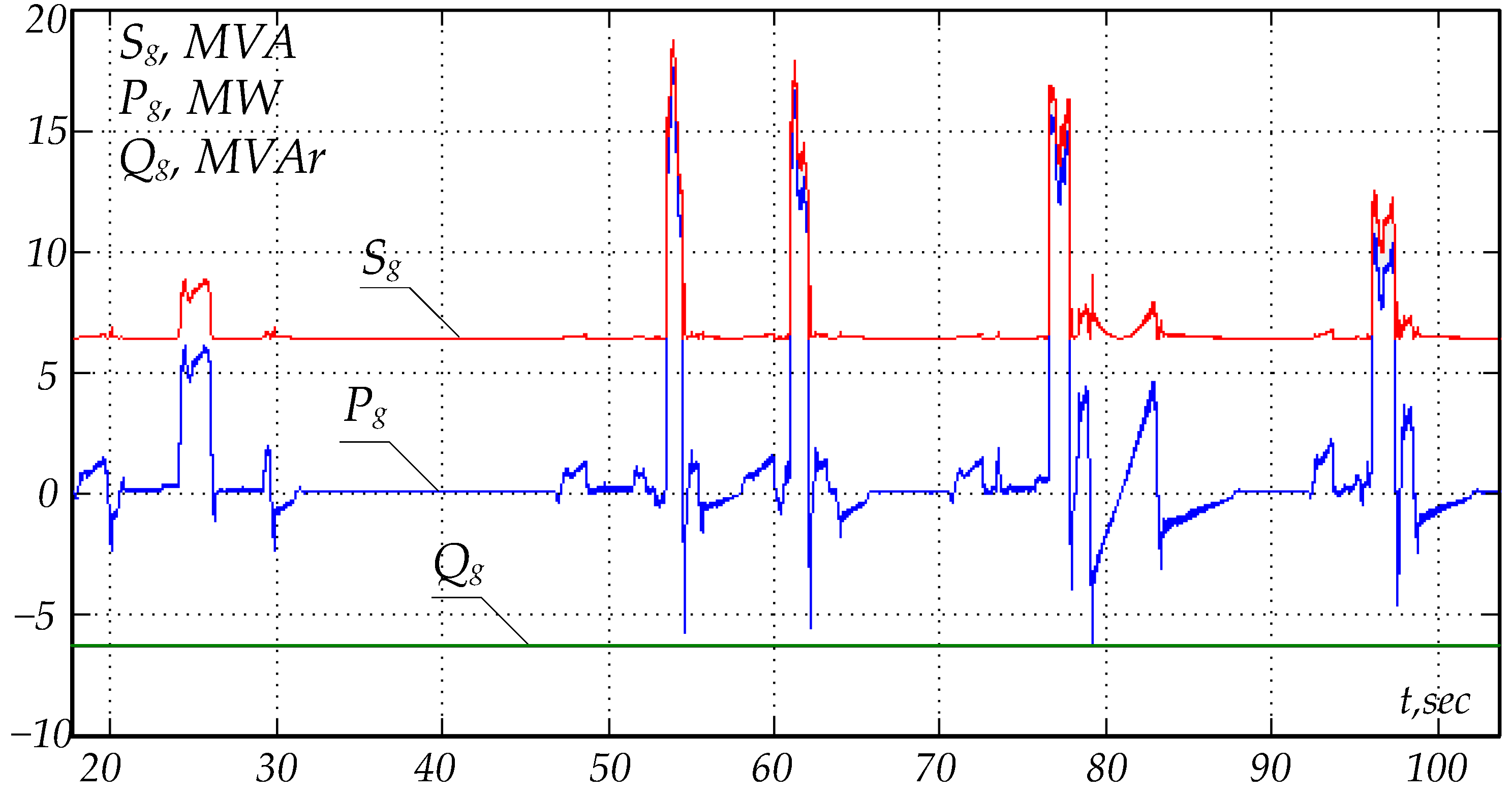
5.2. Industrial Experiment
6. Conclusions
- The review of previous studies revealed underestimated limitations when implementing reactive power compensation modes using a powerful regenerative controlled-speed synchronous motor drive based on a 3L-NPC-AFE-VSI;
- Industrial 3L-NPC-AFE-VSI-SMD systems are developed without considering the possibility of reactive power compensation in the grid. Active power control is a priority; furthermore, it significantly limits the reactive power generation range;
- Increasing the DC link voltage and/or the 3L-NPC-AFE modulation index allows for the increasing and controlling of the compensated reactive power. This paper proposes formulas for determining the maximum reactive power and current;
- Experimental studies at a rolling mill showed that with the recommended modulation index and DC link voltage values, it was virtually impossible to generate reactive power. It was proposed to increase the modulation index to 1.1 during low-load SDM operation modes and at idle, which allowed generating reactive power at a level of 15% of the rated active power;
- The proposed 3L-NPC-AFE reactive power control technique with a dependent current limitation can be used as part of an industrial smart grid to reduce the reactive power at the boundary.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abu-Rub, H.; Bayhan, S.; Moinoddin, S.; Malinowski, M.; Guzinski, J. Medium-Voltage Drives: Challenges and existing technology. IEEE Power Electron. Mag. 2016, 3, 29–41. [Google Scholar] [CrossRef]
- Rajesh, D.; Ravikumar, D.; Bharadwaj, S.K.; Vastav, B.K.S. Design and control of digital DC drives in steel rolling mills. In Proceedings of the International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016. [Google Scholar] [CrossRef]
- Jing, T.; Maklakov, A.S. A Review of Voltage Source Converters for Energy Applications. In Proceedings of the International Ural Conference on Green Energy, Chelyabinsk, Russia, 4–6 October 2018. [Google Scholar] [CrossRef]
- Steczek, M.; Jefimowski, W.; Szeląg, A. Application of Grasshopper Optimization Algorithm for Selective Harmonics Elimination in Low-Frequency Voltage Source Inverter. Energies 2020, 13, 6426. [Google Scholar] [CrossRef]
- Al-Hitmi, M.; Ahmad, S.; Iqbal, A.; Padmanaban, S.; Ashraf, I. Selective Harmonic Elimination in a Wide Modulation Range Using Modified Newton–Raphson and Pattern Generation Methods for a Multilevel Inverter. Energies 2018, 11, 458. [Google Scholar] [CrossRef]
- Orcajo, G.A.; Diez, J.R.; Cano, J.M.; Norniella, J.G.; Pedrayes González, J.F.; Rojas, C.H. Coordinated Management of Electrical Energy in a Steelworks and a Wind Farm. IEEE Trans. Ind. Appl. 2022, 58, 5488–5502. [Google Scholar] [CrossRef]
- Alonso Orcajo, G.; Rodríguez, D.J.; Cano, J.M.; Norniella, J.G.; Ardura, G.P.; Llera, T.R.; Cifrián, R.D. Retrofit of a Hot Rolling Mill Plant with Three-Level Active Front End Drives. IEEE Trans. Ind. Appl. 2018, 54, 2964–2974. [Google Scholar] [CrossRef]
- Orcajo, G.A.; Rodríguez, J.; Ardura, P.; Cano, J.M.; Norniella, J.G.; Llera, R.; Cifrián, D. Dynamic Estimation of Electrical Demand in Hot Rolling Mills. IEEE Trans. Ind. Appl. 2016, 52, 2714–2723. [Google Scholar] [CrossRef]
- Pandit, P.; Mazumdar, J.; May, T.; Koellner, W.G. Real-Time Power Quality Measurements from a Conventional AC Dragline. IEEE Trans. Ind. Appl. 2010, 46, 1755–1763. [Google Scholar] [CrossRef]
- Dybko, M.A.; Brovanov, S.V.; Kharitonov, S.A. Mathematical Simulation Technique for Power Systems based on Diode-Clamped Multilevel VSC. In Proceedings of the Eurocon 2013, Zagreb, Croatia, 1–4 July 2013; pp. 941–948. [Google Scholar] [CrossRef]
- Slezhanovskii, O.V.; Datskovsky, L.K.; Kuznetsov, I.S.; Lebedev, E.D.; Tarasenko, L.M. Systems of Subordinate Regulation of AC Electric Drives with Valve Converters; Energoatomizdat: Moscow, Russia, 1983. [Google Scholar]
- Cheng, J.; Xu, T.; Chen, D.; Chen, G. Dynamic and steady state response analysis of selective harmonic elimination in high power inverters. IEEE Access 2021, 9, 75588–75598. [Google Scholar] [CrossRef]
- Steczek, M.; Chudzik, P.; Szeląg, A. Combination of SHE- and SHM-PWM techniques for VSI DC-link current harmonics control in railway applications. IEEE Trans. Ind. Electron. 2017, 64, 7666–7678. [Google Scholar] [CrossRef]
- Khattak, F.A.; Rehman, H.U. Improved Selective Harmonics Elimination Strategy for Multilevel Inverters with Optimal DC Values. In Proceedings of the International Conference on Emerging Power Technologies, Topi, Pakistan, 1–6 April 2021. [Google Scholar] [CrossRef]
- Patil, S.D.; Kadu, A.; Dhabe, P. Improved Control Strategy for Harmonic Mitigation in Multilevel Inverter. In Proceedings of the 5th International Conference on Intelligent Computing and Control Systems, Madurai, India, 6–8 May 2021. [Google Scholar] [CrossRef]
- Moeini, A.; Dabbaghjamanesh, M.; Kimball, J.W.; Zhang, J. Artificial neural networks for asymmetric selective harmonic current mitigation-PWM in active power filters to meet power quality standards. IEEE Trans. Ind. Appl. 2020. [Google Scholar] [CrossRef]
- de Carvalho Alves, M.D.; Leão e Silva Aquino, R.N.A. Digital implementation of SHE-PWM modulation on FPGA for a multilevel inverter. In Proceedings of the Simposio Brasileiro de Sistemas Eletricos (SBSE), Niteroi, Brazil, 1–6 May 2018. [Google Scholar] [CrossRef]
- Chen, J.; Shen, Y.; Chen, J.; Bai, H.; Gong, C.; Wang, F. Evaluation on the Autoconfigured Multipulse AC/DC Rectifiers and Their Application in More Electric Aircrafts. IEEE Trans. Transp. Electrif. 2020, 6, 1721–1739. [Google Scholar] [CrossRef]
- Padmanaban, S.; Dhanamjayulu, C.; Khan, B. Artificial neural network and Newton Raphson (ANN-NR) algorithm based selective harmonic elimination in cascaded multilevel inverter for PV applications. IEEE Access 2021, 9, 75058–75070. [Google Scholar] [CrossRef]
- Radionov, A.A.; Gasiyarov, V.R.; Maklakov, A.S. Hybrid PWM on the basis of SVPWM and SHEPWM for VSI as part of 3L-BtB-NPC converter. In Proceedings of the IECON 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 1232–1236. [Google Scholar] [CrossRef]
- Nikolaev, A.A.; Gilemov, I.G.; Denisevich, A.S. Analysis of Influence of Frequency Converters with Active Rectifiers on the Power Quality in Internal Power Supply Systems of Industrial Enterprises. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing, Moscow, Russia, 1–4 May 2018. [Google Scholar]
- Wu, B.; Narimani, M. High-Power Converters and AC Drives, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2017. [Google Scholar]
- Nikolaev, A.; Maklakov, A.; Bulanov, M.; Gilemov, I.; Denisevich, A.; Afanasev, M. Current Electromagnetic Compatibility Problems of High-Power Industrial Electric Drives with Active Front-End Rectifiers Connected to a 6–35 kV Power Grid: A Comprehensive Overview. Energies 2023, 16, 293. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2003. [Google Scholar]
- Maklakov, A.S.; Jing, T.; Radionov, A.A.; Gasiyarov, V.R.; Lisovskaya, T.A. Finding the best programmable PWM pattern for three-level active front-ends at 18-pulse connection. Machines 2021, 9, 127. [Google Scholar] [CrossRef]
- Nikolaev, A.A.; Gilemov, I.G.; Bulanov, M.V.; Kosmatov, V.I. Providing Electromagnetic Compatibility of High-Power Frequency Converters with Active Rectifiers at Internal Power Supply System of Cherepovets Steel Mill. In Proceedings of the International Scientific-Technical Conference Alternating Current Electric Drives, Ekaterinburg, Russia, 1–8 May 2021. [Google Scholar]
- Marquez Alcaide, A.; Leon, J.I.; Laguna, M.; Gonzalez-Rodriguez, F.; Portillo, R.; Zafra-Ratia, E.; Vazquez, S.; Franquelo, L.G.; Bayhan, S.; Abu-Rub, H. Real-Time Selective Harmonic Mitigation Technique for Power Converters Based on the Exchange Market Algorithm. Energies 2020, 13, 1659. [Google Scholar] [CrossRef]
- Martínez, C.; Rohten, J.; Garbarino, M.; Andreu, M.; Silva, J.; Baier, C.; Morales, R. Operating Region for AFE Configuration under Variable Frequency Grid. In Proceedings of the IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Valparaíso, Chile, 22–26 March 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Espinosa, E.E.; Melin, P.E.; Garcés, H.O.; Baier, C.R.; Espinoza, J.R. Multicell AFE Rectifier Managed by Finite Control Set–Model Predictive Control. IEEE Access 2021, 9, 137782–137792. [Google Scholar] [CrossRef]
- Chowdhury, M.M.R.; Sütő, Z. Validation of a real-time simulation model of a three-phase Active-Front-End (AFE) rectifier. In Proceedings of the 8th International Youth Conference on Energy (IYCE), Eger, Hungary, 6–9 July 2022; pp. 1–5. [Google Scholar] [CrossRef]


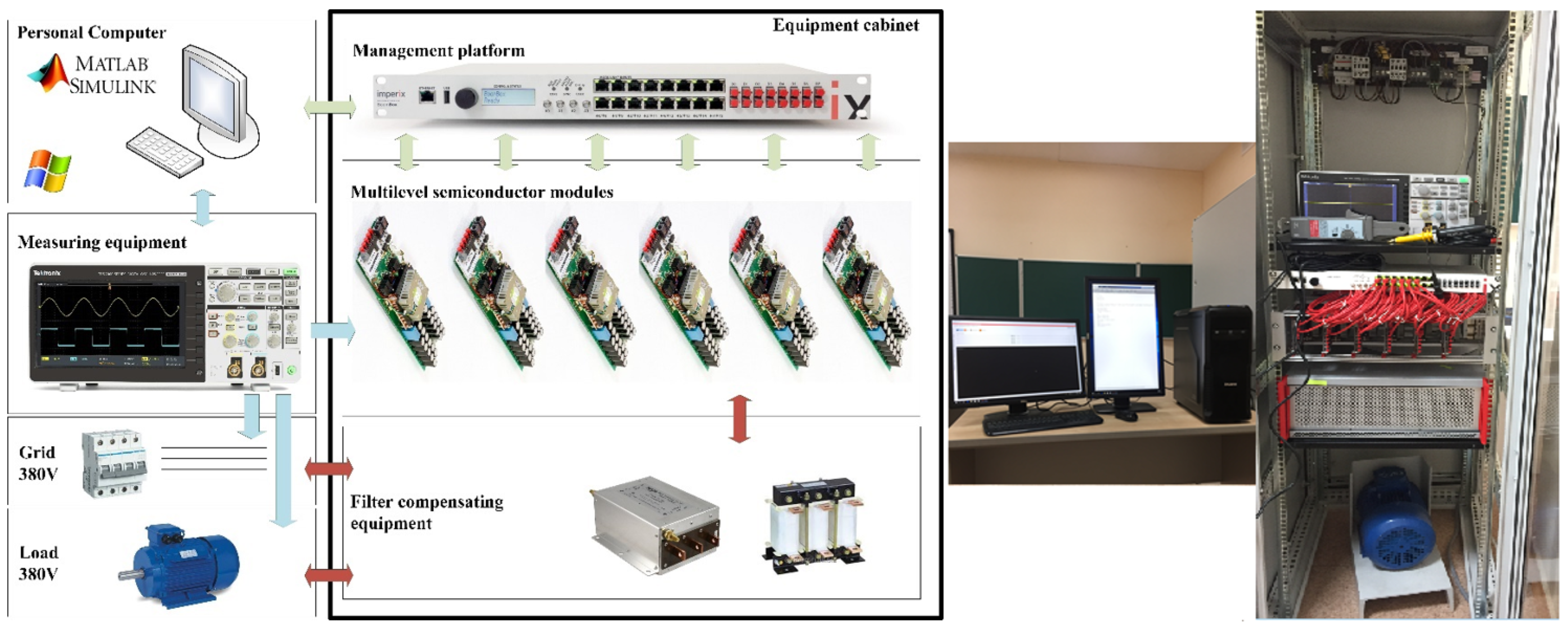

| Power modules | 1 × P924F33 Vincotech; reverse voltage IGBT, 600 V; permissible continuous current IGBT, 30 A; admissible continuous current of the reverse diode, 27 A; maximum switching frequency IGBT, 50 kHz; voltage drop, 1.5–2 V |
| Capacitors | 2 × 517 μF Panasonic EEU-EE2W470S (two batteries of 11 × 47 μF each); maximum voltage, 450 V |
| Control drivers | 4 × Avago ACPL-P345 |
| Current sensor | 1 × LEM HLSR 20-P/SP33; nominal range, ±20 A, 450 kHz; instrument error, ±1% |
| Voltage sensor | 1 × resistive voltage divider + Avago ACPL-C87B; bandwidth, 25 kHz; instrument error, ±0.1% |
| FPGA | 1 × Xilinx XC9536XL-10VQG44C, 10 ns; 36 microelements |
| Microcontrollers | 2 × Microchip PIC24F04KA201, 16 bit, 16 MHz; 9 × 10-bit ADCs; sampling rate, 500 ksps |
| Parameter | Designation | Value |
|---|---|---|
| Rated power | P2, MW | 12 |
| Rated stator current | Is, A | 3600 |
| Rated stator voltage | Us, kV | 3.3 |
| Rated frequency | fs, Hz | 10 |
| Stator’s active resistance | Rs, Ohm | 0.167 |
| Rotor’s active resistance | Rr, Ohm | 0.066 |
| Inductive reactance in the D-axis | Xd, Ohm | 0.12 |
| Inductive reactance in the Q-axis | Xq, Ohm | 0.113 |
| Overload capacity | 3 |
| Parameter | Designation | Value |
|---|---|---|
| Maximum active power | PAFE, MW | 12 |
| Rated current | IAFE, A | 2400 |
| Rated voltage | UAFE, kV | 3.3 |
| Rated frequency | fg, Hz | 50 |
| DC voltage | Udc, V | 5020 |
| Modulation index | p.u. | 0.85 |
| AFE input inductance | mH | 7.5 |
| DC link capacity | µF | 6170 |
| Overload capacity | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maklakov, A.S.; Nikolaev, A.A.; Lisovskaya, T.A. Control over Grid Reactive Power by Using a Powerful Regenerative Controlled-Speed Synchronous Motor Drive. Designs 2023, 7, 62. https://doi.org/10.3390/designs7030062
Maklakov AS, Nikolaev AA, Lisovskaya TA. Control over Grid Reactive Power by Using a Powerful Regenerative Controlled-Speed Synchronous Motor Drive. Designs. 2023; 7(3):62. https://doi.org/10.3390/designs7030062
Chicago/Turabian StyleMaklakov, Aleksandr S., Aleksandr A. Nikolaev, and Tatyana A. Lisovskaya. 2023. "Control over Grid Reactive Power by Using a Powerful Regenerative Controlled-Speed Synchronous Motor Drive" Designs 7, no. 3: 62. https://doi.org/10.3390/designs7030062
APA StyleMaklakov, A. S., Nikolaev, A. A., & Lisovskaya, T. A. (2023). Control over Grid Reactive Power by Using a Powerful Regenerative Controlled-Speed Synchronous Motor Drive. Designs, 7(3), 62. https://doi.org/10.3390/designs7030062









