Design of a Takagi–Sugeno Fuzzy Exact Modeling of a Buck–Boost Converter
Abstract
1. Introduction
2. Materials and Methods
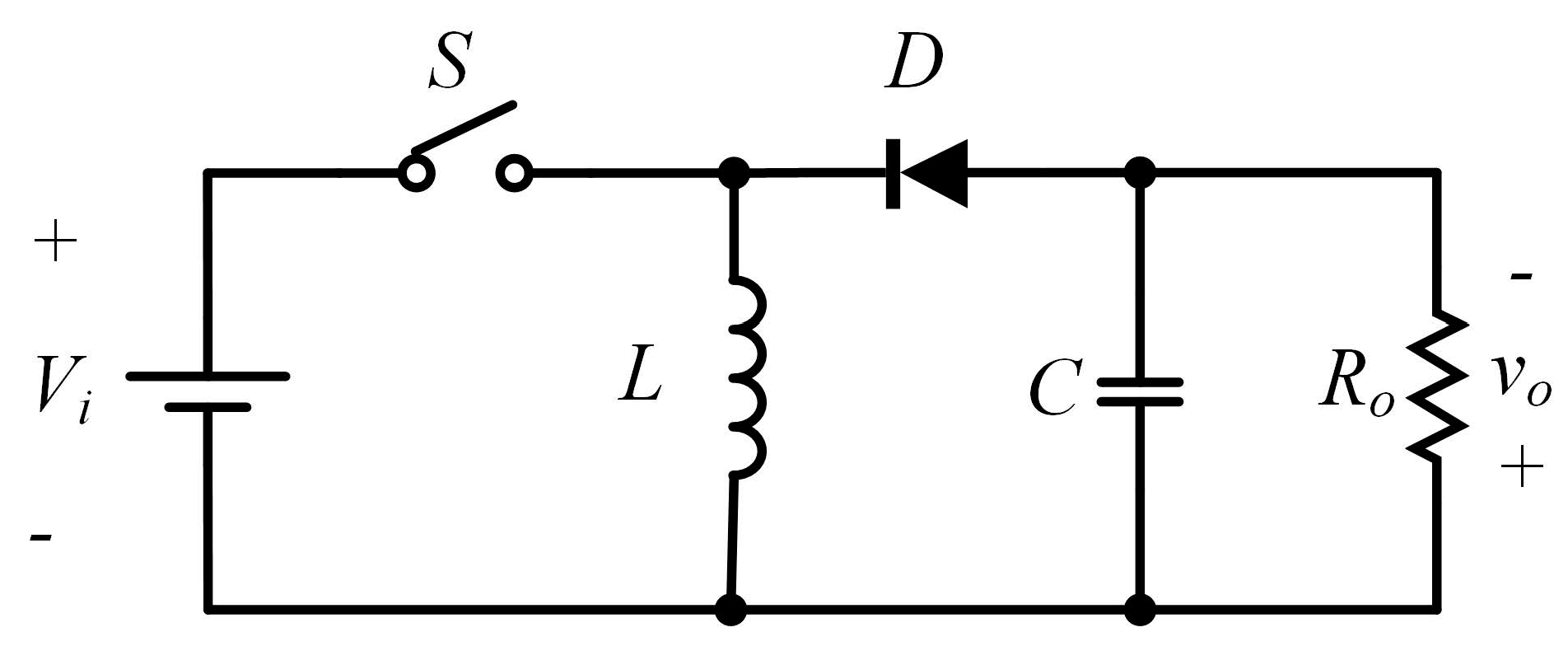
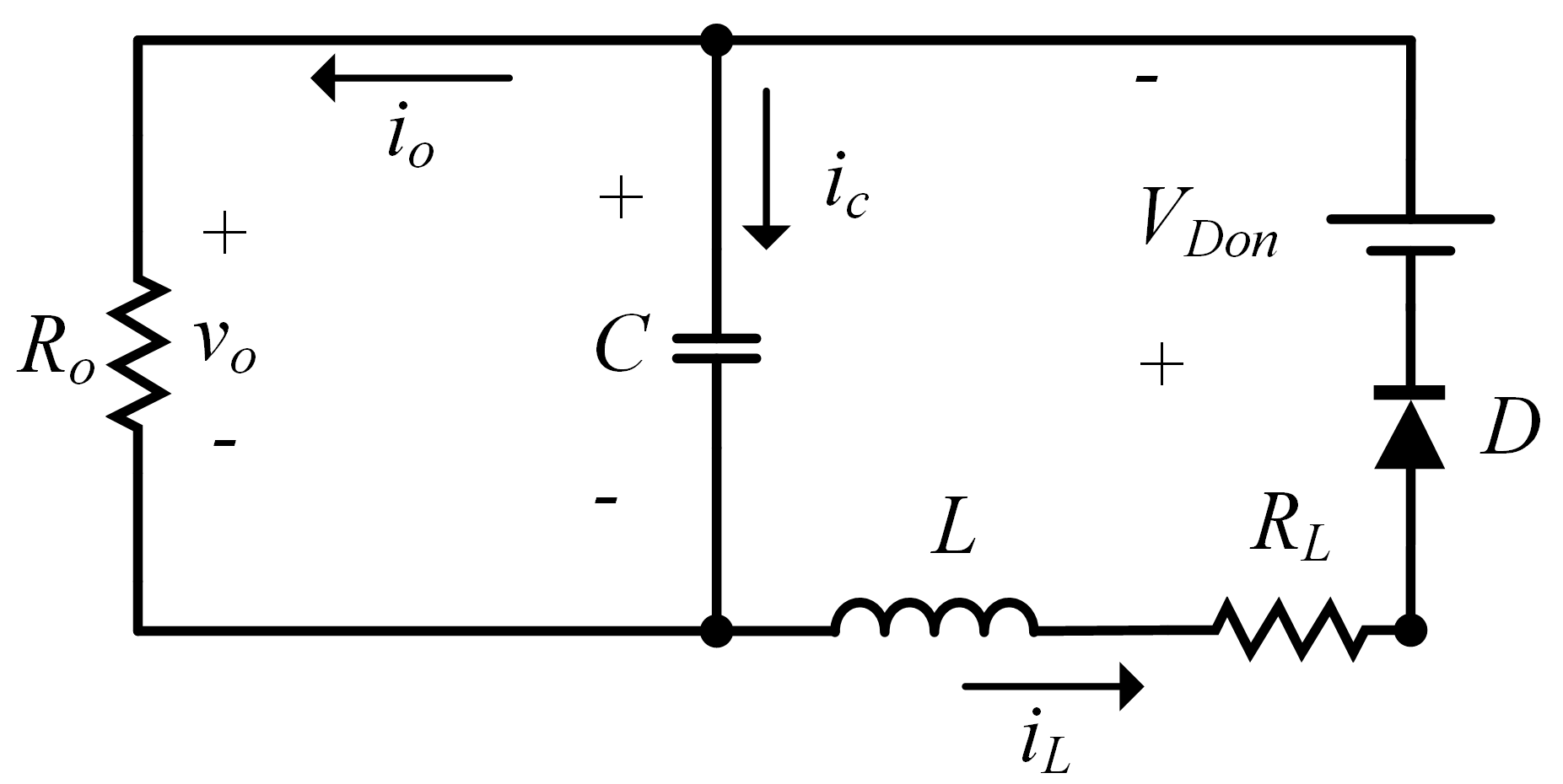
2.1. Buck–Boost Converter
2.1.1. Overview of DC–DC Converters
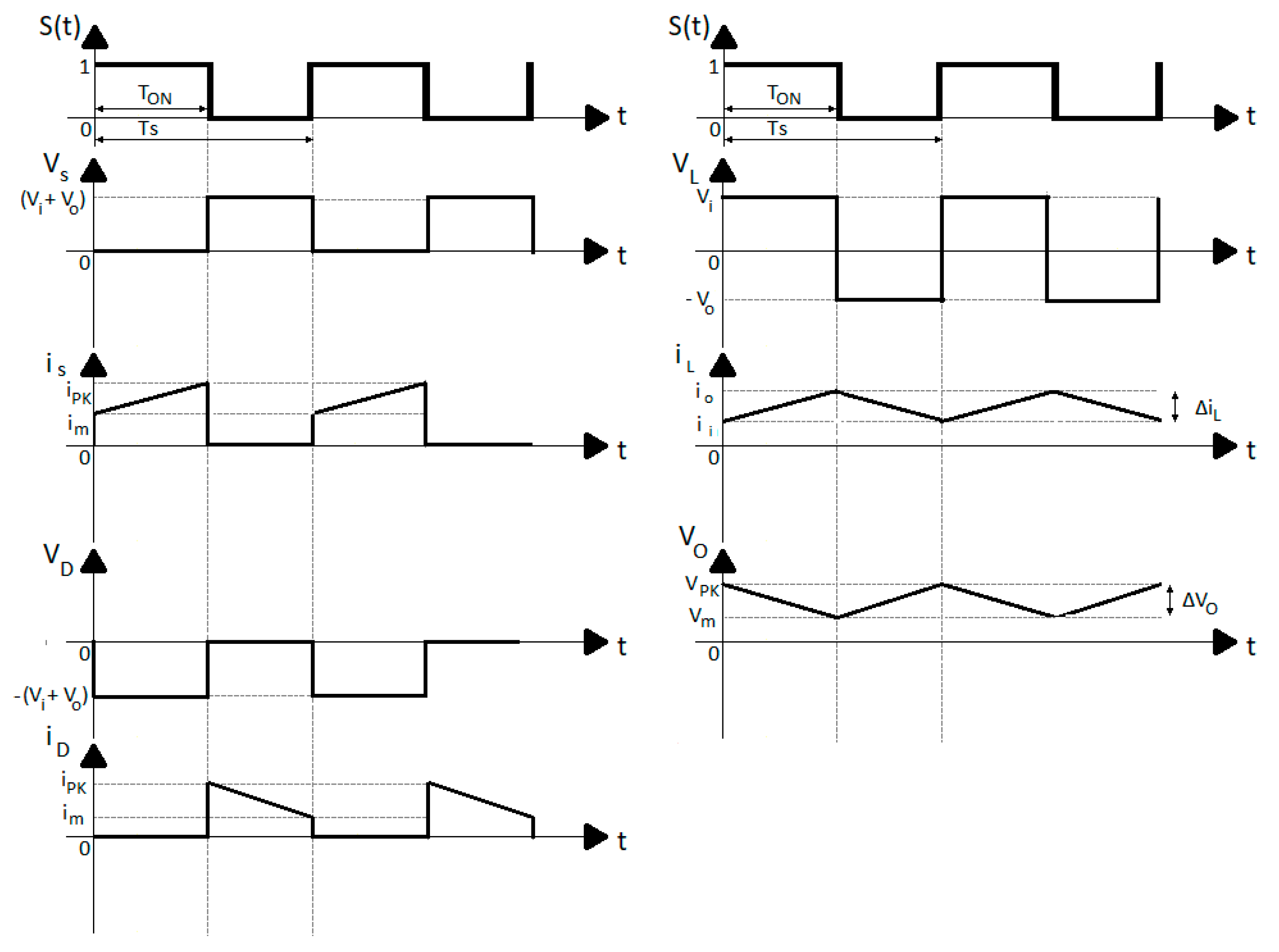
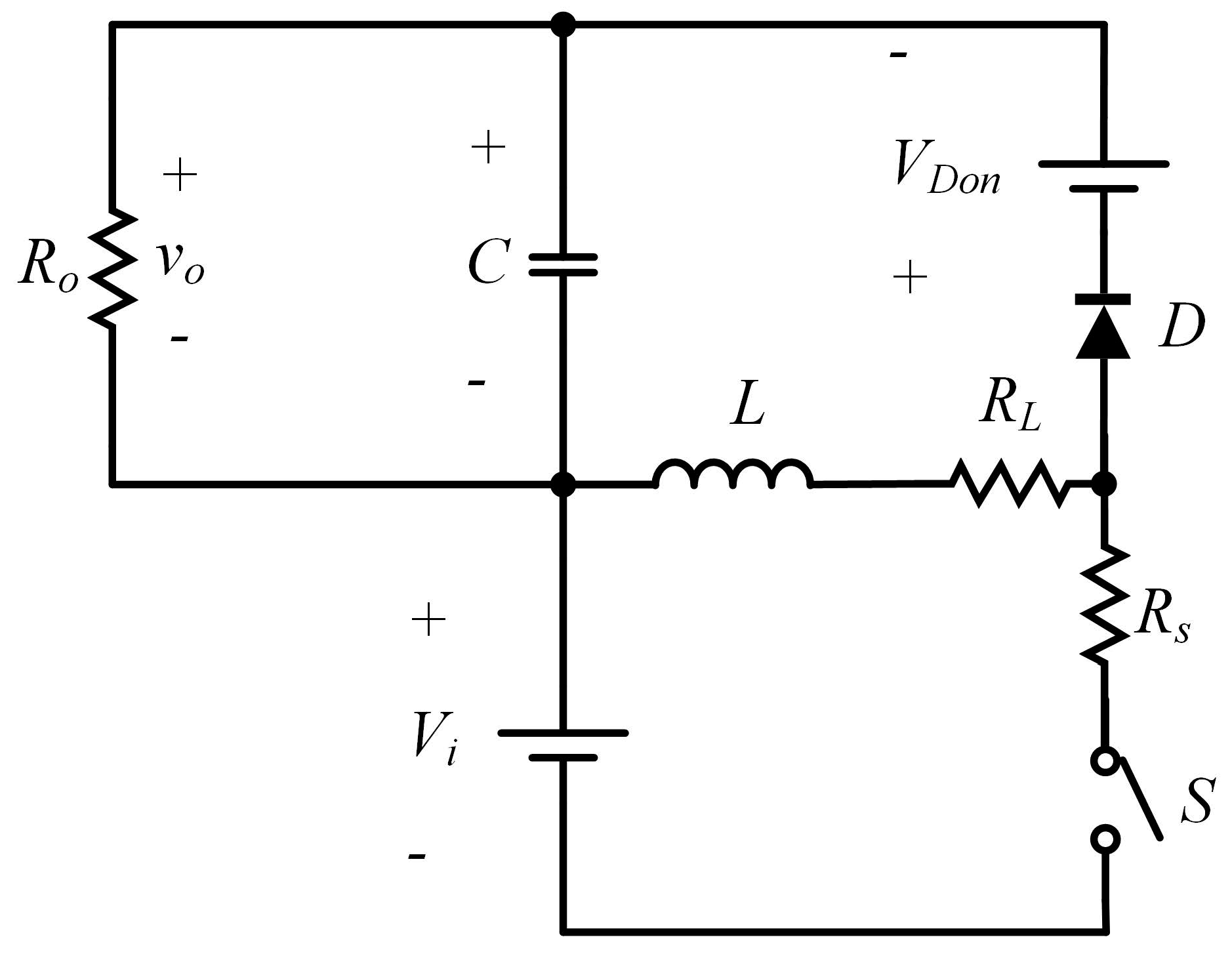
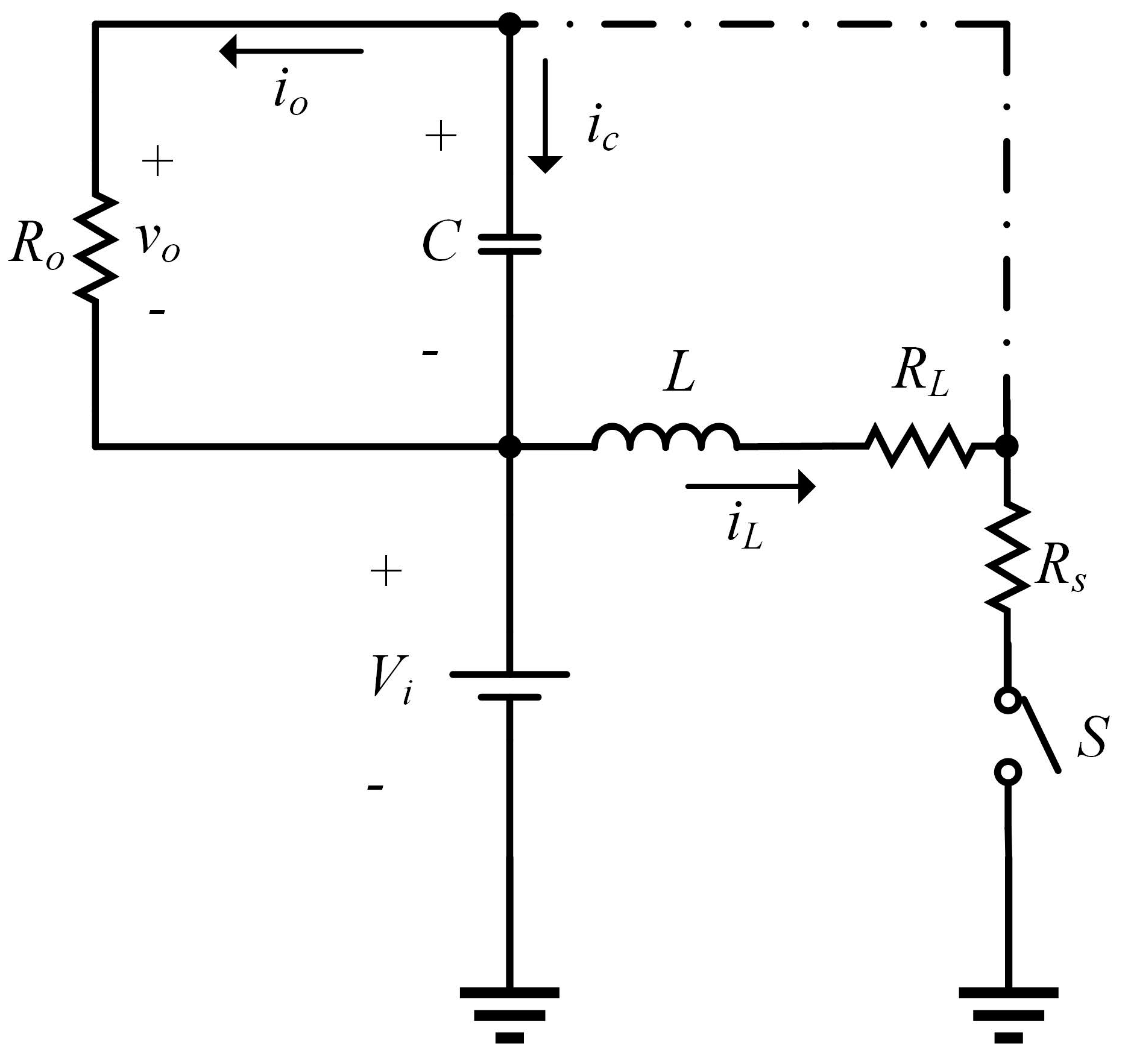
2.1.2. Buck–Boost Converter Project
2.1.3. Mathematical Representation by State Space
2.2. Takagi–Sugeno Fuzzy Modeling
- Scenario 1 (B1):
- Scenario 2 (B2):
- Scenario 3 (B3):
- Scenario 4 (B4):
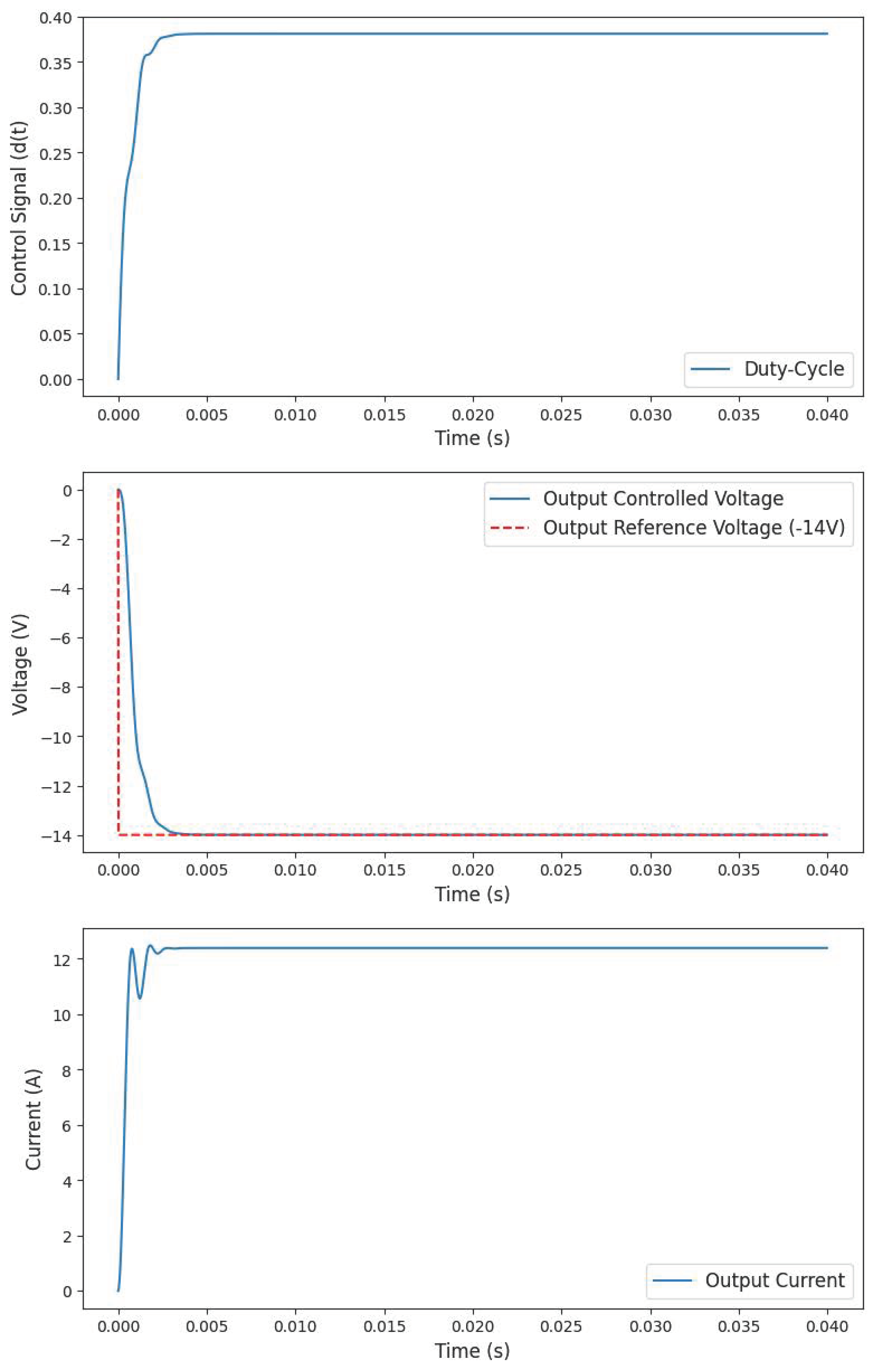
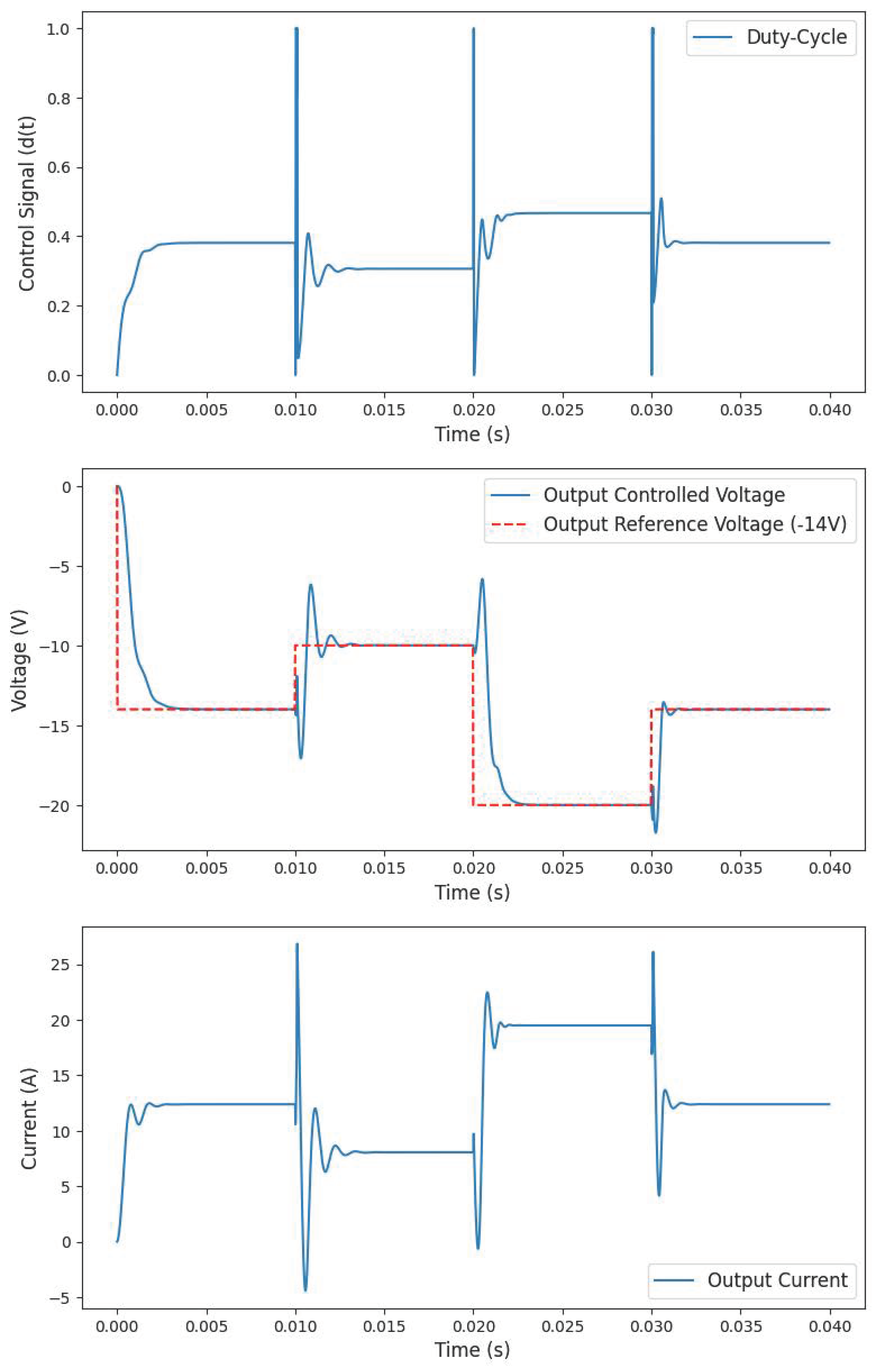
3. Discrete PID Control Design
- Zero stationary error for the reference voltages of −14 V (typical operating point).
- Overshoot percentage of 10% (buck–boost design parameter).
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010; Volume 5. [Google Scholar]
- de Kremes, W.J.; de Andrade, J.M.; Chokkalingam, B.; Illa Font, C.H.; Lazzarin, T.B. Input parallel–output parallel connected modular nonisolated DC-DC converters with current self-sharing capability operating in discontinuous conduction mode. Int. J. Circuit Theory Appl. 2023, 51, 340–359. [Google Scholar] [CrossRef]
- Syed, Z.A.; Wagner, J.R. Modeling and Control of a Multiple-Heat-Exchanger Thermal Management System for Conventional and Hybrid Electric Vehicles. Designs 2023, 7, 19. [Google Scholar] [CrossRef]
- Wester, G.W.; Middlebrook, R.D. Low-frequency characterization of switched DC-DC converters. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 376–385. [Google Scholar] [CrossRef]
- Cuoghi, S.; Ntogramatzidis, L.; Padula, F.; Grandi, G. Direct digital design of PIDF controllers with ComPlex zeros for DC-DC buck converters. Energies 2018, 12, 36. [Google Scholar] [CrossRef]
- Chander, S.; Agarwal, P.; Gupta, I. Auto-Tuned, Discrete PID Controller for DC-DC Converter for Fast Transient Response. In Proceedings of the India International Conference on Power Electronics 2010 (IICPE2010), New Delhi, India, 28–30 January 2011; pp. 1–7. [Google Scholar]
- Mirzaei, E.; Mojallali, H. Auto Tuning PID Controller Using Chaotic PSO Algorithm for a Boost Converter. In Proceedings of the 2013 13th Iranian Conference on Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Puchta, E.D.P.; Lucas, R.; Ferreira, F.R.V.; Siqueira, H.V.; Kaster, M.S. Gaussian Adaptive PID Control Optimized via Genetic Algorithm Applied to a Step-Down DC-DC Converter. In Proceedings of the 2016 12th IEEE International Conference on Industry Applications (INDUSCON), Curitiba, Brazil, 20–23 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R.; Dong, S.; Wang, X. Adaptive Fuzzy Finite-time Attitude Controller Design for Quadrotor UAV with External Disturbances and Uncertain Dynamics. In Proceedings of the 2022 8th International Conference on Control, Automation and Robotics (ICCAR), Xiamen, China, 8–10 April 2022. [Google Scholar]
- Gadari, S.K.; Kumar, P.; Mishra, K.; Bhowmik, A.R.; Chakraborty, A.K. Detailed analysis of fuzzy logic controller for second order DC-DC converters. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019. [Google Scholar]
- Hazil, O.; Bououden, S.; Chadli, M.; Filali, S. Fuzzy Model Predictive Control of DC-DC Converters. In AETA 2013: Recent Advances in Electrical Engineering and Related Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 423–432. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Reda, A.; Vásárhelyi, J. Design and Implementation of Reinforcement Learning for Automated Driving Compared to Classical MPC Control. Designs 2023, 7, 18. [Google Scholar] [CrossRef]
- Neto, P.S.D.M.; Firmino, P.R.A.; Siqueira, H.; Tadano, Y.D.S.; Alves, T.A.; De Oliveira, J.F.L.; Marinho, M.H.D.N.; Madeiro, F. Neural-based ensembles for particulate matter forecasting. IEEE Access 2021, 9, 14470–14490. [Google Scholar] [CrossRef]
- Liu, X.; Yang, C.; Luo, B.; Dai, W. Suboptimal control for nonlinear slow-fast coupled systems using reinforcement learning and Takagi–Sugeno fuzzy methods. Int. J. Adapt. Control Signal Process. 2021, 35, 1017–1038. [Google Scholar] [CrossRef]
- Ghany, M.A.A.; Bahgat, M.E.; Refaey, W.M.; Sharaf, S. Type-2 fuzzy self-tuning of modified fractional-order PID based on Takagi–Sugeno method. J. Electr. Syst. Inf. Technol. 2020, 7, 2. [Google Scholar] [CrossRef]
- Torres-Pinzón, C.; Paredes-Madrid, L.; Flores-Bahamonde, F.; Ramirez-Murillo, H. LMI-Fuzzy control design for non-minimum phase DC-DC converters: An application for output regulation. Appl. Sci. 2021, 11, 2286. [Google Scholar] [CrossRef]
- Borges, F.G.; Guerreiro, M.; Monteiro, P.E.S.; Janzen, F.C.; Corrêa, F.C.; Stevan, S.L., Jr.; Siqueira, H.V.; Kaster, M.d.S. Metaheuristics- Based Optimization of a Robust GAPID Adaptive Control Applied to a DC Motor-Driven Rotating Beam with Variable Load. Sensors 2022, 22, 6094. [Google Scholar] [CrossRef] [PubMed]
- Itaborahy Filho, M.A.; Puchta, E.; Martins, M.S.; Antonini Alves, T.; Tadano, Y.d.S.; Corrêa, F.C.; Stevan, S.L., Jr.; Siqueira, H.V.; Kaster, M.d.S. Bio-inspired optimization algorithms applied to the GAPID control of a Buck converter. Energies 2022, 15, 6788. [Google Scholar] [CrossRef]
- Taniguchi, T.; Tanaka, K.; Ohtake, H.; Wang, H.O. Model construction, rule reduction, and robust compensation for generalized form of Takagi-Sugeno fuzzy systems. IEEE Trans. Fuzzy Syst. 2001, 9, 525–538. [Google Scholar] [CrossRef] [PubMed]
- Cervantes, M.H.; Montiel, M.F.; Marín, J.A.; Anguiano, A.T.; Ramírez, M.G. Takagi-Sugeno Fuzzy Model for DC-DC Converters. In Proceedings of the 2015 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 4–6 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Nachidi; Meriem; El Hajjaji, A.; Bosche, J. An enhanced control approach for dc–dc converters. Int. J. Electr. Power Energy Syst. 2013, 45, 404–412. [Google Scholar] [CrossRef]
- Tatikayala, V.K.; Dixit, S. Takagi-Sugeno Fuzzy based Controllers for Grid Connected PV-Wind-Battery Hybrid System. In Proceedings of the 2021 International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bangalore, India, 27–28 August 2021. [Google Scholar]
- Quispe, B.B.; e Melo, G.d.A.; Cardim, R.; Ribeiro, J.M.d.S. Single-Phase Bidirectional PEV Charger for V2G Operation with Coupled-Inductor Cuk Converter. In Proceedings of the 2021 22nd IEEE International Conference on Industrial Technology (ICIT), Valencia, Spain, 10–12 March 2021; Volume 1. [Google Scholar]
- Abe, S.; Zaitsu, T.; Obata, S.; Shoyama, M.; Ninomiya, T. Pole-Zero-Cancellation Technique for DC-DC Converter. In Advances in PID Control; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef]
- Awada, A.; Younes, R.; Ilinca, A. Optimized active control of a smart cantilever beam using genetic algorithm. Designs 2022, 6, 36. [Google Scholar] [CrossRef]
- TKDs. Aluminum Electrolytic Capacitors, 2019. Rev. 1. Available online: https://www.tdk-electronics.tdk.com/inf/20/30/db/aec/B41895.pdf (accessed on 10 January 2023).
- Siliconix, V. N-Channel 100 V (D-S) MOSFET, 2016. Rev. A. Available online: https://www.vishay.com/docs/62634/si7252dp.pdf (accessed on 10 January 2023).
- ON Semiconductor. Ultrafast Rectifiers 16 Amperes, 100600 Volts, 2015. Rev. 8. Available online: https://www.onsemi.com/pdf/datasheet/mur1620ct-d.pdf (accessed on 10 January 2023).
- Puchta, E.D.P.; Bassetto, P.; Biuk, L.H.; Itaborahy Filho, M.A.; Converti, A.; Kaster, M.d.S.; Siqueira, H.V. Swarm-Inspired Algorithms to Optimize a Nonlinear Gaussian Adaptive PID Controller. Energies 2021, 14, 3385. [Google Scholar] [CrossRef]
- Ogata, K. Discrete-Time Control Systems; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Fuller, S.; Greiner, B.; Moore, J.; Murray, R.; van Paassen, R.; Yorke, R. The Python Control Systems Library (Python-Control). In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 14–17 December 2021. [Google Scholar]
- Siqueira, H.; Macedo, M.; Tadano, Y.d.S.; Alves, T.A.; Stevan, S.L., Jr.; Oliveira, D.S., Jr.; Marinho, M.H.N.; Neto, P.S.G.d.M.; Oliveira, F.L.d.; Luna, I.; et al. Selection of Temporal Lags for Predicting Riverflow Series from Hydroelectric Plants Using Variable Selection Methods. Energies 2020, 13, 4236. [Google Scholar] [CrossRef]
- Lian, K.Y.; Liou, J.J.; Huang, C.Y. LMI-based integral fuzzy control of DC-DC converters. IEEE Trans. Fuzzy Syst. 2006, 14, 71–80. [Google Scholar] [CrossRef]
- Siqueira, H.; Santana, C.; Macedo, M.; Figueiredo, E.; Gokhale, A.; Bastos-Filho, C. Simplified binary cat swarm optimization. Integr. Comput. Aided Eng. 2021, 28, 35–50. [Google Scholar] [CrossRef]
- Santos, P.; Macedo, M.; Figueiredo, E.; Santana, C.J.; Soares, F.; Siqueira, H.; Maciel, A.; Gokhale, A.; Bastos-Filho, C.J. Application of PSO-Based Clustering Algorithms on Educational Databases. In Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Arequipa, Peru, 8–10 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Puchta, E.D.P.; Siqueira, H.V.; Kaster, M.D.S. Optimization Tools Based on Metaheuristics for Performance Enhancement in a Gaussian Adaptive PID Controller. IEEE Trans. Cybern. 2020, 50, 1185–1194. [Google Scholar] [CrossRef] [PubMed]

| Term | Acronym |
|---|---|
| DC–DC | Direct Current |
| TS | Takagi–Sugeno |
| PID | Proportional–integral–derivative |
| RL | Reinforcement learning |
| LMI | Linear matrix inequality |
| PSO | Particle swarm optimization |
| Topology | Static Gain (M) |
|---|---|
| Buck | D |
| Boost | 1/(D − 1) |
| Buck–Boost | D/(1 − D) |
| Cúk | D/(1 − D) |
| SEPIC | D/(1 − D) |
| Zeta | D/(1 − D) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gotz, J.D.; Bigai, M.H.; Harteman, G.; Martins, M.S.R.; Converti, A.; Siqueira, H.V.; Borsato, M.; Corrêa, F.C. Design of a Takagi–Sugeno Fuzzy Exact Modeling of a Buck–Boost Converter. Designs 2023, 7, 63. https://doi.org/10.3390/designs7030063
Gotz JD, Bigai MH, Harteman G, Martins MSR, Converti A, Siqueira HV, Borsato M, Corrêa FC. Design of a Takagi–Sugeno Fuzzy Exact Modeling of a Buck–Boost Converter. Designs. 2023; 7(3):63. https://doi.org/10.3390/designs7030063
Chicago/Turabian StyleGotz, Joelton Deonei, Mario Henrique Bigai, Gabriel Harteman, Marcella Scoczynski Ribeiro Martins, Attilio Converti, Hugo Valadares Siqueira, Milton Borsato, and Fernanda Cristina Corrêa. 2023. "Design of a Takagi–Sugeno Fuzzy Exact Modeling of a Buck–Boost Converter" Designs 7, no. 3: 63. https://doi.org/10.3390/designs7030063
APA StyleGotz, J. D., Bigai, M. H., Harteman, G., Martins, M. S. R., Converti, A., Siqueira, H. V., Borsato, M., & Corrêa, F. C. (2023). Design of a Takagi–Sugeno Fuzzy Exact Modeling of a Buck–Boost Converter. Designs, 7(3), 63. https://doi.org/10.3390/designs7030063











