Abstract
Additive manufacturing is a potentially disruptive technology with a high impact on supply chains and part design. While generally allowing much higher degrees of freedom in design than formative and subtractive manufacturing techniques, the necessity of support structures can diminish the impact of additive manufacturing. This article presents a methodology based on finite spheres to integrate knowledge about process limitations into topology optimization for the direct extrusion-based additive manufacturing of parts with maximized stiffness and strength and minimized support structures. This methodology has been included within our self-developed Freeware Z88 Arion® V3. We investigated the impact of the manufacturing constraints on the additive manufacturing process regarding effective material usage on application test examples. The test results showed that the design proposals created while applying the finite spheres and two-step smoothing needed significantly less or no support material for all application examples.
1. Introduction
Sustainability and resource efficiency are vital aspects of product design in modern society and are more critical than ever. Topology optimization (TO) aims to find the best material distribution within a design space under given loads [1] and, therefore, is a powerful computer-aided engineering tool for addressing the demands of sustainability and resource efficiency. TO has gained a certain maturity over the past few years and has thus transformed from experimental design to performance design with application in many industry fields [2,3,4]. While many commercial software tools and open-source projects for TO are available, freeware solutions providing the functionalities of meshing, preprocessing, optimization, and smoothing are scarce. To the best of our knowledge, the only two are TopOpt (TopOpt group, technical university of Denmark, Lyngby) and Z88Arion® (Engineering Design and CAD, University of Bayreuth, Bayreuth, Germany).
Design proposals, which are the results of TO simulations, represent a structure close to the mathematical optimum and, hence, are, in most cases, nearly impossible to manufacture by conventional manufacturing processes. The integration of manufacturing constraints into TO is, therefore, crucial to turn the design proposal into a manufacturable geometry [5,6,7]. While in the early 2000s, casting processes were the focus of research [8,9,10,11,12], additive manufacturing (AM) is currently of most interest [13,14,15,16,17,18,19], as it allows the fabrication of bio-inspired [20] and numerical optimized structures [21,22,23,24] with ease. Nevertheless, even AM processes have restrictions, most prominently, the overhang-angle needed to provide temporary supports to prevent collapsing or warping, which have to be considered during TO [25,26]. As the overhang angle describes the limit within an additively manufactured structure that is self-supporting [15,27], it differs between extrusion-based [26,28] and powder bed fusion AM [29,30].
Generally, the objective of manufacturing constraints is to provide design proposals dedicated to specific manufacturing processes, which significantly lower, or—at least potentially—omit the postprocessing effort of transforming the design proposal into an actual design. Accordingly, the manufacturing constraints establish a certain synergy between computer-aided engineering and computer-aided design tools. This synergy is even more relevant for the field of generative design, which can be understood as a highly automatized method to generate multiple design proposals, for instance, for various manufacturing processes [31]. Accordingly, the generative design enables workflows, which can design solutions nearly automatically, as Belluomo et al. demonstrated through the example of supporting structures for cultural heritage artifacts [32]. Nevertheless, to provide design solutions for different manufacturing processes, manufacturing constraints are also relevant for generative design. However, the scope of this article is not the combination and automation of various computer-aided engineering and design processes, respectively, but the development of manufacturing constraints as a crucial part of the structural optimization process.
The implementation of manufacturing constraints is possible in multiple ways. Vatanabe et al. used a unified projection approach to define them [6], while Pellens et al. combined a minimum length scale and maximum overhang-angle by spatial filters [25]. Gaynor et al. addressed this issue by embedding a minimum self-supporting angle into the TO framework by using a series of projection operations to ensure the minimum length scale requirements were reached and that the feature was sufficiently supported from the build plate, which they demonstrated on 2D standard minimum compliance TO problems [13]. Guo et al. addressed self-supporting structures using the frameworks moving morphable components and moving morphable voids, which is demonstrated in numerical examples [14]. Further, Leary et al. defined robust manufacturing zones for extrusion-based AM within the common density-based single material with a penalization TO approach and modified geometries outside these robust areas [15] and demonstrated their approach by manufacturing a 2.5 D cantilever beam. Fernández et al. presented an approach for large-scale AM where TO design proposals were tailored to the deposition size. The method defines a structural skeleton, to be interpreted as a deposition path, which is thickened according to the nozzle size through projection and filtering methods [28]; the results on 2D and 3D benchmarks show improved manufacturability.
However, in general, the task for implementing manufacturing constraints is to describe the knowledge about a manufacturing process in a way that it can be used within a TO framework. Accordingly, for experimental findings, the overhang angle, for instance, must be transformed into a mathematical description. In our previous work, we developed a method based on finite spheres to describe manufacturing conflicts in casting and AM processes [2] and incorporated it into the freeware Z88Arion®.
The objective of this article is to demonstrate how to turn AM process knowledge into a framework for manufacturing constraints in TO. Further, we investigate the effect of these manufacturing constraints on the optimized structure through three application examples by evaluating the AM process time and material efficiency to analyze the robustness of the finite-sphere concept. The presented manufacturing conflicts are incorporated in the freeware Z88Arion®, which allows us to deploy our method for improving the material efficiency of topology-optimized and additively manufactured components.
2. Materials and Methods
In our proposed method, we describe the manufacturing constraint for extrusion-based AM as the resolution of manufacturing conflicts. Thereby, we define a manufacturing conflict if an element is not manufacturing without (de-) activating another element within the design space’s volume mesh. Accordingly, all possible manufacturing conflicts are defined a priori; after each TO-iteration, the manufacturing conflicts are solved by (de-) activating elements, and the quantity of the remaining potential manufacturing conflicts is updated. We outlined the overall process in Figure 1.
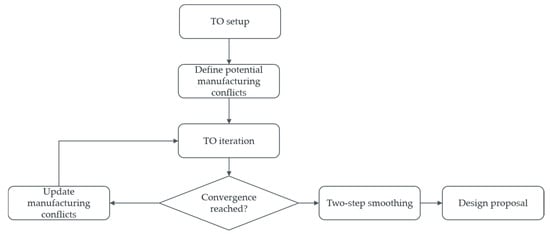
Figure 1.
Overall process flow chart of the proposed method.
The following sections describe the TO framework, the development of manufacturing constraints, and the adjacent smoothing of the design proposals in detail. Further, it introduces the application examples and explains the evaluation process.
2.1. Topology Optimization
One of the most common frameworks for TO is to solve a minimum compliance problem using the optimality criterion (OC) [1]. Hence, the resulting design proposals show maximized stiffness. However, the component’s strength is neglected during the optimization process, which results in design proposals that often show stress overloads. Analogously, if algorithms optimize a homogenized stress distribution, for instance, the soft kill option (SKO) [33], stiffness-increasing structures are only rarely formed. We addressed this issue by using a hybrid TO algorithm for the optimization of stiffness and strength (TOSS), which was developed in [34] and is implemented in Z88Arion®. Within the TOSS algorithm, firstly, a minimum compliance problem is solved using the optimality criterion (OC) for maximized stiffness, and subsequently, the stiffness design proposal is optimized for homogenized surface stresses. We present the concept of the TOSS algorithm in Figure 2.
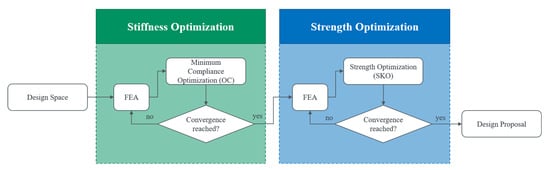
Figure 2.
Concept of the TOSS algorithm, re-drawn from [2].
The material interpolation within the minimum compliance problem was conducted using the solid isotropic material with penalization (SIMP) [1] approach, which is defined as the following:
where E describes the adapted Young’s modulus of the material and E0 represents the solid material which is affected by the density ρ and the penalty exponent p.
Within the first step of the TOSS, we used the optimality criterion method [1] to solve the following optimization problem:
with C denoting the compliance matrix, K the stiffness matrix, respectively, and u the displacement vector. After convergence, the SKO algorithm is started, which is based on the biological rule of growth [33].
In contrast to the OC, the elements of Young’s Modulus are modified directly, which can be easily performed by varying the node temperature of the finite elements. It is important to note here that these nodal temperatures are solely modifying Young’s modulus and have no physical meaning. A virtual temperature Tk is computed for each node j inside the design space:
with
where the scaling factor s and reference stress σref are user-defined inputs. This allows calculating the virtual temperature of each element via:
Here, nE represents the number of nodes per element, and nf describes the first node which belongs to the element and nl the last node, respectively. Therefore, Young’s modulus per element is obtained by:
2.2. Manufacturing Constraints
The objective behind manufacturing constraints is to obtain a design proposal that is directly manufacturable or, at least, with minor geometry adaptions. Hence, an efficient way to analyze and evaluate the manufacturability after each iteration of the TO algorithm is desirable. Therefore, we discretized the elements of the finite element mesh as finite spheres. By doing this abstraction, we could neglect the detailed shapes of the elements, which is appropriate since the design proposals must be smoothed after the TO anyway. In our approach, the simplification of the part results in finite spheres with an identical volume Vi and center of gravity as the actual elements. The radius of a finite sphere is described by:
This procedure allows for defining conflicts between finite spheres, which we will use to define manufacturing conflicts. In this context, we also introduced the tolerance angle as a technical assistance tool to define the existence of a conflict between the elements, with one element moving alongside its manufacturing direction. If two finite spheres collide at the maximum angle , they conflict with each other, which is determined by the overlap of the effective spherical volumes.
A manufacturing conflict is then solved by (de-)activating the elements. The illustration in Figure 3 visualizes the presented concept of finite spheres. An element is moved along a manufacturing direction s (which can be, for example, a solidification direction in casting or a printing direction in AM) and a certain manufacturing angle ω (which denotes the demolding angle in casting or the overhang angle in AM). Elements that penetrate other elements’ spheres have potential manufacturing conflicts with each other. As we present in Figure 3, a finite-sphere (grey) simplifies the actual shape of a tetrahedral element and is moved along a manufacturing direction s and angle ω (indicated by the grey spheres). A manufacturing conflict exists for τ ≤ α = 30° (noted in blue), which is determined by the overlapping finite-sphere volumes. If the colliding angle τ is below 30°, a potential manufacturing conflict between the two elements exist, which is noted in orange. If the colliding angle τ is greater than 30°, no potential manufacturing conflict between the two elements can exist, which is noted in violet.
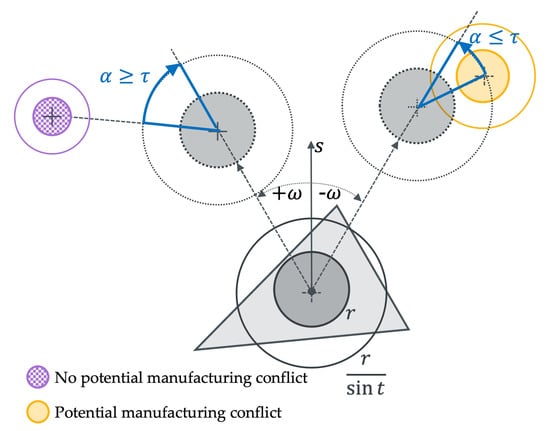
Figure 3.
The finite-sphere that simplifies the actual shape of a tetrahedral element is noted in grey. Elements without a potential manufacturing conflict are noted in violet and elements with a potential manufacturing conflict are noted in orange. Adapted from [2].
In the context of extrusion-based AM, we can now define the overhang constraint as a manufacturing conflict. The overhang constraint describes parts of the structure that would collapse if not supported by additional, so-called support material. Accordingly, the manufacturing angle ω represents the critical overhang angle in extrusion-based AM. Thereby, all elements on the parts’ surface, which have a manufacturing conflict, in this context penetrating spheres, are considered not self-supporting. Within the TO framework, all relevant self-supporting elements must be considered as solid material (xi = 1), while the non-self-supporting elements are removed from the design space.
This procedure is explained in Figure 4. The grey-shaded design space (Figure 4a) consists of deactivated elements, which make a non-self-supporting structure. By activating (green) and deactivating (red) elements, the design space grey is modified so that the resulting design proposal becomes self-supporting.
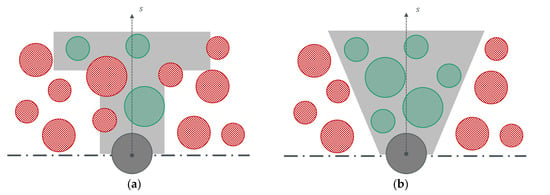
Figure 4.
Schematic procedure of the proposed method; (a) The initial design space (grey) with deactivated elements (red) causing a manufacturing conflict. (b) Conflicted elements are activated (green) iteratively, so that the modified design space is free of deactivated elements causing manufacturing conflicts.
To describe this manufacturing conflict mathematically, the sets are introduced, which consist of all potential conflict elements for each element :
with the adjacent manufacturing direction s, center of gravity and manufacturing angle .
These sets are updated along with the TO algorithm as the elements are (de-)activated iteratively and used to remove relevant manufacturing conflicting elements from the optimization problem. For efficient removal of conflict elements, the part is changed stepwise in the direction of the local mass difference towards the nearest conflict-free structure. As real existing parts have a continuous geometry, it is sufficient to determine the optimal surface of the part in the manufacturing direction. For the evaluation of the optimal surface, the design variable x for all elements on the surface is set to , respectively, for all elements outside of the part. The following equation defines the remaining loss Mi, which describes the deviation between the density distribution of the design space and the elements on the optimal surface:
for all , where is the mass of the elements. The optimal surface is chosen so that Mi is minimal. Therefore, the set for the optimal surface:
with the maximizing objective function:
determines the next adaption of the solution geometry. The geometry adaption is conducted by the activation or deactivation of elements in the design space based on the updated element densities ρi. It was not intended to overwrite the density distribution of the TO; accordingly, the (de-)activation of the elements depends on the actual design variable (). For symmetry reasons, we defined the deactivating function as the following:
Thereby describes the activating function. Within the maximizing function in Equation (11), an element was activated ( if it was inside the design proposals and deactivated () if the element was outside of the design proposal. Further, we introduced the manufacturing rate to control the weighting of the manufacturing constraints. For , no manufacturing conflicts were calculated. Henceforth, we used the manufacturing rate to describe the trade-off between manufacturability and mechanical performance. The activating function is given by:
with the elements density and design variable .
Accordingly, the presented method allows for the describing and solving of manufacturing conflicts in 3D design spaces based on the manufacturing direction s, the manufacturing angle ω, and the manufacturing rate g.
For further background on the implementation of the finite-sphere concept, we refer to [2] or the Z88Arion documentation (www.z88.de, accessed on 11 December 2022). The presented concept shows the integration of the process knowledge about a critical printing angle into a manufacturing constraint for TO, which we applied to the three application examples in the following.
2.3. Smoothing
After the convergence of the TO algorithm, an implicit two-step smoothing algorithm developed by [35] was used to prepare the design proposal for the subsequent re-design or manufacturing. In the first smoothing step, a slightly modified marching cube algorithm decides which elements to consider for the smoothed design proposal based on their design variable value. Hence, the first smoothing leads to a triangulated surface whose roughness correlates with the chosen element size of the TO volume mesh. The second smoothing step is based on the implicit fairing approach, built upon the Laplace smoothing and solved using implicit integration. Its purpose is to align the surface triangles’ coordinates so that the surface roughness of the triangulated geometry is minimized [35].
2.4. Application Examples
We relied on the three application examples, shown in Figure 5, for the subsequent experiments, a cantilever beam, a bracket, and a rocker.
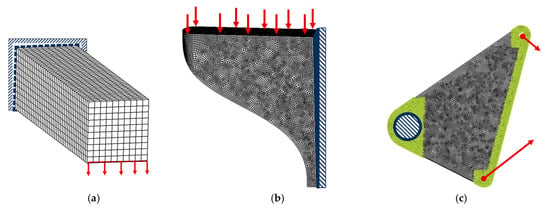
Figure 5.
Overview of the application examples’ TO-setup: (a): Cantilever beam, (b): Bracket, (c): Rocker. Dark blue represents displacement constraints, the force vectors are displayed in red and green denote passive regions, if applicable.
In these examples, we investigated the influence of the manufacturing rate and manufacturing angle when investigated and compared with the reference solution without manufacturing constraints. The printing direction of each specimen is displayed in the example of the reference design proposal in Figure 6.
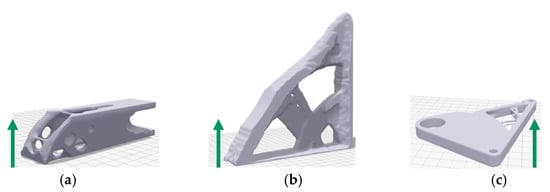
Figure 6.
Visualization of the manufacturing, respectively, with printing direction indicated by the green arrow for the cantilever (a), the bracket (b), and the rocker (c) application-examples.
We provide a summary of all TO-experiments in Table 1.

Table 1.
Summary of all TO-experiments for the three application examples, where ∆ defines the step length.
To evaluate the design proposals in the context of the manufacturing constraints’ effectiveness, the slicing software Eiger™ (Markforged Inc., Boston, MA, USA) was used to analyze the total volume of the print job Vges, respectively and the parts’ remaining support-volume Vsup. Based on this, we calculated the effective material usage as:
3. Results
3.1. Cantilever
All TO experiments for the cantilever were conducted successfully; its results in Figure 7 display that 14 out of 20 design proposals reached a better effective material usage than the reference, while two design proposals were equivalent to the reference. Further, two design proposals reached a material usage of 100%.
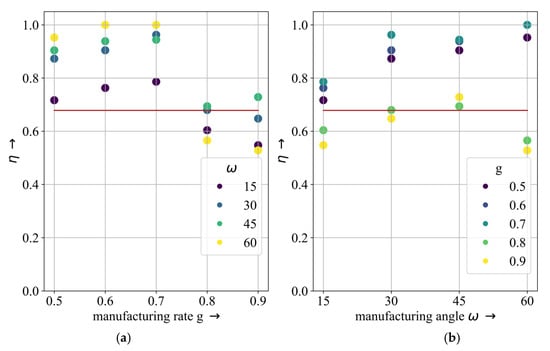
Figure 7.
The effective material usage of the cantilever design proposals. The red line indicates of the reference design proposal. (a) Shows the effective material usage as a function of manufacturing rate g; (b) Shows the effective material usage as a function of manufacturing angle ω. By application of the proposed method, was increased to 100%.
Further, the results in Figure 7 show that a manufacturing degree of 45° for all manufacturing rates leads to an increase in , while the best results were reached at 60°. Additionally, the change in between ω 15° and the other manufacturing angles was quite significant, while for ω, it was greater than 30°, the changes becoming smaller. Figure 7a further shows that until the effective material usage increased but dropped for values of greater than 0.7. Figure 7b elucidates that the highest mean of was reached for manufacturing angles 30° and 45°. For the cantilever, the effective material usage was increased by 32% from 68% to 100%, which presents a fully self-supporting design proposal. We have visualized the two design proposals in Figure 8.
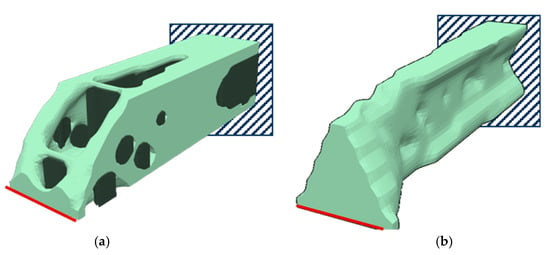
Figure 8.
Comparison of the reference design proposal (a) and the design proposal with the highest effective material usage (b) for the cantilever application example. The support-material is displayed in dark green, while constraints are visualized in dark blue and loaded areas in red.
3.2. Bracket
In the case of the bracket example, the TO-simulations for ω = 60° diverged for all manufacturing rates and were consequently excluded from evaluation. The remaining 16 TO-experiments all lead to design proposals with a higher effective material usage than the reference, as shown left in Figure 9.
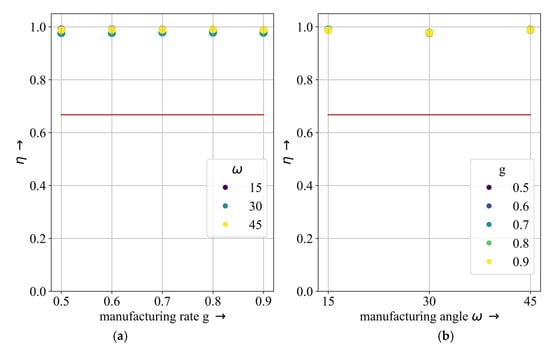
Figure 9.
The effective material usage of the bracket design proposals. The red line indicates of the reference design proposal. (a) Shows the effective material usage as a function of manufacturing rate g; (b) Shows the effective material usage as a function of manufacturing angle ω. For the bracket, all settings led to a of minimum 98%.
The design proposals with ω = 45° showed a slightly better performance. Besides this, the influence of the manufacturing angle or rate on the bracket example was so marginal that it did not impact the design proposal relevantly, as displayed in in Figure 9. Though an increase in effective material usage from 32% to 67%, 99% was reached, but no fully self-supporting structure was found. The difference between the reference and the best design proposal is visualized in Figure 10.
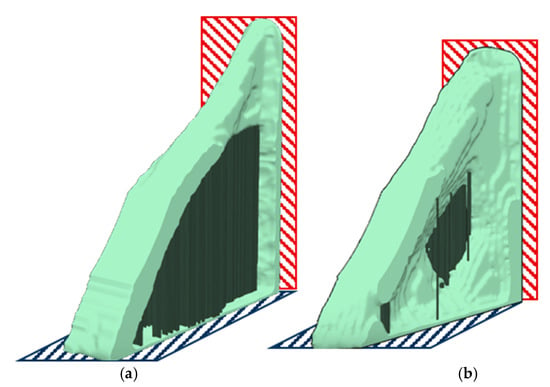
Figure 10.
Comparison of the reference design proposal (a) and the design proposal with the highest effective material usage (b) for the bracket application example. The support-material is displayed in dark green, while constraints are visualized in dark blue and loaded areas in red.
3.3. Rocker
For the rocker example, all TO experiments were conducted successfully. Since its reference solution already had an effective material usage of 93%, there was little space for improvement beforehand. For all the TO simulations, 17 design proposals had an increased effective material usage, as shown left in Figure 11.
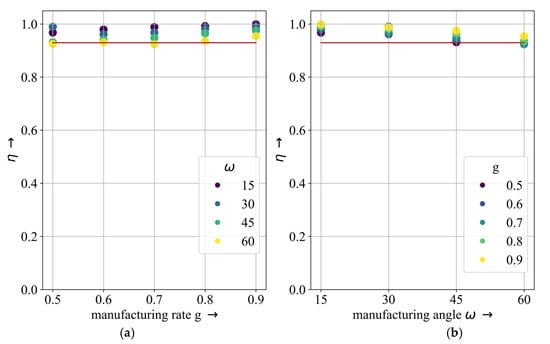
Figure 11.
The effective material usage of the rocker design proposals. The red line indicates of the reference design proposal. (a) Shows the effective material usage as a function of manufacturing rate g; (b) Shows the effective material usage as a function of manufacturing angle ω. The parameters resulted in a of 99.91%.
Though all changes were within a range of 8%, the rocker’s results showed trends contrary to the previous two examples. Here, the effective material usage continuously decreased with the increasing manufacturing angle, which respectively increased with the increasing manufacturing rate. Figure 11 further shows that increased with increasing g, while it decreased with increasing ω. The best design proposal resulted in an effective material usage of 99.91%, which denoted an improvement of circa 7% compared to the reference design proposal. The differences between these two design proposals are displayed in Figure 12.
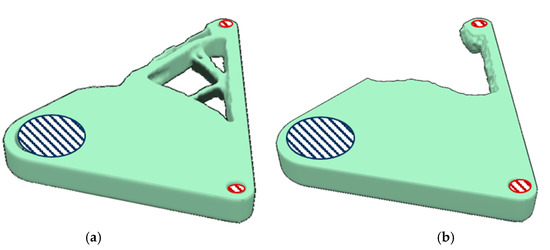
Figure 12.
Comparison of the reference design proposal (a) and the design proposal with the highest effective material usage (b) for the rocker application example. The support-material is displayed in dark green, while constraints are visualized in dark blue and loaded areas in red.
4. Discussion
The results show that the application of the presented method of manufacturing conflicts based on finite spheres lead to an improvement in effective material usage. While, in other works, the proposed methods for manufacturing constraints are demonstrated on numerical, 2D, and 2.5 D structures, respectively [13,14,15], we studied the influence of various settings on our proposed methods on three different 3D structures. We showed that the common manufacturing angle for extrusion-based AM of 45° led to an increase in the effective material used for all application examples. However, superior results could be achieved with other settings. Hence, the effective material used for all application examples was increased to at least 99%, while only the cantilever was manufacturable entirely without support material. According to our definition of manufacturing conflicts, effective material usage should rise with an increasing manufacturing rate. Nevertheless, the abstracted finite sphere and not the real elements were evaluated, and the design proposal was further smoothed after the TO with manufacturing constraints converged. Due to these abstractions, manufacturing conflict-free design proposals may still have manufacturing conflicts for the real elements, or some features may become non-self-supporting during the smoothing.
In addition, the results show that these drawbacks are minor, so for the cantilever and the bracket example, an improvement in the effective material usage by 32% was achieved. However, these significant improvements were only possible as the reference design proposal’s effective material usage was below 70%. The material usage improvement for the rocker resulted in nearly 7% since its reference effective material usage was already 93%. These results prove that the initial design space and selection of the manufacturing direction heavily influence the effectiveness, respectively, and the necessity of manufacturing constraints. Table 2 summarizes the results for all three application examples with their settings for the three best configurations.

Table 2.
Overall summary of the results for all three application examples. For each example, the best three configurations are shown with their corresponding .
Based on these results, default settings are hard to propose. The cantilever’s results tend to use manufacturing rates lower than 0.8, while the rocker’s results emphasize higher rates.
However, in total, an improvement was detected for 78% of all TO experiments, while the best parameters led to effective material used in all cases, which demonstrates the effectiveness of our proposed method. To further improve and ease the application of the presented concept, future work will investigate how to cluster geometries in categories for the manufacturing conflict settings to avoid unnecessary parameter studies beforehand.
5. Conclusions
In this article, we presented the concept of finite spheres and applied it to the description of manufacturing conflicts in extrusion-based AM. The purpose was to investigate the impact of the manufacturing rate and manufacturing angle on effective material usage for three application examples. The results led to the effective material usage of at least 99% for each application example, demonstrating the method’s viability. Moreover, the results show that, for optimal material utilization, the manufacturing conflict settings must be selected considering the particular TO setup. Thus, the presented method leads to support-free or nearly support-free structures for arbitrary geometries. The presented method is integrated into the freeware Z88Arion®, making it easier for product developers to optimize their parts for extrusion-based AM.
Author Contributions
Conceptualization, T.R.; methodology, T.R. and T.B.; software, T.R. and T.B.; validation, C.O. and T.B.; formal analysis, T.R. and C.O.; investigation, T.R., C.O. and T.B.; resources, B.A.-L. and S.T.; data curation, T.R.; writing—original draft preparation, T.R., C.O. and T.B.; writing—review and editing, B.A.-L. and S.T.; visualization, T.R., T.B. and C.O.; supervision, B.A.-L. and S.T.; project administration, B.A.-L. and S.T.; funding acquisition, B.A.-L. and S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Social Fund (ESF) within the project OpAL (StMBW-W-IX4-6-210091). The APC was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—491183248. This research was also funded by the Open Access Publishing Fund of the University of Bayreuth.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The software and data used in this study are available at www.z88.de, accessed on 11 December 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003; ISBN 978-3-540-42992-0. [Google Scholar]
- Rosnitschek, T.; Hentschel, R.; Siegel, T.; Kleinschrodt, C.; Zimmermann, M.; Alber-Laukant, B.; Rieg, F. Optimized one-click development for topology-optimized structures. Appl. Sci. 2021, 11, 2400. [Google Scholar] [CrossRef]
- Wu, Z.; Xiao, R. A topology optimization approach to structure design with self-supporting constraints in additive manufacturing. J. Comput. Des. Eng. 2022, 9, 364–379. [Google Scholar] [CrossRef]
- Orme, M.; Madera, I.; Gschweitl, M.; Ferrari, M. Topology optimization for additive manufacturing as an enabler for light weight flight hardware. Designs 2018, 2, 51. [Google Scholar] [CrossRef]
- Liu, J.; Ma, Y. A survey of manufacturing oriented topology optimization methods. Adv. Eng. Softw. 2016, 100, 161–175. [Google Scholar] [CrossRef]
- Vatanabe, S.L.; Lippi, T.N.; de Lima, C.R.; Paulino, G.H.; Silva, E.C. Topology optimization with manufacturing constraints: A unified projection-based approach. Adv. Eng. Softw. 2016, 100, 97–112. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, Z. Structural shape and topology optimization of cast parts using level set method: Structural shape and topology optimization of cast parts using level set method. Int. J. Numer. Methods Eng. 2017, 111, 1252–1273. [Google Scholar] [CrossRef]
- Harzheim, L.; Graf, G. A review of optimization of cast parts using topology optimization: II-Topology optimization with manufacturing constraints. Struct. Multidiscip. Optim. 2006, 31, 388–399. [Google Scholar] [CrossRef]
- Wang, C.; Xu, B.; Meng, Q.; Rong, J.; Zhao, Y. Topology optimization of cast parts considering parting surface position. Adv. Eng. Softw. 2020, 149, 102886. [Google Scholar] [CrossRef]
- Gersborg, A.R.; Andreasen, C.S. An explicit parameterization for casting constraints in gradient driven topology optimization. Struct. Multidiscip. Optim. 2011, 44, 875–881. [Google Scholar] [CrossRef]
- Tavakoli, R.; Davami, P. Optimal riser design in sand casting process by topology optimization with SIMP method I: Poisson approximation of nonlinear heat transfer equation. Struct. Multidiscip. Optim. 2008, 36, 193–202. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Q. Numerical simulation of stress-based topological optimization of continuum structures under casting constraints. Eng. Comput. 2022, 38, 4919–4945. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Guest, J.K. Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Struct. Multidiscip. Optim. 2016, 54, 1157–1172. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, J.; Zhang, W.; Du, Z.; Liu, C.; Liu, Y. Self-supporting structure design in additive manufacturing through explicit topology optimization. Comput. Methods Appl. Mech. Eng. 2017, 323, 27–63. [Google Scholar] [CrossRef]
- Leary, M.; Merli, L.; Torti, F.; Mazur, M.; Brandt, M. Optimal topology for additive manufacture: A method for enabling additive manufacture of support-free optimal structures. Mater. Des. 2014, 63, 678–690. [Google Scholar] [CrossRef]
- Perumal, V.I.; Najafi, A.R.; Kontsos, A. A novel digital design approach for metal additive manufacturing to address local thermal effects. Designs 2020, 4, 41. [Google Scholar] [CrossRef]
- Nvss, S.; Esakki, B.; Yang, L.-J.; Udayagiri, C.; Vepa, K.S. Design and development of unibody quadcopter structure using optimization and additive manufacturing techniques. Designs 2022, 6, 8. [Google Scholar] [CrossRef]
- Rastegarzadeh, S.; Wang, J.; Huang, J. Two-scale topology optimization with isotropic and orthotropic microstructures. Designs 2022, 6, 73. [Google Scholar] [CrossRef]
- Tyflopoulos, E.; Steinert, M. Combining macro and mesoscale optimization: A case study of the general electric jet engine bracket. Designs 2021, 5, 77. [Google Scholar] [CrossRef]
- Ryan-Johnson, W.P.; Wolfe, L.C.; Byron, C.R.; Nagel, J.K.; Zhang, H. A systems approach of topology optimization for bioinspired material structures design using additive manufacturing. Sustainability 2021, 13, 8013. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. Mater. Des. 2019, 183, 108164. [Google Scholar] [CrossRef]
- Saadlaoui, Y.; Milan, J.-L.; Rossi, J.-M.; Chabrand, P. Topology optimization and additive manufacturing: Comparison of conception methods using industrial codes. J. Manuf. Syst. 2017, 43, 178–186. [Google Scholar] [CrossRef]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for additive manufacturing: Trends, opportunities, considerations and constraints. CIRP Ann. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Delyová, I.; Frankovský, P.; Bocko, J.; Trebuňa, P.; Živčák, J.; Schürger, B.; Janigová, S. Sizing and topology optimization of trusses using genetic algorithm. Materials 2021, 14, 715. [Google Scholar] [CrossRef] [PubMed]
- Pellens, J.; Lombaert, G.; Lazarov, B.; Schevenels, M. Combined length scale and overhang angle control in minimum compliance topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2019, 59, 2005–2022. [Google Scholar] [CrossRef]
- Patterson, A.E.; Chadha, C.; Jasiuk, I.M. Identification and mapping of manufacturability constraints for extrusion-based additive manufacturing. J. Manuf. Mater. Process. 2021, 5, 33. [Google Scholar] [CrossRef]
- Van de Ven, E.; Maas, R.; Ayas, C.; Langelaar, M.; van Keulen, F. Overhang control based on front propagation in 3D topology optimization for additive manufacturing. Comput. Methods Appl. Mech. Eng. 2020, 369, 113169. [Google Scholar] [CrossRef]
- Fernández, E.; Ayas, C.; Langelaar, M.; Duysinx, P. Topology optimisation for large-scale additive manufacturing: Generating designs tailored to the deposition nozzle size. Virtual Phys. Prototyp. 2021, 16, 196–220. [Google Scholar] [CrossRef]
- Ameen, W.; Al-Ahmari, A.; Mohammed, M.K. Self-supporting overhang structures produced by additive manufacturing through electron beam melting. Int. J. Adv. Manuf. Technol. 2019, 104, 2215–2232. [Google Scholar] [CrossRef]
- Barroqueiro, B.; Andrade-Campos, A.; Valente, R.A.F. Designing self supported SLM structures via topology optimization. J. Manuf. Mater. Process. 2019, 3, 68. [Google Scholar] [CrossRef]
- Vlah, D.; Žavbi, R.; Vukašinović, N. Evaluation of topology optimization and generative design tools as support for conceptual design. Proc. Des. Soc. Des. Conf. 2020, 1, 451–460. [Google Scholar] [CrossRef]
- Belluomo, L.; Bici, M.; Campana, F. A generative design method for cultural heritage applications: Design of supporting structures for artefacts. Comput. Aided Des. Appl. 2022, 20, 663–681. [Google Scholar] [CrossRef]
- Baumgartner, A.; Harzheim, L.; Mattheck, C. SKO (Soft Kill Option): The biological way to find an optimum structure topology. Int. J. Fatigue 1992, 14, 387–393. [Google Scholar] [CrossRef]
- Frisch, M. Entwicklung Eines Hybridalgorithmus Zur Steifigkeits- UND Spannungsoptimierten Auslegung von Konstruktionselementen; Fortschritte in Konstruktion und Produktion; Shaker Verlag: Aachen, Germany, 2015; ISBN 978-3-8440-4028-9. [Google Scholar]
- Deese, K.; Geilen, M.; Rieg, F. A two-step smoothing algorithm for an automated product development process. Int. J. Simul. Model. 2018, 17, 308–317. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).