A Novel Reverse Hinge Spoiler for Flight Loads Control
Abstract
1. Introduction
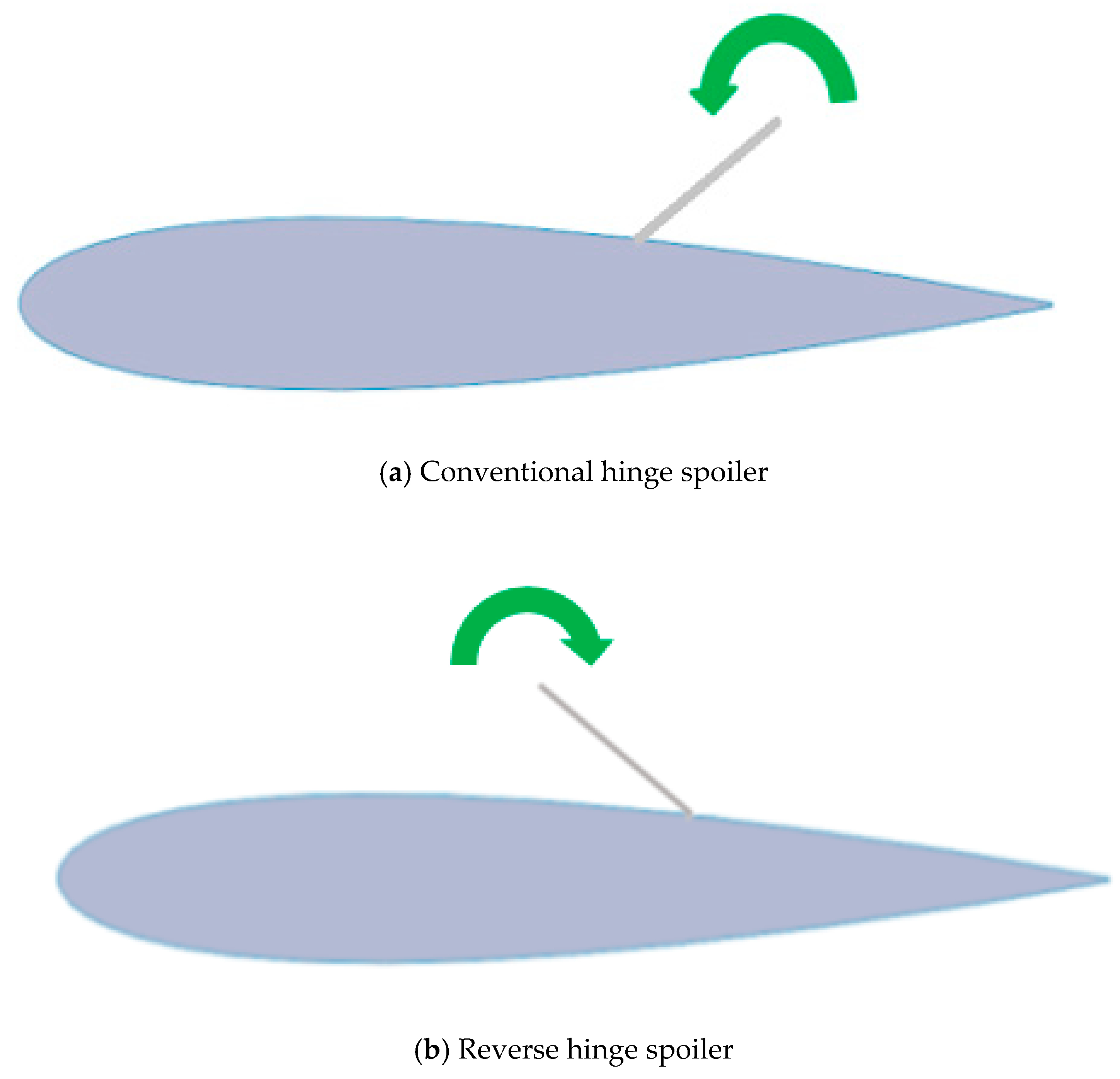
2. The Reverse Spoiler Concept
3. Computational Fluid Dynamics
3.1. The Mathematical Model
3.2. Spoiler Variables
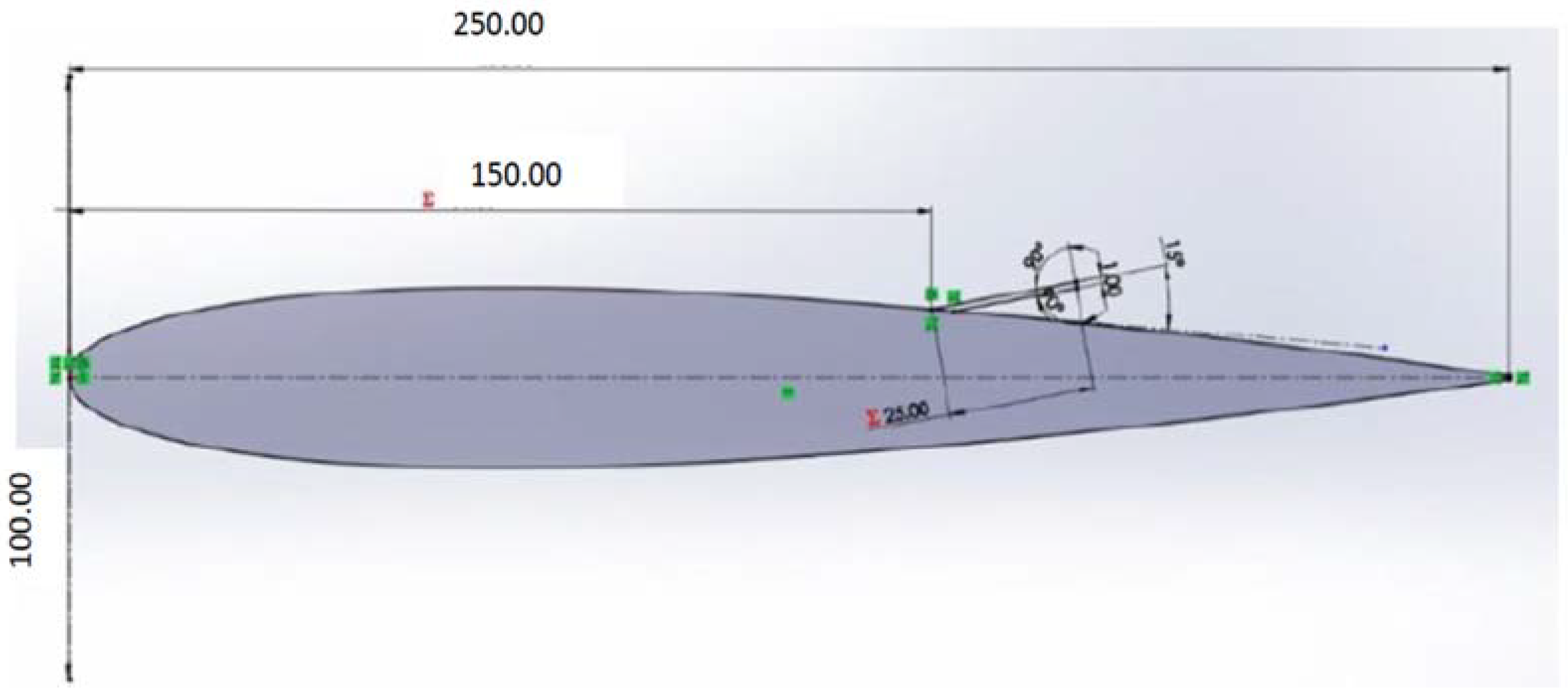
- Non-Dimensional Spoiler Length, L/C;
- Non-Dimensional Hinge Location of the Spoiler, X/C;
- Spoiler Deflection, θ (relative to a tangent drawn on the airfoil surface).
3.3. Geometry
3.4. Mesh Generation and Boundary Conditions
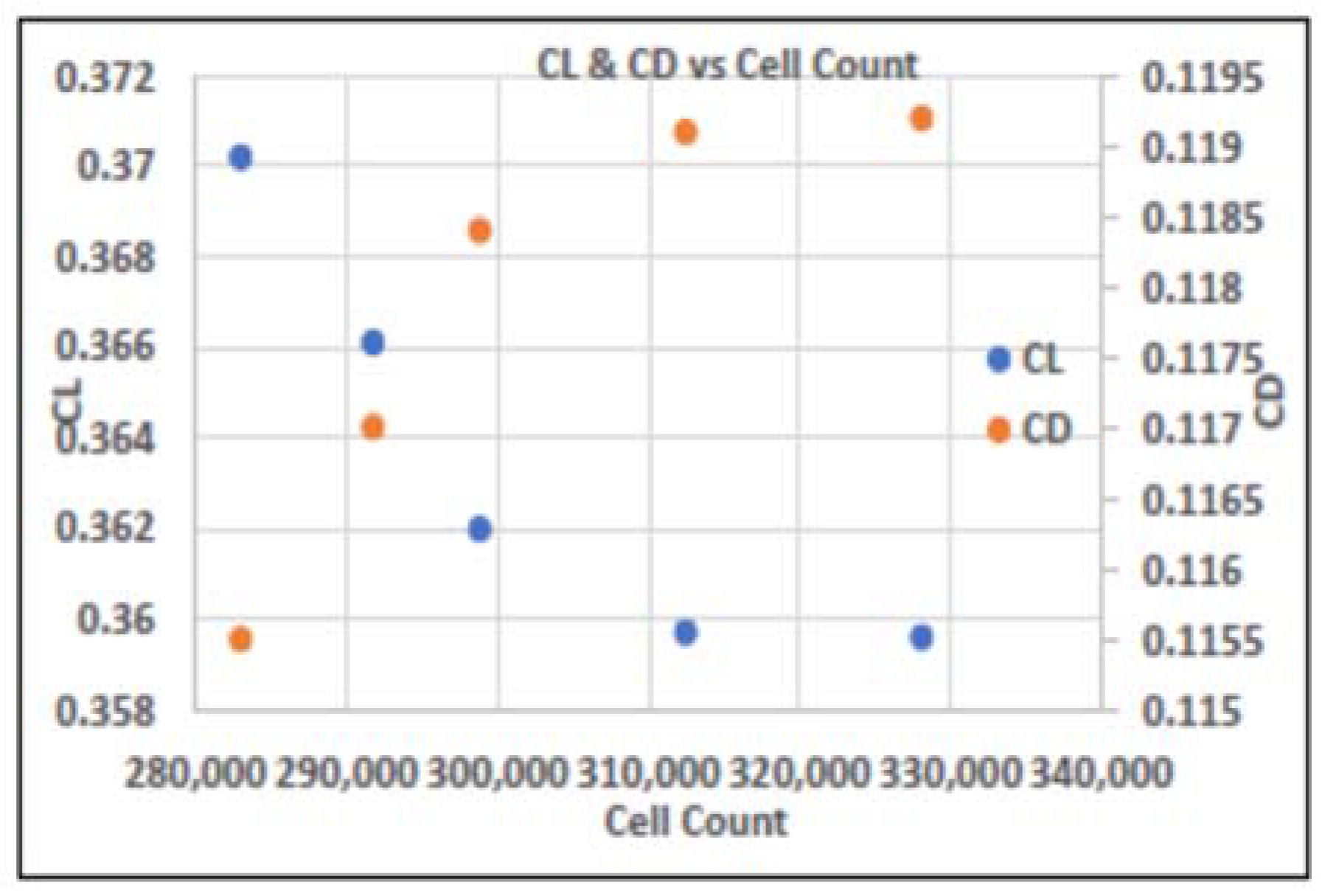
3.5. Grid Independence and Verification Analysis
Grid Uncertainty Analysis
3.6. Validation
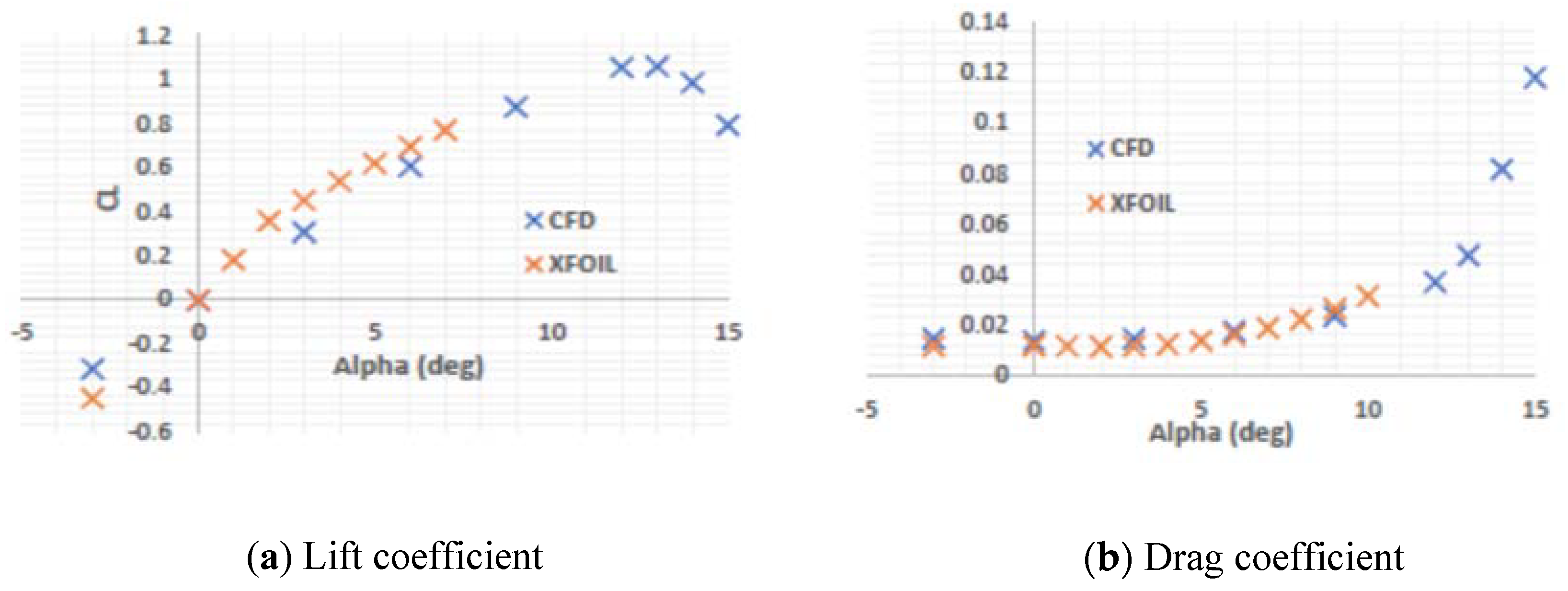
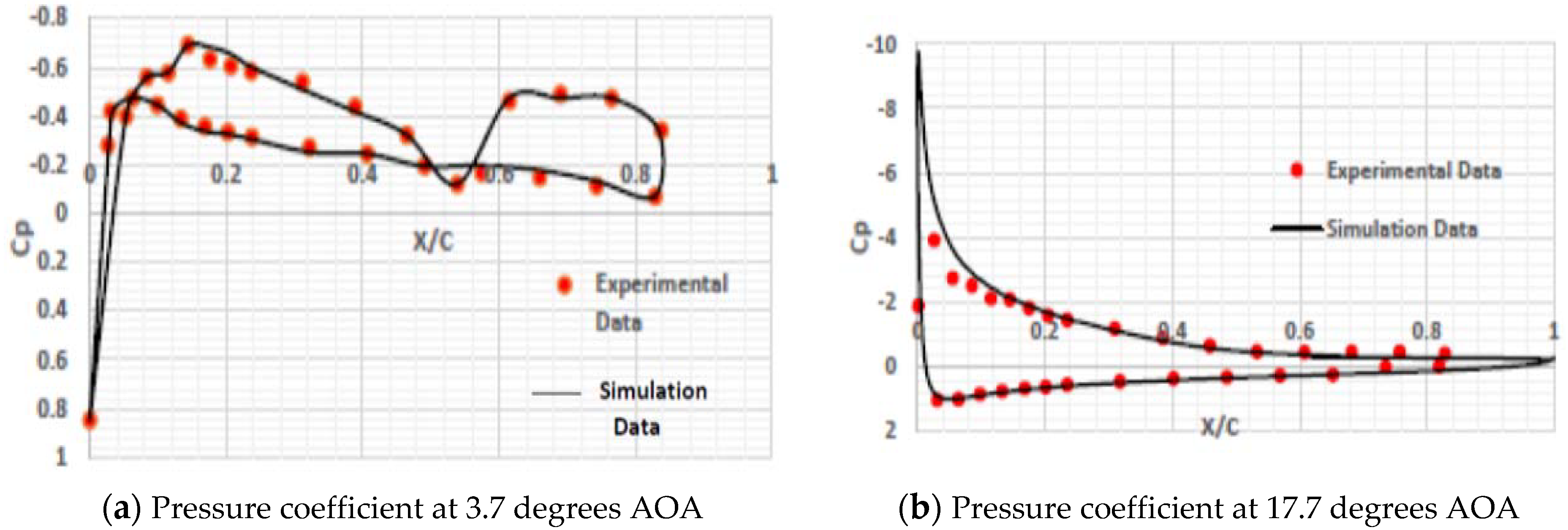
3.6.1. Clean NACA0012 CFD Results Validation with XFOIL
3.6.2. NACA 2412 with a Conventional Spoiler CFD Validation by Experiment
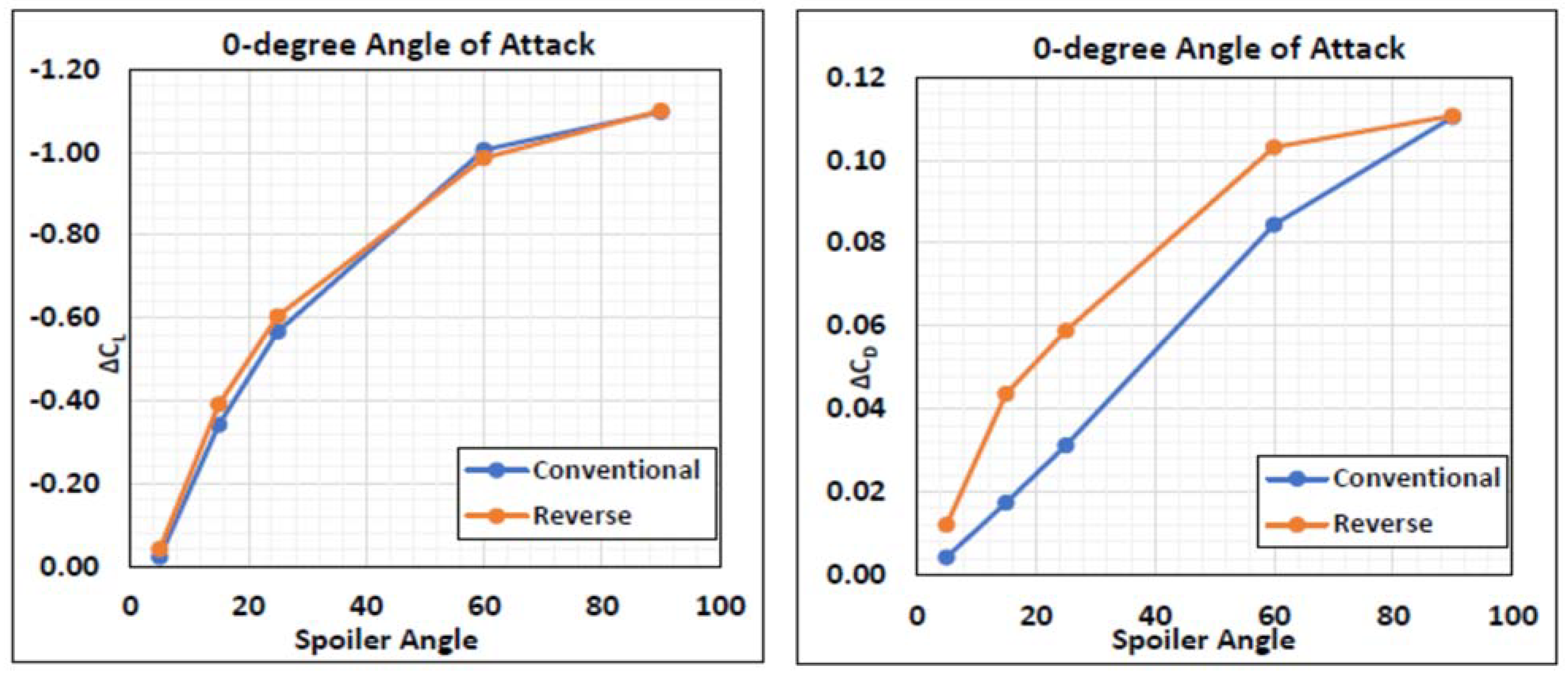
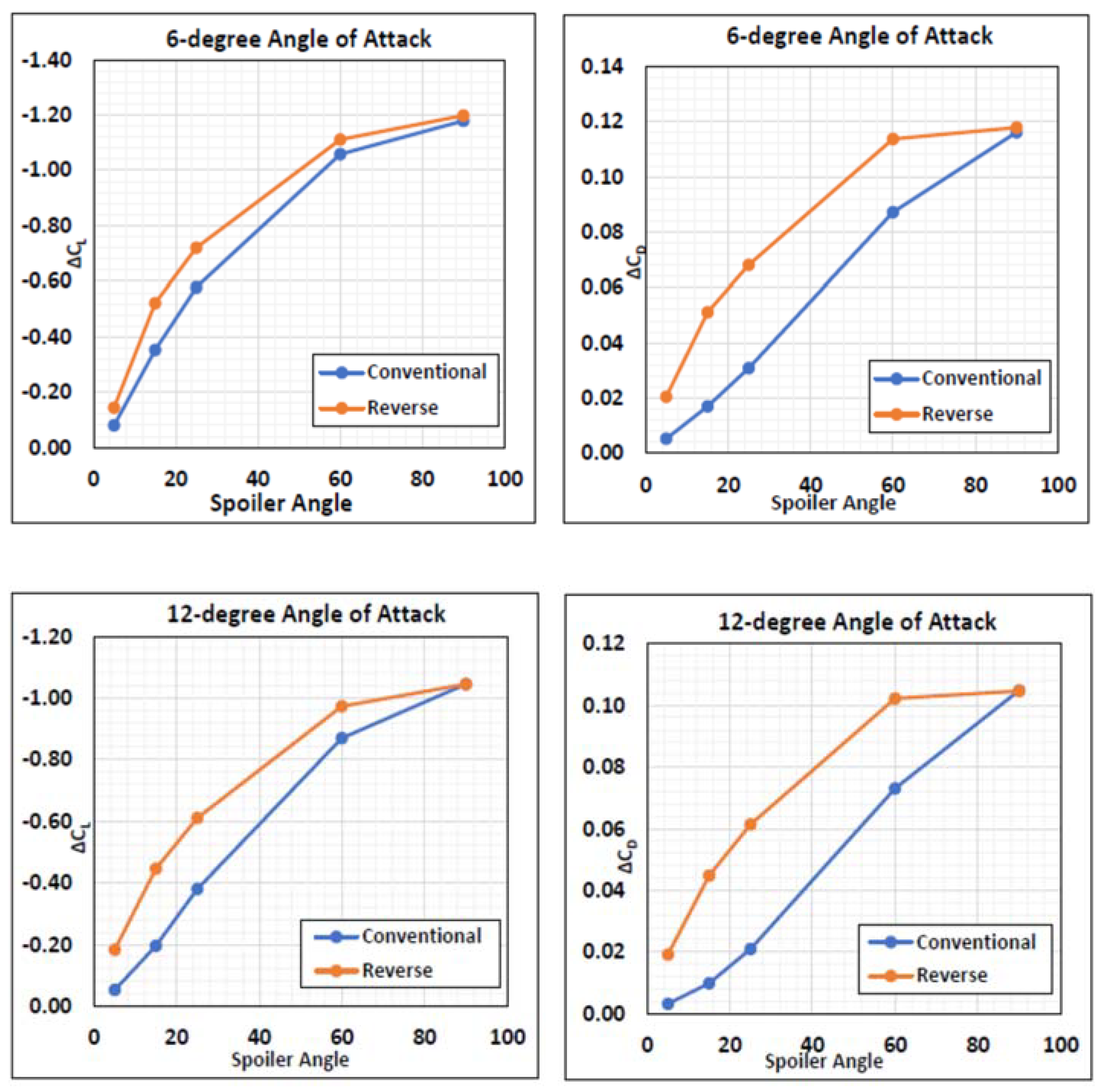
4. Conventional vs. Reverse Hinge Spoilers—Performance Analysis
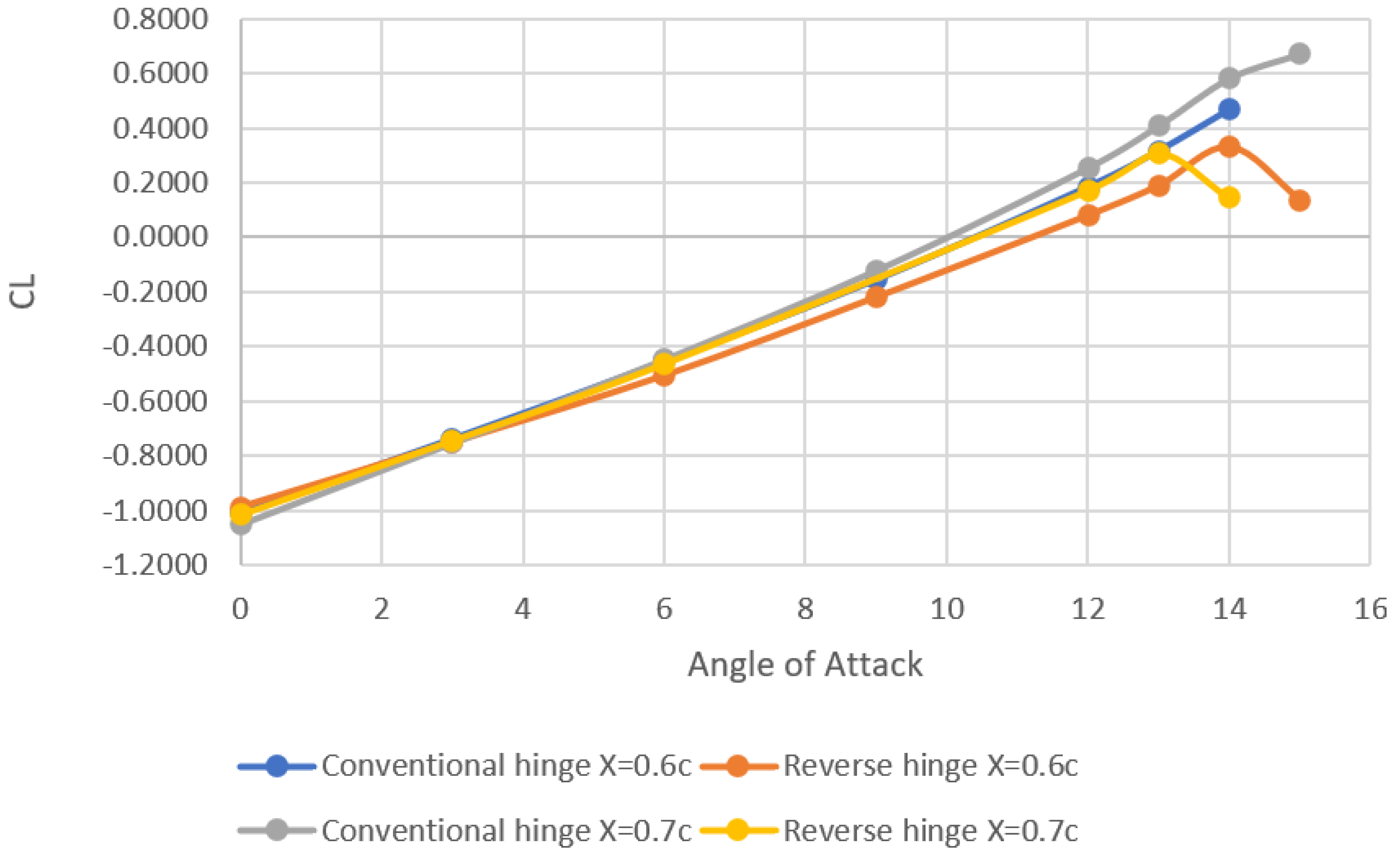
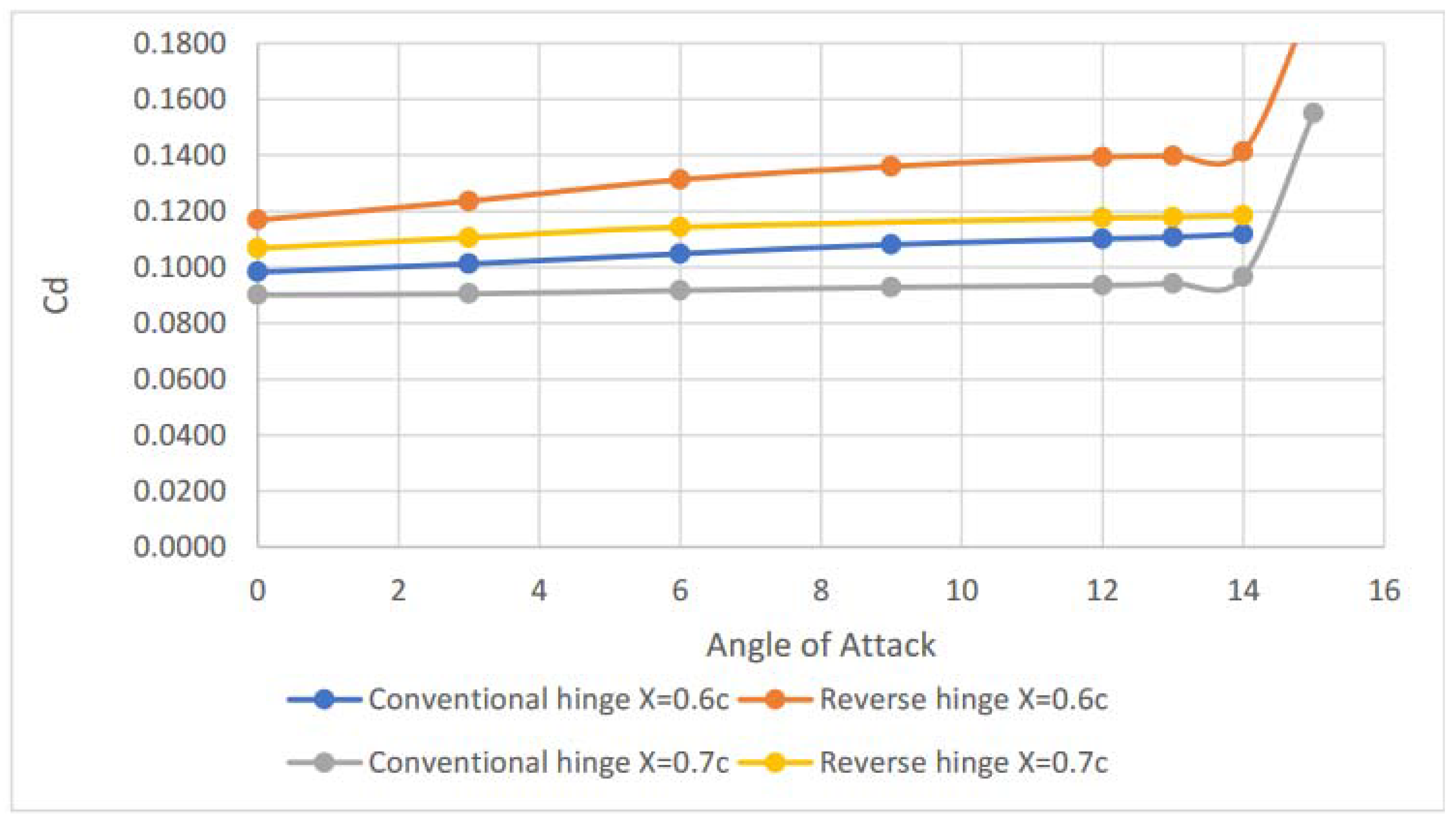
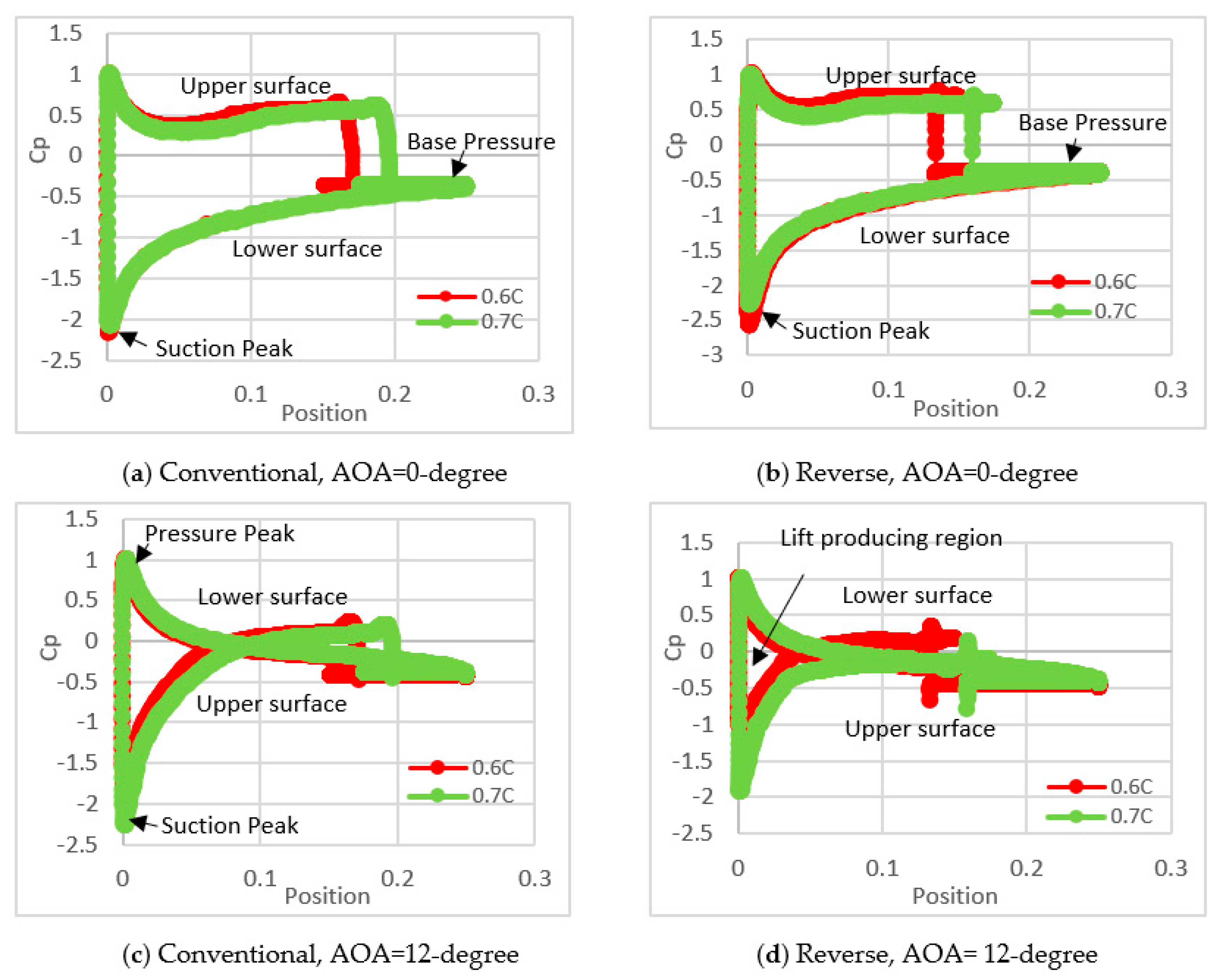
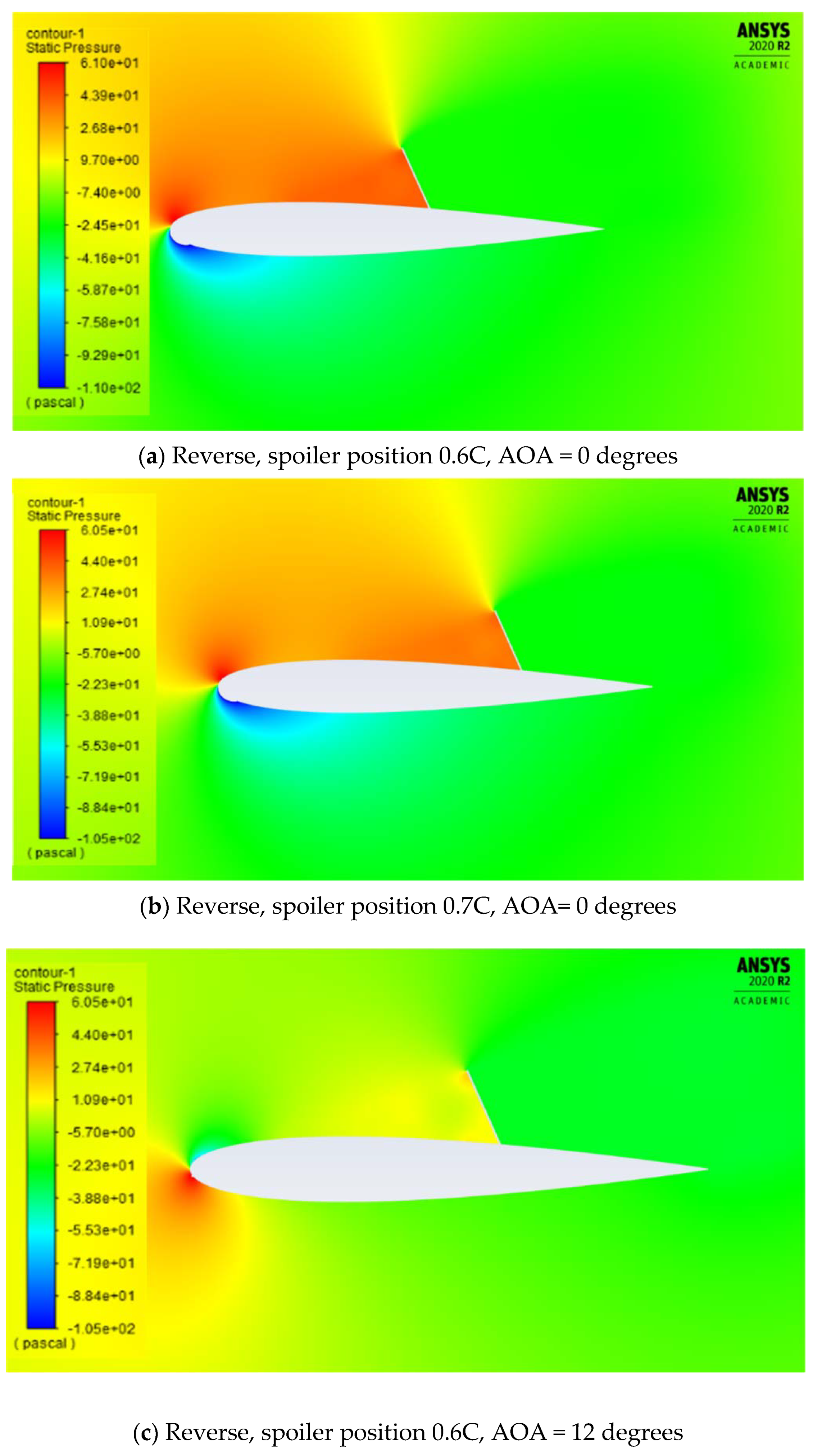
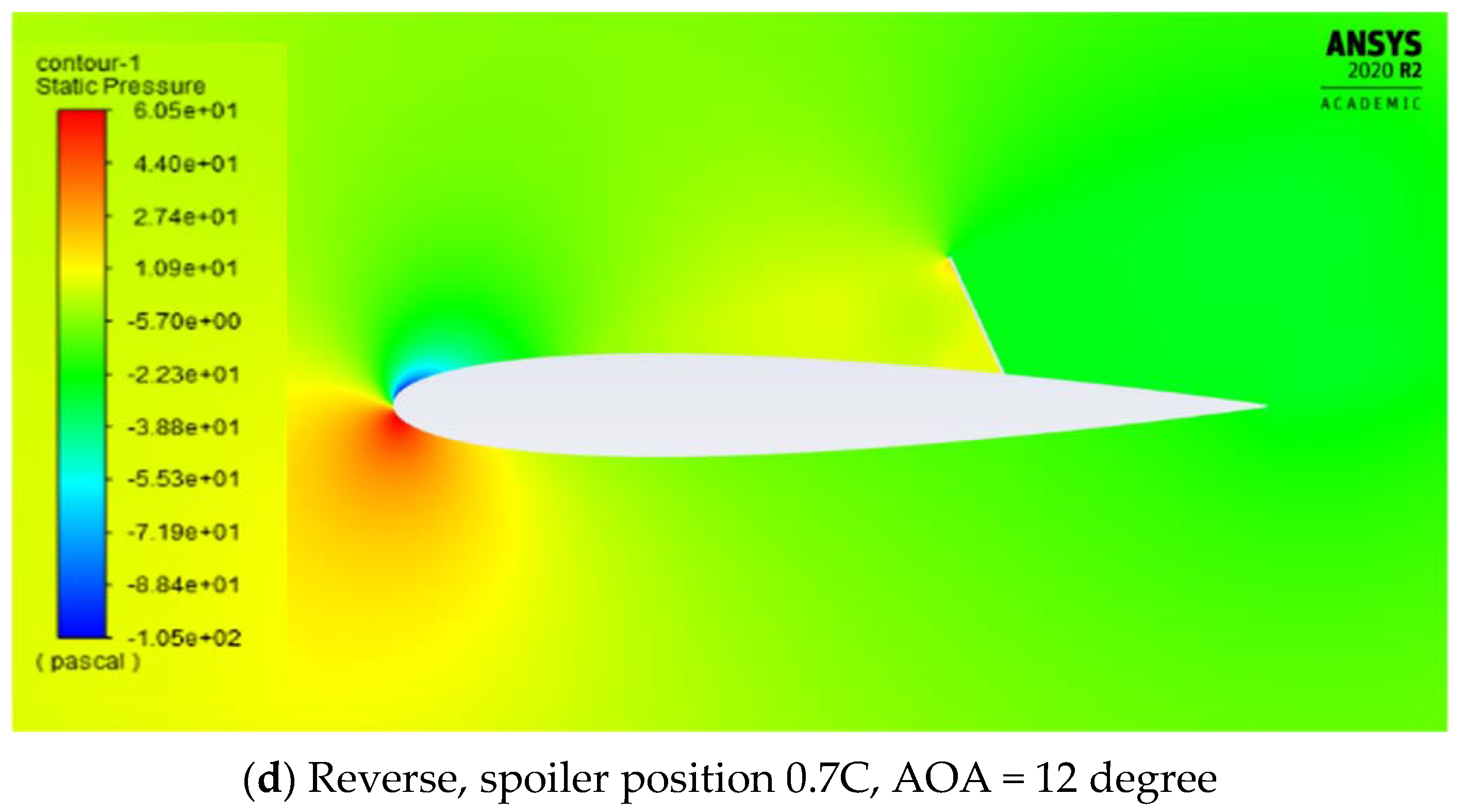
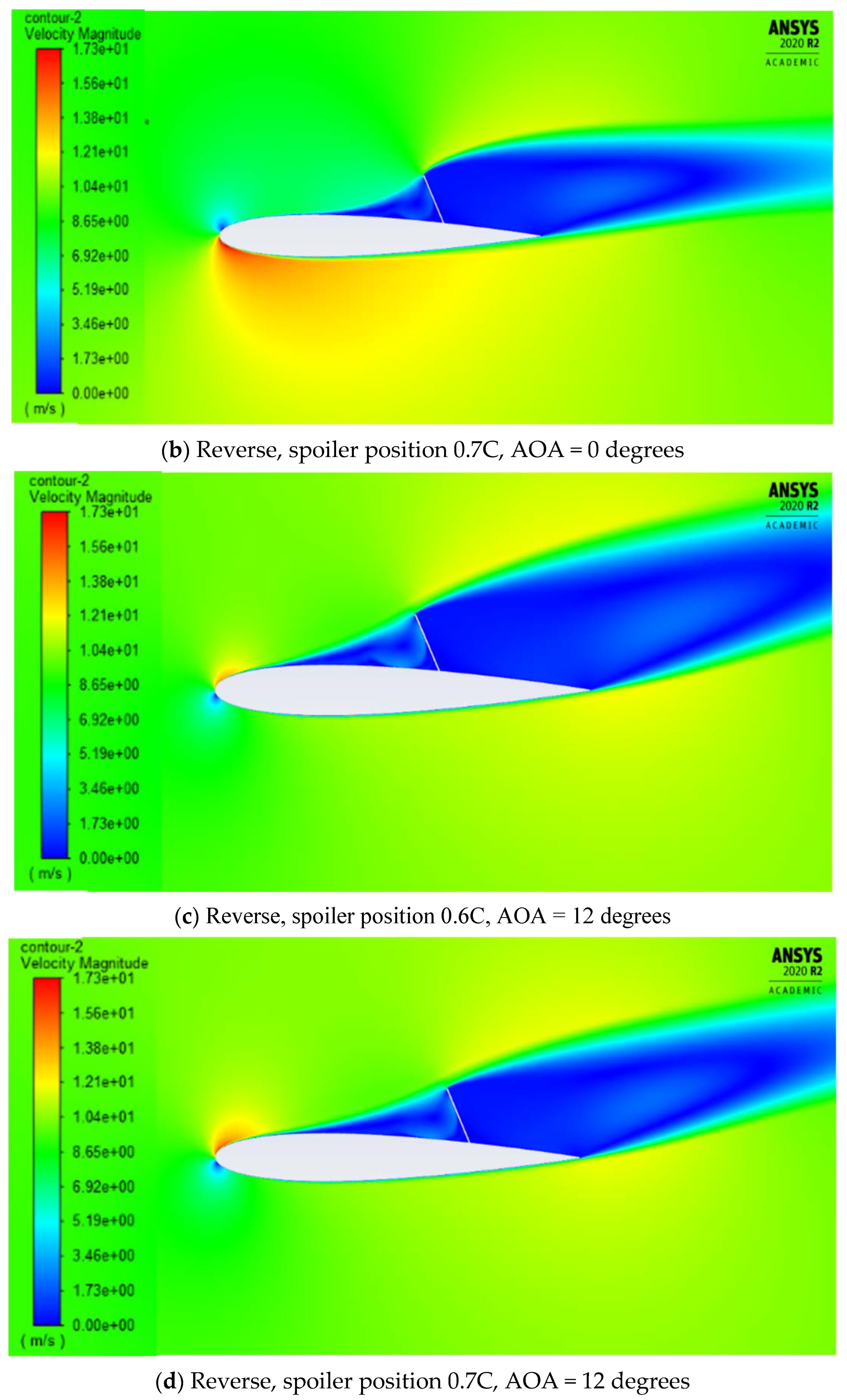
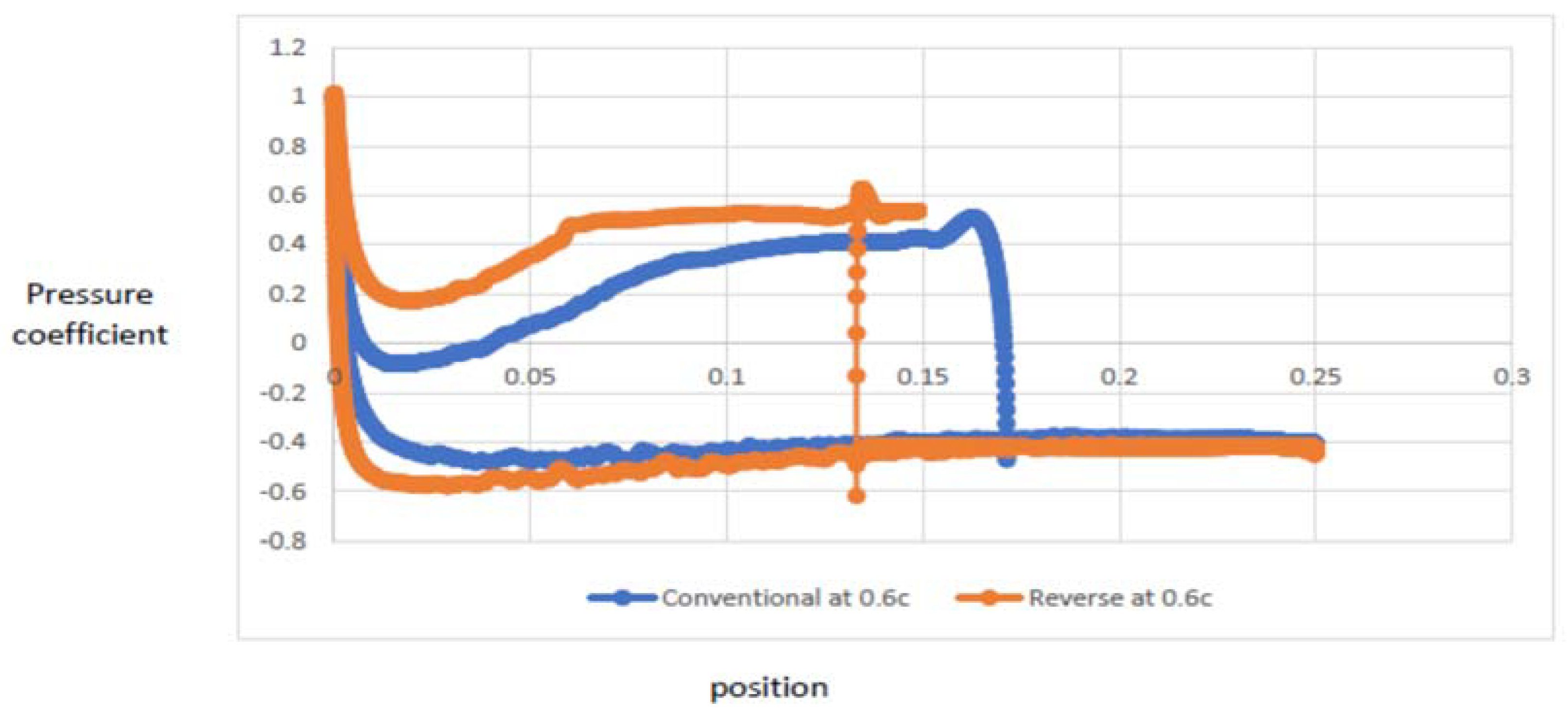
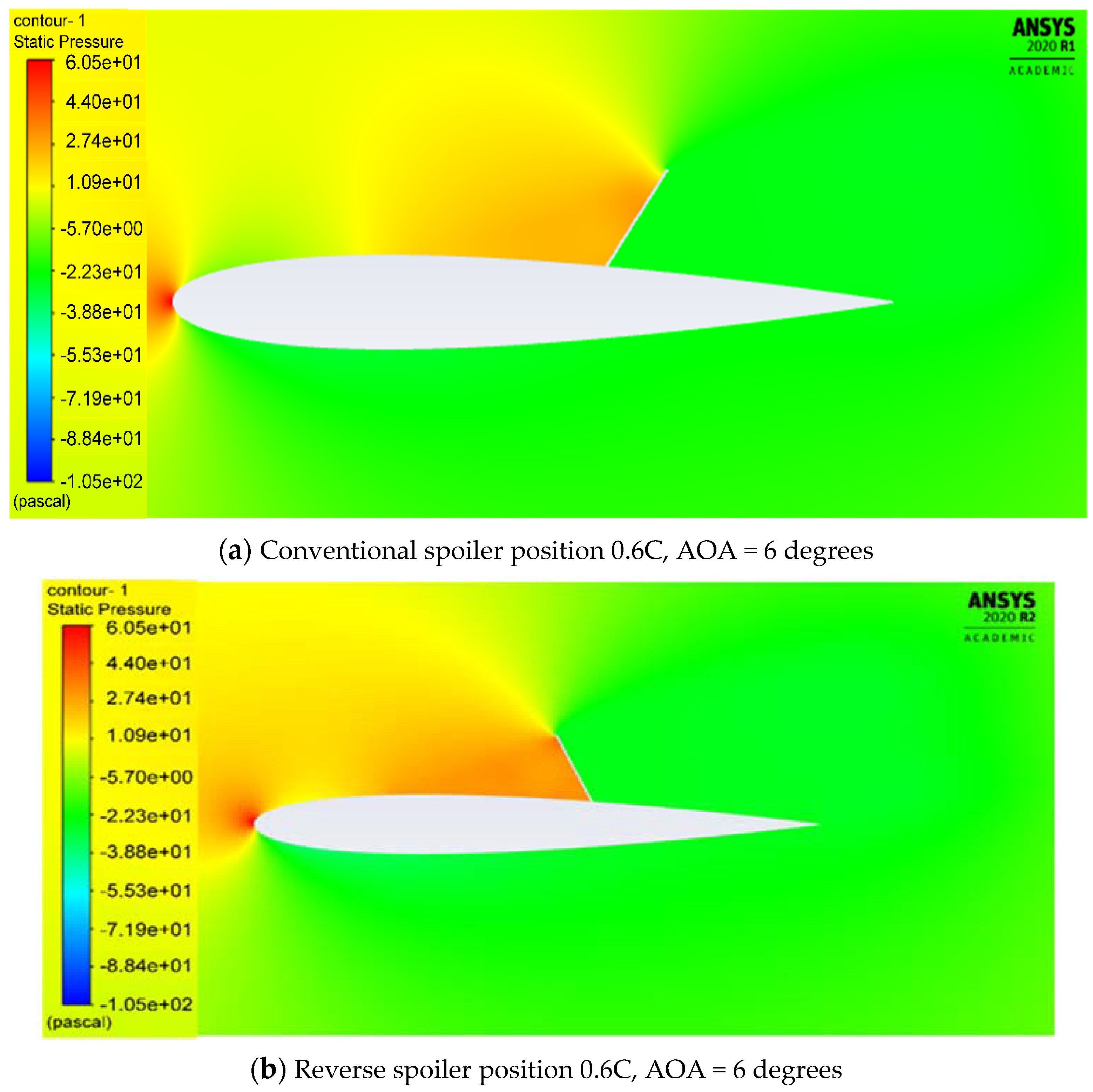
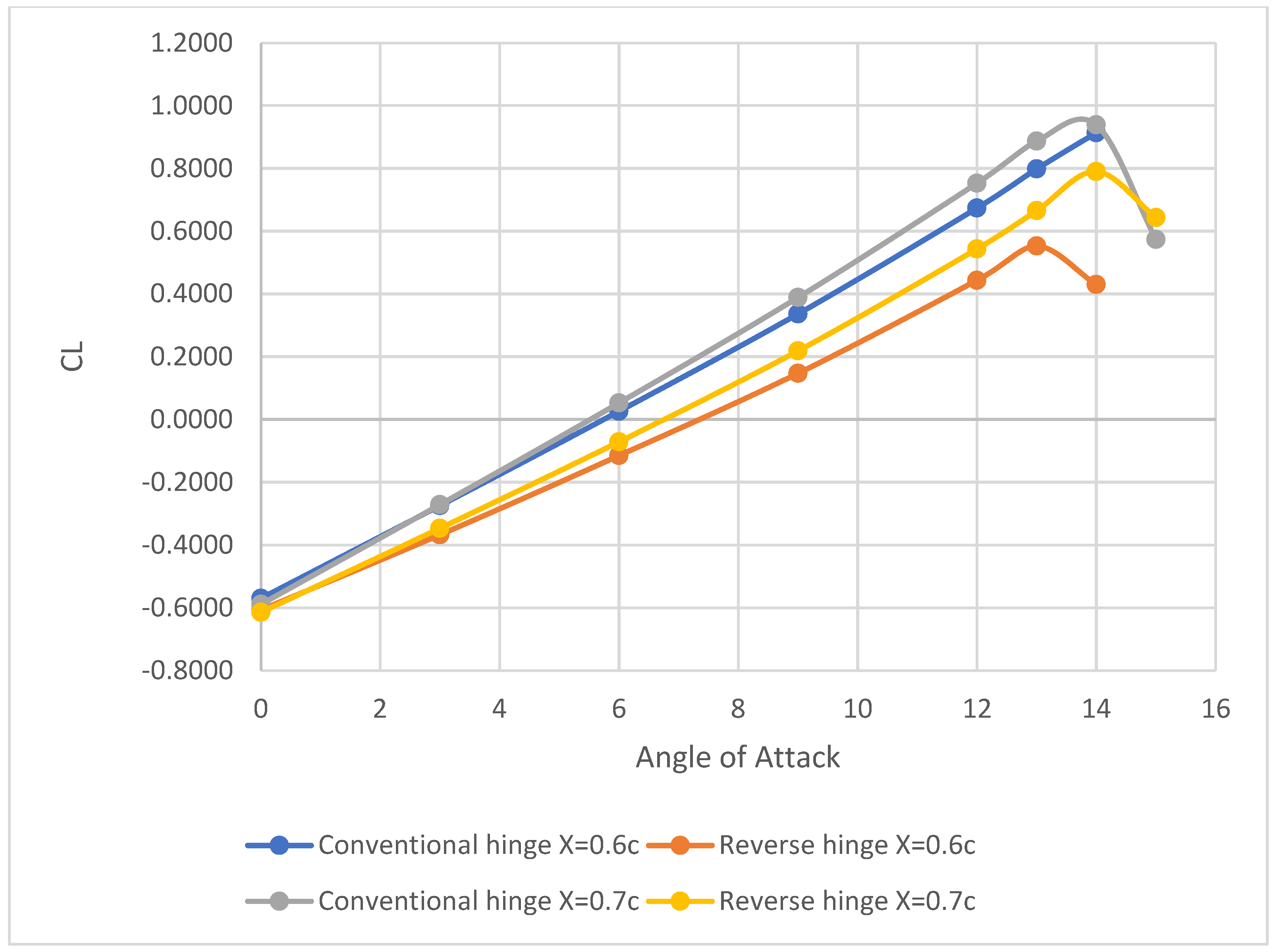
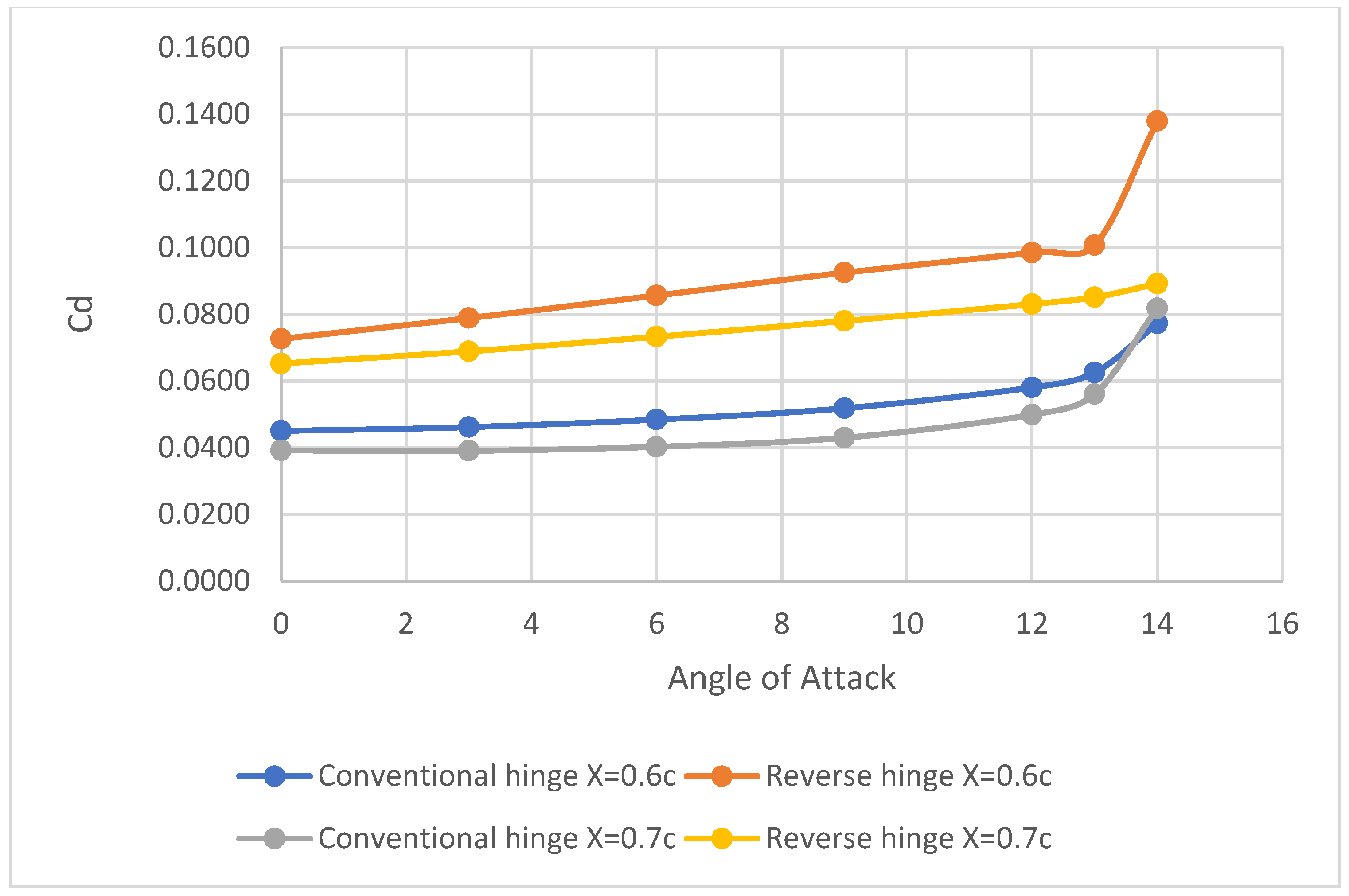
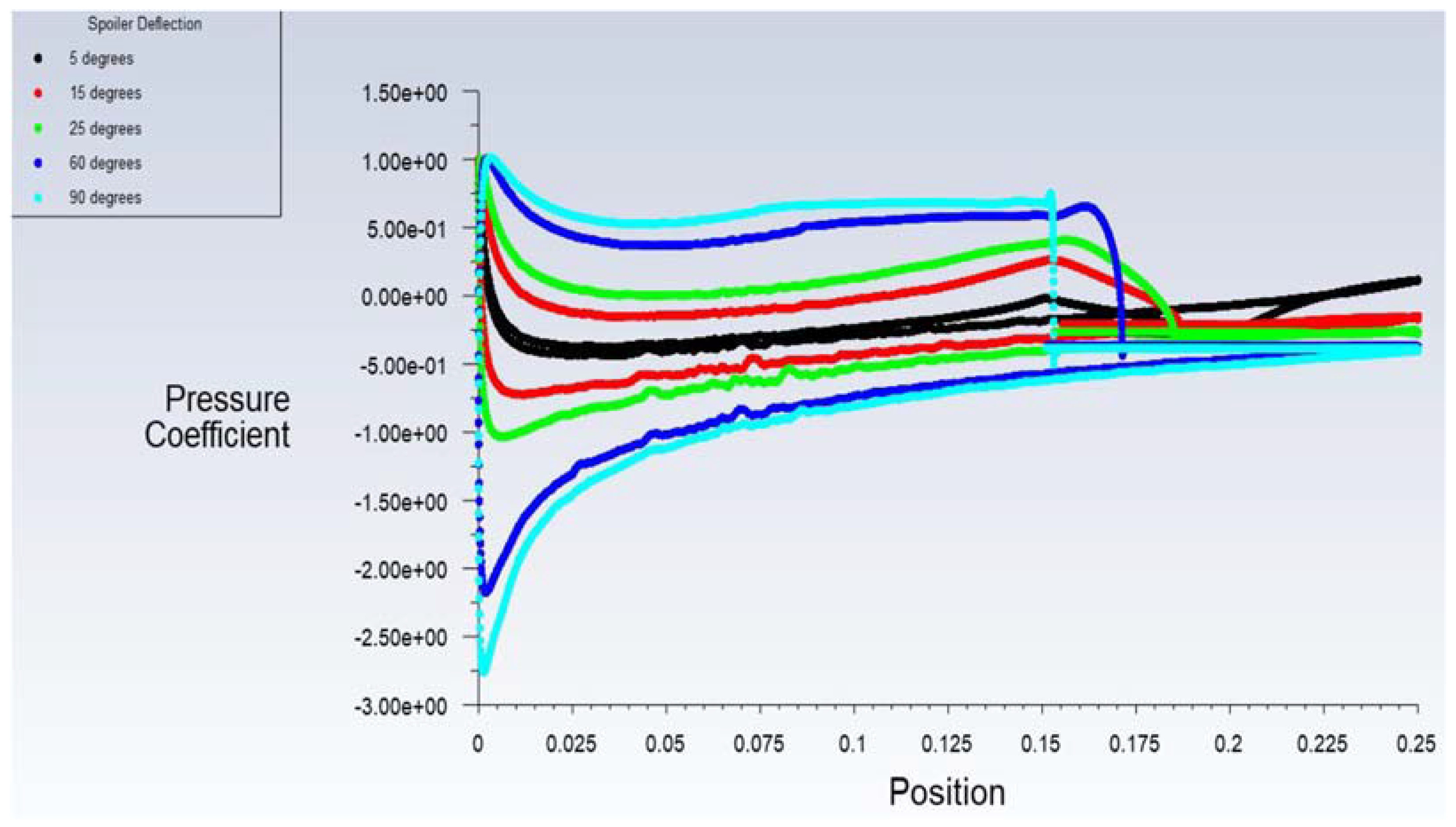
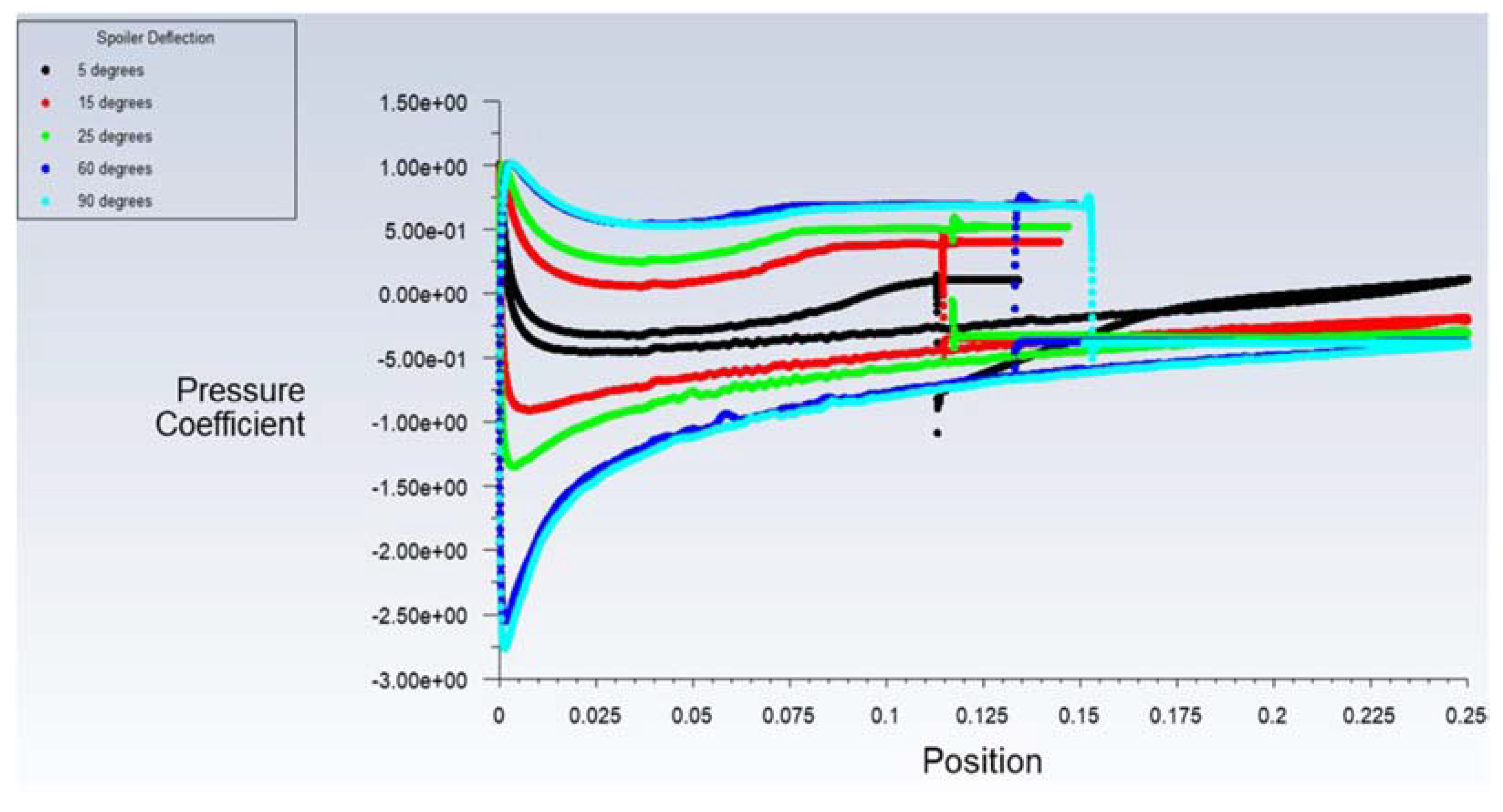
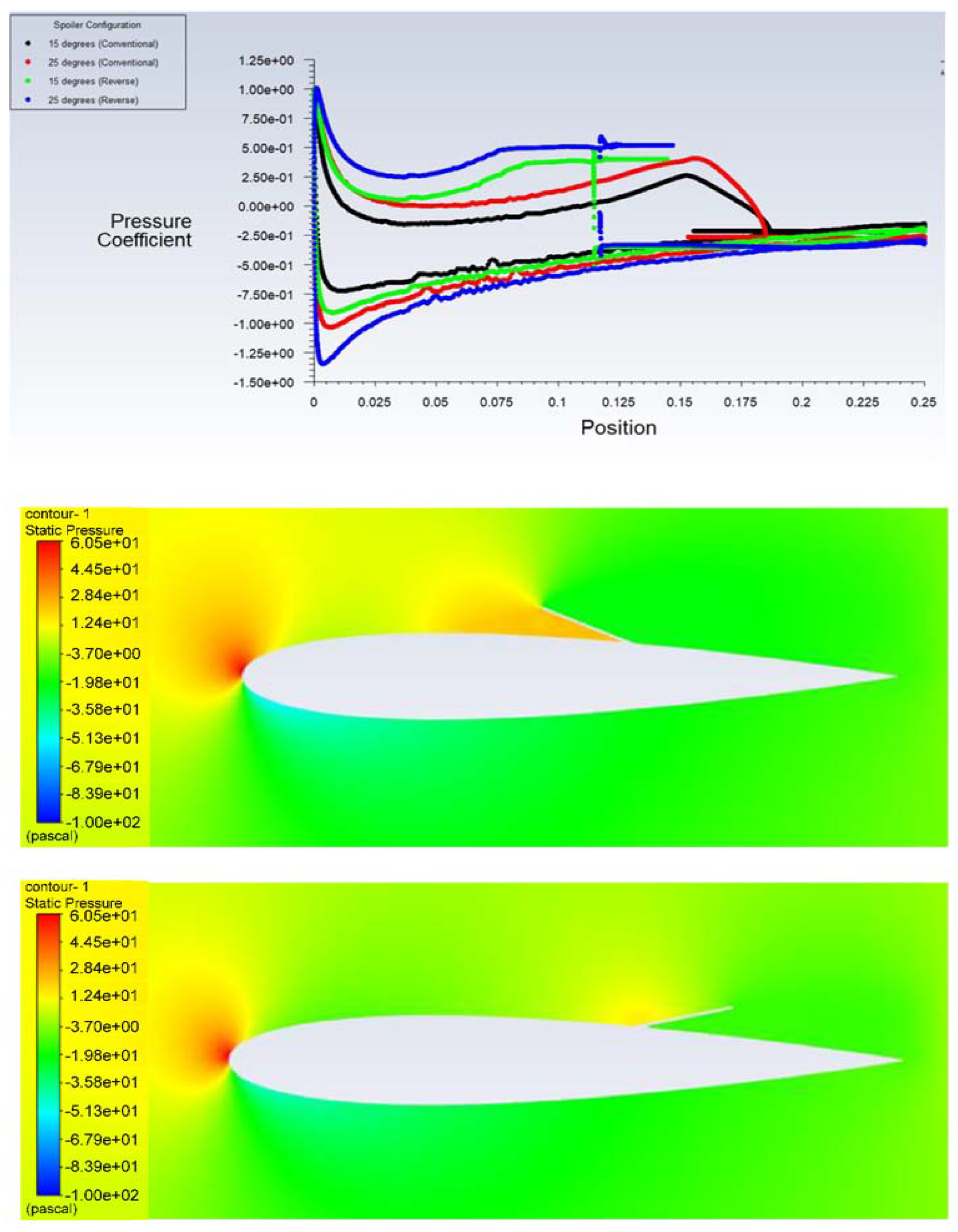
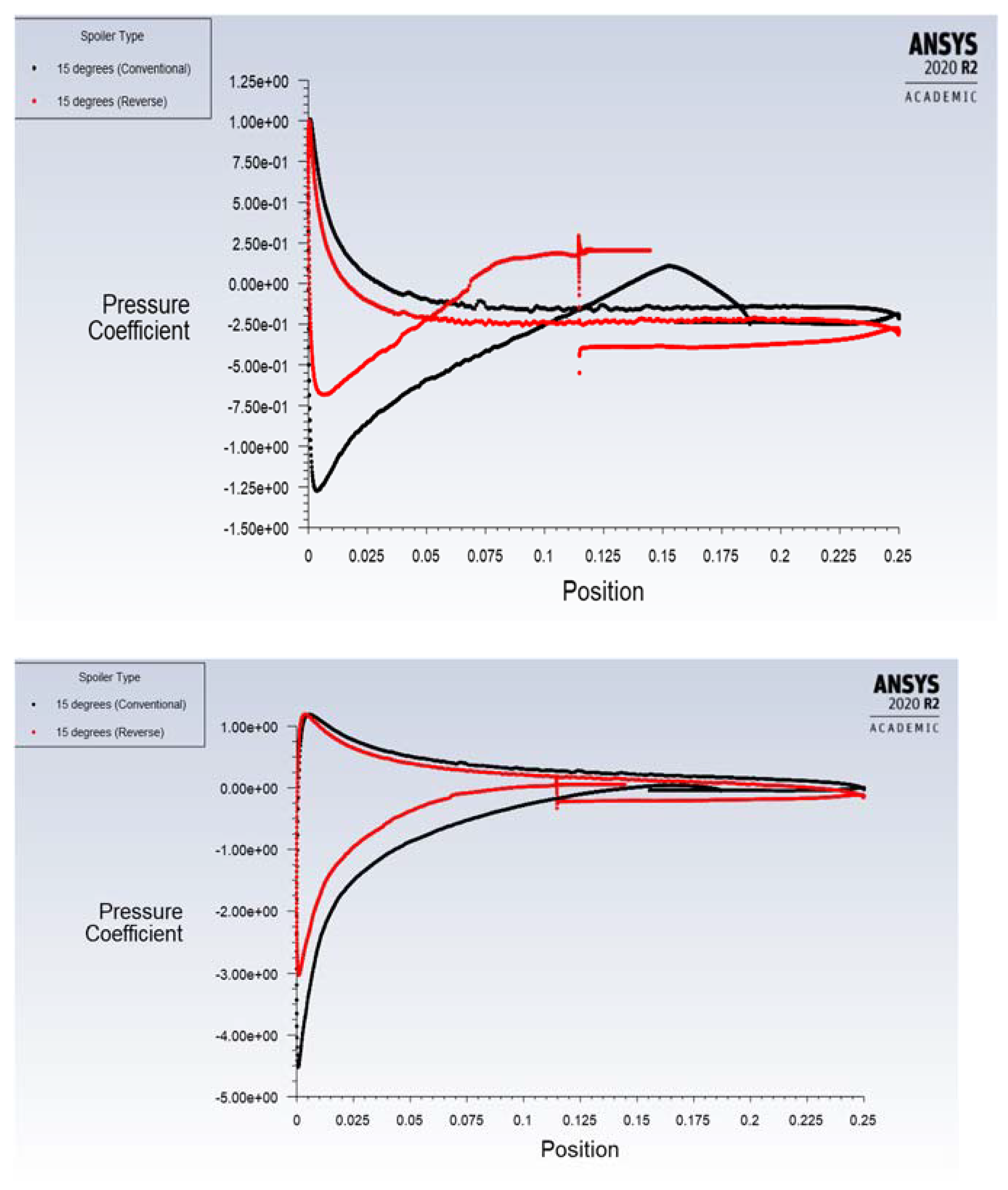
4.1. Effect of Spoiler Hinge Location
Flow-Field Analysis
4.2. Effect of Spoiler Deflection
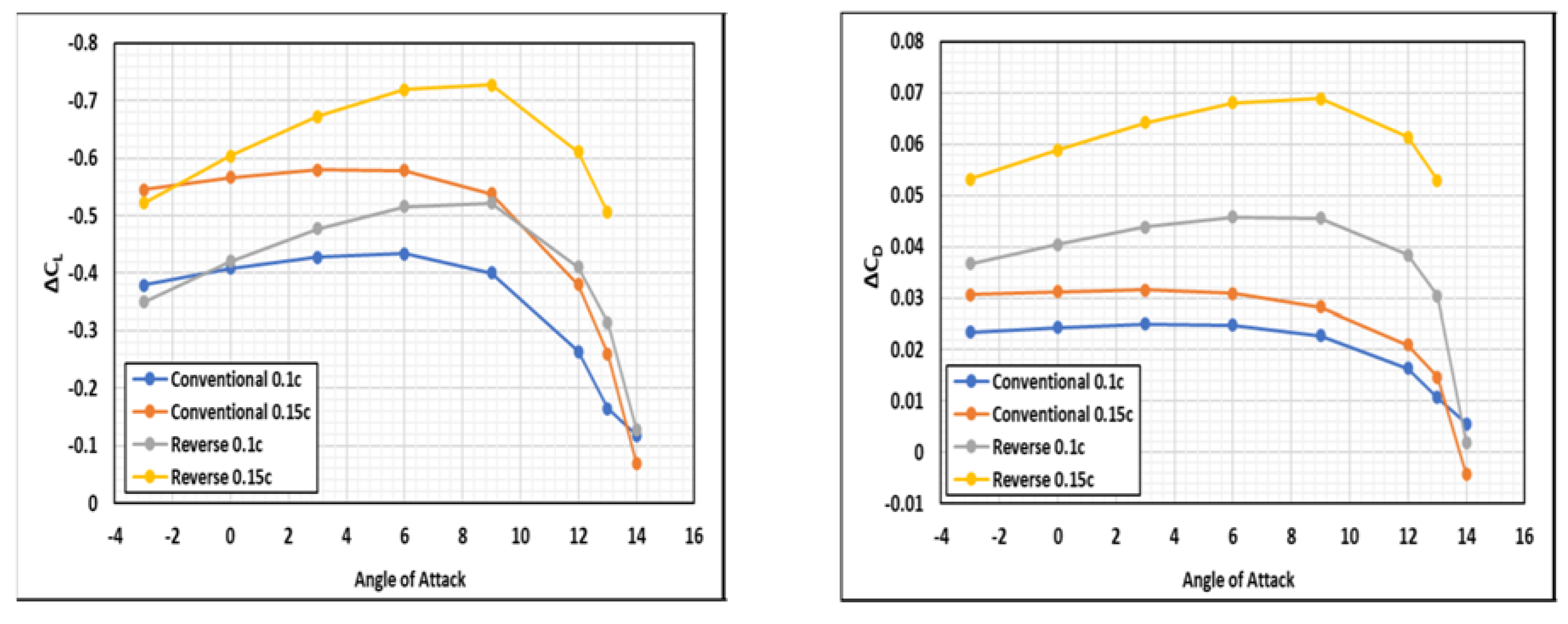
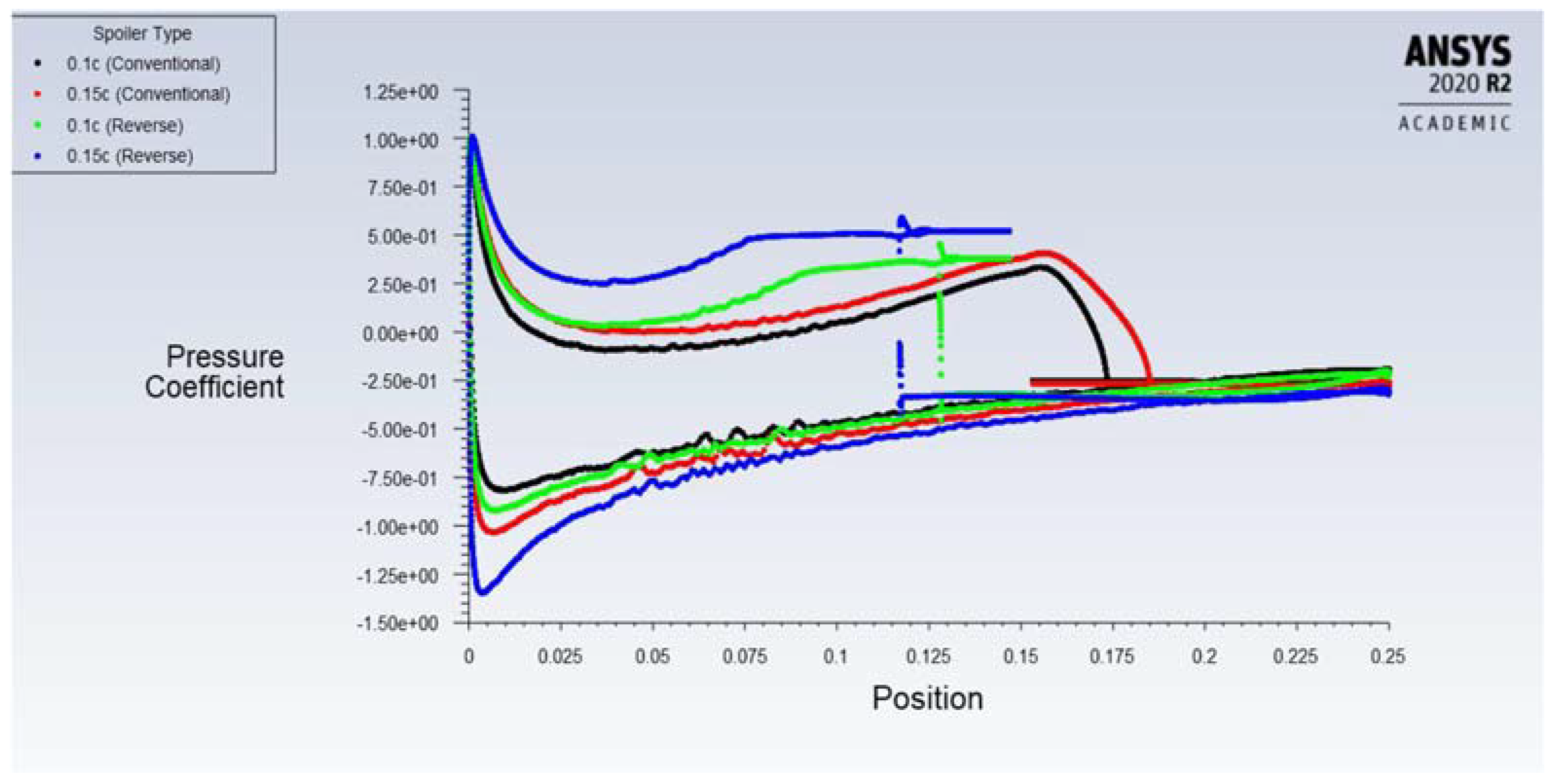
4.3. Effect of Spoiler Length
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andrisani, D.; Gentry, G.L.; Stickle, J.W. Wind Tunnel Study of Slot Spoilers for Direct Lift Control; NASA Technical Report; Langley Research Centre: Hamtpon, VA, USA, 1972. [Google Scholar]
- Harley, C. Aerodynamic Performance of Low Form Factor Spoilers. Ph.D. Thesis, University of Manchester, Manchester, UK, 2010. [Google Scholar]
- Fitzpatrick, J.E.; Furlong, G.C. Effect of Spoiler-Type Lateral-Control Devices on the Twisting Moments of a Wing of NACA 230-Series Airfoil Sections; Langley Memorial Aeronautical Laboratory: Hampton, VA, USA, 1947. [Google Scholar]
- Waszak, M.R. Robust Multivariable Flutter suppression for benchmark active control technology wind tunnel model. AIAA J. 2001, 24, 147–153. [Google Scholar] [CrossRef]
- Payne, B.W. Designing a load alleviation system for a modern civil aircraft. In Proceedings of the 15th International Council of the Aeronautical Sciences, London, UK, 7–12 September 1986; pp. 283–291. [Google Scholar]
- Weick, F.E.; John, R.T. Resume and Analysis of NACA Lateral Control Research. NACA; Langley Memorial Aeronautical Laboratory: Hampton, VA, USA, 1937. [Google Scholar]
- Wentz, J.R.; Ostowari, C.; Seetharam, H.C. Effects of design variables on spoiler control effectiveness, hinge moments and wake. In Proceedings of the 19th AIAA Aerospace Sciences Meeting, St. Louis, MO, USA, 12–15 January 1981. [Google Scholar]
- McLachlan, B.G.; Karamcheti, K.; Joint Institute for Aeronautics and Acoustics. An Experimental Study of Airfoil Spoiler Aerodynamics; Stanford University: Stanford, CA, USA, 1984. [Google Scholar]
- Mashud, M.; Ferdous, M.; Omee, S.H. Effect of spoiler position on aerodynamic characteristics of an airfoil. Int. J. Mech. Mechatron. Eng. 2012, 12, 1–6. [Google Scholar]
- Lee, C.S.; Bodapati, S. Experimental investigations of the flowfield of an airfoil with spoiler. AIAA J. 1987, 25, 1411–1416. [Google Scholar] [CrossRef]
- Kalkanis, P. Numerical Simulation of Spoiler Flows. Ph.D. Thesis, Imperial College of Science and Technology, South Kensington, UK, 1988. [Google Scholar]
- Geisbauer, S. Numerical spoiler wake investigations at the borders of the flight envelope. In Proceedings of the 29th AIAA Applied Aerodynamics Conference, Honolulu, HU, USA, 27–30 June 2011. [Google Scholar]
- Alhawwary, M.A.; Owis, F.M.; Abdelrahman, M.M. Numerical simulation of the flowfield around airfoil with spoiler using the higher-order spectral difference method. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Guaily, A.; Abdelrahman, M. Numerical simulation of the vortex shedding behind an airfoil-spoiler configuration. Am. J. Aerosp. Eng. 2018, 5, 16–23. [Google Scholar] [CrossRef][Green Version]
- Askar, M.K.A.; Hameed, A.Q.; Suffer, K.H.; Razlan, Z.M. Numerical simulation of a new spoiler on upper surface of Clark Y14 wing. IOP Conf. Ser. Mat. Sci. Eng. 2018, 429, 012080. [Google Scholar] [CrossRef]
- Lindsay, S.D.; Walsh, P. Experimental investigation of spoiler deployment on wing stall. Open J. Fluid Dyn. 2018, 8, 308–320. [Google Scholar] [CrossRef]
- Tian, Y.; Feng, P.; Liu, P.; Hu, T.; Qu, Q. Spoiler Upward Deflection on Transonic Buffet Control of Supercritical Airfoil and Wing. J. Aircr. 2017, 54, 1229–1233. [Google Scholar] [CrossRef]
- Geisbauer, S.; Loeser, T. Towards the investigation of unsteady spoiler aerodynamics. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Geisbauer, S. Numerical simulation and validation of aerodynamics of static and dynamic spoilers. J. Aircr. 2021, 58, 1187–1203. [Google Scholar] [CrossRef]
- Juretic, F.; Kozmar, H. Computational modeling of the atmospheric boundary layer using various two-equation turbulence Models. Wind. Struct. 2014, 19, 687–708. [Google Scholar] [CrossRef]
- Fillola, G.; Carrier, G.; Rodde, A.M.; Dor, J.B. Experimental study and numerical simulation of flow around wing control surface. In Proceedings of the 25th International Congress of Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ansys Fluent. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/node67.htm (accessed on 15 May 2022).
- Roache, P.J. Code verification by the method of manufactured solutions. J. Fluid Eng. 2002, 1, 4–10. [Google Scholar] [CrossRef]
- Coleman, H.; Freitas, C.J.; Crane, R.L.; Blackwell, B.F.; Dowding, K.J.; Ghia, U.; Hills, R.G.; Logan, R.W.; Roache, P.J.; Steele, W.G., Jr. ASME V&V 20–2009; Standard for Verification and Validation in Computational Fluid Dynamics and 24 Heat Transfer; ASME: New York, NY, USA, 2009. [Google Scholar]
- Slater, J.W. Examining Spatial (Grid) Convergence, NASA. 2008. Available online: https://www.grc.nasa.gov/www/wind/valid/tutorial/spatconv.html (accessed on 15 May 2022).
- Mark, D. XFOIL Subsonic Airfoil Development System. Available online: https://web.mit.edu/drela/Public/web/xfoil (accessed on 15 May 2022).






| Variable | Values |
|---|---|
| Spoiler deflection ( | 0, 5, 15, 25, 60, and 90 |
| Length of spoiler | 0.1 and 0.15 |
| Hinge location (X/C) | 0.6 and 0.7 |
| Cell Count | CL Percentage | CD Percentage | Difference in CL % | Difference in CD % |
|---|---|---|---|---|
| 282,992 291,743 298,834 312,457 328,078 | 0.3702 0.3661 0.3620 0.3597 0.3596 | 0.1155 0.1170 0.1184 0.1191 0.1192 | 1.14 1.12 0.63 0.019 | 1.27 1.13 0.62 0.059 |
| Validation Case | Re | # of Cells | Average y+ |
|---|---|---|---|
| NACA0012 NACA2412 with Conventional spoiler | 166023 783761 | 272014 296104 | 1.2 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajaj, R.M.; Djidjeli, K. A Novel Reverse Hinge Spoiler for Flight Loads Control. Designs 2022, 6, 92. https://doi.org/10.3390/designs6050092
Ajaj RM, Djidjeli K. A Novel Reverse Hinge Spoiler for Flight Loads Control. Designs. 2022; 6(5):92. https://doi.org/10.3390/designs6050092
Chicago/Turabian StyleAjaj, Rafic M., and Kamal Djidjeli. 2022. "A Novel Reverse Hinge Spoiler for Flight Loads Control" Designs 6, no. 5: 92. https://doi.org/10.3390/designs6050092
APA StyleAjaj, R. M., & Djidjeli, K. (2022). A Novel Reverse Hinge Spoiler for Flight Loads Control. Designs, 6(5), 92. https://doi.org/10.3390/designs6050092







