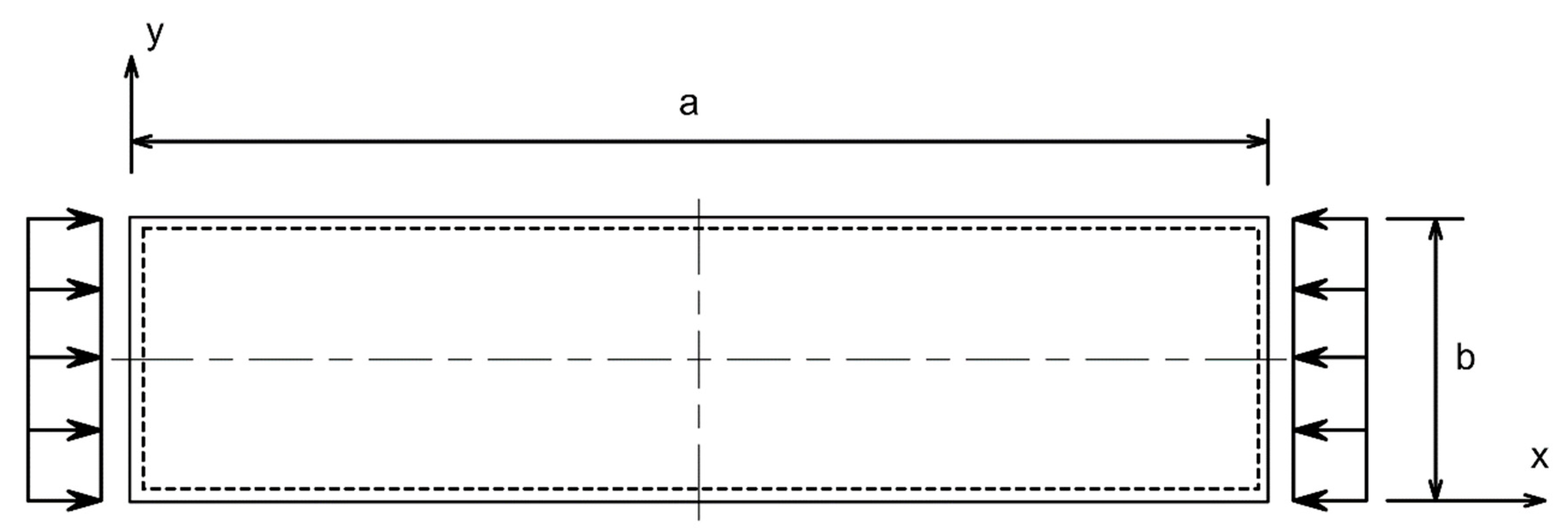
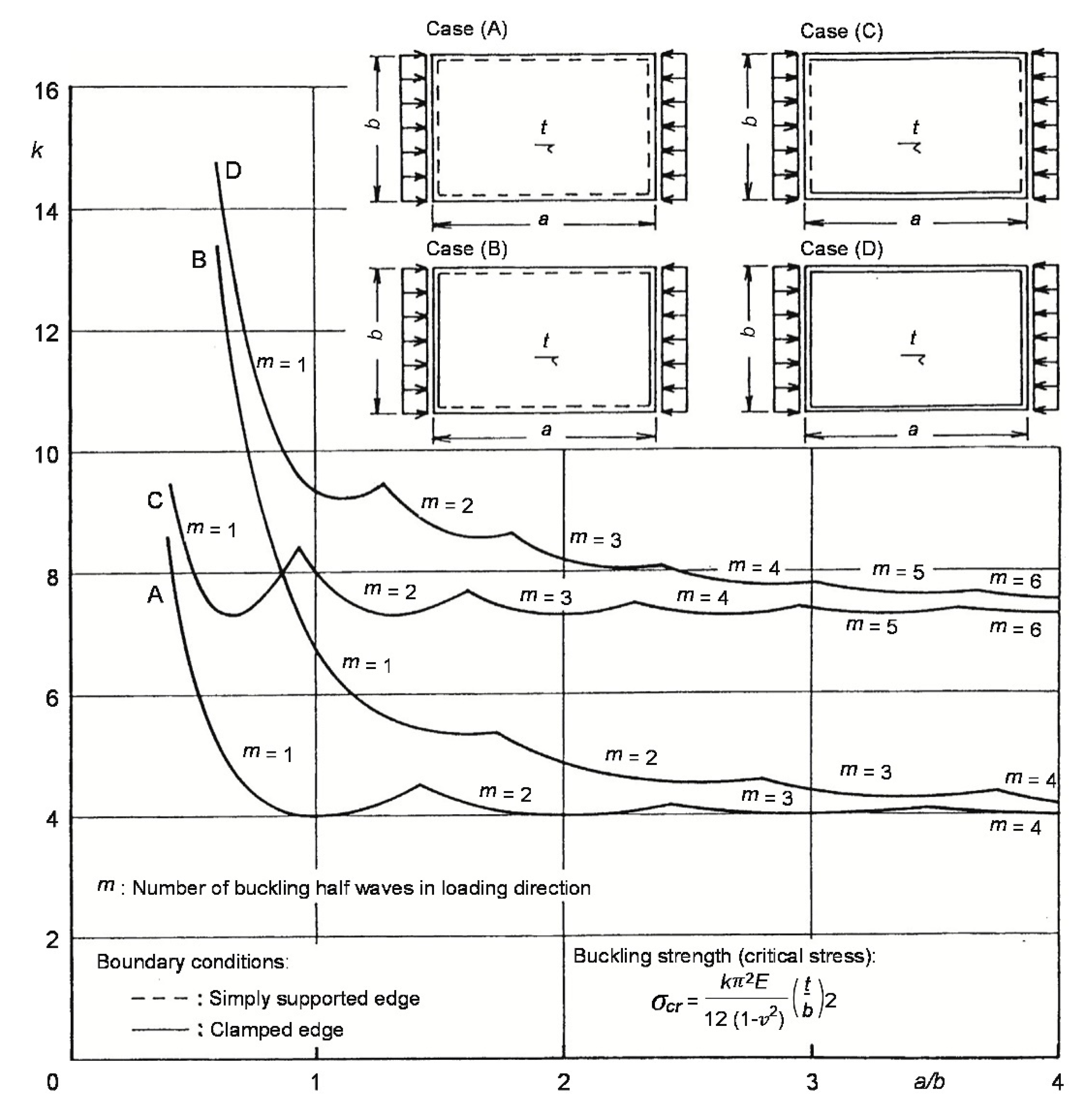
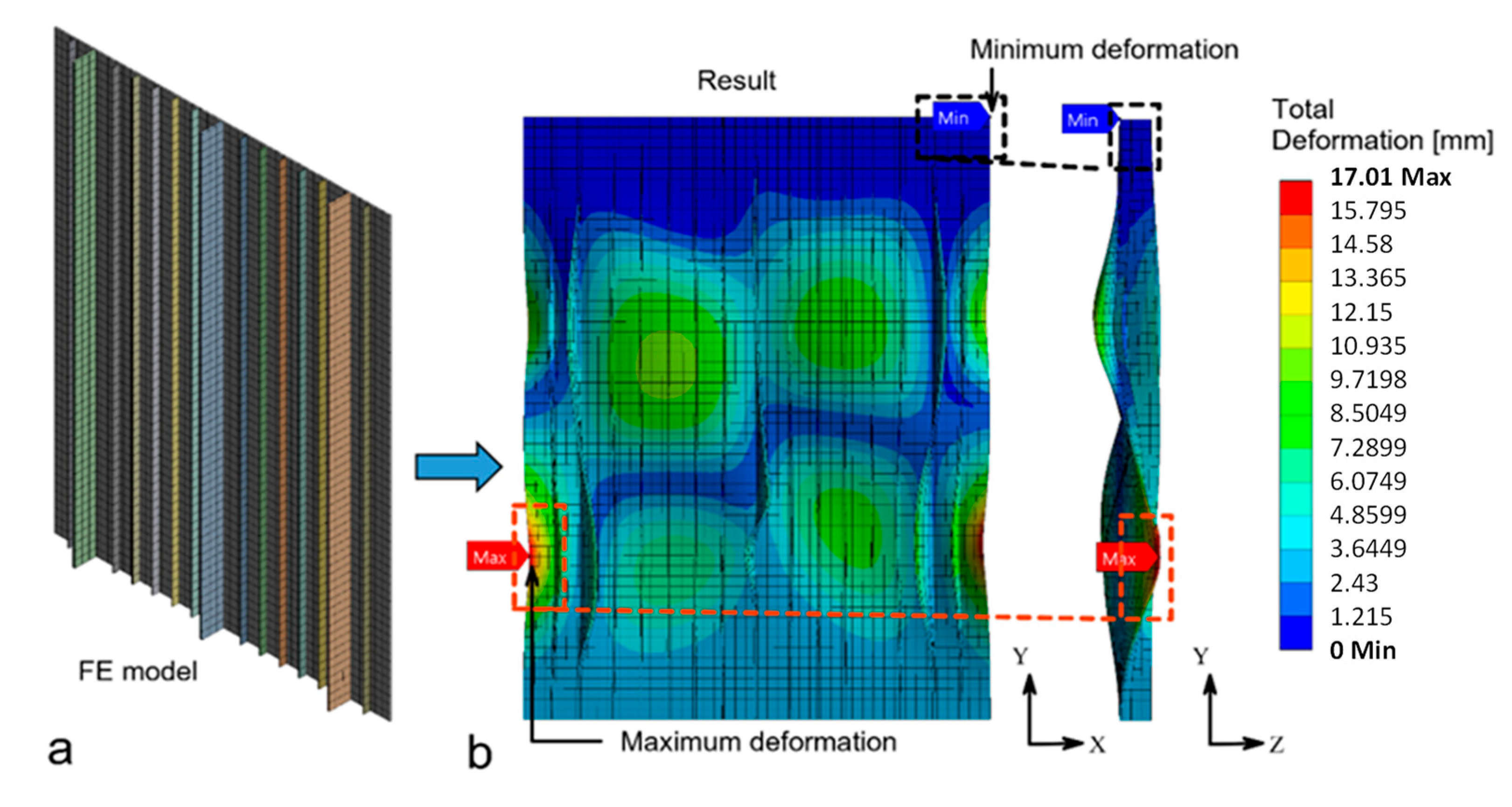
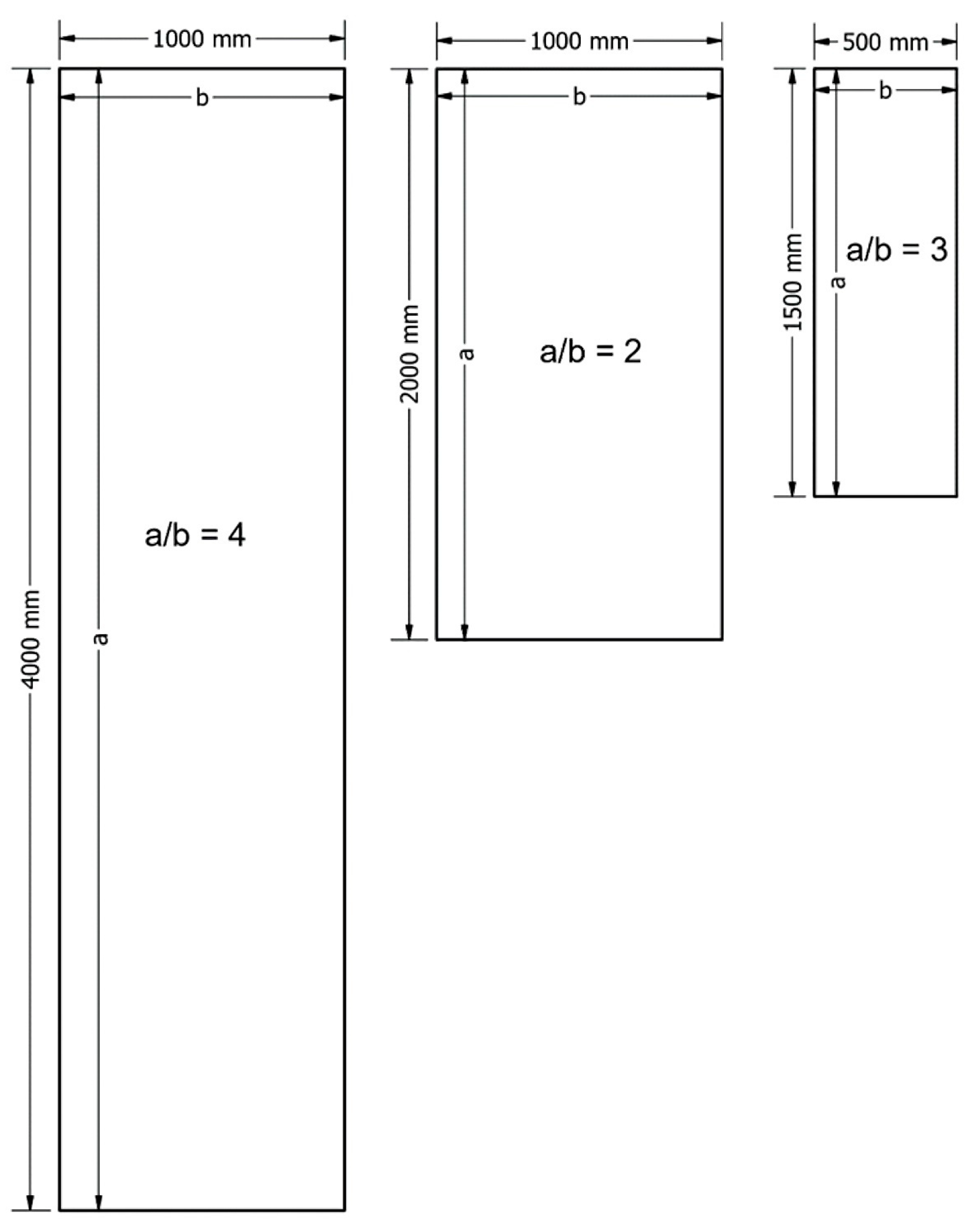
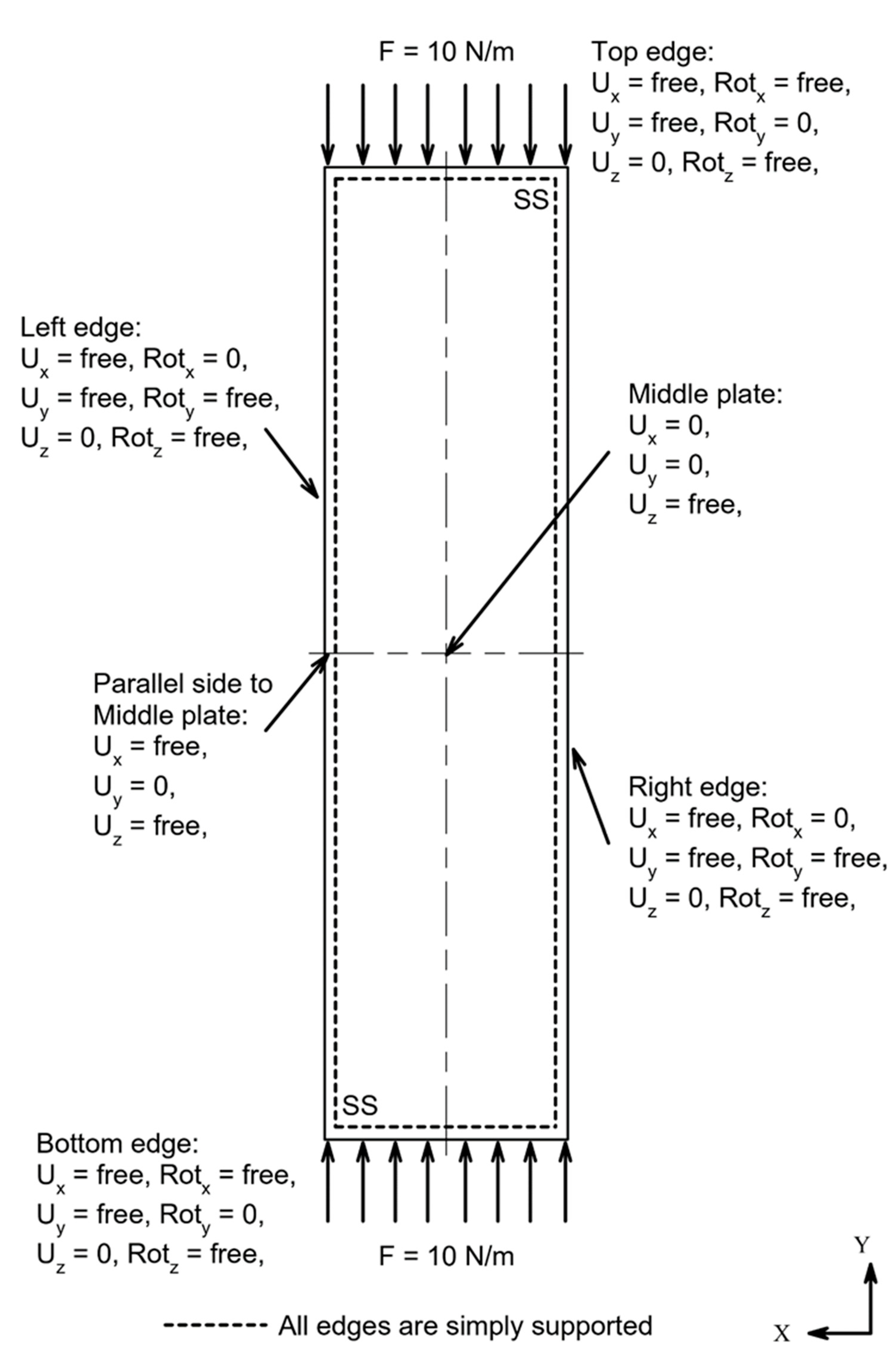
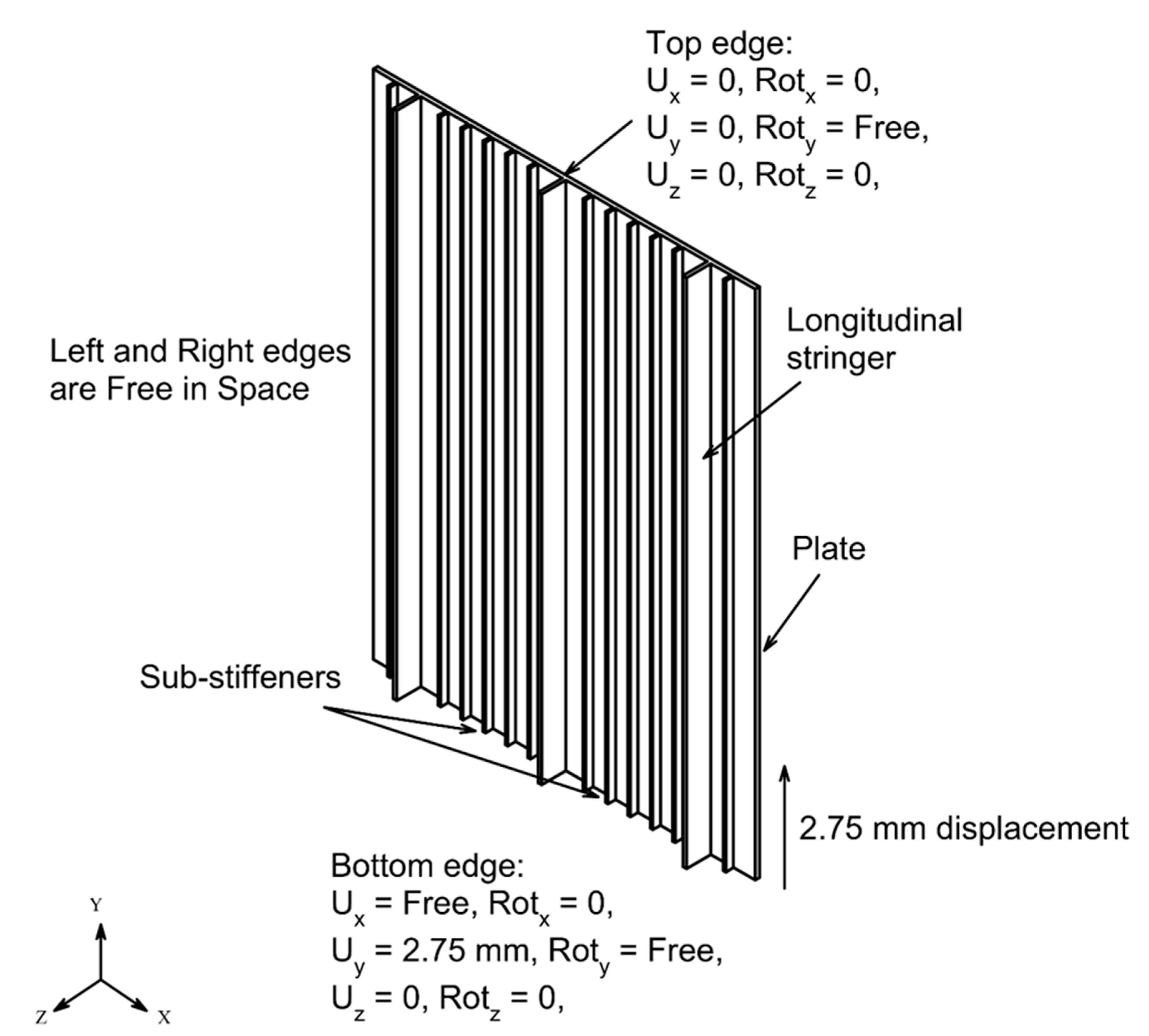
1. Introduction
The buckling phenomenon is a condition where the stiffeners in a structural member such as a plate or column, are under a thrust load and are deflected in an out-of-plane direction when the load reaches a certain critical value. This deflection in an out-of-plane direction begins to increase rapidly following the buckling. As a result, the stiffness in-plane is reduced, and the load-carrying capacity is decreased. If the load is increased further, the collapse of the entire structure may occur due to progressive buckling [
1].
Buckling collapse behavior can be determined using both analytical and numerical methods. Durban and Zuckerman [
2] showed that the critical buckling load of the rectangular plate could be measured with the flow and deformation theory. The aspect ratio
a/b that was examined ranged from 0.25–4. Furthermore, Elgaaly [
3] found that the nonlinear finite element analysis programs, NONSAP and ANSR-III, are able to depict the post-buckling behavior of thin plates to an extraordinary degree of accuracy when compared with analytical solutions and experimental results. This numerical method has several advantages, which are the parameters that can be considered, the reasonable cost, and relatively short time period. The calculation of the dynamic buckling of thin isotropic plates subjected to an in-plane impact can also be performed using a stress failure criterion [
4]. In the same year, Cheung et al. [
5] showed that the finite strip method (FSM) can be used to perform buckling analysis of plates with abrupt changes in thickness and complex support conditions. In 2007, Shimizu [
6] conducted a study on the tension buckling strength of a plate which had a hole in the middle. The study used the numerical method for calculation purposes and seven deferent types of holes (e.g., rectangular, circular, etc.) were proposed. He found that plates which have holes influence the outcome of the tension buckling strength. In the last decade, a study that performed numerical analysis on plates that have curvature has been carried out by Amani et al. [
7]. They found that an increase in the curvature of plates raises the elastic buckling load. Parameters such as fire also can be included in the numerical method, as shown in the study by Xing et al. [
8] on the local buckling response of stainless-steel plates.
Buckling collapse behavior of the stiffened panels are also of interest for researchers. For instance, Danielson and Wilmer [
9] conducted a study (analytical and numerical methods) on the buckling behavior of a rectangular plate with a bulb flat stiffener attached to one side of the panel. In 2011, buckling analysis on the effect of longitudinal stiffeners on stiffened panels was carried out by Kwon and Park [
10]. The study was performed using both experimental and numerical methods. They found that the amount of longitudinal stiffeners attached to the panel influences the ultimate panel collapse load. Furthermore, a numerical study conducted by Layachi and Xu [
11] showed that the type of sub-stiffeners and the dimension also influences the ultimate panel collapse load. In 2020, an experimental and numerical buckling test of stiffened panels subjected to an in-plane compressive load was conducted by Kong et al. [
12]. This study reported that the differences in plate size (i.e., length and width of the stiffened plate) affect the load vs. displacement curve; however, the thickness of the stiffeners attached on the stiffened plate were not the focus of the study and were neglected. Furthermore, the studies that have been mentioned above did not examine the energy produced during the buckling process. Neither of the studies used were based on the element to thickness ratio (ELT) to choose the mesh size in numerical calculations.
In this paper, analytical and numerical analysis of linear buckling on simply supported rectangular plates subjected to in-plane uniaxial load were carried out. Numerical calculation was performed using the finite element (FE) with three deferent elements for the length to thickness ratio (ELT). Rectangular plates were varied into three different aspect ratios a/b and three different plate thicknesses h. The objective was to find the most accurate result of element length to thickness ratio (ELT) compared with analytical calculations. Furthermore, nonlinear buckling analysis of the stiffened panels that were subjected to an in-plane compressive load were also carried out. The effect of the thickness of the longitudinal stringers and sub-stiffeners on the ultimate panel collapse load and the generated energy was carried out using finite element. The main purpose was to determine which is the most satisfactory way of increasing the strength of the stiffened panel, by comparing the load and energy versus displacement curves, respectively. The specimens that were used are based on a real experimental buckling test specimen. Benchmarks were performed to confirm that the methodology and boundary conditions are suitable.
2. Characteristics of Ship Hull Structure
In the last two decades, research that focuses on the analysis of buckling collapse behavior on plates and stiffened panels has been carried out by researchers in considerable detail. In 2003, analysis on compressive buckling and vibration behavior of a stiffened plate subjected to non-uniform in-plane stress distribution has been carried out by Srivastava et al. [
13]. In his research, the aspect ratio of the plate
a/b ranged from 0.5 to 2. The results show that, due to uniform stress distribution on the long-stiffened plate, the buckling loads of the higher aspect ratios are not significantly affected by the position and load bandwidth. Three years afterwards, Kumar et al. [
14] found that the presence of a cutoff in the middle of the plate has a major influence on the strength of the stiffened plate. Seifi and Khoda-yari [
15] and Sujiatanti et al. [
16] have investigated the effect of the cracked plate on the critical buckling load and ultimate plate collapse load, respectively. Their result shows that the crack on the plate reduces the critical buckling load and ultimate plate collapse load, respectively. In 2018, Xu et al. [
17] conducted a study on the ultimate strength of stiffened panels of ship structures. Three different types of stiffeners were proposed and attached to the plates (e.g., flat, angle, and Tee bars). They found very close results of average stress versus displacement curves obtained from the angle and Tee bars. However, average stress versus displacement curves is extremely different when using the flat bar compared with the angle and Tee bars. Xu et al. [
17] found that when the column slenderness is 1.010 (weak stiffener), the stiffened panels with angle and Tee bars have a greater ultimate strength than the flat bar; however, the opposite occurs when strong stiffeners were used (column slenderness is 0.165).
Table 1 lists the milestone research on the buckling analysis of the plates and stiffened panels in last two decades.
4. Fundamental FE Algorithm
The finite element technique was introduced in 1956 by Turner et al. [
38] who described it as a direct stiffness approach. The assumption of the actual structure is represented by an approximation by the discretized structure; that is, with a collection of finite elements having simple elastic properties, which are then connected, so as to represent a true continuum [
39].
Mukhopadhyay and Mukherjee [
40] and Srivastava et al. [
13] have discussed the stiffness matrix of the plate, which arbitrarily orients the stiffener, in great detail. The following presumptions are used in the basic equation of the stiffened panels:
Hooke’s law is applied to the plate and stiffener material;
Mindlin’s theory is applied to the bending deformation, which is a state before the bending in the plate happens, and the linear elements remain straight when they are perpendicular to the middle plane of the plate;
The x- and y-directions become a function of the deflection that occurs in the z-direction;
The deflections of the plate are small—less than the thickness of the plate;
After bending occurs, it is common and normal for the plate and stiffener to stand straight before bending.
For the stiffened plate that is subjected to in-plane loads, the equation of equilibrium can be written as the following
where
and
are the elastic and geometric stiffness matrices, respectively.
is the displacement vector.
The buckling and vibration problems
and Equation (6) can be simplified as
For the free vibration problem with angular frequency
Equation (6) can be written as
The stiffness matrix of the plate element is expressed as follows
where
and
are the elastic and geometric stiffness matrices, respectively.
is the mass matrix of the plate.
and
can be expressed as
and
The stiffness matrix of the stiffener element is expressed as follows
where
and
are the elastic and geometric stiffness matrices, respectively.
is the mass matrix of the stiffener. Here,
is the Jacobian of the stiffener and represents half of the actual length in an element.
and
can be expressed as
The expression for the matrices is given by
where
and
are the area, and the first moment of area with respect to the reference plane, respectively.
and
are the second moment of area with respect to the reference plane and the torsional constant, respectively.
7. Results: Linear Buckling
7.1. Effect of Thickness Change
The analytical and finite element results of the critical buckling load on simply supported rectangular plates are presented in
Table 7. The critical buckling load was significant depending on the thickness of the plate. As is evident, the critical buckling load was significantly larger with an increase in the thickness of the plate. This phenomenon was found in all aspect ratios
a/
b = 2, 3, and 4.
At a 3 mm thickness of the plate, the analytical calculation results showed that the critical buckling load was at 20,498 N/m, 81,994 N/m, and 20,498 N/m for aspect ratio a/b = 2, 3, and 4, respectively. Compared with the 5 mm plate thickness, results showed the critical buckling load values of 94,900 N/m, 379,600 N/m, and 94,900 N/m. These three values increased by exactly 362.97% when compared with the critical buckling load values of the 3 mm plate thickness.
The critical buckling load results from the finite element using the ELT ratio showed that the largest difference compared with the analytical data occurred at ELT ratio = 7 from a/b ratio = 3 with a 5 mm plate thickness. The critical buckling load value was 0.65%, which is higher than the value from the analytical result. The lowest error occurred when the ELT ratio of 5 and 7 were used in the aspect ratio a/b = 2 and 4 with a 3 mm plate thickness. The value of the critical buckling load was 0.01% higher than the analytical value.
7.2. Effect of Geometrical Change
Element length to thickness (ELT) ratios of 5, 6, and 7 showed no significant difference in the outcome; therefore, the result of the analysis of the data from the ELT ratio 5 is presented.
Figure 16 shows the first four mode shapes for the
a/b ratio = 2, 3, and 4. As is evident, three aspect ratios gave a different total number of half-wavelengths. Neither one gave the same number of half-wavelengths. The number of half-wavelengths increased as the
a/b ratio increased. The total number of half-wavelengths did not depend on the thickness of the plate [
1].
For the aspect ratio of plate, a/b = 2, the number of half-wavelengths for the 1st mode shape indicated the presence of two half-wavelengths; however, for aspect ratios a/b = 3 and 4, the number of half-wavelengths increased, and the number of half-wavelengths appeared to be three and four, respectively.
There were three, one, and four half-wavelengths for a/b = 2 that appeared in the 2nd, 3rd, and 4th mode shapes, respectively. For the aspect ratio a/b = 3, the half-wavelengths that appeared in the 2nd, 3rd, and 4th shapes were four, two, and five, respectively. The mode shown in the five, three, and six number of half-wavelengths appeared in the 2nd, 3rd, and 4th mode shapes when the aspect ratio of the plate a/b was 4.
The critical buckling load obtained from the analytical data and from the first four mode shapes is shown in
Figure 17. As is evident, the 1st mode shape was in extremely good agreement compared with the analytical calculation. This phenomenon was found in all aspect ratios
a/
b = 2, 3, and 4. At a thickness of the plate equal to 3 mm, the critical buckling load in 1st mode shape was slightly lower, at about 0.02%, for the
a/
b = 2 and 4 compared with the analytical data (
Figure 17a). Furthermore, the critical buckling load in 1st mode shape in
a/
b = 3 was slightly higher, at about 0.1%, compared with the analytical data. The 4th mode shape showed a fairly higher critical buckling load value. The difference in the 28.73% error was found in the 4th mode shape at
a/
b = 3. The highest error was found in plate thicknesses of 3 mm, 4 mm, and 5 mm in the 4th shape mode (
Figure 17) which was only found at
a/
b ratio = 2. For this aspect ratio, 4th mode shapes gave a difference of 56.35%, 56.64%, and 56.49%, which is higher than the analytical data for plate thicknesses of 3 mm, 4 mm, and 5 mm, respectively.
9. Overall Discussion: Linear vs. Nonlinear Behaviors
For the linear buckling analysis, the findings of this study show that the element length to thickness ratios (ELT) can provide quite good results for the critical buckling load compared with analytical calculations. The highest error of critical buckling load value was only 0.65% higher than the value from the analytical result. This error was obtained when the ELT ratio = 7 and from the specimen with
a/b ratio = 3 with the 5 mm plate thickness. No errors higher than 0.65% were found in the all ELT ratios (5, 6, and 7) compared to the analytical data. On the other hand, the smallest error was found in the 5 and 7 ELT ratio with the specimen aspect ratio
a/b = 2 dan 4, with 3 mm plate thickness. The error was not more than 0.01% compared to the analytical value. All calculations with the finite element and analytical showed good results and were in accordance with the literature [
1]. The number of half-half-wavelengths depending on the aspect ratio
a/b is the same as in the literature [
1] (
Figure 2 and
Figure 3).
It is a fact that the
a/
b ratio of the specimen affects the number of half-wavelengths and the critical buckling load [
1]. This fact also can be seen in the simulation with the finite element in this study (
Figure 16 and
Figure 17). In particular, all the buckling deformation patterns that are shown in
Figure 16 exhibit cartesian symmetry. This behavior is due to the fact that the structural system under consideration is symmetric and the material is isotropic, as described by Zucco and Weaver in “The role of symmetry in the postbuckling behaviour of structures” [
52]. A total number of two, three, and four half-wavelengths appear in the 1st mode shape of the specimen with an
a/
b ratio of 2, 3, and 4, respectively. The 1st mode shape gives remarkably good agreement of the critical buckling load compared with the analytical calculation (e.g., the error is not more than 0.02% for the
a/
b = 2 and 4, and 0.1% for the
a/
b = 3 compared with the analytical). In the case of plate thickness, it severely affects the value of the critical buckling load, but the reverse is true for the number of apparent half-wavelengths. For instance, the 3 mm thickness of the plate produces the critical buckling load of 20,498 N/m, 81,994 N/m, and 20,498 N/m for aspect ratio a/b = 2, 3, and 4, respectively. These three values are increased exactly by 362.97% compared to 5 mm plate thickness, which is 94,900 N/m, 379,600 N/m, and 94,900 N/m. However, the thickness of the plate seems to not affect the number of half-wavelengths.
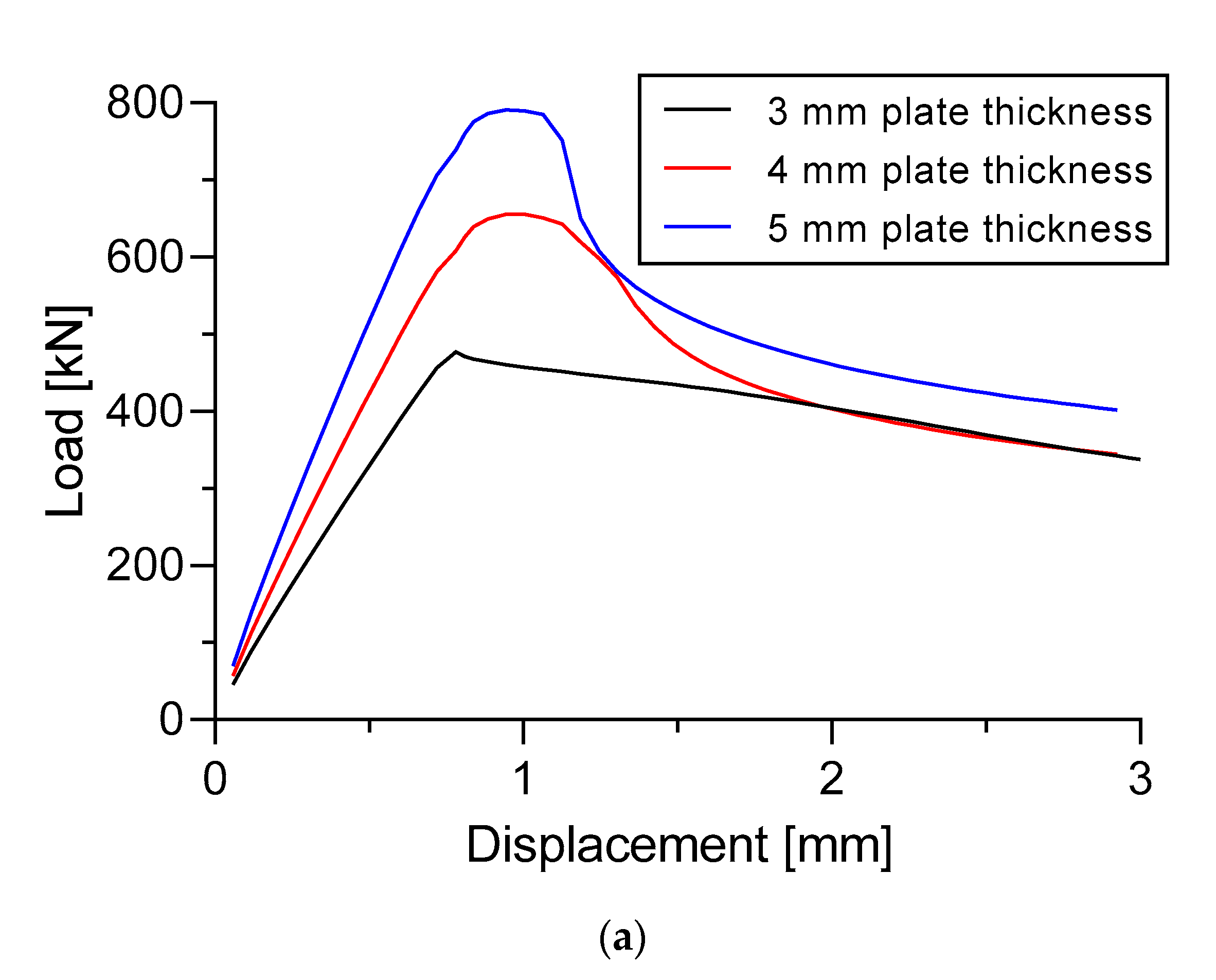
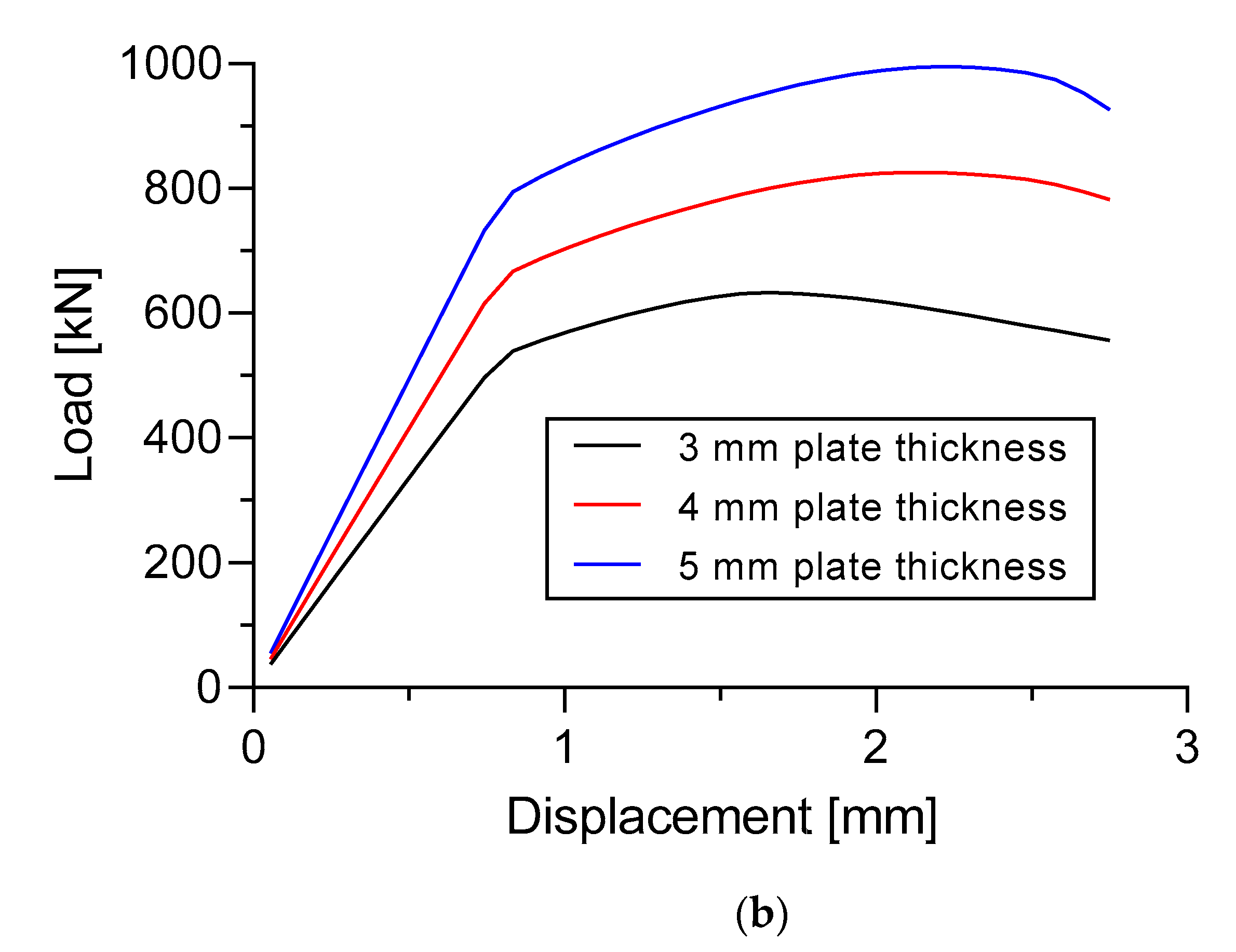
For the nonlinear buckling analysis, the findings of this study indicate that increase in the plate thickness and thickness of the longitudinal stringers attached to the specimens seem to increase the strength of the stiffened panel. As seen in
Section 8.1, the plate thickness of 5 mm in Specimen A and Specimen B have higher ultimate buckling collapse load values compared to the plate thicknesses of only 3 mm and 4 mm. This is also supported by the presence of a fairly high strain in the center of the plate in Specimen A and Specimen B when a plate thickness of 3 mm is used. When compared with the 5 mm thickness of the plate, the strain is less pronounced in the center of the plate (
Figure 20 and
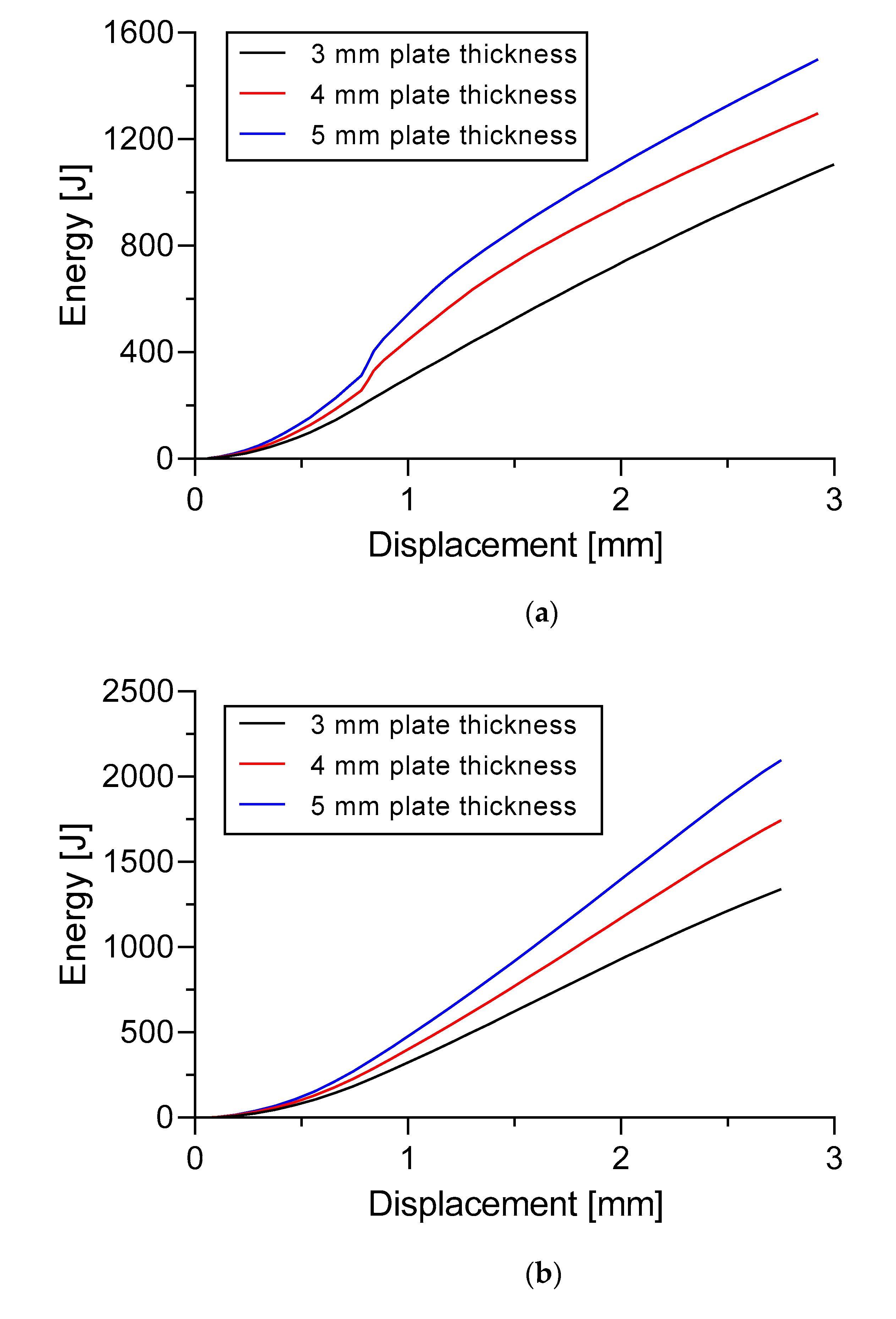
Figure 21). In Specimen A, the ultimate buckling collapse resulting from 5 mm plate thickness is 65.7% and 20.61% higher compared to 3 mm and 4 mm plate thickness. The values of this situation are 790.7 kN, which is compared with 477.2 kN and 655.6 kN, respectively. The same tendency is also found in Specimen B which gives the highest ultimate buckling load value when 5 mm of plate thickness is applied. An increase from 633.0 kN and 825.8 kN to 995.2 kN appear to be found when increasing the thickness of the plate from 3 mm and 4 mm to 5 mm, respectively. These had increases of 57.22% and 20.51%. In terms of the energy that is generated during the buckling process shows that, 5 mm plate thickness in Specimen A and Specimen B provides a more comprehensive total energy of 35.72% and 56.46% higher than the 3 mm thickness of the plate (
Table 8). Prabowo et al. [
53], Bae et al. [
54], and Prabowo et al. [
50] suggested that the total energy obtained from structural damage also can indicate the strength of a structure. Increased structural strength can be a significant advantage and they play a significant role in improving the stability of the structure for instance while under tensile load or impact load [
55,
56]. This finding can also be implemented into a new design such as the in savonius turbine technology [
57].
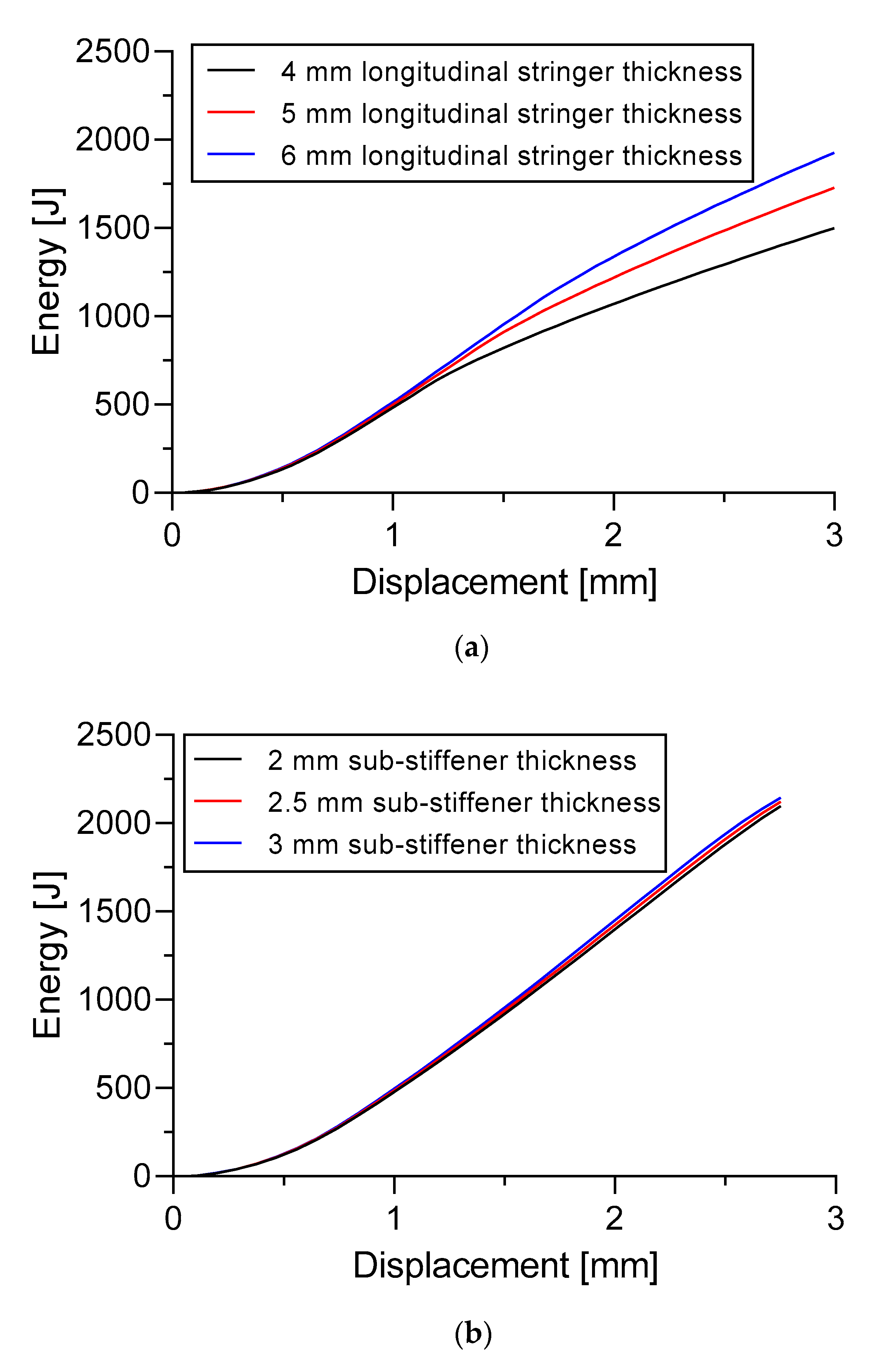
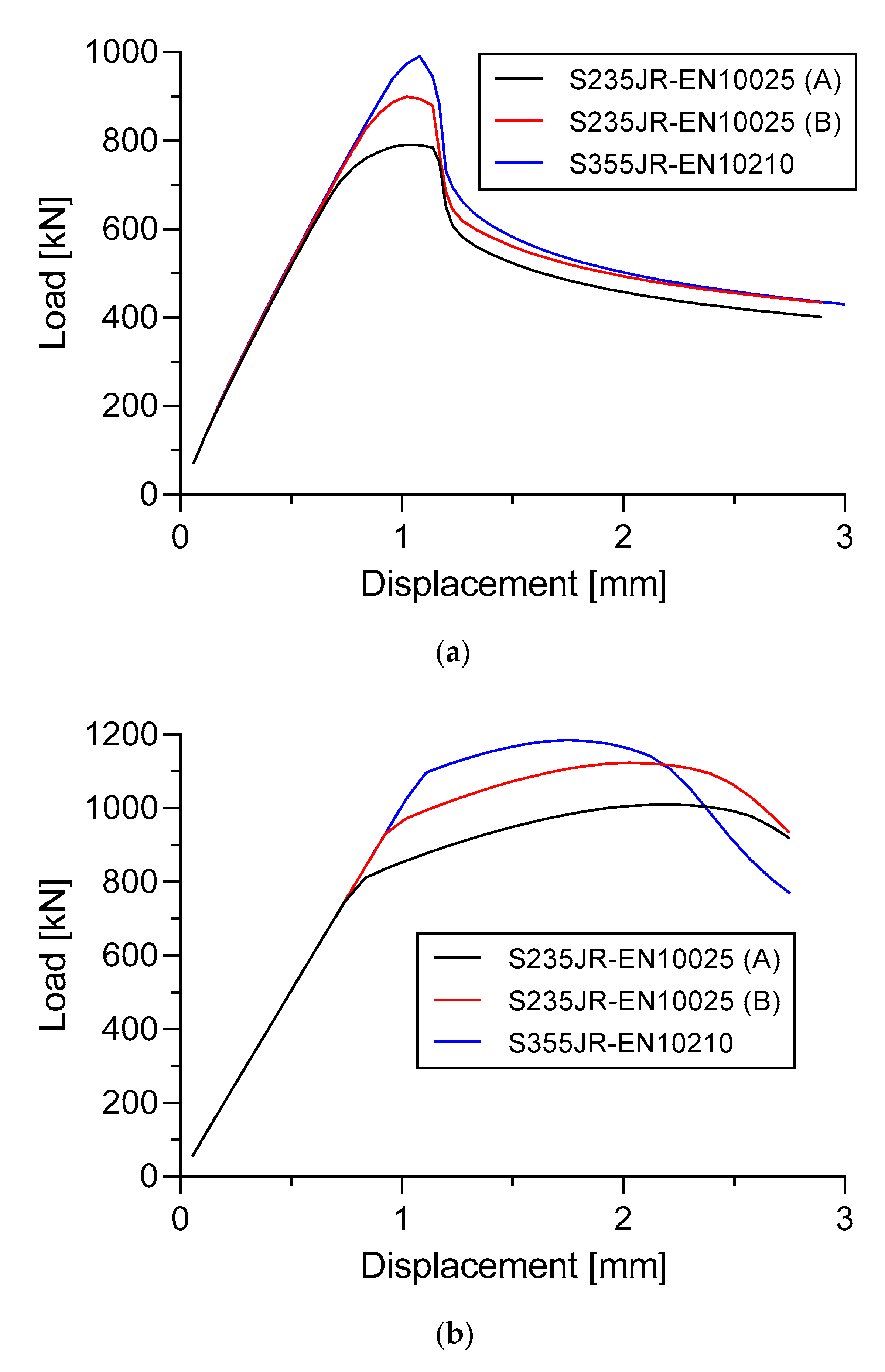
There is an increase in ultimate buckling collapse load if the thickness of the longitudinal stringers is increased, as was the case in Specimen A. The thickness of the longitudinal stringers in Specimen A moderately affected the strength of the stiffened panels (
Section 8.2). This is also supported by the existence of a different strain distribution when the thickness of longitudinal stringers changes, for example, when the thickness is 6 mm which gives a quite small deformation compared to the thickness of 4 mm and 5 mm (
Figure 24). In the case of 6 mm thickness, the stiffened panel increased its strength by 6.18% and 11.8% compared to the thickness of 5 mm and 4 mm, respectively. The values obtained from these thicknesses are 884.0 kN, 839.6 kN, and 790.7 kN, respectively. These thicknesses also seem to moderately affect the total energy in Specimen A. Less total energy was produced when the 4 mm thickness was applied which was 1499.7 J. Slightly more energy was provided when the 5 mm and 6 mm thickness was applied which was 1727.7 J and 1927 J respectively.
Quite surprisingly, the thickness of the sub-stiffeners in Specimen B does not really seem to affect the strength of the stiffened panel and the total energy generated during the buckling process. There was no strong evidence that the thickness of the sub-stiffeners in Specimen B increases the strength of the stiffened panel. This occurrence is also observed in the strain distribution section which has a fairly similar strain distribution for the three thicknesses of the proposed sub-stiffeners. There was negligible visible result when the 3 mm sub-stiffeners increased only 3% the strength of the stiffened panel compared with the thickness of the 2 mm sub-stiffeners. This percentage increase was obtained from the original value of 995.2 kN to 1025.1 kN. The same condition also occurs in the total energy generated during the buckling process (e.g., 3 mm thickness of the sub-stiffeners increased by only 2.25% compared with the 2 mm. Although, the total number of sub-stiffeners that were attached to the stiffened panel was 12. Further work is needed to reveal how the thickness of the sub-stiffeners influences the strength of the stiffened panels.
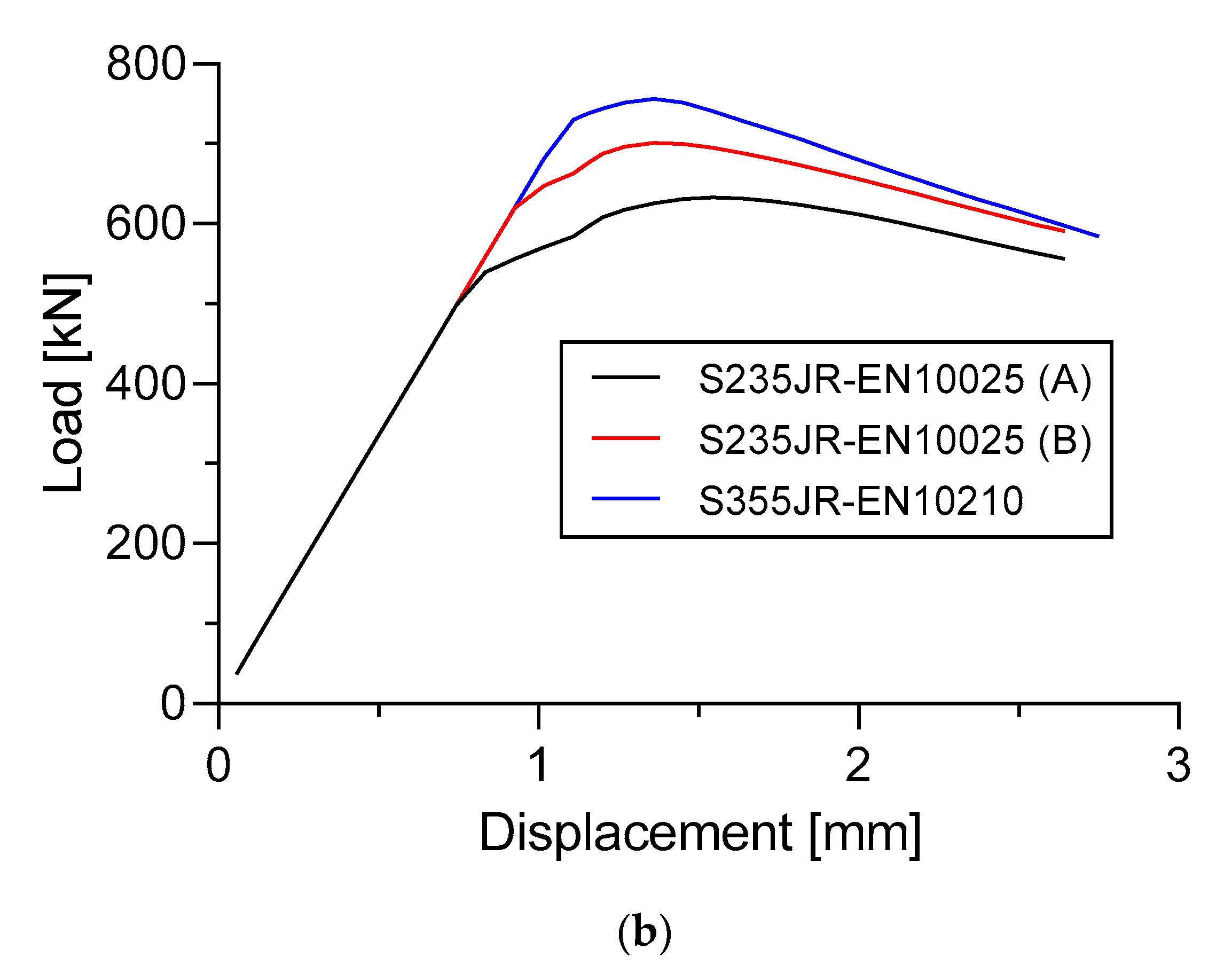
The materials that were used show that the S355JR-EN10210 material produces more comprehensive strength of the stiffened panel (Specimen A and Specimen B) followed by the S235JR-EN10025 (B) and S235JR-EN10025 (A) materials. This increase in strength can be affected by the properties of the material, such as yield stress, ultimate stress, Poisson’s ratio, and the exponent of this material (strain hardening) [
35,
36]. It is possible that the strength of the specimen can be influenced by the material that has been used [
27]. A recently study also showed that fibers from the agave cantala plant can also be used to increase the strength of the material [
58]. There is also some evidence that Rad and Panahandeh-Shahraki [
35] found that the material properties of Poisson’s ratio give descent the critical load when its value increases. Furthermore, Ndubuaku et al., [
36] found that the material properties of strain hardening affect ultimate compressive strength and strain on the plate. In this study, there are still many parameters of material properties that have been used such as yield stress, ultimate stress, and the exponent of this material (strain hardening). Where the only constant parameters are the material properties of density, Young’s modulus, and Poisson’s ratio. Therefore, to show how the S355JR-EN10210 material produces higher strength requires further research.