Lot Streaming in Different Types of Production Processes: A PRISMA Systematic Review
Abstract
1. Introduction
2. Methodology
2.1. Research Questions
2.2. Sources of Information
2.3. Search Methodology
2.4. Eligibility Criteria
- Study design: All studies were included in which solutions to the Lot Streaming problem were outlined, and the literature reviews and comparative studies are discarded.
- Years considered: There are ten years, i.e., publications are reviewing from 2010 to 2020. Although there are previous papers, it is decided to limit the search in this way to present fresher information, in essence, due to this paper being based on previous studies.
- Language: English papers are searched as there are a more significant number of publications in that language.
- Publishing region: Papers from all regions of the world will be reviewed as this will result in further comparative analysis.
- Publication status: Papers published by indexed journals are considered, taking as a decisive factor of acceptance, with DOI (Digital Object Identifier).
2.5. Risk of Bias in Individual Studies
2.6. Selection of Studies
3. Results
3.1. Initial Data
3.1.1. Base
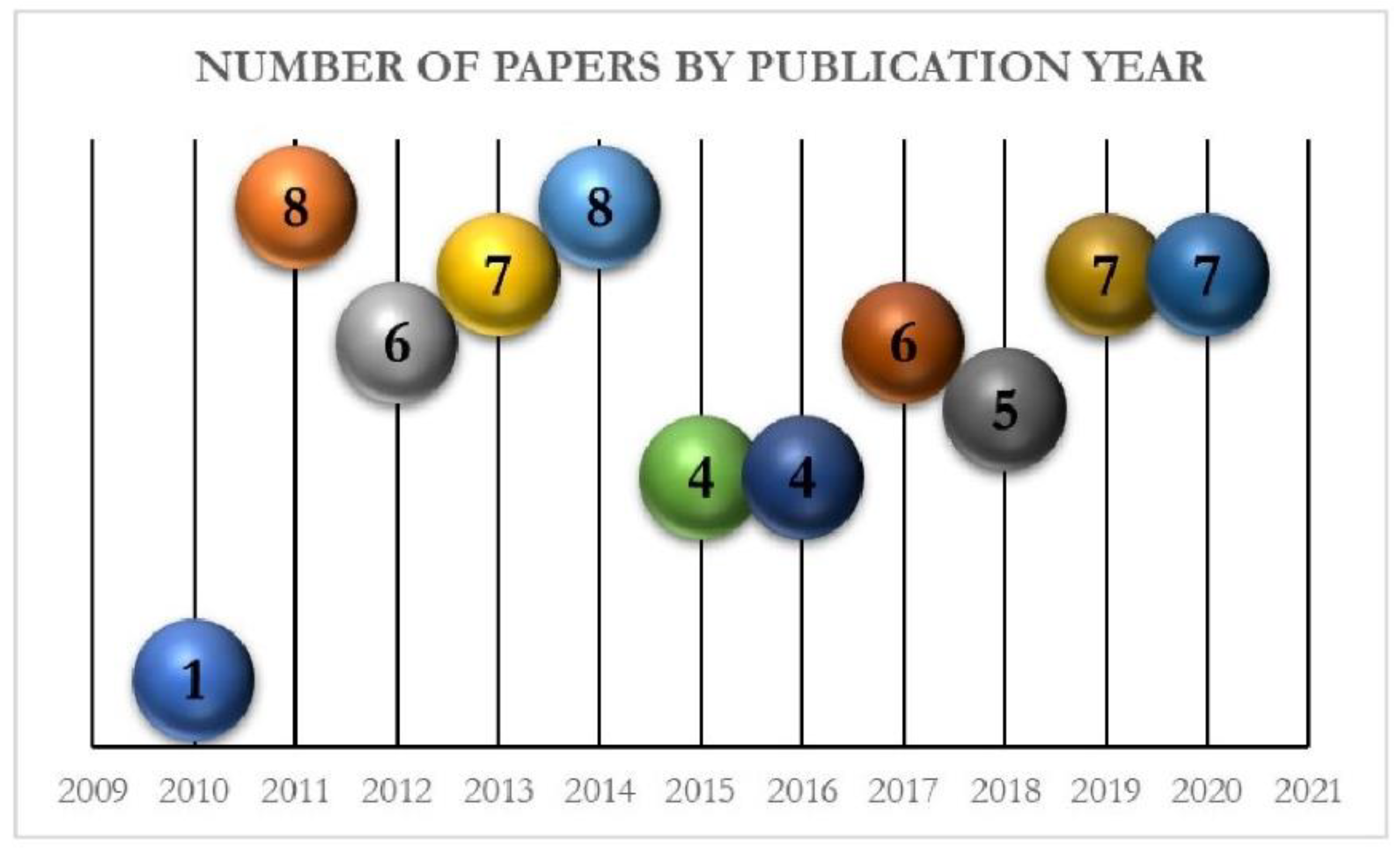
3.1.2. Year
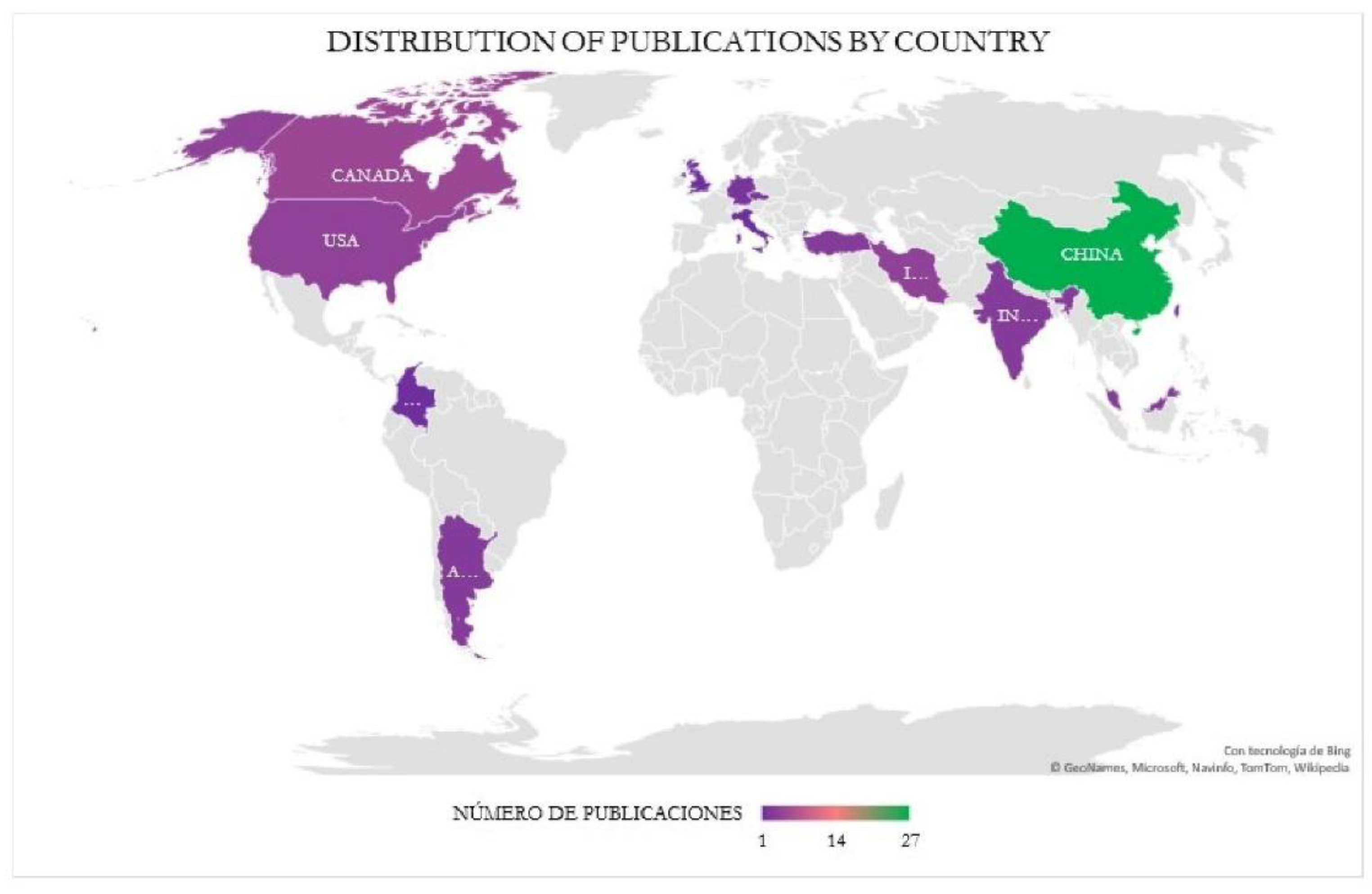
3.1.3. Country
3.2. Background Data
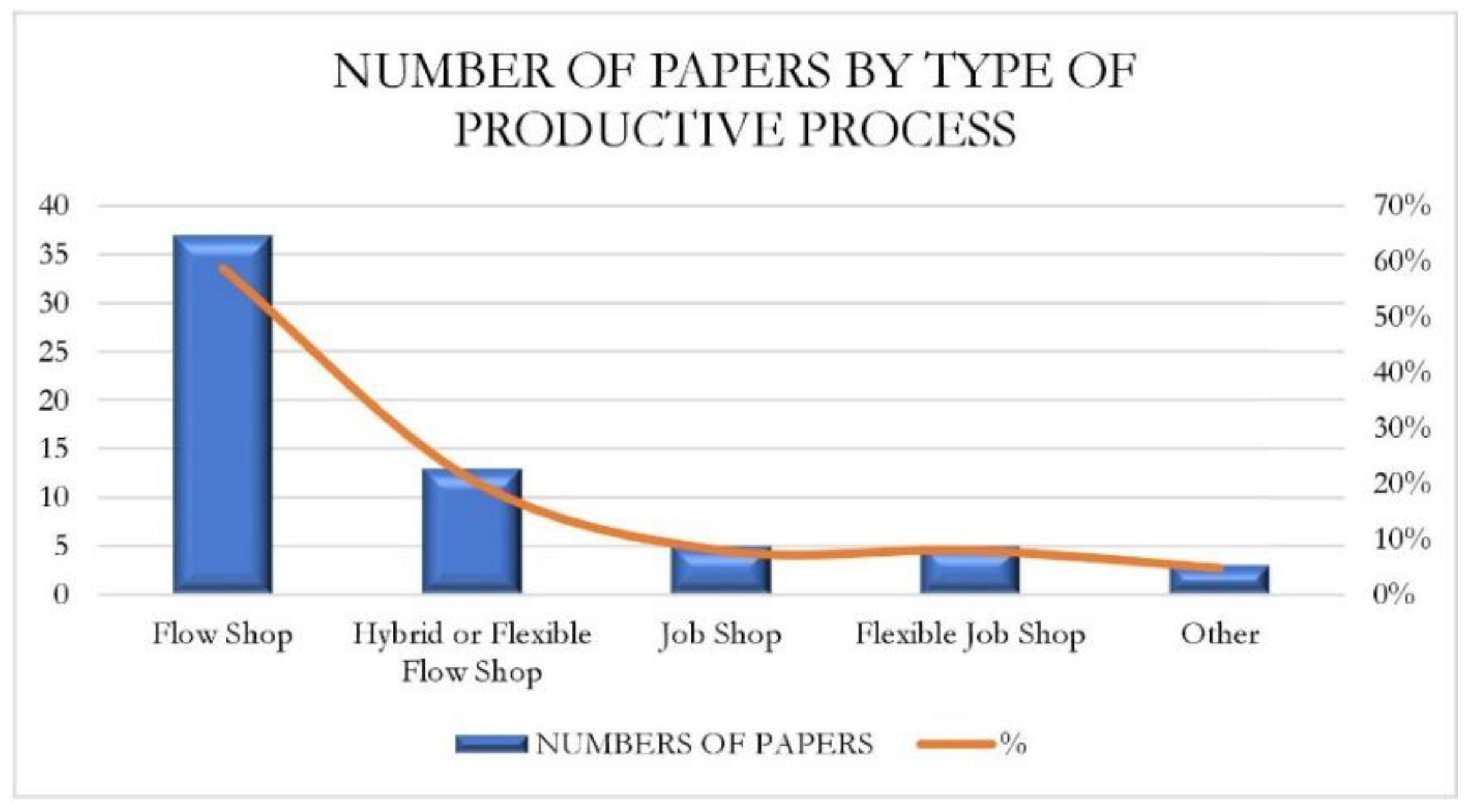
3.2.1. Problem/Type of Production Process Studied
3.2.2. Additional Features and Times Considered
3.2.3. Configuration/Work Number-Machines
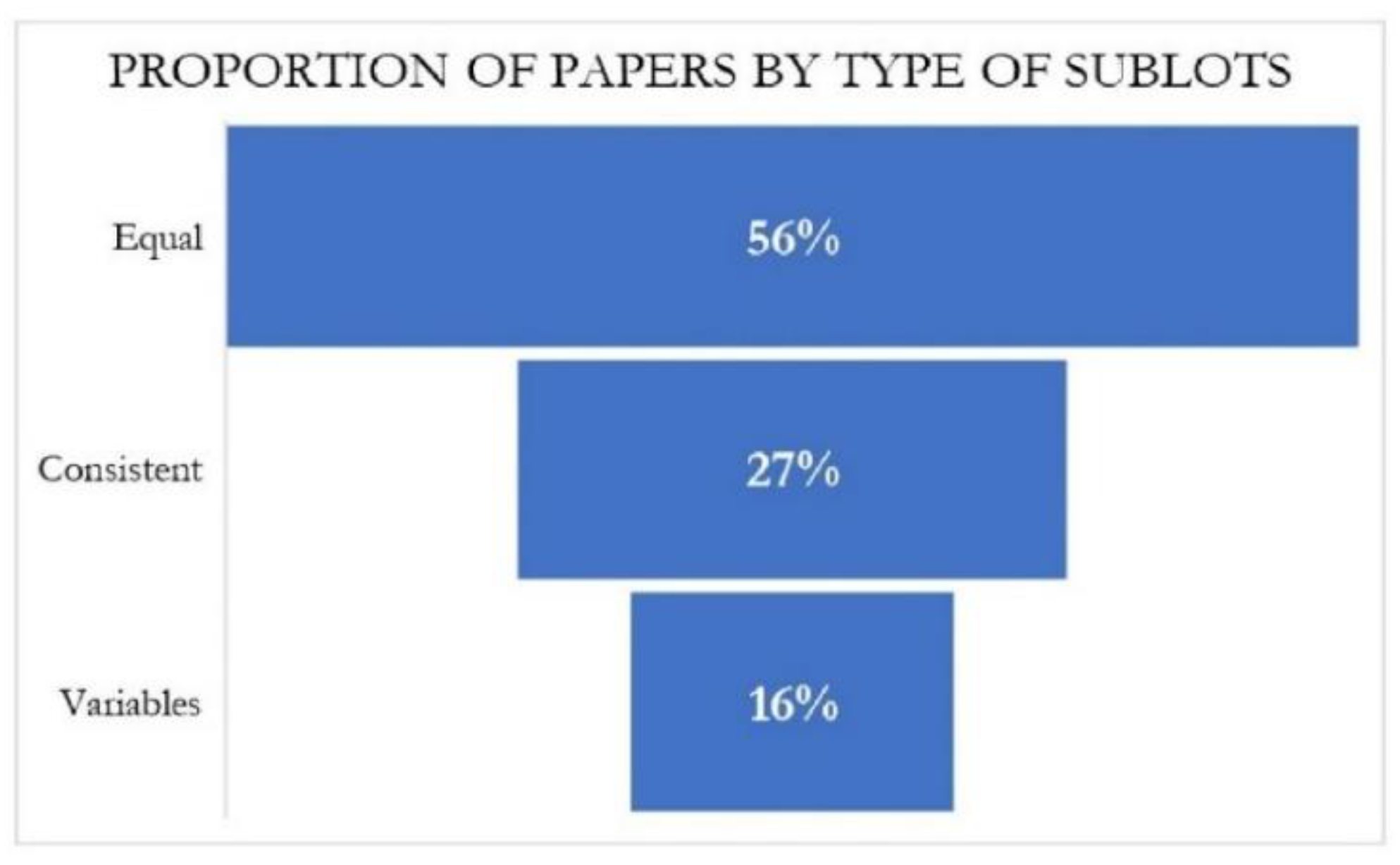
3.2.4. Types of Sublots or Jobs
3.2.5. Idling
3.2.6. Buffer
3.2.7. Setup Time
3.2.8. Objectives
3.2.9. Calculating the Problem Solution
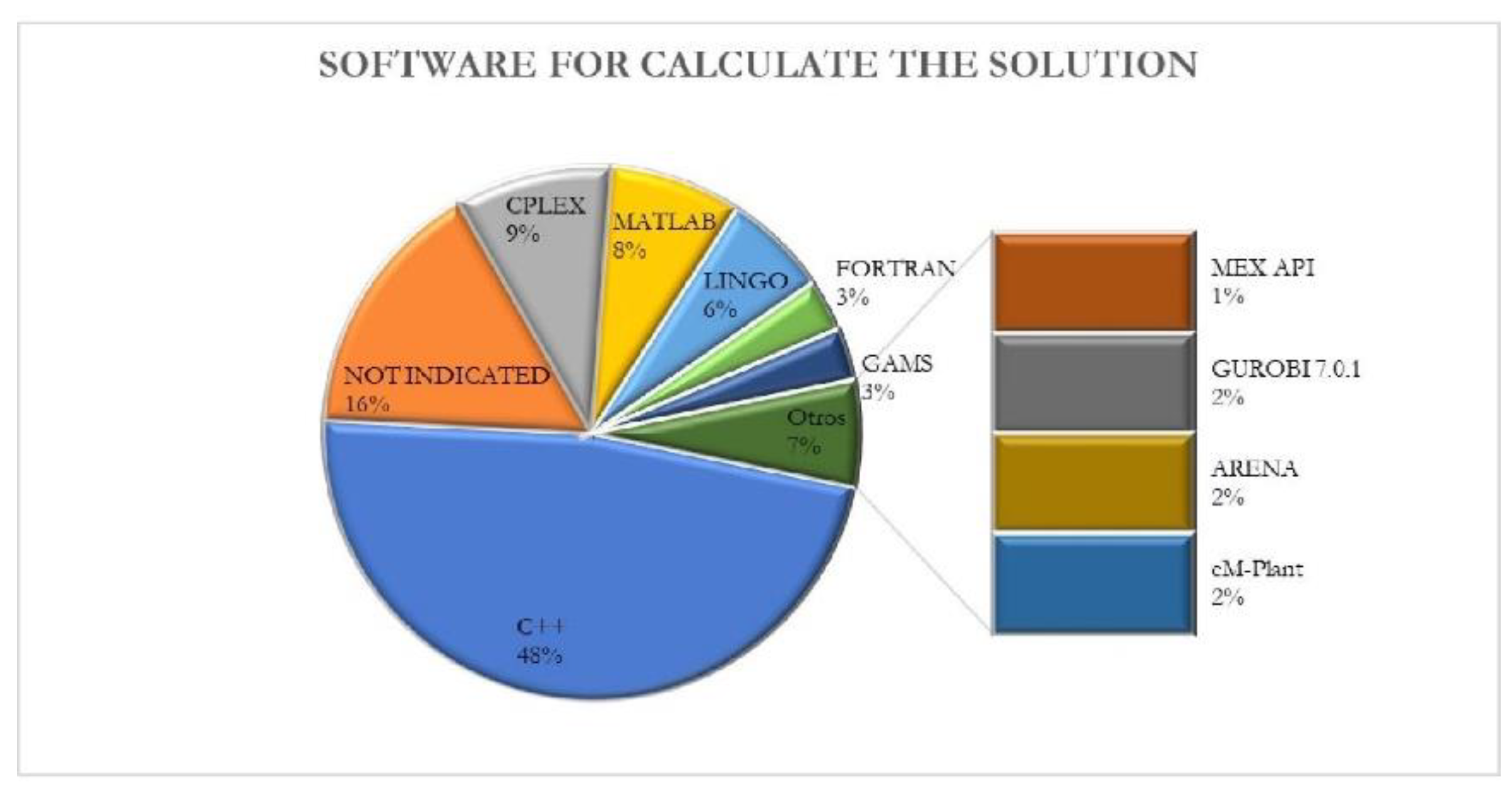
3.2.10. Software for Solving the Problem
3.2.11. Compared to
3.2.12. Metrics to Evaluate
- The objective function and the maximum, minimum, and standard deviations.
- Central Pocessing Unit (Cpu) Time.
- AverageRetail Price Index (Rpi) Value.
- Hypervolume, Convergence.
- Statistical tests such as Analysis of Variance (ANOVA), Mood Median Test, Mann–Whitney Test, Student’s T-Test, Mann-Whitney U-Test.
3.3. Final Data
3.3.1. Conclusion
3.3.2. Future Works
4. Discussion
4.1. Research Questions
4.2. Comparison of Current Work with Existing Work
4.3. Contributions to Literature
4.4. Implications for Practice
4.5. Limitations
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hill, A.V. The Encyclopedia of Operations Management: A Field Manual and Glossary of Operations Management Terms and Concepts; FT Press: Upper Saddle River, NJ, USA, 2012; ISBN 978-0-13-288370-2. [Google Scholar]
- Anil Kumar, S.; Suresh, N. Production and Operations Management (with Skill Development, Caselets and Cases); New Age International (P) Ltd.: New Delhi, India, 2008; ISBN 978-81-224-2177-4. [Google Scholar]
- Chapman, S.N. The Fundamentals of Production Planning and Control; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2006; ISBN 978-0-13-017615-8. [Google Scholar]
- Stewart, J. The Toyota Kaizen Continuum: A Practical Guide to Implementing Lean, 1st ed.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 978-1-4398-4605-6. [Google Scholar]
- Rao, S.S. Engineering Optimization: Theory and Practice, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-18352-6. [Google Scholar]
- Sarin, S.C.; Jaiprakash, P. Flow Shop Lot Streaming; Springer: New York, NY, USA; London, UK, 2007; ISBN 978-0-387-47687-2. [Google Scholar]
- Welch, V.; Petticrew, M.; Petkovic, J.; Moher, D.; Waters, E.; White, H.; Tugwell, P. Extending the PRISMA Statement to Equity-Focused Systematic Reviews (PRISMA-E 2012): Explanation and Elaboration. Int. J. Equity Health 2015, 14, 92. [Google Scholar] [CrossRef]
- Cheng, M.; Mukherjee, N.J.; Sarin, S.C. A Review of Lot Streaming. Int. J. Prod. Res. 2013, 51, 7023–7046. [Google Scholar] [CrossRef]
- Chang, J.H.; Chiu, H.N. A Comprehensive Review of Lot Streaming. Int. J. Prod. Res. 2005, 43, 1515–1536. [Google Scholar] [CrossRef]
- Gómez-Gasquet, P.; Segura-Andrés, R.; Andrés-Romano, C. A Review of Lot Streaming in a Flow Shop Environment with Makespan Criteria. JIEM 2013, 6, 761–770. [Google Scholar] [CrossRef][Green Version]
- Bagchi, T.P.; Gupta, J.N.D.; Sriskandarajah, C. A Review of TSP Based Approaches for Flowshop Scheduling. Eur. J. Oper. Res. 2006, 169, 816–854. [Google Scholar] [CrossRef]
- Camara Gradim, L.C.; Archanjo Jose, M.; Marinho Cezar da Cruz, D.; de Deus Lopes, R. IoT Services and Applications in Rehabilitation: An Interdisciplinary and Meta-Analysis Review. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2043–2052. [Google Scholar] [CrossRef] [PubMed]
- Diószegi, J.; Llanaj, E.; Ádány, R. Genetic Background of Taste Perception, Taste Preferences, and Its Nutritional Implications: A Systematic Review. Front. Genet. 2019, 10, 1272. [Google Scholar] [CrossRef] [PubMed]
- Alam, S.A.N. Managing Organizational Knowledge by Unlearning? A Systematic Literature Review. In Proceedings of the 2019 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), IEEE, Dubai, United Arab Emirates, 11–12 December 2019; pp. 81–86. [Google Scholar]
- Alarcón Palacios, M.; Ojeda Gómez, R.C.; Ticse Huaricancha, I.L.; Cajachagua Hilario, K. Análisis crítico de ensayos clínicos aleatorizados: Riesgo de sesgo. Rev. Estomatol. Herediana 2015, 25, 304–308. [Google Scholar] [CrossRef]
- Higins, J.; Green, S. Updated March 2011; The Cochrane Collaboration: London, UK, 2011. [Google Scholar]
- Yavuz, Y. Lot Streaming with Flexible Process Plans. Int. J. Prod. Res. 2013, 51, 5055–5072. [Google Scholar] [CrossRef]
- Meng, T.; Pan, Q.-K.; Li, J.-Q.; Sang, H.-Y. An Improved Migrating Birds Optimization for an Integrated Lot-Streaming Flow Shop Scheduling Problem. Swarm Evol. Comput. 2018, 38, 64–78. [Google Scholar] [CrossRef]
- Sang, H.-Y.; Pan, Q.-K.; Duan, P.-Y.; Li, J.-Q. An Effective Discrete Invasive Weed Optimization Algorithm for Lot-Streaming Flowshop Scheduling Problems. J. Intell. Manuf. 2018, 29, 1337–1349. [Google Scholar] [CrossRef]
- Li, J.; Tao, X.; Jia, B.; Han, Y.; Liu, C.; Duan, P.; Zheng, Z.; Sang, H. Efficient Multi-Objective Algorithm for the Lot-Streaming Hybrid Flowshop with Variable Sub-Lots. Swarm Evol. Comput. 2020, 52, 100600. [Google Scholar] [CrossRef]
- Alfieri, A.; Zhou, S.; Scatamacchia, R.; van de Velde, S.L. Dynamic Programming Algorithms and Lagrangian Lower Bounds for a Discrete Lot Streaming Problem in a Two-Machine Flow Shop. 4OR-Q J. Oper. Res. 2020, 19, 265–288. [Google Scholar] [CrossRef]
- Pinedo, M. Scheduling: Theory, Algorithms, and Systems, 4th ed.; Springer: New York, NY, USA, 2012; ISBN 978-1-4614-1986-0. [Google Scholar]
- Han, Y.; Gong, D.; Jin, Y.; Pan, Q. Evolutionary Multiobjective Blocking Lot-Streaming Flow Shop Scheduling with Machine Breakdowns. IEEE Trans. Cybern. 2019, 49, 184–197. [Google Scholar] [CrossRef] [PubMed]
- Gong, D.; Han, Y.; Sun, J. A Novel Hybrid Multi-Objective Artificial Bee Colony Algorithm for Blocking Lot-Streaming Flow Shop Scheduling Problems. Knowl.-Based Syst. 2018, 148, 115–130. [Google Scholar] [CrossRef]
- Han, Y.; Li, J.-Q.; Gong, D.; Sang, H. Multi-Objective Migrating Birds Optimization Algorithm for Stochastic Lot-Streaming Flow Shop Scheduling with Blocking. IEEE Access 2019, 7, 5946–5962. [Google Scholar] [CrossRef]
- Han, Y.; Gong, D.; Jin, Y.; Pan, Q. Evolutionary Multi-Objective Blocking Lot-Streaming Flow Shop Scheduling with Interval Processing Time. Appl. Soft Comput. 2016, 42, 229–245. [Google Scholar] [CrossRef]
- Han, Y.-Y.; Gong, D.; Sun, X.-Y.; Pan, Q.-K. An Improved NSGA-II Algorithm for Multi-Objective Lot-Streaming Flow Shop Scheduling Problem. Int. J. Prod. Res. 2014, 52, 2211–2231. [Google Scholar] [CrossRef]
- Ventura, J.A.; Yoon, S.-H. A New Genetic Algorithm for Lot-Streaming Flow Shop Scheduling with Limited Capacity Buffers. J. Intell. Manuf. 2013, 24, 1185–1196. [Google Scholar] [CrossRef]
- Chakaravarthy, G.V.; Marimuthu, S.; Sait, A.N. Performance evaluation of proposed Differential Evolution and Particle Swarm Optimization algorithms for scheduling m-machine flow shops with lot streaming. J. Intell. Manuf. 2013, 24, 175–191. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Ruiz, R. An Estimation of Distribution Algorithm for Lot-Streaming Flow Shop Problems with Setup Times. Omega 2012, 40, 166–180. [Google Scholar] [CrossRef]
- Davendra, D.; Senkerik, R.; Zelinka, I.; Pluhacek, M.; Bialic-Davendra, M. Utilising the Chaos-Induced Discrete Self Organising Migrating Algorithm to Solve the Lot-Streaming Flowshop Scheduling Problem with Setup Time. Soft. Comput. 2014, 18, 669–681. [Google Scholar] [CrossRef]
- Rossit, D.; Tohmé, F.; Frutos, M.; Bard, J.; Broz, D. A Non-Permutation Flowshop Scheduling Problem with Lot Streaming: A Mathematical Model. Int. J. Ind. Eng. Comput. 2016, 7, 507–516. [Google Scholar] [CrossRef]
- Sang, H.; Gao, L.; Li, X. An Iterated Local Search Algorithm for the Lot-Streaming Flow Shop Scheduling Problem. Asia Pac. J. Oper. Res. 2014, 31, 1450045. [Google Scholar] [CrossRef]
- Fang, K.; Luo, W.; Che, A. Speed Scaling in Two-Machine Lot-Streaming Flow Shops with Consistent Sublots. J. Oper. Res. Soc. 2020, 71, 1–13. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Suganthan, P.N.; Liang, J.J.; Tasgetiren, M.F. A Local-Best Harmony Search Algorithm with Dynamic Sub-Harmony Memories for Lot-Streaming Flow Shop Scheduling Problem. Expert Syst. Appl. 2011, 38, 3252–3259. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Wang, L.; Gao, L.; Li, J. An Effective Shuffled Frog-Leaping Algorithm for Lot-Streaming Flow Shop Scheduling Problem. Int. J. Adv. Manuf. Technol. 2011, 52, 699–713. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Fatih Tasgetiren, M.; Suganthan, P.N.; Chua, T.J. A Discrete Artificial Bee Colony Algorithm for the Lot-Streaming Flow Shop Scheduling Problem. Inf. Sci. 2011, 181, 2455–2468. [Google Scholar] [CrossRef]
- Ferraro, A.; Rossit, D.; Toncovich, A.; Frutos, M. Lot Streaming Flow Shop with a Heterogeneous Machine. Eng. Manag. J. 2019, 31, 113–126. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, F.; Gao, H.; Sutherland, J.W. A Three-Stage Method with Efficient Calculation for Lot Streaming Flow-Shop Scheduling. Front. Inf. Technol. Electron. Eng. 2019, 20, 1002–1020. [Google Scholar] [CrossRef]
- Ramesh, C.; Kamalakannan, R.; Karthik, R.; Pavin, C.; Dhivaharan, S. A Lot Streaming Based Flow Shop Scheduling Problem Using Simulated Annealing Algorithm. Mater. Today Proc. 2021, 37, 241–244. [Google Scholar] [CrossRef]
- Mukherjee, N.J.; Sarin, S.C.; Singh, S. Lot Streaming in the Presence of Learning in Sublot-Attached Setup Times and Processing Times. Int. J. Prod. Res. 2017, 55, 1623–1639. [Google Scholar] [CrossRef]
- Mortezaei, N.; Zulkifli, N. Integration of Lot Sizing and Flow Shop Scheduling with Lot Streaming. J. Appl. Math. 2013, 2013, 216595. [Google Scholar] [CrossRef]
- Li, Y.G.; Zhang, M.S. A Multi-Objective Lot-Streaming Optimization Scheduling Model Considering the Blocking Effect. Int. J. Simul. Model. 2016, 16, 731–741. [Google Scholar] [CrossRef]
- Sang, H.; Gao, L.; Pan, Q. Discrete Artificial Bee Colony Algorithm for Lot-Streaming Flowshop with Total Flowtime Minimization. Chin. J. Mech. Eng. 2012, 25, 990–1000. [Google Scholar] [CrossRef]
- Fattahi, P.; Azizi, V.; Jabbari, M. Lot Streaming in No-Wait Multi Product Flowshop Considering Sequence Dependent Setup Times and Position Based Learning Factors. IJE 2015, 28, 1031–1039. [Google Scholar] [CrossRef]
- Yoon, S.-H. Minimizing the Total Stretch when Scheduling Flows of Divisible Requests without Interruption. J. Soc. E-Bus. Stud. 2015, 20, 79–88. [Google Scholar] [CrossRef][Green Version]
- Defersha, F.M.; Chen, M. A Genetic Algorithm for One-Job m-Machine Flowshop Lot Streaming with Variable Sublots. IJOR 2011, 10, 458. [Google Scholar] [CrossRef]
- Glass, C.A.; Possani, E. Lot Streaming Multiple Jobs in a Flow Shop. Int. J. Prod. Res. 2011, 49, 2669–2681. [Google Scholar] [CrossRef]
- Mortezaei, N.; Zulkifli, N. A Study on Integration of Lot Sizing and Flow Shop Lot Streaming Problems. Arab. J. Sci. Eng. 2014, 39, 9283–9300. [Google Scholar] [CrossRef]
- Mortezaei, N.; Norzima, Z.; Tang, S.H.; Rosnah, M.Y. Lot Streaming and Preventive Maintenance in a Multiple Product Permutation Flow Shop with Intermingling. AMM 2014, 564, 689–693. [Google Scholar] [CrossRef]
- Mortezaei, N.; Zulkifli, N. Mixed-Integer Formulation for Integration of Lot Sizing and Lot Streaming Problem with Scheduled Preventive Maintenance. RJASET 2014, 7, 2563–2568. [Google Scholar] [CrossRef]
- Davendra, D.; Senkerik, R.; Zelinka, I.; Pluhacek, M.; Bialic-Davendra, M. Utilising the Chaos-Induced Discrete Self Organising Migrating Algorithm to Schedule the Lot-Streaming Flowshop Scheduling Problem with Setup Time. In Nostradamus 2013: Prediction, Modeling and Analysis of Complex Systems; Zelinka, I., Chen, G., Rössler, O.E., Snasel, V., Abraham, A., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; Volume 210, pp. 31–45. ISBN 978-3-319-00541-6. [Google Scholar]
- Yang, L.; Pan, Y.X. Discrete Particle Swarm Optimization Algorithm for Lot-Streaming No-Wait Flow Shop Scheduling Problem. AMR 2012, 538–541, 863–868. [Google Scholar] [CrossRef]
- Defersha, F.M.; Chen, M. A Hybrid Genetic Algorithm for Flowshop Lot Streaming with Setups and Variable Sublots. Int. J. Prod. Res. 2010, 48, 1705–1726. [Google Scholar] [CrossRef]
- Alfieri, A.; Glass, C.; van de Velde, S. Two-Machine Lot Streaming with Attached Setup Times. IIE Trans. 2012, 44, 695–710. [Google Scholar] [CrossRef]
- Han, H.Y. The Lot-Streaming Flow Scheduling Shops Based on a Hybrid Discrete Harmony Search Algorithm. AMR 2011, 204–210, 563–568. [Google Scholar] [CrossRef]
- Nejati, M.; Mahdavi, I.; Hassanzadeh, R.; Mahdavi-Amiri, N. Lot Streaming in a Two-Stage Assembly Hybrid Flow Shop Scheduling Problem with a Work Shift Constraint. J. Ind. Prod. Eng. 2016, 33, 459–471. [Google Scholar] [CrossRef]
- Chen, T.-L.; Cheng, C.-Y.; Chou, Y.-H. Multi-Objective Genetic Algorithm for Energy-Efficient Hybrid Flow Shop Scheduling with Lot Streaming. Ann. Oper. Res. 2020, 290, 813–836. [Google Scholar] [CrossRef]
- Cheng, M.; Sarin, S.C.; Singh, S. Two-Stage, Single-Lot, Lot Streaming Problem for a $$1+2$$ 1 + 2 Hybrid Flow Shop. J. Glob. Optim. 2016, 66, 263–290. [Google Scholar] [CrossRef]
- Wang, P.; Sang, H.; Tao, Q.; Guo, H.; Li, J.; Gao, K.; Han, Y. Improved Migrating Birds Optimization Algorithm to Solve Hybrid Flowshop Scheduling Problem with Lot-Streaming. IEEE Access 2020, 8, 89782–89792. [Google Scholar] [CrossRef]
- Defersha, F.M.; Chen, M. Mathematical Model and Parallel Genetic Algorithm for Hybrid Flexible Flowshop Lot Streaming Problem. Int. J. Adv. Manuf. Technol. 2012, 62, 249–265. [Google Scholar] [CrossRef]
- Cheng, M.; Sarin, S.C. Lot Streaming in a Two-Stage Assembly System. Annu. Rev. Control. 2020, 50, 303–316. [Google Scholar] [CrossRef]
- Wang, S.; Kurz, M.; Mason, S.J.; Rashidi, E. Two-Stage Hybrid Flow Shop Batching and Lot Streaming with Variable Sublots and Sequence-Dependent Setups. Int. J. Prod. Res. 2019, 57, 6893–6907. [Google Scholar] [CrossRef]
- Nejati, M.; Mahdavi, I.; Hassanzadeh, R.; Mahdavi-Amiri, N.; Mojarad, M. Multi-Job Lot Streaming to Minimize the Weighted Completion Time in a Hybrid Flow Shop Scheduling Problem with Work Shift Constraint. Int. J Adv. Manuf. Technol. 2014, 70, 501–514. [Google Scholar] [CrossRef]
- Zhang, B.; Pan, Q.; Gao, L.; Zhang, X.; Sang, H.; Li, J. An Effective Modified Migrating Birds Optimization for Hybrid Flowshop Scheduling Problem with Lot Streaming. Appl. Soft Comput. 2017, 52, 14–27. [Google Scholar] [CrossRef]
- Defersha, F.M. A Simulated Annealing with Multiple-Search Paths and Parallel Computation for a Comprehensive Flowshop Scheduling Problem: A Simulated Annealing with Multiple-Search Paths and Parallel Computation for a Comprehensive Flowshop Scheduling Problem. Intl. Trans. Op. Res. 2015, 22, 669–691. [Google Scholar] [CrossRef]
- Defersha, F.M. A Comprehensive Mathematical Model for Hybrid Flexible Flowshop Lot Streaming Problem. IJIEC 2011, 2, 283–294. [Google Scholar] [CrossRef]
- Lalitha, J.L.; Mohan, N.; Pillai, V.M. Lot Streaming in [N-1] (1) + N (m) Hybrid Flow Shop. J. Manuf. Syst. 2017, 44, 12–21. [Google Scholar] [CrossRef]
- Lei, D.; Guo, X. Scheduling Job Shop with Lot Streaming and Transportation through a Modified Artificial Bee Colony. Int. J. Prod. Res. 2013, 51, 4930–4941. [Google Scholar] [CrossRef]
- Güçdemir, H.; Selim, H. Integrating Simulation Modelling and Multi Criteria Decision Making for Customer Focused Scheduling in Job Shops. Simul. Model. Pract. Theory 2018, 88, 17–31. [Google Scholar] [CrossRef]
- López, M.L.N.; Díaz, H.L.; Sanmiguel, P.J.J.; González, J.V.R. Transfer Batch Size Impact on a Job Shop Environment Performance. IJMR 2017, 12, 318. [Google Scholar] [CrossRef]
- Xu, X.Q.; Lei, D.M. Research on Swarm Intelligence Algorithm with an Artificial Bee Colony Algorithm for Lot Streaming Problem in Job Shop. AMR 2014, 951, 239–244. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chen, L.-S.; Lin, P.-S. Lot Streaming Multiple Jobs with Values Exponentially Deteriorating over Time in a Job-Shop Environment. Int. J. Prod. Res. 2013, 51, 202–214. [Google Scholar] [CrossRef]
- Bożek, A.; Werner, F. Flexible Job Shop Scheduling with Lot Streaming and Sublot Size Optimisation. Int. J. Prod. Res. 2018, 56, 6391–6411. [Google Scholar] [CrossRef]
- Novas, J.M. Production Scheduling and Lot Streaming at Flexible Job-Shops Environments Using Constraint Programming. Comput. Ind. Eng. 2019, 136, 252–264. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zhang, B.; Wang, S. Multi-Objective Optimisation in Flexible Assembly Job Shop Scheduling Using a Distributed Ant Colony System. Eur. J. Oper. Res. 2020, 283, 441–460. [Google Scholar] [CrossRef]
- Yousefi Yegane, B.; Nakhai Kamalabadia, I.; Khanlarzade, N. Critical Path Method for Lot Streaming Problem in Flexible Job Shop Environment. IJE 2017, 30, 216–269. [Google Scholar] [CrossRef]
- Kesen, S.E.; Güngör, Z. How Important Is the Batch Splitting Activity in Scheduling of Virtual Manufacturing Cells (VMCs)? Int. J. Prod. Res. 2011, 49, 1645–1667. [Google Scholar] [CrossRef]
- Almeder, C.; Klabjan, D.; Traxler, R.; Almada-Lobo, B. Lead Time Considerations for the Multi-Level Capacitated Lot-Sizing Problem. Eur. J. Oper. Res. 2015, 241, 727–738. [Google Scholar] [CrossRef]
- Ye, T. Analysis on Multi-Stage Lot Streaming: The Effect of Transfer. Comput. Ind. Eng. 2012, 62, 1046–1054. [Google Scholar] [CrossRef]
- Sun, Y. Fuzzy Approaches and Simulation-Based Reliability Modeling to Solve a Road–Rail Intermodal Routing Problem with Soft Delivery Time Windows When Demand and Capacity Are Uncertain. Int. J. Fuzzy Syst. 2020, 22, 2119–2148. [Google Scholar] [CrossRef]
- Kovács, P. Minimum-Cost Flow Algorithms: An Experimental Evaluation. Optim. Methods Softw. 2015, 30, 94–127. [Google Scholar] [CrossRef]

| N° | Research Question | Motivation |
|---|---|---|
| RQ1 | In what types of production processes has LS been applied? | Identify the production processes in which LS can be applied. |
| RQ2 | For what types of sublots are LS used? | Identify the different sublots to consider in LS. |
| RQ3 | What optimization algorithms were used for LS calculation? | Identify the use of optimization algorithms. |
| RQ4 | Has LS been used to decrease Makespan? | Identify the LS’s goal about Makespan. |
| Database | Search | Papers |
|---|---|---|
| SCOPUS | (“lot streaming”; AND (“production processes” OR “operation lots” OR “decrease in lead time” OR “lot size” OR “optimization algorithms” OR “Makespan” OR “decrease in resource use”) AND (LIMIT-TO (PUBYEAR, 2020) OR LIMIT-TO (PUBYEAR, 2019) OR LIMIT-TO (PUBYEAR, 2018) OR LIMIT-TO (PUBYEAR, 2017) OR LIMIT-TO (PUBYEAR, 2016) OR LIMIT- TO (PUBYEAR, 2015) OR LIMIT-TO (PUBYEAR, 2014) OR LIMIT-TO (PUBYEAR, 2013) OR LIMIT-TO (PUBYEAR, 2012) OR LIMIT-TO (PUBYEAR, 2011) OR LIMIT-TO (PUBYEAR, 2010)). | 73 |
| WEB OF SCIENCE | (“lot streaming” AND (“production processes” OR “operation batches” OR “decrease in lead time” OR “lot size” OR “optimization algorithms” OR “Makespan” OR “decrease in resource use”). | 69 |
| SCIENCEDIRECT | (“lot streaming” AND (“production processes” OR “operation batches” OR “decrease in lead time” OR “lot size” OR “optimization algorithms” OR “Makespan” OR “decrease in resource use”). | 25 |
| TAYLOR and FRANCIS | (All: “lot streaming”) AND (All: “production processes”) O (All: “operation lots”) O (All: “decrease in lead time”) O (All: “lot size”) O (All: “optimization algorithms”) OR (All: “Makespan”) OR (All: “decrease in resource use”)) AND (Publication Date: (01/01/2010 TO 12/31/2020)). | 19 |
| IEEE | (“lot streaming” AND (“production processes” OR “operation batches” OR “decrease in lead time” OR “lot size” OR “optimization algorithms” OR “Makespan” OR “decrease in resource use”). | 4 |
| SEMANTIC SCHOLAR | (“lot streaming” AND (“production processes” OR “operation batches” OR “decrease in lead time” OR “lot size” OR “optimization algorithms” OR “Makespan” OR “decrease in resource use”). | 7 |
| SPRINGER | (“lot streaming” AND (“production processes” OR “operation batches” OR “decrease in lead time” OR “lot size” OR “optimization algorithms” OR “Makespan” OR “decrease in resource use”). | 3 |
| Total | 200 |
| Initial Data | Background Data | Final Data |
|---|---|---|
|
|
|
| Country | Number of Papers | % |
|---|---|---|
| China | 27 | 43% |
| Canada | 5 | 8% |
| Iran | 4 | 6% |
| USA | 4 | 6% |
| India | 3 | 5% |
| Argentina | 3 | 5% |
| Turkey | 3 | 5% |
| Malaysia | 3 | 5% |
| Taiwan | 2 | 3% |
| Germany | 2 | 3% |
| Czech Republic | 2 | 3% |
| Singapore | 1 | 2% |
| Colombia | 1 | 2% |
| South Korea | 1 | 2% |
| United Kingdom | 1 | 2% |
| Italy | 1 | 2% |
| Total | 63 | 100% |
| Process | Papers |
|---|---|
| Flow Shop | [18,19,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56] |
| Hybrid or Flexible Flow Shop | [20,57,58,59,60,61,62,63,64,65,66,67,68] |
| Job Shop | [69,70,71,72,73] |
| Flexible Job Shop | [74,75,76,77,78] |
| Other | [17,79,80] |
| Configuration | Number of Papers | % |
|---|---|---|
| j jobs m machines | 35 | 55% |
| j jobs m parallel machines s stages | 7 | 11% |
| j jobs m machines s stages | 2 | 3% |
| j jobs m non-identical machines | 2 | 3% |
| j jobs m identical parallel machines s stages | 2 | 3% |
| j jobs m non-identical machines | 2 | 3% |
| j jobs m heterogenous machines | 1 | 2% |
| j jobs m series machines | 1 | 2% |
| Total | 52 | 81% |
| Configuration | Number of Papers | % |
|---|---|---|
| j jobs 2 machines | 3 | 5% |
| 1 job m machine | 1 | 2% |
| 1 jobs on machine 1 j jobs on machine 2 2 machines | 1 | 2% |
| 1 machine at Stage 1 2 identical parallel machines at Stage 2 2 stages | 1 | 2% |
| 2 parallel machines 2 stage | 1 | 2% |
| 3 jobs 1 machine on Stage 1 2 machines on Stage 3 3 stages | 1 | 2% |
| j jobs m parallel machines on Stage 1 n parallel machines on Stage 2 2 stages | 1 | 2% |
| j jobs 1 machine s stages | 1 | 2% |
| j jobs m machines 3 stages | 1 | 2% |
| j jobs 2 machines 2 stages | 1 | 2% |
| Total | 52 1 | 81% |
| Algorithm | Papers |
|---|---|
| HA: Heuristic algorithm | [62,63,68] |
| HGA: Hybrid genetic algorithm | [46,47,54] |
| SA: Simulated annealing | [40,57,66] |
| DABC: Discrete artificial bee colony | [37,44] |
| DPA: Dynamic programming algorithms | [21,55] |
| DSOMA: Discrete self-organizing migrating algorithm | [31,52] |
| GA: Genetic algorithm | [61,64] |
| IMMBO: Improved migrating birds optimization | [18,60] |
| DEA: Differential Evolution Algorithm/PSO: Particle Swarm Optimization | [29] |
| GLASS–POTTS/JOHNSON’S | [48] |
| ABC: Artificial bee colony | [72] |
| DACS: Distributed ant colony system | [76] |
| DIWO: Discrete invasive weed optimization | [19] |
| DLHS: Local-best harmony search with dynamic sub-harmony memories | [35] |
| DPSO: Discrete particle swarm optimization | [53] |
| EDA: Estimation of distribution algorithm | [30] |
| EMMBO: Effective modified migrating birds optimization (EMBO) | [65] |
| GAJS: Genetic algorithm-based job splitting approach | [73] |
| GEA: Greedy constructive algorithm | [74] |
| HDABC: Hybrid discrete artificial bee colony | [24] |
| HDHS: Hybrid discrete harmony search | [56] |
| ILS: Iterated local search | [33] |
| INSGA-II: Improved Non-dominated Sorting Genetic Algorithm II | [27] |
| MA: Memetic algorithm | [77] |
| MABC: Modified artificial bee colony | [69] |
| MHA: Metaheuristic algorithm | [45] |
| MOMBO: Multi-Objective Migrating Birds Optimization | [25] |
| NEMO: Novel evolutionary multi-objective optimization | [26] |
| NGA: New genetic algorithm | [28] |
| NSGA II: Non-dominated Sorting Genetic Algorithm II | [58] |
| ONSGA-II: Optimization Improved Non-Dominated Sorting Genetic Algorithm | [43] |
| PA: Polynomial-time algorithm | [41] |
| PH-MOEAD: Problem-specific heuristics multi-objective evolutionary algorithm based on decomposition. | [20] |
| REMO: Evolutionary multiobjective robust scheduling | [23] |
| SFLA: Shuffled frog leaping algorithm | [36] |
| TF-HI algorithm | [59] |
| Algorithm | Papers |
|---|---|
| MILMM: Mixed-integer linear mathematical model | [32,42,49,50,51] |
| Mathematical model | [38,67,79,80] |
| MILP: Mixed-integer linear programming | [71,78] |
| Existing convex programming techniques | [34] |
| CP: Constraint Programming | [75] |
| TSM: Three-stage method | [39] |
| DSS: Integrated decision support system that combines multicriteria/AHP simulation and decision-making approaches: Analytical Hierarchy Process/WAM: Weighted Aggregation Method | [70] |
| IMM: Integer mathematical models | [17] |
| Algorithm | Compared to |
|---|---|
| HA: Heuristic algorithm | The same TSAS-MP-MIP/TSAS-CP-MIP issue resolved in Solver, RK: Random Key Method/WSPT: Weighted Shortest Processing Time/JR: Johnson’s Rule, and the same issue resolved in LINGO 11.0 with a Brauch and Bound algorithm |
| HGA: Hybrid genetic algorithm | GA, the same problem solved in Cplex, and the same problem but comparing the use of Variable Sublots and Consistent Sublots |
| SA: Simulated annealing | The same problem solved in Lingo, GA, Baker, the same problem solved in Cplex, and the performance of the parallel SA is evaluated against a sequential SA |
| DABC: Discrete artificial bee colony | HGA, HDPSO, SA, TA, ACO y DPSO |
| DPA: Dynamic programming algorithms | Proposal by Bukchin et al. (2002) and the same algorithm with different working values |
| DSOMA: Discrete self-organizing migrating algorithm | The same algorithm using the venerable Mersenne Twister, and the same but generic algorithm |
| GA: Genetic algorithm | The same algorithm executed on both sequential and parallel computing platforms (using the PGA island model), SA and MILP solved in Lingo |
| IMMBO: Improved migrating birds optimization | TLGA, iFOA, DIWO, DE-ABC, EMBO, MBO, EGA, DIWO Y ABC |
| DEA: Differential Evolution Algorithm/PSO: Particle Swarm Optimization | TEA y ACO |
| GLASS–POTTS/JOHNSON’S | |
| ABC: Artificial bee colony | GA y TS |
| DACS: Distributed ant colony system | PSO and CP |
| DIWO: Discrete invasive weed optimization | EDA, ISFH, and ABC |
| DLHS: Local-best harmony search with dynamic sub-harmony memories | HGA y HDPSO |
| DPSO: Discrete particle swarm optimization | GA, GOOD, ACO y TA |
| EDA: Estimation of distribution algorithm | EDA (and variants), DABC, ACO, DPSO, HGA, SA (and variants), TA (and variants), and TS |
| EMMBO: Effective modified migrating birds optimization (EMBO) | MBO, IMBO, MMBO, GA, GAR, DPSO y DABC |
| GAJS: Genetic algorithm-based job splitting approach | Fixed Number Work Division Approach (FNJS), taking into account different dispatch rules |
| GEA: Greedy constructive algorithm | CPO, MILP-CN /MILP-MM solved with Solver and the same problem with and without Lot Streaming |
| HDABC: Hybrid discrete artificial bee colony | TA, INSGA, NGA y BBEDA |
| HDHS: Hybrid discrete harmony search | DPSO |
| ILS: Iterated local search | HGA, DPSO y DLHS |
| INSGA-II: Improved Non-dominated Sorting Genetic Algorithm II | DHS, TA, basic NSGA-II |
| MA: Memetic algorithm | The same algorithm allowing or not to preemption |
| MABC: Modified artificial bee colony | GA, OPGA y TS |
| MHA: Metaheuristic algorithm | SA y TS |
| MOMBO: Multi-Objective Migrating Birds Optimization | BASIC MBO, h-MOEA, m-MOEA/D y REMO |
| NEMO: Novel evolutionary multi-objective optimization | INSGA-II and PBEDA |
| NGA: New genetic algorithm | GA |
| NSGA II: Non-dominated Sorting Genetic Algorithm II | i-AWGA, SPEA2 |
| ONSGA-II: Optimization Improved Non-Dominated Sorting Genetic Algorithm | DHS, NSGA-II, and TA |
| PA: Polynomial-time algorithm | |
| PH-MOEAD: Problem-specific heuristics multi-objective evolutionary algorithm based on decomposition. | EMBO, GA, GAR, DPSO y DABC |
| REMO: Evolutionary multiobjective robust scheduling | INSGA-II, PBEDA, MMSA, MOMA |
| SFLA: Shuffled frog leaping algorithm | HGA, TA y ACO |
| TF-HI algorithm | TF-I y TSHF-LSP |
| Solution | Compared to |
|---|---|
| MILMM: Mixed-integer linear mathematical model | The same problem with and without Lot Streaming and using various conditions and constraints (lot size, intermingling, maintenance times, sublot types) |
| Mathematical model | The same problem solved in Cplex, using different sublot sizes and transfer types and pure Flowshop against Hybrid Flowshop |
| MILP: Mixed-integer linear programming | The same problem with and without Lot Streaming using various conditions and restrictions |
| Existing convex programming techniques | |
| CP: Constraint Programming | The same problem with and without Lot Streaming using various conditions and restrictions |
| TSM: Three-stage method | GA, DEA, PSO, y HEA |
| DSS: Integrated decision support system that combines multicriteria/AHP simulation and decision-making approaches: Analytical Hierarchy Process/WAM: Weighted Aggregation Method | Use of different dispatch rules |
| IMM: Integer mathematical models | Flexible Lot Streaming against Basic Lot Streaming |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salazar-Moya, A.; Garcia, M.V. Lot Streaming in Different Types of Production Processes: A PRISMA Systematic Review. Designs 2021, 5, 67. https://doi.org/10.3390/designs5040067
Salazar-Moya A, Garcia MV. Lot Streaming in Different Types of Production Processes: A PRISMA Systematic Review. Designs. 2021; 5(4):67. https://doi.org/10.3390/designs5040067
Chicago/Turabian StyleSalazar-Moya, Alexandra, and Marcelo V. Garcia. 2021. "Lot Streaming in Different Types of Production Processes: A PRISMA Systematic Review" Designs 5, no. 4: 67. https://doi.org/10.3390/designs5040067
APA StyleSalazar-Moya, A., & Garcia, M. V. (2021). Lot Streaming in Different Types of Production Processes: A PRISMA Systematic Review. Designs, 5(4), 67. https://doi.org/10.3390/designs5040067






