Design and Mechanical Testing of 3D Printed Hierarchical Lattices Using Biocompatible Stereolithography
Abstract
1. Introduction
2. Methods
2.1. Lattice Design
2.2. Build Process
2.3. Mechanical Testing
3. Results
3.1. Material Characterization
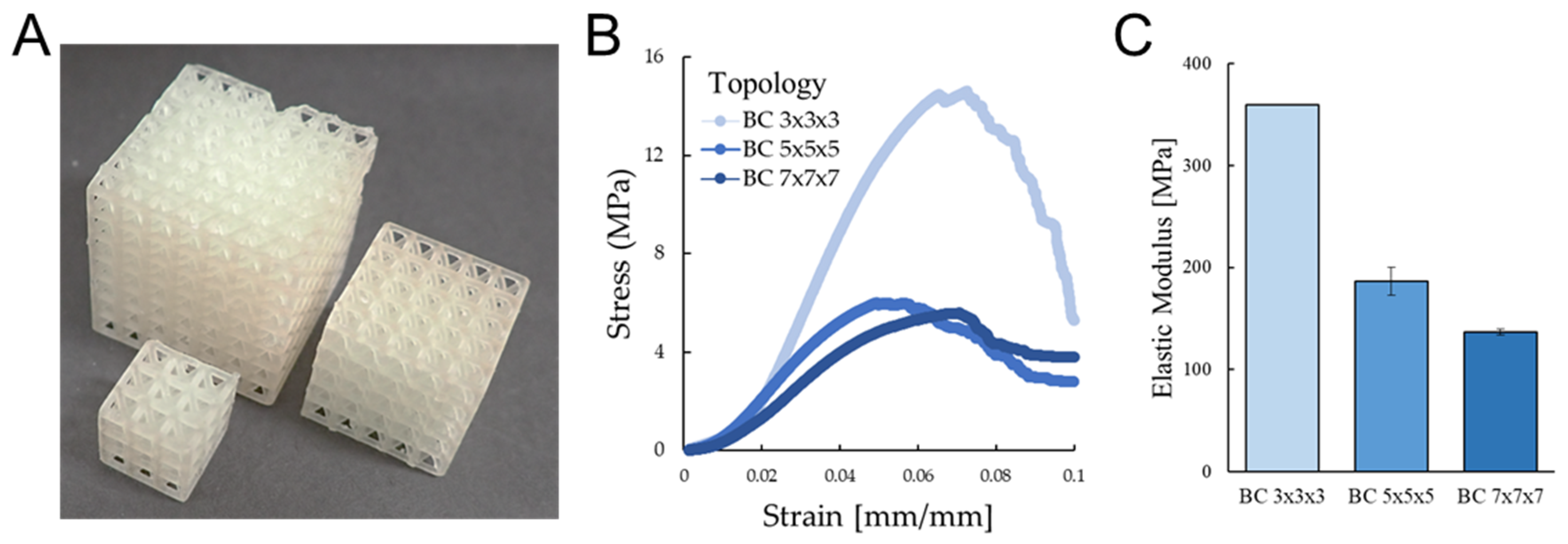
3.2. Lattice Rescaling
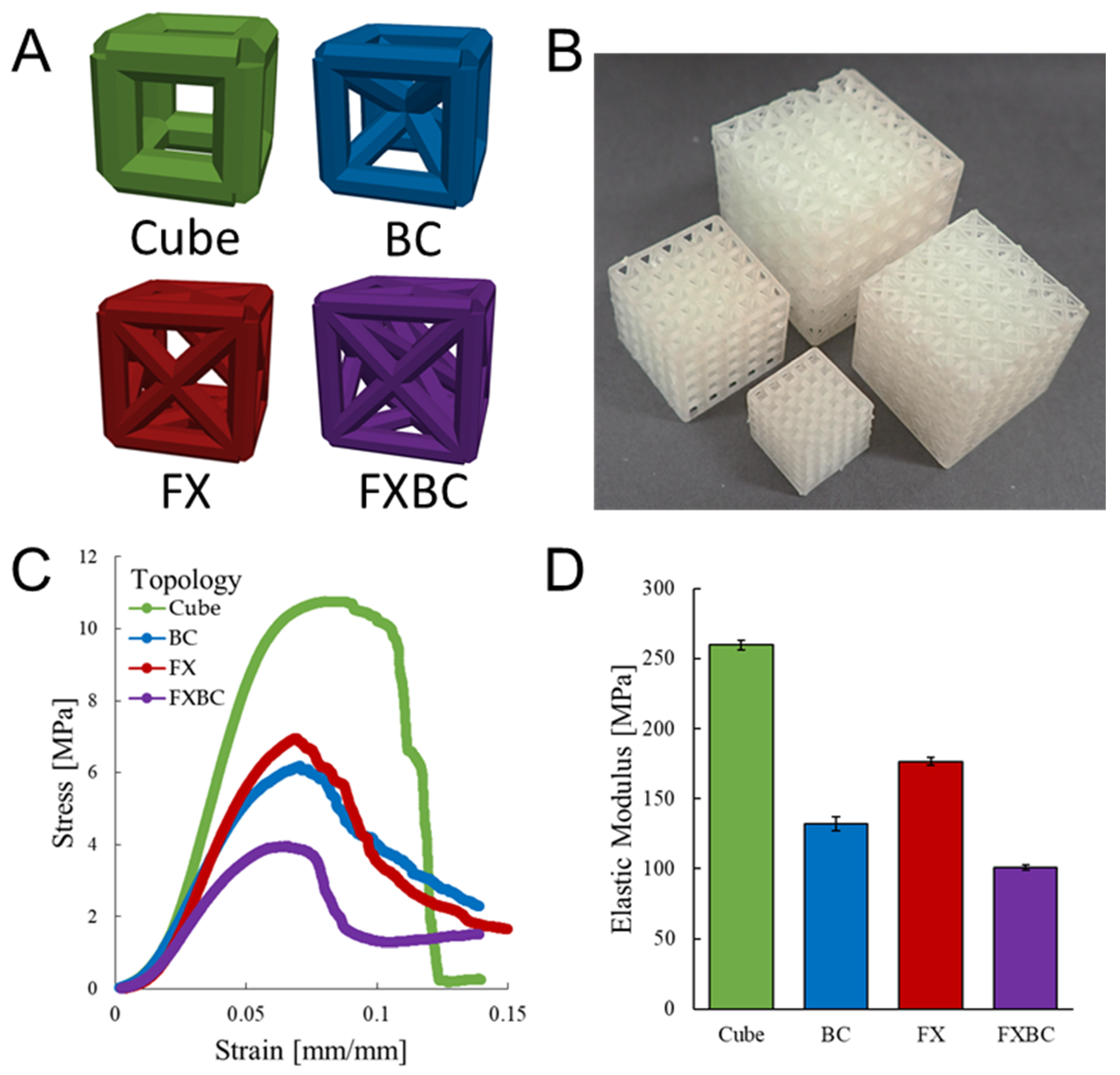
3.3. Unit Cell Topology
3.4. Hierarchical Lattices
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Egan, P.F.; Bauer, I.; Shea, K.; Ferguson, S.J. Mechanics of Three-Dimensional Printed Lattices for Biomedical Devices. J. Mech. Des. 2019, 141, 031703. [Google Scholar] [CrossRef]
- Kang’iri, S.; Gradl, C.; Byiringiro, J.; Ngetha, H. Design and Calibration of a 3D-Printed Cup-Vane Wireless Sensor Node. Designs 2018, 2, 21. [Google Scholar] [CrossRef]
- Goulas, A.; Zhang, S.; Cadman, D.A.; Järveläinen, J.; Mylläri, V.; Whittow, W.G.; Vardaxoglou, J.Y.C.; Engstrøm, D.S. The impact of 3D printing process parameters on the dielectric properties of high permittivity composites. Designs 2019, 3, 50. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Zhao, Y.F. A Survey of Modeling of Lattice Structures Fabricated by Additive Manufacturing. J. Mech. Des. 2017, 139, 100906. [Google Scholar] [CrossRef]
- Ling, C.; Cernicchi, A.; Gilchrist, M.D.; Cardiff, P. Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef] [PubMed]
- Ashby, M. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Egan, P.F. Integrated Design Approaches for 3D Printed Tissue Scaffolds: Review and Outlook. Materials 2019, 12, 2355. [Google Scholar] [CrossRef] [PubMed]
- Langer, R.; Vacanti, J. Tissue engineering. Tissue Eng. Union Biol. Eng. 1993, 98, 920–926. [Google Scholar] [CrossRef]
- Yang, S.; Leong, K.-F.; Du, Z.; Chua, C.-K. The design of scaffolds for use in tissue engineering. Part II. Rapid prototyping techniques. Tissue Eng. 2002, 8, 1–11. [Google Scholar] [CrossRef]
- Leong, K.; Cheah, C.; Chua, C. Solid freeform fabrication of three-dimensional scaffolds for engineering replacement tissues and organs. Biomaterials 2003, 24, 2363–2378. [Google Scholar] [CrossRef]
- Yeong, W.-Y.; Chua, C.-K.; Leong, K.-F.; Chandrasekaran, M. Rapid prototyping in tissue engineering: Challenges and potential. TRENDS Biotechnol. 2004, 22, 643–652. [Google Scholar] [CrossRef] [PubMed]
- Egan, P.; Wang, X.; Greutert, H.; Shea, K.; Wuertz-Kozak, K.; Ferguson, S. Mechanical and Biological Characterization of 3D Printed Lattices. 3D Print. Addit. Manuf. 2019, 6, 73–81. [Google Scholar] [CrossRef]
- Melchels, F.P.; Bertoldi, K.; Gabbrielli, R.; Velders, A.H.; Feijen, J.; Grijpma, D.W. Mathematically defined tissue engineering scaffold architectures prepared by stereolithography. Biomaterials 2010, 31, 6909–6916. [Google Scholar] [CrossRef] [PubMed]
- Alifui-Segbaya, F.; Varma, S.; Lieschke, G.J.; George, R. Biocompatibility of Photopolymers in 3D Printing. 3D Print. Addit. Manuf. 2017, 4, 185–191. [Google Scholar] [CrossRef]
- Rong, Z.; Zeng, W.; Kuang, Y.; Zhang, J.; Liu, X.; Lu, Y.; Cheng, X. Enhanced bioactivity of osteoblast-like cells on poly (lactic acid)/poly (methyl methacrylate)/nano-hydroxyapatite scaffolds for bone tissue engineering. Fibers Polym. 2015, 16, 245–253. [Google Scholar] [CrossRef]
- Pepelanova, I.; Kruppa, K.; Scheper, T.; Lavrentieva, A. Gelatin-Methacryloyl (GelMA) hydrogels with defined degree of functionalization as a versatile toolkit for 3D cell culture and extrusion bioprinting. Bioengineering 2018, 5, 55. [Google Scholar] [CrossRef]
- Byrne, D.P.; Lacroix, D.; Planell, J.A.; Kelly, D.J.; Prendergast, P.J. Simulation of tissue differentiation in a scaffold as a function of porosity, Young’s modulus and dissolution rate: Application of mechanobiological models in tissue engineering. Biomaterials 2007, 28, 5544–5554. [Google Scholar] [CrossRef]
- An, J.; Teoh, J.E.M.; Suntornnond, R.; Chua, C.K. Design and 3D printing of scaffolds and tissues. Engineering 2015, 1, 261–268. [Google Scholar] [CrossRef]
- Sanyal, A.; Gupta, A.; Bayraktar, H.H.; Kwon, R.Y.; Keaveny, T.M. Shear strength behavior of human trabecular bone. J. Biomech. 2012, 45, 2513–2519. [Google Scholar] [CrossRef]
- Barba, D.; Alabort, E.; Reed, R. Synthetic bone: Design by additive manufacturing. Acta Biomater. 2019, 97, 637–656. [Google Scholar] [CrossRef] [PubMed]
- Kengla, C.; Renteria, E.; Wivell, C.; Atala, A.; Yoo, J.J.; Lee, S.J. Clinically Relevant Bioprinting Workflow and Imaging Process for Tissue Construct Design and Validation. 3D Print. Addit. Manuf. 2017, 4, 239–247. [Google Scholar] [CrossRef]
- Hollister, S.J.; Flanagan, C.L.; Zopf, D.A.; Morrison, R.J.; Nasser, H.; Patel, J.J.; Ebramzadeh, E.; Sangiorgio, S.N.; Wheeler, M.B.; Green, G.E. Design control for clinical translation of 3D printed modular scaffolds. Ann. Biomed. Eng. 2015, 43, 774–786. [Google Scholar] [CrossRef] [PubMed]
- Briguiet, G.; Egan, P. Structure, process, and material influences for 3D printed lattices designed with mixed unit cells. In Proceedings of the ASME International Design Engineering Technical Conference, St. Louis, MO, USA, 16–29 August 2020. [Google Scholar]
- Cui, H.; Hensleigh, R.; Chen, H.; Zheng, X. Additive Manufacturing and size-dependent mechanical properties of three-dimensional microarchitected, high-temperature ceramic metamaterials. J. Mater. Res. 2018, 33, 360–371. [Google Scholar] [CrossRef]
- Egan, P.F.; Gonella, V.C.; Engensperger, M.; Ferguson, S.J.; Shea, K. Computationally designed lattices with tuned properties for tissue engineering using 3D printing. PLoS ONE 2017, 12, e0182902. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review. Biomaterials 2016, 83, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Du, Z.; Zhang, W.; Zhu, Y.; Guo, X. Additive manufacturing-oriented design of graded lattice structures through explicit topology optimization. J. Appl. Mech. 2017, 84, 081008. [Google Scholar] [CrossRef]
- Meza, L.R.; Zelhofer, A.J.; Clarke, N.; Mateos, A.J.; Kochmann, D.M.; Greer, J.R. Resilient 3D hierarchical architected metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 11502–11507. [Google Scholar] [CrossRef]
- Maggi, A.; Li, H.; Greer, J.R. Three-Dimensional nano-architected scaffolds with tunable stiffness for efficient bone tissue growth. Acta Biomater. 2017, 63, 294–305. [Google Scholar] [CrossRef]
- Ma, Q.; Cheng, H.; Jang, K.-I.; Luan, H.; Hwang, K.-C.; Rogers, J.A.; Huang, Y.; Zhang, Y. A nonlinear mechanics model of bio-inspired hierarchical lattice materials consisting of horseshoe microstructures. J. Mech. Phys. Solids 2016, 90, 179–202. [Google Scholar] [CrossRef]
- Egan, P.; Ferguson, S.; Shea, K. Design of hierarchical 3D printed scaffolds considering mechanical and biological factors for bone tissue engineering. J. Mech. Des. 2017, 139, 061401-1–061401-9. [Google Scholar] [CrossRef]
- Kang, H.; Lin, C.-Y.; Hollister, S.J. Topology optimization of three dimensional tissue engineering scaffold architectures for prescribed bulk modulus and diffusivity. Struct. Multidiscip. Optim. 2010, 42, 633–644. [Google Scholar] [CrossRef]





| Topology | Designed | Measured Data | ||||
|---|---|---|---|---|---|---|
| Beam Diameter | Cell Length | Lattice Length | Lattice Length | Porosity | Elastic Modulus | |
| (mm) | (mm) | (mm) | (mm) | (%) | (MPa) | |
| Solid | 0.8 | 4 | 4 | 4.11 | 0 | 1673.5 |
| ± 0.01 | ± 0 | ± 62.7 | ||||
| BC | 0.8 | 3.3 | 17.3 | 17.35 | 63.1 | 132 |
| ± 0.02 | ± 0.38 | ± 4.9 | ||||
| Topology | Designed | Measured Data | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Beam Diameter | Cell Length | Lattice Length | Lattice Length | Porosity | Elastic Modulus | Yield Stress | Yield Strain | Ultimate Strength | |
| (mm) | (mm) | (mm) | (mm) | (%) | (MPa) | (MPa) | (-) | (MPa) | |
| BC 3 × 3 × 3 | 0.8 | 3.3 | 10.7 | 10.92 | 50.69 | 359.8 | 11.8 | 0.05 | 14.8 |
| ± 0.02 | ± 0.33 | ± 0.5 | ± 0.1 | ± 0.001 | ± 0.2 | ||||
| BC 5 × 5 × 5 | 0.8 | 3.3 | 17.3 | 17.39 | 57.68 | 186.1 | 5.1 | 0.04 | 6.2 |
| ± 0.05 | ± 3.74 | ± 13.7 | ± 0.2 | ± 0.003 | ± 0.3 | ||||
| BC 7 × 7 × 7 | 0.8 | 3.3 | 23.9 | 23.95 | 61.52 | 136.7 | 4.5 | 0.04 | 5.6 |
| ± 0.03 | ± 0.27 | ± 2.8 | ± 0.1 | ± 0.08 | ± 0.1 | ||||
| Topology | Designed | Measured Data | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Beam Diameter | Cell Length | Lattice Length | Lattice Length | Porosity | Elastic Modulus | Yield Stress | Yield Strain | Ultimate Strength | |
| (mm) | (mm) | (mm) | (mm) | (%) | (MPa) | (MPa) | (-) | (MPa) | |
| Cube | 0.8 | 2.16 | 11.60 | 11.63 | 67.91 | 259.6 | 9.2 | 0.050 | 10.8 |
| ± 0.02 | ± 0.55 | ± 3.4 | ± 0.3 | ± 0.002 | ± 0.4 | ||||
| BC | 0.8 | 3.30 | 17.30 | 17.35 | 63.07 | 132.0 | 5.3 | 0.050 | 6.3 |
| ± 0.02 | ± 0.38 | ± 4.9 | ± 0.2 | ± 0.001 | ± 0.2 | ||||
| FX | 0.8 | 3.97 | 20.65 | 20.71 | 65.24 | 176.4 | 5.6 | 0.050 | 7.1 |
| ± 0.02 | ± 0.35 | ± 2.8 | ± 0.1 | ± 0.002 | ± 0.2 | ||||
| FXBC | 0.8 | 4.84 | 25.00 | 25.03 | 64.20 | 101.0 | 3.3 | 0.050 | 4.1 |
| ± 0.02 | ± 0.11 | ± 1.9 | ± 0.1 | ± 0.001 | ± 0.1 | ||||
| Topology | Designed | Measured Data | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Beam Diameter | Cell Length | Lattice Length | Lattice Length | Porosity | Elastic Modulus | Yield Stress | Yield Strain | Ultimate Strength | Stiffness | |
| (mm) | (mm) | (mm) | (mm) | (%) | (Mpa) | (Mpa) | (-) | (MPa) | (kN/mm) | |
| BC | 0.8 | 3.3 | 17.3 | 17.39 | 57.68 | 186.1 | 5.1 | 0.040 | 6.2 | 3.22 |
| ± 0.05 | ± 3.74 | ± 13.7 | ± 0.2 | ± 0.003 | ± 0.3 | ± 0.24 | ||||
| BC-Void | 0.8 | 3.3 | 17.3 | 17.31 | 74.86 | 158.2 | 5.3 | 0.050 | 6.5 | 2.74 |
| ± 0.02 | ± 1.33 | ± 3.8 | ± 0.1 | ± 0.001 | ± 0.1 | ± 0.07 | ||||
| BC-Cage | 0.8 | 3.3 | 23.9 | 23.90 | 71.02 | 144.7 | 5.7 | 0.050 | 7.1 | 7.72 |
| ± 0.02 | ± 0.22 | ± 4.8 | ± 0.2 | ± 0.006 | ± 0.1 | ± 0.26 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moniruzzaman, M.; O'Neal, C.; Bhuiyan, A.; Egan, P.F. Design and Mechanical Testing of 3D Printed Hierarchical Lattices Using Biocompatible Stereolithography. Designs 2020, 4, 22. https://doi.org/10.3390/designs4030022
Moniruzzaman M, O'Neal C, Bhuiyan A, Egan PF. Design and Mechanical Testing of 3D Printed Hierarchical Lattices Using Biocompatible Stereolithography. Designs. 2020; 4(3):22. https://doi.org/10.3390/designs4030022
Chicago/Turabian StyleMoniruzzaman, Md, Christopher O'Neal, Ariful Bhuiyan, and Paul F. Egan. 2020. "Design and Mechanical Testing of 3D Printed Hierarchical Lattices Using Biocompatible Stereolithography" Designs 4, no. 3: 22. https://doi.org/10.3390/designs4030022
APA StyleMoniruzzaman, M., O'Neal, C., Bhuiyan, A., & Egan, P. F. (2020). Design and Mechanical Testing of 3D Printed Hierarchical Lattices Using Biocompatible Stereolithography. Designs, 4(3), 22. https://doi.org/10.3390/designs4030022