Shaft Integrated Electromagnetic Energy Harvester with Gravitational Torque

Abstract

This paper presents the development of an electromagnetic energy harvester for electrical supply of a sensor unit integrated on the rotating inner ring of a rolling bearing. This energy harvester is of special interest for condition monitoring tasks on rotating shafts. A sensory monitor on the inner ring can detect wear conditions at an early stage. The harvester works without mechanical and energetic contact to surrounding components by utilizing the rotational energy of the shaft. The functionality of the Energy Harvester is enabled by the inertia principle, which is caused by an asymmetrical mass distribution. We provide simulations to validate the designs. This work includes simulation studies on the electrical power output of the harvester. Therefore, the necessary simulation of the magnetic problems is realized in a substitute simulation environment. The harvester design enables existing machines to be equipped with the harvester to provide an energy supply on rotating shafts. This clamp connection enables shaft mounting independent of location without mechanical work on the shaft. With an electrical power of up to 163.6 m W, at 3600 rpm, the harvester is used as an energy supply, which enables sensor-based monitoring of slow wear processes.

1. Introduction

In order to increase machine productivity, there is a need for continuous information about the current wear condition of a machine. Based on the wear condition, necessary machine maintenances can be planned in terms of time and costs. Up to 20% of unplanned failures of a production machine are caused by rolling bearing damage [1]. Previous technologies have made it possible to monitor rolling bearings, which monitor the lubrication condition, outer ring temperature, cage speed and bearing load. For this, acoustic surface waves are coupled into the bearing outer ring with a piezo element and received by another piezo element. Due to the different propagation speeds and damping of the acoustic wave, conclusions can be drawn about the bearing condition [2,3].

The disadvantage of this method is the damping of the inner ring signal because of the acoustic transfer paths to the outer ring. This is based on the fact that the signal must be transferred from the inner ring to the rolling elements and from the rolling elements to the outer ring. Condition monitoring of the rotating inner ring is therefore suitable for early diagnosis of bearing failure, because the tribological rolling contacts on the inner ring are subject to higher loads than on the outer ring.

Condition monitoring of the rotating inner ring requires an energy supply to the sensor components. Energy-autonomous sensor networks can be used, because such networks do not require wired installation. Especially when moving and stationary components are connected, wired installations have high wear characteristics. For example, wear is caused by sliding contacts between the moving and static components. In addition, mechanical moving cable connections are highly susceptible to errors. Battery-powered sensor networks also do not offer a practical solution due to the high maintenance costs resulting from battery replacement [4].

Based on the generally decreasing energy consumption of electrical components, micro energy harvesting solutions are used as energy sources, which generate power in the range of a few microwatts to milliwatts [5].

There are numerous conversion principles for energy harvesting. For example, the thermoelectric effect uses temperature differences to generate electrical energy from the environment [6]. Piezoelectric transducers are often applied when vibration energy in the form of a spring-mass oscillator is to be used [7]. Furthermore, photoelectric and electromagnetic conversion principles are utilized [8,9]. For the conversion of rotational energy into electrical energy, triboelectric nanogenerators (TENG) can also be considered [10]. Generators of this type are based on a frictional contact between two materials, resulting in an electrostatic charge of the surfaces. These generators are initially used as micro and nano energy sources. Triboelectric generators achieve high efficiency especially at low motion frequency [11]. Due to the friction-bound operating principle, this conversion principle has high wear characteristics, especially due to high speeds. Electromagnetic converters offer a wear-free conversion principle and a high energy density compared to other technologies [12]. The functionality of the Energy Harvester presented here is based on a generator design, which does not have to be adapted to any property parameters (resonance frequency or similar), as is absolutely necessary for vibration energy harvesters [13]. Similar works in that area, which follow the intention of a voltage supply at rotating shafts, have clear boundaries to the presented development in this paper.

Table 1. Comparable works and their similarities and differences.

Comparable Works	Similarities	Differences
Gravitational moment generator [14]	electromagnetic gravitational moment	mounting location on shaft ends development of the generator unit
Rotatory vibration energy generator [15]	electromagnetic mounting location flexible on shafts use the principle of inertia	spring-mass oscillator adjust to the characteristic parameter resonance frequency use of rotary non-uniformity movements
Axlebox generator, Siemens Schaeffler Mobilities [16]	electromagnetic	mechanical contact to surrounding components required

lists comparable works with similarities and differences to this work.

Patents (e.g., EP0594550B1 [17], US20160123401A1 [18], US20160254725A1 [19]) in this area of development also show a mechanical connection to surrounding components, in addition the energy gain takes place at the stator assembly.

Due to the limited amount of solutions for maintenance-free energy supply of sensor network nodes on rotating shafts, the implementation of condition monitoring is problematic. The issue is increased by the fact that the Energy Harvester can be installed on existing machines. For this reason, this design is constructed in such a way that it can be adapted to different shaft sizes and there is no contact to surrounding components (stator of the diagnostic object). During the implementation of this project, problems arise in the amount of energy to be obtained in order to use a sensory monitoring system. A high energy consumption results from the data transfer between the rotating shaft and a receiving unit. It is essential that the use of the harvester does not cause any additional maintenance effort and that it is absolutely maintenance-free. Furthermore, a service life expectancy must be achieved that is longer than that of the diagnostic object.

The aim is to develop a new integrated electromagnetic energy harvester for energy self-sufficient sensor systems. The harvester is used to supply energy to a sensor system integrated on the rotating inner ring of a bearing. This construction of the harvester allows installation in existing systems without contact between the harvester and the stator unit of the diagnostic object.

2. Operating Principle

In order to generate electrical energy based on the induction principle, a relative movement between an inductive component and a magnetic field is required (Figure 1). To enable this relative movement, a movable or pivoted connection must be created—by using a bearing, for example. With regard to the frictional forces between the bearing inner ring, the rolling elements, the bearing outer ring and other damping factors, it is to be expected that no relative movement occurs between the components. To achieve a braking torque or a rotational inertia at the stator component, an asymmetrical mass distribution takes place at the bearing outer ring, resulting in an unevenly distributed weight force on the bearing outer ring. This force ensures that a braking torque or increased inertia is generated at the outer ring, resulting in relative movement.

3. Modeling

The harvester design is accompanied by a simulation in Matlab Simulink. With the simulation model, the kinematic behavior and the electrical performance of the harvester is simulated. For the electrical performance a simulation of the magnetic parameters is necessary. This simulation takes place in a separate simulation environment, FEMM (Finite Element Method Magnetics). FEMM is specialized in two-dimensional simulation of magnetic parameters. For simplification this simulation is limited to a single coil-magnet pair. The separation of the two simulation environments results in the following advantages:

• Simple replication of the geometrical structure in a two-dimensional simulation environment.
• Fast simulation process, by reducing the simulation to one coil–magnet pair.
• The simple geometrical structure allows a quick adaptation of the simulation object.
• Increase in the simulation speed, because within a simulation there is no cross-program data exchange.
• No simulation of the magnetic parameters, if not absolutely necessary.

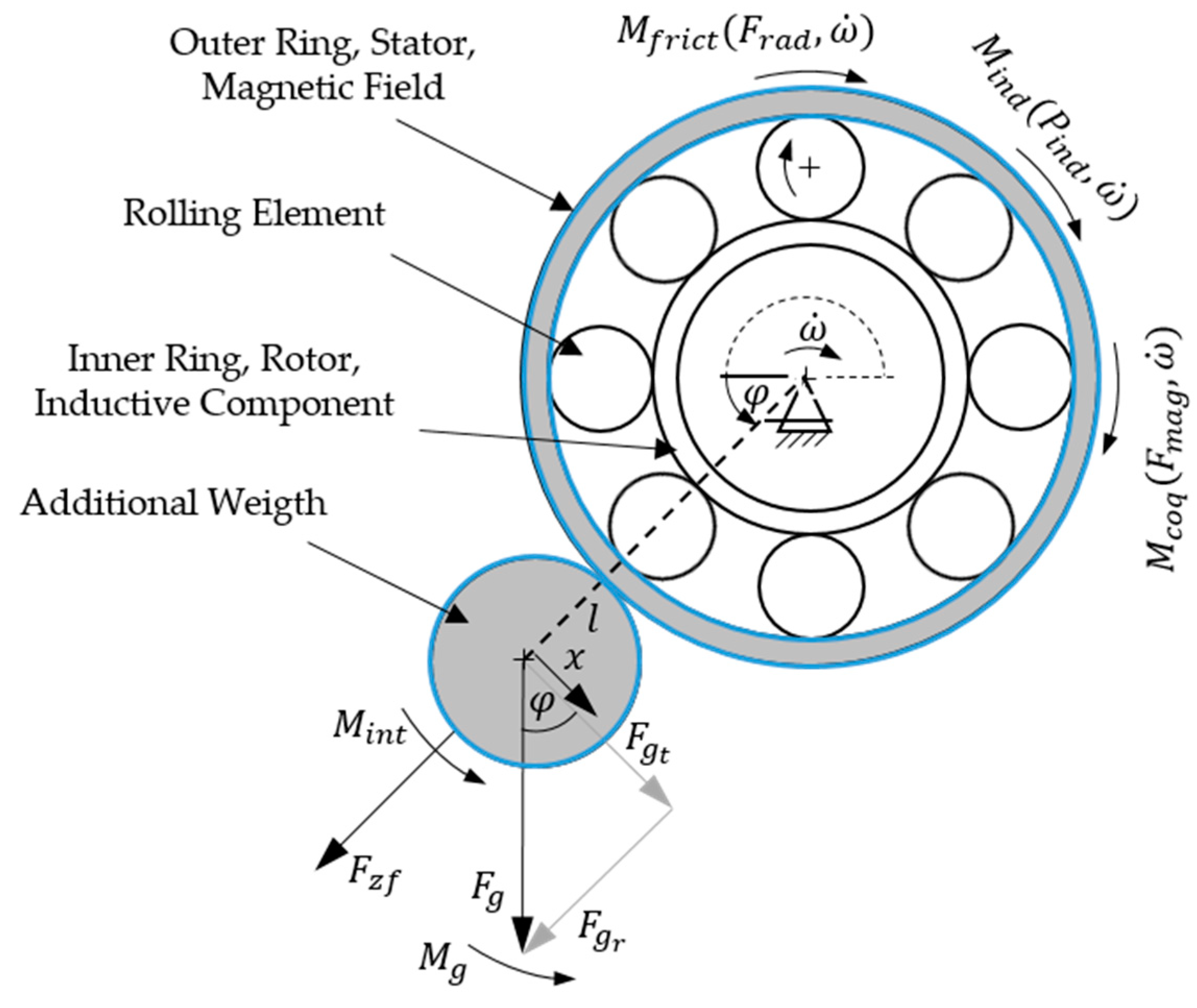
This model reflects the operating principle described in Figure 1. Specifically, the simulation of the operating principle includes the calculation of the gravitational torque $M_g$, the torque of inertia $M_{int}$, the cogging torque $M_{coq}$, and the friction torque $M_{frict}$. By the variable $\phi$, the deflection of the additional mass is described and $\dot{\omega }$ represents the rotational speed of the drive shaft. The friction torque describes the behaviour of the bearing unit used in the harvester. It results from the bearing design, the lubricant and the bearing speed. Calculation of the frictional torque is based on a calculation algorithm from SKF [20].

Cogging torque arises from the magnetic force acting on the iron cores and coils. Further influence on the kinematic behavior is the induction torque $M_{ind}$. A mathematical relationship between the above-mentioned moments is shown in Figure 1 and formula (1).

$$0=M_{frict}+M_{coq}+M_{ind}-M_g-M_{int}$$

(1)

The calculation of the induction voltage is shown in formula (2) [21]. For a coil, the induction voltage is calculated from the number of turns n, the magnetic flux density B and the coil surface A, the magnetic flux density is passed through which the magnetic flux density is passed. The number of turns n is a constant depending on the coil size.

$$U_{ind}=-n\ast \frac{d\left(B\ast A\right)}{dt}$$

(2)

The penetrated area A of the coil results from the area of a magnet and the area of the iron core, resulting in a sliced plane. The path (Figure 2b) of the slice plane is represented as a sub-function depending on the angle of rotation. For the implementation of the slice plane in Matlab Simulink, an entire function is created that illustrates the complete surface of one rotation from the harvester. Within one rotation, the slice plane is dependent on the number of magnet pairs and coils being used. To represent the entire harvester, the individual sub-functions are arranged in a row according to the number of coil–magnet pairs.

The magnetic flux density is also combined from created partial functions to an entire function (Figure 2c) and integrated into the simulation environment. In the simulation environment FEMM, a substitute simulation model (Figure 2a) is created, which is used to determine the magnetic flux density in one of a coil-magnet pair. In particular, the intensity and the course of the magnetic flux density in the magnetic back iron and in the iron core can be determined. Furthermore, the effect of the material thickness on the magnetic flux can be verified. If the magnetic flux is supersaturated, the magnetic flux density in the iron core decreases, resulting in a loss of power. Therefore, an optimum of material thickness and maximum magnetic flux density must be found. During the simulation, the iron core passes through the idealized circular path (Figure 2a) between the magnets and calculates the discrete course of the magnetic flux density in the iron core. Figure 2 shows how the simulation model is built. Figure 2a shows the substitute simulation model for the magnetic parameters. The course from the substitute simulation model is idealized and corresponds to the course of the idealized circular path of the iron core in Figure 2b. Figure 2c illustrates the quantitative course of the flux density from Figure 2a,b, at one rotation of the rotor.

The induction voltage represents the input variable for calculating the induction torque $M_{ind}$. It represents the mechanical losses resulting from the use of electrical energy. From the aspect of power adjustment, an operating point results after the basic circuit where the maximum electrical power can be expected. The operating point is set by a resistance ratio between internal resistance $R_i$ and load resistance $R_a$ [22]. At this point, the following relationship applies:

$$R_i=R_a.$$

(3)

As shown in Equation (4), maximum power is accompanied by maximum induction torque.

$$M_{ind}=\frac{P}{2\pi n}$$

(4)

Similar to the modelling of the magnetic flux density, the simulation of the magnetic force takes place in FEMM. The simulation program enables us to solve two-dimensional problems, whereby geometrical images in depth are represented as cuboid. Due to this, a substitute simulation model is necessary to perform a realistic simulation of the magnetic force. In the simulation model, the magnetic surface has been adjusted to correspond to a cylindrical magnetic surface. Like in Figure 2a, the iron core passes the simulation path and determines the force $F_{y mag}$, which acts on the iron core in y-direction. Depending on the differential rotation angle $\Delta \dot{\omega }$ and the radius of the coil rotation path $r=\mathrm{l}$, the result is a cogging torque $M_{coq}$ using formula (5).

$$M_{coq}=F_{y mag}\ast \Delta \omega \ast l$$

(5)

This simulation model is used to perform a simulation calculating the electrical power in a stepwise method for the speed range 0–3600 rpm. During the simulation the behavior of the inertial mass is ignored. The simulation is parameterized with the design parameters of

Table 2. Constructive and electrical parameters.

Constructive Parameter		Electrical Parameters
Diameter	98 mm	Number of coils	6
Length	105 mm	Coil connection	Serial
Weight	1.3 kg	Number of turns	185
Bearing	61810-2RZ-Y	Wire diameter	0.2 mm
-	-	Iron core length	5 mm
-	-	Internal resistance	15.2 Ω
-	-	Magnet pairs	8

. A voltage rectification is carried out in the simulation to compare the simulation values with the measured values of the final harvester design. For this purpose, a voltage drop of 0.4 V is subtracted from the rectified value of the alternating voltage. Based on this, the electrical power can be calculated according OHM’s law. Figure 6 shows the results of the simulation.

4. Shaft integrated Generator

The Energy Harvester is a generator mountable on shafts—its installation does not require structural changes to existing machines. It is designed for a shaft diameter of 40 mm. For installation on shaft diameters $\varnothing$ > 40 mm, the individual components are scalable in size, so that after constructive adaptation, installation on other shaft diameters is possible. The fixing mechanism is based on a force-locked conical clamp connection, which reduces the installation effort at the application place. Table 2 lists the constructive and electrical design parameters of the harvester. The electrical parameters can be modified by using other coils. For example, the wire diameter, the number of turns and the size of the iron core can be modified depending on the available installation space.

In Figure 3, the sectional view of the harvester is shown, which represents the construction of the harvester.

Table 3. Energy Harvester components.

No.	Component	No.	Component
1	Case cover	7	Cone ring
2	Back iron with asymmetrical mass distribution	8	Socket
3	Bearing	9	Electronic board
4	Central nut	10	Shaft seal
5	Magnets	11	Case
6	Coil unit

lists the main components of the energy harvester. The harvester is designed to achieve the highest grade of miniaturization available with conventional production methods.

The stator component of the harvester comprises the back iron (Figure 3, no. 2) and the outer ring of the bearing unit (3). The remaining components, central nut (4), coil unit (6), cone ring (7) and socket (8), form the rotor assembly of the harvester unit. To ensure maintenance free operation, the bearing unit is lifetime lubricated. The electrical voltage is connected to the rotor component and is used to supply energy to the sensor system.

5. Evaluation of the Energy Harvester Design Principle

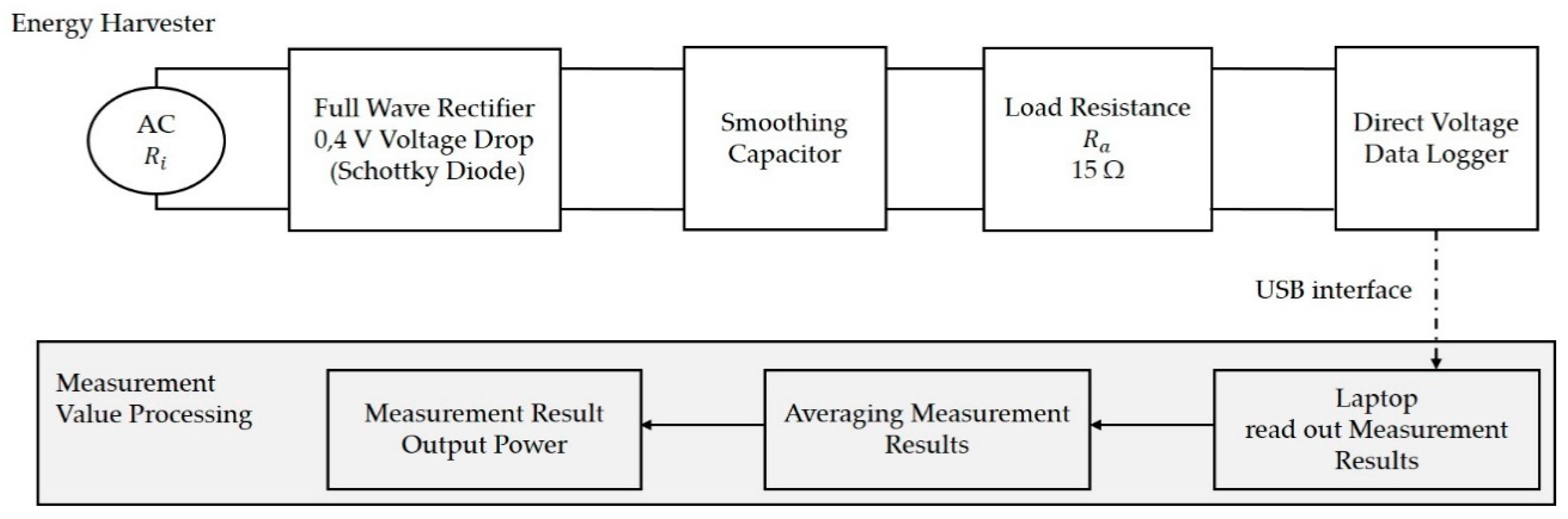
To evaluate the Energy Harvester design principle, speed-dependent measurements (1000–2000 rpm) are carried out. The measurement analysis is limited to a power output test of the harvester, because of the rotating induction coils, the measured variables must be recorded on the rotor component. A direct voltage data logger is used for this purpose. The AC voltage of the Energy Harvester is rectified by a rectifier circuit consisting of Schottky diodes and a smoothing capacitor. The voltage drop at the load resistor (15 ohm) can be used to determine the electrical power at the consumer. To measure the maximum power, the harvester is loaded with a load resistance that is almost equal to the internal resistance (15.2 ohm). The internal resistance of the harvester is derived from the OHM resistance of the coils. In Figure 4, the schematic diagram illustrates the measuring principle and the process for evaluating the measured values. The upper part of the diagram shows the procedure for recording the measured values. After the measured values have been recorded, they are downloaded and prepared via USB interface. The evaluation includes the averaging of the measured values, recorded over a constant speed range.

Figure 5 illustrates the experimental setup with the necessary measuring equipment for evaluating the harvester. It shows an electric motor driving the rotor component. A data logger with the measuring circuit shown in Figure 5 is mounted on the shaft. In addition, the Energy Harvester is supplied with weights to increase the inertial mass.

Figure 6 shows the measured values of the power output test and the simulation results. Due to the mounting of the data logger on the shaft, unbalance influences on the test setup result. In order to keep these forces low, an upper speed limit of 2000 RPM is specified. To be able a performance specification for the speed range of 2000–3600 RPM, the measured values for this range are extrapolated. Due to the proportional relationship between the induction voltage and the speed, the voltage measurements are linearly extrapolated. From the extrapolated values, the power can be calculated according to formula (6).

The measurements of the output power test result in an electrical power of 41.4 m W and 163.6 m W at 2000 and 3600 rpm respectively. For these speeds, the simulation results in an output of 58.8 m W and 227.6 m W respectively. There is a difference of up to 29% between these results. Reasons for the differences are found in the procedure for simulating the electrical power. Based on the relation

$$\mathrm{P}=\frac{U^2}{R}$$

(6)

the power calculation is implemented in the simulation. Differences that occur in the simulated electric voltage have quadratic effects on the simulated power. For the simulation of the electric voltage, a two-dimensional simulation of the magnetic flux is used. In this process, simplifications are created upon which the differences are attributed. For example, by reducing the simulation to one coil–magnet pair and the simplified representation of the design conditions.

In addition to the measured property parameters, empirical knowledge was gained. This includes in particular the operating behavior of the harvester in relation to the inert mass. During the performance test, the stator mass with an additional weight of 167.8 g, at approx. 600 rpm, was found to be entrained. After longer running periods and heating of the bearings, an operating range of up to 1200 rpm can be achieved with a constant increase in speed without the stator unit rotating. With regard to the thermal bearing load, a balance must be maintained between the frictional power $N_R$ and the heat flow $\dot{Q}$ to be dissipated, demonstrated by formula (7) [23]:

$$N_R=\dot{Q}$$

(7)

This balance results in a limit speed ${\mathit{n}}_{\mathit{G}}$, which may not be exceeded [23]. For the bearing used here, the limiting speed is 12,900 rpm, so from a mechanical point of view, no thermal overload of the bearing is expected. Due to the surrounding components with a high thermal conductivity, heat dissipation is ensured. Further investigations are necessary within the scope of the research work with regard to the electrical losses. The geometric design of the magnetic back iron has a positive effect on the cooling of the electrical components (Figure 5). The back iron is cut out on one side and thus allows the coil unit to be cooled in the ambient air.

6. Conclusions

The design of the electromagnetic Energy Harvester permits mounting it on shafts independent of location. Therefore, an existing machine can be equipped with the Energy Harvester if the shaft diameter has been adapted. This harvester provides an energy supply of up to 163.6 m W, at 3600 rpm, on rotating shafts. With that amount of power, sensor-based monitoring of inert wear processes is possible. This includes all areas of application for rolling bearing technology—for example, in machine tools or wind power plants.

During the development of the harvester, a simulation model was created, which is used to carry out simulations of power output. When comparing the simulation and measurement results, approximations of up to 29% were reached. With regard to the mentioned simplifications in the two-dimensional magnetic simulation models, these results offer a sufficient approximation. Taking these differences into consideration, further developments of the harvester can first be simulated, and their influences quantitatively evaluated.

From a mechanical perspective, there is a potential for further developments of the underlying bearing technology. Reducing the frictional torque between the stator and rotor assembly is important. If necessary, a further adjustment of the internal resistance to the external resistance can be made. For instance, a phase connection of the coils is conceivable to improve the reliability. The use of AC voltage measurement technology is necessary for further investigations of the harvester AC voltage. With this, the induction behavior of single and several connected coils can be analyzed. Furthermore, the simulation model can be validated with regard to the induction behavior.