Experimental and Numerical Investigation of Tip Leakage Flows in a Roots Blower
Abstract
1. Introduction
2. Experimental Study
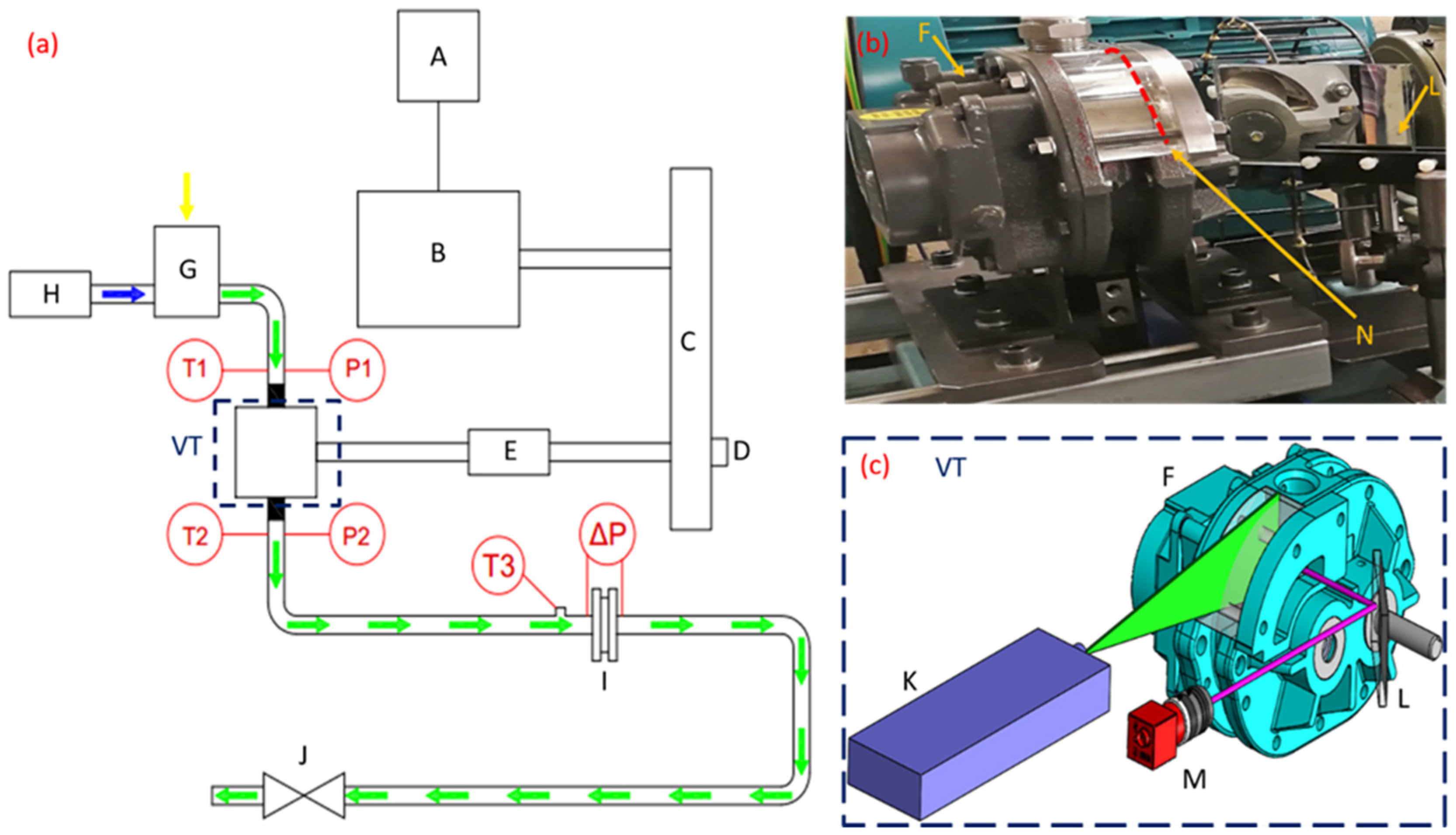
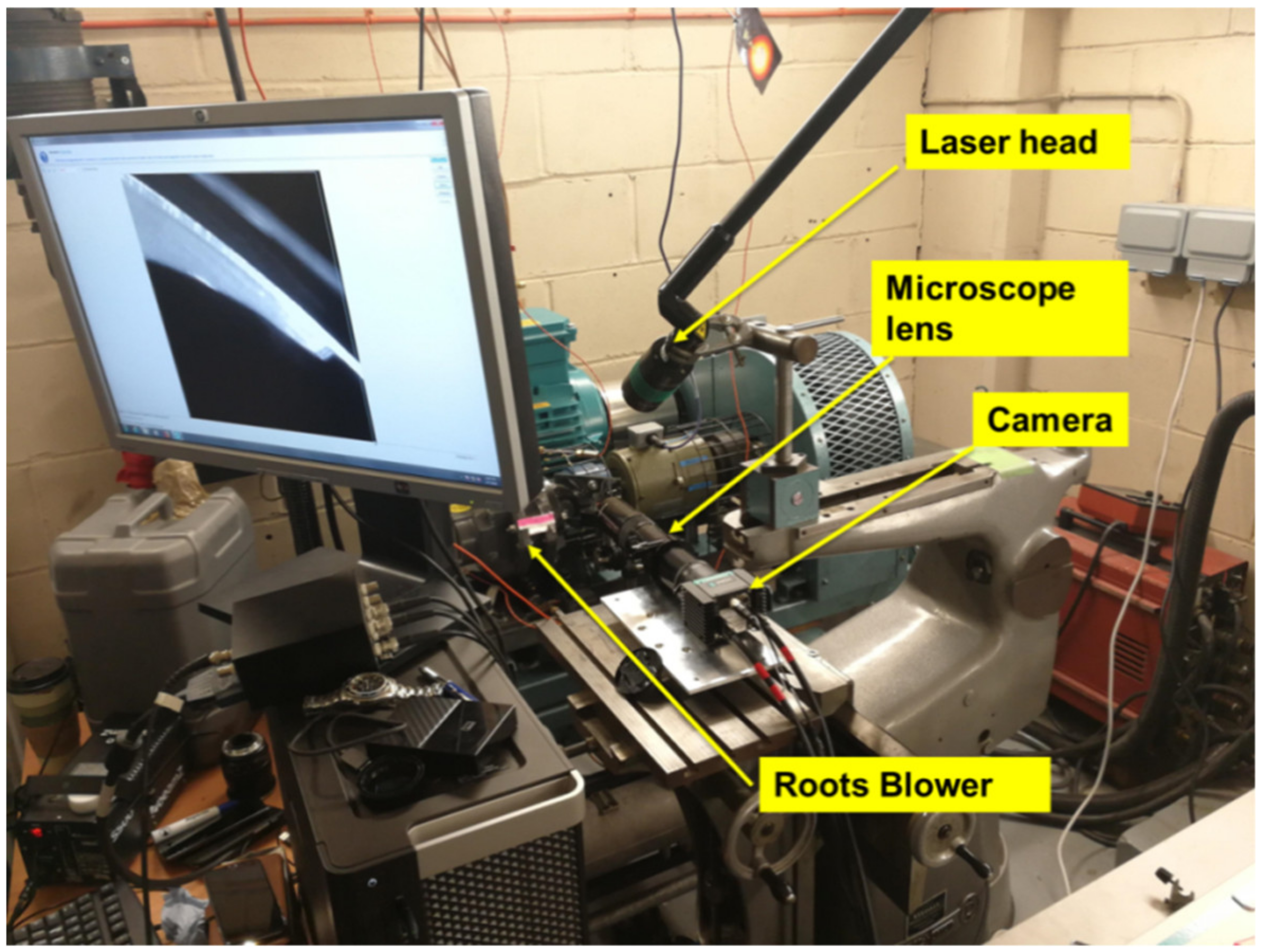
2.1. Experimental Setup and Data Processing
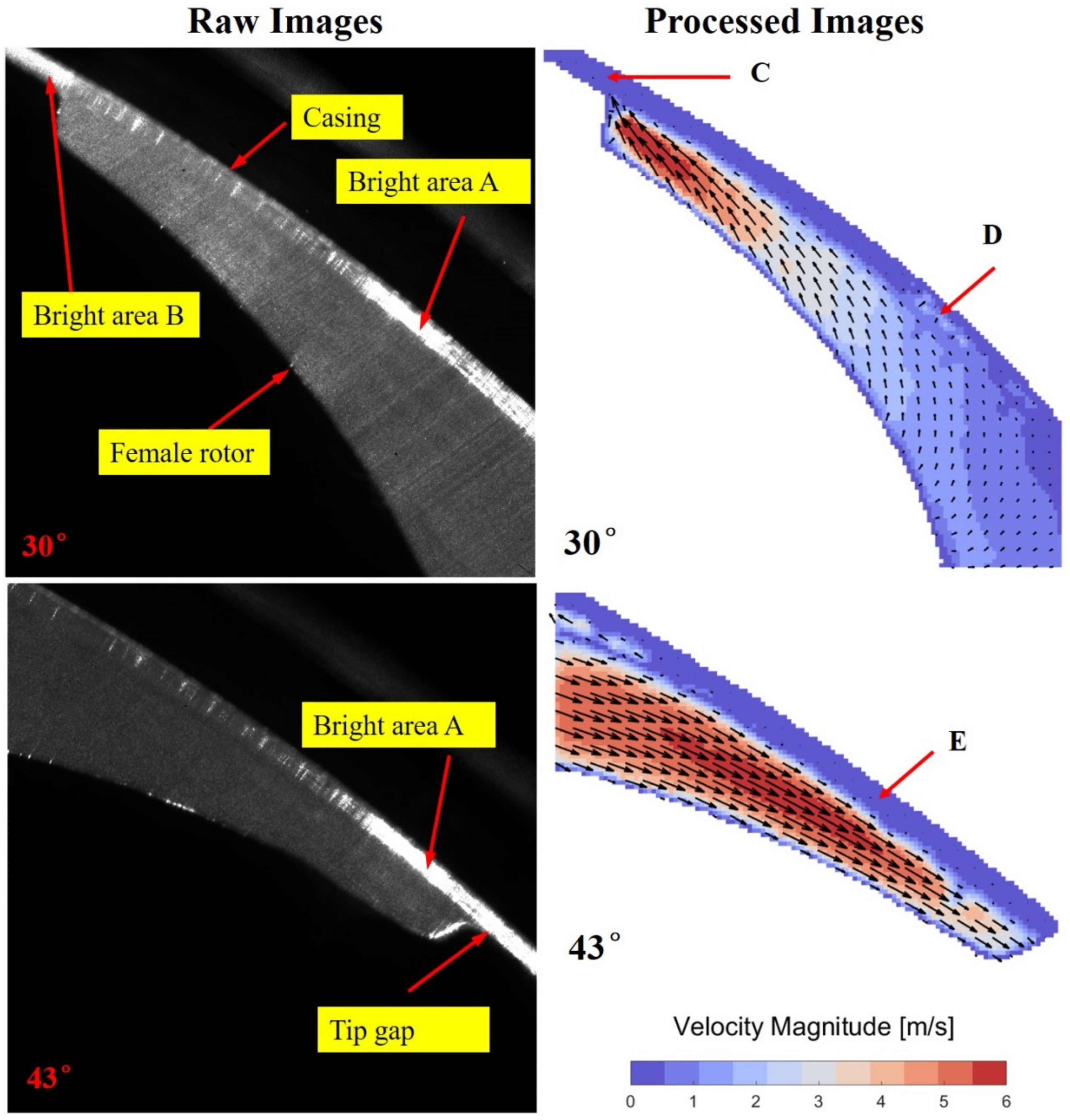
2.2. Experimental Findings
3. CFD Model for Roots Blower
3.1. CFD Settings and Boundary Conditions
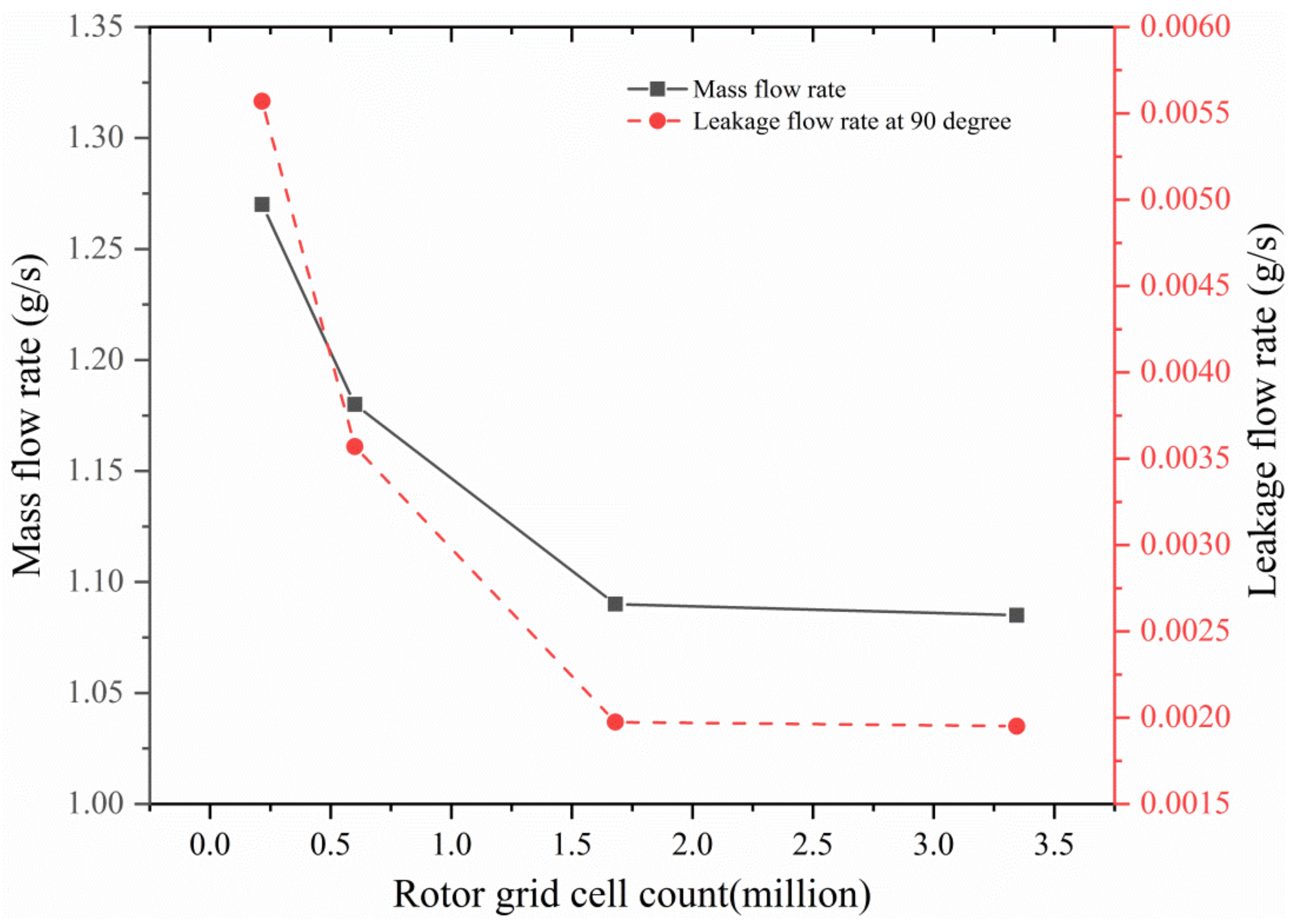
3.2. Grid Generation and Grip Independence Study
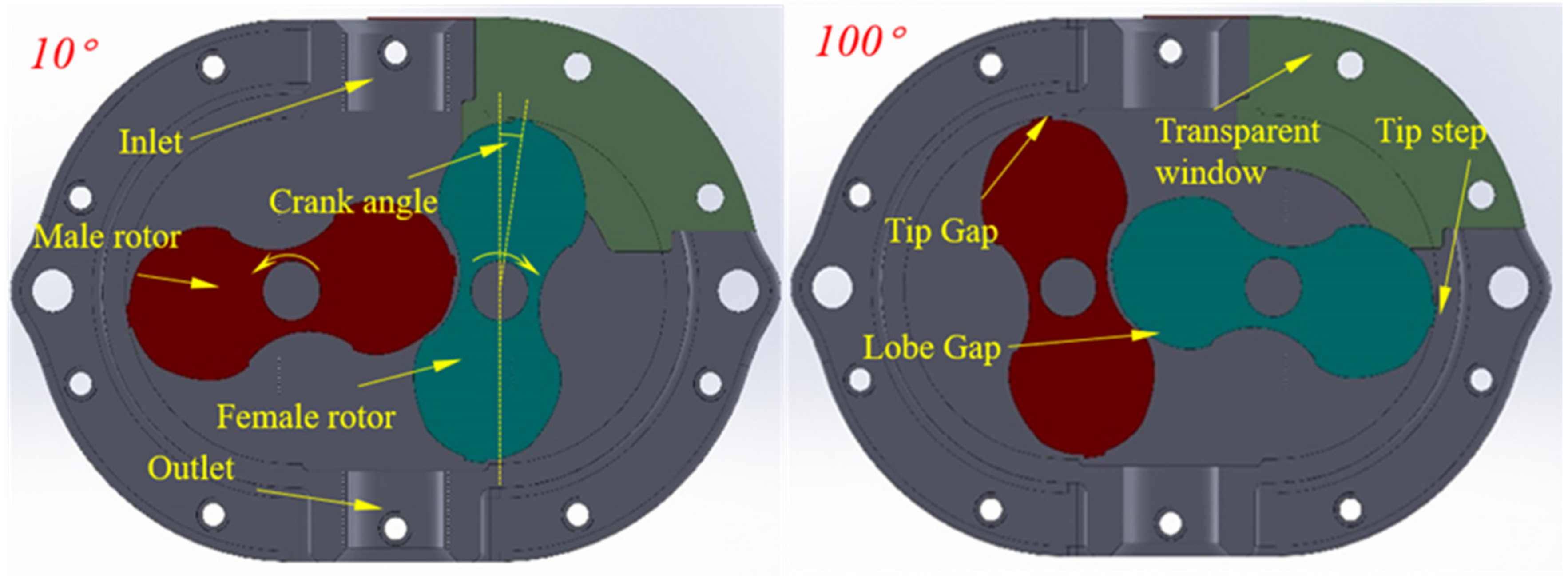
4. Analysis of the Tip Leakage Flow
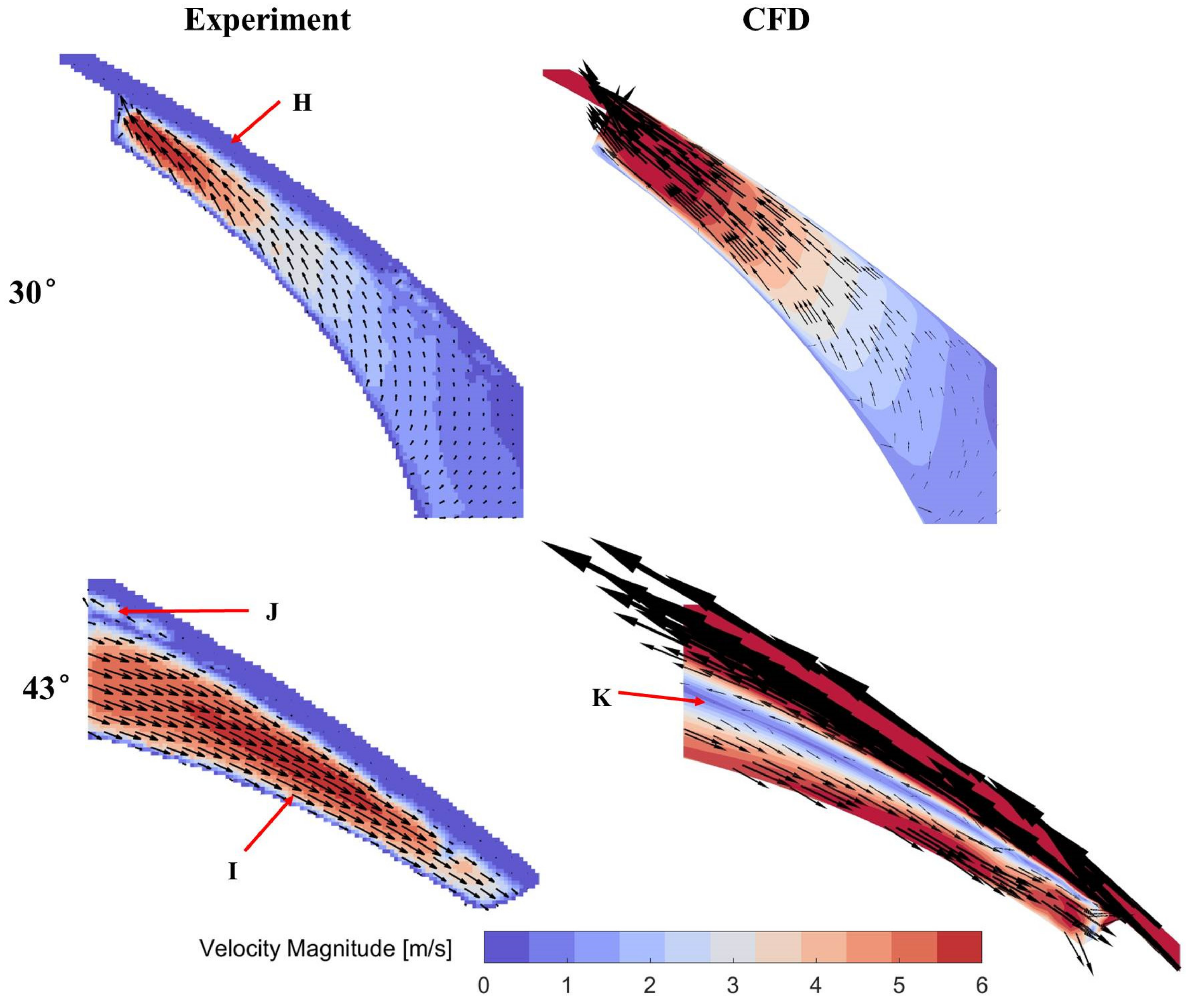
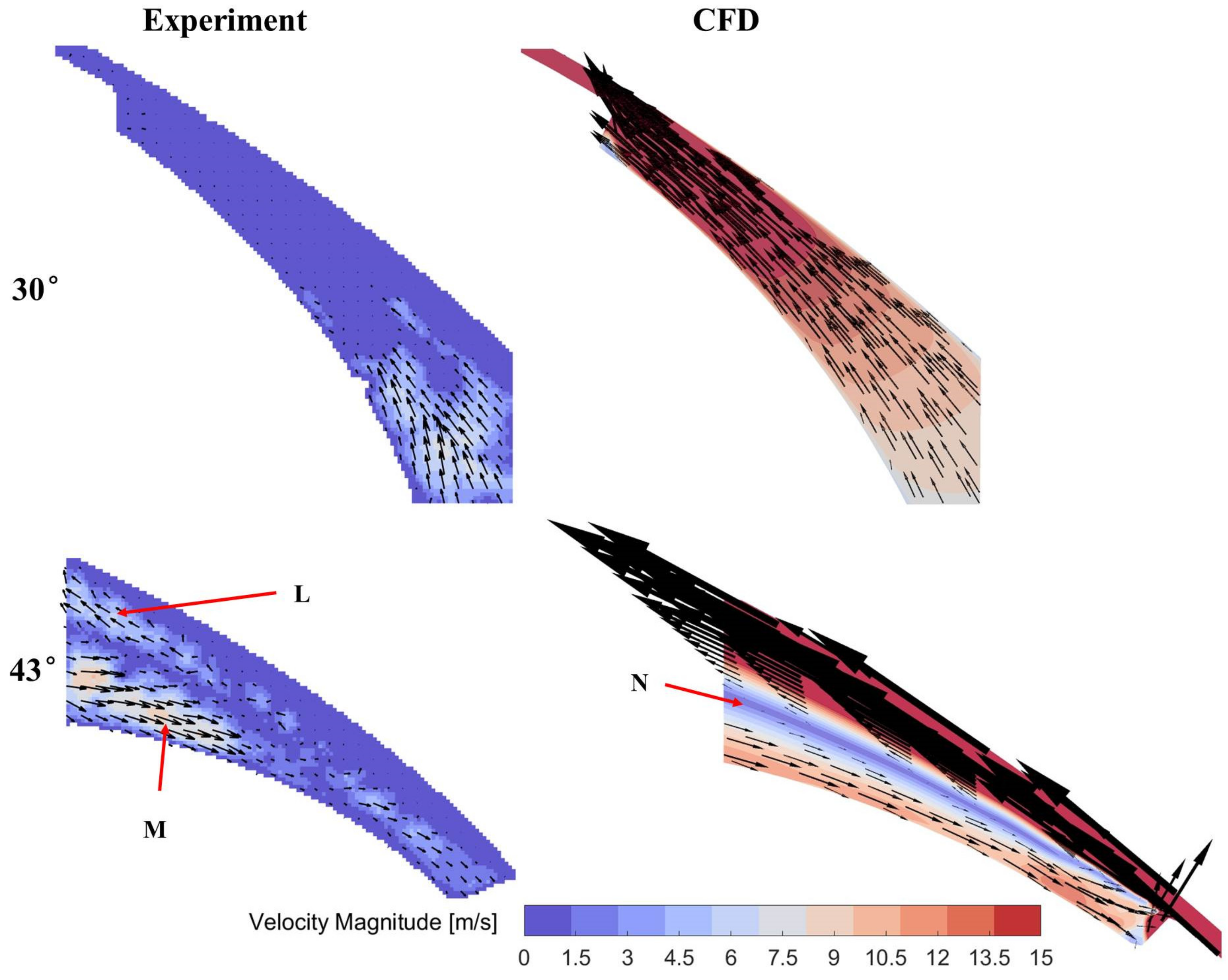
4.1. Comparison between the Experimental and Simulation Results
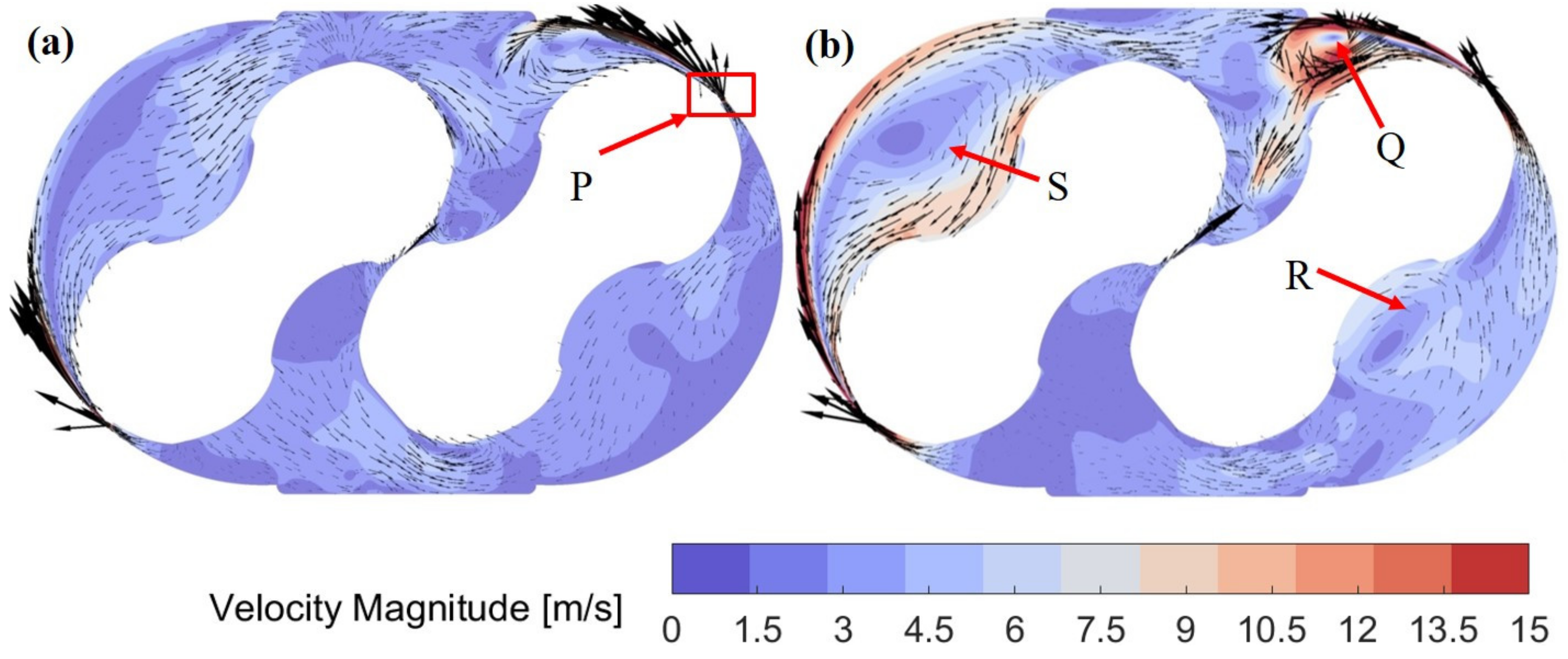
4.2. Analysis of the Overall Flow Field
5. Discussion
6. Conclusions
- (1)
- A series of factors deteriorating the results of the PIV test were observed as follows: the surface flaws of the transparent window, the reflection of the surface, the jitter in the phase-locking due to uncertainties in the transmission of the synchronized gear, the accumulation of the liquid particles and the pressure fluctuations. These factors caused an increase in erroneous vectors and limited the quality of measured velocity fields. The solutions to these problems were discussed and will be implemented in future measurements in our lab.
- (2)
- The CFD flow field agrees with experimental results in the flow pattern and velocity magnitude at certain areas but overestimates the leakage flow velocity.
- (3)
- The vortex induced by the leakage flow through the tip gap results in the separation of high and low-velocity areas in the downstream region of the leakage flow. The main flow field changes significantly with the increased pressure ratio.
- (4)
- The leakage flow in the tip gap is laminar under the pressure ratios in this paper. The main flow losses occur upstream at the entrance of the tip gap. The total pressure changes moderately along the gap since the leakage flow does not diffuse much. The step at the rotor tip can be redesigned to increase pressure losses and reduce the leakage flow.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fujiwara, M.; Mori, H.; Suwama, T. Prediction of the Oil Free Screw Compressor Performance Using Digital. In Proceedings of the International Compressor Engineering Conference 1974, Purdue University, West Lafayette, IN, USA, 10–12 July 1974; p. 119. [Google Scholar]
- Stošić, N.; Smith, I.K.; Kovačević, A. Screw Compressors: Mathematical Modelling and Performance Calculation; Springer: Berlin, Germany, 2005. [Google Scholar]
- Kovačević, A. Boundary adaptation in grid generation for CFD analysis of screw compressors. Int. J. Numer. Methods Eng. 2005, 64, 401–426. [Google Scholar] [CrossRef]
- Kovačević, A.; Stošić, N.; Smith, I.K. Screw Compressors—Three-Dimensional Computational Fluid Dynamics and Solid Fluid Interaction; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Sun, S.H.; Wang, X.W.; Guo, P.C.; Wu, K.; Luo, X.Q.; Liu, G.B. Numerical analysis of the transient leakage flow in axial clearance of a scroll refrigeration compressor. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2019. [CrossRef]
- Chen, Y.; Halm, N.P.; Groll, E.A.; Braun, J.E. Mathematical modeling of scroll compressors—Part I: Compression process modeling. Int. J. Refrig. 2002, 25, 731–750. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimizu, T. Leakage losses with a rolling piston type rotary compressor. I. Radical clearance on the rolling piston. Int. J. Refrig. 1985, 8, 75–84. [Google Scholar] [CrossRef]
- Ucer, A.S.; Celik, I. Analysis of Flow through Roots Blower Systems. In Proceedings of the International Compressor Engineering Conference 1980, Purdue University, West Lafayette, IN, USA, 23–25 July 1980; p. 319. [Google Scholar]
- Sun, S.; Kovačević, A.; Brücker, C.; Leto, A.; Singh, G.; Ghavami, M. Numerical and Experimental Analysis of Transient Flow in Roots Blower. IOP Conf. Ser. Mater. Sci. Eng. 2018, 425, 012024. [Google Scholar] [CrossRef]
- Rane, S. Grid Generation and CFD Analysis of Variable Geometry Screw Machines. Ph.D. Thesis, City University of London, London, UK, 2015. [Google Scholar]
- Rane, S.; Kovačević, A. Algebraic generation of single domain computational grid for twin screw machines Part I—Implementation. Adv. Eng. Softw. 2017, 107, 38–50. [Google Scholar] [CrossRef]
- Kovačević, A.; Rane, S. Algebraic generation of single domain computational grid for twin screw machines Part II—Validation. Adv. Eng. Softw. 2017, 109, 31–43. [Google Scholar] [CrossRef]
- Casari, N.; Pinelli, M.; Suman, A.; Kovačević, A.; Rane, S.R.; Ziviani, D. Full 3D Numerical Analysis of A Roots Blower with Open-Source Software. In Proceedings of the International Compressor Engineering Conference 2018, Purdue University, West Lafayette, IN, USA, 9–12 July 2018; p. 2620. [Google Scholar]
- Liu, X.M.; Lu, J.; Gao, R.H.; Xi, G. Numerical Investigation of the Aerodynamic Performance Affected by Spiral Inlet and Outlet in a Positive Displacement Blower. Chin. J. Mech. Eng. 2013, 26, 957–966. [Google Scholar] [CrossRef]
- Liu, X.M.; Lu, J. Unsteady Flow Simulations in a Three-lobe Positive Displacement Blower. Chin. J. Mech. Eng. 2014, 27, 575–583. [Google Scholar] [CrossRef]
- Sun, S.K.; Zhao, B.; Jia, X.H.; Peng, X.Y. Three-dimensional numerical simulation and experimental validation of flows in working chambers and inlet/outlet pockets of Roots pump. Vacuum 2017, 137, 195–204. [Google Scholar] [CrossRef]
- Sun, S.K.; Jia, X.H.; Xing, L.F.; Peng, X.Y. Numerical study and experimental validation of a Roots blower with backflow design. Eng. Appl. Comput. Fluid Mech. 2018, 12, 282–292. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, Z. Numerical study of a positive displacement blower. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 2309–2316. [Google Scholar] [CrossRef]
- Xing, L.; He, Y.; Wen, J.; Peng, X. Three-Dimensional CFD Modelling of a Roots Blower for Hydrogen Recirculation in Fuel Cell System. In Proceedings of the International Compressor Engineering Conference 2018, Purdue University, West Lafayette, IN, USA, 9–12 July 2018; p. 2562. [Google Scholar]
- Joshi, A.; Blekhman, D.; Felske, J.; Lordi, J.; Mollendorf, J. Clearance Analysis and Leakage Flow CFD Model of a Two-Lobe Multi-Recompression Heater. Int. J. Rotating Mach. 2006, 2006, 1–10. [Google Scholar] [CrossRef]
- Kovačević, A.; Rane, S.; Stosic, N.; Jiang, Y.; Lowry, S.; Furmanczyk, M. Influence of Approaches in CFD Solvers on Performance Prediction in Screw Compressors. In Proceedings of the International Compressor Engineering Conference 2014, Purdue University, West Lafayette, IN, USA, 14–17 July 2014; p. 2252. [Google Scholar]
- Ronald, S. Experimental Investigation of Gas Flows in Screw Machines. Ph.D. Thesis, University of Dortmund, Dortmund, Germany, 2002. [Google Scholar]
- Guerrato, D.; Nouri, J.M.; Stosic, N.; Constantine, A.; Smith, I.K. Flow measurements in the discharge port of a screw compressor. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2007, 222, 201–210. [Google Scholar] [CrossRef]
- Kovačević, A.; Arjeneh, M.; Rane, S.; Stosic, N.; Gavaises, M. Flow Visualization at Suction of a Twin Screw Compressor. In Proceedings of the International Screw Compressor Conference 2014, Dortmund, Germany, 23–24 September 2014; pp. 309–318. [Google Scholar]
- Sun, S.H.; Kovačević, A.; Bruecker, C.; Leto, A.; Ghavami, G.; Rane, S.; Singh, G. Experimental Investigation of the Transient Flow in Roots Blower. In Proceedings of the International Compressor Engineering Conference 2018, Purdue University, Chicago, IL, USA, 9–12 July 2018; p. 2615. [Google Scholar]
- Singh, G.; Sun, S.; Kovacevic, A.; Li, Q.; Bruecker, C. Transient flow analysis in a Roots blower: Experimental and numerical investigations. Mech. Syst. Signal Process. 2019, 134, 106305. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS CFX Modeling Guide, Release 18.0; Ansys Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Coleman, H.; Stern, F. Uncertainties and CFD code validation. J. Fluid Eng. 1997, 119, 795–803. [Google Scholar] [CrossRef]
- PDM Analysis Ltd. SCORGTM Help Manual, V5.7; PDM Analysis Ltd.: London, UK, 2019. [Google Scholar]




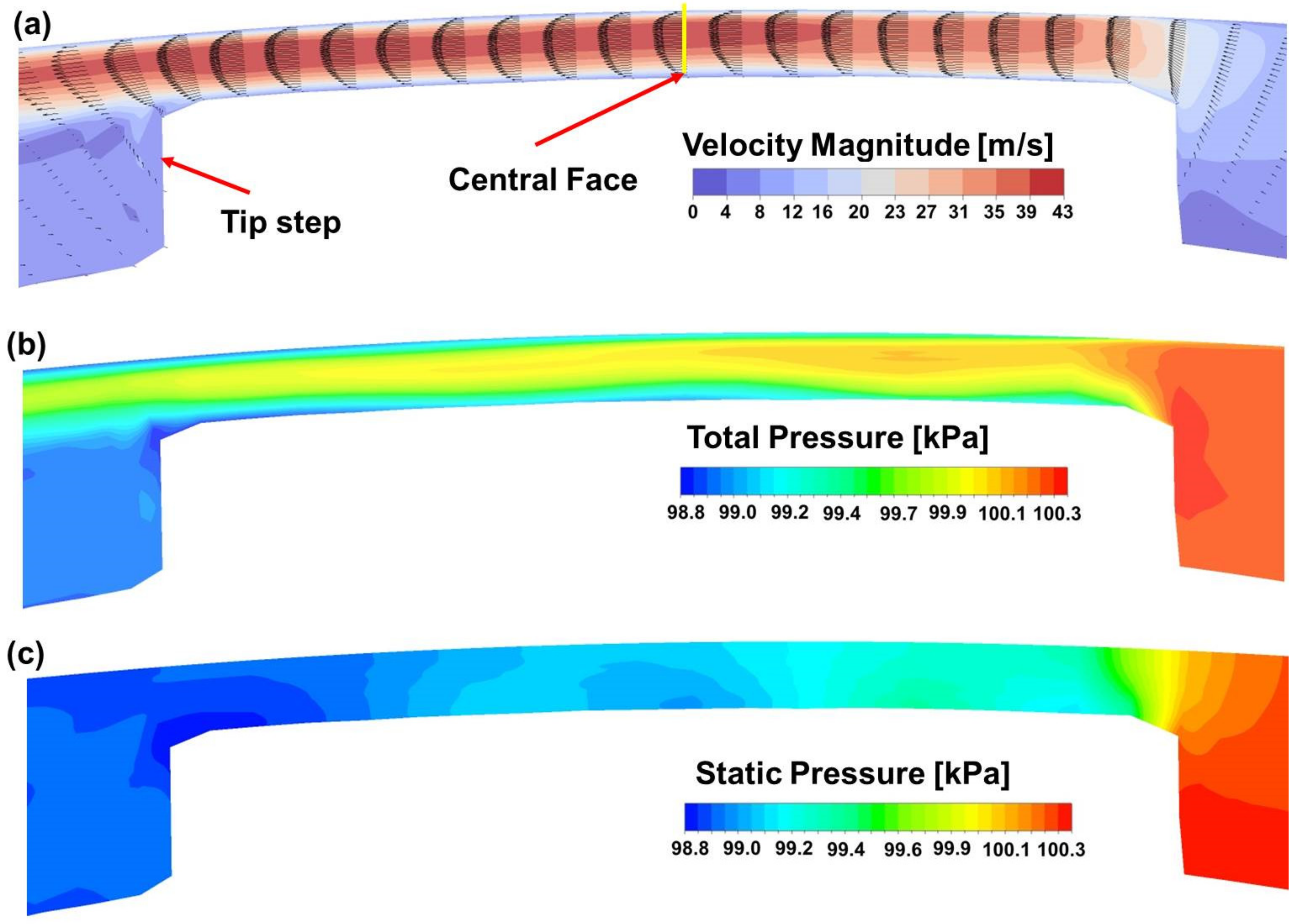
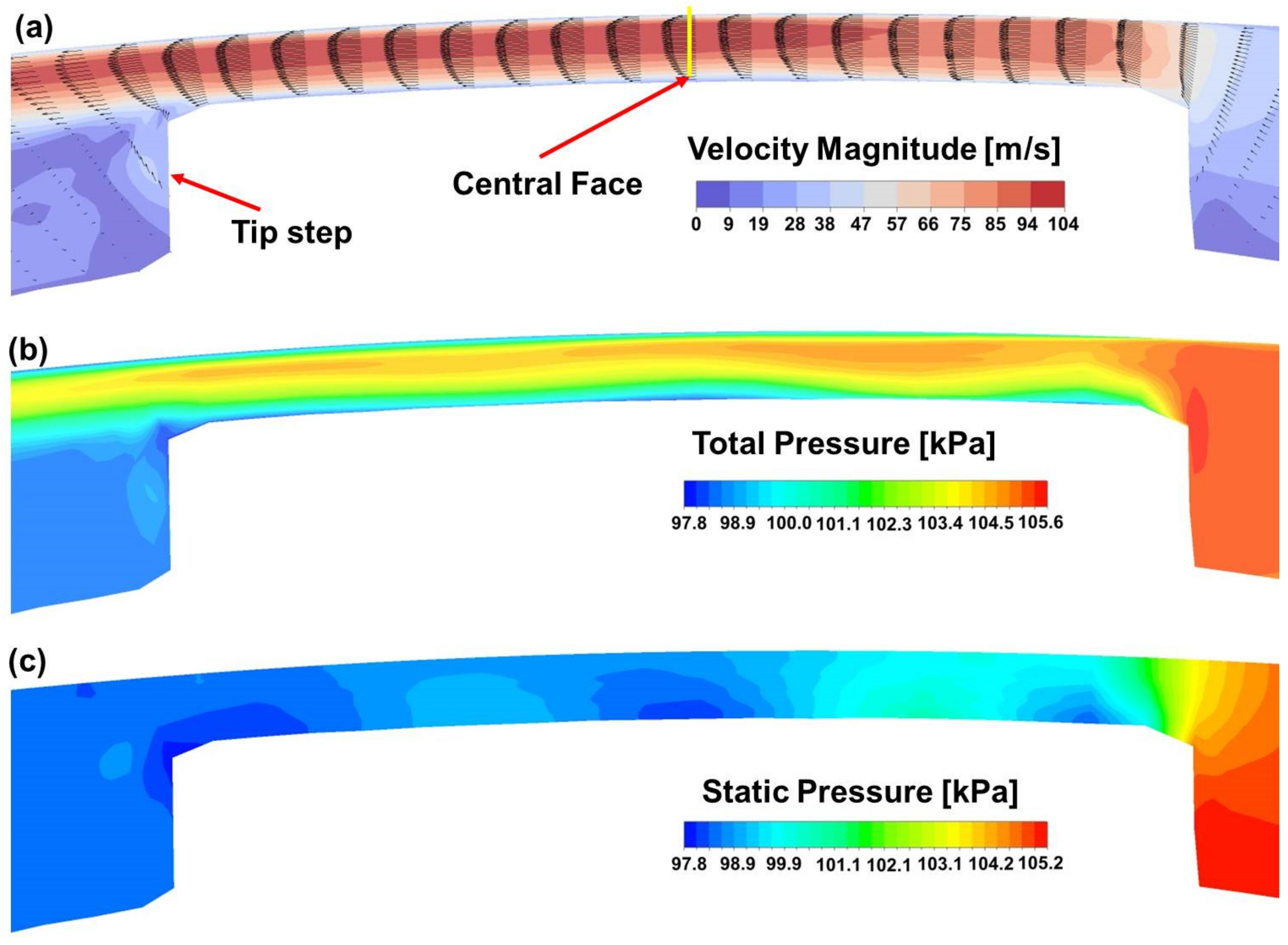
| Items | Specification | Items | Specification |
|---|---|---|---|
| Diameter of the rotor (mm) | 101.3 | Tip gap (mm) | 0.4 |
| Axis distance (mm) | 63.12 | Lobe gap (mm) | 0.17 |
| Rotor length (mm) | 50.5 | Axial gap (mm) | 0.15 |
| Displacement volume (L/rev) | 0.4618 | Width of tip step (mm) | 6.4 |
| Inlet Pressure (Bar) | Inlet Temperature (K) | Outlet Pressure (Bar) | Outlet Temperature (K) | Pressure Ratio (-) | Speed (rpm) | Mass Flow Rate (g/s) |
|---|---|---|---|---|---|---|
| 0.990 | 300.1 | 1.005 | 301.2 | 1.015 | 464 | 1.71 |
| 0.990 | 300.6 | 1.061 | 306.9 | 1.072 | 464 | 1.18 |
| Setting | Specification | Setting | Specification |
|---|---|---|---|
| Advection scheme | High-resolution | Turbulence numeric | 1st order |
| Transient scheme | 2nd order backward Euler | Wall model | No-slip with adiabatic walls |
| Turbulence model | SST k-w with automatic wall functions | Iteration per time step | 20 |
| Heat transfer model | Total energy including viscous terms | Inlet/Outlet condition | Opening with static pressure & temperature |
| Working fluid | Air as Ideal gas | Inlet turbulence intensity | 5% |
| Domain initialization | Standard atmospheric conditions | Convergence criteria | RMS 1E-4 |
| Time step at 464 rpm | 3.592 × 10−4 |
| Level | Circumference | Radial | Angular | Axial | Number of Grid Cells in Rotors |
|---|---|---|---|---|---|
| Grid-1 | 200 | 15 | 180 | 18 | 216,000 |
| Grid-2 | 285 | 21 | 180 | 25 | 600,600 |
| Grid-3 | 400 | 30 | 180 | 35 | 1,680,000 |
| Grid-4 | 500 | 38 | 180 | 44 | 3,344,000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Singh, G.; Kovacevic, A.; Bruecker, C. Experimental and Numerical Investigation of Tip Leakage Flows in a Roots Blower. Designs 2020, 4, 3. https://doi.org/10.3390/designs4010003
Sun S, Singh G, Kovacevic A, Bruecker C. Experimental and Numerical Investigation of Tip Leakage Flows in a Roots Blower. Designs. 2020; 4(1):3. https://doi.org/10.3390/designs4010003
Chicago/Turabian StyleSun, Shuaihui, Gursharanjit Singh, Ahmed Kovacevic, and Christoph Bruecker. 2020. "Experimental and Numerical Investigation of Tip Leakage Flows in a Roots Blower" Designs 4, no. 1: 3. https://doi.org/10.3390/designs4010003
APA StyleSun, S., Singh, G., Kovacevic, A., & Bruecker, C. (2020). Experimental and Numerical Investigation of Tip Leakage Flows in a Roots Blower. Designs, 4(1), 3. https://doi.org/10.3390/designs4010003






