CFD Simulations of Single- and Twin-Screw Machines with OpenFOAM
Abstract
1. Introduction
2. Mesh Moving Techinques in OpenFOAM and Analysis of Single—Screw Expanders
2.1. Creating the Mesh
2.2. Moving the Mesh—Numerical Strategies Available
2.2.1. Rigid Mesh Motion—IBM
2.2.2. Rigid Mesh Motion—Overset
2.2.3. Mesh Deformation—Mesh Adaption Dynamic Remeshing
2.2.4. Mesh Deformation—Key Frame Remeshing
3. Custom Predefined Mesh Generation—Twin Screw Machines
3.1. Creating and Moving The Mesh
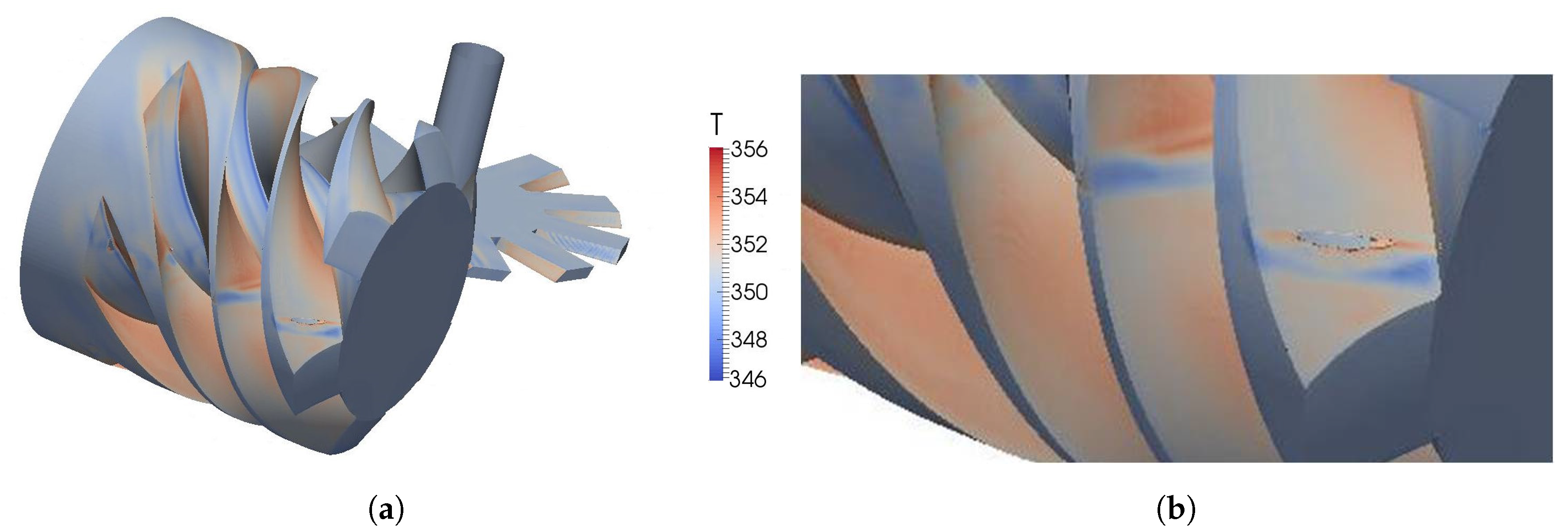
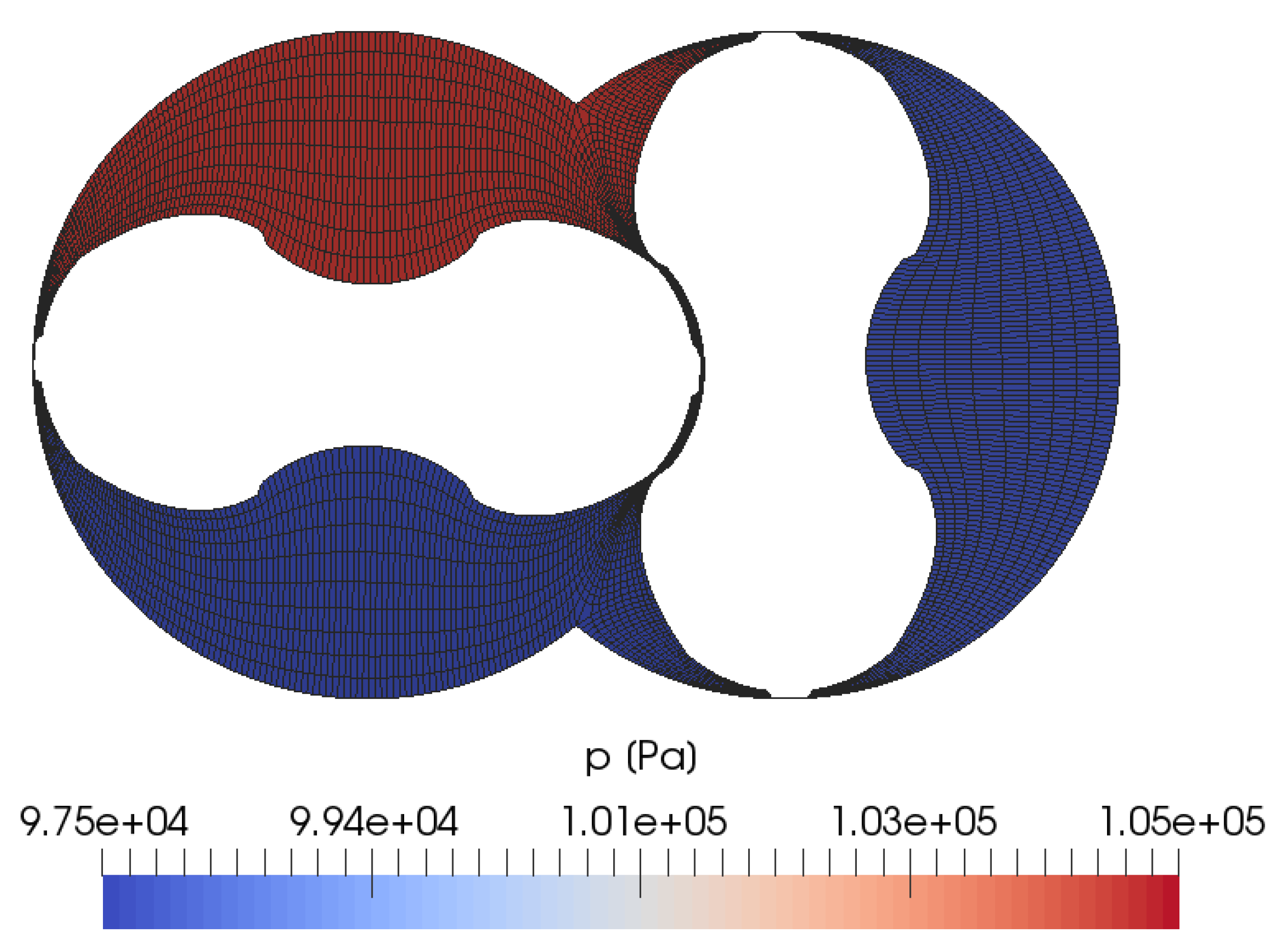
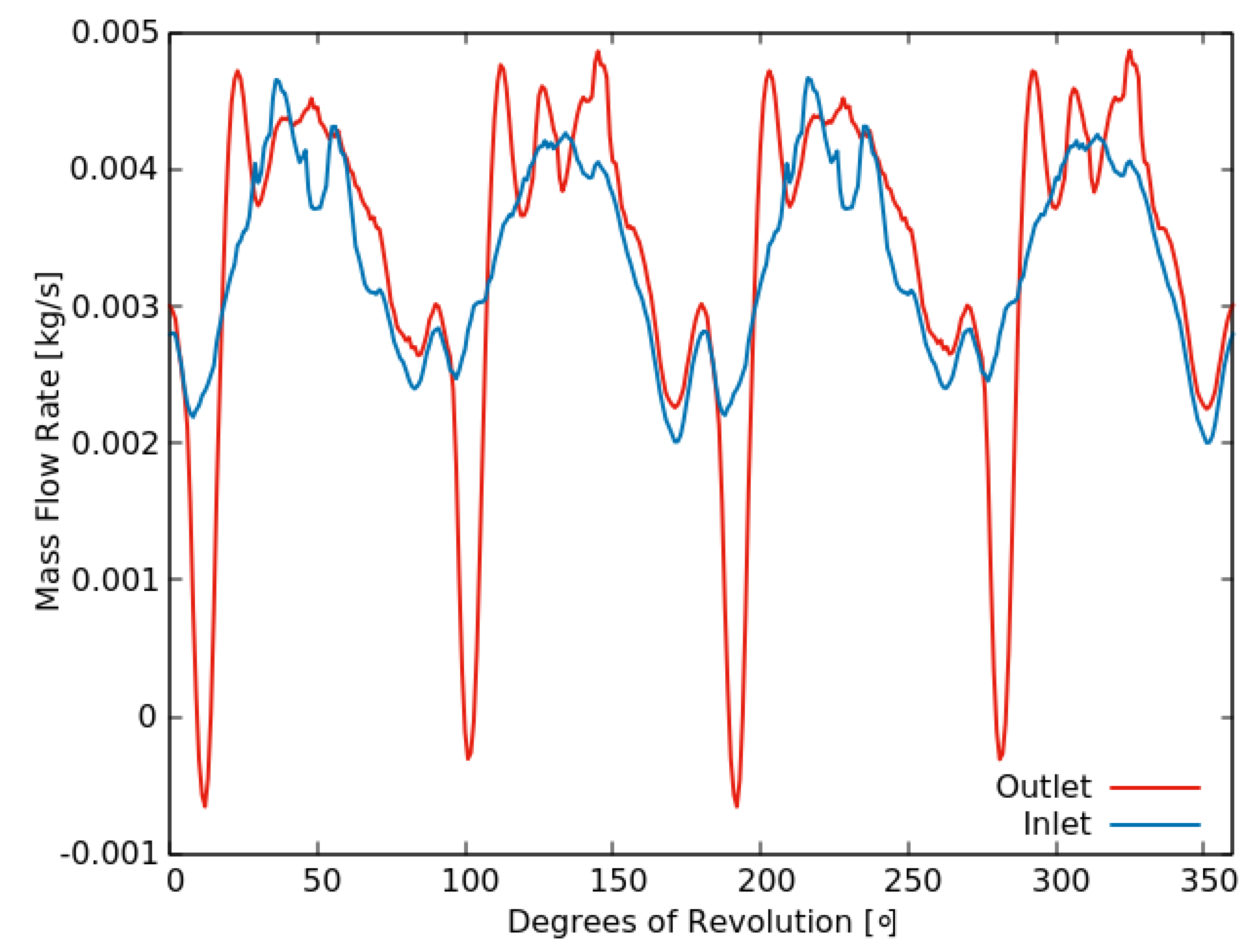
3.2. Applications: Twin-Screw and Roots Blower
3.3. OpenFOAM Thermophysical Models
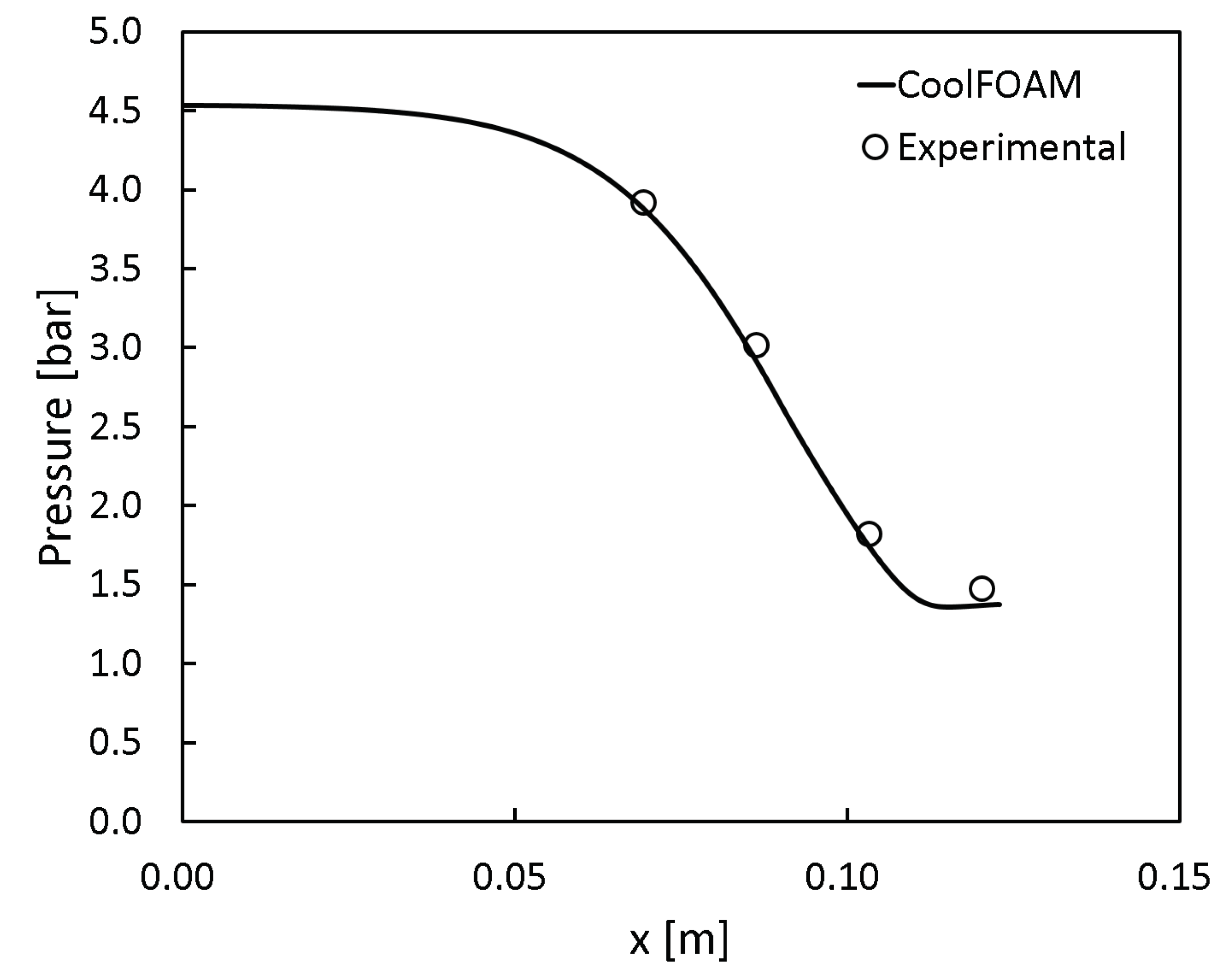
3.4. CoolProp Thermophysical Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Macchi, E.; Astolfi, M. Organic Rankine Cycle (ORC) Power Systems, Technologies and Applications; Woodhead Publishing Series in Energy; Woodhead Publishing: Duxford, UK, 2016; Volume 107. [Google Scholar]
- Montenegro, G.; Della Torre, A.; Onorati, A.; Broggi, D.; Schlager, G.; Benatzky, C. CFD Simulation of a Sliding Vane Expander Operating inside a Small Scale ORC for Low Temperature Waste Heat Recovery; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2014. [Google Scholar]
- Kovacevic, A.; Stosic, N.; Smith, I. Screw Compressors: Three Dimensional Computational Fluid Dynamics and Solid Fluid Interaction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 46. [Google Scholar]
- Mujic, E.; Kovacevic, A.; Stosic, N.; Smith, I. The influence of port shape on gas pulsations in a screw compressor discharge chamber. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2008, 222, 211–223. [Google Scholar] [CrossRef]
- Tang, H.; Wu, H.; Wang, X.; Xing, Z. Performance study of a twin-screw expander used in a geothermal organic Rankine cycle power generator. Energy 2015, 90, 631–642. [Google Scholar] [CrossRef]
- Ziviani, D.; Groll, E.A.; Braun, J.E.; De Paepe, M. Review and update on the geometry modeling of single-screw machines with emphasis on expanders. Int. J. Refrig. 2018, 92, 10–26. [Google Scholar] [CrossRef]
- Stosic, N.; Smith, I.K.; Kovacevic, A. A twin screw combined compressor and expander for CO2 refrigeration systems. In Proceedings of the International Compressor Engineering Conference, West Lafayette, Indiana, 16–19 July 2002. [Google Scholar]
- Lemort, V.; Guillaume, L.; Legros, A.; Declaye, S.; Quoilin, S. A comparison of piston, screw and scroll expanders for small scale Rankine cycle systems. In Proceedings of the 3rd International Conference on Microgeneration and Related Technologies, Napoli, Italy, 15–17 April 2013. [Google Scholar]
- Montenegro, G.; Della Torre, A.; Onorati, A.; Broggi, D.; Schlager, G.; Benatzky, C. Directive 2005/32/EC Establishing a Framework for the Setting of Ecodesign Requirements for Energy-Using Products and Amending Council Directive 92/42/EEC and Directives 96/57/EC and 2000/55/EC. OJ, 2005; L191/29; Technical Report; European Parliament: Brussels, Belgium, 2009. [Google Scholar]
- Kennedy, S.; Wilson, M.; Rane, S. Combined Numerical and Analytical Analysis of an Oil-Free Twin Screw Compressor; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 232, p. 012080. [Google Scholar]
- Sun, S.; Kovacevic, A.; Bruecker, C.; Leto, A.; Singh, G.; Ghavami, M. Numerical and Experimental Analysis of Transient Flow in Roots Blower; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 425, p. 012024. [Google Scholar]
- Casari, N.; Pinelli, M.; Suman, A.; Kovacevic, A.; Rane, S.; Ziviani, D. Full 3D Numerical Analysis of a Twin Screw Compressor by Employing Open-Source Software; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 425, p. 012017. [Google Scholar]
- Randi, S.; Suman, A.; Casari, N.; Pinelli, M.; Ziviani, D. Numerical Analysis of Oil Injection Effects in a Single Screw Expander; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 425, p. 012001. [Google Scholar]
- Suman, A.; Ziviani, D.; Gabrielloni, J.; Pinelli, M.; De Paepe, M.; Van Den Broek, M. Different Numerical Approaches for the Analysis of a Single Screw Expander. Energy Procedia 2016, 101, 750–757. [Google Scholar] [CrossRef]
- Morini, M.; Pavan, C.; Pinelli, M.; Romito, E.; Suman, A. Analysis of a scroll machine for micro ORC applications by means of a RE/CFD methodology. Appl. Therm. Eng. 2015, 80, 132–140. [Google Scholar] [CrossRef]
- Chang, J.C.; Chang, C.W.; Hung, T.C.; Lin, J.R.; Huang, K.C. Experimental study and CFD approach for scroll type expander used in low-temperature organic Rankine cycle. Appl. Therm. Eng. 2014, 73, 1444–1452. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Tillner-Roth, R. A Helmholtz energy equation of state for calculating the thermodynamic properties of fluid mixtures. Fluid Phase Equilibria 1999, 165, 1–21. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J.N. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Aungier, R. A fast, accurate real gas equation of state for fluid dynamic analysis applications. Trans.-Am. Soc. Mech. Eng. J. Fluids Eng. 1995, 117, 277. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed]
- snappyHexMesh Algorithm. Available online: https://cfd.direct/openfoam/user-guide/v6-snappyhexmesh/ (accessed on 1 October 2019).
- Juretić, F. cfMesh User Guide; Creative Fields: Zagreb, Croatia, 2015. [Google Scholar]
- Bergeaud, V.; Lefebvre, V. SALOME. A software integration platform for multi-physics, pre-processing and visualisation. In Proceedings of the Joint International Conference on Supercomputing in Nuclear Applications and Monte Carlo, Tokyo, Japan, 17–21 October 2010. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh Reference Manual; Free Software Foundation Inc.: Boston, MA, USA, 2003. [Google Scholar]
- Ferziger, J.H.; Perić, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; Volume 3. [Google Scholar]
- Peskin, C.S. Flow Patterns around Heart Valves: A Digital Computer Method for Solving the Equations of Motion. Ph.D. Thesis, Yeshiva University, New York, NY, USA, 1972. [Google Scholar]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Jasak, H.; Tukovic, Z. Immersed Boundary Method in FOAM: Theory, Implementation and Use. Available online: http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2015/H-rvojeJasak/ImmersedBoundary.pdf (accessed on 1 January 2015).
- Benek, J.; Steger, J.; Dougherty, F.C. A flexible grid embedding technique with application to the Euler equations. In Proceedings of the 6th Computational Fluid Dynamics Conference Danvers, Danvers, MA, USA, 13–15 July 1983; p. 1944. [Google Scholar]
- Benek, J.; Buning, P.; Steger, J. A 3-D chimera grid embedding technique. In Proceedings of the 7th Computational Physics Conference, Cincinnati, OH, USA, 15–17 July 1985; p. 1523. [Google Scholar]
- Menon, S.; Mooney, K. Using the dynamicTopoFvMesh class in OpenFOAM. Available online: www.personal.psu.edu/dab143/OFW6/Training/mooney_slides.pdf (accessed on 30 January 2020).
- Brewer, M.L.; Diachin, L.F.; Knupp, P.M.; Leurent, T.; Melander, D.J. The Mesquite Mesh Quality Improvement Toolkit. In Proceedings of the 12th International Meshing Roundtable, IMR, Santa Fe, NM, USA, 14–17 September 2003. [Google Scholar]
- Casari, N.; Suman, A.; Ziviani, D.; Van Den Broek, M.; De Paepe, M.; Pinelli, M. Computational Models for the Analysis of positive displacement machines: Real Gas and Dynamic Mesh. Energy Procedia 2017, 129, 411–418. [Google Scholar] [CrossRef]
- SCORG V5.7 Manual; PDM Analysis Ltd.: Barnet, UK, 2019; Available online: http://pdmanalysis.co.uk/online-documentation/online-documentation/ (accessed on 7 September 2019).
- Farrell, P.; Maddison, J. Conservative interpolation between volume meshes by local Galerkin projection. Comput. Methods Appl. Mech. Eng. 2011, 200, 89–100. [Google Scholar] [CrossRef]
- Singh, G.; Sun, S.; Kovacevic, A.; Li, Q.; Bruecker, C. Transient flow analysis in a Roots blower: Experimental and numerical investigations. Mech. Syst. Signal Process. 2019, 134, 106305. [Google Scholar] [CrossRef]
- Kunz, O.; Wagner, W. The GERG-2008 Wide-Range Equation of State for Natural Gases and Other Mixtures: An Expansion of GERG-2004. J. Chem. Eng. Data 2012, 57, 3032–3091. [Google Scholar] [CrossRef]
- Valderrama, J. The state of the cubic equations of state. Ind. Eng. Chem. Res. 2003, 42, 1603–1618. [Google Scholar] [CrossRef]
- Gernert, J.; Jäger, A.; Span, R. Calculation of phase equilibria for multi-component mixtures using highly accurate Helmholtz energy equations of state. Fluid Phase Equilibria 2014, 375, 209–218. [Google Scholar] [CrossRef]
- Lazhar Abdelli, J.D.; Vierendeels, J. CFD Analysis of an Expansion Process Using Different Real Gas Models. Master’s Thesis, Ghent University, Ghent, Belgium, 2015. [Google Scholar]
- Allison, T. JANAF Thermochemical Tables, NIST Standard Reference Database 13; NIST: Gaithersburg, MD, USA, 1996. [CrossRef]
- Thorade, M.; Saadat, A. Partial derivatives of thermodynamic state properties for dynamic simulation. Environ. Earth Sci. 2013, 70, 3497–3503. [Google Scholar] [CrossRef]
- Span, R. Multiparameter Equations of State; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Lemmon, E.; Jacobsen, R.; Penoncello, S.; Friend, D. Thermodynamic properties of air and mixtures of nitrogen, argon, and oxygen from 60 to 2000 K at pressures to 2000 MPa. J. Phys. Chem. Ref. Data 2000, 29, 331–362. [Google Scholar] [CrossRef]
- Sengers, J. Transport properties of fluids near critical points. Int. J. Thermophys. 1985, 6, 203–232. [Google Scholar] [CrossRef]
- Huber, M.L.; Perkins, R.A.; Laesecke, A.; Friend, D.G.; Sengers, J.V.; Assael, M.J.; Metaxa, I.N.; Vogel, E.; Mareš, R.; Miyagawa, K. New International Formulation for the Viscosity of H2O. J. Phys. Chem. Ref. Data 2009, 38, 101–125. [Google Scholar] [CrossRef]
- Bock, S.; Bich, E.; Vogel, E.; Dickinson, A.S.; Vesovic, V. Calculation of the transport properties of carbon dioxide. III. Volume viscosity, depolarized Rayleigh scattering, and nuclear spin relaxation. J. Chem. Phys. 2004, 121, 4117–4122. [Google Scholar] [CrossRef] [PubMed]
- Fadiga, E.; Casari, N.; Suman, A.; Pinelli, M. CoolFOAM: The CoolProp wrapper for OpenFOAM. Comput. Phys. Commun. 2019. [Google Scholar] [CrossRef]
- Spinelli, A.; Cammi, G.; Gallarini, S.; Zocca, M.; Cozzi, F.; Gaetani, P.; Dossena, V.; Guardone, A. Experimental evidence of non-ideal compressible effects in expanding flow of a high molecular complexity vapor. Exp. Fluids 2018, 59. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casari, N.; Fadiga, E.; Pinelli, M.; Suman, A.; Ziviani, D. CFD Simulations of Single- and Twin-Screw Machines with OpenFOAM. Designs 2020, 4, 2. https://doi.org/10.3390/designs4010002
Casari N, Fadiga E, Pinelli M, Suman A, Ziviani D. CFD Simulations of Single- and Twin-Screw Machines with OpenFOAM. Designs. 2020; 4(1):2. https://doi.org/10.3390/designs4010002
Chicago/Turabian StyleCasari, Nicola, Ettore Fadiga, Michele Pinelli, Alessio Suman, and Davide Ziviani. 2020. "CFD Simulations of Single- and Twin-Screw Machines with OpenFOAM" Designs 4, no. 1: 2. https://doi.org/10.3390/designs4010002
APA StyleCasari, N., Fadiga, E., Pinelli, M., Suman, A., & Ziviani, D. (2020). CFD Simulations of Single- and Twin-Screw Machines with OpenFOAM. Designs, 4(1), 2. https://doi.org/10.3390/designs4010002







