Reliability-Based Design Optimization of Load Sharing Systems Using SSI-Markov Models

Abstract

This paper presents a novel single loop approach to design the components of the load sharing systems by optimally allocating the failure probabilities to each component, thereby satisfying the overall system reliability requirement. The Reliability–Based Design Optimization (RBDO) of load sharing systems is computationally intensive due to the dynamic nature of component failure probabilities, since the failure of one component will vary the failure probabilities of other working components. Many RBDO methods have been successfully utilized to design individual components, however using these methods for handling system level reliability constraints is still a challenging task. This is because of a drop in accuracy and computational efficiency, especially when considering a load sharing system, where there is dependency in failure probabilities of components. The key idea is to integrate Stress–Strength Interference (SSI) theory with discrete (or) continuous time-discrete state Markov model for the reliability assessment of system, with the states being the condition of components (working/failed). This method takes advantage of the state transition probability matrix to represent the dynamic nature of the system performance. A numerical example of a simple load sharing system with two I-Beams is presented to illustrate and evaluate the performance of the proposed methodology.

1. Introduction

The RBDO of mechanical systems is an iterative process and involves two steps, one being optimization and the other being reliability assessment [1,2]. Over the years, several improvements have been proposed for the reliability analysis of different types of systems, with most of them strongly predicated on the assumption that failure of components in the system is independent to each other, i.e., the failure probability of components is considered to be constant throughout its operation [1,2,3,4]. However, the central concern is that, utilizing these methods to evaluate a load sharing system, where the failure probability of a component varies depending on the state of other components in the system, the results will not be accurate. In addition, few methods can handle both the system and component level reliability, with most of them devoid of handling repair rates of the system [1,5,6,7,8,9]. Traditional methods such as joint distribution approach, compound events, minimal cut sets, probability modeling or minimal path sets method are not efficient and intractable when the number of components increases [1,5,6,7]. Hence, the development of efficient and accurate RBDO framework for the system level design optimization, especially for the load sharing systems is essential but not an easy task.

For general cases of the Reliability Based Design (RBD), the SSI theory plays a major role in formulating the system reliability model [10,11,12,13]. The reason that SSI theory is widely used to model the system reliability is that it is easy to represent the limit states of the components directly in terms of stress and strength. However, the conventional SSI theory results in a static reliability model and cannot be used for designing load sharing system, since it does not reflect the relationship between lifetime and failure probability [12,13,14]. The reliability function from the conventional SSI model is derived by evaluating the joint probability density function of stress (L) and strength (S) and is given by Equation (1).

$$R={\int }_0^{\infty }{f}_L\left(L\right){\int }_L^{\infty }{f}_S\left(S\right)dSdL$$

(1)

The SSI model shown in Equation (1) does not reflect the reliability of components with respect to frequency of load applications or time duration of applied load. The SSI model in Equation (1) is not time dependent and it is hard to represent the dynamic failure rate of components in order to design the load sharing system. Several single loop, decoupled loop and double loop strategies for the component and system level design have been proposed, and each of these strategies are selected based on the trade-off between computational efficiency and accuracy [1,5,6,7,10]. In the case of RBDO of load sharing systems, due to the presence of large number of probability constraints, the double loop strategy is not recommended, as it is computationally intensive [1,10] and the decoupled loop is not efficient since there is dependency in component failure probabilities. Therefore, in this paper, an efficient single loop method for the RBDO of load sharing systems considering the dynamic failure probabilities of components is developed.

Du et al. [10] developed Sequential Optimization and Reliability Analysis (SORA) decoupled loop formulation for the RBDO framework, which can handle any type of reliability analysis and optimization technique. Zhuang and Pan [11,12,13] used SORA decoupled loop approach to design individual component for a given reliability level. The shifting vector strategy worked well for designing individual components, but this method cannot handle system level reliability constraints. Cheng and Du [5] conducted feasibility study on evaluating system level reliability for the independent component failures, but incorporating their method into RBDO framework and suitability for load sharing systems was not discussed. McDonald and Mahadevan [1] developed a single loop strategy for designing systems with dependent and independent component failure modes. A correlation matrix between failure modes of components was established and used in the evaluation of reliability indices for each component. The evaluation of probability constraints for the multi-normal integrals is explained in [15]. However, this single loop method was computationally efficient and accurate to solve only simple numerical problems. In addition, the authors used a method where component reliability targets were arbitrarily assigned and updated by evaluating these discrete indices for system reliability. This process of arbitrarily assigning component reliabilities can save computational time but might not produce an optimum result. In addition, this method cannot be used for designing a load sharing system as the dependency in component failure rates has to be taken into consideration.

From all the above-mentioned theories, the most important task in RBDO of load sharing systems is the incorporation of time dependent failure rates of the components into the optimization framework. It has been proven that, in the case of reliability analysis of complex systems with dynamic failure rate, the Markov theory provides a good analytical solution for reliability assessment of the system as the state transition probabilities can be easily computed [16,17,18,19]. The use of Markov theory for reliability evaluation of engineering systems is explained in [20]. This method is efficient because it is easy to represent the dynamic failure rate of components in the system and obtain the transition probability matrix. Shah and Lamberson [17] proposed a generalized analytical methodology using Markov model for shared load system with repairable components, consisting of equations for both time dependent and steady state availability. The assumption of this method is that the failure rate of all the functioning components remains constant for each state, with each state representing the state of the system when a component breaks. Gao et al. [16] developed a reliability analysis methodology for dynamic load sharing model considering the strength degradation path dependence of components over time. A discrete time-discrete state Markov process theory was used to represent the probability of system in different states after specified number of load applications. However, this method has some limitations and might only be applicable to systems with only limited components and is not computationally efficient.

Overall, the system reliability modeling using Markov theory provides a way to represent the time dependent failure rate. However, it is hard to represent the failure rate of components in terms of design variables, which is the major requirement for RBDO. Hence, our hypothesis is that combining the SSI theory of mechanical components with Markov theory would give a good solution to aid the design problem and model the load sharing system [21,22]. The fundamental idea of this paper is to use Markov model to capture the dynamics of the system along with SSI theory to include the design variables and integrate into the RBDO single loop framework to design the system [21,22,23,24,25]. The paper is organized as follows: Section 2 presents the proposed single loop formulation using Discrete Time Markov Chain (DTMC) and Continuous Time Markov Chain (CTMC) framework, followed by a case study on designing I-Beam and results in Section 3 and Section 4, respectively. Before moving on to the Methodology section, some of the assumptions are stated in the next subsection.

Assumptions

• Only the brittle failures are considered in our approach. The plastic deformation phase of the system/components with respect to time is not considered in addition to other material related phenomena such as corrosion, change in material properties over time, etc. However, these changes could be incorporated into our RBDO formulation when the material’s deterioration rate is known. In such cases, the system cost will vary from the cost obtained from this approach since we add more information about the failure into the model. When the strength degrades with respect to time, the cost of the components increases in order to meet the reliability requirement.
• The system is assumed to have zero-simultaneous failure probability. This means that all the components in the system cannot fail simultaneously from a single load application.
• The loading duration on a component and load redistribution time after a component failure are assumed to be constant and occur in a very short interval of time. Hence, they are considered negligible.
• The component repair time is not considered, i.e., once a component fails, it is removed from operation and not put back into operation. However, the component repair process can be easily included in the transition probability/rate matrix in SSI-DTMC/CTMC to find the optimum design.

2. Materials and Methods

In practice, a Markov process is the generalization of a dynamic system in discrete or continuous time [19]. The Markov property is referred to as the memoryless property of a stochastic process, i.e., the conditional probability distribution of transferring to the future state depends only on the present state and does not depend on any of the previous states. A DTMC is a sequence of random numbers $X_1,X_2,\dots ,X_n$ such that the probability P($X_{n+1}=x_{n+1}|X_1=x_1,X_2=x_2,\dots ,X_n=x_n$) is the same as the probability P($X_{n+1}=x_{n+1}|X_n=x_n$). Note that all possible values of $X_i$ form the state space of the model. A CTMC is similar to DTMC with the difference being that CTMC has transition rate matrix instead of transition probability matrix defined on the finite state space. The elements of this transition rate matrix is non-negative since it denotes the rate of transition of the process from one state to another [19]. With that said, the integration of SSI with both discrete and continuous time Markov model for the design optimization of load sharing systems is presented in this section. Let the random variable “B” denote the bending stress applied on the component and “Y” the yield strength of the component. Using the conventional SSI theory, the probability of failure for each component $\left(P{f}_c\right)$ in terms of limit state function (where G(x) is the performance function with design variable (x) and G(x)<0 represents the component failure) can be written as given in Equations (2) and (3). In a simple way, Equations (2) and (3) represent that the failure occurs whenever the bending stress (B) exceeds the yield strength (Y) of the component.

$$P{f}_c=Probability(Y<B)$$

(2)

$$or,P{f}_c=Probability(G\left(x\right)<0)$$

(3)

A simple flowchart to demonstrate the proposed methodology to design the system for a given reliability target is shown in Figure 1. Note that the Genetic algorithm [26] is used to solve the problem but the framework can be modified to accommodate other optimization algorithms.

A single cycle consists of an optimization part and reliability assessment part. The optimization process begins with a set of random design points that are used to form a group of fittest individuals. The key to calculating the failure probability is to locate the most probable point in standard normal U-space. One of the methods to locate this point is using the reliability index approach (RIA), as given in [27]. In each cycle, a nested deterministic optimization problem given in Equations (4) and (5) is solved to find the most probable point in addition to the original problem.

Objective:

$$Minimize\left|\right|u\left|\right|$$

(4)

Subject to:

$$g_i\left(u_i\left({\beta }_i\right)\right)\ge 0,\forall i\in Ilimitstatefunctions$$

(5)

To solve the above problem, a recursive formula given in [27] is used. The idea is to construct the normalized gradients of the limit state function at that search point given in Equation (6), and locate the next search point on the limit state function using a vector pointing in a reverse direction from that of the gradient of the limit state function.

$$u_i\left({\beta }_i\right)=-{\alpha }_i{\beta }_i,\forall i\in Ilimitstatefunctions$$

(6)

where the value of alpha is given in Equation (7) [27].

$${\alpha }_i=\frac{\Delta g\left(u_i\right)}{\left|\right|g\left(u_i\right)\left|\right|},\forall i\in Ilimitstatefunctions$$

(7)

Note that the design point is converted to standard normal u-space and hence the initial value of $u_i$ is zero. The value of $\beta$ is termed as the reliability index and is used to generate the transition probability matrix. The initially value of $\beta$ is also taken to be zero at the start of the iteration and the update rule is as follows:

$${\beta }_i={\beta }_i+\frac{g\left(u_i\right)}{\Delta g\left(u_i\right){\alpha }_i},\forall i\in Ilimitstatefunctions$$

(8)

Once the $\beta$ values are updated, then the iteration of Equations (6)–(8) is continued until the value of $\beta$ converges. Upon convergence, the corresponding point $u_i$ is the optimum for the given optimization problem (Equations (4) and (5)). The values of $\beta$ vector can be converted to failure probabilities using the cdf of normal distribution. The obtained probability values are used to represent the state transition probabilities for each of the components in a system using the DTMC or CTMC, and assessed for system reliability requirement.

Each individual is a solution to the problem and a group of individuals are selected to form a Population set. An individual is characterized by a set of parameters known as genes and they are joined to form a chromosome, represented by a binary string. The cost function is used to determine the fitness of an individual, i.e., to measure the ability of the individual to compete with others. This process is continued by selecting the fittest individuals and passing to the next generation. Two pairs of individuals are selected based on their fitness scores, termed as parents. The next significant phase is to perform crossover. For each pair of parents to be mated, a crossover point is chosen at random from within the genes. Offspring are created by exchanging the genes of parents among themselves until the crossover point is reached. In certain new offspring formed, some of their genes can be subjected to a mutation with a low random probability, taken to be 0.1. This is done to maintain diversity within the population and prevent premature convergence. The next subsection details the proposed DTMC and CTMC load sharing model.

2.1. SSI–DTMC Load Sharing Model

In this section, the single loop formulation of SSI–discrete time Markov chain model for the design optimization of load sharing systems is presented. The methodology is similar for the most part to the regular single loop formulation [1,9,10,23,24,27] but the difference being that the transition probability values are added as constraint for the overall system reliability. The SSI–DTMC single loop formulation is given in Equations (6)–(9).

Objective:

$$Minimizef(d,{\mu }_X)$$

(9)

Subject to:

$$g_i(d,u_i\left({\beta }_i\right))\ge 0,\forall i\in Ilimitstatefunctions$$

(10)

$${\Sigma }_{j\in J}P{\left(n\right)}_j\ge R_{sys}$$

(11)

$$d^L\le d\le d^U$$

(12)

$${\mu }_X^L\le {\mu }_X\le {\mu }_X^U$$

(13)

The method starts with the initial design point, converting it to standard normal u-space to locate the most probable point and the reliability index $\beta$. The values of $\beta$ are used to estimate the failure probability using normal distribution cdf and generate the transition probability values $P_j$ in the transition probability matrix $\mathbf{Z}$ for each state combination of the system given in Equation (14), where $P_k$ denotes the probability of transition from one state to other. Let A and B denote two components in a system and the notation A’ the failed state of component A. For simplification purpose, it is assumed that the component B will survive the entire mission, i.e., only component A can fail anytime. At the start of the mission, both components will be working. There is a chance that both components will survive the load applied on them. Let the probability that both the components survive, i.e., the system starts at state AB and remains in state AB after the load application be P1. If component A breaks with probability P2, then the probability that the system goes from state AB to state A’B is also P2. If component A fails, the system has a chance to remain at the same state A’B and this probability is taken as P3. Similarly, if there are many components, all their corresponding values of the probability transition matrix are derived. Based on the stated assumption, there is no repair process considered in our case. Hence, the state transitions from A’B to state AB is zero.

$$\begin{array}{ccccc}& & & \begin{array}{cc}AB& A^{\prime }B\end{array}& \\ \mathbf{Z}=& \hfill \begin{array}{c}AB\\ A^{\prime }B\end{array}& \parallel & \begin{array}{cc}P1& P2\\ 0& P3\end{array}& \parallel \end{array}$$

(14)

The exponential of the transition probability matrix, i.e., $P_j$ with “n” steps, is obtained by solving Equation (15) using the procedure given in [20,28]. The complete discussion of the matrix decomposition approach for solving Equation (15) and obtaining the transition probability values from Moler and Van Loan [20,28] is provided in Section 2.3.

$$Z^n=M{D}^n{M}^{-1}\ast Z^0$$

(15)

Similar to the regular single loop formulation, the cycle starts with an initial guess for the design point. The deterministic optimization problem is solved by calculating the negative normalized gradient “${\alpha }_i$” value at current iteration point for each limit state function $g_{\left(i\right)}$ associated with the probability functions in the transition matrix. From there, a new design point is searched and the Most Probable Point (MPP) is located using the reliability index (${\beta }_i$) with the relation in Equation (6). Usually, the normal distribution assumption holds good to calculate the new design point and the value of ${\beta }_i$ is obtained from the normal distribution table. Now, the old design point is updated with the newly calculated design point and checked for convergence. If the new design point converges to the specified reliability target (Equation (11)), it is a candidate for optimal design, otherwise, the gradient (${\alpha }_i$) value is calculated for this new design point and the cycle continues. Some of the methods for evaluating the gradient “${\alpha }_i$” is summarized in [9]. In our system level single loop formulation, the limit state function is evaluated for all combinations of shared load, i.e., in the case of a system with two components sharing equal load, there will be limit states representing the shared load state as well as full loading state. This is because, when one component fails, the entire load gets redistributed over other component. The values in the transition probability matrix will aid in moving the design points beyond half loading limit state to accommodate for load sharing phenomenon but not beyond the full loading limit state since it will be trivial and costly to design each component to carry full system load and it deviates from the definition of load sharing. To illustrate, let the random variable “L” denote the stress applied on a component and “S” the yield strength of the same component. Using SSI theory, the probability of failure $\left(P{f}_c\right)$ in terms of limit state function can be written as Equations (16) and (17).

$$P{f}_c=Probability(S<L)$$

(16)

$$\mathrm{i}.\mathrm{e}.,P{f}_c=Probability(G\left(x\right)<0)$$

(17)

For a load sharing system with two components (e.g., $C_1$ and $C_2$), the transition probability ($P_1$) from both components in working state to one component in working state (e.g., $C_1$ fails) in terms of SSI using Equations (16) and (17), is given by Equation (18).

$$P_1=Probability[(S_1<\frac{L}{2})\cap (S_2\ge \frac{L}{2})]$$

(18)

Assuming an equal load sharing rule, $S_1$ and $\frac{L}{2}$ are the strength and shared load of component $C_1$, respectively; and $S_2$ and $\frac{L}{2}$ are the strength and shared load of component $C_2$, respectively. According to the law of conditional probability, the value of transition probability ($P_1$) is given in Equation (19).

$$P_1=Probability[(S_1<\frac{L}{2})|(S_2\ge \frac{L}{2})].Probability[(S_2\ge \frac{L}{2})]$$

(19)

Likewise, all the probability values in transitional probability matrix “Z” are calculated and updated, respectively. The First Order Reliability Method (FORM) [1,10,11] is used to evaluate the probability function in Equation (19). After the first iteration, the values in the state transition probability matrix gets updated and the n-step transition probabilities are found by Equation (15). The constraint on the $n^{th}$ step transition probabilities (given by Equation (11)) denotes the system reliability target after “n” steps. In this formulation, each value in the transition probability matrix has similar function to the reliability constraint defined in regular single loop formulation [9]. The Most Probable Point (MPP) $u_i\left({\beta }_i\right)$, should satisfy the limit state constraint for the respective values in the transition probability matrix. The values $P_j,\forall j\in J$ and $P_y,\forall y\in Y$, collectively represent all the state transition probabilities and are updated during each iteration. Note that the total sum is $P_j+P_y=1$. Hence, ${\Sigma }_{j\in J}{P}_j$, where J is the set of all possible combinations of component states that contribute to overall working condition of the system is nothing but the overall system reliability. In addition, the states in the set “Y” are absorbing states. The value of each step (n) in the above-mentioned SSI–DTMC formulation denotes the application of load. However, for some systems, the failure process can occur at any time instead of fixed time steps as in DTMC. For such cases, the integration of SSI theory with continuous time Markov chain formulation will provide a good solution, which is explained in the next section.

2.2. SSI–CTMC Load Sharing Model

The SSI–DTMC formulation is useful for systems with failures occurring at discrete load steps but some systems fail at any time interval rather than discrete steps as in SSI–DTMC formulation. For such system behavior, the SSI–CTMC load sharing model is used to model the state of the system. Different from the discrete time Markov model, the rate transition matrix is used to represent the failure rate ($\delta$) for each state combination. In some cases, if the number of loads acting on a component before failure is known, then the failure rate ($\delta$) is calculated as follows.

Let “$\lambda$” be the rate at which loading occurs. The relationship among the failure rate ($\delta$), the loading rate ($\lambda$) and the probability of transition at time “t” from state “i” $\left(P_i\right)$ is given in Equations (20) and (21) [18].

$$\delta \left(t\right)=\lambda \left(t\right).Probability(S<L)$$

(20)

$$\mathrm{i}.\mathrm{e}.,\delta \left(t\right)=\lambda \left(t\right).Probability\left(G\right(x)<0)$$

(21)

For a load sharing system with two components $C_1$ and $C_2$, the transition rate at time “t” ($\delta \left(t\right)$) from both components in working state to one component working (e.g., $C_1$ fails) in terms of SSI is given in Equation (22).

$$\delta \left(t\right)=\lambda \left(t\right)\times Probability[(S_1<\frac{L}{2})\cap (S_2\ge \frac{L}{2})]$$

(22)

In this case, $\delta \left(t\right)$ is the transition rate, $S_1$ and $\frac{L}{2}$ are the strength and shared load of component $C_1$, respectively; and $S_2$ and $\frac{L}{2}$ are the strength and shared load of component $C_2$, respectively. According to the law of conditional probability, the failure rate $\delta \left(t\right)$ is given in Equation (23).

$$\delta \left(t\right)=\lambda \left(t\right)\times Probability[(S_1<\frac{L}{2})|(S_2\ge \frac{L}{2})].Probability[(S_2\ge \frac{L}{2})]$$

(23)

Hence, the SSI-CTMC formulation is as follows.

Objective:

$$\mathrm{Minimize}f(d,{\mu }_X)$$

(24)

Subject to:

$$g_i(d,u_i\left({\beta }_i\right))\ge 0,\forall i\in Ilimitstatefunctions$$

(25)

$${\Sigma }_{j\in J}{P}_{j\left(t\right)}\ge R_{sys-required}$$

(26)

The values of $P_{j\left(t\right)}$ are derived from the transition rate matrix (Z), which is obtained by solving Equations (27) and (28). The failure rate of the components is represented in terms of its geometric dimension and loading rate. The solution for SSI–CTMC formulation is similar to that of SSI–DTMC, as discussed in the previous subsection. For each iteration, the optimization algorithm updates the design variable, as failure rate is connected with the limit state function in Equation (21) until the reliability requirement given in Equation (26) is met.

$$P_{j\left(t\right)}=e^{Zt}{P}_{j\left(0\right)},\forall j\in J$$

(27)

$$e^{Zt}=M{e}^{Dt}{M}^{-1}$$

(28)

The most important part is the transient analysis of CTMC in order to calculate the transition probabilities for different states of the load sharing system. The time–dependent state probabilities of the Markov process can be derived using Equations (27) and (28) [19]. However, the evaluation of Equation (28) to compute the state transition probabilities is not an easy task. Moler and Van Loan [20,28] reviewed several methods in order to calculate the exponential ($e^{Zt}$) of matrix “Z”. These methods can be classified into five different categories and can be characterized based on their generality, reliability, stability, accuracy, efficiency, storage requirements, ease of use and simplicity [20,28]. In this paper, the Eigenvalue–Jordan (EJ) approach is used since it is simple, handles complex matrices and deal with the problem of non–distinct eigenvectors. The details of this matrix decomposition approach is given in the next subsection.

2.3. Matrix Decomposition Approach

The time–dependent state probabilities of an n–state Markov process can be found by solving the Markov differential equations for that process. These equations have the general form given in Equation (29) and the corresponding solution with known initial conditions $X_t$ at time t = 0 is given in Equation (30) [19,25]. In general, the computation of the state transition matrix $e^{Zt}$, where Z is the n–order coefficient matrix of the Markov differential equations, can be done in several ways. As mentioned above, Moler and Van Loan [20,28] explained various methods to calculate the exponential of a matrix, which are classified based on several different characteristics such as their generality, stability, etc.

$$\dot{X}=ZX$$

(29)

$$X_t=e^{Zt}{X}_0$$

(30)

In this paper, the matrix decomposition approach [20,28] is utilized to solve the RBDO formulation taking advantage of the eigenvalues of a matrix. Although some specific algorithms have been developed to solve the exponential of matrices, the eigenvalues of the matrix play a fundamental role in calculation of $e^{Zt}$. This matrix decomposition method is widely used when the problem involves large matrices and repeated evaluation of $e^{Zt}$ is performed. This is the exact situation that will be encountered during our product design optimization involving reliability constraints, where the design variables need to be constantly updated through the repeated evaluation of $e^{Zt}$ for finding the failure probability and meet the required reliability target. Hence, this approach is selected to solve our single loop RBDO formulation. All the matrix decompositions are based on the similarity transformations of the form given in Equation (31), followed by the power series definition of $e^{Zt}$ given in Equation (32).

$$Z=MD{M}^{-1}$$

(31)

$$e^{Zt}=M{e}^{Dt}{M}^{-1}$$

(32)

The idea is to find matrix “M” in such a way that $e^{Dt}$ is easy to compute. In some cases, the matrix “M” may be close to singular, which means that cond(M) may be large. One of the basic approaches is to define matrix “M” as the matrix whose columns are eigenvectors of coefficient matrix “Z” [20,28]. The detailed description of eigenvalue method is explained in the following subsection, in which there are two cases to be considered: a matrix with distinct eigenvalues and a matrix with repeated eigenvalues.

Eigenvalue Method

Let “Z” be the n–order coefficient matrix of the Markov differential equations. One of the basic approaches in matrix decomposition is to define the matrix “M” whose columns are the eigenvectors of “Z”. Once this is done, there are two different cases to be considered. The first one is when the matrix “Z” has distinct eigenvalues $d_1,\dots ,d_n$. In this case, $e^{Dt}$ is defined by Equation (33), where “M” is the modal matrix of “Z” given by Equation (34) in which $m_k$ is the eigenvector corresponding to the eigenvalue $d_k$, where $k=1,2,\dots ,n$.

$$e^{Zt}=M{e}^{Dt}{M}^{-1}$$

(33)

$$M=[m_1{m}_2...m_n]$$

(34)

where,

$$e^{Dt}=\left(\begin{array}{cccc}{e}^{d_{1}t}& & & \\ & e^{d_{2}t}& & \\ & & \ddots & \\ & & & e^{d_{n}t}\end{array}\right)$$

(35)

After substituting the value of $e^{Dt}$ in Equation (33), the solution to the original problem is found by further substituting Equation (33) into Equation (30). This process works well when the matrix “Z” has distinct eigenvalues. However, in cases where the matrix “Z” does not have distinct eigenvalues and has repeated eigenvalues $d_1,\cdots ,d_n$, the value of $e^{Zt}$ is calculated using Equation (36). In this formulation, J is the Jordan canonical form, which is found using Equation (37) and “M” is the modal matrix of “Z” given in Equation (38).

$$e^{Zt}=M{e}^{Jt}{M}^{-1}$$

(36)

$$J=M^{-1}ZM$$

(37)

$$M=[m_1{m}_2\dots m_n]$$

(38)

In the above formulation, $m_k$ is the eigenvector corresponding to the eigenvalue $d_k$, $k=1,2,\cdots ,n$. After substituting the value of $e^{Jt}$ in Equation (36), the solution to the problem is found by further substituting Equation (36) into Equation (30) as discussed previously.

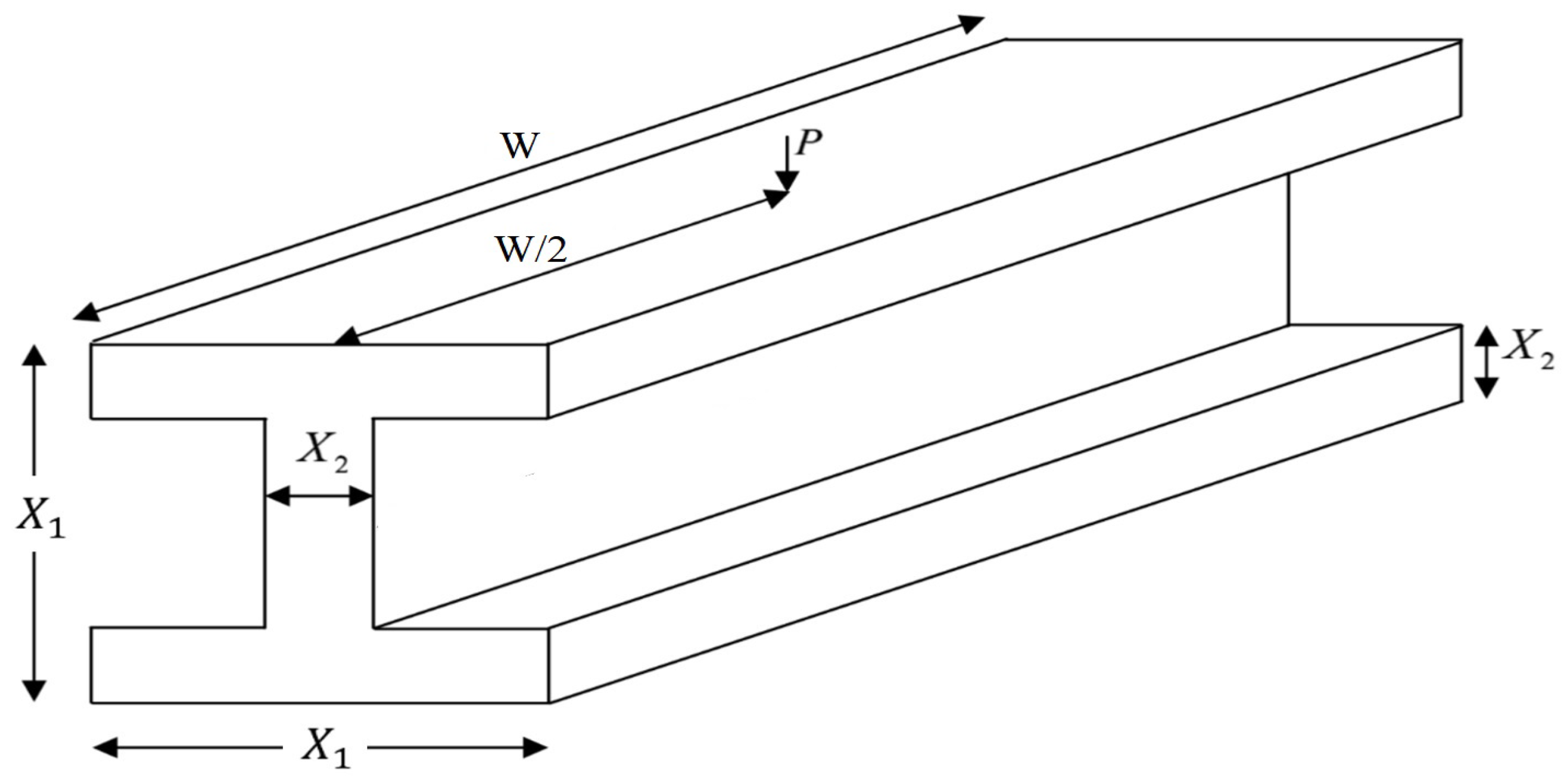
3. Case Study: System with Two Identical Components

In this section, a numerical example for both SSI–DTMC and SSI–CTMC formulation is provided to demonstrate the proposed methodology. A simple system with two components is considered for easy understanding but the methodology can be extended to design system with any number of components (identical or non–identical) without loss of generality. The SSI–DTMC formulation is provided in the next subsection followed by SSI–CTMC formulation.

3.1. SSI–DTMC Formulation

Consider an equal load sharing system consisting of two identical I-Beams “A” and “B”, as shown in Figure 2. Since the beams are identical, the dimensions of a single beam is given in Figure 3. These two beams constitute a single system, which is subjected to an overall load “L”, with each beam carrying a load “P”. Since an equal load sharing rule is applied for this case, the value of P equals L/2. The failure criterion is that the system fails when both of its components fail.

In Figure 3, the geometric parameters of the cross section of the beam $X_1$ and $X_2$ are random variables due to the manufacturing variability and is normally distributed with ${\sigma }_{X_1}=2.025$ cm and ${\sigma }_{X_2}=0.225$ cm, respectively [11]. The total load “L” acting on the system is normally distributed with ${\mu }_L=600 \mathrm{KN}$ and ${\sigma }_L=10 \mathrm{KN}$. The yield strength ($\xi$) of the beam is distributed normally with mean ${\mu }_{\xi }=16$ KN/cm${}^2$ and ${\sigma }_{\xi }$ = 0.1 KN/cm${}^2$. The required system reliability from the customer is 95% for load application of n = 100 times with an objective to reduce the overall manufacturing cost of the system.

To simplify the solution procedure, assuming the beam length and the material density to be constants, the overall objective of reducing the system cost will come down to reducing the weight of each beam, which is equivalent to minimizing the cross sectional area of the beams, i.e., $f\left(x\right)=2(3x_1{x}_2-2{x_2}^2)$. Since the design variables are random, the cost function $f\left(\mu \right)=2(3{\mu }_1{\mu }_2-2{{\mu }_2}^2)$ is derived, where ${\mu }_1$ and ${\mu }_2$ are the means of the corresponding random variables $x_1$ and $x_1$, respectively [11]. Further, it is assumed that the random parameters such as load (L) and yield strength ($\xi$) are equal to their mean values. The different possible system states are listed in

Table 1. Possible states of a system with two components (identical/non-identical).

State	Component A	Component B
AB	working	working
A’B	failed	working
AB’	working	failed
A’B’	failed	failed

.

In our case, since both components A and B are identical, their corresponding limit states and the cost function are same. The transition probability matrix $\mathbf{Z}$ for each state combination of the system is given in Equation (39), where $P_k$ denotes the probability of transition from one state to other. The notations A’ and B’ denote the failed states of components A and B, respectively. At the start of the mission, both components will be working. There is a chance that both components will survive the load applied on them. Let the probability that both the components survive, i.e., the system starts at state AB and remains in state AB after the load application be P1. If component A breaks with probability P2, then the probability that the system going from state AB to state A’B is also P2. If component A fails, the system has a chance to remain at the same state A’B and this probability is taken as P4. Similarly, all the other values of the probability transition matrix are derived for other components. Based on the stated assumption, the system cannot go directly from state AB to A’B’ due to single load application. Hence, the probability of transition from state AB to A’B’ is zero. Similarly, there is no repair process considered in our case. Hence, all the state transitions such as A’B to AB, AB’ to AB are zero. At the end, when both components fail, the system will fail since there is no repair process later on. Therefore, the probability of going back to other states from state A’B’ is zero and remaining at the state A’B’ is 1.

$$\mathbf{Z}=\begin{array}{rrrrr}\begin{array}{c}\\ \begin{array}{cc}\begin{array}{r}AB\\ A^{\prime }B\\ A{B}^{\prime }\\ A^{\prime }{B}^{\prime }\end{array}& \parallel \end{array}\end{array}& \begin{array}{c}AB\\ \begin{array}{r}P1\\ 0\\ 0\\ 0\end{array}\end{array}& \begin{array}{c}{A}^{\prime }B\\ \begin{array}{r}P2\\ P4\\ 0\\ 0\end{array}\end{array}& \begin{array}{c}A{B}^{\prime }\\ \begin{array}{r}P3\\ 0\\ P6\\ 0\end{array}\end{array}& \begin{array}{cc}{A}^{\prime }{B}^{\prime }& \hspace{1em}\\ \begin{array}{cc}\begin{array}{r}0\\ P5\\ P7\\ 0\end{array}& \parallel \end{array}\end{array}\end{array}$$

(39)

Let $G_i(x_1,x_2)$ denote the limit state function (performance function) for component i, which is the difference between the given bending threshold ($\xi$) of the component and the actual bending stress ($f\left(p\right)$) applied (i.e., $G\left(x\right)=\xi -f\left(p\right)$). Theoretically, the safety region for each component is $G_i(x_1,x_2)\ge 0$ because when the actual bending stress exceeds the bending threshold, then the component breaks, i.e., $G\left(x\right)=\xi -f\left(p\right)$ will become negative. Initially, each component carries half the system load but when one component fails, the load gets redistributed and the other surviving component carries the entire system load. The analytical limit state function for the I-Beam is given in Equation (40) [11,22]. This function is used to update the transitional probability values in terms of SSI and the complete mathematical formulation of the problem is given as follows.

$$G(x_1,x_2)=\xi -\frac{0.3P{x}_1}{x_2{(x_1-2x_2)}^3+2x_1{x}_2(4x_2^2+3x_1^2-6x_1{x}_2)}$$

(40)

Objective:

$$Minimize2(3{\mu }_1{\mu }_2-2{{\mu }_2}^2)$$

(41)

Constraints:

$$g_i(d,u_i\left({\beta }_i\right))\ge 0,\forall i\in Ilimitstatefunctions$$

(42)

$${\Sigma }_{j\in J}{P}^{(}{100)}_j\ge 0.95$$

(43)

$$30\le {\mu }_1\le 55$$

(44)

$$0.9\le {\mu }_2\le 2$$

(45)

In the above formulation, the objective function is to minimize the total cost of the system. The constraint in Equation (42) denotes the safety region and the values of $P_j$ in Equation (43) are obtained from the probability transition matrix (Z), derived by solving Equation (46) with $n=100$ using the matrix decomposition approach explained in Section 2.3. For each iteration, the transition probabilities is updated in the matrix “Z” and the 100–step transition probabilities are found by Equation (46). Equations (44) and (45) are just the boundary constraints for the design variable of interest.

$$Z^{100}=M{D}^{100}{M}^{-1}\ast Z^0$$

(46)

The constraint on the transition probabilities, given by Equation (43), ensures that the system reliability target is met. The set “J” consists of component states which constitute the working state of the system, i.e., J = {AB, A’B, AB’}. The set “Y” consists of the component states which lead to system failure, i.e., Y = {A’B’}. The set “K” is given by K = {AB}, with probability $P_K^0=1$, i.e., the system always works at initial time (t = 0).

3.2. SSI–CTMC Formulation

The same system presented in Section 3.1 is designed using a continuous time Markov chain. In addition to the parameters described in Section 3.1, let the failure rate of components A and B be ${\delta }_A$ and ${\delta }_B$, respectively, with the assumption that loading occurs at a rate $\lambda \left(t\right)=4$/month. The required system reliability from the customer is 95% for t = 25 years (i.e., t = 300 months). Let ${\delta }_A^{\prime }$ denote the failure rate of component A when component B fails and ${\delta }_B^{\prime }$ denote the failure rate of component B when component A fails. Obviously, ${\delta }_A^{\prime }>{\delta }_A$ and ${\delta }_B^{\prime }>{\delta }_B$ because, when one component fails, the entire load acting on the system is redistributed, which increases the failure rate of the surviving components. The transition rate matrix ${\mathbf{Z}}^{\ast }$ is represented by Equation (47) and the description is similar to the transition probability matrix, as explained in the previous subsection.

$${\mathbf{Z}}^{\ast }=\begin{array}{rrrrr}\begin{array}{c}\\ \begin{array}{cc}\begin{array}{r}AB\\ A^{\prime }B\\ A{B}^{\prime }\\ A^{\prime }{B}^{\prime }\end{array}& \parallel \end{array}\end{array}& \begin{array}{c}AB\\ \begin{array}{r}0\\ 0\\ 0\\ 0\end{array}\end{array}& \begin{array}{c}{A}^{\prime }B\\ \begin{array}{r}\delta A\\ 0\\ 0\\ 0\end{array}\end{array}& \begin{array}{c}A{B}^{\prime }\\ \begin{array}{r}\delta B\\ 0\\ 0\\ 0\end{array}\end{array}& \begin{array}{rr}{A}^{\prime }{B}^{\prime }& \\ \begin{array}{rr}\begin{array}{c}0\\ {\delta }_B^{\prime }\\ {\delta }_A^{\prime }\\ 0\end{array}& \parallel \end{array}\end{array}\end{array}$$

(47)

Let $S_A$ and $S_B$ denote the yield strengths of components A and B, respectively. From Equation (22), the failure rate in terms of SSI is given in Equations (48)–(51) [18], followed by the mathematical formulation of the problem in Equations (52)–(56).

$${\delta }_A\left(t\right)=\lambda \left(t\right)\times Probability[(S_A<\frac{L}{2})|(S_B\ge \frac{L}{2})].Probability[(S_B\ge \frac{L}{2})]$$

(48)

$${\delta }_A^{\prime }\left(t\right)=\lambda \left(t\right)\times Probability[S_A<L]$$

(49)

$${\delta }_B\left(t\right)=\lambda \left(t\right)\times Probability[(S_B<\frac{L}{2})|(S_A\ge \frac{L}{2})].Probability[(S_A\ge \frac{L}{2})]$$

(50)

$${\delta }_B^{\prime }\left(t\right)=\lambda \left(t\right)\times Probability[S_B<L]$$

(51)

Objective:

$$Minimize2(3{\mu }_1{\mu }_2-2{{\mu }_2}^2)$$

(52)

Constraints:

$$g_i(d,u_i\left({\beta }_i\right))\ge 0,\forall i\in Ilimitstatefunctions$$

(53)

$${\Sigma }_{j\in J}{P}_{j\left(300\right)}\ge 0.95$$

(54)

$$30\le {\mu }_1\le 55$$

(55)

$$0.9\le {\mu }_2\le 2$$

(56)

The working procedure is similar to the SSI–DTMC model discussed in the previous subsection. Instead of transition probabilities, during the iteration process, the failure rates are updated in the transition rate matrix (Z${}^{\ast }$). The values of $P_j$ are derived from the transition rate matrix (Z), which is obtained by solving Equations (57) and (58). The limiting state probabilities at t = 300 for the problem is found using the Eigenvalue Methodology (EM), as explained in the Section 2.3. The Genetic algorithm [26] is used to solve the problem with population size of 100 with 50 generations. The results of both SSI–DTMC and SSI–CTMC along with a static system are detailed in the next section.

$$P_{j\left(300\right)}=e^{300Z}{P}_{j\left(0\right)},\forall j\in J$$

(57)

$$e^{300Z}=M{e}^{300D}{M}^{-1}$$

(58)

4. Results and Discussion

In this section, the results for the case study using the proposed single loop methodology is provided. To validate the results of our single loop formulation, the Monte Carlo (MC) simulation was used as benchmark [27].

Table 2. Case study results.

Type	Method	${\mathit{R}}_{\mathit{sys}}$	${\mathit{R}}_{\mathit{comp}}$	Duration	${\mathit{\mu }}_1$ cm	${\mathit{\mu }}_2$ cm	Cost ($)	${\mathit{R}}_{\mathit{comp},\mathit{MC}}$	${\mathit{R}}_{\mathit{sys},\mathit{MC}}$
	Static	95	93.23	-	41.32	0.92	224.70	94.21	96.12
Single loop	DTMC	95	96.48	100 steps	36.71	1.21	260.65	97.56	98.39
	CTMC	95	99.62	25 years	50.22	1.14	338.30	99.28	99.99

summarizes the results of single loop formulation of static system (traditional SSI without Markov chain), single loop SSI–DTMC and single loop SSI–CTMC for different system reliability target levels. The R${}_{sys}$ column is the required reliability level from the customer for the number of load applications on the system (e.g., $n=100$ load applications). In the case of SSI–CTMC, the time unit of 25 years is specified by the customer. Since the components are identical, the values of the design variables (${\mu }_1,{\mu }_2$) and allocated component reliabilities ($R_{comp}$) are the same for both components A and B. Table 2 shows that, although the required system reliability target is the same for the three different cases (static, DTMC and CTMC), the allocated component reliabilities are different. This is because the load application happens only once for static system and remains constant thereafter. However, in the cases of dynamic loads, which is the main theme of this paper, SSI–DTMC and SSI–CTMC provide the required design dimensions for the components. The total system cost is the total value of the objective function expressed in dollars. Note that the system cost for SSI–CTMC is higher than for SSI–DTMC because of the presence of the loading rate factor in SSI–CTMC, which is higher than the SSI–DTMC case.

In addition, the results of the MC simulation ($R_{comp,MC}$ and $R_{sys,MC}$) of the same static, SSI–DTMC and SSI–CTMC system are provided for comparison. The obtained design points from the proposed methodology are nothing but the mean value of the design variables and their corresponding variance is also known as per the problem definition. Hence, a random sample of 100,000 design points were drawn and the corresponding reliability values of the component ($R_{comp,MC}$) and the system ($R_{comp,MC}$) were tabulated [27]. In terms of computational cost of single loop formulation, the static system calculations are quick because the Markov chain calculations are not involved. In terms of the accuracy of the proposed single loop formulation, it can be seen that the maximum deviation of the allocated reliability values for static, DTMC and CTMC models are within 10% deviation when compared to that of MC simulation. This deviation could be well traded–off with the computational cost for the MC simulation as well as other RBDO methodologies.

As far as the matrix decomposition methods are concerned, there are some possible limitations that might occur for the complex performance functions. The results from the Eigenvalue–Jordon method would be similar to the results from Squaring and Scaling with Pade Approximation (another popular matrix decomposition method [20,28]) with little variation occurring after three decimal digits. However, when the number of components increases, the accumulated errors between the matrix decomposition methods will lead to a large variation in results. However, there is no single method that is deemed to be more accurate than the others [20,28]. In addition, some rounding errors will cause multiple eigenvalues to become distinct or vice versa, thereby altering the entire structure of Jordan canonical form [20,28]. In general, since it is easy to represent a matrix in the form of eigenvectors, the eigenvalue method is chosen in this paper. The methodology works well for any matrix whose eigenvectors can be chosen orthogonal. However, there is a drop in accuracy when the matrix becomes large and when eigenvectors are linearly dependent. If there is a complex ill-conditioned matrix with large number of components (e.g., $n>25$), then there will be a problem with convergence, and the results might be far away from the true value. However, for well behaved and small matrices, especially when there is a need to perform repeated calculations of the exponential of a matrix, such as in the case of RBDO, this eigenvalue method is really helpful. The efficiency of this method is better than that of Ordinary Differential Equation (ODE) and polynomial methods, which require large storage space and are prohibitively expensive. However, there is no conclusive evidence as to which matrix decomposition method is the best, since each method has its own advantages and limitations depending on the requirements.

5. Conclusions

Reliability Based Design Optimization of load sharing systems is a challenging problem due to the dynamic nature of component failure probabilities. The use of Markov theory and SSI theory provides a better way to model the load sharing system for a given reliability target. Unlike the conventional static SSI model, the proposed methodology captures the complete dynamics of the system with respect to time as well as load application and depicts the real nature of stresses acting on the system, thus making it best suited for designing the load sharing systems. It is to be noted that, based on the design requirement and loading behavior (e.g., steady load, time varying load, etc.), SSI–DTMC or SSI–CTMC should be chosen accordingly. In addition, the computational requirement increases for complex systems with increase in number of components and the use of high performance computing clusters is recommended to implement the methodology. When the number of components increases and each component has its own failure mode, then the Z matrix will be huge. However, due to the availability of computational power from high performance computing clusters, the matrix calculations can still be done in a considerable time. The Z matrix in our case will still be manageable when compared to the matrices involved in deep neural network architectures. If possible, the given complex system can be broken down into simple subsystems and the final results can be aggregated, but a thorough investigation is needed before breaking the system links.

In terms of optimization algorithms, the user needs to be cautious when there are large number of non–identical components in the system. This is because, when the reliability level of some components drops below a specific threshold, the feasible region will not be convex and it will be hard to reach an optimum point [29]. In addition, the nonlinear objective functions and constraints may cause difficulty in reaching global optimum in some cases as there is no guarantee on the convexity of the feasible region and not much is known about the continuity of the functions. Hence, it is necessary to choose an optimizer that will provide a good local optimum. In our case study, the algorithm was started with different initial values to check for convergence and validate the final solution.

In terms of reliability assessment, the user needs to be wise in choosing the matrix exponential evaluation methods as there is no conclusive evidence for a best method, since each one has its own advantages and drawbacks [20,28]. However, in our framework, any method can be integrated depending on requirements such as reliability, stability, efficiency, storage requirements, etc. In addition, the developed SSI–Markov methodology is very flexible to design systems with non–identical components for equal load sharing, local load sharing and monotone load sharing rule [30], with or without considering the repair time.