PV Microgrid Design for Rural Electrification

1. Introduction

As per the World Bank, about 13% of the world population still have no access to electricity. There are more than 30 countries with less than 50% electrification rates [1]. In India, there are still around 31 million village homes which are not yet electrified [2]. Most remote villages in India, which have not yet been electrified have some common characteristics such as [3]:

• Being located in areas with difficult terrain such as hills, forests, deserts and islands. Being part of a protected forest area could isolate the village and prevent live conductors from being drawn through it.
• Being located far from the nearest existing grid.
• Very low population (below 500) and low number of households (ranging between 2 and 200).
• Low power demand, probably even in the near future, as the loads are mostly lighting.
• Minimal transport and communication facilities.
• Low income level and low affordability.
• Poor literacy levels and technical skills.

Due to their remote locations, high costs are involved in grid extension and also high losses will be encountered while transporting power to the village from the central grid. On-site generation/distributed generation (DG) based on renewable sources would be an economic option to enable faster electrification of villages as compared to extension of a central grid [4]. Advantages of distributed generation-based rural electrification include energy loss reduction, reliability of supply, and reduction of indoor pollution arising from use of conventional fuel (wood or kerosene) for lighting [5]. Of the renewable energy technologies, photovoltaics (PV) is ideally suited for remote villages due to resource availability, its modular nature which makes transportation convenient, the low maintenance requirement and long life (up to 25 years). Moreover, PV system costs have continually declined over the last two decades increasing their affordability [6].

The supply systems for rural electrification are mostly isolated power systems of capacities ranging from 1 kW for villages/hamlets to around 100 kW for large islands. Most of these low capacity systems are single-phase systems with a supply duration of around 4–6 h per day. Microgrids are ideally suited for the small power capacity needed by the remote villages in India. A microgrid is a self-controlled isolated power distribution system, having sources which are based on power electronics to provide control on flow of real and reactive power, voltage, current etc., loads and storage devices [7]. To the utility, the microgrid can be thought of as a controlled cell of the power system. It can be designed to meet their specific needs, such as enhance local reliability, reduce feeder losses, support local voltages, provide increased efficiency, voltage sag correction or provide uninterruptible power supply [8].

When the planning of a distribution system with DG is considered, the greatest attention should be paid to the siting and sizing of DG units because their installation in non-optimal locations can result both in an increase of power losses and reduction of reliability levels [9,10]. In rural distribution systems, the resistance in the distribution lines is often larger than, or at least similar to, the inductive impedance. The distribution line resistance causes a significant proportion of voltage drop along the distribution lines as well as of line losses [11]. The effect becomes prominent when a small amount of power needs to be taken over longer distances as in cases of villages far from the existing grid poles. The connection of DG can therefore have a significant influence on the local voltage level [11].

Considerable amount of research work has been done in the issue of optimal placement and sizing of DGs such as PV systems [12,13,14,15]. However, these studies were focused on larger capacity three-phase microgrids, whereas most of the rural electrification systems are single-phase. In the existing literature, proper tools that will enable the planner to design such small capacity PV microgrids while satisfying the technical constraints are not available. This study aims to address this knowledge gap in the planning of PV microgrids intended for rural electrification. An improved design procedure is introduced in this work based on the use of centre of moments for central PV system siting given the estimate of spatial load distribution, simulated annealing for network structure optimisation and load flow based parametric analysis for confirming the PV microgrid structure before detailed software-based PV design. Two isolated remote villages in India with existing PV microgrids namely Ghotiya village, Chattisgarh and Rajmachi village, Maharashtra are used as case studies. Case studies of Ghotiya village is used to formulate the design procedure and that of Rajmachi village to illustrate the design procedure. A comparison of industrial standard PV system design software PVsyst™ (PVsyst SA, Satigny, Switzerland) and free online tool PVGIS5 (European Commission, Joint Research Centre Institute for Energy, Ispra, Italy) for designing the central PV system is also carried out.

The rest of the paper is organised as follows: Section 2 describes the design problem; Section 3 provides details of the case study systems and describes the analysis and design methodologies followed for formulating the improved PV microgrid design procedure; Results of analysis are examined in Section 4; The improved design procedure is presented in Section 5 along with a case study illustration; Conclusions are drawn in Section 6.

2. The Design Problem

The constraints of microgrid planning are derived from the requirements for a technically acceptable operation of distribution systems. There are criteria for the dimensioning of the equipment as well as criteria for a minimum quality of power supply, specified by the voltage quality and the reliability of power supply. These requirements can be written as follows [16]:

Restriction of maximum power flow on every line:

$$I_k\le I_{k,max} k=1,2\dots N_k$$

(1)

where I_k is the power flowing in the kth line and k is the line number.

Restriction of the upper and lower voltage at every node:

$$V_{l,min}\le V_l\le V_{l,max} l=1,2\dots N_l$$

(2)

where V_l is voltage at the lth node (bus) and l is the node number. A node is the point of consumer connection on the network.

Restriction of the maximum frequency of interruptions (H_U) and the maximum unavailability (Q_U) for every consumer:

$$\begin{array}{c}{H}_{u,m}\le H_{u,max}\\ Q_{u,m}\le Q_{u,max} m=1,2\dots N_m\end{array}$$

(3)

where m is the month of the year.

Factors that are to be considered by the planner when designing a rural distribution system are [17]:

• Voltage drop limits the design: The loads are distributed over large distances, which increase the voltage drop at the extreme consumer point in a radial system.
• Losses costs are high: Moving relatively small amounts of power over long distances results in losses which are high in proportion to the amount of power delivered.
• Layout and customers are restricted to the road network.
• Loads vary from very small single-phase to medium sized three-phase. Water pumps for irrigation purpose may require three-phase supply.
• Reliability requirements are below average.

The design problem involves answering the questions given the spatial distribution of load and estimate of magnitudes:

• What should be the network (microgrid) structure?
• What should be the size of the central PV system?
• Where the PV system should be located?
• What should be the specifications of cables, protective equipment?

The inputs needed in the design process are:

• Spatially distributed ‘point’ loads and estimate of its magnitudes
• Location details and/or local resource availability
• Roads and other obstacles
• Expected load growth
• Cost of PV system and power network feeders

  ∙

  Installation cost

  ∙

  Operating cost

The design objective is to develop an optimal PV microgrid subject to the following constraints:

• The minimum PV system and battery bank size determined is adequate to ensure continuity of supply to the load
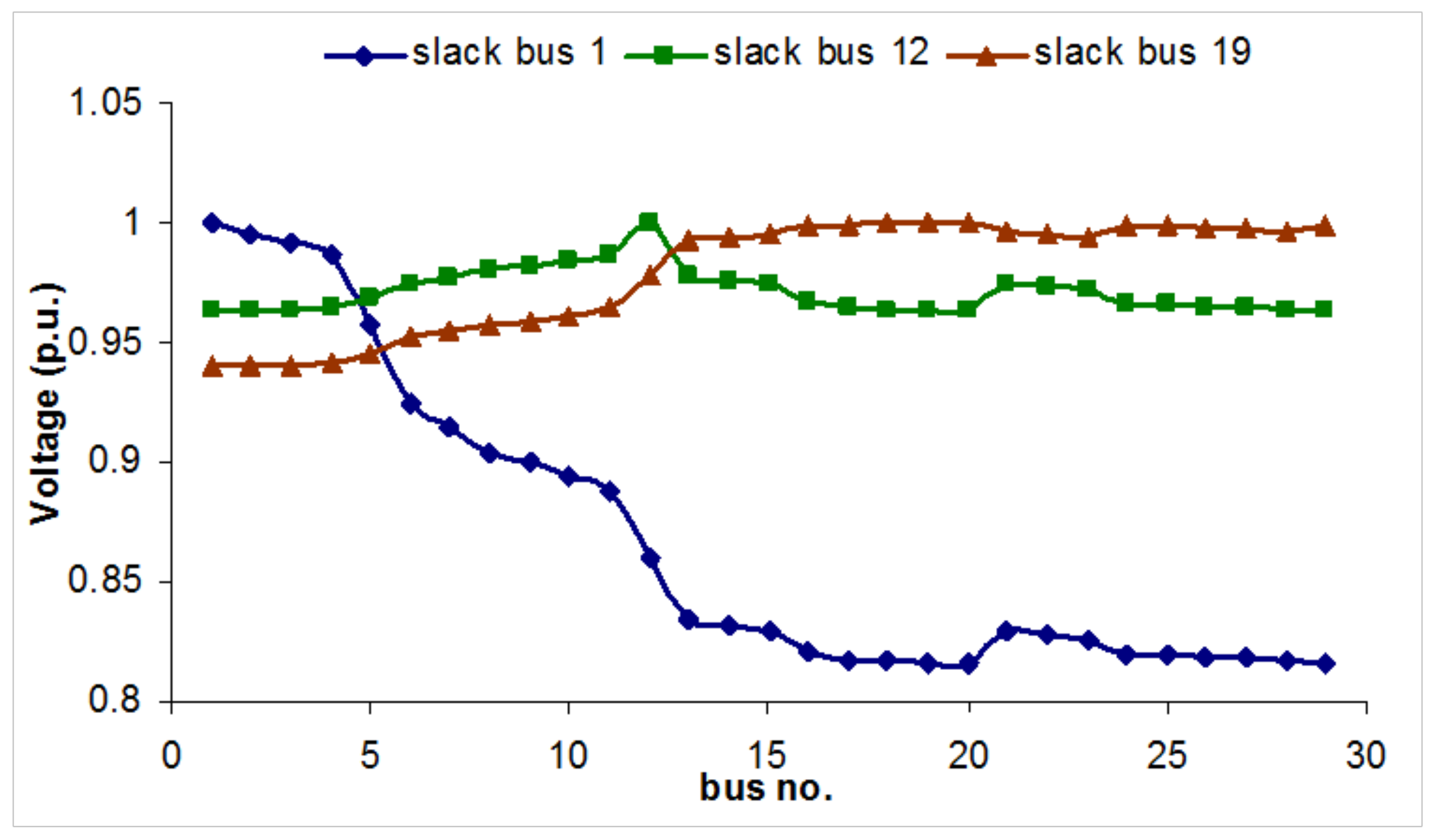
• Voltage at each bus/node should be within limits
• Feeder capacity should not be exceeded
• The energy losses are minimized
• The PV system design is based on parameters of practical components.

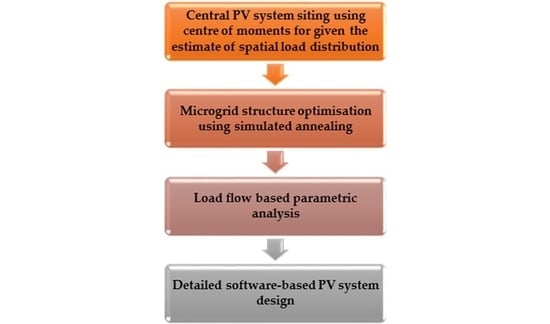
3. Methodology

From the literature review, it is observed that no generic set of guidelines are available to help the planner decide the location, size and structure of the PV microgrid for rural electrification. The typical procedure adopted by planners for design of such systems is given in Figure 1. The inclusion of power network requirements into the design process is essential to reduce the overall costs, reduce power loss and maximize supply reliability. An improved method for planning is formulated using the case studies of two existing isolated rural power systems in India namely Ghotiya village, Chattisgarh and Rajmachi village, Maharashtra. Optimal location of central PV system as a function of spatial distribution of load points can be obtained using the centre of moments approach [18]. Network structure is another major issue to be considered in the planning phase of a distribution system. Given the spatial distribution of system and location of the PV system, the optimal network structure can be obtained using simulated annealing [19]. Parametric analysis using single-phase power flow can be performed to examine whether the PV system and network structure meet the technical requirements. In parametric analysis the variation of losses, power generation at slack bus (bus where the source PV system is connected) and voltage profile with the following parameters is obtained:

• Siting of source PV system
• Size of PV system
• Slack bus voltage (p.u.)

Based on the observations from parametric analysis general rules for sizing and siting of the central PV system and structure of the network is evolved.

3.1. Case Study Systems

In the Indian context, there are a large number of villages which are electrified using small isolated power systems and many more are under the planning stage. To understand the characteristics of systems for rural electrification systems, two real remote rural isolated networks were considered as case studies. Their details are as follows:

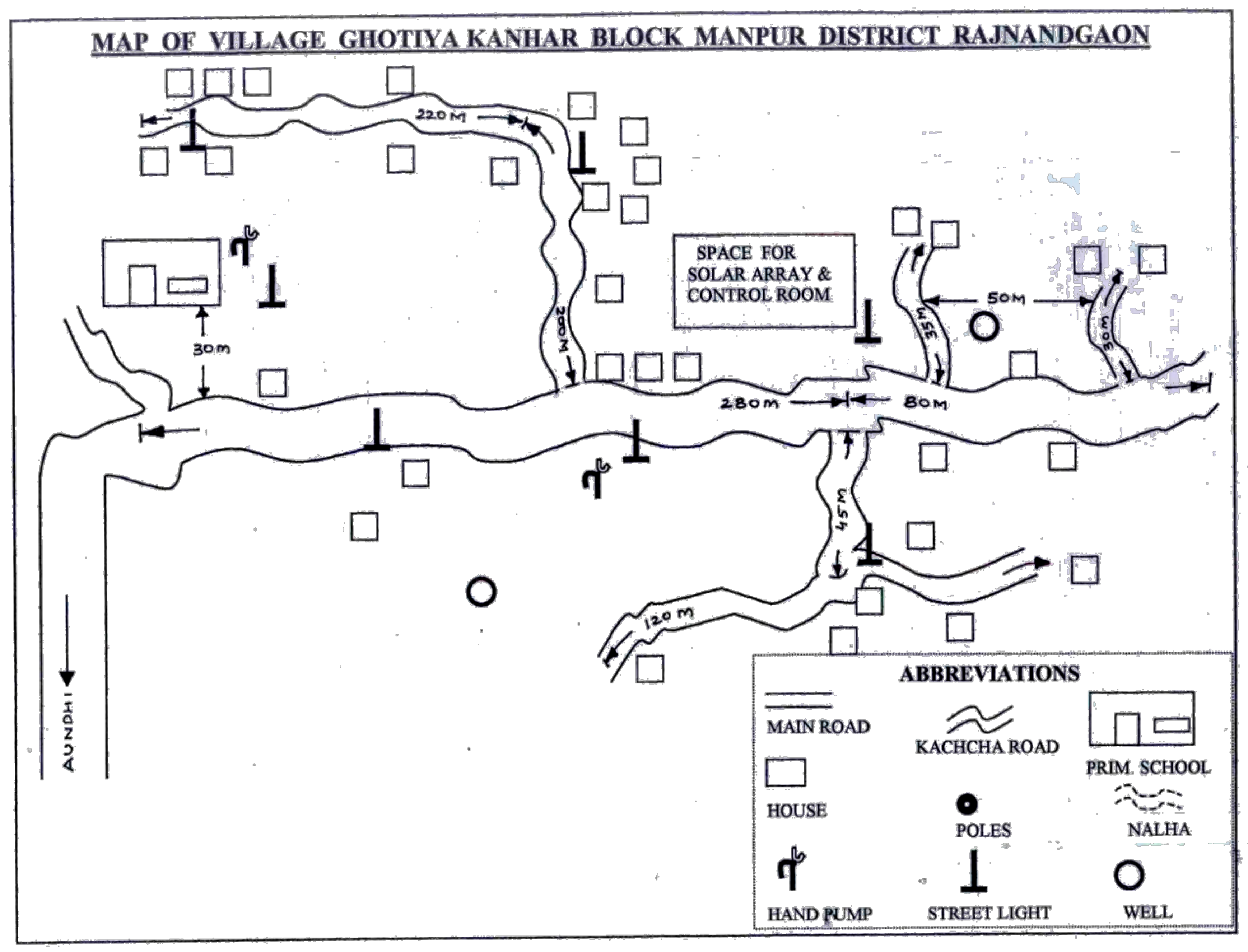
3.1.1. Ghotiya Village in Raipur, Chattisgarh

The map of Ghotiya village is shown in Figure 2. The geography of the place is covered by dense forests and mountainous landscape making it an extremely difficult terrain for development activities. It is difficult to provide grid connectivity from the central transmission network of the country to such villages due to the harsh geographical conditions. Ghotiya was one of the villages electrified using PV systems by Tata BP Solar Ltd. along with Chattisgarh Renewable Energy Development Authority (CREDA).

3.1.2. Rajmachi Village near Lonawala, Maharashtra

Figure 3 shows the village and the extent of its isolation. The geography of the location includes hilly terrain, heavy monsoons, with landslides and continuous rains for 5–6 days, making it more difficult to access the place. Figure 4 gives the map of the village as obtained from MEDA (Maharashtra Energy Development Agency). Though there are many villages electrified by isolated power systems, none of them have been documented under running conditions. Hence, the variation of load (Figure 5) and voltages at different load points over a day for the village microgrid were documented using the experimental setup shown in Figure 6. The existing PV system which supplies the village has a rating of 5 kW and a 120 V 800 Ah battery bank. During experimentation, it was observed that the voltage at the bus furthest from the PV source at near peak load conditions is around 210 V. This is 30 V less than the statutory voltage of 240 V. The point is less than 500 m from source. The impedance of the line was calculated as around 8.6 ohms/km (7.4 + 4.3i) which is quite high as compared to the central electricity utility recommended distribution line resistance of 1.88 ohms/km.

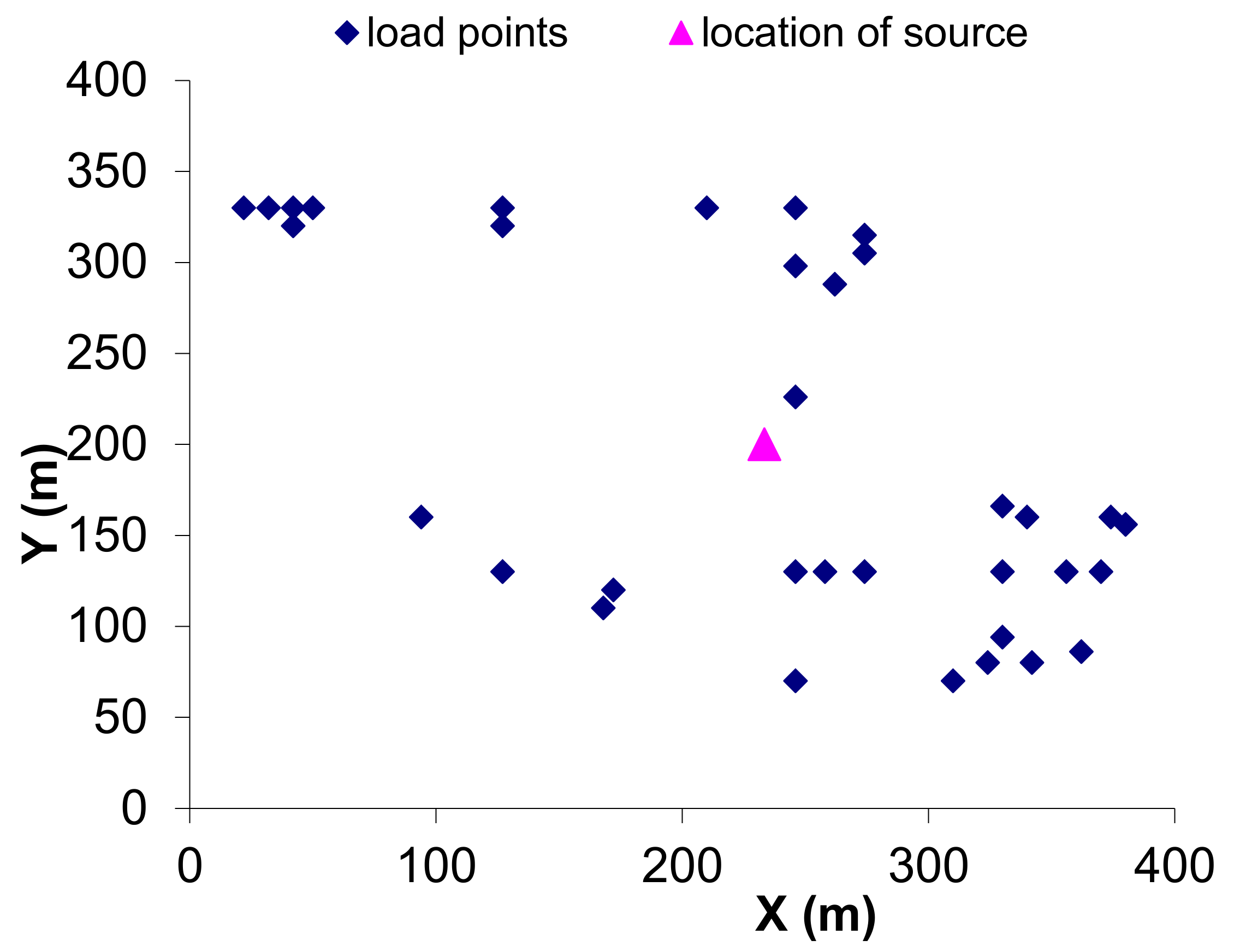
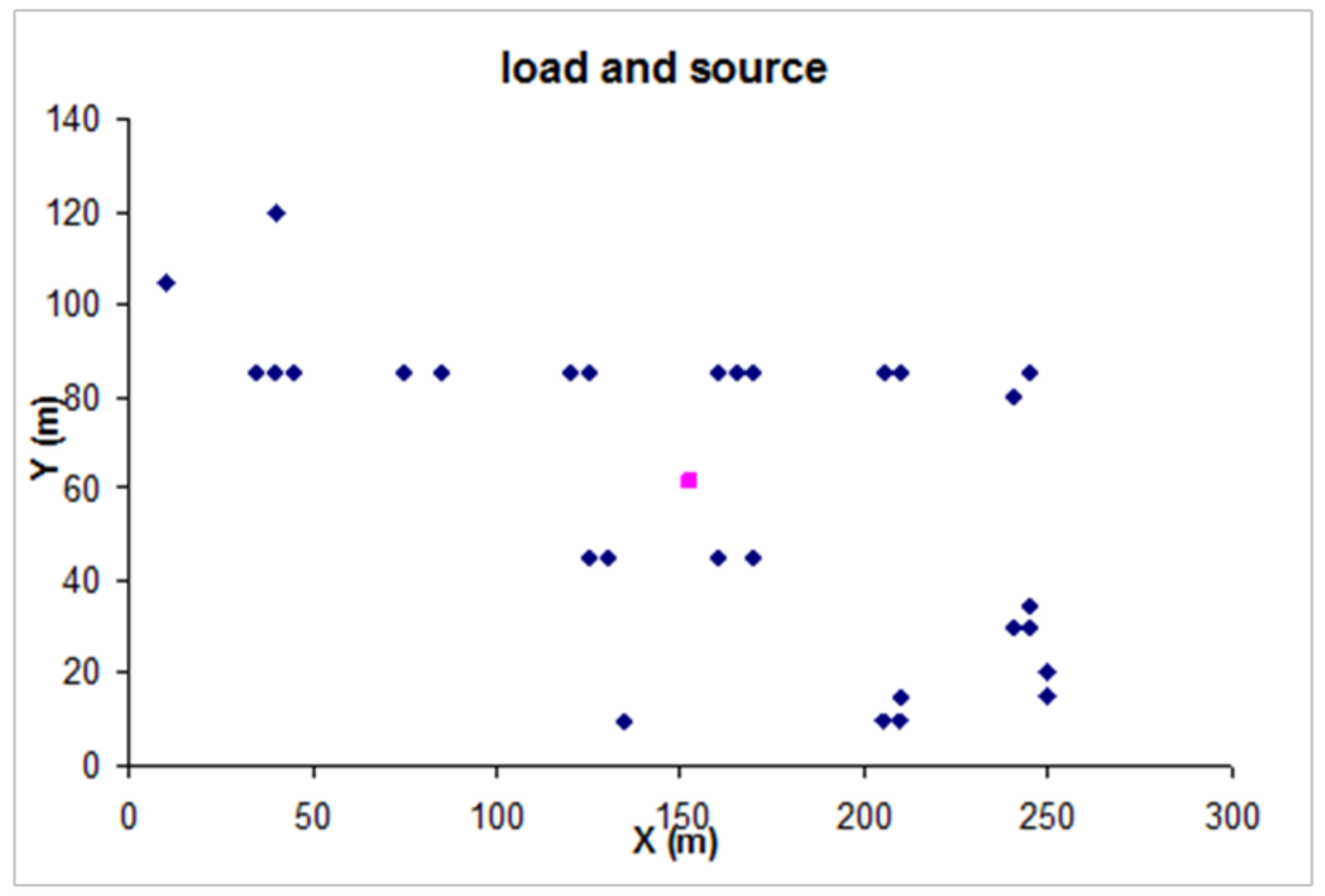
3.2. PV System Location Siting Using Centre of Moments

In a power system, the power loss in a line is proportional to the line current and the distance between the two points. The system can be represented in a 2-dimensional space as point loads with a weight equal to the load at each point. Assuming a constant power factor, point loads can be represented by their active power consumption in watts. For total loss of the system to a minimum, sum of weighted distances of load from source should be minimal. The optimal location of the source (central PV system) can be obtained by finding out the centre of moments of the points assuming the weight associated with each point as its mass [18].

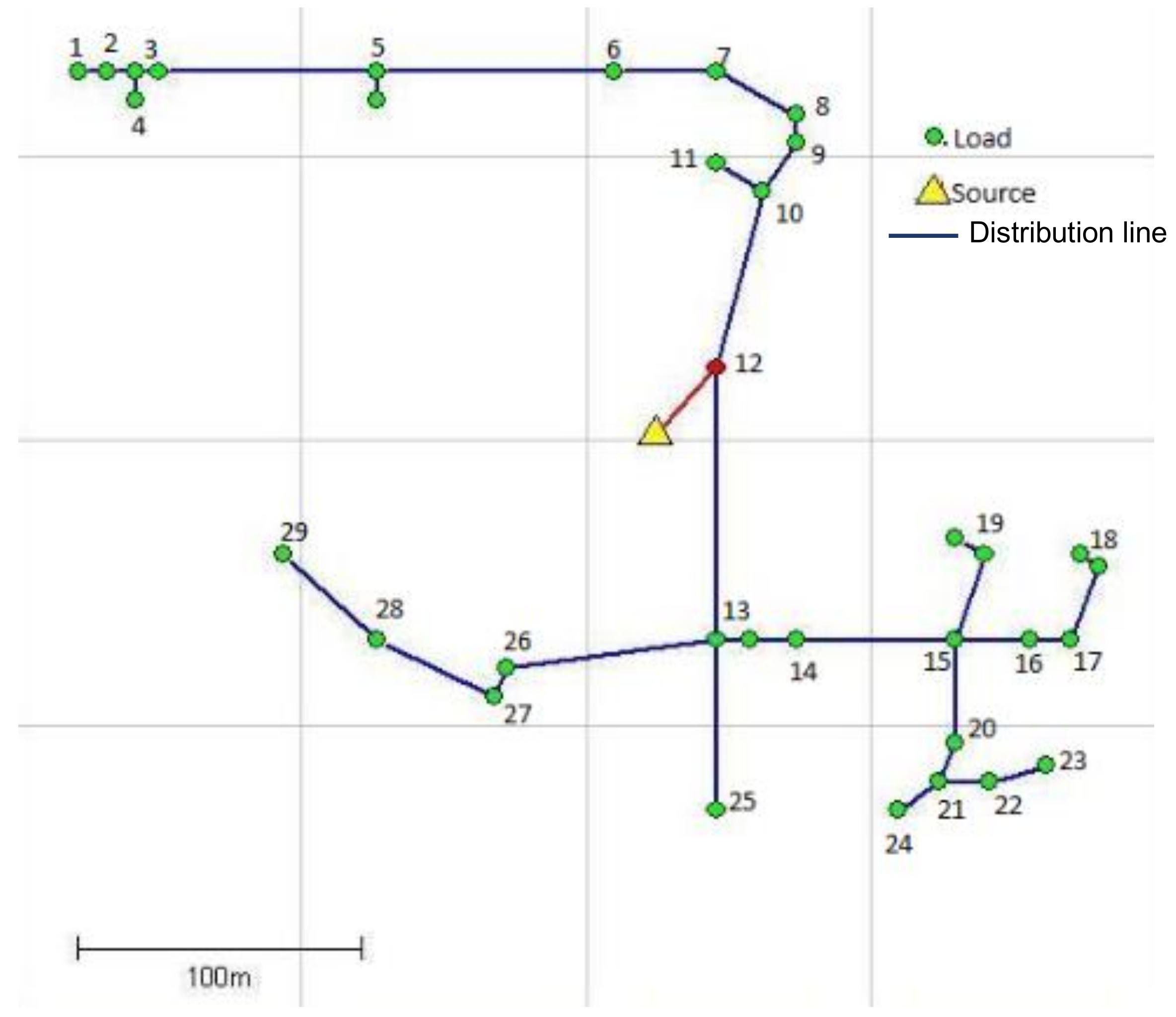
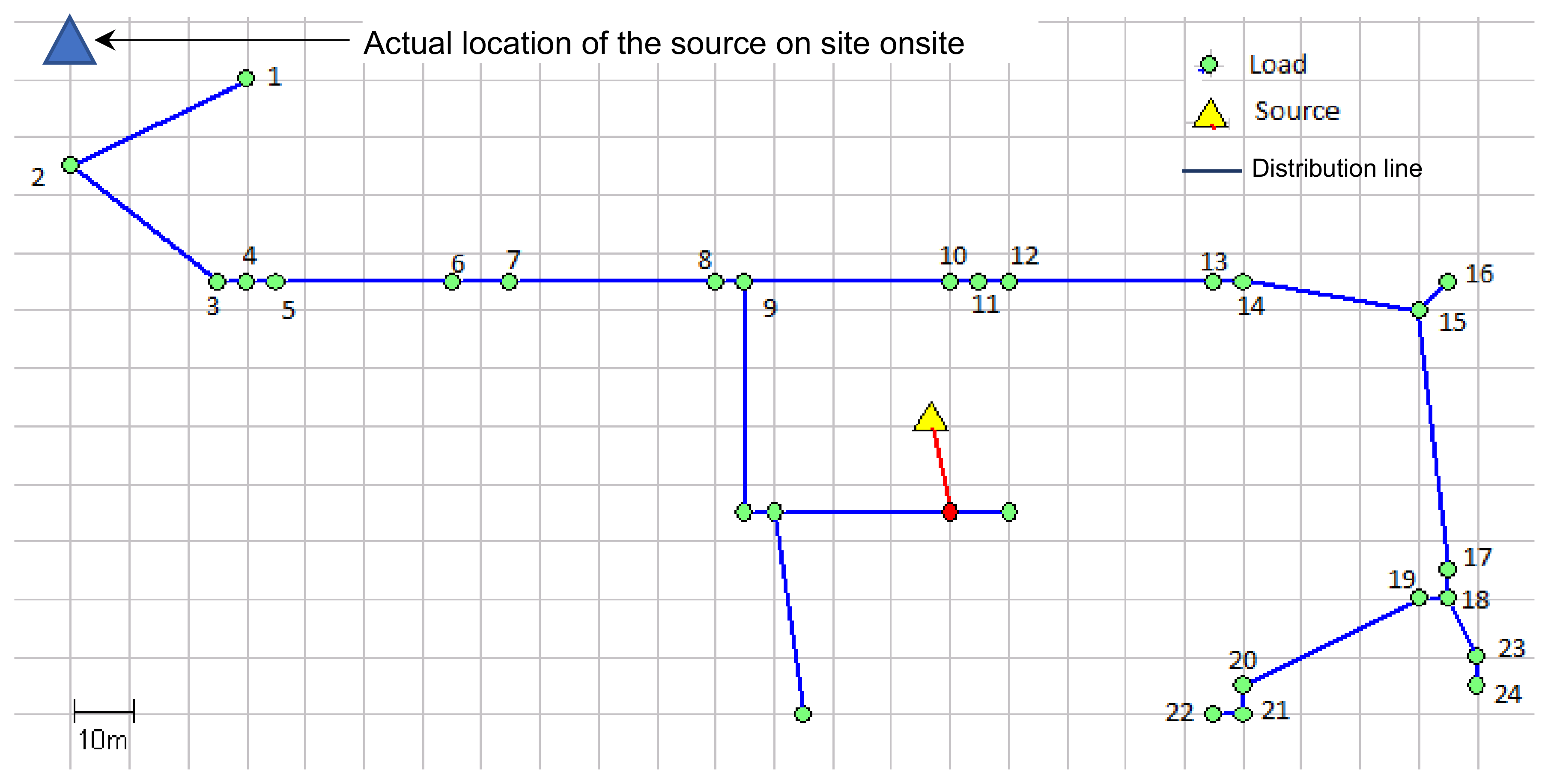
3.3. Network Topology Design

The structure of the power network (topology) should be such that feeders should be able to cover the whole area where service is to be provided and include all the houses in that area. In case of rural feeder design, the two major goals are: cost should be minimized, and electrical performance must be satisfactory. A “Backward-Trace” layout procedure generally produces the best results for finding an optimal network structure. The procedure to find the configuration with least cost is [17]:

• Identify all the geographic constraints; areas that cannot be crossed, areas where construction is difficult etc.
• Identify all special opportunities; diagonal routes which contribute to lower cost.
• Identify a set of load points on the periphery of the area to be served by the feeder, as well as a load point that is the “worst case” in terms of each constraint
• One by one for each load points identified in step 3, work backward from it toward the substation (power source) trying to find out the shortest route(s). As feeders generally follow roads it is better to consider $D=\left|X\right|+\left|Y\right|$ than $D=\sqrt{{\left|X\right|}^2+{\left|Y\right|}^2}$ (X and Y are the feeder lengths along the two coordinates of the site map).
• As a shortest path from each point is traced, commonalities among the paths can be used as major trunk or branch routes.

Simulated annealing is a mathematical optimisation technique that mimics the process that misplaced atoms in a metal undergo when the metal is slowly cooled after heating. Simulated annealing is able to find a near optimal solution even with a large number of variables and noisy data [20]. The quality of the solution provided by this algorithm is dependent on the amount of time it is given to solve the optimization problem. In this study, simulated annealing was carried out using an early version of ViPOR (Village Power Optimization Tool box, NREL NREL, Golden, CO, USA) as the authors were conversant with the software. However, users do not have to restrict to this software as there are a number of other software such as MATLAB, Global Optimization Software etc. that allow users to solve optimization problems using simulated annealing. NREL has now replaced ViPOR with REOPT™ (Renewable Energy Integration and Optimization) software.

To determine the cost and the ideal layout of the distribution grid, ViPOR requires a spatial or description of the village which must include the location and type of each load point (such as houses, schools, stores, etc.) and at least one potential centralized power source location. The spatial description may also include linear features (such as roads, rivers, and shorelines) and terrain information. Other inputs needed include:

• the type of source and cost of generating electricity
• the costs of running wire across different types of terrain
• the maximum low voltage line length. This input restricts the length of low voltage wire runs. It refers to the length of wire between a load point and the transformer to which it is connected. This restriction is meant to limit voltage drops and line losses.

At the end of the simulated annealing process, ViPOR displays a map of the optimal network structure. The distribution network follows the road wherever possible in order to avoid more expensive terrain. A breakdown of the costs and revenues associated with the optimal solution can also be obtained.

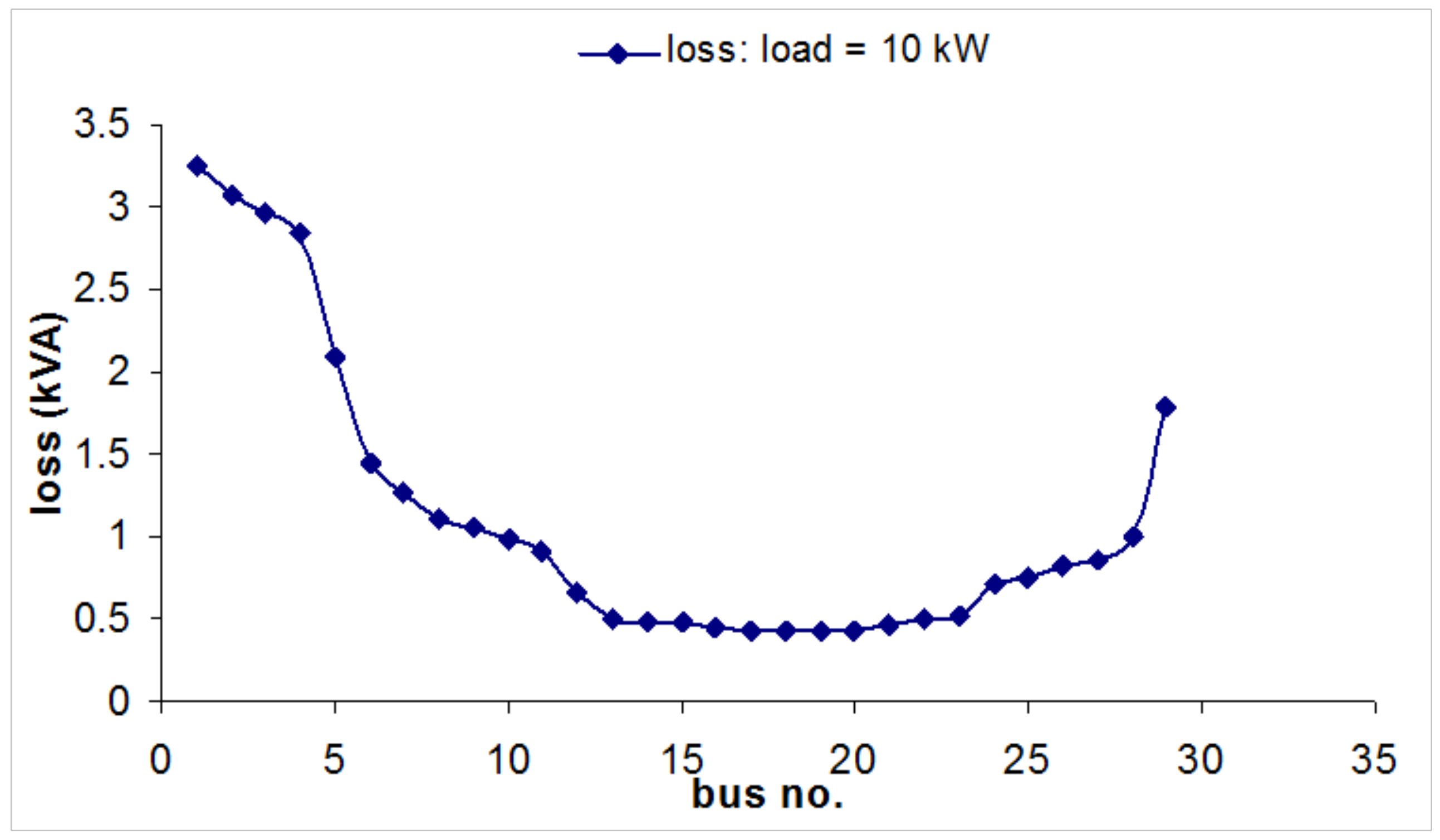
3.4. Parametric Analysis Based on Load Flow

To obtain the steady state parameters of a power network, load flow analysis needs to be done. Load flow analysis of the system gives an efficient way to the following by phase and total three-phase:

• Voltage magnitudes and angles at all nodes of the feeder
• Line flow in each line section specified in kW and kVAr, amps and degree, or amps and power factor
• Power loss in each line section
• Total feeder input kW and kVAr
• Total feeder power loss
• Load kW and kVAr based upon the specified model for the load.

Normally, load flow analysis is conducted for three phase systems, with the assumption that the phases are balanced and can be represented by a single phase. Owing to this feature, the single phase network considered in this study can also be analysed by standard balanced load flow algorithms. In this study, the Gauss–Seidel method of balanced load flow analysis [21] was conducted using the standard MATLAB code available in free software MATPOWER (Power Systems Engineering Research Center, Tempe, AZ, USA) [22].

In distribution networks, which are more resistive, the active power injection will affect the voltage profile throughout the grid and as the active power injected varies, the losses in the system also vary. For the same network topology, the optimal placement is different for different load profiles. In such a case, the PV source should be placed such that the voltage drops at any point in the worst case is within the limits. Hence, the parametric analysis of this study focuses on the node voltages and total feeder power loss with regards to the location of the PV source. As the PV microgrid is single-phase in nature, single-phase load flow analysis is performed.

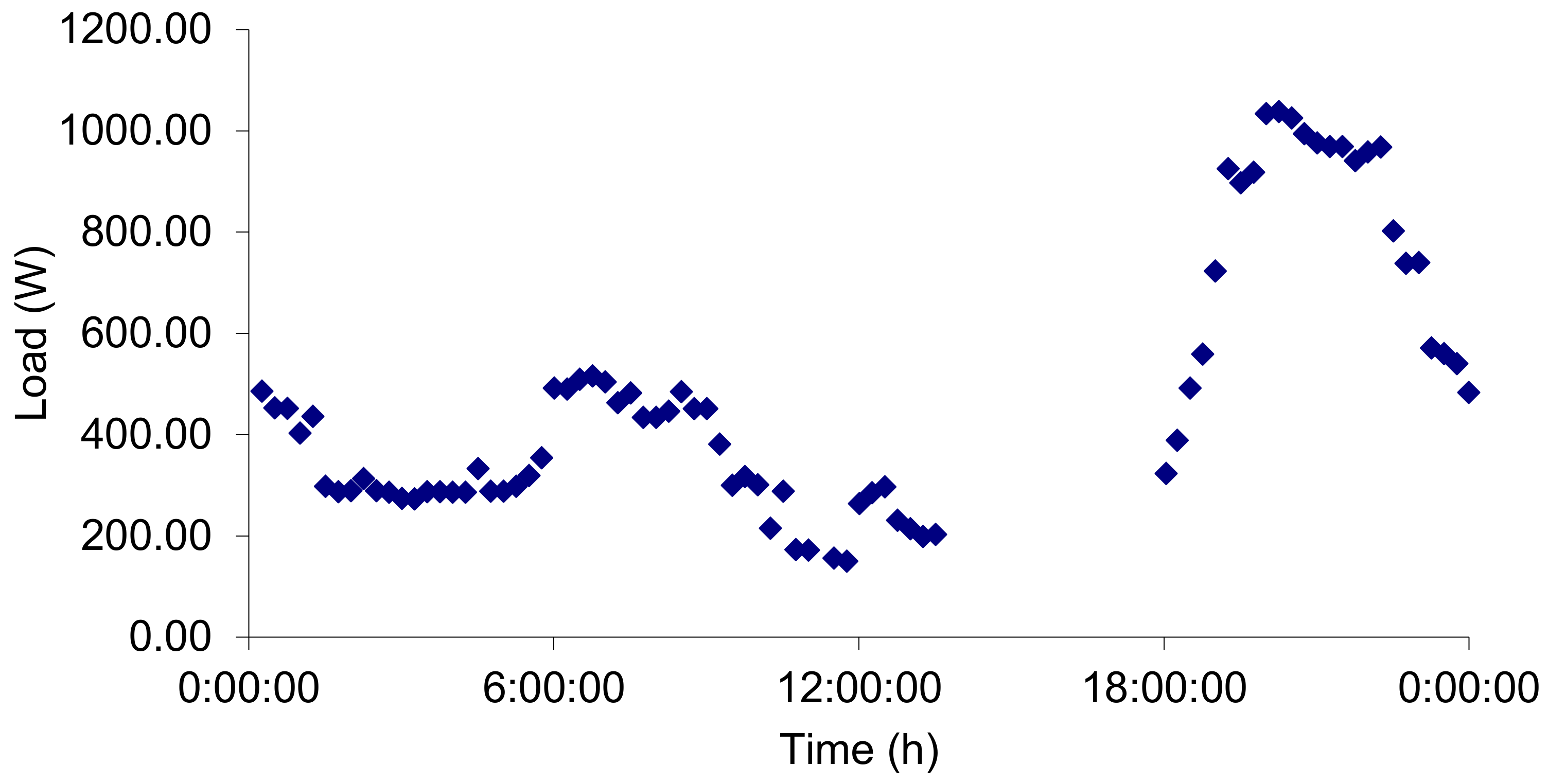
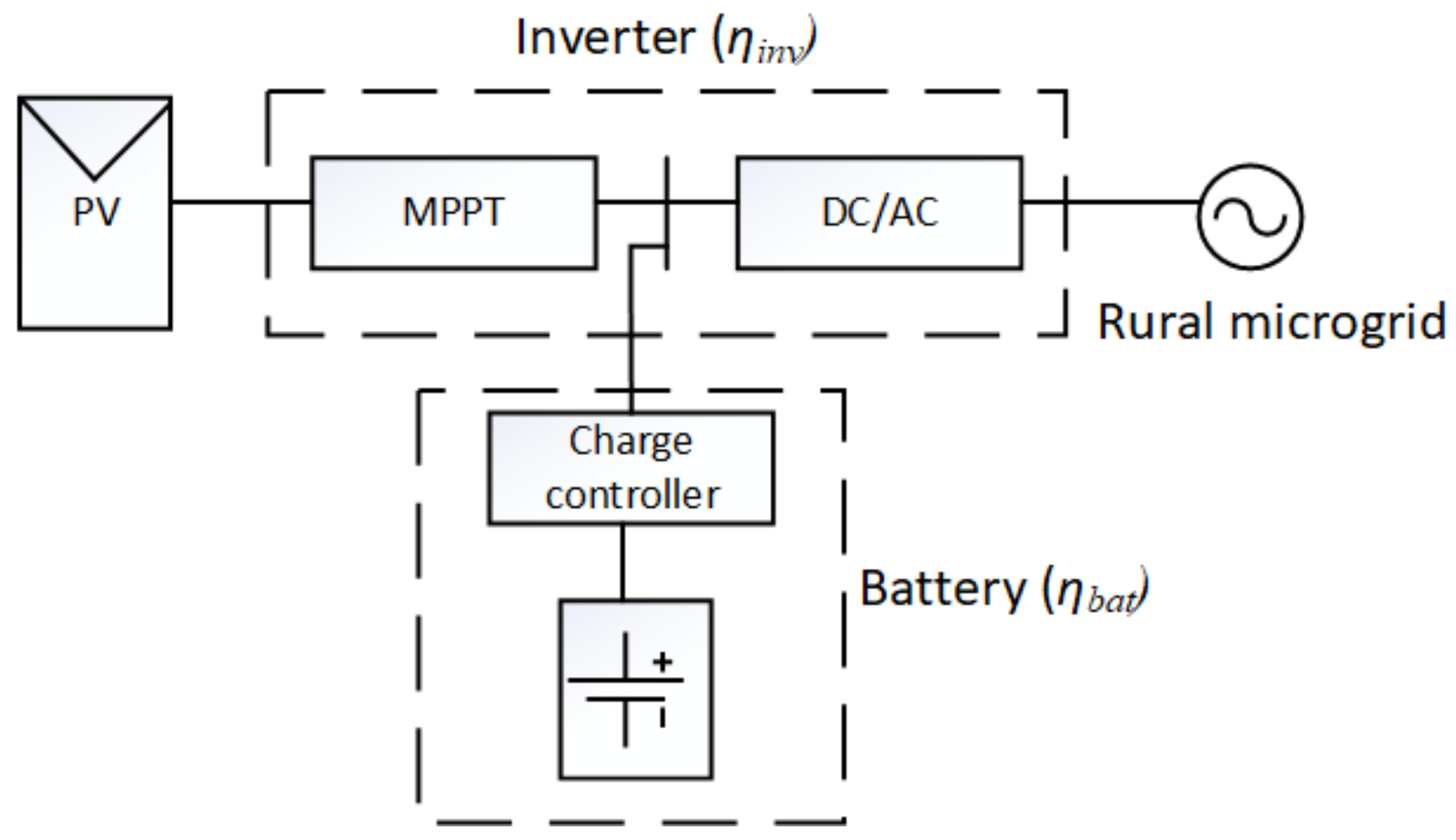
3.5. PV System Sizing

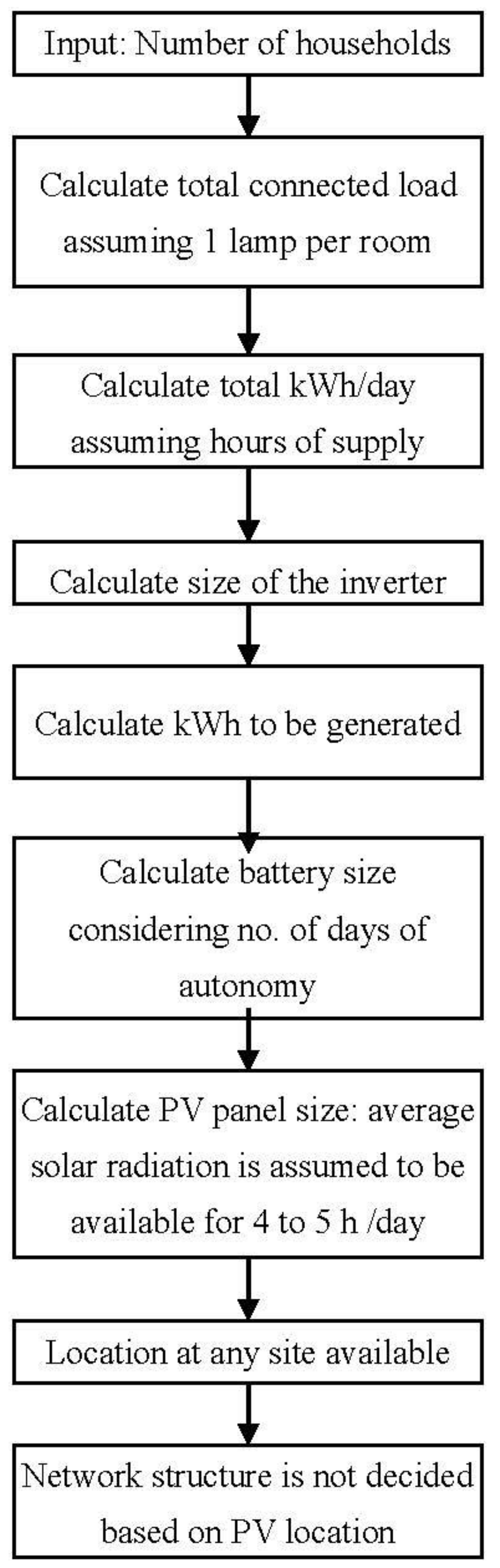
3.5.1. Pre-Sizing

Pre-sizing of the central PV system has to be based on the load curve of the remote village for a typical day. A block diagram of the PV system with its main components are shown in Figure 7. The area under the curve gives the total kWh required per day (E_d). The total energy to be generated per day by the PV array (kWh/day _{to be generated}) is determined using the inverter efficiency (η_inv) as:

$$kWh/da{y}_{to be generated}=\frac{E_d}{{\eta }_{inv}\times {\eta }_{bat}}$$

(4)

The value of η_inv is specific to the PV technology used (monocrystalline, polycrystalline, amorphous etc.) and the inverter topology (H5, HERIC etc. [23]). η_bat is the battery round trip efficiency (the fraction of energy put into the storage that can be retrieved). An η_bat of 80% can be assumed for lead acid batteries commercially available at present. With the current commercially available inverters, efficiency does not fall below 80% during PV generation hours.

The average daily energy from incident global solar insolation (I_t, unit kW/m²) at the location can be identified from meteorological data or onsite recording using pyranometers. The average daily photovoltaic energy conversion efficiency (η) will depend mainly on the PV array orientation (tilt and azimuth) and the PV technology. An η of 10% can be assumed for crystalline silicon with the current commercially available PV modules. The area of PV array is then be calculated as:

$$Area=\frac{\left(kWh/da{y}_{to be generated}\right)}{I_t\times t\times \eta }$$

(5)

where t is the average daily sunshine hours over the year.

As PV is the only source of power it is essential to include a battery bank to ensure continuity of supply. The battery size depends on the number of days of autonomy required and the permissible battery Depth of Discharge (DOD). For remote villages in India the battery technology to be considered is lead acid due to the low cost and easy availability. Lead acid batteries degrade quickly if they are completely discharged frequently. So, a DOD limit of 40% is imposed. The battery size is calculated as:

$$B=\frac{\left(\frac{kWh}{da{y}_{to be generated}}\right) \times No. of days of autonomy}{Battery DOD}$$

(6)

Typical lead acid battery has terminal voltage of 2 V/cell and 900 Ah @ C10 (i.e., it can supply at the rate of 90 A/h for 10 h before getting fully discharged).

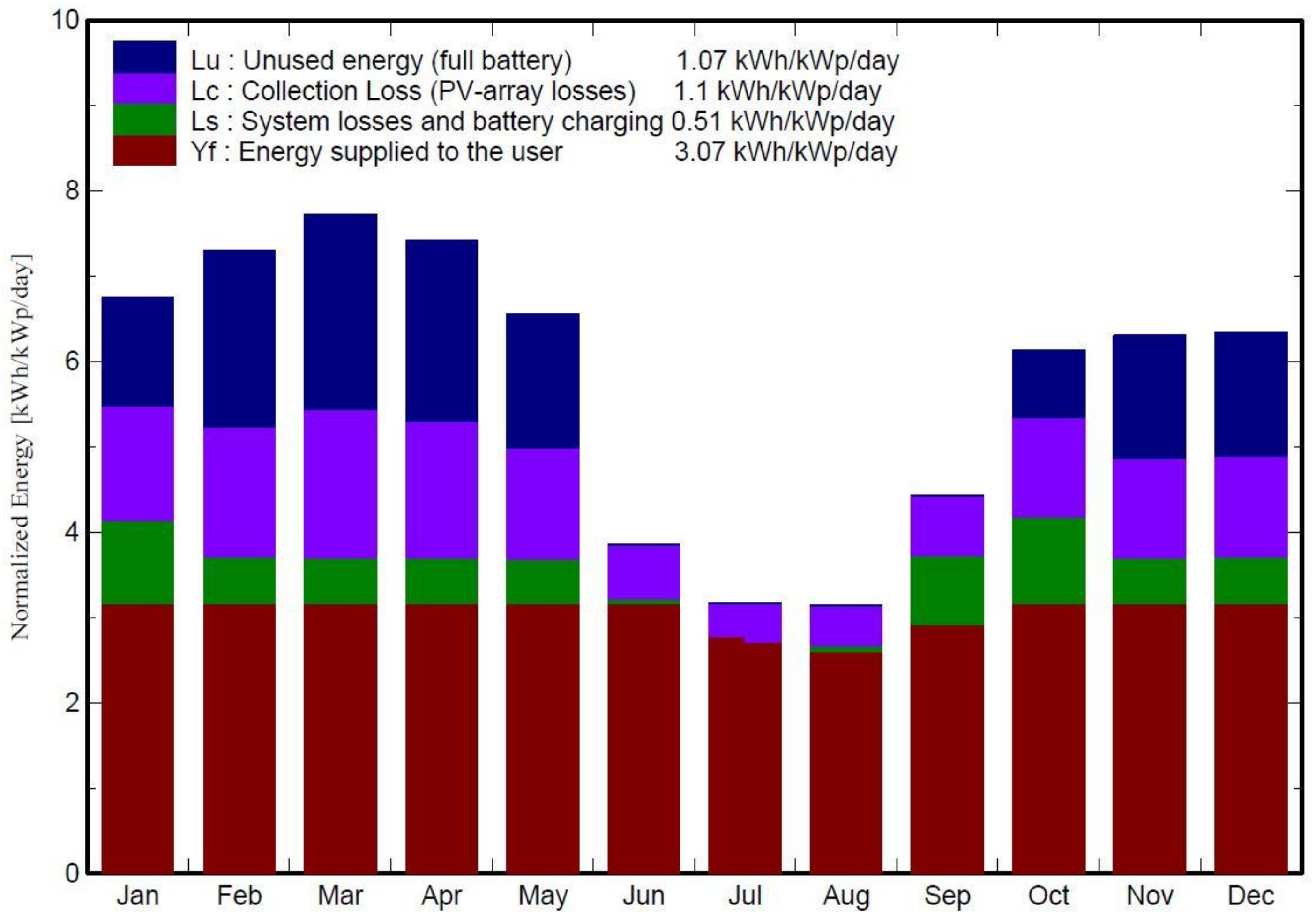
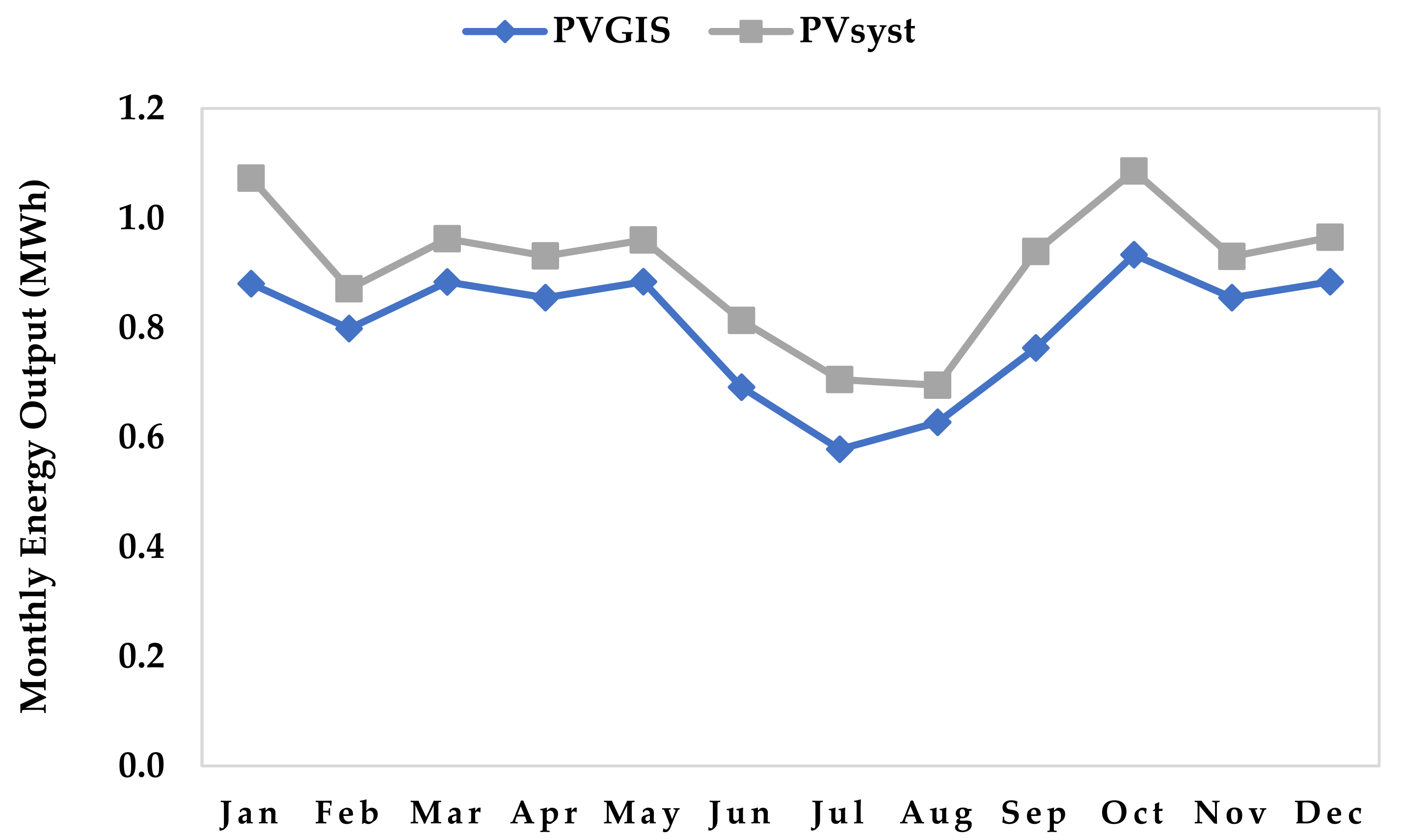
3.5.2. Detailed Design

The PV system pre-sizing does not consider the variability of the solar resource over the year. This can lead to over/underestimating the PV system size. While overestimation is financially unfavourable, underestimating can cause continuity of supply issues in months with lower solar insolation. Therefore, the availability of weather data (mainly irradiation and temperature data) for a typical meteorological year and its use in system sizing is essential. JRC (EU Joint Research Centre, Ispra, Italy) has recently released a solar dataset, SARAH which provides data for Europe, Africa, a large proportion of Asia and parts of South America [24]. The dataset is within PVGIS Climate—SAF (Photovoltaic Geographical Information System Climate Monitoring Satellite Application Facility), has a high temporal and spatial resolution and is available free of charge. JRC also provides PVGIS 5, which is a set of web-based tools for the assessment of PV systems and solar resource [25].

PVSyst™ is one of the standard software that is commonly used for design and optimisation of the PV system operation. It has been validated for different climates and PV module and inverter technologies and has an inbuilt library of currently available PV modules and inverters [26]. PVSyst™ has the facility to input meteorological data manually from different databases. For the remote village location considered, the annual energy generation for the pre-sized PV system design can be simulated using PVSyst™ based on data imported from PVGIS SARAH database. As PVSyst™ simulation considers commercially available modules and inverter parameters it can be used to modify and finalize the PV system design. For remote rural system design in India, the cost of the software could be excessive for it to be used in the PV microgrid planning stage. In such case, the web-based tools of PVGIS could be a viable alternate. Georgitsioti [27] identified that difference in PV system annual energy outputs simulated by PVGIS only differs by a few percentages from PVSyst™ outputs.

4. Results and Discussion

4.1. Location of PV System and Determination of Network Structure

4.1.1. Location of Central PV System in Terms of Spatial Distribution of Load

One of the specific objectives of the study is to determine the location of the source in terms of the spatial distribution of loads and also the network structure. Figure 8 shows the map of Ghotiya village with dark blue dots representing the location of houses. The load at each house has been considered as two Compact fluorescent lamps (CFL) lamps each of 11 W rating and a table fan of 20 W rating (total 42 W).

Algebraic sum of all moments around y-axis and x-axis are calculated and divided by the total load respectively to get the X and Y co-ordinates of the source as discussed in Section 3.2 using the following equation:

$$x_{source}=\frac{{{\displaystyle \sum }}_{i=1}^N{x}_i\times P_i}{{{\displaystyle \sum }}_{i=1}^N{P}_i};y_{source}=\frac{{{\displaystyle \sum }}_{i=1}^N{y}_i\times P_i}{{{\displaystyle \sum }}_{i=1}^N{P}_i}$$

(7)

where, $x_i$ is the x-co-ordinate of the ith load (P_i), $y_i$ is the y- co-ordinate of the ith load and N is the total number of loads.

The magenta triangle shown in Figure 8 represents the ideal central PV system location arrived at using the centre of moments approach. The central PV system in Ghotiya village should be located as close to this as possible depending on the availability of land and source of energy so that total losses are minimized.

4.1.2. Determination of Network Topology Using Simulated Annealing

The map of Ghotiya village, the location, the load points and that of central PV system based on the centre of moments approach (Figure 8), information about load sizes, equipment costs, terrain information and low voltage conductor data (sizes, voltage limits and costs) were used as the inputs to ViPOR software. The costs were taken from a sample system in ViPOR itself. Figure 9 shows the network structure for the isolated remote rural microgrid system with a central PV source generated by ViPOR. The data shown as green circles indicate that these are houses, the triangle indicates the location of the source and the blue lines represent the network feeder lines.

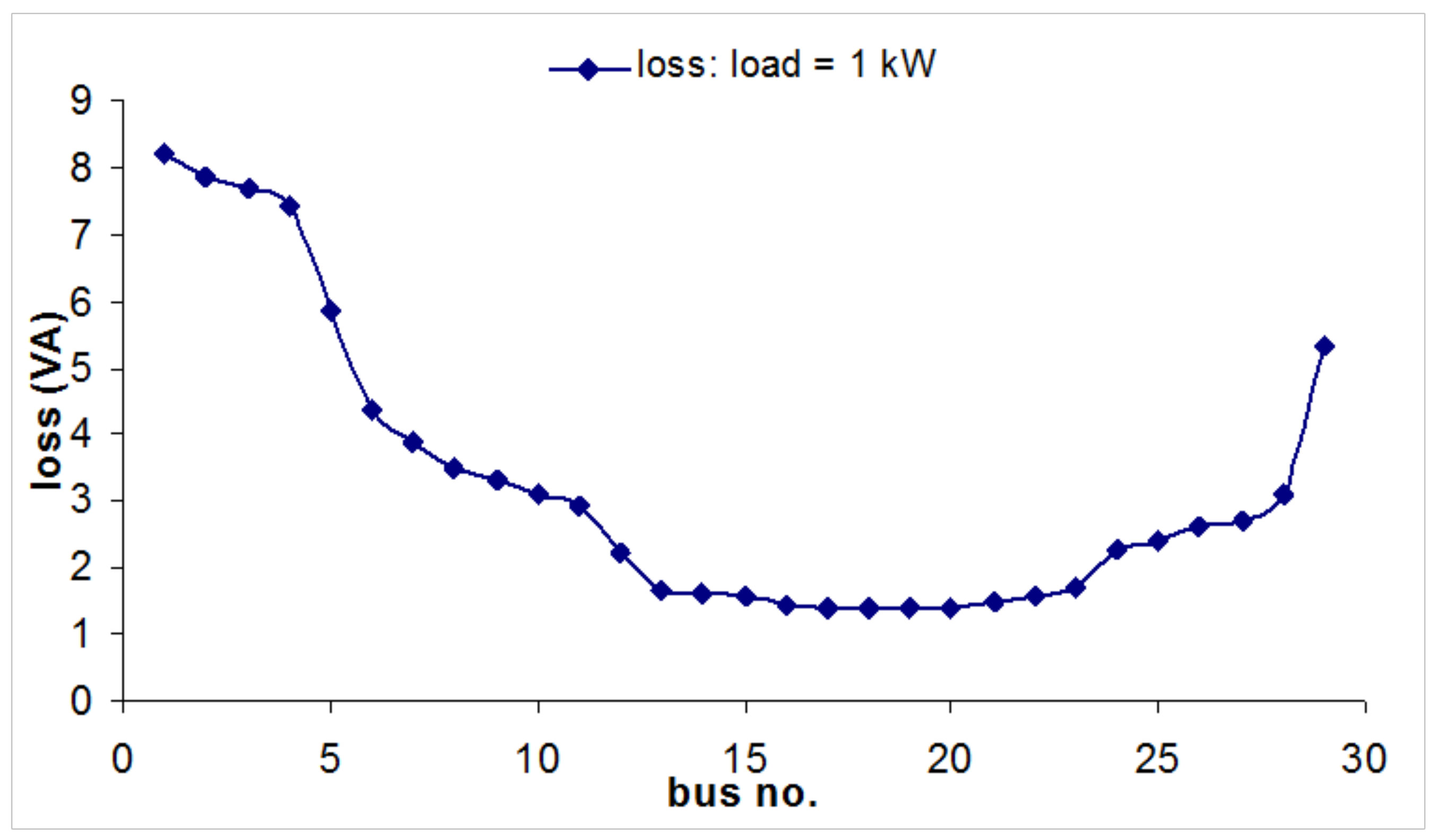
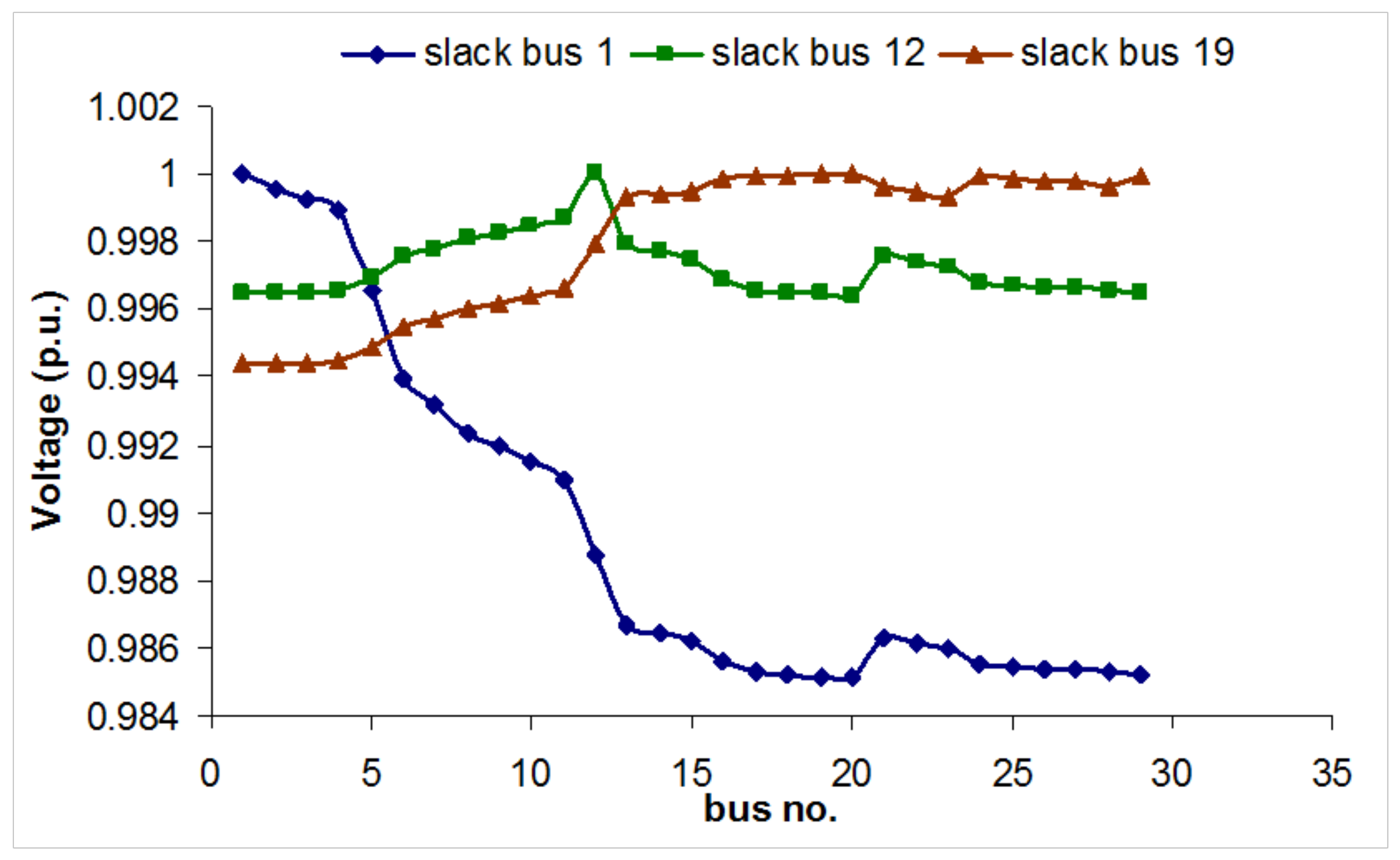
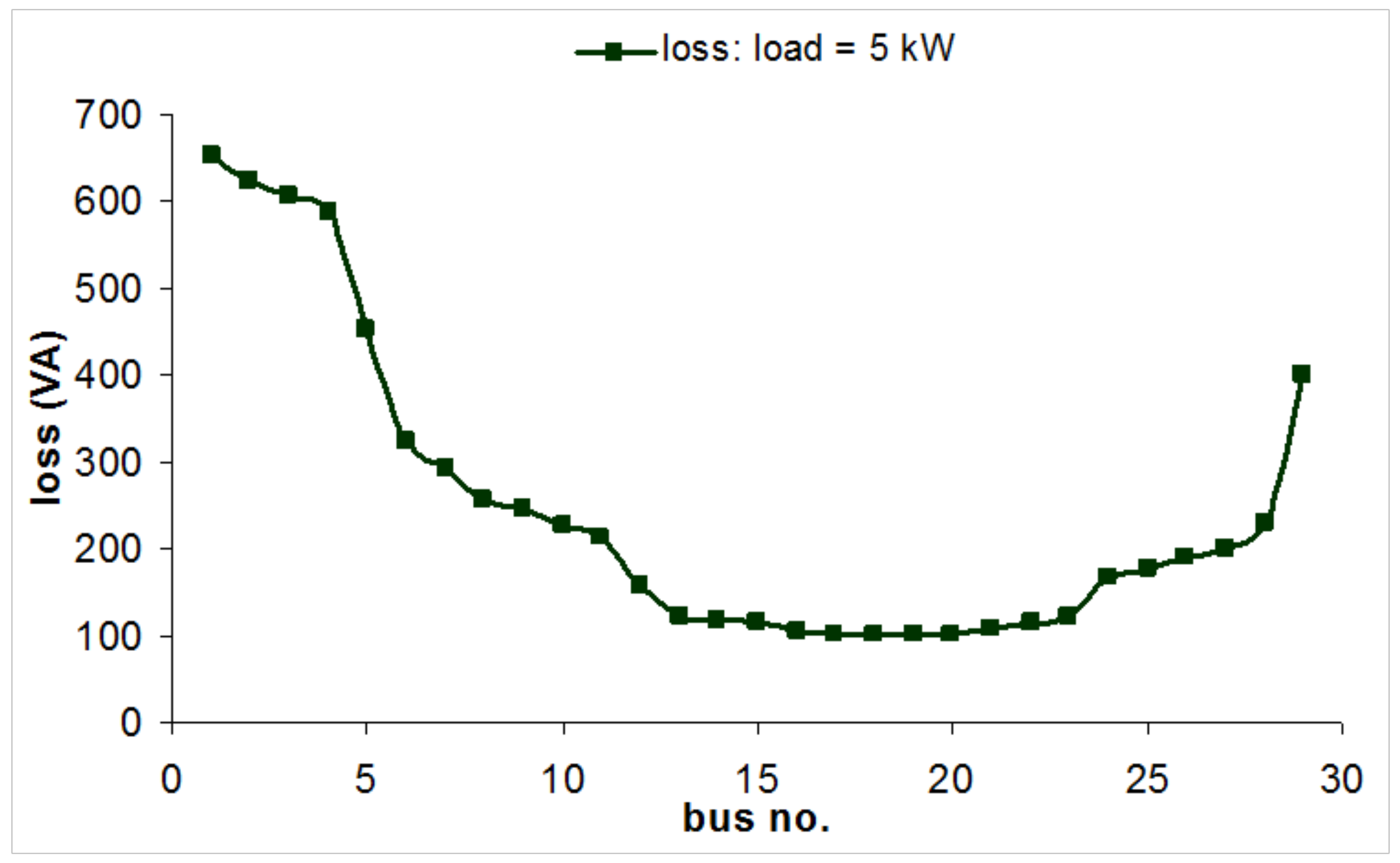
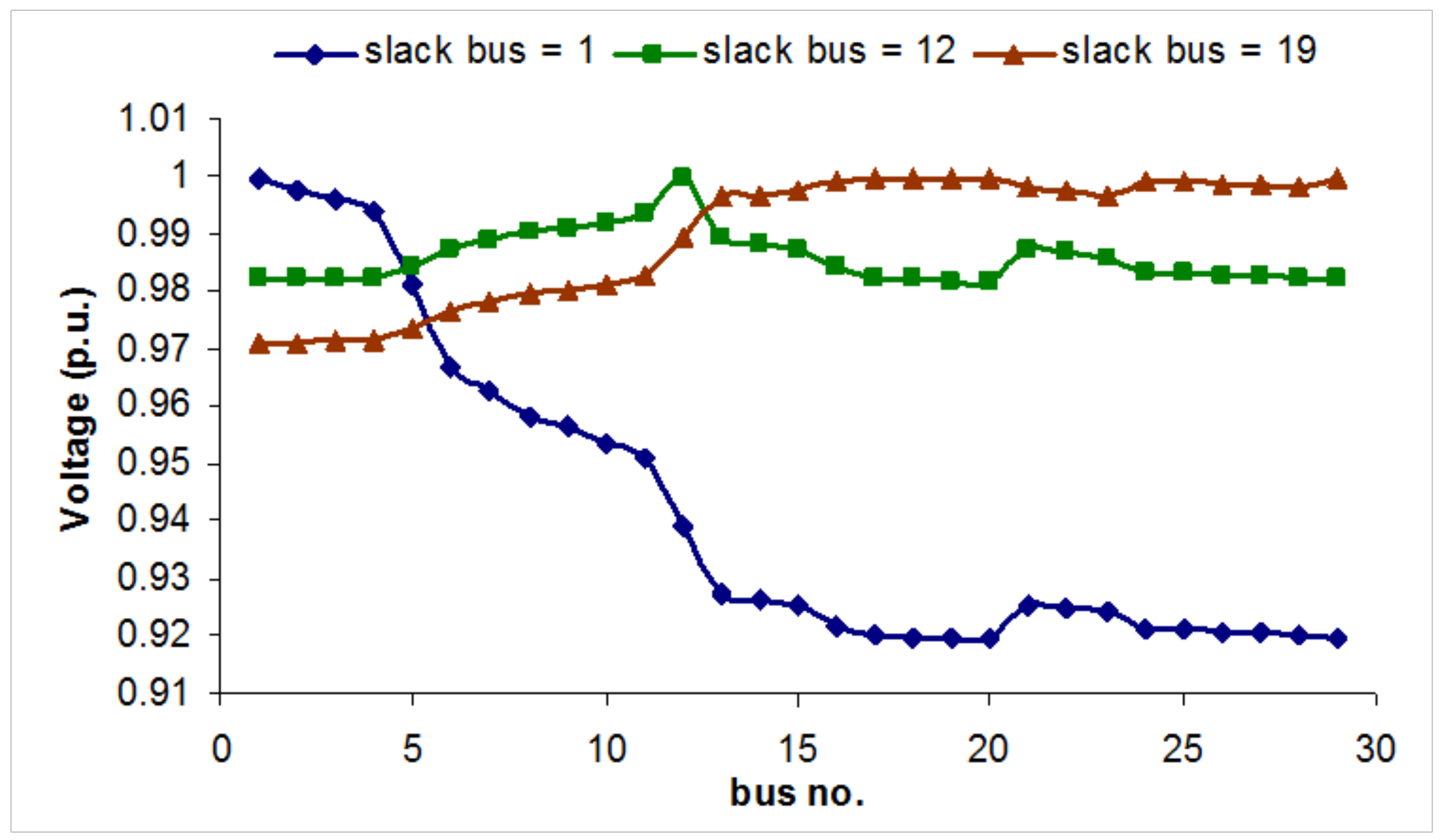
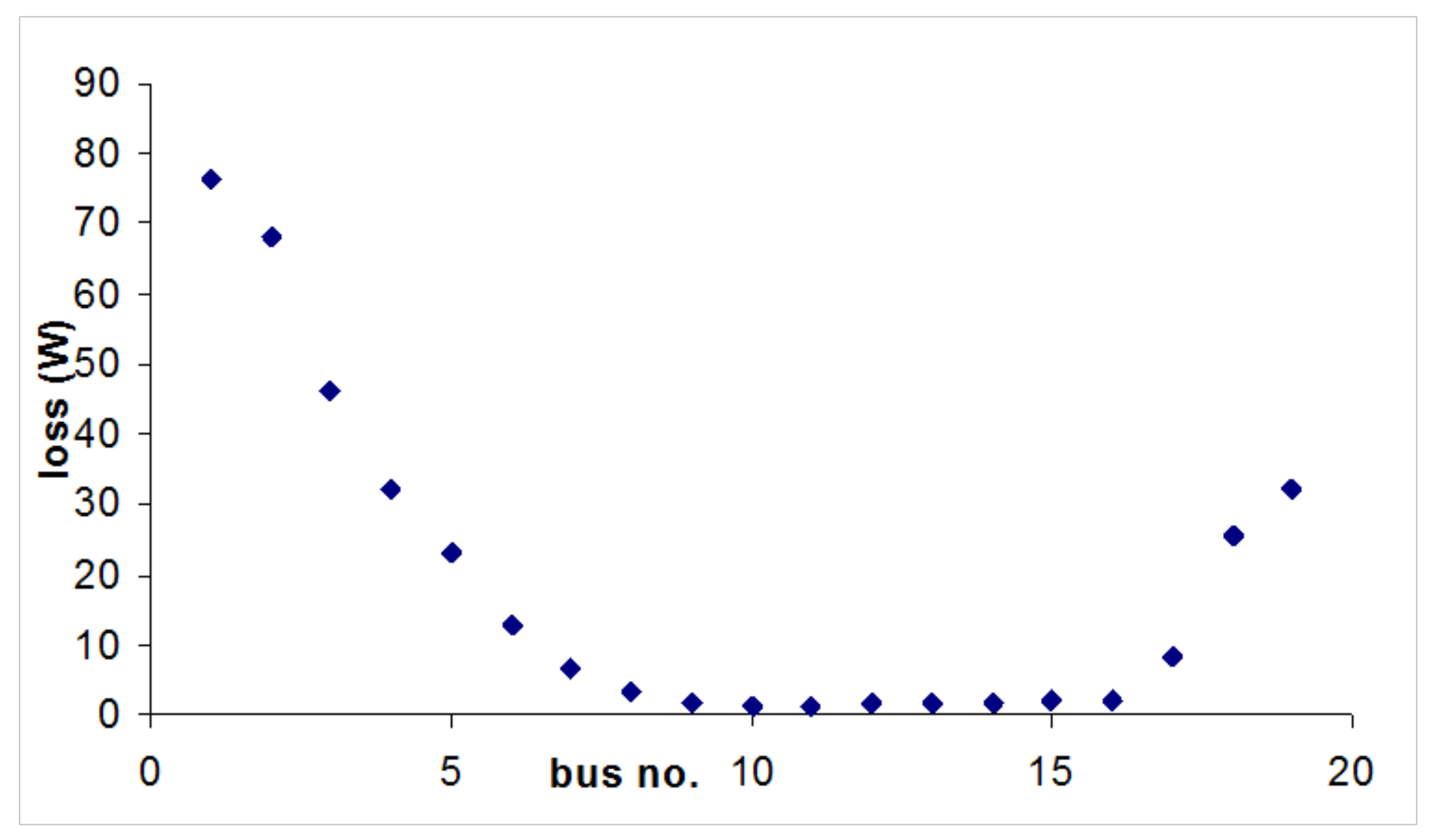
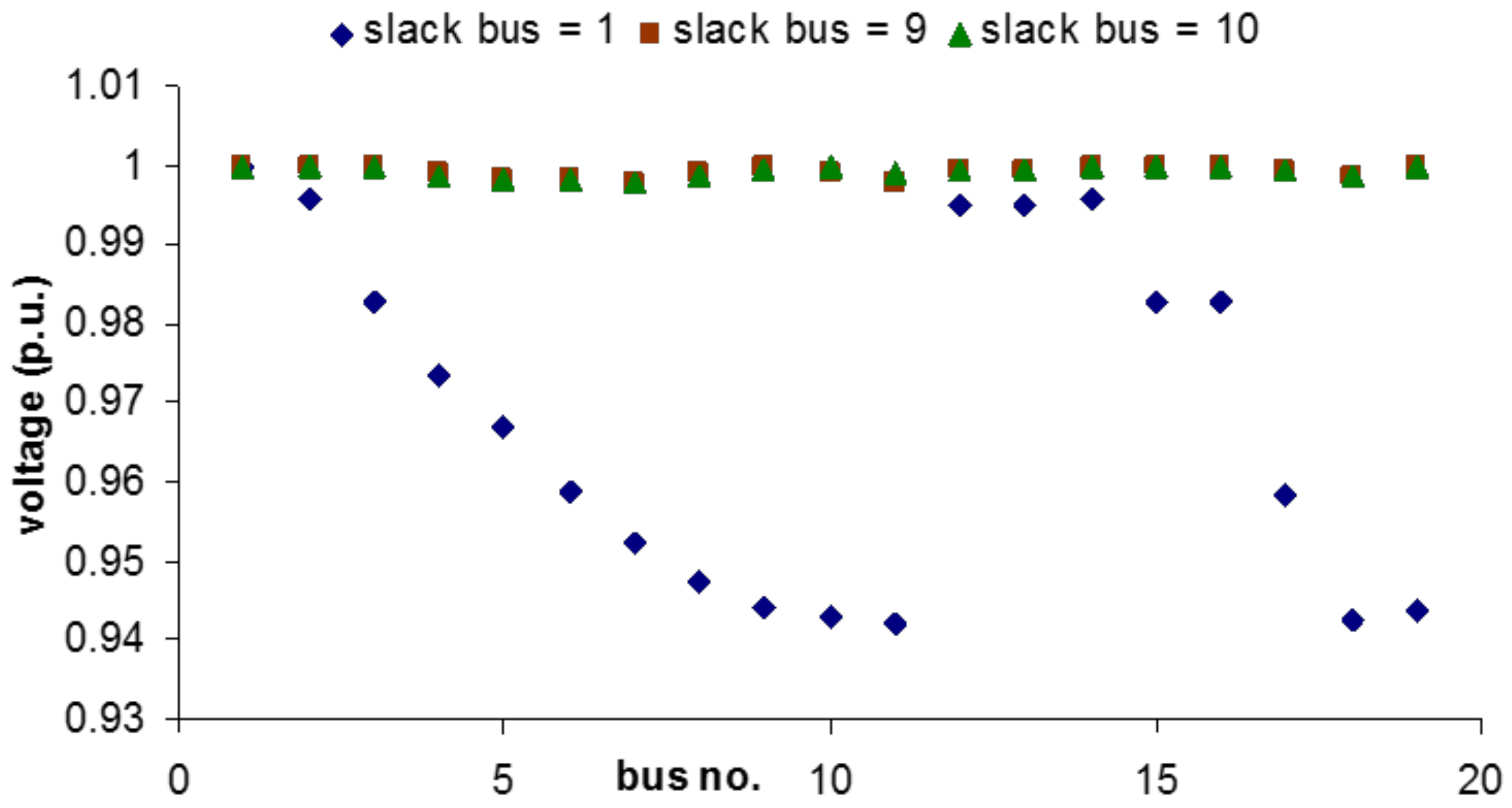
4.1.3. Parametric Analysis Using Load Flow

To estimate the steady state parameters of the network, a single-phase Gauss–Seidel load flow analysis is used.

Table 1. Branch data for the Ghotiya village network.

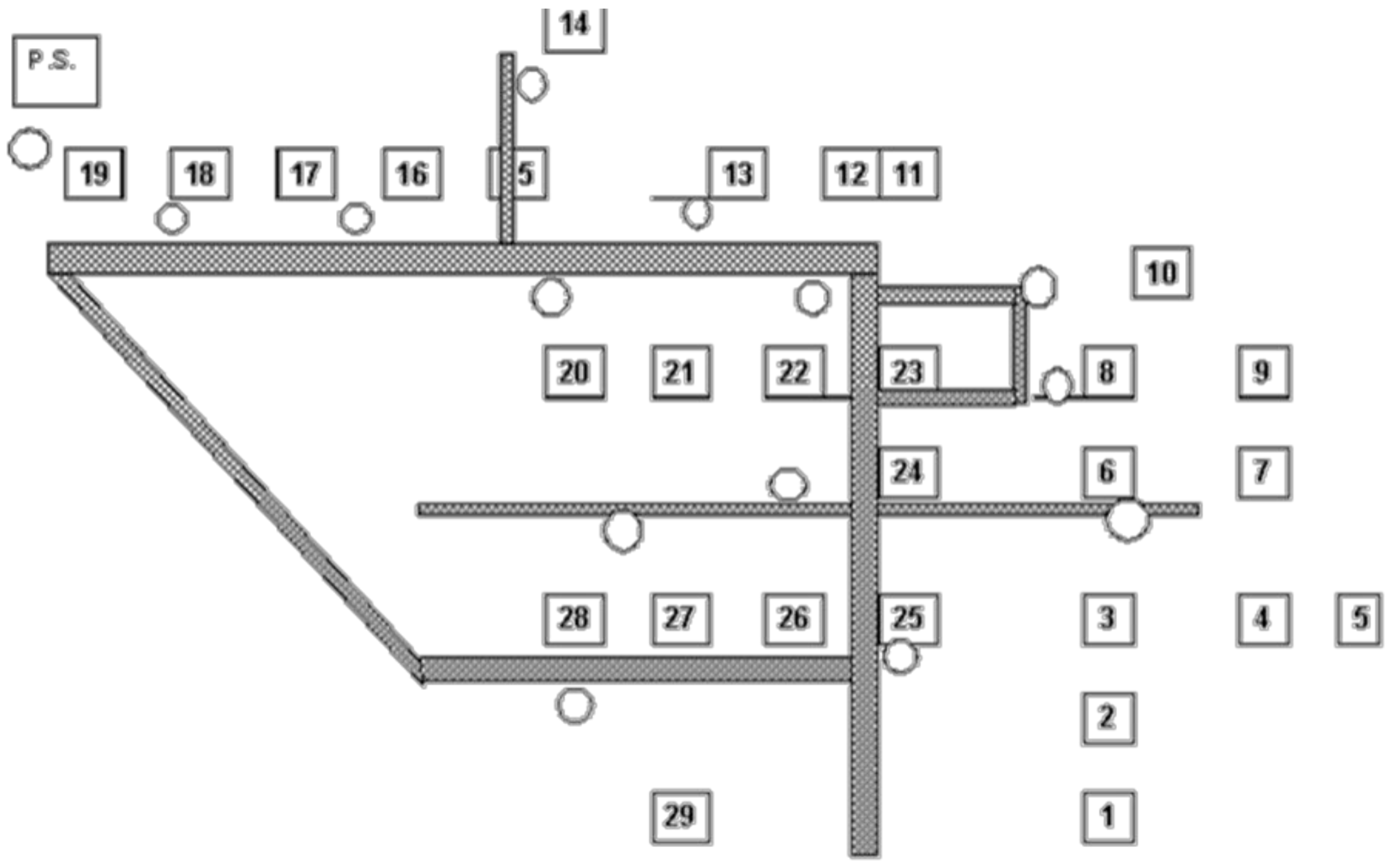
From	To	Distance (m)	R (in p.u.)	X (in p.u.)
1	2	11	0.013	0.011
2	3	11	0.013	0.011
3	4	12	0.015	0.012
3	5	78	0.095	0.076
5	6	78	0.095	0.076
6	7	59	0.072	0.057
7	8	42	0.051	0.041
8	9	12	0.015	0.012
9	10	31	0.038	0.030
10	11	31	0.038	0.030
10	12	77	0.094	0.075
12	13	94	0.115	0.091
13	14	17	0.021	0.016
14	15	56	0.068	0.054
15	16	26	0.032	0.025
16	17	13	0.016	0.013
17	18	38	0.046	0.037
15	19	39	0.048	0.038
15	20	35	0.043	0.034
20	21	20	0.024	0.019
21	22	19	0.023	0.018
22	23	19	0.023	0.018
21	24	27	0.033	0.026
13	25	59	0.072	0.057
13	26	83	0.101	0.080
26	27	14	0.017	0.014
27	28	56	0.068	0.054
28	29	63	0.077	0.061

gives the branch data for the network developed for Ghotiya village. Bus no. 12 corresponds to the source location near the point obtained by the centre of moments approach. In order to analyse the impact of the PV source location on voltage profile and losses, the load flow algorithm was run multiple times. The node on which the central PV system is connected (slack bus) was changed in each run of the load flow program until all nodes were covered. Furthermore, the location variation analysis was conducted with different load levels in order to identify the impact of loading levels on the PV source location.

As the system is rural, a fixed power factor of 0.6 pf lagging was considered. Three values of total connected load of 1 kW, 5 kW and 10 kW were considered. Figure 10 and Figure 11 respectively show the variation of apparent power losses and voltage profile with location of PV source for a load level of 1 kW. The corresponding variations for a load of 5 kW is shown in Figure 12 and Figure 13, and for a load of 10 kW is shown in Figure 14 and Figure 15.

The losses amount to only 1% of total load when the total connected load considered is 1 kW. However, the percentage reduction in losses is high (around 80%) when placement of the PV source is varied from bus no. 1 to bus no. 19. In this case, economics will play a major role as the absolute value of the losses is very small.

As the load is increased from 1 kW to 5 kW, it can be observed that the voltage at the extreme buses tends to drop below 0.95 p.u., which is not acceptable. Here again the percentage reduction of losses is around 80% and the total loss amounts to around 8% of total load when placed in bus no. 1.

When the load is increased from 5 kW to 10 kW it can be observed that the total losses account to around 20% of the total connected load. Hence, in this system both losses and voltage profiles need to be considered for optimization. A total connected load of 10 kW is at the higher end of the loading level. Normally, when the load increases, the spatial distribution of loads and the area covered by the system increase. When the feeder lengths increase, voltage drop will become a more stringent constraint and losses may account for more than 20% of the total load.

From Figure 14 it can be observed that even when the load is increased to 10 kW the voltage drop remains within limits when the PV source is connected to bus no. 12 as compared to bus no. 1. This confirms that the PV source location and network structure determined in Section 4.1.1 and Section 4.1.2 are optimal.

5. PV Microgrid Design Method for Rural Electrification

Based on the analysis presented in Section 4.1.1, Section 4.1.2 and Section 4.1.3 and findings from the literature, an improved method for the design of isolated PV microgrids for rural electrification is proposed as in Figure 16.

Illustration of Proposed Method

For illustration purposes, it is assumed that the village of Rajmachi, Maharashtra is yet to be electrified. The map as obtained from MEDA (Figure 4) is used. The details of the total connected load estimation are given in

Table 2. Load data of Rajmachi village.

Load	No. of Units	Wattage	Coverage (fraction)	Connected Load (W)	No. of Households	Total
Domestic Lighting	3	11	1	33	29	957
Street Lights	1	11	0.5	5.5	29	159.5
Fans	1	40	0.5	20	29	580
Refrigeration	1	100	-	100	29	100
Television	1	80	0.4	32	29	928
Radio	1	5	0.4	1.75	29	58
Other Loads	1	100	0.1	10	29	290

. The total connected load is around 3 kW. The load curve obtained from the case study (Figure 6) is normalized and then multiplied by 3 to get the load curve for the estimated connected load as shown in Figure 17.

The area under the curve gives the total kWh required per day which is 28.5 kWh for the considered case. Inverter and battery round trip efficiencies are assumed to be 80%; this gives the total energy to be generated per day as 44.5 kWh. The total global horizontal irradiation energy available over PV generation hours (E_d) at the location is 5.037 kWh/m²/day (source PVGIS CMSAF). Considering monocrystalline PV technology, the average daily system efficiency (η) is assumed to be 10%. The PV array is calculated using (4) as approx. 88 m². A generic 75 Wp monocrystalline PV module of length 1208 mm and width 538 mm is considered. For an area of 10 m², a series parallel arrangement of the 75 Wp module is equivalent to 1 kWp. Hence, the rating of the central PV system for Rajmachi is estimated as 8.9 kWp. Battery size calculated using (5) lead to an energy rating of 223 kWh. The autonomy considered was 2 days. The battery bank voltage is assumed to be 48 V. This gives the battery bank specification as 24 cells in series and 6 such strings in parallel.

The map of the village and the load magnitudes are used to calculate the location of the source which reduces the total losses (using the centre of moments approach). The load points and the PV system location determined are shown in Figure 18. These are given as input to ViPOR for determining the network structure. In the ViPOR simulation, the connected load is clubbed at some points where the distance between the houses is less than 5 m. The optimum network structure obtained using simulated annealing is shown in Figure 19. The actual source location at the village site is also shown. Evidently, the actual source location is not optimum as the total loss in the system is not minimized.

Figure 20 shows the variation of losses and Figure 21 gives the variation of voltage profile with respect to location of the PV system resulting from the parametric analysis. Even for the comparatively low total connected load, the losses amount to around 5% of the load value. The improvement in losses is very high (around 98%, from 76 W to 2 W) when the location of the PV source is changed from bus no. 1 to bus no. 10 (identified as optimal from centre of moments analysis). The voltage profile also shows considerable improvement on varying the location of the PV source. With the present location even at a nominal load of 1.5 kW the voltage at the bus furthest from the source is 0.95 p.u. This indicates that when the system operates at even half the total load rating, the voltage at the last nodes/buses will be less than 0.95 (which is the minimum statutory voltage limit). This result also matches the actual voltage at the furthest house point measured experimentally. For the actual system in Rajmachi, the houses are clustered in the midst of the village which makes it difficult for the placement of the PV system close to bus no. 10.

Central PV System Design

The PV system and battery sizes (8.9 kWp and 48 V, 5400 Ah, respectively) obtained from pre-sizing were used as inputs to both PVsyst™ and PVGIS5 online software. The meteorological data of Rajmachi village (Latitude 18.826° N, Longitude 73.396° E) was imported into PVsyst™ from the PVGIS Climate SAF database. Figure 22 shows the monthly PV energy output simulated by PVGIS5 for a typical meteorological year normalised per kWp. Figure 23 shows the monthly PV energy output estimates normalised per kWp obtained from the detailed PVsyst™. The PV array size had to be increased to 9 kWp to match with commercial module specifications from 8.9 kWp. The figure also shows PV array losses (due its orientation, module temperature and insolation coefficients etc.), the rest of system losses (due to Maximum Power Point Tracking (MPPT), due to battery charging and discharging etc.) and PV energy unused (due to battery being fully charged). A detailed description of the losses and the calculation methodology is available on PVsyst’s user manual and the software vendor’s website.

The seasonal variation in PV energy output obtained from both software are very similar. From a comparison of the monthly energy outputs as shown in Figure 24, it was observed that the output estimated by PVGIS is marginally lower than that from PVsyst™. Over the year, PVGIS energy outputs were 12% lower than PVsyst™ on average. This is expected as the PVsyst™ design is detailed and uses data of commercially available PV modules and batteries whilst PVGIS is based on generic PV and battery models. As PVGIS online tool does not overestimate PV generation potential, it could be a viable alternative in the absence of detailed design software like PVsyst™.

It was noticed from both PVsyst™ and PVGIS simulations that the ratings of the PV system and battery from pre-sizing were inadequate for supplying the load. As per PVsyst™ calculations, the system design would lead to a shortage of 0.32 MWh/year. The design was modified to alleviate energy shortage for the consumers and the final rating of the PV array was found to be 9.9 kWp and the battery bank rating 48 V, 7200 Ah. The main parameters of the system are shown in

Table 3. The main parameters of the central PV system from the final PVsyst design.

Parameter	Value
PV module technology	Monocrystalline Silicon
Manufacturer and model	Ecosol PV tech Mono 75 Wp 36 cells
No. of PV modules in series	4
No. of parallel strings	33
Array nominal (STC) power	9.9 kWp
MPPT converter maximum and European efficiencies	97%/95%
Battery technology	Lead acid
Battery bank voltage	48 V
Nominal capacity	7200 Ah
Number of units	24 in series × 8 in parallel

.

6. Conclusions

Microgrids based on a central PV system could be a potential way forward for the electrification of isolated remote villages in developing countries. This is subject to the country having a good solar resource. PV technology is particularly suited for remote location with difficult terrains due to the modularity of the technology and the lowering technology costs. It was identified that unlike larger isolated power systems, rural microgrids have a low energy demand as the loads are mainly residential and street lighting. Hence, these microgrids could be of a single-phase configuration. The literature on microgrids and the standard test distribution network are for three-phase systems with high power factor, which is not the case for rural microgrids in developing countries. Furthermore, the typical procedure followed currently by planners of rural networks is not comprehensive as it does not consider the importance of PV source siting and optimisation of network structure.

The centre of moments approach (Section 3.2) can be used for identifying the optimal location of the central PV source in a rural microgrid. The determination of network structure is a complex problem owing to the number of variables to be considered such as location map, terrain information, conductor costs etc. It can be solved as an optimisation problem using simulated annealing. Load flow analysis can determine voltage profiles and power losses. Hence, a parametric analysis based on load flow can confirm the PV source location for the network structure developed. Hence an improved PV microgrid design procedure was introduced in this work based on these methods and survey of existing isolated power systems. Two isolated remote villages in India with existing PV microgrids namely Ghotiya village, Chattisgarh and Rajmachi village, Maharashtra are used as case studies. The case study of Ghotiya village was used to formulate the design procedure and that of Rajmachi village to illustrate the design procedure. A comparison of industrial standard PV system design software PVsyst™ and free online tool PVGIS5 from JRC indicated that PVGIS5 could be a viable alternative for designing the central PV system in the microgrid. At present, water-pumping and other irrigation loads in remote villages are fed by independent standalone PV systems. Future work is expected to focus on their integration into the village microgrid.