Suitability of Electrical Coupling in Solar Cell Thermoelectric Hybridization
Abstract
1. Introduction
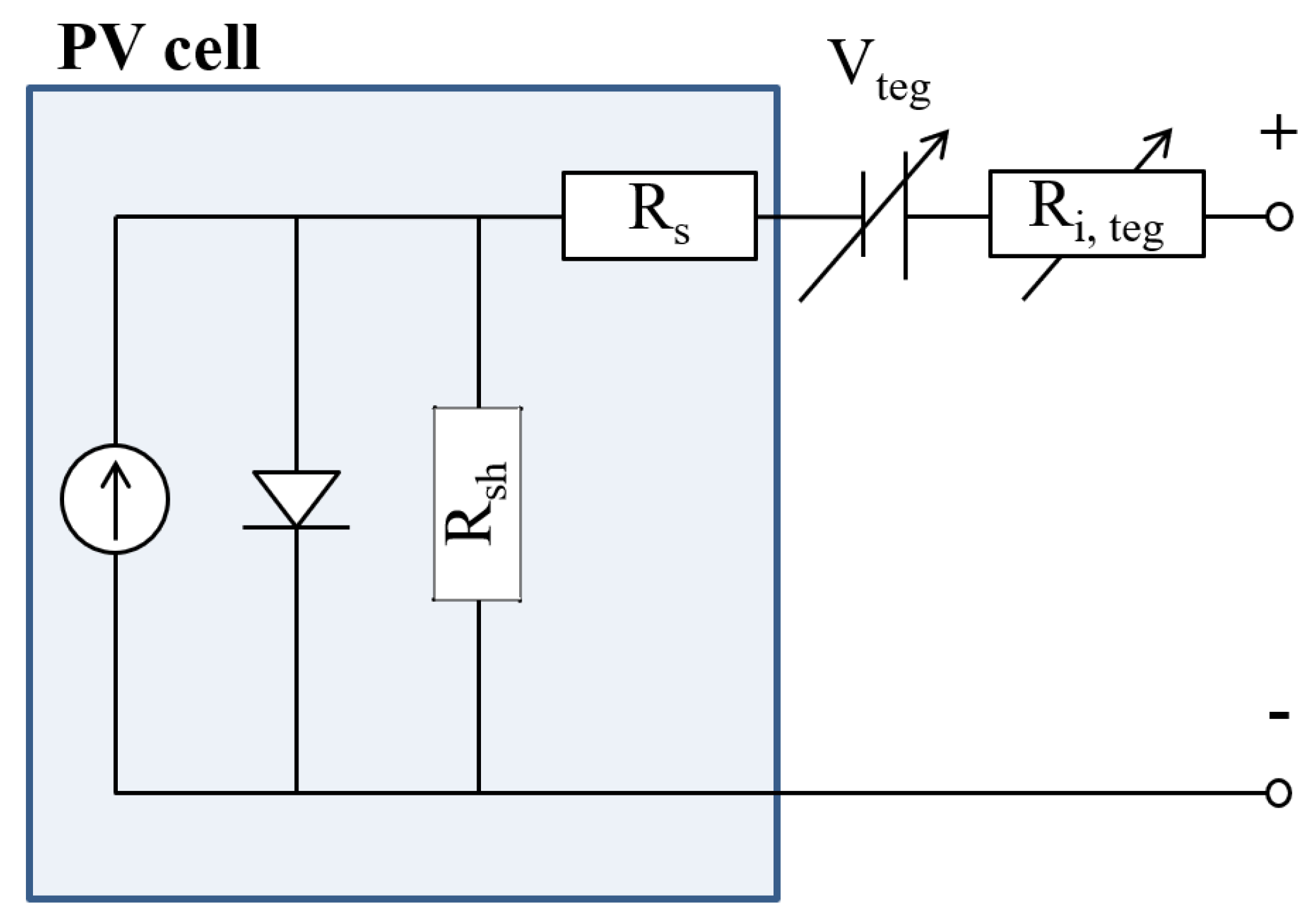
2. Materials and Methods
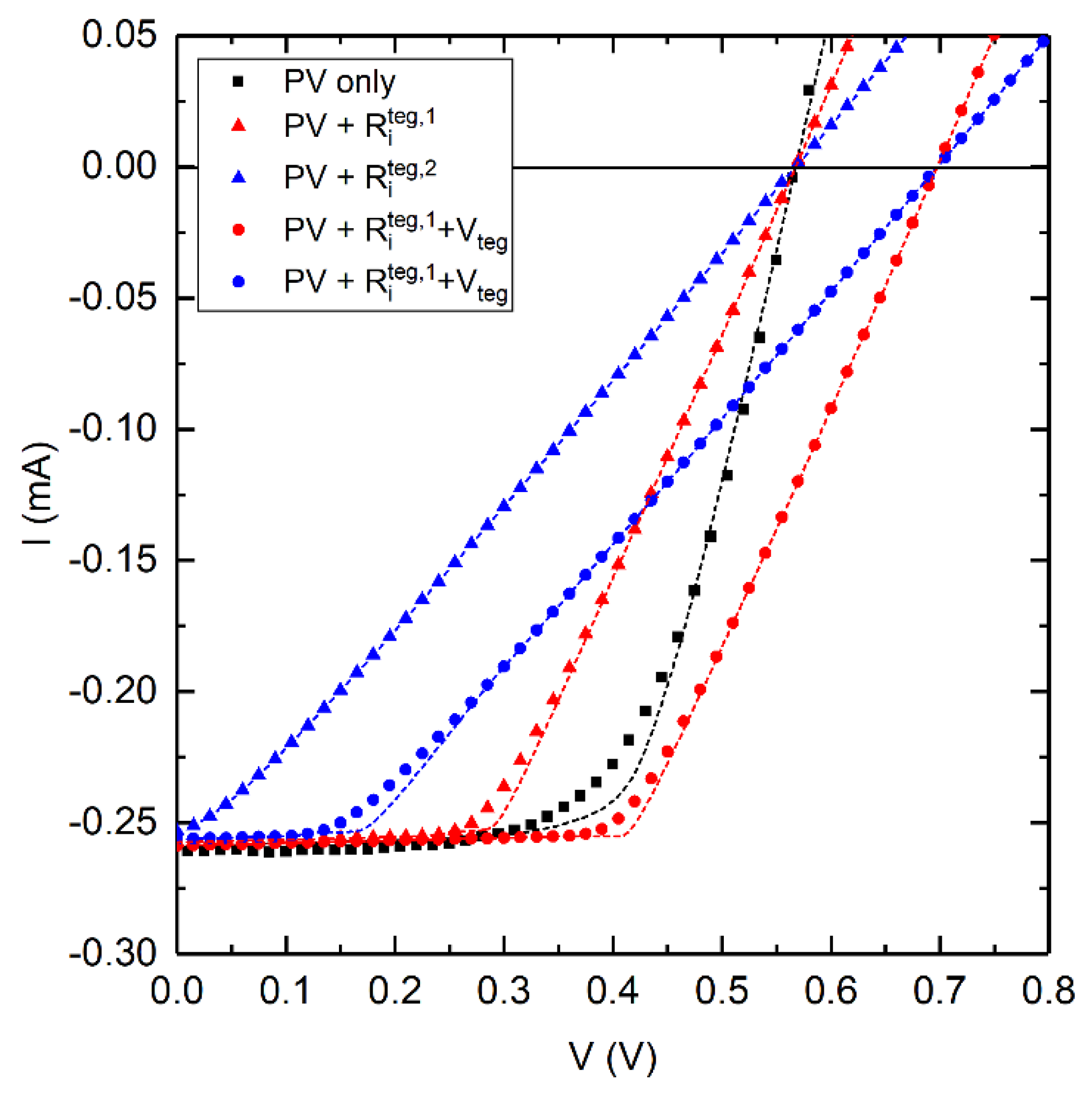
3. Results
3.1. Lossless Conditions
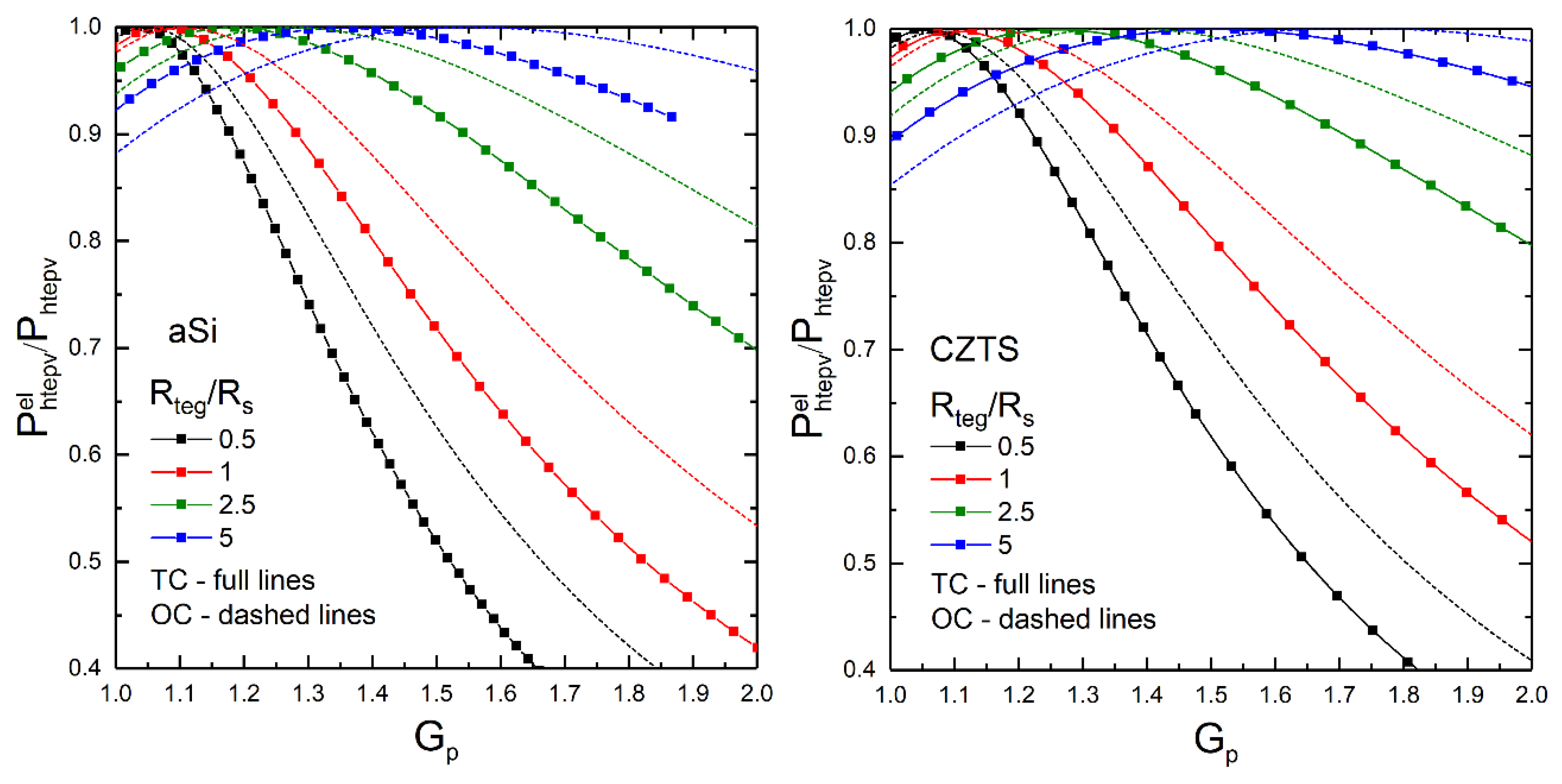
3.2. vs Lossless Conditions
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chow, T.T. A review on photovoltaic/thermal hybrid solar technology. Appl. Energy 2010, 87, 365–379. [Google Scholar] [CrossRef]
- Yazawa, K.; Shakouri, A. System optimiztion of hot water concentrated solar thermoelectric generation. In Proceedings of the Thermal Issues Emerging Technologies, ThETA 3, Cairo, Egypt, 19–22 December 2010; pp. 283–290. [Google Scholar]
- Tyagi, V.V.; Kaushik, S.C.; Tyagi, S.K. Advancement in solar photovoltaic/thermal (PV/T) hybrid collector technology. Renew. Sustain. Energy Rev. 2012, 16, 1383–1398. [Google Scholar] [CrossRef]
- Vorobiev, Y.; González-Hernández, J.; Vorobiev, P.; Bulat, L. Thermal-photovoltaic solar hybrid system for efficient solar energy conversion. Sol. Energy 2006, 80, 170–176. [Google Scholar] [CrossRef]
- Chavez-Urbiola, E.A.; Vorobiev, Y.V.; Bulat, L.P. Solar hybrid systems with thermoelectric generators. Sol. Energy 2012, 86, 369–378. [Google Scholar] [CrossRef]
- Narducci, D.; Lorenzi, B. Challenges and perspectives in tandem thermoelectric-photovoltaic solar energy conversion. IEEE Trans. Nanotechnol. 2016, 15, 348–355. [Google Scholar] [CrossRef]
- Li, Y.; Witharana, S.; Cao, H.; Lasfargues, M.; Huang, Y.; Ding, Y. Wide spectrum solar energy harvesting through an integrated photovoltaic and thermoelectric system. Particuology 2014, 15, 39–44. [Google Scholar] [CrossRef]
- Zhang, J.; Xuan, Y.; Yang, L. Performance estimation of photovoltaic-thermoelectric hybrid systems. Energy 2014, 78, 895–903. [Google Scholar] [CrossRef]
- Liao, T.; Lin, B.; Yang, Z. Performance characteristics of a low concentrated photovoltaic-thermoelectric hybrid power generation device. Int. J. Therm. Sci. 2014, 77, 158–164. [Google Scholar] [CrossRef]
- Bjørk, R.; Nielsen, K.K. The performance of a combined solar photovoltaic (PV) and thermoelectric generator (TEG) system. Sol. Energy 2015, 120, 187–194. [Google Scholar] [CrossRef]
- Cui, T.; Xuan, Y.; Li, Q. Design of a novel concentrating photovoltaic–thermoelectric system incorporated with phase change materials. Energy Convers. Manag. 2016, 112, 49–60. [Google Scholar] [CrossRef]
- Li, D.; Xuan, Y.; Li, Q.; Hong, H. Exergy and energy analysis of photovoltaic-thermoelectric hybrid systems. Energy 2017, 126, 343–351. [Google Scholar] [CrossRef]
- Beeri, O.; Rotem, O.; Hazan, E.; Katz, E.A.; Braun, A.; Gelbstein, Y. Hybrid photovoltaic-thermoelectric system for concentrated solar energy conversion: Experimental realization and modeling. J. Appl. Phys. 2015, 11. [Google Scholar] [CrossRef]
- Luo, B.; Deng, Y.; Wang, Y.; Gao, M.; Zhu, W.; Hashim, H.T. Synergistic photovoltaic–thermoelectric effect in a nanostructured CdTe/Bi2Te3 heterojunction for hybrid energy harvesting. RSC Adv. 2016, 6, 114046–114051. [Google Scholar] [CrossRef]
- Yan, X.; Poudel, B.; Ma, Y.; Liu, W.S.; Joshi, G.; Wang, H. Experimental studies on anisotropic thermoelectric properties and structures of n-type Bi2Te2.7Se0.3. Nano Lett. 2010, 10, 3373–3378. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Xiong, Y.; Mei, A.; Hu, Y.; Rong, Y.; Zhou, Y. Efficient perovskite photovoltaic-thermoelectric hybrid device. Adv. Energy Mater. 2018, 8, 1702937. [Google Scholar] [CrossRef]
- Narducci, D.; Bermel, P.; Lorenzi, B.; Wang, N.; Yazawa, K. Hybrid and Fully Thermoelectric Solar Harvesting, 1st ed.; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Lorenzi, B.; Contento, G.; Sabatelli, V.; Rizzo, A.; Narducci, D. Theoretical analysis of two novel hybrid thermoelectric–photovoltaic systems based on CZTS solar cells. J. Nanosci. Nanotechnol. 2017, 17, 1608–1615. [Google Scholar] [CrossRef] [PubMed]
- Contento, G.; Lorenzi, B.; Rizzo, A.; Narducci, D. Efficiency enhancement of a-Si and CZTS solar cells using different thermoelectric hybridization strategies. Energy 2017, 131, 230–238. [Google Scholar] [CrossRef]
- Fisac, M.; Villasevil, F.X.; López, A.M. High-efficiency photovoltaic technology including thermoelectric generation. J. Power Sources 2014, 252, 264–269. [Google Scholar] [CrossRef]
- Park, K.T.; Shin, S.M.; Tazebay, A.S.; Um, H.D.; Jung, J.Y.; Jee, S.W. Lossless hybridization between photovoltaic and thermoelectric devices. Sci. Rep. 2013, 3, 422–427. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhou, K.; Song, Z.; Zhao, X.; Ji, J. Inconsistent phenomenon of thermoelectric load resistance for photovoltaic–thermoelectric module. Energy Convers. Manag. 2018, 161, 155–161. [Google Scholar] [CrossRef]
- Verma, V.; Kane, A.; Singh, B. Complementary performance enhancement of PV energy system through thermoelectric generation. Renew. Sustain. Energy Rev. 2016, 58, 1017–1026. [Google Scholar] [CrossRef]
- Cotfas, D.T.; Cotfas, P.A.; Ursutiu, D.; Samoila, C. The methods to determine the series resistance and the ideality factor of diode for solar cells-review. In Proceedings of the 2012 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 24–26 May 2012; pp. 966–972. [Google Scholar]
- Lorenzi, B.; Acciarri, M.; Narducci, D. Conditions for beneficial coupling of thermoelectric and photovoltaic devices. J. Mater. Res. 2015, 30. [Google Scholar] [CrossRef]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W.; Dunlop, E.D. Solar cell ef fi ciency tables (version 46). Prog. Photovolt. Res. Appl. 2015, 23, 805–812. [Google Scholar] [CrossRef]
- Green, M.A.; Hishikawa, Y.; Warta, W.; Dunlop, E.D.; Levi, D.H.; Hohl-Ebinger, J. Solar cell efficiency tables (version 50). Prog. Photovolt. Res. Appl. 2017, 25, 668–676. [Google Scholar] [CrossRef]
- Kondo, M.; Yoshida, I.; Saito, K.; Matsumoto, M.; Suezaki, T.; Sai, H. Development of highly stable and efficient amorphous silicon based solar cells. In Proceedings of the 28th European Photovoltaic Solar Energy Conference, Villepinte, France, 30 September–4 October 2013; pp. 2213–2217. [Google Scholar]
- Sun, K.; Yan, C.; Liu, F.; Huang, J.; Zhou, F.; Stride, J.A. Over 9% efficient kesterite Cu2ZnSnS4 solar cell fabricated by using Zn1−xCdxS buffer layer. Adv. Energy Mater. 2016, 6, 1600046. [Google Scholar] [CrossRef]
- Sze, S.M. Physics of Semiconductor Devices, 2nd ed.; John Wiley & Sons, Ltd.: New York, NY, USA, 1981; pp. 84–89. [Google Scholar]
- Friesen, G.; Pavanello, D.; Virtuani, A. Overview of temperature coefficients of different thin film photovoltaic technologies. In Proceedings of the 5th World Conference on Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010; pp. 422–427. [Google Scholar]
- Lin, P.; Lin, L.; Yu, J.; Cheng, S.; Lu, P.; Zheng, Q. Numerical simulation of Cu2ZnSnS4 based solar cells with In2S3 buffer layers by SCAPS-1D. J. Appl. Sci. Eng. 2014, 17, 383–390. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lorenzi, B.; Acciarri, M.; Narducci, D. Suitability of Electrical Coupling in Solar Cell Thermoelectric Hybridization. Designs 2018, 2, 32. https://doi.org/10.3390/designs2030032
Lorenzi B, Acciarri M, Narducci D. Suitability of Electrical Coupling in Solar Cell Thermoelectric Hybridization. Designs. 2018; 2(3):32. https://doi.org/10.3390/designs2030032
Chicago/Turabian StyleLorenzi, Bruno, Maurizio Acciarri, and Dario Narducci. 2018. "Suitability of Electrical Coupling in Solar Cell Thermoelectric Hybridization" Designs 2, no. 3: 32. https://doi.org/10.3390/designs2030032
APA StyleLorenzi, B., Acciarri, M., & Narducci, D. (2018). Suitability of Electrical Coupling in Solar Cell Thermoelectric Hybridization. Designs, 2(3), 32. https://doi.org/10.3390/designs2030032








