1. Introduction
Gas turbine technology proved to be essential in multiple applications throughout the last few decades, thanks to its unequaled power density and reliability. Advancements in micro- and nano- technologies push the gas turbine engine to become smaller and more efficient [
1], in order to be competitive in sectors where to which it did not belong; as an example, a small power generator for civilian buildings or military individual generators. The intention of reducing emissions leads to a different approach to one of the main sources of CO
2 emissions of the transport sector, which is road transport, with about 72% of CO
2 (European Union, 2012) produced by road vehicles. While the light vehicle sector is slowly converting to hybrid or electric solutions, which results in a reduction of both emissions (CO, CO
2, NOx) and operation costs, heavy duty hybrid vehicles are still uncommon, with some exceptions. In particular, the hybrid design for large urban transport vehicles, such as buses, offers the possibility of improvements both on the economic and environmental side of public service duty. Some solutions have been widely used with good success in some major cities; in particular, New York has one of the world’s biggest hybrid bus fleets, counting 1677 units in 2013.
The advantages of this solution for the environmental aspect of the problem are evident: hybrid vehicles allow noise and emission reduction, while operative cost is estimated to be generally lower, and fuel efficiency is increased. The beneficial impact is more evident in heavily-crowded areas such as large city centers, where air pollution and noise are indeed a serious concern. This solution has thus found convenient applications, combined with regenerative braking, in low-speed routes (city centers), while for higher speeds and longer distances, experience suggests conventional diesel buses are still more convenient. From [
2,
3], the mean power required during transit bus operations, on urban tracks like SORT (Standardized On-Roat Test Cycle) and DUBC (Dutch Urban Bus Cycle), is variable between 20 and 57 kW; using a series hybrid configuration, a 50-kW generator should be enough to power a wide range of hybrid bus models. In this sense, the reliability, power density and cleaner combustion of turbogas turbine (TG) could prove to be a valid alternative to the widely-used reciprocating generators. The present work aims at designing a competitive micro TG, which can recharge the battery pack of a hybrid transit bus, thus extending its operational range through its daily road schedule. Battery capacity for a standard hybrid bus is around 150 kWh, and the purpose of the TG is not to fully recharge it in a few minutes but to constantly produce a lower amount of power, enough to keep the battery level relatively constant. This approach is preferred for two reasons: firstly, high power implies higher weights, fuel consumption and costs, all of which must be limited in order to have a competitive product. Secondly, each engine startup adds equivalent operative hours to the turbine, especially on this kind of small turbine, which must operate at high rpm (above 60,000): so, it is preferable to make them operate for a longer time at a constant rate, limiting transitory regimes. Since constant power supply is the strategy, the turbine produces just enough power to guarantee a constant battery level or, depending on the specific drive cycle, a slight increase in its charge. For this reason, and for the difficulty of yielding more than 50 kW with a single-stage axial turbine, the cited power is the limit of this specific design. It is to be noted that the present design is based on a commercial KJ-66 aircraft model TG, which is not intended to have any residual shaft power since its purpose is to propel the aircraft. The attempt to obtain a bigger, power-generating exemplar of this machine resulted in the proposed design. In this sense, the present work can be seen as an attempt to investigate the limits in terms of the power of a micro TG based on a single-stage radial compressor-axial turbine geometry.
The most critical aspect of a TG is the combustion chamber: fuel mixing is the key to achieve high efficiency and reduce noxious combustion products. This is why larger machines have a swirler to allow a vortical mixing of fuel and compressed air entering the combustion chamber. In this case, a different chamber design has been proposed, mainly because the stock KJ-66 TG creates fuel mixing by injecting it in stems, which leads to a rather inhomogeneous mix of air and fuel against the back wall of the machine; this leads to poor mixing [
4,
5] and, consequently, poor combustion quality [
6]. The complete simulation of the combustion chamber was not possible due to limitations in computational resources, but the study of swirlers and fuel injection has been investigated via CFD simulations.
2. Materials and Methods
The philosophy used to achieve the intended design is to design a compact machine, which can be housed even in small spaces; this of course allows for application not only on buses, but in many other vehicles, potentially even in cars, thus increasing the product’s versatility. Size limitations, though, imply power limitations: one single turbine stage creates complications in the design if it is intended to yield more than 30 kW. The main limitation is turbine blade tip speed, as in this case, shaft speed is 70,000 rpm. High peripheral speed (and then high centrifugal stress), combined with high temperature, pose a serious risk for blade integrity in the long run. The reaction stage allows a good turbine efficiency (reaction blades can reach an efficiency of about 90%). The impulse stage, on the other hand, would allow lower rotational speed, but would introduce higher friction losses, caused by higher gas speed at the nozzle outlet section. A comparison with similar machines, produced by Capstone, Ingersoll-Rand, Elliott Energy System, shows that micro TG are usually radial compressor-radial turbine machines; this design choice is better suited for high peripheral velocities, because the thin section at the tip rapidly grows moving towards the hub in radial turbines, thus increasing the resisting section and allowing higher rotational speed. The general shape of radial turbines is thus more solid than axial ones, which, as in this case, simply extend in a constant section from hub to tip (with or without twisting), making the blades more stressed and thus more subject to thermomechanical effects (creep). However, a radial-radial design requires higher radial encumbrance, due to the combustion chamber usually extending radially. Since similarity to the KJ-66 layout was required, we opted for an axial turbine, with a simpler design of the combustion chamber and a reduction of associated pressure losses, while limiting dimensions both in the longitudinal and most of all in the radial direction. This design choice implies some power output reduction (Capstone C65 yields 65 kW with a single-stage radial turbine) in favor of compact dimensions of the assembly, but, as stated above, 50 kW are enough and consistent with the purpose.
An axial compressor, although allowing a straight air flow from compressor to combustion chamber, is not acceptable in this case, since the pressure ratio (2.75) would require at least two stages, with larger longitudinal encumbrance; thus, a radial compressor has been chosen.
The combustion chamber shape has been designed keeping in mind the necessity of coupling a radial compressor and an axial turbine, while trying to follow the compactness and simple design approach, which are required in the proposed TG. Swirler optimization has been performed using computational fluid dynamics, in order to achieve a good mixing of the injected fuel [
6]; however, simulating the whole combustion chamber was out of reach in terms of computational resources, but it would indeed be necessary as further work, before creating a prototype of the machine.
Another important consideration is the absence of a heat regenerator, which is commonly used in micro turbines for on-ground power production [
1,
7]. In fact, its use is costly, requires a higher maintenance effort and can hardly be practiced in a bus engine compartment without increasing the whole group size considerably: its presence would not be consistent with the purpose of designing a small, simple, low-maintenance and economic TG. For these reasons and due to the possibility of using high-temperature exhaust heat in an ORC cycle [
8], as studied in our department, we decided not to include heat recovery in the design process.
The thermodynamic cycle for the TG is the standard Brayton cycle, with an upper temperature of 1236 K (963 °C) and exhaust temperature of 972 K (699 °C), with an ideal thermodynamic efficiency of 21% and a global efficiency of 19%, consistent with similar machines [
9]. Air temperature at the compressor inlet is 300 K (27 °C) and after compression, the air temperature is:
having chosen a pressure ratio
, a polytropic efficiency
and a polytropic coefficient
(as adopted in the literature, e.g., [
10]). The combustion chamber operates with strong air excess, defined as the ratio
between the air mass flow rate and fuel mass flow rate, and equal to
, and the gas temperature at the chamber outlet is
. The turbine expansion ratio has been chosen equal to 2.55 because of the necessity of a small overpressure at the outlet to allow exhaust gases to leave the turbine quickly enough; therefore, the exhaust temperature is:
An intermediate temperature , which is the temperature at the nozzle outlet and turbine impeller inlet, was calculated once the reaction ratio was determined.
The pressure ratio for the compressor has been chosen both from a comparison with already built machines and, mostly, from compressor maps: in fact, the idea was to employ existing compressor maps as design tools. Moreover, the idea of possibly relying on a commercial, already designed compressor, allows more flexibility in the design, especially relating to the necessity of part replacement. Furthermore, technological reasons are behind the choice. Low-pressure compressors, with pressure ratios up to 2.2, would permit an insufficient expansion ratio, considering the required power to be yielded by the turbine: in other words, the turbine would yield just enough power to keep the compressor in rotation, without any more power available on the shaft. As an example, a 2.2-pressure ratio for the compressor would lead to a reduction of shaft power to 40 kW while requiring an increase in turbine blade height and thus tensile stress. On the other hand, pressure ratios of 3 or higher, while increasing thermodynamic efficiency and power (55 kW for a pressure ratio of 3), would require a multi-stage turbine solution [
9] or higher peripheral velocity with supersonic flow conditions: both solutions, as explained above, are out of the specific design philosophy with which we are complying.
The mass flow rate is another key parameter. High mass flow rates imply a higher compressor power requirement, and this directly influences the available shaft power. We have fixed an optimum value of mass flow rate of 0.5 kg/s, which is consistent with similar-power micro turbines.
The target design parameter is the shaft power; it has to be converted into electric power by means of a generator, mounted, for obvious thermal reasons, at the compressor-side end of the shaft. The shaft output has been obtained by evaluating different pressure ratios and mass flow rates and subtracting the compressor power requirement from the turbine output, keeping as a limit the turbine enthalpy drop, which as mentioned above, cannot be however large. After calculations, we fixed the maximum cycle temperature at 963 °C and then chose the maximum enthalpy drop of
, which is a very large value for a single-stage turbine, while the compressor increases air enthalpy by
. The determination of turbine and compressor power requires the assumption of their actual efficiencies, which will be discussed later. For the moment, we can estimate that the turbine net power output is 118 kW and that the compressor requires 65 kW, from which:
This outcome however does not consider yet the electric and mechanical efficiency, which we chose reasonably equal to 0.96 and 0.98, respectively [
11]. Consequently, the net electric power generated is
.
As for rotational speed, it is limited mainly by stresses on blade roots, and, also for consistency with already built machines and individual compressors, it has been chosen equal to 70,000 rpm.
2.1. Compressor Design
First of all, it is necessary to calculate enthalpy change during compression. Having obtained the value of the temperature after the compression, assuming a
, enthalpy, the increase is:
This must be equated by Euler work for the compressor:
Choosing
is a natural condition on the compressor, since ideally the air at inlet flows normally to the impeller front plane, and this is also the condition of maximum work, as is evident from (5).
is the compressor impeller outlet peripheral speed and is limited by the material choice: a standard value is 400 m/s for steel impellers, while titanium impellers could reach up to 700 m/s. In this case, however, since the Euler work is not particularly high, a steel impeller is adequate [
12], hence the choice of
. Inverting (5), we obtain the value of
, from which we can have an idea of the required blade shape, which is backward-facing. The reaction ratio, defined as the ratio between rotor enthalpy gain and total (rotor + stator) enthalpy gain, is:
Meanwhile, knowing the rotational speed of 70,000 rpm and converting it to radians, , we can compute the external diameter .
At this point, we have to impose the flow coefficient
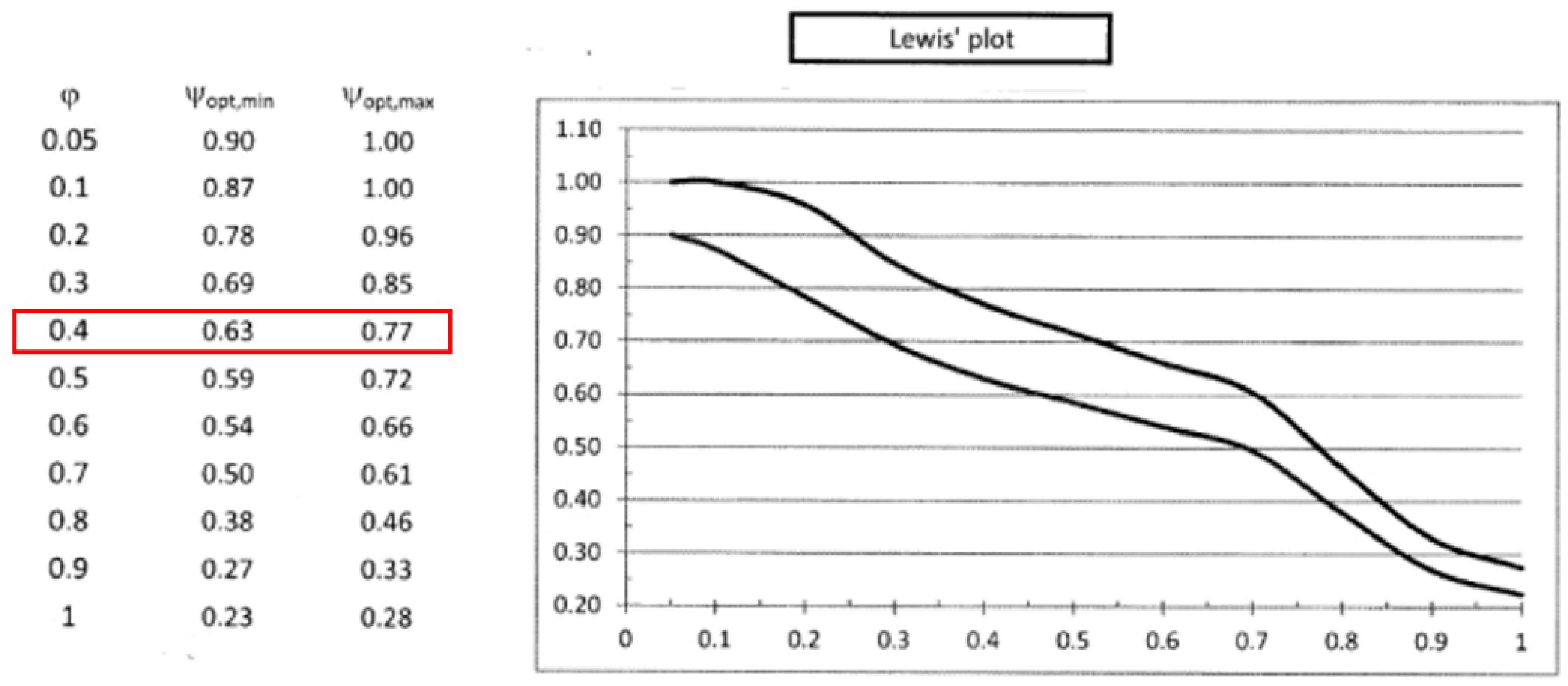
. This has to be assumed consistently with constructive practice, using the Lewis plots (
Figure 1) [
13], which relate
and
, as a design tool. Entering in the plot with the obtained value of
, the corresponding
is equal to 0.4.
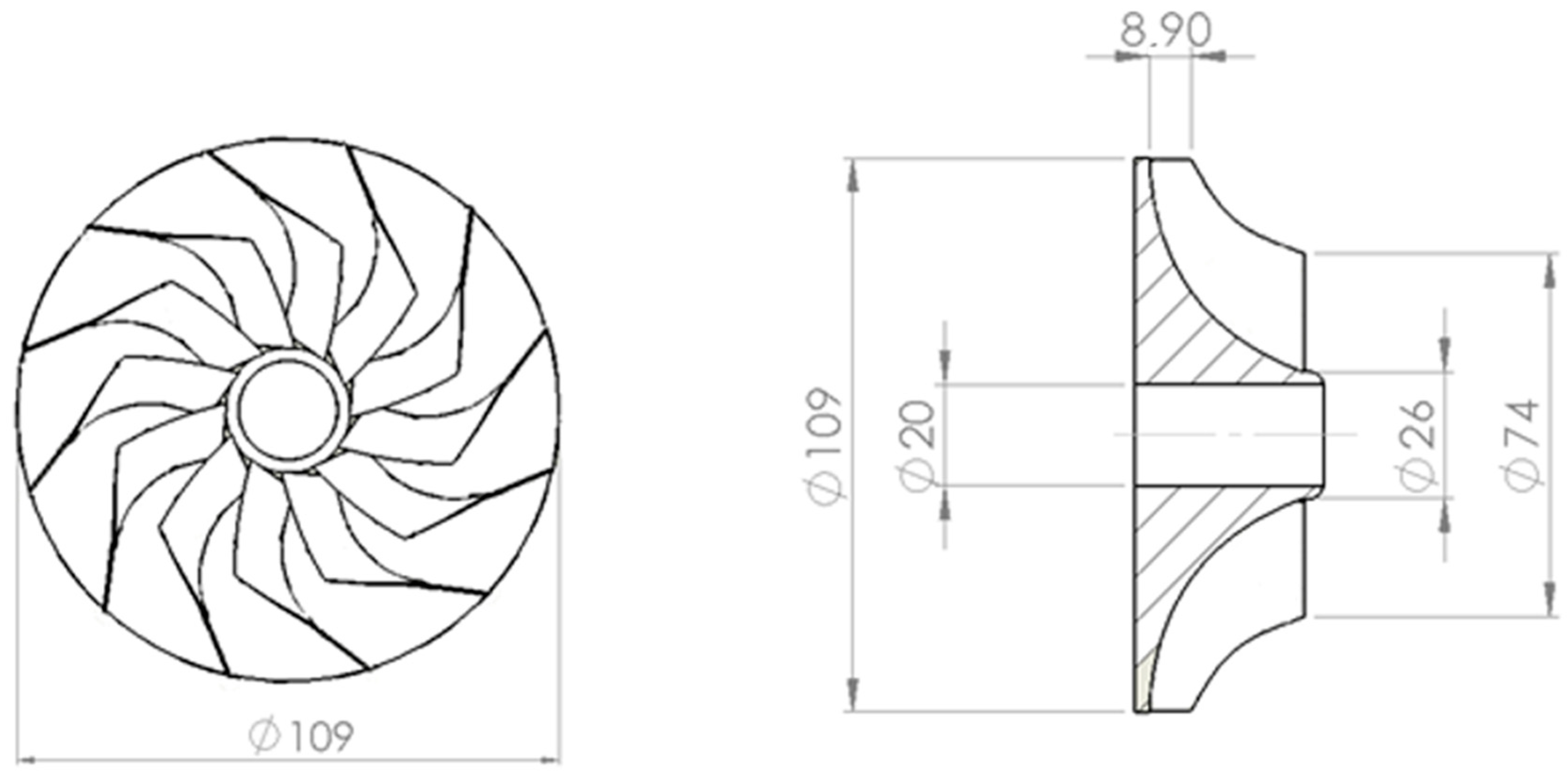
Another design degree of freedom is the ratio between impeller outlet diameter and outer diameter of the inlet section: this is particularly important because in this location, air velocity might approach sonic conditions. Usually, the ratio is chosen by comparison with similar compressors; in this case, a value of 0.68 has been used, and the inlet section external diameter has been obtained: .
The calculation proceeds with
and thus
, which is the meridian velocity of air flow at the impeller inlet. By knowing densities both at the inlet and outlet, we can derive
, and then, absolute velocity angles and constructive blade angles can be determined using the relations:
Table 1 shows the values of the angles and intensities of velocities involved. An important check is the one regarding the choking phenomenon, which is the reaching of sonic velocity at the inlet. Problems can occur when the relative velocity between incoming air and the rotating compressor inlet is too large; this can happen if impeller inlet diameter is too large or flow coefficient
is excessive. If sonic velocity is reached, beyond the shock waves, which reduce compression efficiency, a blockage of mass flow occurs, thus reducing both the compression ratio and mass flow at the compressor outlet. In this specific case, however, relative velocity is small enough with respect to local sound velocity,
, and the conservative good practice design condition
is respected. Velocity triangles for both the inlet and outlet are shown in
Figure 2.
Blade inlet and outlet geometry have now to be defined; this is performed by applying and solving, for the blade height at outlet
, the volumetric flow equation:
which, choosing blade encumbrance factor
, yields a blade height
.
As for the inlet section, the ratio must be fixed in order to obtain the value of the innermost diameter, at the impeller inlet: this is not a degree of freedom, because it influences directly the compressor inlet area, and applying the relation , the calculated velocity must be equal to the one obtained by using the flow coefficient . By applying an iterative procedure, the value of has been obtained, yielding , which is very close to the value obtained by velocity triangles theory ().
We obtain the internal diameter
, which means a blade height at the inlet
. The shaft diameter is a function of the power it has to transmit, and an empirical formula from the literature [
14] allows a simple and conservative calculation:
where
P is the total power (in kW),
is the maximum shear stress for carbon steel (Ni-based alloys allow an even higher
),
is the shaft rotational speed in
and
is a safety coefficient, which in our case was set equal to 3. In order to increase shaft reliability (which is one of the main goals of this design) and shape rigidity (the shaft is more than 40 cm long), a conservative value of shaft diameter is chosen equal to 2 cm. This result shows how the on-design compressor impeller is not suited for being cast on the shaft itself, because the two diameters (
and
) differ too much; therefore, but also for turbine casting and dynamic equilibrium correction possibility, an assembling system must be adopted to assemble the compressor impeller on the shaft, which is realized on the same casting of the turbine wheel.
As for the number of blades, the Stepanoff equation [
14] is used:
but this value is not definitive, since the phenomenon of slip must be taken into account. Using the “slip factor”
:
We can apply the following formula, which yields the corrected constructive angle
:
This value will be the constructive angle and will replace the one obtained by velocity triangle theory.
The correction to the number of blades is done applying again the Stepanoff equation using , and the result is .
In order to complete the compressor design, diffuser geometry must be determined. In this case, since radial displacement must be limited, a vaned diffuser is appropriate, in order to contain the size while forcing the conversion of kinetic energy to pressure in a short duct. External diffuser diameter has been limited by the relation , where is the diffuser inlet diameter, which is assumed equal to the impeller outlet diameter.
The meridian velocity at the diffuser outlet is obtained by:
Diffuser outlet angle
is chosen equal to 60°, and adopting this value, the tangential velocity at the diffuser outlet is:
By the vectorial sum of the two components, velocity intensity at the pressure outlet is .
Compressor efficiency has been evaluated by comparing different commercial compressors (Garrett, Mitsubishi, BorgWarner, etc.) characterized by the same approximate size, pressure ratio and mass flow rate; from compressor maps, an efficiency range of 76–74% has been identified for
and
; hence, the estimated efficiency has been chosen as 75%. The estimated value is consistent with the literature results [
15,
16,
17,
18].
2.2. Turbine Design
The critical design parameter to be chosen is the reaction ratio:
A zero value means the turbine impeller will not expand the gas; with increasing , aerodynamic forces begin to become more and more important, until, for , being the only ones acting on the profile, which has become basically an airfoil without any stator. Impulse blades require very high velocity at the nozzle outlet, since the whole enthalpy drop must be processed in nozzle guide vanes; this is undesirable, in most cases, because the higher the velocity, the higher the friction losses. Moreover, the use of a convergent-divergent de Laval nozzle is often required, because the local sound velocity is easily exceeded in the nozzle, thus introducing additional losses. A reaction stage is indeed more suitable than an impulse stage due to its higher efficiency, and it guarantees acceptable temperature conditions (818 °C) for rotor blades, while stresses at the blade hub have still acceptable values for the construction material; these conditions allow reaching the intended power of 50 kW, which could not be achieved using an impulse stage. Maximum efficiency for axial gas turbines is usually obtained for , but the choice has to take into account sonic phenomena in the nozzle outlet. Using would lead to air conditions very close to the sonic limit, and consequently, this forced the choice of the reaction ratio to . Since , we obtain .
By adopting the Balje diagrams approach in order to estimate stage efficiency, a calculation of specific speed and specific diameter has been performed using the relations [
16]:
The required values are all known, since diameter
is obtained from the value of
and
, which is known by inverting:
by entering these values in this diagram for single-stage turbines [
14,
16], the expected efficiency, according to Balje, is very close to 0.9.
However, while Balje suggests this high efficiency, some considerations are required over this topic; during the calculation, some errors are unavoidably present, since the design of turbomachines is based, as a second design step, on velocity triangle calculations, which are near-1-dimensional calculations representing the fluid behavior, but with no consideration of tridimensional phenomena and motions. For these reasons, and for the fact that pressure losses in the combustion chamber could not be evaluated, we decided to use a conservative turbine efficiency
, consistent with similar machines’ performance [
10].
Gas conditions at the stage inlet are:
Since expansion happens evenly in the stator and in the rotor, nozzle expansion reduces the temperature to 1084 K (811 °C). Sonic conditions are avoided, since local sound velocity at the nozzle inlet is
and at the nozzle outlet
, while the nozzle expansion velocity is
. The tangential component of absolute velocity is known, by remembering the relation
. The meridian velocity, on the other hand, has to be obtained by choosing an appropriate value of
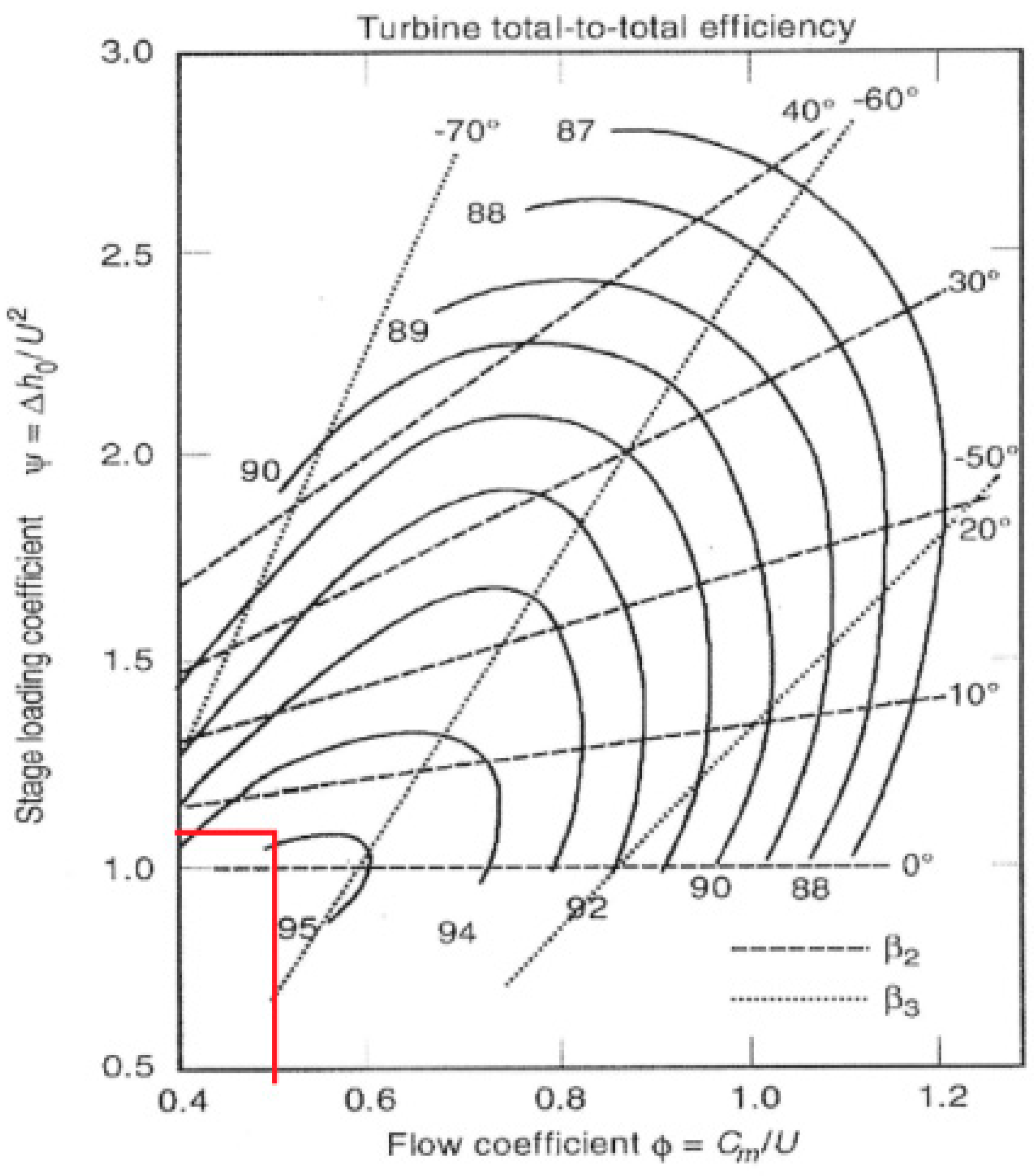
: help in this decision is provided by Smith charts [
14] (
Figure 5), which are based on actual turbines and give indications about the efficiency, as a function of the coupling of
and
. By this graph, a value of
is suitable. According to Smith, this turbine should have an efficiency of 94%, but this high value is referred to a turbine never reaching sonic conditions, while the on-design turbine operates with relative velocity at the outlet in the sonic condition; for this reason, assuming such an efficiency would be unrealistic. At this point, velocity triangles can be drawn (
Figure 6);
Table 2 shows the values of velocities and characteristic angles for the turbine stage.
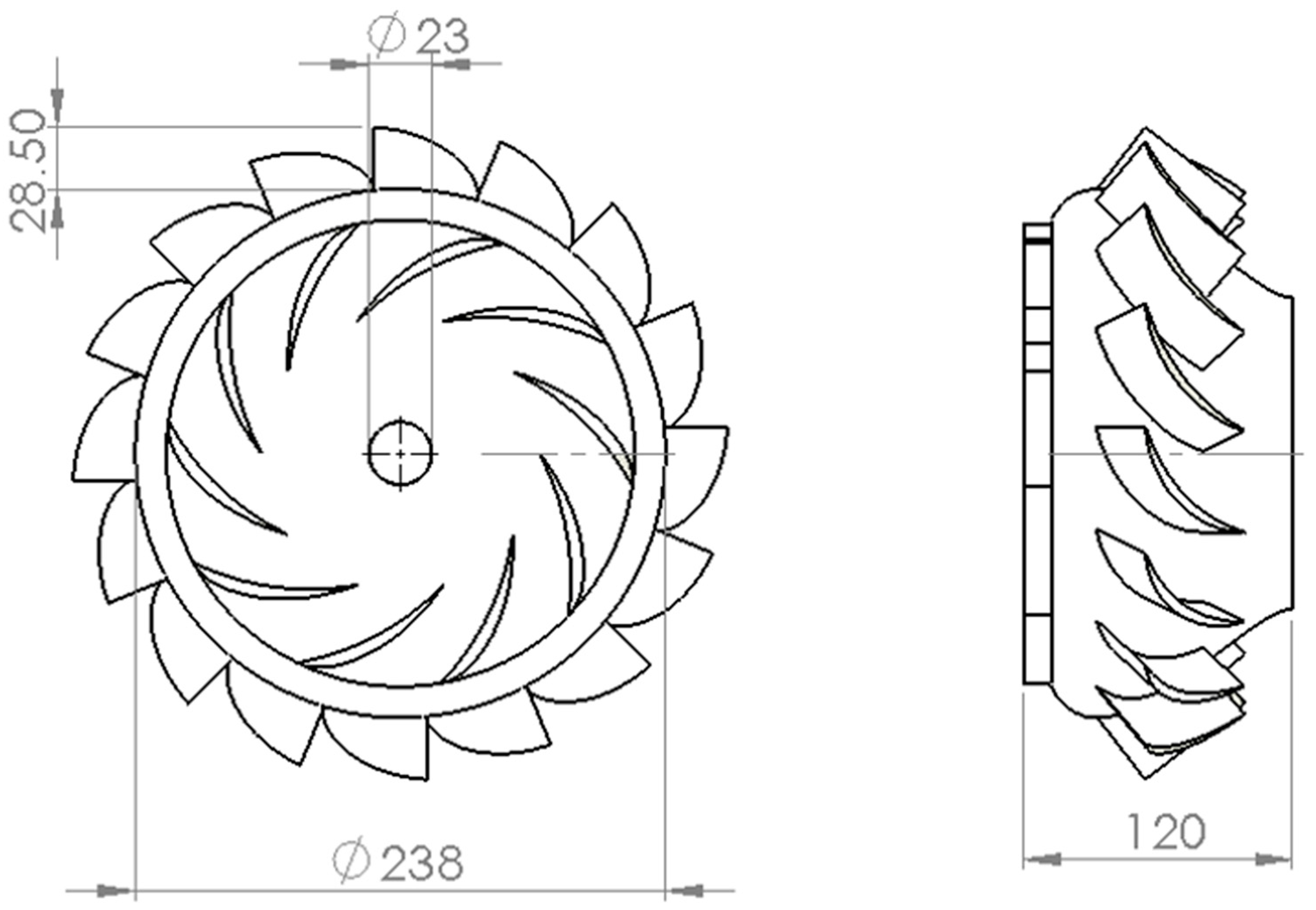
To define blade height,
has to be determined. The calculation is based on volumetric flow rate conservation; by inverting the equation:
we obtain
, having considered for reaction blades an encumbrance
; this leads to external and internal diameters,
and
, respectively, and a blade height
From these values, the peripheral velocity at the tip
and hub
. Now, by imposing blade aspect ratio, defined as the ratio between blade height and blade length, equal to 1, the blade length results
. As for the pitch between the blades, it has been chosen as
, due to similar reasons for other turbines. Therefore, the number of blades has been calculated as:
While blades should be twisted, in order to have equally-distributed Euler work along the blade height, in this situation, it was not advisable, for two reasons. Firstly, the blade height ratio
is high, which means the blades are very short in the radial direction; this means that free-vortex effects and the difference between tip and hub velocities are not relevant. In this case, simplicity in manufacturing suggests avoiding blade twisting, since it would be more complex to obtain, while offering very little gain. The second reason is a technological one: given the very small blade height, creating individual, single-crystal twisted blades to be inserted individually by shaped joints would be very complex and would require a highly miniaturized production process. As a simpler solution, machining the blades directly from the rotor disk would be easier and produce a more reliable product. For these two reasons, we have decided to design untwisted blades, to be directly milled on the rotor disk surface; therefore, Euler work
does vary along the diameter. However, given the low blade height, the design process can be carried out by considering all properties and parameters at blade midspan; in fact, at the blade tip, the work is higher, while at the hub, it is lower than at midspan, so that their combined effects compensate each other. A view of the turbine impeller is available in
Figure 7.
2.3. Combustion Chamber Design
In the combustion chamber, the heat released during combustion increases the produced gases’ temperature up to the design temperature of 963 °C. The temperature in the chamber has been fixed as a compromise between maximum turbine enthalpy allowance and power requirements; by inverting the following:
the fuel mass flow rate is obtained, equal to
and
for diesel fuel and CNG, respectively, and having a LHW (lower heating value) of
for diesel fuel and
for CNG. The air-to-fuel ratio is:
Fuel consumption is using diesel fuel and for CNG; the difference in measurement units is due to the different nature of the two fuels and their stocking modes.
The proposed design is a different concept than the one composing the KJ-66, which is known to be rather inefficient in fuel burning [
4,
19], due to the absence of swirling motion.
The compressed air leaves the diffuser vanes in a radial direction, with a tangential component of velocity. This component can be used to force the air into the combustion chamber in such a way to create a single, wide vortex, which runs along the combustion chamber; the objective of this flow behavior is a uniform combustion and thus an increase in combustion efficiency. A curvature in the adduction channels is necessary, changing the air flow radial component until inverting it, so that the air enters the chamber with a “shaftward” radial component. This curvature is realized by an ad hoc shape of both the compressor stator block and the external casing, keeping the section of flow passage constant. Tangential velocity is conserved during flow turning around the compressor stator block, but in order to guide it precisely into the swirlers, some vanes are required to adjust the flow tangential velocity to correctly align with the swirler inlet, since in this design, the swirler is not produced after a wall-rebound effect such as in the KJ-66 model and in [
10,
20].
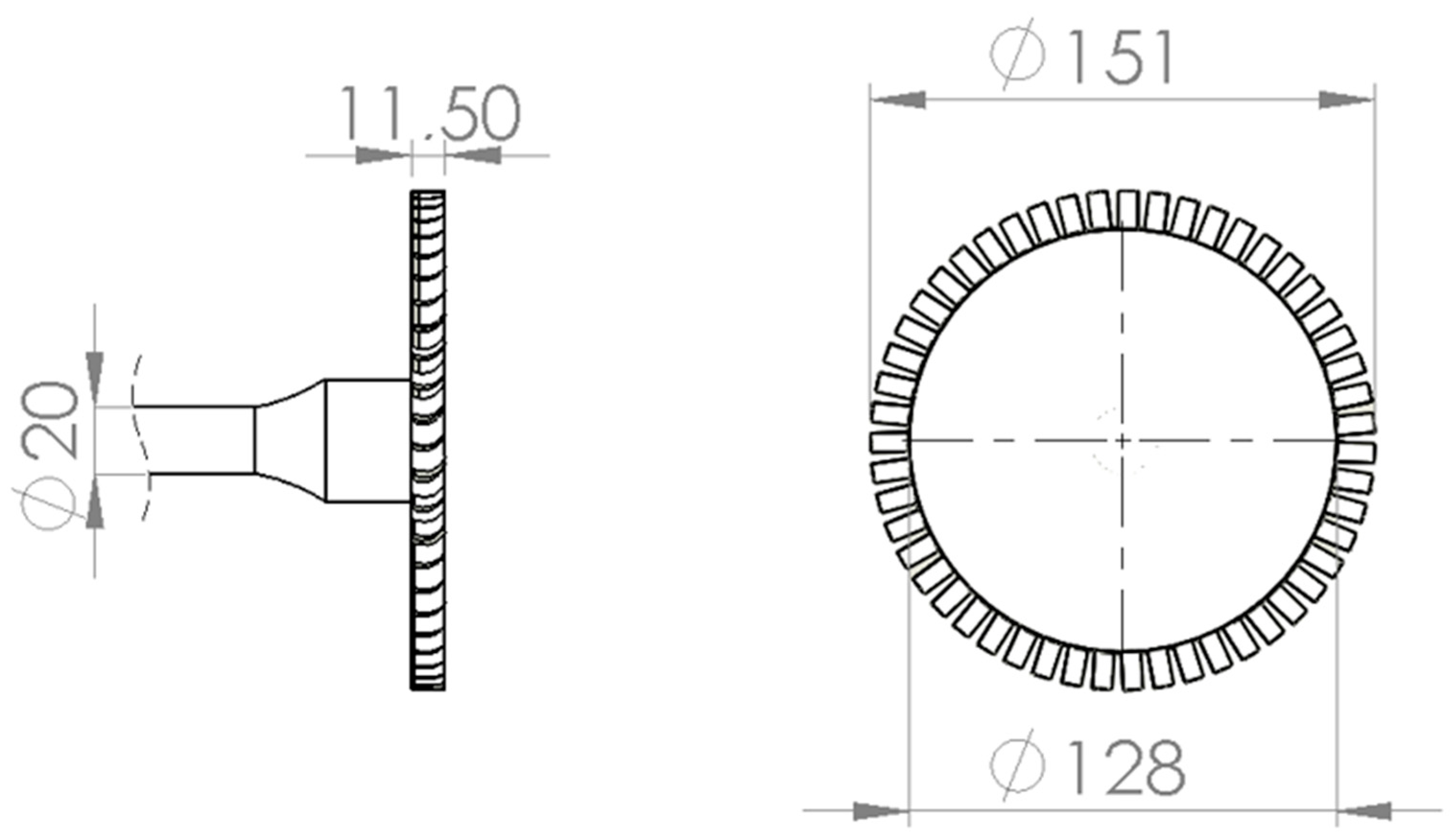
The 5 swirlers elaborate approximately 20% of the compressed air flow, as usually this is the amount of primary air in which the fuel is injected, and the swirlers have been designed such that their inlet area is about 20% of the area of the inlet section of the chamber. They are composed of a cylindrical body, which presents a diverging shape in the end; before the divergence, 14 swirler vanes are mounted on a central hub. Through this hub is inserted the injector in the illustrated model, otherwise the injector is positioned before the swirling device. The injection angle is 70° from the swirler longitudinal axis, realized with micro holes in the injection surface, and injection overpressure is about 2 bar, as from the similar TG present in our department; this corresponds to an injection velocity of . An injection of per injector is realized via micro holes, with a total surface of .
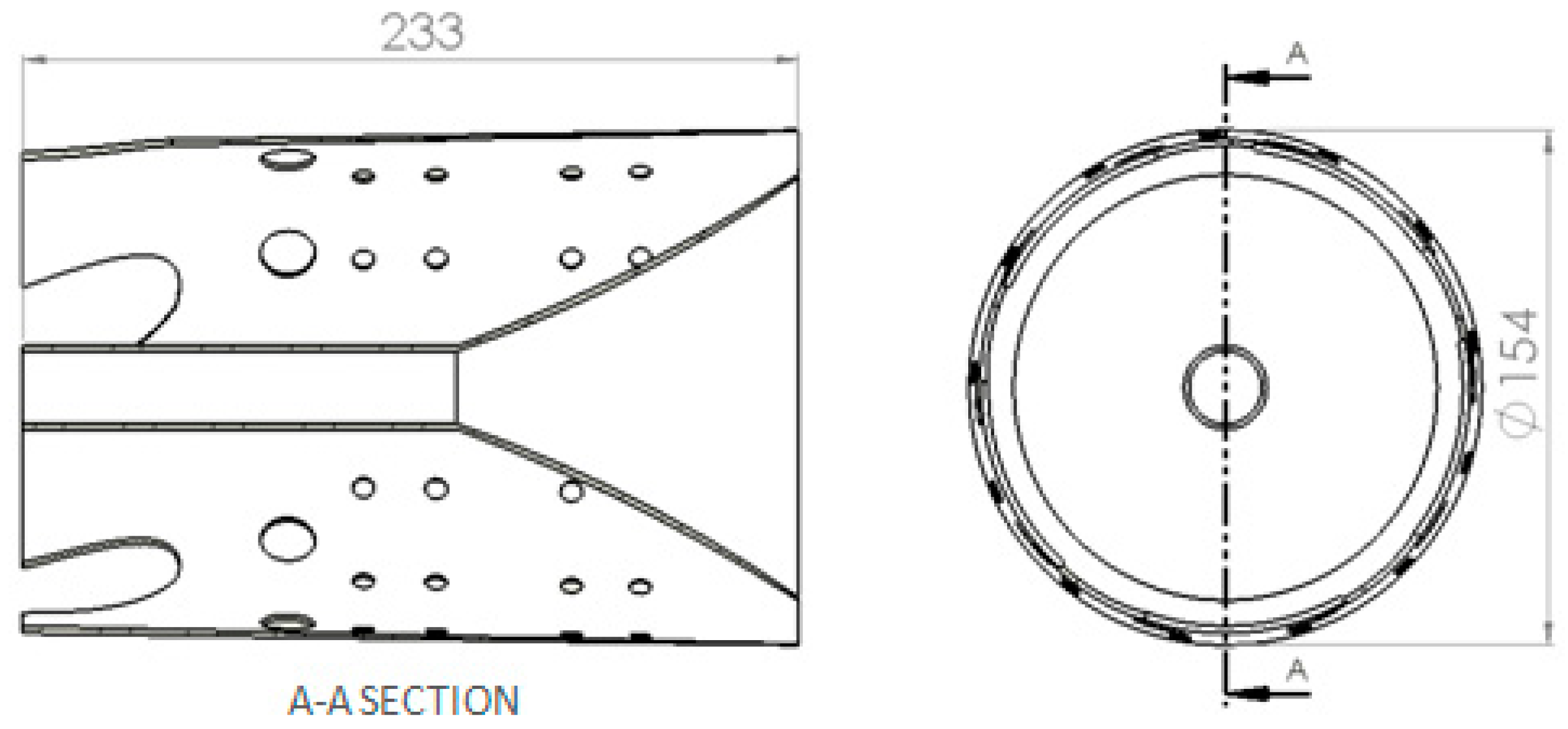
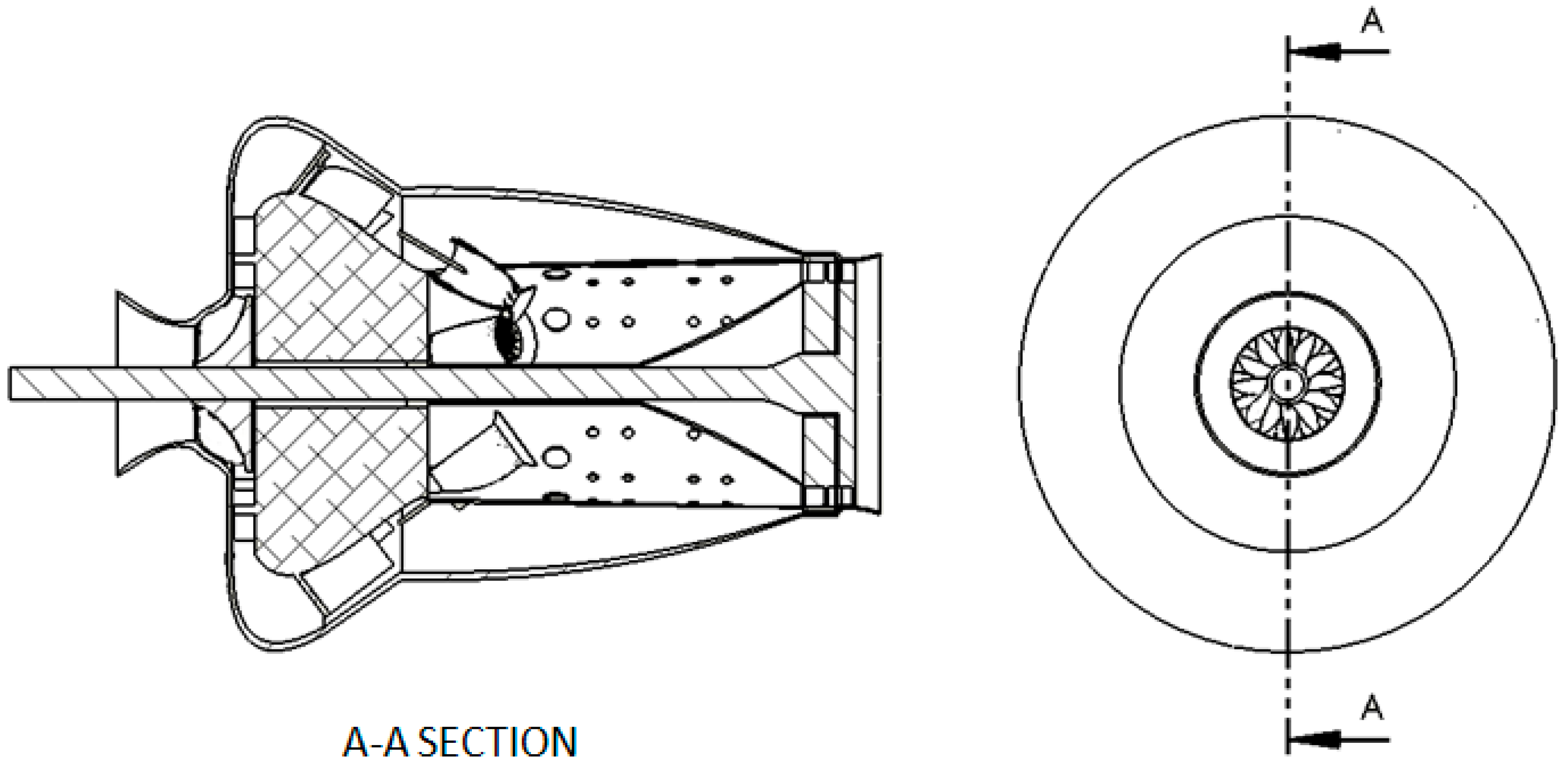
The chamber shape, illustrated in
Figure 8, has been chosen by keeping in mind the aim of the product, and its simplicity in manufacturing. The external part of the chamber is a simple holed cylinder 23.3 cm long, with holes of different sizes in the longitudinal direction. The first holes are destined to host the swirler and injector assemblies, which are the most critical parts of the design. The second hole set is composed of 10 and 20 mm-diameter holes whose purpose is to allow the entry of secondary air directly above the swirled mix of air and fuel, and their number has been fixed to 10 so that two holes serve one swirler. The next hole sets are smaller 7 mm-diameter holes, with the function of feeding extra air, contributing to mass flow in the last part of the chamber and cooling the central and final part of the combustion chamber. Their number, which has been set to 52 (13 per set, 4 sets), and position are to be adjusted with CFD simulations of the combustion process in future works. The inner part of the chamber is composed of a tube, which surrounds the shaft, with the turbine-side end forming a cone, to invite the gas flow from the (radially) deepest part of the chamber to the nozzle guide vanes.
The design of the combustion chamber is the most critical task when designing gas turbines, since the power output of the machine depends on its efficiency. The proposed design has not been simulated yet, and for its efficiency, a hypothesis can be made based on a similar machine.
2.4. Stress and Materials
Stress evaluation has been performed for the turbine blades by applying the following general equation [
14]:
where the second term inside the brackets is zero, since the blades are not tapered for production simplicity so that the ratio
(blade section area at the tip/blade section area at the hub) is equal to one. Blade stress has a rather high value, considering that operative temperature of the blades is about 818 °C; consequently, even special steel performances are not enough. Nickel-based superalloys are necessary. From nickel alloys’ property charts, the commercial MAR-M 200 and MAR-M 246 alloys have been selected as candidates for the turbine blades [
21], disk and shaft materials, since they present a 1000-hours rupture strength, at 818 °C, of 415 MPa and 435 MPa, respectively; these materials allow the turbine-shaft assembly to endure operative conditions beyond the 1000-h target [
21], a primary goal for such an extreme turbine design. The shaft torque is:
which leads to a maximum shear stress of:
a value well within the limits even of carbon steels, even better considering the superalloys’ choice.
Other components do not face the same harsh operative conditions as the turbine impeller; for this reason, the material choice for the other components of the TG is less critical. The combustion chamber must withstand, as the NGV (nozzle guide vanes), the highest temperatures in an oxidizing environment; thus, a generic stainless steel alloy could be used. The same has to be said for the casing, which can be made in two sections: however, stainless steel is recommended, in the form of a sheet, since the temperature of the air leaking from the turbine side and at the turbine outlet is still beyond aluminum operative capabilities. As for the compressor impeller, the choice could be stainless steel or a high-strength aluminum alloy [
12]; the compressor stator, which also acts as a guide for the flow into the combustion chamber and as the closing end of the same chamber, could be made in an aluminum alloy.
2.5. Fuel Injection Modelling
Fuel mixing, in the present design, is characterized by 5 swirlers positioned circumferentially in the first part of the combustion chamber [
5,
6]. They process about 20% of the air coming from the compressor and give it a vortical motion using static blades. Fuel injection, in the two proposed models, whose geometry is shown in
Figure 9 and
Figure 10, is realized via an injection stem, in the first case before or, as in the second case, just after the splitting blades, with an angle of 70° from the swirler axis. Comparison of the particle density and qualitative spreading at a fixed section in the combustion chamber allows one to determine the better performing among the two geometries proposed.
ANSYS Fluent software has been used to simulate each swirler alone and, subsequently, a wider portion of the chamber. Since this problem is strongly related to turbulent stress generations [
22], second moment closure is an appropriate [
17,
23,
24] way of treating it: its higher computational cost with respect to a standard k-
model, however, limited the size of the simulation domain, limiting it to one (two in the final simulation) swirler at a time. In Fluent, this is called the Reynolds stress model (RSM), and it solves each stress generation component (uu, vv, ww, uv, uw, vw). The non-equilibrium wall function [
4] has been used, in order to account for small pressure gradients during the interaction with swirler vanes. Fuel injection has been modeled with discrete phase modeling (DPM) in Fluent; it allows the injection of particles from surfaces, or (with pre-defined injection types) from user-defined points; in our case, since an injection conic surface was modeled in the swirler assembly, surface injection has been used. The DPM iteration interval has been set to 5 (meaning one DPM iteration every 5 air iterations). As for the fuel, in these simulations, diesel fuel was injected, but it must be noted that this type of machine uses poly-fuel. The injection velocity has been set to
, and the angle of injection is about 70° from the injector axial direction. Initial velocity and pressure have been set according to the compressor outlet conditions, slightly reduced by a fraction in order to account for friction losses in the adduction channel: velocity at the swirler inlet has then been chosen equal to
. The secondary air holes are present in the simulation, two per swirler, and their purpose is dual: they contribute to the dilution of the mixed air, which is almost in stoichiometric conditions, and to the need to push the flow in a radial, axis-facing direction. The air incoming through is slower, due to the wider space it occupies and due to the losses in entering the chamber through small, 1 cm-diameter holes; consequently, holes’ admission air has been set to enter the chamber at
. Pressure conditions, theoretically being the same in the whole chamber, have been set to 275 KPa, from the design.
The meshing (shown in
Figure 11) has been realized with the ANSYS built-in meshing tool ICEM. Obviously, the number of mesh nodes and elements varies between the single cases, but they present the same order of magnitude both in number and in mesh quality. The selected meshing method is tetrahedrons with the patch-independent algorithm, which created a better quality mesh with respect to patch-conforming.
Mesh characteristics for the two cases are approximately the same; here are shown the values for the post-swirler injection case:
Element number 2,350,000 (4,000,000 in the extended domain case)
Node number 400,000
Max. element size m
Average aspect ratio
Max skewness
Average orthogonal quality
Simulations have been performed until the 2000th iteration with second order upwind convergence tolerance and with Fluent standard under-relaxation factors; this was enough for reaching stability in the residuals trend. At this point, scaled residual order has been checked; for velocities, stress components, k and equations, at least a order of magnitude has been achieved, while for continuity, the order is ; this is not a surprising result, since usually, the continuity equation has greater residuals than velocities and is harder to converge.
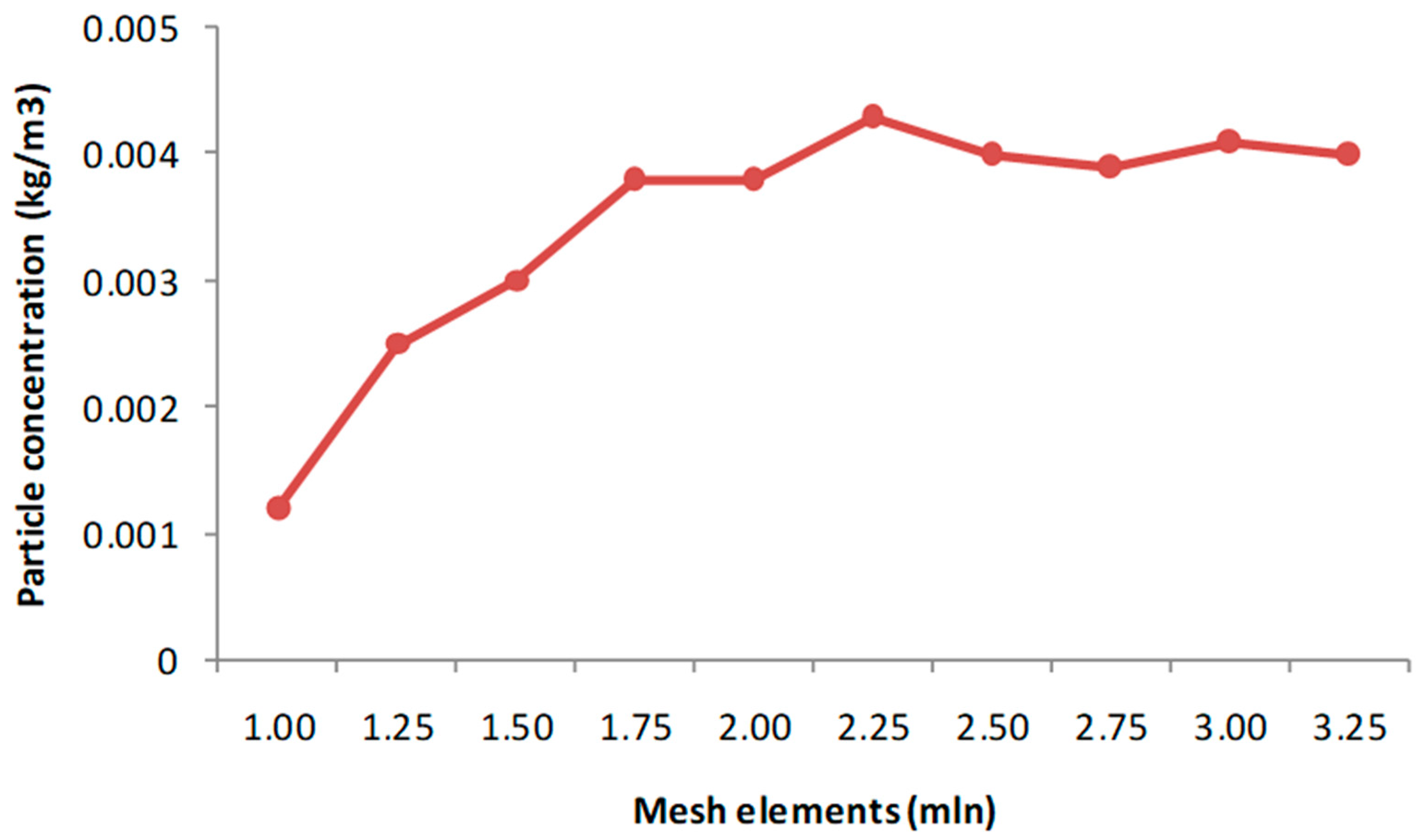
Mesh independency has been verified via particle concentration at the outlet section, as shown in
Figure 12.
3. Results
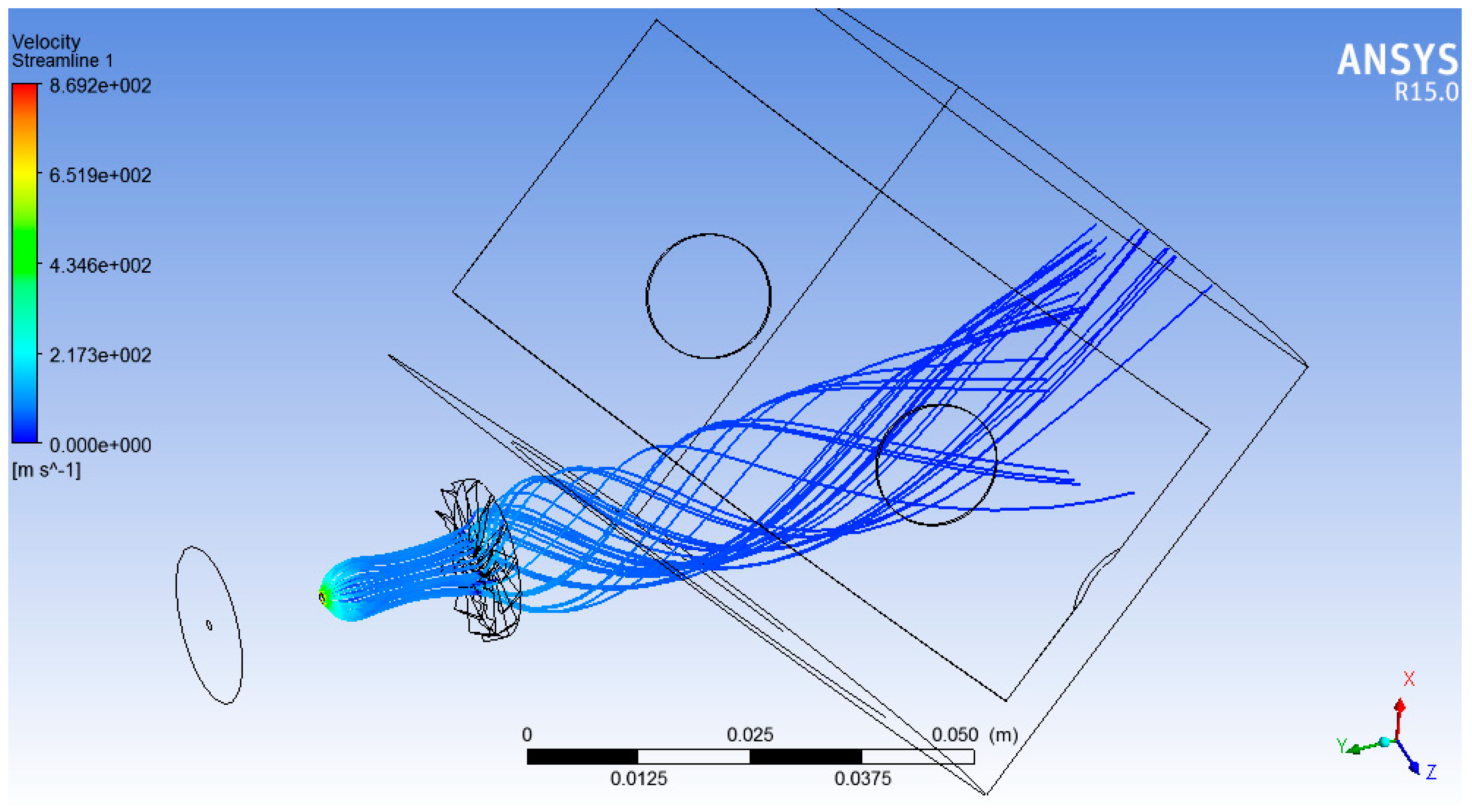
The pre-blades’ injection geometry gives the results shown in
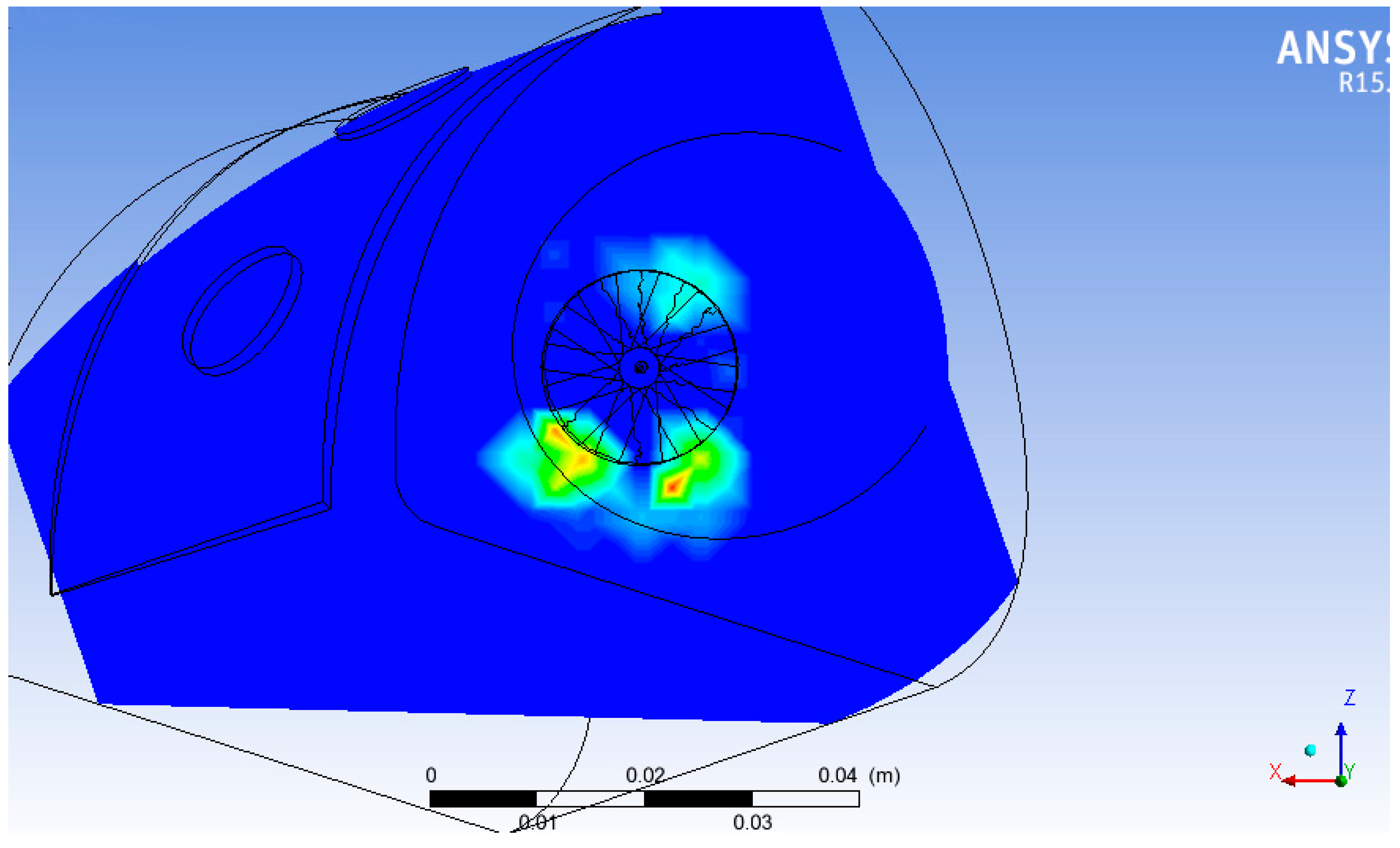
Figure 13. After injection, the particles proceed axially, transported by the air, until reaching the blades; there, a strongly vortical motion is created, where air and diesel droplets are scrambled and slightly accelerated. When entering the combustion chamber, the flow presents a strong helical motion, which acts as a vortex extending straight into the chamber; a deviation, appreciable in the axial view, is due to secondary air holes’ contribution in the air supply (not visible in the figures). However, the vortex seems to be too strong to allow the particles to move away from it, and the spreading begins only in the final part of the domain. Considering the reduced length of the designed chamber (about 23 cm), dispersion is required to be remarkable after only a few centimeters into the chamber. Since the vorticity induced by the blades appeared to be too strong, but reducing the number of blades would not allow the creation of the correct vortical structure, due to the tendency of the air to bypass the blades, passing into the free areas between them, a good solution has been identified in a post-blade injection.
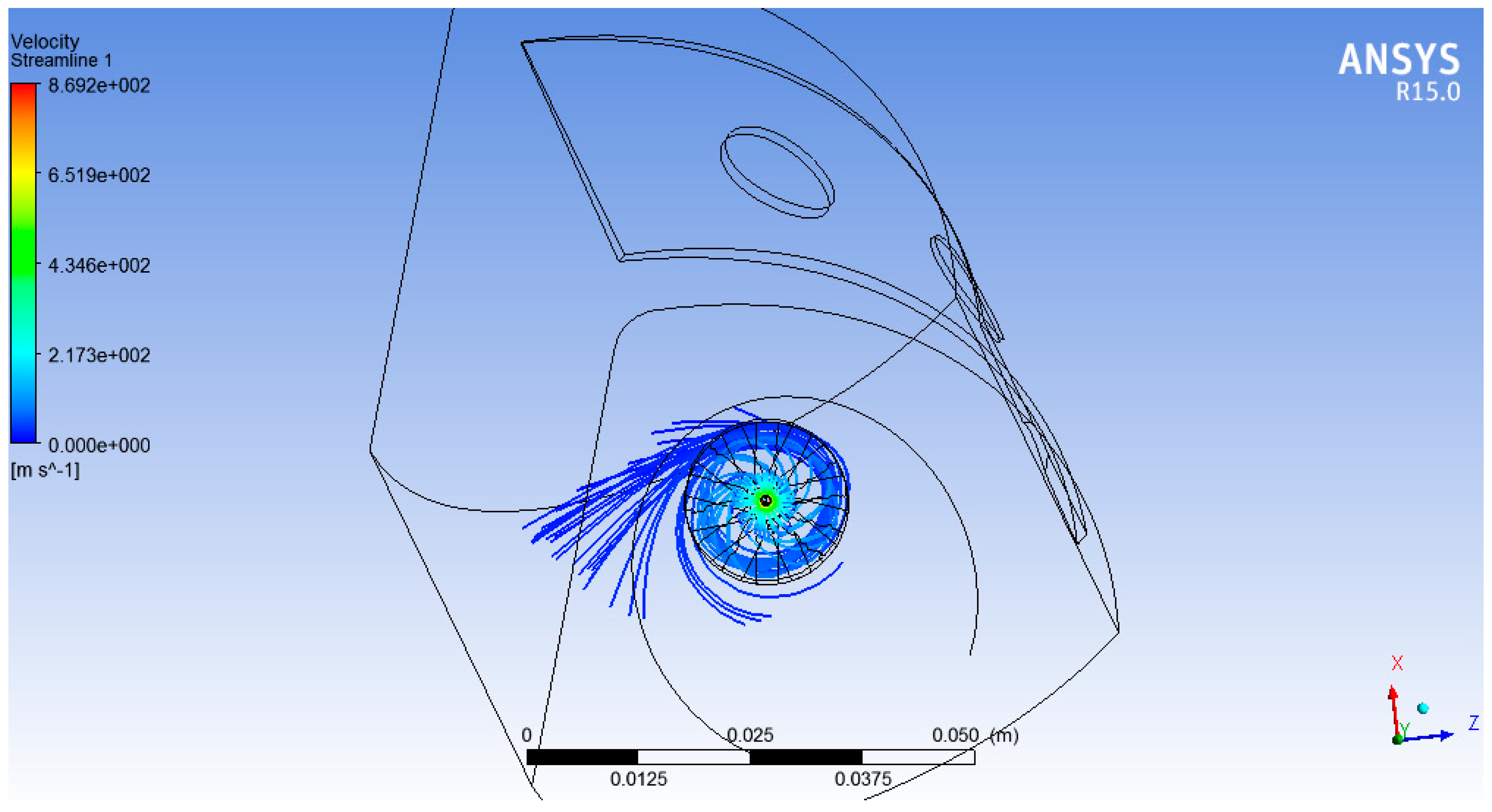
This approach takes advantage of two velocity components: the injection velocity component, which is inclined by 70° from the axial direction of the swirler, and consequently tends to send the particles away, in a radial direction, from the vortex, with limited disturbance from the main flow, which has lost a part of its axial velocity component due to the splitting blades’ action; and the vortical motion, which tends to scramble the particles. Performing the injection just after the splitting blades yields far better results; the particles are pushed away from the center of the vortex; a part of them is captured, while a group is able to escape.
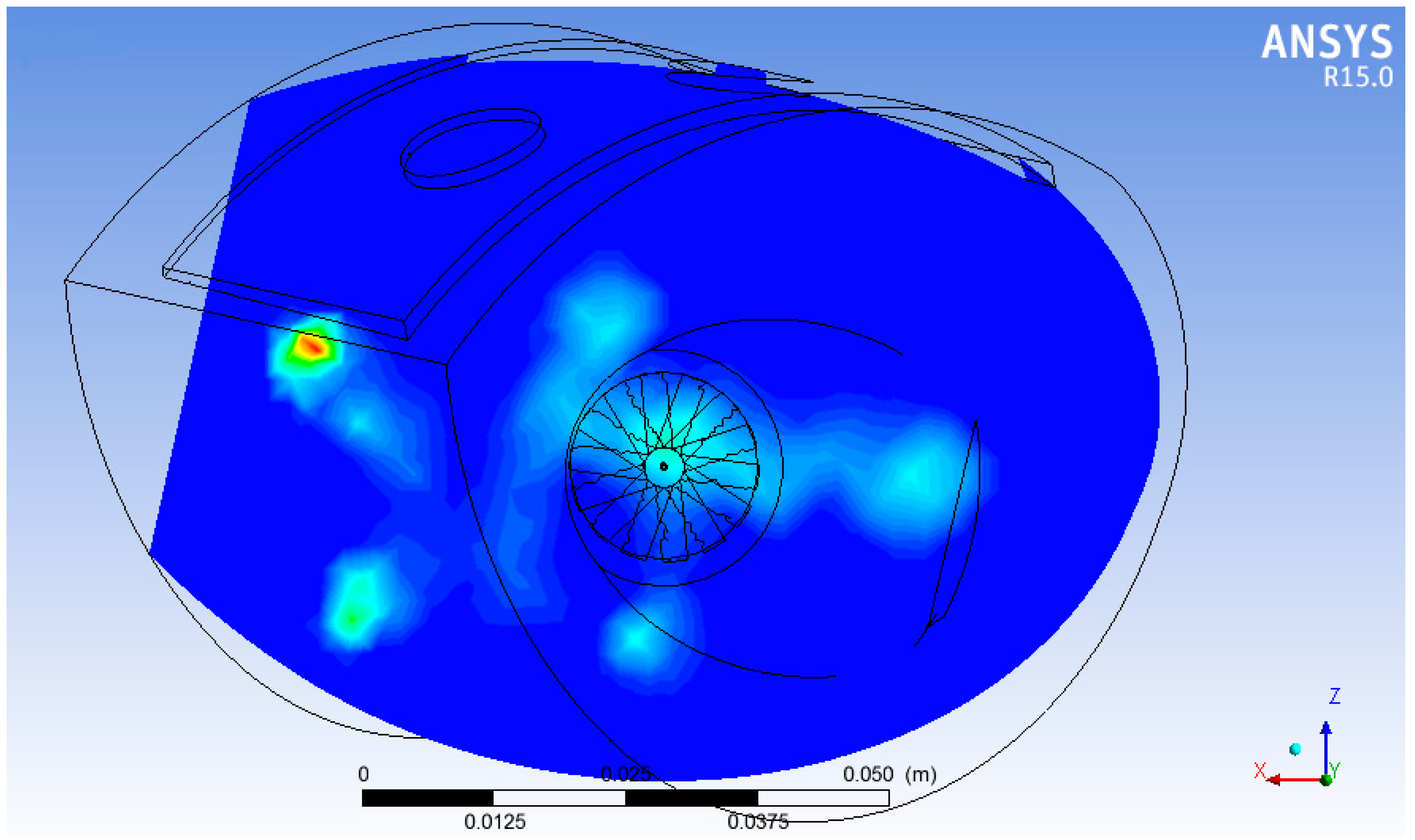
However, the vortical motion tends to attract the escaped particles, keeping them in a peripheral zone. The results show this behavior (
Figure 14); the vortical structure is clearly visible on the swirler axis, while the suction effect is also visible, causing the outgoing particles to deviate; moreover, secondary air contribution bends the main vortex downward.
The spreading is evidently improved, covering a much wider portion of the domain. A comparison between these two injection approaches has been performed by comparing particle density on the same plane (located at a depth corresponding to the right-side hole edge).
In
Figure 15, the difference in the spreading appears evident. After the same axial distance traveled by the particles, the dispersion area is almost three-times wider in the post-blades’ injection case, while in the pre-blades’ injection case, the droplets can hardly cover more surface than the one crossed by the main vortex. It is clear that the post-blade injection swirler is the most appealing one and is hence selected for the application.
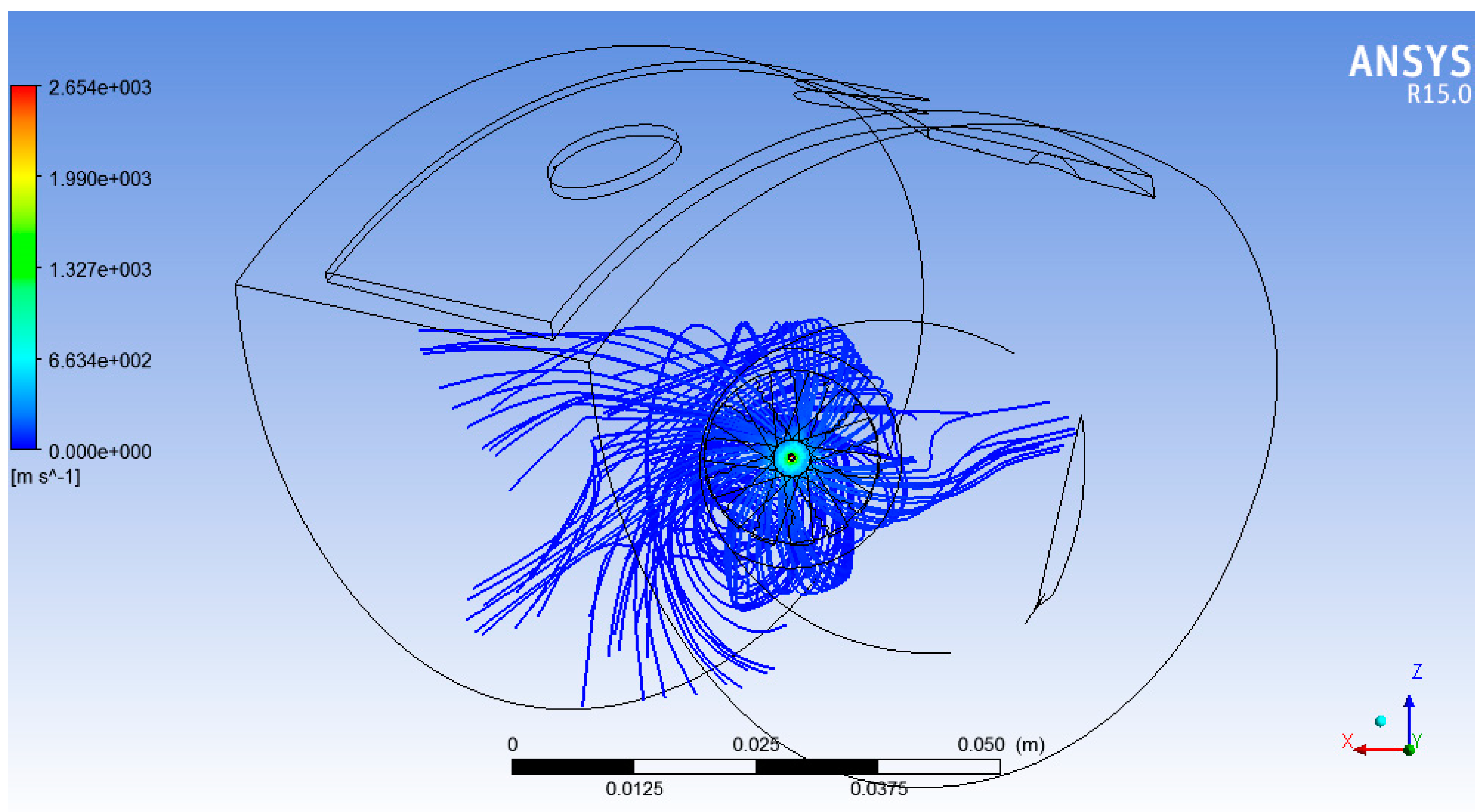
In order to evaluate the spreading on a larger portion of the combustion chamber, a final simulation of a wider portion of the chamber has been performed, covering an arc of about 150° and counting two swirlers and injectors.
On the complete circumference, a good uniformity in dispersion is achieved. The whole chamber, due to its extension and complex meshing around each of the five swirlers, was out of reach; the mesh of the last simulation counts 4,000,000 elements even with coarse elements in the regions of no interest, reaching the limit of our present computational resources.
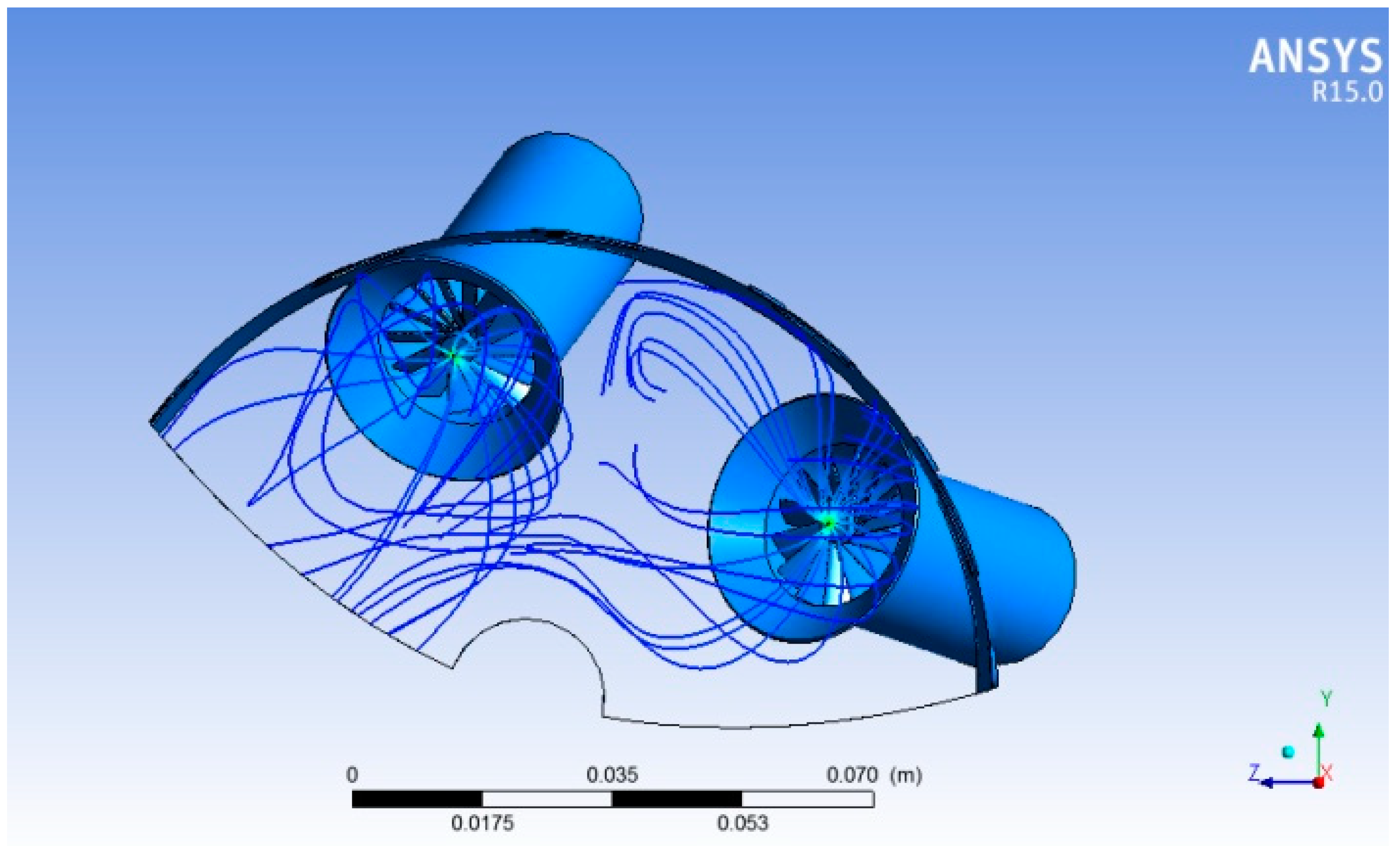
The interaction of particle dispersion from multiple swirlers is indeed beneficial for the complete filling of the chamber: in fact, as suggested from
Figure 16, where particles’ streamlines have been limited in order to make the image clearer, the filling of the section of the chamber is satisfying.
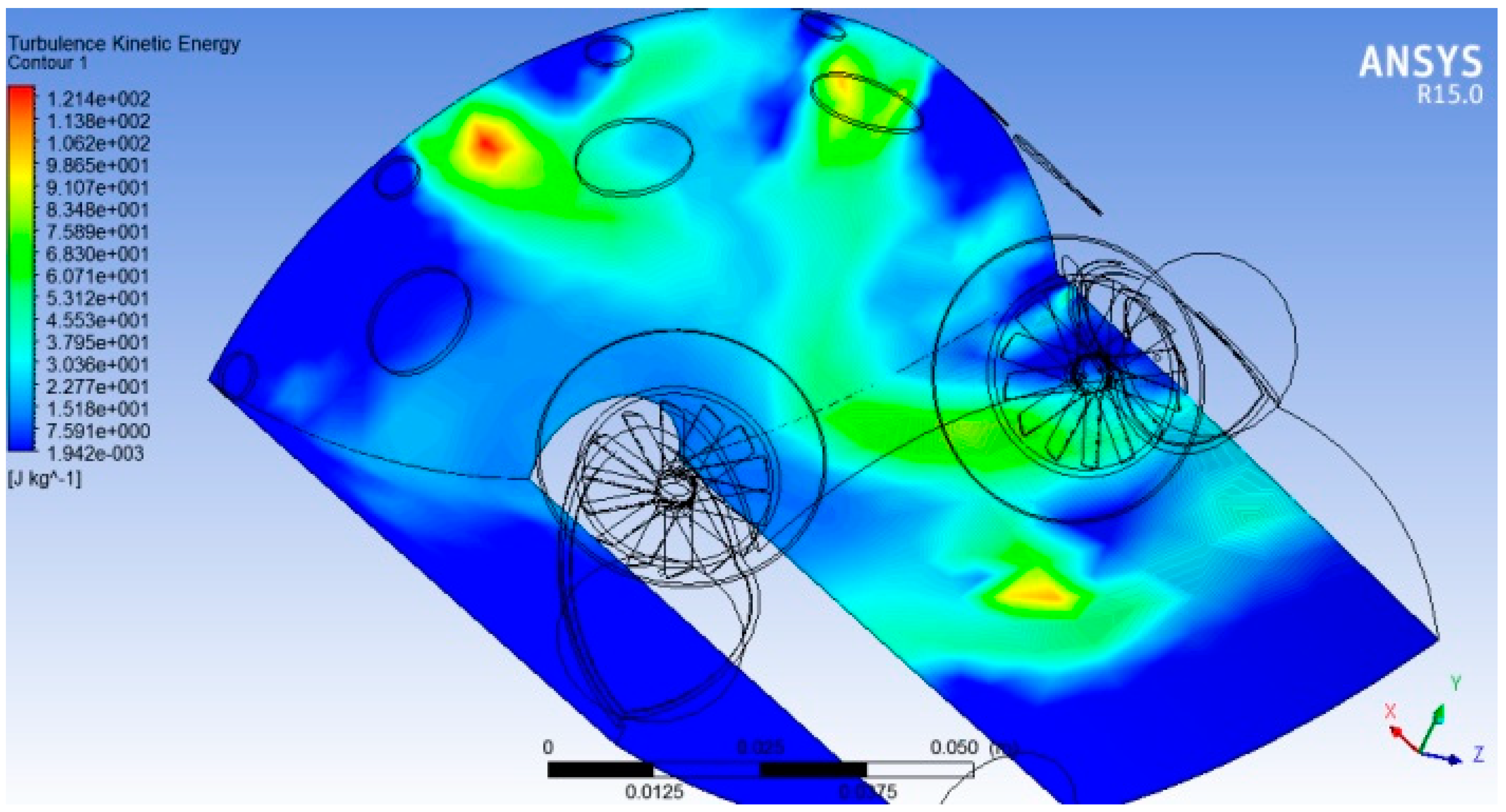
On the complete circumference, a good uniformity in dispersion is achieved. In
Figure 17, turbulent kinetic energy intensity is presented, and a good turbulence distribution on the domain outlet can be observed, which is beneficial for the mixing purpose.