Analytical Expression of Parabolic Trough Solar Collector Performance
Abstract
:1. Introduction
2. Material and Methods
2.1. Mathematical Modeling
2.1.1. Model Assumptions
- The PTC is assumed to be in steady-state conditions.
- There are no contact thermal losses.
- The receiver is an evacuated tube and the heat convection losses between absorber and cover are neglected.
- There is uniform heat flux over the absorber.
- The receiver temperature does not have great variation along the tube because the collector has a reasonable length (~10 m).
- The solar collector radiates thermally to the ambient.
- There is no great difference between cover and ambient temperature level.
- There is no great difference between the receiver and fluid temperature level.
- The flow is fully developed and it can be characterized by a constant heat transfer coefficient along the tube.
- This model needs the knowledge of the fluid thermal properties, as well as of the heat transfer coefficient.
- All the thermal properties, as well as the receiver emittance, can be estimated for the temperature level of the inlet temperature.
2.1.2. Steps of the Developed Modeling
STEP 1
STEP 2
STEP 3
STEP 4
STEP 5
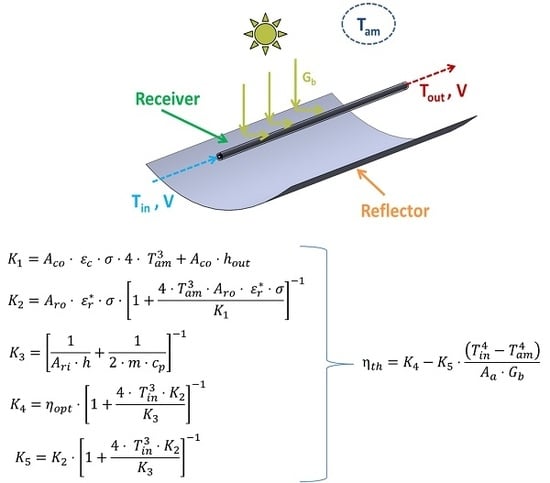
2.1.3. Other Parameter Calculations
2.1.4. Extra Equations for the Developed Model
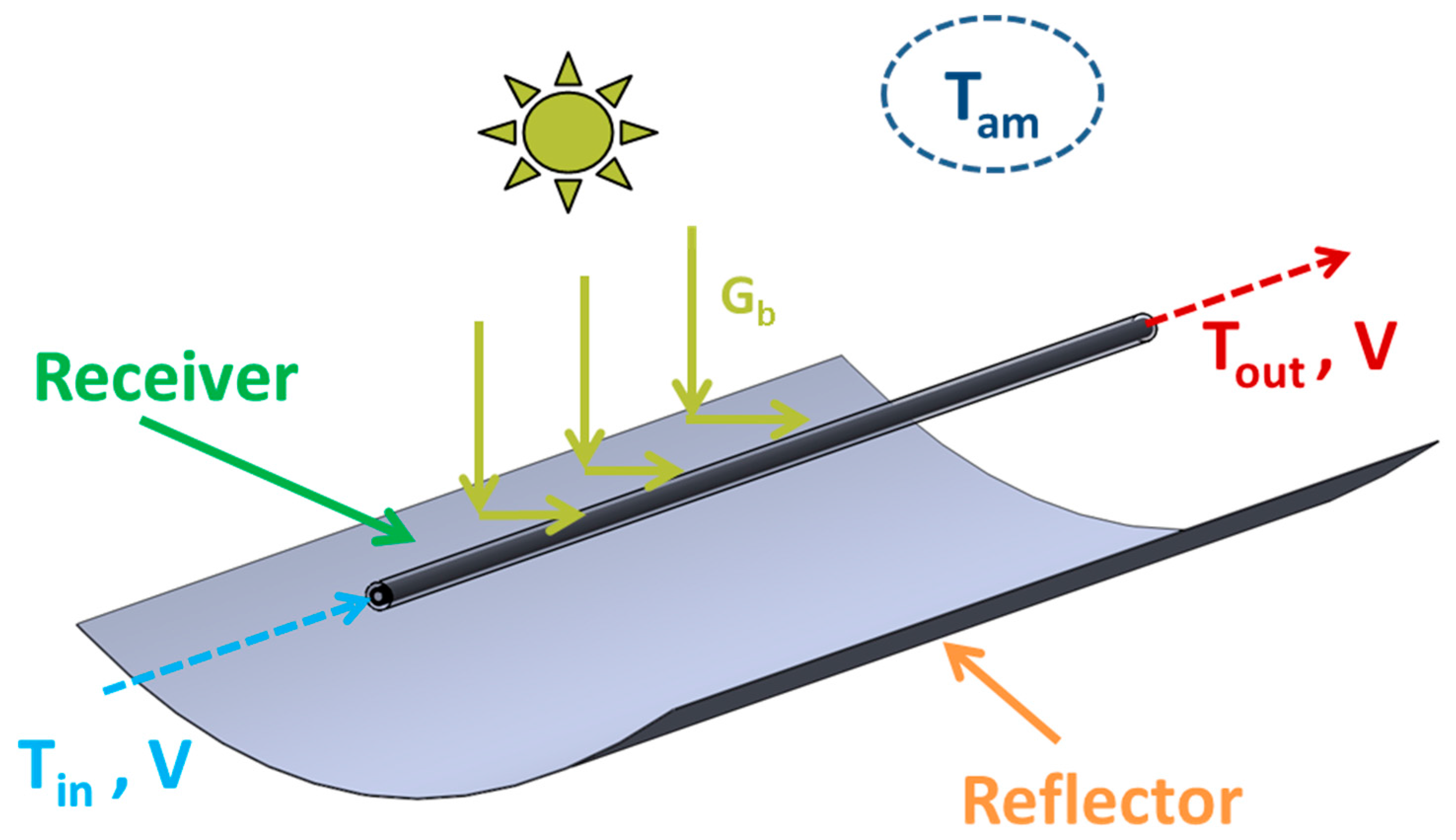
2.2. The Examined Parabolic Trough Collector (PTC)
3. Results
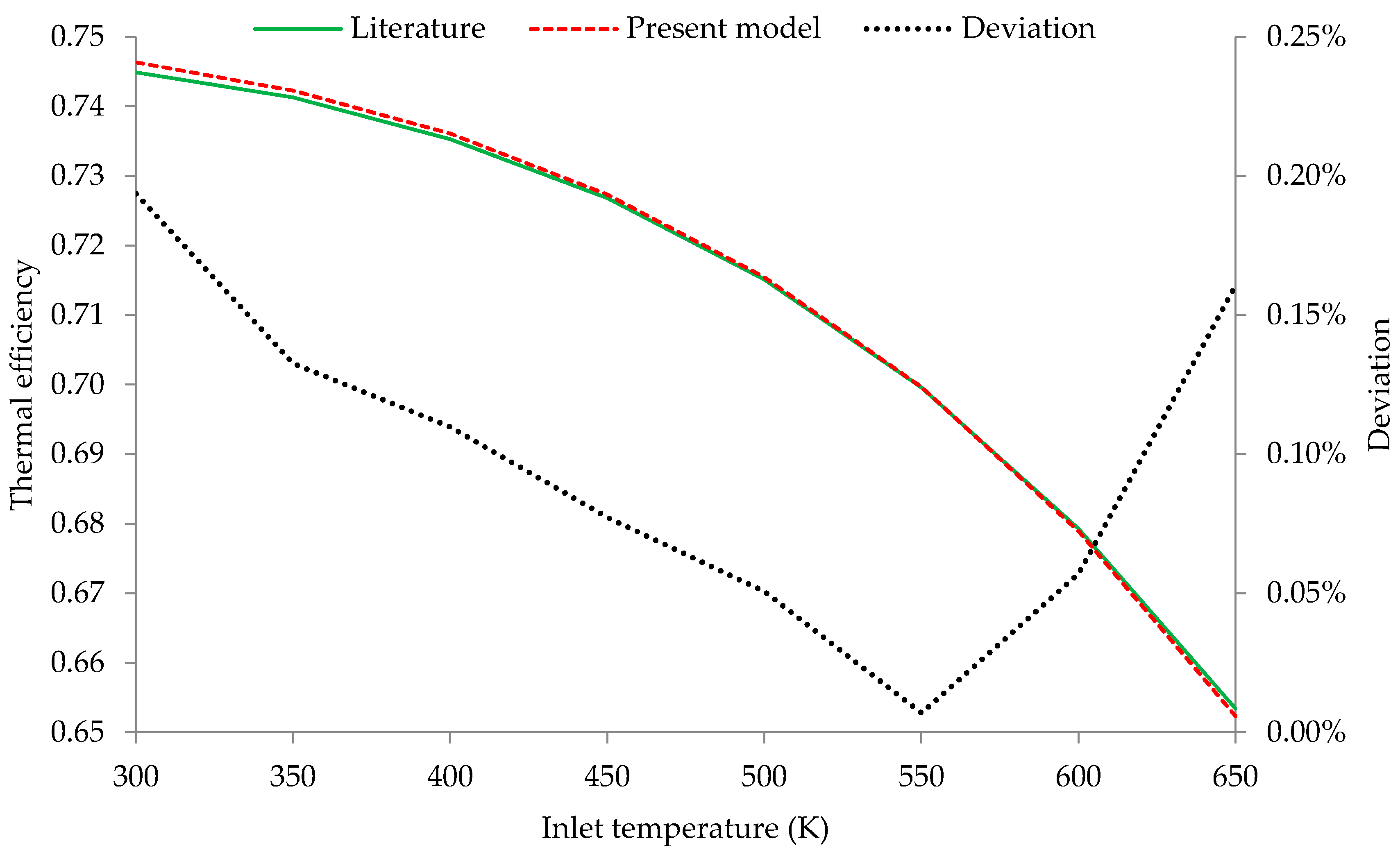
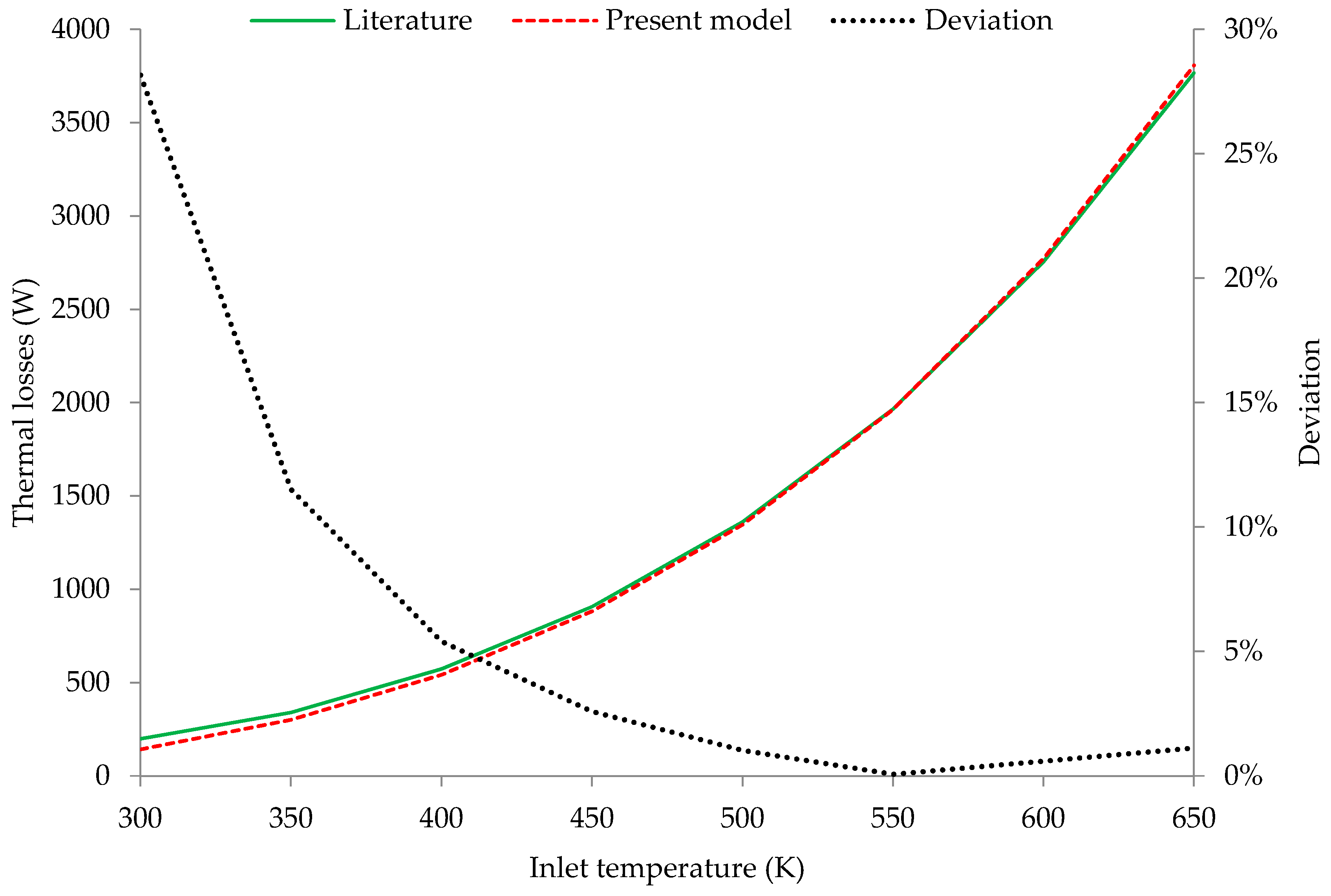
3.1. Model Validation
3.2. Parametric Investigation
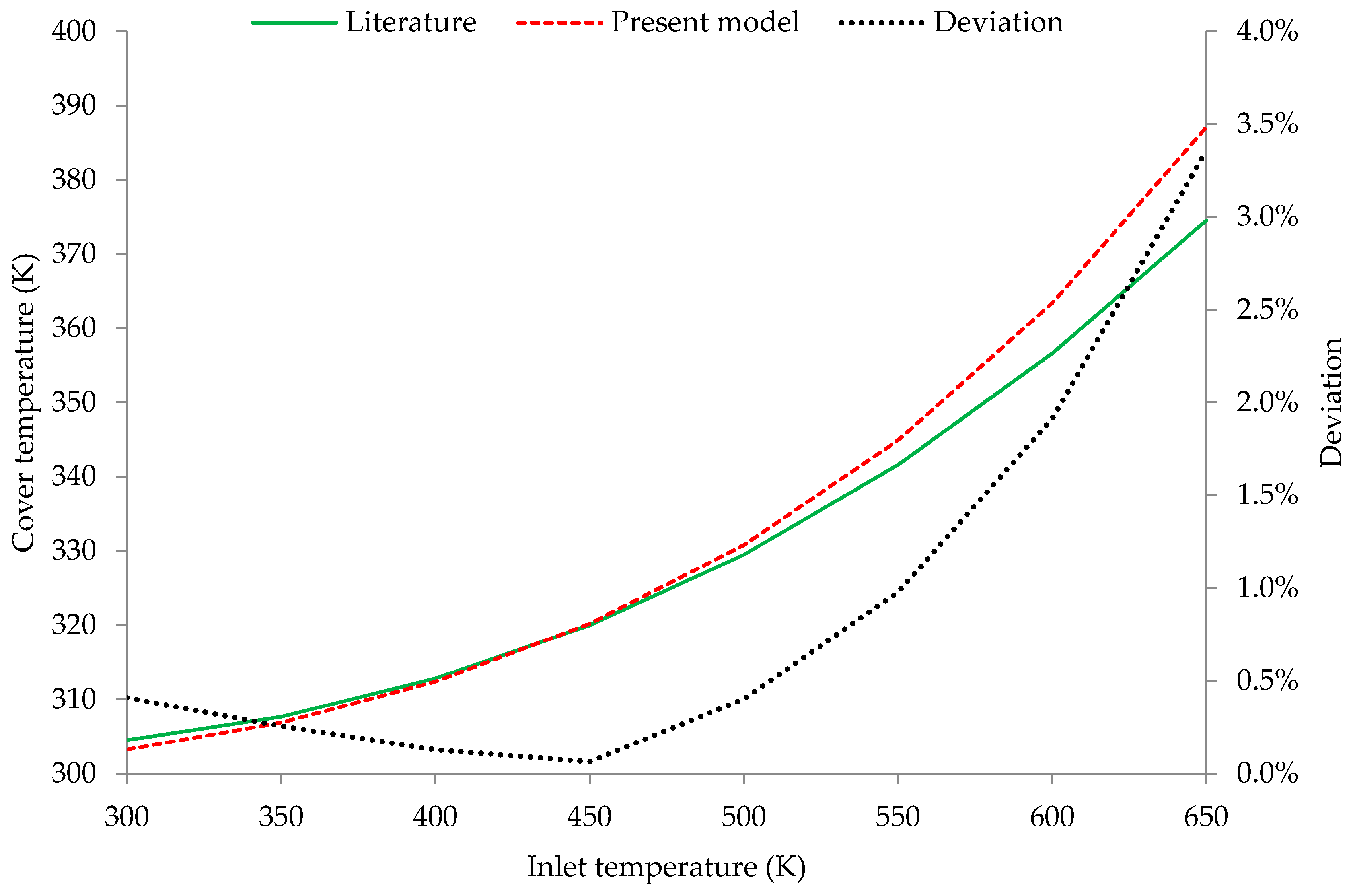
3.2.1. The Impact of the Inlet Temperature on the Results
3.2.2. The Impact of Various Parameters on the Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | Area, m2 |
| C | Concentration ratio |
| cp | Specific heat capacity under constant pressure, J/kg K |
| D | Diameter, m |
| f | Collector focal distance, m |
| Gb | Solar direct beam radiation, W/m2 |
| h | Heat transfer coefficient between fluid and absorber, W/m2 K |
| hout | Heat transfer coefficient between cover and ambient, W/m2 K |
| k | Thermal conductivity, W/mK |
| K | Incident angle modifier |
| K1 | Coefficient of Equation (4), W/K |
| K2 | Coefficient of Equation (11), W/K4 |
| K3 | Coefficient of Equation (17), W/K |
| K4 | Coefficient of Equation (25) |
| K5 | Coefficient of Equation (25), W/K4 |
| L | Collector length, m |
| m | Mass flow rate, kg/s |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Q | Heat flux, W |
| Re | Reynolds number |
| T | Temperature, K |
| V | Volumetric flow rate, m3/s |
| W | Collector width, m |
| Greek Symbols | |
| α | Absorbance |
| γ | Intercept factor |
| εc | Cover emittance |
| εr | Absorber emittance |
| εc* | Equivalent emittance |
| η | Efficiency |
| θ | Incident angle, o |
| μ | Dynamic viscosity, Pa s |
| ρ | Density, kg/m3 |
| ρc | Reflectance |
| σ | Stefan–Boltzmann constant [=5.67 × 10−8 W/m2 K4] |
| τ | Cover transmittance |
| Subscripts and Superscripts | |
| a | aperture |
| am | ambient |
| c | cover |
| ci | inner cover |
| co | outer cover |
| fm | mean fluid |
| in | inlet |
| loss | losses |
| max | maximum |
| opt | optical |
| out | outlet |
| r | receiver |
| ri | inner receiver |
| ro | outer receiver |
| s | solar |
| th | thermal |
| u | useful |
Abbreviations
| CFD | Computational Fluid Dynamics |
| EXP | Experimental |
| EES | Engineer Equator Solver |
| FEM | Finite Element Method |
| PTC | Parabolic trough collector |
References
- Kumaresan, G.; Sudhakar, P.; Santosh, R.; Velraj, R. Experimental and numerical studies of thermal performance enhancement in the receiver part of solar parabolic trough collectors. Renew. Sustain. Energy Rev. 2017, 77, 1363–1374. [Google Scholar] [CrossRef]
- Pavlovic, S.; Bellos, E.; Loni, R. Exergetic investigation of a solar dish collector with smooth and corrugated spiral absorber operating with various nanofluids. J. Clean. Prod. 2018, 174, 1147–1160. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Belessiotis, V. Daily performance of parabolic trough solar collectors. Sol. Energy 2017, 158, 663–678. [Google Scholar] [CrossRef]
- Qu, W.; Wang, R.; Hong, H.; Sun, L.; Jin, G. Test of a solar parabolic trough collector with rotatable axis tracking. Appl. Energy 2017, 207, 7–17. [Google Scholar] [CrossRef]
- Dudley, V.E.; Kolb, G.J.; Mahoney, A.R.; Mancini, T.R.; Matthews, C.W.; Sloan, M.; Kearney, D. Test Results: SEGS LS2 Solar Collector; Report of Sandia National Laboratories, SAN94-1884; Sandia National Laboratories: Livermore, CA, USA, 1994.
- Sallaberry, F.; Valenzuela, L.; Palacin, L.G. On-site parabolic-trough collector testing in solar thermal power plants: Experimental validation of a new approach developed for the IEC 62862-3-2 standard. Sol. Energy 2017, 155, 398–409. [Google Scholar] [CrossRef]
- Wang, R.; Sun, J.; Hong, H.; Liu, Q. An on-site test method for thermal and optical performances of parabolic-trough loop for utility-scale concentrating solar power plant. Sol. Energy 2017, 153, 142–152. [Google Scholar] [CrossRef]
- Chafie, M.; Aissa, M.F.B.; Guizani, A. Energetic end exergetic performance of a parabolic trough collector receiver: An experimental study. J. Clean. Prod. 2018, 171, 285–296. [Google Scholar] [CrossRef]
- Wu, Z.; Li, S.; Yuan, G.; Lei, D.; Wang, Z. Three-dimensional numerical study of heat transfer characteristics of parabolic trough receiver. Appl. Energy 2014, 113, 902–911. [Google Scholar] [CrossRef]
- Mwesigye, A.; Huan, Z.; Meyer, J.P. Thermodynamic optimisation of the performance of a parabolic trough receiver using synthetic oil–Al2O3 nanofluid. Appl. Energy 2015, 156, 398–412. [Google Scholar] [CrossRef]
- Mwesigye, A.; Huan, Z.; Meyer, J.P. Thermal performance of a receiver tube for a high concentration ratio parabolic trough system and potential for improved performance with Syltherm 800-CuO nanofluid. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition IMECE2015, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Mwesigye, A.; Huan, Z. Thermodynamic analysis and optimization of fully developed turbulent forced convection in a circular tube with water–Al2O3 nanofluid. Int. J. Heat Mass Transf. 2015, 89, 694–706. [Google Scholar] [CrossRef]
- Ghasemi, S.E.; Ranjbar, A.A. Thermal performance analysis of solar parabolic trough collector using nanofluid as working fluid: A CFD modelling study. J. Mol. Liq. 2016, 222, 159–166. [Google Scholar] [CrossRef]
- Ghasemi, S.E.; Ranjbar, A.A. Effect of using nanofluids on efficiency of parabolic trough collectors in solar thermal electric power plants. Int. J. Hydrogen Energy 2017, 42, 21626–21634. [Google Scholar] [CrossRef]
- Tzivanidis, C.; Bellos, E.; Korres, D.; Antonopoulos, K.A.; Mitsopoulos, G. Thermal and optical efficiency investigation of a parabolic trough collector. Case Stud. Therm. Eng. 2015, 6, 226–237. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A.; Gkinis, G. Thermal enhancement of solar parabolic trough collectors by using nanofluids and converging-diverging absorber tube. Renew. Energy 2016, 94, 213–222. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Tsimpoukis, D. Thermal, hydraulic and exergetic evaluation of a parabolic trough collector operating with thermal oil and molten salt based nanofluids. Energy Convers. Manag. 2018, 156, 388–402. [Google Scholar] [CrossRef]
- Forristall, R. Heat Transfer Analysis and Modeling of a Parabolic Trough Solar Receiver Implemented in Engineering Equation Solver; National Renewable Energy Laboratory (NREL): Lakewood, CO, USA, 2003.
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A.; Daniil, I. The use of gas working fluids in parabolic trough collectors—An energetic and exergetic analysis. Appl. Therm. Eng. 2016, 109, 1–14. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A. A detailed working fluid investigation for solar parabolic trough collectors. Appl. Therm. Eng. 2017, 114, 374–386. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Parametric investigation of nanofluids utilization in parabolic trough collectors. Therm. Sci. Eng. Prog. 2017, 2, 71–79. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. A detailed exergetic analysis of parabolic trough collectors. Energy Convers. Manag. 2017, 149, 275–292. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Parametric investigation of supercritical carbon dioxide utilization in parabolic trough collectors. Appl. Therm. Eng. 2017, 127, 736–747. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Thermal analysis of parabolic trough collector operating with mono and hybrid nanofluids. Sustain. Energy Technol. Assess. 2017. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Assessment of the thermal enhancement methods in parabolic trough collectors. Int. J. Energy Environ. Eng. 2018, 9, 59–70. [Google Scholar] [CrossRef]
- Kalogirou, S.A. A detailed thermal model of a parabolic trough collector receiver. Energy 2012, 48, 298–306. [Google Scholar] [CrossRef]
- Behar, O.; Khellaf, A.; Mohammedi, K. A novel parabolic trough solar collector model—Validation with experimental data and comparison to Engineering Equation Solver (EES). Energy Convers. Manag. 2015, 106, 268–281. [Google Scholar] [CrossRef]
- Guo, J.; Huai, X.; Liu, Z. Performance investigation of parabolic trough solar receiver. Appl. Therm. Eng. 2016, 95, 357–364. [Google Scholar] [CrossRef]
- Padilla, R.V.; Demirkaya, G.; Goswami, D.Y.; Stefanakos, E.; Rahman, M.M. Heat transfer analysis of parabolic trough solar receiver. Appl. Energy 2011, 88, 5097–5110. [Google Scholar] [CrossRef]
- Cheng, Z.-D.; He, Y.-L.; Qiu, Y. A detailed nonuniform thermal model of a parabolic trough solar receiver with two halves and two inactive ends. Renew. Energy 2015, 74, 139–147. [Google Scholar] [CrossRef]
- Liang, H.; You, S.; Zhang, H. Comparison of different heat transfer models for parabolic trough solar collectors. Appl. Energy 2015, 148, 105–114. [Google Scholar] [CrossRef]
- Jeter, S.M. Analytical determination of the optical performance of practical parabolic trough collectors from design data. Sol. Energy 1987, 39, 11–21. [Google Scholar] [CrossRef]
- Khanna, S.; Kedare, S.B.; Singh, S. Analytical expression for circumferential and axial distribution of absorbed flux on a bent absorber tube of solar parabolic trough concentrator. Sol. Energy 2013, 92, 26–40. [Google Scholar] [CrossRef]
- Fraidenraich, N.; Oliveira, C.; da Cunha, A.F.V.; Gordon, J.M.; Vilela, O.C. Analytical modeling of direct steam generation solar power plants. Sol. Energy 2016, 98, 511–522. [Google Scholar] [CrossRef]
- Eck, M.; Feldhoff, J.F.; Uhlig, R. Thermal modelling and simulation of parabolic trough receiver tubes. In Proceedings of the ASME 2010 4th International Conference on Energy Sustainability, Phoenix, AZ, USA, 17–22 May 2010. [Google Scholar]
- Eck, M.; Steinmann, W.-D. Modelling and Design of Direct Solar Steam Generating Collector Fields. J. Sol. Energy Eng. 2005, 127, 371–380. [Google Scholar] [CrossRef]
- Conrado, L.S.; Rodriguez-Pulido, A.; Calderón, G. Thermal performance of parabolic trough solar collectors. Renew. Sustain. Energy Rev. 2017, 67, 1345–1359. [Google Scholar] [CrossRef]
- Sandeep, H.M.; Arunachala, U.C. Solar parabolic trough collectors: A review on heat transfer augmentation techniques. Renew. Sustain. Energy Rev. 2017, 69, 1218–1231. [Google Scholar] [CrossRef]
- Fuqiang, W.; Ziming, C.; Jianyu, T.; Yuan, Y.; Yong, S.; Linhua, L. Progress in concentrated solar power technology with parabolic trough collector system: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 1314–1328. [Google Scholar] [CrossRef]
- Lienhard, J.H. A Heat Tranfer Textbook, 4th ed.; Philogiston Press: Cambridge, MA, USA, 2012; pp. 354–360. [Google Scholar]
- Silicon Heat Transfer Fluid. Available online: http://www.loikitsdistribution.com/files/syltherm-800-technical-data-sheet.pdf (accessed on 15 January 2018).





| Parameter | Symbol | Value |
|---|---|---|
| Width of the PTC | W | 5.0 m |
| Length of the PTC | L | 7.8 m |
| Focal distance of the PTC | f | 1.71 m |
| Aperture of the PTC | Aa | 39.0 m2 |
| Concentration ratio of the PTC | C | 22.74 |
| Receiver inner diameter | Dri | 66 × 10−3 m |
| Receiver outer diameter | Dro | 70× 10−3 m |
| Cover inner diameter | Dci | 109 × 10-3 m |
| Cover outer diameter | Dco | 115 × 10−3 m |
| Receiver inner surface | Ari | 1.617 m2 |
| Receiver outer surface | Aro | 1.715 m2 |
| Cover inner surface | Aci | 2.671 m2 |
| Cover outer surface | Aco | 2.818 m2 |
| Receiver emittance | εr | 0.2 |
| Cover emittance | εc | 0.9 |
| Absorber absorbance | α | 0.96 |
| Cover transmittance | τ | 0.95 |
| Concentrator reflectance | ρc | 0.83 |
| Intercept factor | γ | 0.99 |
| Incident angle modifier (zero incident angle) | K(θ = 0o) | 1 |
| Incident angle | θ | 0o |
| Maximum optical efficiency (zero incident angle) | ηopt,max | 75% |
| Parameter | Symbol | Value | Range |
|---|---|---|---|
| Ambient temperature | Tam | 300 K | 280–320 K |
| Solar direct beam irradiation | Gb | 1000 W/m2 | 500–1000 W/m2 |
| Heat transfer coefficient between cover and ambient | hout | 10 W/m2 K | 5–20 W/m2 K |
| Volumetric flow rate | V | 0.025 m3/s | 0.001–0.004 m3/s |
| Inlet temperature | Tin | 500 K | 300–650 K |
| Cases | Gb | Tam | Tin | V | Tout (K) | ηth (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| (W/m2) | (K) | (K) | (m3/s) | EXP | Model | Deviation | EXP | Model | Deviation | |
| 1 | 933.7 | 294.35 | 375.35 | 47.7 | 397.15 | 397.55 | 0.10% | 72.51 | 73.10 | 0.82% |
| 2 | 968.2 | 295.55 | 424.15 | 47.8 | 446.45 | 446.97 | 0.12% | 70.90 | 72.21 | 1.85% |
| 3 | 982.3 | 297.45 | 470.65 | 49.1 | 492.65 | 493.10 | 0.09% | 70.17 | 71.13 | 1.37% |
| 4 | 909.5 | 299.45 | 523.85 | 54.7 | 542.55 | 542.48 | 0.01% | 70.25 | 69.33 | 1.31% |
| 5 | 937.9 | 299.35 | 570.95 | 55.5 | 589.55 | 589.96 | 0.07% | 67.98 | 67.42 | 0.83% |
| 6 | 880.6 | 301.95 | 572.15 | 55.6 | 590.35 | 589.90 | 0.08% | 68.92 | 67.07 | 2.69% |
| 7 | 903.2 | 300.65 | 629.05 | 56.3 | 647.15 | 647.24 | 0.01% | 63.82 | 63.94 | 0.18% |
| 8 | 920.9 | 304.25 | 652.65 | 56.8 | 671.15 | 671.23 | 0.01% | 62.34 | 62.48 | 0.23% |
| Mean | - | - | - | - | - | - | 0.06% | - | - | 1.16% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellos, E.; Tzivanidis, C. Analytical Expression of Parabolic Trough Solar Collector Performance. Designs 2018, 2, 9. https://doi.org/10.3390/designs2010009
Bellos E, Tzivanidis C. Analytical Expression of Parabolic Trough Solar Collector Performance. Designs. 2018; 2(1):9. https://doi.org/10.3390/designs2010009
Chicago/Turabian StyleBellos, Evangelos, and Christos Tzivanidis. 2018. "Analytical Expression of Parabolic Trough Solar Collector Performance" Designs 2, no. 1: 9. https://doi.org/10.3390/designs2010009
APA StyleBellos, E., & Tzivanidis, C. (2018). Analytical Expression of Parabolic Trough Solar Collector Performance. Designs, 2(1), 9. https://doi.org/10.3390/designs2010009